Investigation of joist floor diaphragm flexibility on inelastic behavior of steel braced structures

Abstract

The flexibility of floor diaphragms has a significant influence on the behavior of building structures. Commonly, in analyzing structures, floor diaphragms are considered rigid. This assumption distributes lateral loads between the resistant elements according to their rigidities, and decreases the degree of freedom that creates easier analysis. However, in steel structures with braced frames and long span floors, diaphragms usually behave flexibly. The seismic responses of such structures vary to the expected response of typical rigid floor structures. Ignoring the effects of diaphragm flexibility can lead to non-economic or unsafe structural design. In this paper, the nonlinear responses of braced steel buildings with flexible concrete block-joist floor diaphragms are investigated under both static lateral load and dynamic ground motion, and they are compared with the responses of structures with the assumption of rigid diaphragms. This study demonstrates that span ratio is an important parameter in the flexibility of floor diaphragms, and if this ratio exceeds three, the variation of results between the two assumptions of flexible and rigid diaphragms may not be ignored. In addition, results show that diaphragm flexibility changes the seismic response of the structures and linear analysis is not sufficient to explain this behavior.

Keywords

Rigid floor ; Flexible diaphragm ; Concrete joist floor ; Braced steel structures ; Nonlinear seismic response

1. Introduction

The seismic response of buildings subjected to earthquake ground motion depends not only on the characteristics of its vertical lateral force resisting systems, such as braces and frames, but also on horizontal lateral force resisting elements. The horizontal elements typically consist of floor diaphragms. Diaphragms transmit inertial forces from the floor system to the vertical elements of the seismic force-resisting system. They also tie the vertical elements together, thereby stabilizing and transmitting forces between these elements, as required during earthquake shaking. Thus, diaphragms are an essential part of seismic force-resisting systems and require design attention to ensure that the structural system gives an appropriate performance during earthquake shaking  [1] . In the analysis and design of structures under lateral forces, floor diaphragms are frequently assumed to be perfectly rigid in their planes and distribute horizontal forces between vertical lateral load resisting elements in proportion to their relative stiffness. In addition, this assumption reduces the degrees of freedom and simplifies the seismic analysis of many types of building. Although this assumption may be justified for many structures, for some types of structural system, such as structures with a large span ratio, the effects of diaphragm deformability cannot be disregard. Span ratio is defined as ${\textstyle L/W}$ , where ${\textstyle W}$ is the diaphragm dimension parallel to the weak axis plan, and ${\textstyle L}$ is the largest distance in the orthogonal direction between two adjacent vertical lateral load resisting elements  [2] , [3]  and [4] . In addition, structures with long narrow floor plans  [5] , structures with several wings  [6] and cross wall structures  [7] are other types of structures with flexible diaphragms. In current seismic codes, four analysis procedures are used for the seismic analysis of buildings, two linear procedures (linear static and linear dynamic), and two nonlinear procedures (nonlinear static and nonlinear dynamic). The linear procedures are proper when the expected level of nonlinearity is low  [8] . As the performance objective of the structure implies greater inelastic demands, the uncertainty with linear procedures increases. Also, linear procedures have been found by various researchers to under-estimate the acceleration of floors, particularly in the lower levels of the building  [7]  and [9] . In addition, floor diaphragm behavior is a combination of both in-plane and out-of-plane loadings. However, in some previous research, the diaphragm behavior of a floor slab was represented by its behavior under in-plane forces only  [10] . With this assumption, analysis of the floor diaphragm was simplified to the two dimensional plane stress problem. For low-rise buildings, the lateral stiffness of the structure is usually higher than high-rise buildings, and then the study of diaphragm behavior and the calculation of interstory drift in these structures are more important  [11]  and [12] .

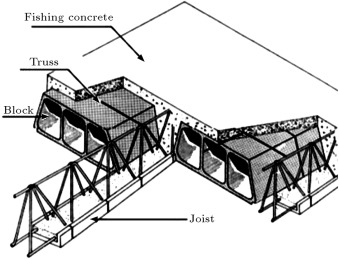
Investigations on pre-stressed beams and filler blocks have shown that a 4 cm thick slab for these floors assures the validity of the “rigid diaphragm” hypothesis. Moreover, the horizontal resistance capacity of floors without cast-in-place concrete and transversal reinforcement is about one-half of floors with cast-in-place concrete and transversal reinforcement  [13] . Studies on low-rise steel buildings with metal roof decks have indicated that the period of the structure is influenced by the diaphragm in-plane flexibility, and the forces in the resistant elements can amplify due to the dynamic behavior of the flexible diaphragm  [14] . The studies of Sarkissian et al. on the composite floor diaphragm show that one of the most important parameters in diaphragm behavior and strength is the direction of the joists relative to lateral loads  [15] . The direction of joists in block-joist floors is an important parameter in diaphragm rigidity, too. Especially, in the case of braced steel structures with block-joist floors and large span ratios, there is a lack of quantitative information to confirm that the use of a rigid diaphragm assumption is appropriate for building analysis and design. In these structures, the vertical components consist of braces with high lateral stiffness, connected to the floors with less rigidity in one direction of their own planes; according to Figure 1 , the floor made by a 20 cm×10 cm reinforced concrete joist with a minimum thickness of 5 cm finishing concrete. In this type of building, the floor diaphragms usually act flexibly and the bending deformation of the floor diaphragm becomes significant. Therefore, the actual distribution of lateral forces between vertical members can be different from the distribution obtained based on the rigid assumption.

Figure 1. Block joist floors details.

In this paper, by using pushover or Nonlinear Static Procedure (NSP) and nonlinear dynamic procedure (NDP) methods, the 3D model of the structures is analyzed. The nonlinear responses of the braced steel buildings with flexible concrete block-joist floor diaphragms are calculated and compared with the responses of structures with the assumption of rigid diaphragms. The effects of some parameters, such as span ratio and number of stories, are also studied.

2. Structural modeling

The structural finite element software, SAP2000, is used for nonlinear static (pushover) and dynamic ground motion (time–history) analysis. For each structure, two 3D finite element models are developed. In the first models, the floors are modeled by rigid diaphragm assumption, and, in these models, the story masses are assumed to be concentrated at the center mass of the story. In the second models, the flexibility of floor diaphragms is considered and the stories masses are distributed in the floor diaphragms. In this parametric study, to consider in-plane diaphragm flexibility, the floors are modeled with SHELL elements, and to model a floor with a rigid diaphragm assumption, the diaphragm constraint and master joints are used. A diaphragm constraint causes all of its constrained joints to move together as a planar diaphragm that is rigid against membrane deformation. Effectively, all constrained joints are connected to each other by links that are rigid in the plane, but do not affect out-of-plane deformation. The joists, beams, columns, and bracings are modeled by FRAME elements. Simply supported connections (hinge connection) are used for column bases and beam to column connections. In nonlinear analysis, because the lateral resistance of concrete diaphragms, with respect to the other members, is very high, the floors will not show non-linear behavior and remain linear, while the other members are in the non-linear phase  [16] . Hence, the non-linear behavior of the floor diaphragm is not considered in this study.

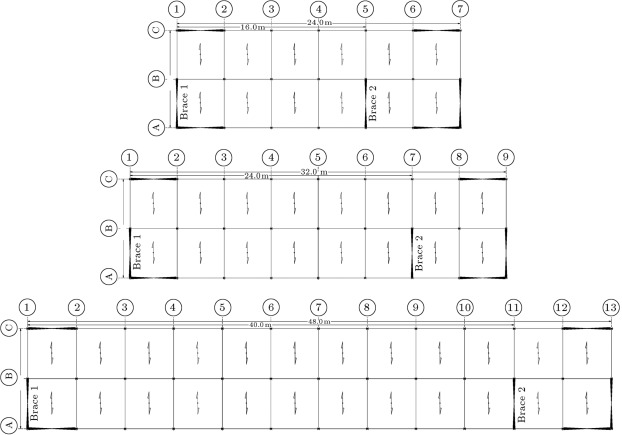
In this research, 3 and 5 story rectangular shaped buildings with 2:1, 3:1 and 5:1 span ratios are analyzed. The plan dimensions of the buildings with 2:1, 3:1 and 5:1 span ratios are 24 m×8 m, 32 m×8 m and 48 m×8 m, respectively. The length of the longitudinal and transverse bays is 4 m, and the height of the floors is 4 m. The properties of materials are summarized in Table 1 , and the planar layout of X-braced frames and the direction of floor joists are illustrated in Figure 2 .

Table 1. Mechanical properties of material.

Mechanical properties of concrete material		Mechanical properties of steel material
Modulus of elasticity, E	2×104  MPa	Modulus of elasticity, E	2×10 5  MPa
Poisson ratio, ν	0.2	Poisson ratio, ν	0.3
Compression strength, fc	23.0 MPa	Yield strength, fy	240 MPa

Figure 2. Plan layout and braces location.

The seismic loads subjected to the structures are based on the equivalent static analysis, according to the Iranian Seismic Code  [17] . For this purpose, the seismic parameters are selected as response reduction factor ${\textstyle R=6}$ (for a X-Braced system), importance factor, ${\textstyle I=1}$ , and peak ground acceleration, ${\textstyle A=0.35g}$ . All buildings are designed, based on AISC-UBC97, according to rigid diaphragm assumptions.

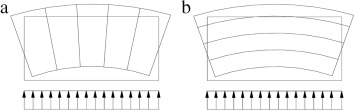
The direction of the joists in the models is considered parallel to the direction of the lateral load, according to Figure 3 (a). The diaphragm has a lower stiffness in the joist direction, because the joists bending stiffness is not effective in this direction (Figure 3 (a)). However, in the direction perpendicular to the joist, the floor joist strengthens the floor diaphragm by increasing the moment of inertia, and the area and bending stiffness of the floor diaphragm, as shown in Figure 3 (b).

Figure 3. Behavior of joists: (a) floor joists parallel to lateral load; and (b) floor joists perpendicular to lateral load.

3. Nonlinear static analysis

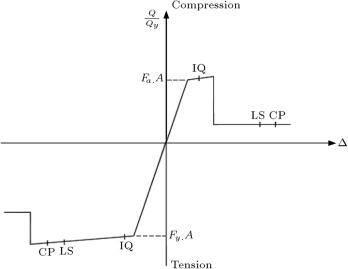
In nonlinear static (pushover) analysis, the structure is subjected to a monotonically increasing pattern of lateral forces, representing the inertial forces, which would be experienced by the structure when subjected to ground shaking. Under an incremental event, the structure experiences a loss in stiffness until the roof displacement reaches the target displacement, or the building collapses. For the nonlinear static procedure, the FEMA356 guidelines are used to determine the response and internal forces in the building  [8] . Two lateral loads patterns are applied for pushover analysis: the first is a uniform pattern load and the second is a modal pattern load. Lateral loads monotonically increase until collapse occurs  [18] . In order to model nonlinear behavior in any structural element, a corresponding nonlinear hinge must be assigned to the building model. In this study, FEMA356 hinges are used for columns and x-braces. For columns, PMM hinges are assigned at column ends (plastic hinges formed by axial loads and bi-axial bending moments), and, for braces, ${\textstyle P}$ hinges are assigned at the brace ends. For beams with pinned connections that bear only gravitational loads, non-linear hinges are not considered. Material behavior (force–displacement) is considered based on the provisions of FEMA356 documents. The post-yield stiffness of columns and braces is assumed to be 2%. For x-braces in compression, the residual strength after degradation is 20% of the buckling strength, and life safety plastic deformation, ${\textstyle \Delta _{LS}}$ , is equal to 5 ${\textstyle \Delta _{C}}$ (${\textstyle \Delta _{C}}$ is the axial deformation at expected buckling load). For conventional braces in the tension and buckling restrained brace, the life safety plastic deformation, ${\textstyle \Delta _{LS}}$ , is equal to ${\textstyle 7\Delta _{T}}$ (${\textstyle \Delta _{T}}$ is the axial deformation at expected tensile yielding load). Figure 4 presents the typical force–displacement (moment–rotation) relation proposed by FEMA356 for steel brace elements.

Figure 4. Generalized force–deformation relation for steel brace elements (FEMA-356).

3.1. Result of nonlinear static analysis

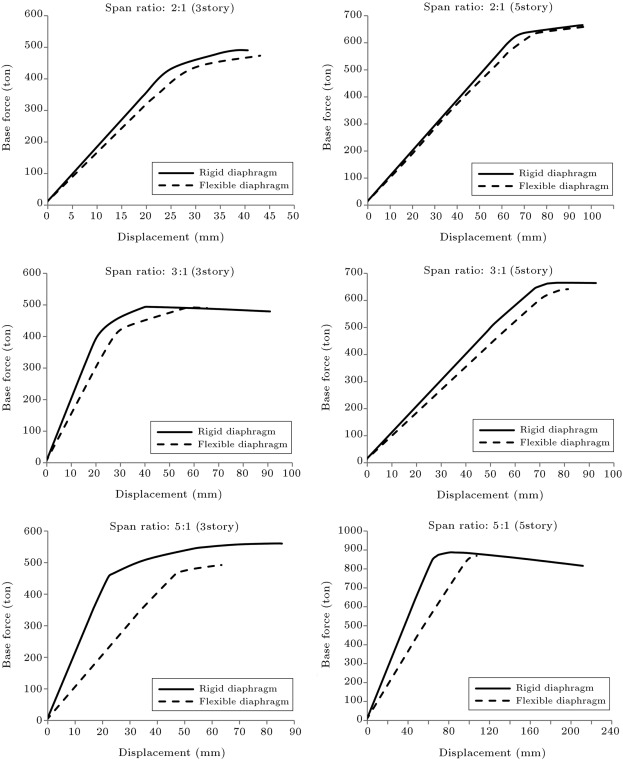
The base shear–displacement curves obtained from the pushover analyses for two cases (flexible and rigid floor assumptions) are presented in Figure 5 . The base-shear versus top-floor displacement can represent the shear capacity of the building. This graph is very useful in estimating the seismic behavior of a building in a pushover analysis.

Figure 5. Comparison of push-over curves for buildings with rigid and flexible diaphragms.

As shown in Figure 5 , all pushover curves in the flexible floor analysis have lower shear capacity, with respect to the rigid floor analysis. However, in buildings with span ratios greater than 3:1, it is observed that the ultimate base shear decreases remarkably in flexible analysis compared to rigid floor analysis. This discrepancy increases when the number of stories decreases. Also, as shown in Figure 5 , in buildings with flexible floors, whose span ratios are greater than 3:1, the termination displacement points of the pushover curve are lower than those of the rigid floor models. Furthermore, from Figure 5 , it can be observed that the number of stories has a similar effect on the capacity curve. Therefore, as the number of stories of flexible models decreases, reduction in the ultimate shear capacity is increased, with respect to rigid floor models. Figure 5 also shows the initial stiffness and yield base shears of the rigid models, which, especially in three story buildings with span ratios greater than 3:1, are higher than in the flexible floor models.

In Table 2 and Figure 6 , formations of plastic hinges at each step of the pushover analysis are shown. As shown in this table, increasing the span ratio and decreasing the number of stories in the flexible models lead to the production of more plastic hinges in the lower steps of loading. Also, the number of plastic hinges in the performance levels, such as Life Safety (LS) or Collapse Prevention (CP), is more than in rigid models.

Table 2. Formation of plastic hinges at each step of pushover analysis.

Step	B-IO		IO-LS		LS-CP		CP-C		C-D		D-E		${\textstyle >E}$
	Rigid	Flex	Rigid	Flex	Rigid	Flex	Rigid	Flex	Rigid	Flex	Rigid	Flex	Rigid	Flex
Aspect ratio:2 (3 story)
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	0	0	0	0	0	0	0	0	0	0	0	0	0
2	0	0	0	0	0	0	0	0	0	0	0	0	0	0
3	2	2	0	0	0	0	0	0	0	0	0	0	0	0
4	7	6	0	3	0	0	0	0	0	1	0	0	0	0
5	3	2	3	7	0	0	0	0	6	6	0	2	0	1
6	7	–	4	–	1	–	0	–	6	–	2	–	2	–
Aspect ratio:2 (5 story)
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	0	0	0	0	0	0	0	0	0	0	0	0	0
2	0	0	0	0	0	0	0	0	0	0	0	0	0	0
3	0	2	0	0	0	0	0	0	0	0	0	0	0	0
4	4	6	0	3	0	0	0	0	0	1	0	0	0	0
5	9	2	0	7	0	0	0	0	1	6	0	0	0	0
6	12		0		0		0		1		0		0
7	11		4		0		0		2		0		0
8	10		4		0		0		3		0		0
Aspect ratio:3 (3 story)
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	2	0	0	0	0	0	0	0	0	0	0	0	0	0
2	6	2	0	0	0	0	0	0	0	0	0	0	0	0
3	2	4	4	2	0	0	0	0	2	0	0	0	0	0
4	4	2	6	4	0	0	0	0	4	2	0	0	0	0
5	4	6	4	8	0	0	0	0	6	4	0	0	0	0
6	3	8	7	8	2	0	0	0	6	4	0	0	0	0
7	2	8	7	6	0	0	0	0	10	6	0	0	0	0
8	3	6	7	7	0	1	0	0	10	7	0	0	0	0
Aspect ratio:3 (5 story)
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	2	0	0	0	0	0	0	0	0	0	0	0	0	0
2	8	2	0	0	0	0	0	0	0	0	0	0	0	0
3	6	10	4	2	0	0	0	0	2	0	0	0	0	0
4	12	12	4	2	0	0	0	0	2	2	0	0	0	0
5	10	8	4	6	0	0	0	0	4	4	0	0	0	0
6	8	9	4	4	0	0	0	0	6	6	0	0	0	0
7	7	9	7	6	0	1	0	0	6	6	0	0	0	0
8	8	9	6	7	1	0	0	1	6	6	0	0	0	0
9	8	9	7	7	1	0	0	0	7	7	0	0	0	0
10	8	9	7	8	0	0	0	0	8	8	0	0	0	0
	9		7		0		0		8		0		0
Aspect ratio:5 (3 story)
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	2	0	0	0	0	0	0	0	0	0	0	0	0	0
2	4	2	0	0	0	0	0	0	0	0	0	0	0	0
3	4	4	0	2	0	0	0	0	2	0	0	0	0	0
4	2	4	4	0	0	0	0	0	2	2	0	0	0	0
5	8	3	4	4	1	0	0	1	4	5	0	0	0	0
6	11	2	7	5	0	0	0	1	6	6	0	0	0	0
7	8		11		2		0		6		0		0
8	9		11		1		0		9		0		0
9	8		10		1		0		11		0		0
10	8		7		2		2		13		0		0
Aspect ratio:5 (5 story)
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	2	2	0	0	0	0	0	0	0	0	0	0	0	0
2	12	6	2	6	0	0	0	0	0	2	0	0	0	0
3	12	8	2	6	0	0	0	0	4	4	0	0	0	0
4	10	9	6	8	0	0	0	0	4	6	0	0	0	0
5	2	5	10	9	0	0	0	0	8	10	0	0	0	0
6	4	7	10	13	0	0	0	1	8	14	0	0	0	0
7	6	4	10	11	0	5	0	0	8	17	0	0	0	0
8	2		12		1		0		14		0		0
9	1		10		6		0		15		2		0

Figure 6. Formation of plastic hinges in pushover analysis.

4. Nonlinear dynamic analysis

The pushover analysis based on static loading approximately demonstrates the natural behavior of the building, but it cannot represent the dynamic response of the structure with a large degree of accuracy. However, nonlinear dynamic analysis is the most accurate method used for structural analysis. Nonlinear dynamic analysis can be performed with two general methods: Direct Integration and Modal Analysis. Direct integration includes different methods, such as Hilber, Central Difference, Wilson-${\textstyle \Theta }$ and Newmark  [19] . In this research, the Newmark Method with (${\textstyle \beta =0.25}$ and ${\textstyle \gamma =0.5}$ ) is used in the direct integration  [19]  and [20] . The scaled record of the Tabas Earthquake (Iran 1978) is selected as the input ground motion with the maximum acceleration of ${\textstyle 0.35g}$ .

The damping matrix (${\textstyle C}$ ) is Rayleigh damping, and it is assumed to be a linear combination of mass (${\textstyle M}$ ) and stiffness (${\textstyle K}$ ) matrices, as shown in Eq. (1) :

$C=\alpha M+\beta K{\mbox{,}}$

( 1)

where ${\textstyle \alpha }$ and ${\textstyle \beta }$ are Rayleigh damping factors. These factors can be determined by the solution of simultaneous equations if the damping ratios, ${\textstyle \xi _{m}}$ and ${\textstyle \xi _{n}}$ , associated with two specific modes, ${\textstyle m}$ and ${\textstyle n}$ (${\textstyle \omega _{m},\omega _{n}}$ ), are known  [19] . In this study, to calculate the Rayleigh damping, the damping ratio for all significant structural modes is specified equal to 5% (${\textstyle \xi _{m}=\xi _{n}=\xi =0.05}$ ).

Then, the factors can be determined from a simplified equation as below:

$\lbrace {\begin{array}{c}\alpha \\\beta \end{array}}\rbrace ={\frac {2\xi }{\omega _{m}+\omega _{n}}}\lbrace {\begin{array}{c}\omega _{m}\omega _{n}\\1\end{array}}\rbrace {\mbox{.}}$

( 2)

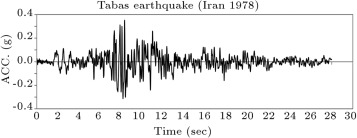
In order to use the accelerograms in nonlinear dynamic analysis, the response spectrum of this accelerogram should be as much as possible in harmony with the design spectrum of the site. In fact, they should be scaled before using the accelerograms. In this research, six accelerograms from three earthquakes (each with a north and south component) have been used for calculating the scaled accelerograms. The chosen earthquake records were Tabas (Iran 1978), Rudbar (Iran 1990), and ElCentro (Imperial Valley 1940). The records were scaled according to the Iranian Seismic Code  [17] to match the site-specific design spectra. Because the results of nonlinear dynamic analysis are very extensive, in this paper, only the results of structural analysis under the scaled Tabas earthquake are presented. For example, the record of the Tabas earthquake is shown in Figure 7 .

Figure 7. Tabas (Iran 1978) earthquake accelerogram (${\textstyle PGA=0.35g}$ ).

4.1. Result of nonlinear dynamic analysis

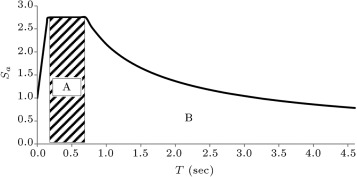
The results of dynamic analysis for all cases subjected to the scaled Tabas (Iran 1978) earthquake, using flexible floor and rigid floor assumptions, are summarized in Table 3 . As shown in Figure 2 , the results include the natural period, base shear and axial force in brace 2. It is observed that in the structures with span ratio 2:1, considering diaphragm flexibility does not have a significant effect on the natural periods of structures, especially when the number of stories increases. However, for structures with span ratios greater than 3:1, the actual assumption of a flexible diaphragm increases the natural period of the structure. This period elongation is noticeable when the number of stories decreases. For example, as shown in Table 3 , for three story buildings, the fundamental period of the structure with span ratio 5:1, obtained from the flexible model, is 0.537 s, which is 1.45 times greater than similar models with a rigid diaphragm assumption. Therefore, when a structure with a flexible diaphragm is considered to have a rigid diaphragm, the calculated period will be underestimated. Then, for most structures with periods on the descending branch of the acceleration spectrum (zone B in Figure 8 ), the use of periods smaller than actual periods causes base shear greater than actual value. Hence, the assumption of a rigid diaphragm may lead to an overstraining of the base shear.

Table 3.

Summary of results for dynamic analysis using Tabas earthquake.

Output	Span ratio 2:1				Span ratio 3:1				Span ratio 5:1
	3 story		5 story		3 story		5 story		3 story		5 story
	Rigid	Flex	Rigid	Flex	Rigid	Flex	Rigid	Flex	Rigid	Flex	Rigid	Flex
Period, T (s)	0.309	0.321	0.382	0.397	0.315	0.402	0.551	0.596	0.371	0.537	0.580	0.670
Base shear, V (ton)	108.7	102.0	370.2	349.7	378.1	327.0	533.0	498.5	450.2	391.6	771.5	574.3
Axial force in Brace 2, (ton)	65.9	73.1	78.2	81.9	71.2	80.0	91.6	105.1	125.3	161.9	121.3	147.9

Figure 8. Typical acceleration design spectrum.

As shown in Table 3 , in models with span ratios greater than 3:1, the seismic base shears decrease significantly in the flexible analysis, in respect to the rigid floor assumption analysis. For example, in the three story model with span ratio 5:1, the base shear obtained from the flexible model is less than 75% of that obtained from the rigid model. Table 3 shows that for flexible models, by increasing span ratio and decreasing the number of stories, the axial force in brace 2 increases compared to rigid models. This difference between the results of the flexible model and the rigid model is due to the variation of distribution of dynamic load for flexible diaphragm and rigid diaphragm buildings. On the other hand, deformation of diaphragms causes additional lateral load in middle braced frames. Then, the application of a rigid diaphragm assumption to low-rise building structures with large plan aspect ratios is usually unsafe, and can lead to an underestimated axial force in some structural members (for example, interior braces).

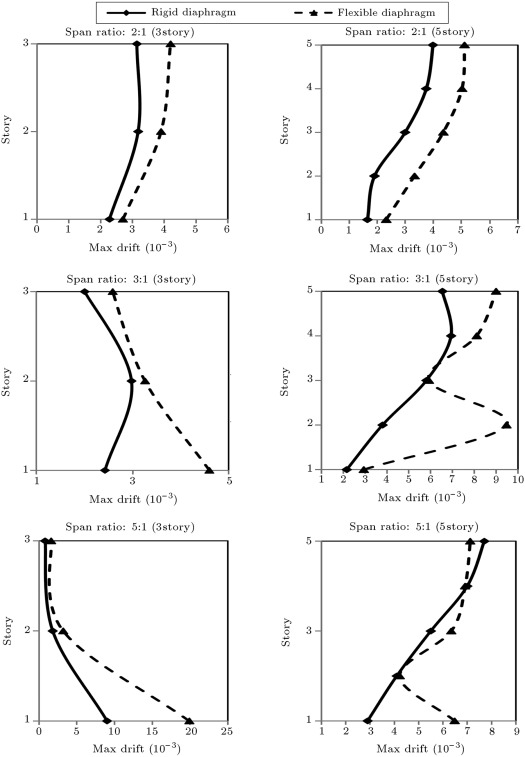
The maximum drift of stories in two flexible and rigid models are compared in Figure 9 . From this figure, it is observed that the story drift in the flexible floor model is more than that of the rigid floor model. The largest difference between storey drifts is observed in the building with three stories and a span ratio of 5:1. In this building, maximum drift in the first story obtained from flexible models is about twice the value obtained from rigid models. In addition, it is observed that the highest drift percentage errors between flexible models and rigid models occurred at the first and second floor levels, which can create the potential for excessive gravity system drifts.

Figure 9. Comparison of interstory drifts obtained by dynamic analysis (Tabas earthquake).

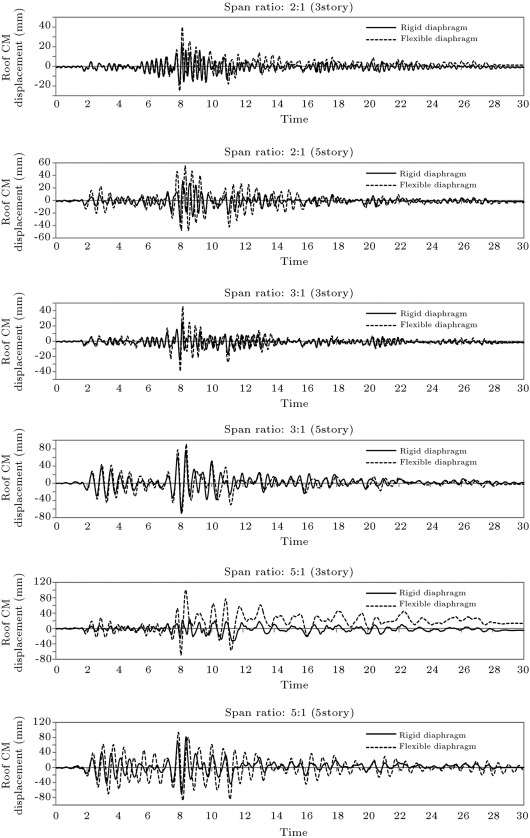
The time history of displacement at the center mass of the top story (roof) for flexible and rigid models is compared in Figure 10 . These figures show that the flexible models produce more frame displacement relative to rigid models during the whole time and application of rigid diaphragm assumption for three story structures with span ratios greater than 3:1 causes significant errors in analysis results. For example, in the three story model with span ratio 5:1, the peak floor displacement at the roof obtained from flexible models is about three times that of the value obtained from rigid models. In addition, these figures show that the peak floor displacement for flexible diaphragm structures is a function of the span ratio and the number of stories. Also, Figure 10 indicates that by decreasing the number of stories, the overall diaphragm peak displacements in flexible models relative to rigid models tend to increase. Hence, diaphragm flexibility has a significant influence on both peak displacements and interstory drifts.

Figure 10. Comparison of displacement time history at top floor (Tabas earthquake).

5. Conclusions

The goal of this research is to investigate the influence of flexible concrete block-joist floor diaphragms on the behavior of steel structure buildings with braced frames, under both static lateral loads (push-over) analysis and dynamic ground motion (time–history) analysis. The results of these analyses are compared with the response of similar buildings with the assumption of rigid diaphragms. Based on the analysis results, the following conclusions are presented:

• Assumption of diaphragm flexibility in the analysis changed the natural period, maximum total base shear and dynamic response of the structures. The estimated results are sensitive to the number of stories and the span ratio.
• In the low-rise buildings (such as three story building) with span ratios greater than 3:1, it can be observed that the ultimate base shear capacities decrease significantly in flexible analysis, in respect to the rigid floor assumption analysis.
• Initial stiffness and yield base shears in the rigid diaphragm models, especially in the three story buildings with span ratios greater than 3:1, are higher than those resulted for flexible models.
• The displacement and maximum drift of flexible floor models is greater than for rigid models. Then, application of rigid diaphragm assumption for structures with span ratios greater than 3:1, and, especially for low-rise buildings, causes significant errors in the analysis results. These unrealistic results may lead to the non-conservative or non-economic design of structures.
• In models with span ratios greater than 3:1, the interior braces may be subjected to additional force due to the shear force redistribution caused by the large in-plane deformation of the diaphragm. It can be made a non-conservative design for interior braces and a non-economical design for exterior braces.

Therefore, in braced steel buildings with concrete block-joist floors and span ratios greater than 3:1, floor flexibility should be considered in the seismic analysis of the structure.

References

1. [1] F. Naeim; The Seismic Design Handbook; Van Nostrand Reinhold Publishers, New York (2002)
2. [2] J.M. Barron, M.B. Hueste; Diaphragm effects in rectangular reinforced concrete; ACI Structural Journal, 101 (5) (2004), pp. 615–624
3. [3] Sadashiva, V.K., MacRae, G.A., Deam, B.L. and Spooner, M.S. “Quantifying the seismic response of structures with flexible diaphragms”, NZSEE Conf. (2009).
4. [4] Al Harash, M., Panahshahi, N. and Truman, K. “Inelastic seismic response of reinforced concrete buildings with floor diaphragm openings”, 14th World Conf. on Earthquake Engrg., Structural and Environmental Engrg. , Beijing, China (2008).
5. [5] Nakashima, M.W., Huang, T. and Lu, L.W. “Effect of diaphragm flexibility on seismic response of building structures”, Proc. 8th World Conf. on Earthquake Engrg. , San Francisco, California (1984).
6. [6] Button, M.R., Kelly, T.E. and Jones, L.R. “The influence of diaphragm flexibility on the seismic response of buildings”, Proc. 8th World Conf. on Earthquake Engrg. , San Francisco, California, 4, pp. 751–758 (1984).
7. [7] R.B. Fleischman, K.T. Farrow, K. Eastman; Seismic response of perimeter lateral system structures with highly flexible diaphragms; Earthq. Spectra, 18 (2002), pp. 251–286
8. [8] Prestandard and Commentary for the Seismic Rehabilitation of Buildings; American Society of Civil Engineers (ASCE). FEMA Publication, 356, Federal Emergency Management Agency, FEMA, Washington, DC (2000)
9. [9] Nakaki, S.D. “Design guidelines for precast and cast-in-place concrete diaphragms”, Tech. Report., EERI Professional Fellowship, Earthquake Research Ins (2000).
10. [10] M.W. Nakashima, T. Huang, L.W. Lu; Experimental study of beam-supported slabs under in-plane loading; ACI Structural Journal, 79 (1) (1982), pp. 59–65
11. [11] H.J. Lee, M.A. Aschheim, D. Kuchma; Interstory drift estimates for low-rise flexible diaphragm structures; Eng. Struct., 29 (2007), pp. 1375–1397
12. [12] H.J. Lee, D. Kuchma, M.A. Aschheim; Strength-based design of flexible diaphragms in low-rise structures subjected to earthquake loading; Eng. Struct., 29 (2007), pp. 1277–1295
13. [13] Damian, A., Kovacs, L.A., Gosa, T.B., Maniu, H., Dico, C.S. and Tokes, A. “Diaphragm behavior of the floor with pre-stressed beam and filler blocks”, 12th World Conf. on Earthquake Engrg. (2000).
14. [14] Tremblay, R., Berair, T. and Filiatrault, A. “Experimental behavior of low-rise steel buildings with flexible roof diaphragms”, 12th World Conf. on Earthquake Engrg. (2000).
15. [15] L. Sarkissian, K. Khalili, S.M. Zahrai; Impact of joists direction on the diaphragm behavior of composite floor systems; Journal of Seismology and Earthquake Engineering, 8 (1) (2006), pp. 29–38
16. [16] J. Colina; In-plane floor flexibility effects on torsionally unbalanced systems; Earthq. Eng., 28 (12) (1992), pp. 1705–1715
17. [17] “BHRC Iranian code of practice for seismic resistant design of buildings”, Standard No. 2800, Tehran, Iran (2005).
18. [18] A.S. Elnashai; Advanced inelastic static (pushover) analysis for earthquake applications; Struct. Eng. Mech., 12 (1) (2001), pp. 51–69
19. [19] R. Clough, J. Penzien; Dynamics of Structures; Computers & Structures, Inc., Berkeley (1995)
20. [20] N. Nakahira; Vibration of plane trusses by the Newmark method; Comput. Struct., 37 (1990), pp. 515–520