Analysis of heatlines and entropy generation during double-diffusive MHD natural convection within a tilted sinusoidal corrugated porous enclosure

Abstract

The natural convection and entropy generation during double-diffusive MHD natural convection in a tilted sinusoidal corrugated porous enclosure is investigated numerically in this work by using heatline visualization technique. The top and bottom horizontal walls are assumed as adiabatic and non-diffusive, while the left and right vertical corrugated sidewalls are maintained at a constant hot and cold temperatures and concentrations respectively. The flow in the enclosure is subjected to an inclined magnetic field. The enclosure is filled with an electrically conducting fluid [Pr = 0.024] saturated with a porous media. The numerical computations are presented for various values of Rayleigh number (Ra), Hartmann number (Ha), Lewis number (Le), Darcy number (Da), buoyancy ratio (N), magnetic field orientation angle (φ) and enclosure inclination angle (Φ). In addition, the entropy generation due to fluid friction, thermal gradients, diffusion, and magnetic field beside the total entropy generation are studied and discussed. It is found that the flow circulation decreases strongly when the magnetic field applied horizontally and the enclosure is considered vertical. Heatline visualization concept is successfully applied to the considered problem. The average Nusselt number decreases when the Lewis number increases, while the average Sherwood number increases when the Lewis number increases. Also, both average Nusselt and Sherwood numbers increase when the Darcy number and buoyancy ratio increase. Moreover, the results show that the entropy generations due to magnetic field when the enclosure is subjected to the horizontal magnetic field are higher than the corresponding values when it subjected to the vertical magnetic field.

Abbreviation

MHD , magneto-hydrodynamics

Keywords

MHD ; Natural convection ; Porous media ; Entropy generation ; Double diffusive ; Corrugated enclosure ; Heatline

Nomenclature

${\textstyle {\overline {Nu}}}$- Average Nusselt number

B- Magnitude of magnetic field, (Tesla)

c- Dimensional concentration, (kg/m³ )

C- Dimensionless concentration

D- Mass diffusivity, (m² /s)

Da- Darcy number

g- Gravitational acceleration, (m/s² )

Ha- Hartmann number

K- Permeability of the porous media, m²

L- Length and width of the sinusoidal corrugated enclosure, (m)

Le- Lewis number

N- Buoyancy ratio

Nu- Local Nusselt number

P- Dimensionless pressure

p- Pressure, (N/m² )

Pr- Prandtl number

Ra- Rayleigh number

S- Dimensionless entropy

T- Temperature, (°C)

u- Dimensional velocity component in x-direction, (m/s)

U- Dimensionless velocity component in X-direction

v- Dimensional velocity component in y-direction, (m/s)

V- Dimensionless velocity component in Y-direction

x- Cartesian coordinate in horizontal direction, (m)

X- Dimensionless coordinate in horizontal direction

y- Cartesian coordinate in vertical direction, (m)

Y- Dimensionless Coordinate in vertical direction

Greek symbols

${\textstyle {\beta }_{c}}$- Coefficient of expansion due to concentration, (m³ .kg⁻¹ )

${\textstyle {\beta }_{T}}$- Coefficient of expansion due to temperature, (K^-1 )

${\textstyle \Pi }$- Dimensionless heat function

${\textstyle \sigma }$- Electrical conductivity (s/m)

${\textstyle \vartheta }$- Fluid kinematics viscosity, (m² /s)

${\textstyle \phi }$- Irreversibility coefficient

${\textstyle \varphi }$- Magnetic field orientation angle, (degree)

α- Thermal diffusivity, (m² /s)

θ- Dimensionless temperature

λ- The corrugation amplitude

ρ- Fluid density, (kg/m³ )

Φ- Enclosure inclination angle, (degree)

Ψ- Dimensionless stream function

Subscripts

c- Cold

C- Diffusion

Cor- Corrugated

h- Hot

M- Magnetic

T- Total

θ- Thermal

Ψ- Friction

1. Introduction

Natural convection in corrugated or wavy enclosures has an increasing attention in the last ten years. This interest has many reasons. One of them, is due to the many technological application of this geometry like in electronic packages, micro-electronic devices, solar heaters, electric machinery and in geometrical design requirements. The important point one can observe in the open literature is that in spite of the significant practical applications of this geometry, the number of published papers dealing with it is still very limited compared with those discussing classical square, rectangular or inclined walled geometries. This is due to its complex geometry, which makes the construction of the mesh generation and the numerical modeling of it are very difficult to build. Moreover, in corrugated or wavy enclosures, the orientation of their sidewalls is not uniform, but it changes from point to point, which increases also the complexity of the numerical simulation. Furthermore, in wavy enclosures many new important factors that are not encountered in classical geometries must be put in the mathematical model such as wave ratio, inter-wall spacing and amplitude of surface waves. These reasons make the published papers deal with this geometry are very restricted [1] , [2] , [3] , [4] , [5]  and [6] . Ali and Husain [7] investigated numerically the natural convection problem in a square enclosure having two vertical sidewalls of vee-corrugated geometry. They concluded that for high Grashof number, the heat transfer rate decreased when the corrugation was decreased. Saha et al. [8] performed a numerical analysis using finite element method on steady-state natural convection in a vee-corrugated square enclosure with discrete heating from below. The length of the heat source was 20% of the total length of the bottom wall. The non-heated parts of the bottom wall and entire upper wall were considered adiabatic. The Grashof number based on the enclosure height varied from 10³ to 10⁶ , corrugated frequency varied from 0.5 to 2 and Prandtl number was taken as 0.71. The results showed that the average Nusselt number was maximum for low corrugation frequency but a reverse trend was found for high corrugation frequency. Hasan et al. [9] numerically investigated the natural convection of air in a two-dimensional laminar steady-state incompressible fluid flow in a modified square enclosure with a sinusoidal corrugated top surface for different inclination angles. A constant flux heat source was flush mounted on the top sinusoidal wall, modeling a wavy tin shaded room exposed to sunlight. The results were obtained for Rayleigh number (Ra) ranging from 10³ to 10⁶ . The results showed that the convective phenomena were greatly influenced by the variation of inclination angles. Saha et al. [10] carried out a numerical simulation to study the effects of discrete isoflux heat source size and angle of inclination on natural convection inside a sinusoidal corrugated inclined enclosure. They concluded that for various heat source sizes, when the angle of inclination was increased, the overall Nusselt number was increased also. Hussain et al. [11] studied numerically the steady natural convection phenomenon in a square inclined enclosure with vertical vee-corrugated sidewalls and horizontal top and bottom surfaces. A discrete heat flux strip of 24% of the total length was flush-mounted on the bottom wall, while the other non-heated parts of the bottom wall and the top wall were considered adiabatic. The two vee-corrugated sidewalls were maintained at constant cold temperature. They concluded that the natural convection phenomenon was greatly affected by increasing the enclosure inclination angle. Bakier [12] studied numerically, by using the finite difference scheme, the free convection in partially C-shape open ended enclosure filled with water-based nanofluid. They concluded that the nanofluid increased both the rate of the heat and mass transfer in the enclosure. Also, he concluded that stream function was decreased by increasing the aspect ratio. Mliki et al. [13] used the Lattice Boltzmann method to simulate numerically the free convection in an L-shaped enclosure filled with copper–water nanofluid. They concluded that heat transfer was increased when the aspect ratio was low.

The natural convection in wavy enclosures filled with electrically conducting fluid subjected to a magnetic field or a fluid saturated with a porous media has a wide range of industrial applications such as sewage purification in sand beds, water storage in heavy porous rocks and nuclear fusion. Examples of recent studies considering the natural convection in wavy enclosures or surfaces subject to a magnetic field or filled with a porous media are reviewed in the following sections. Kumar [14] studied numerically the free convection induced by a vertical wavy surface with heat flux in an enclosure filled with porous medium. He concluded that the surface temperature was very sensitive to drifts in undulations and amplitude of the wavy surface. Misirlioglu et al. [15] numerically investigated the steady-state free convection inside a cavity made of two horizontal adiabatic straight walls and two isothermal vertical bent-wavy walls and filled with a fluid-saturated porous medium. The wavy walls were assumed to follow a profile of cosine curve. Flow and heat transfer characteristics (isothermal, streamlines and local and average Nusselt numbers) were investigated for some values of Rayleigh number, cavity aspect ratio and surface waviness parameter. Misirlioglu et al. [16] performed a numerical investigation by using the finite element method of free convection inside a cavity made of two horizontal adiabatic straight walls and two isothermal vertical wavy walls filled with a heat-generating porous medium. Simulations were carried out for a range of wave ratio [λ  = 0 to 0.6], aspect ratio [A = 1 to 5] and Rayleigh number [Ra = 10 to 1000]. Results were presented in the form of streamlines, isotherms and local and average Nusselt numbers. Khanafer et al. [17] carried out a numerical investigation to analyze natural convection inside a cavity with a sinusoidal vertical wavy wall and filled with a porous medium. The vertical walls were isothermal while the top and bottom horizontal straight walls were kept adiabatic. The implications of Rayleigh number, number of wavy surface undulation and amplitude of the wavy surface on the flow structure and heat transfer characteristics were investigated in detail while the Prandtl number was considered equal to unity. Mushatet [18] numerically studied the natural convection in an inclined wavy porous cavity. The two wavy walls were differentially heated, while the upper and lower walls were insulated. The problem was simulated for different values of Rayleigh number [50 ≤ Ra ≤ 500] and angle of inclination [${\textstyle 0{\mbox{°}}\leq \alpha \leq 90{\mbox{°}}}$ ]. He concluded that the angle of inclination, number of undulation, the amplitude and Rayleigh number had a significant effect on the flow and thermal field. Also, it was found that the heat transfer rate was increased as angle of inclination increased. Mansour et al. [19] studied numerically by using thermal non-equilibrium model the steady natural convection inside wavy enclosures with the effect of thermal radiation. The inter-phase heat transfer coefficient effect, thermal radiation effect, the modified conductivity ratio effect and the Rayleigh number effect were investigated and discussed. They concluded that the average Nusselt number decreased by increasing the modified conductivity ratio. Whereas, increasing the radiation parameter led to the increase in the average Nusselt numbers for fluid and solid phases. Saha [20] studied numerically the magnetohydrodynamic natural convection in a sinusoidal corrugated air-filled enclosure with discrete isoflux heating from below. The results explained that streamlines and isotherms were affected significantly for high Grashof number and zero Hartmann number. Hussain et al. [21] analyzed numerically the effects of the longitudinal magnetic field and the heat source size on natural convection in a tilted sinusoidal corrugated enclosure for different values of enclosure inclination angles. A constant heat flux source was discretely embedded at the central part of the bottom wall, whereas the remaining parts of the bottom wall and the upper wall were assumed adiabatic. The two vertical sinusoidal corrugated walls were maintained at a constant low temperature. An empirical correlation was developed by using Nusselt number versus Hartmann number, Rayleigh number and enclosure inclination angle. They concluded that the increase in the Hartmann number and the ratio of heating element to enclosure width decreased the Nusselt number. Moreover, double-diffusive natural convection in corrugated or wavy enclosures or surfaces has an important applications in various engineering fields such as food industries, solidification in material processing, chemical engineering, cement manufacturing and oil tanks. In this type of heat transfer process, the natural convection is generated due to both temperature and concentration effects. Rathish Kumar and Krishna Murthy [22] analyzed the combined heat and mass transfer process by natural convection from a corrugated vertical surface immersed in a non-Darcy porous medium. Krishna Murthy et al. [23] investigated numerically the double diffusive free convection due to corrugated vertical surface immersed in a fluid saturated semi-infinite porous medium under Darcian assumptions. The effect of various parameters such as wave amplitude (a), Lewis number (Le), buoyancy ratio (B), and Soret (S_r ) and Dufour (D_f ) numbers were analyzed through local and average Nusselt number, and local and average Sherwood number plots. Rahman et al. [24] performed a numerical study of double-diffusive buoyancy induced flow in a triangular cavity with corrugated bottom wall. The results were presented for various wave lengths (0.1 ≤ λ  ≤ 1.0), Rayleigh number (10³  ≤ Ra ≤ 10⁵ ) and Prandtl number (0.071 ≤ Pr ≤ 7). It was found that wave length played a dominant role on flow strength for any Rayleigh numbers. Nikbakhti and Khodakhah [25] made a numerical investigation by using the finite difference method about the double diffusive natural convection in a cavity partially heated and cooled from sidewalls. They found that in the aiding flow, the average Nusselt number was increased with increasing the buoyancy ratio. From the other side, the heat transfer process is considered as an irreversible process, so it already generates entropy. Therefore, to get an optimum heat transfer process it is very recommended to reduce the entropy generation. However, the entropy generation due to natural convection in a corrugated or wavy enclosure has been considered by limited authors. Mahmud and Islam [26] simulated numerically using the finite-volume method the free convection and entropy generation inside an inclined wavy walled enclosure. The second law of thermodynamics was also applied to predict the nature of irreversibility in terms of entropy generation. Simulation was carried out for a range of wave ratio [λ  = 0.0–0.4], aspect ratio [A = 1.0–2.0] and Rayleigh number [Ra = 1–10⁷ ] for a fluid with Prandtl number equal to 0.7 while angle of inclination (θ) was varied from 0° to 360° with 15° interval. They concluded that the entropy generation due to fluid friction and heat transfer were significantly affected by changing the inclination angle of the wavy enclosure. Mahmud and Fraser [27] performed a numerical investigation using finite volume method of free convection and entropy generation characteristics inside a vertical in-phase wavy cavity. The wavy walls were assumed to follow a profile of cosine curve. Results were presented for a range of wave ratio [λ = 0 to 0.6], aspect ratio [A = 1 to 4] and Rayleigh number [Ra = 1 to 10⁷ ]. Mahmud et al. [28] analyzed the natural convection and entropy generation characteristics inside wavy enclosures filled with microstructures. Esmaeilpour and Abdollahzadeh [29] studied numerically the effects of Grashof number and volume fraction of Cu-water nanofluid on natural convection and entropy generation inside a wavy enclosure. Calculation were performed for Grashof numbers from 10⁴ to 10⁶ , nanoparticles volume fraction from 0% to 10% and surface waviness ranging from 0.0 to 0.4 for different patterns of wavy enclosure. The results showed that the heat transfer rate decreased as nanoparticles volume fraction and Grashof number increased. Also, the nanoparticles can be used to decrease the entropy generation. Das et al. [30] investigated numerically the entropy analysis on MHD pseudo-plastic nanofluid flow through a vertical porous channel with convective heating. They concluded that the major source of the entropy and the heat transfer in the channel was their active walls. Eegunjobi and Makinde [31] utilized numerically the second law analysis for MHD permeable channel flow with variable electrical conductivity and asymmetric Navier slips. They computed both the entropy generation and the Bejan numbers by using the obtained temperature and velocity profiles. Mkwizu and Makinde [32] investigated numerically, by using the finite difference method, the entropy generation in a variable viscosity channel flow of water-based nanofluids with convective cooling. The results of the skin friction, Nusselt number, entropy generation and the Bejan number were displayed graphically and discussed extensively. Extra references about the entropy generation can be found in References [33] , [34]  and [35] .

Nowadays, heatline and heatfunction method is considered a very efficient method for visualization of natural convection compared with classical method by isotherms. In fact, a heatline is similar to a streamline, but it visualizes net energy flow in a convection heat transfer situation. The heatline concept was suggested for the first time by Kimura and Bejan [36] and represented mathematically by heatfunctions, which were related to Nusselt number based on some dimensionless form. For comprehensive review about heatlines concept, one can go back to Costa [37] . Dalal and Das [38] investigated numerically using finite-volume method the natural convection inside a two-dimensional cavity with a wavy right vertical wall. The bottom wall was heated by a spatially varying temperature while other three walls were kept at constant lower temperature. The heatfunction equation in the transformed plane was solved in terms of dimensionless variables. The results were presented for three different undulations (1–3) with different wave amplitude (0.00–0.10) and a fluid having Prandtl number 0.71. Basak et al. [39] performed an analysis of heatlines for natural convection within porous trapezoidal enclosures to investigate the effect of uniform and non-uniform heating of bottom wall. The results were presented by using heatlines, isotherms and streamlines. They concluded that the Darcy number had a significant effect on heatlines distribution. Kaluri and Basak [40] performed a heatline analysis of thermal mixing due to natural convection in discretely heated porous cavities filled with various fluids. They concluded that the heatline approach was found to be very useful to analyze thermal mixing in square cavities with discrete heat sources filled with fluid-saturated porous media by visualizing the heat distribution. Basak and Chamkha [41] presented a heatline analysis on natural convection for nanofluids confined within square cavities with various thermal boundary conditions. Enhancement of heat transfer rates were illustrated by isotherms associated with trajectory of heat flow via heatline method. Two types of boundary conditions were considered: hot left and cold right walls in the presence of adiabatic horizontal walls (case 1) and hot bottom wall with cold side walls in presence of adiabatic top wall (case 2). More references related to heatlines concept can be found in References [42] , [43]  and [44] .

In the present paper, a numerical analysis of double-diffusive MHD natural convection and entropy generation inside a tilted sinusoidal corrugated porous enclosure is performed. Also, the visualization of results are presented by using heatfunctions approach. The use of this visualization tool is increased considerably to present the numerical results of the convection heat transfer problems. Our paper contains many original contributions, and among them is a paper considered as the first study to link between many effects such as double-diffusive, magnetohydrodynamic, porous medium and entropy generation within natural convection in a complex geometry like a tilted sinusoidal corrugated porous enclosure.

2. Mathematical model

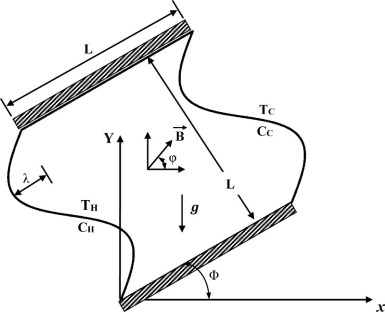
Fig. 1 illustrates a schematic diagram of the considered two-dimensional tilted corrugated porous enclosure with dimensions (L × L). The left and right vertical corrugated sidewalls of the cavity are maintained at fixed but different temperatures (T_h ,T_c ) and concentrations (C_h , C_c ) respectively. The top and bottom horizontal walls are considered adiabatic and non-diffusive. The gravitational force acts in a vertical downward direction. The enclosure is filled with an electrically conducting fluid (Pr = 0.024) subjected to an inclined magnetic field (B) and saturated with a porous media. The enclosure is inclined at an angle (Φ) that is varied as [Φ = 0°, 30°, 60° and 90°], while the magnetic field orientation angle is varied as [φ = 0°, 30°, 45°, 60° and 90°]. The shape of wavy vertical walls is taken as a sine wave with single corrugation frequency and the corrugation amplitude (λ) has been taken fixed at 20% of the enclosure length. The Rayleigh number range is [Ra = 10³ –10⁶ ], the Hartmann number (Ha) is varied as [Ha = 0, 25, 50,75 and 100 ], the Darcy number (Da) is varied as [Da = 10⁻² , 10⁻³ , 10⁻⁴ and 10⁻⁵ ], the Lewis number (Le) is varied as [Le = 1, 2, 4, 6, 8 and 10] and buoyancy ratio (N) is varied as [N = 0,1, 2,4, 6, 8 and 10]. The following assumptions are assumed in the present work:

• The flow is assumed laminar, incompressible, two-dimensional and steady.
• A thermal equilibrium occurs between the electrical conducting Newtonian fluid and the porous media and the latter is modeled based on the Darcy-Brinkman model.
• The fluid physical properties are assumed constant and density variations are ignored except in buoyancy term, which is modeled according to Boussinesq approximation and changes with temperature and concentration only.
• Forchheimers inertia, viscous dissipation, radiation heat exchange and Joule heating are neglected.

The continuity, Navier–Stokes, energy, concentration, heat function equations in their non-dimensional forms are defined as:

${\frac {\partial U}{\partial X}}+{\frac {\partial V}{\partial Y}}=$$0$

( 1)

$U{\frac {\partial U}{\partial X}}-V{\frac {\partial U}{\partial Y}}=$$-{\frac {\partial P}{\partial X}}+Pr\left({\frac {{\partial }^{2}U}{\partial X^{2}}}+\right.$$\left.{\frac {{\partial }^{2}U}{\partial Y^{2}}}\right)-$${\frac {Pr}{\mbox{Da}}}U+RaPr\left(\theta +NC\right)sin\left(\Phi \right)$ ${\mbox{ }}+{\mbox{ }}Ha^{2}Pr\left[Vsin\left(\varphi \right)cos\left(\varphi \right)-\right.$$\left.U{sin}^{2}{\mbox{ }}\left(\varphi \right)\right]$

( 2)

$U{\frac {\partial V}{\partial X}}-V{\frac {\partial V}{\partial Y}}=$$-{\frac {\partial P}{\partial Y}}+Pr\left({\frac {{\partial }^{2}V}{\partial X^{2}}}+\right.$$\left.{\frac {{\partial }^{2}V}{\partial Y^{2}}}\right)-$${\frac {Pr}{\mbox{Da}}}V+RaPr\left(\theta +NC\right)cos\left(\Phi \right)$ ${\mbox{ }}+{\mbox{ }}Ha^{2}Pr\left[Usin\left(\varphi \right)cos\left(\varphi \right)-\right.$$\left.V{cos}^{2}{\mbox{ }}\left(\varphi \right)\right]$

( 3)

$U{\frac {\partial \theta }{\partial X}}+V{\frac {\partial \theta }{\partial Y}}=$$\left({\frac {{\partial }^{2}\theta }{\partial X^{2}}}+{\frac {{\partial }^{2}\theta }{\partial Y^{2}}}\right)$

( 4)

$U{\frac {\partial C}{\partial X}}+V{\frac {\partial C}{\partial Y}}=$${\frac {1}{Le}}\left({\frac {{\partial }^{2}C}{\partial X^{2}}}+\right.$$\left.{\frac {{\partial }^{2}C}{\partial Y^{2}}}\right)$

( 5)

${\frac {{\partial }^{2}\Pi }{\partial X^{2}}}+{\frac {{\partial }^{2}\Pi }{\partial Y^{2}}}=$${\frac {\partial \left(U\theta \right)}{\partial Y}}-$${\frac {\partial \left(V\theta \right)}{\partial X}}$

( 6)

${\frac {\partial \Pi }{\partial Y}}=U\theta -{\frac {\partial \theta }{\partial X}},{\mbox{ }}{\frac {\partial \Pi }{\partial X}}=$$V\theta -{\frac {\partial \theta }{\partial Y}}$

( 7)

Fig. 1. Schematic diagram and coordinate system of the physical domain with boundary conditions.

The dimensionless variables in the above equations are defined as:

$X,{\mbox{ }}Y={\frac {x,{\mbox{ }}y}{L}},{\mbox{ }}U=$${\frac {\mbox{uL}}{\alpha }},{\mbox{ }}V={\frac {\mbox{vL}}{\alpha }},{\mbox{ }}P=$${\frac {pL^{2}}{\rho {\alpha }^{2}}},{\mbox{ }}Pr={\frac {\vartheta }{\alpha }},{\mbox{ }}{\mbox{Da}}=$${\frac {K}{L^{2}}},$ ${\mbox{ }}\theta ={\frac {T-T_{c}}{T_{h}-T_{c}}},{\mbox{ }}{\mbox{Ra}}=$${\frac {g\beta \left(T_{h}-T_{c}\right)L^{3}}{{\vartheta }^{2}}}Pr$

Also, the Hartmann number (Ha), the dimensionless concentration (C), the buoyancy ratio (N) and the Lewis number (Le) are defined respectively as follows:

$Ha=BL{\sqrt {\frac {\sigma }{\rho \vartheta }}};{\mbox{ }}C=$${\frac {c-c_{c}}{c-c_{h}}};{\mbox{ }}N={\frac {{\beta }_{c}{\mbox{ }}\left(c_{h}-c_{c}\right)}{{\beta }_{T}{\mbox{ }}\left(T_{h}-T_{c}\right)}}{\mbox{ }}{\mbox{and}}{\mbox{ }}Le=$${\frac {\alpha }{D}}$

The local and average heat and mass transfer through the hot corrugated left sidewall are given in dimensionless terms by the Nusselt and Sherwood numbers, respectively. They are defined as follow:

$Nu_{h}={\frac {\partial \theta }{\partial n}}{\mbox{ }}{\mbox{and}}{\mbox{ }}Sh_{h}=$${\frac {\partial C}{\partial n}}$

( 8)

${\overline {Nu}}_{h}={\frac {1}{L_{Cor}}}\int _{0}^{L_{Cor}}Nu_{h}dn{\mbox{ }}{\mbox{and}}{\mbox{ }}{\overline {Sh}}_{h}=$${\frac {1}{L_{Cor}}}\int _{0}^{L_{Cor}}Sh_{h}dn$

( 9)

2.1. Entropy generation

Entropy generation due to fluid friction (S_Ψ ), thermal gradients (S_θ ), diffusion (S_C ), magnetic field (S_M ) and total entropy generation (S_T ) in their non-dimensional forms are defined as:

$S_{\Psi }={\phi }_{1}{\mbox{ }}\left[\left[U^{2}+V^{2}\right]+\right.$$\left.Da\times \left[2\left[{\left({\frac {\partial U}{\partial X}}\right)}^{2}+\right.\right.\right.$$\left.\left.\left.{\left({\frac {\partial V}{\partial Y}}\right)}^{2}\right]+\right.\right.$$\left.\left.{\left({\frac {\partial U}{\partial Y}}+{\frac {\partial V}{\partial X}}\right)}^{2}\right]\right]$

( 10)

$S_{\theta }=\left[{\left({\frac {\partial \theta }{\partial X}}\right)}^{2}+\right.$$\left.{\left({\frac {\partial \theta }{\partial Y}}\right)}^{2}\right]$

( 11)

$S_{C}={\phi }_{2}{\mbox{ }}\left[{\left({\frac {\partial C}{\partial X}}\right)}^{2}+\right.$$\left.{\left({\frac {\partial C}{\partial Y}}\right)}^{2}\right]+$${\phi }_{3}{\mbox{ }}\left[\left({\frac {\partial \theta }{\partial X}}\right)\left({\frac {\partial C}{\partial X}}\right)+\right.$$\left.\left({\frac {\partial \theta }{\partial Y}}\right)\left({\frac {\partial C}{\partial Y}}\right)\right]$

( 12)

$S_{M}={\phi }_{1}\times Ha^{2}\times {\left[Usin\varphi -Vcos\varphi \right]}^{2}$

( 13)

$S_{T}=S_{\Psi }+S_{\theta }+S_{C}+S_{M}$

( 14)

2.2. Boundary conditions

The dimensionless boundary conditions that combined with governing equations ((1) , (2) , (3) , (4) , (5)  and (6) ) for the present study can be written as follows:

${\mbox{For}}{\mbox{ }}Y=0{\mbox{ }}{\mbox{and}}{\mbox{ }}0\leq X\leq 1$

$U\left(X,{\mbox{ }}0\right)=V\left(X,{\mbox{ }}0\right)=$$0,{\mbox{ }}{\frac {\partial \theta }{\partial Y}}={\frac {\partial C}{\partial Y}}=$$0,{\mbox{ }}\psi =0,{\mbox{ }}\Pi =0$

${\mbox{For}}{\mbox{ }}X=0{\mbox{ }}{\mbox{and}}{\mbox{ }}0\leq Y\leq 1$

$U\left(0,{\mbox{ }}Y\right)=V\left(0,{\mbox{ }}Y\right)=$$0,{\mbox{ }}\theta =C=1,{\mbox{ }}\psi =0,{\mbox{ }}n\cdot \nabla \Pi =$$0$

${\mbox{For}}{\mbox{ }}X=1{\mbox{ }}{\mbox{and}}{\mbox{ }}0\leq Y\leq 1$

$U\left(1,{\mbox{ }}Y\right)=V\left(1,{\mbox{ }}Y\right)=$$0,{\mbox{ }}\theta =C=0,{\mbox{ }}\psi =0,{\mbox{ }}n\cdot \nabla \Pi =$$0$

${\mbox{For}}{\mbox{ }}Y=1{\mbox{ }}{\mbox{and}}{\mbox{ }}0\leq X\leq 1$

$U\left(X,{\mbox{ }}1\right)=V\left(X,{\mbox{ }}1\right)=$$0,{\mbox{ }}{\frac {\partial \theta }{\partial Y}}={\frac {\partial C}{\partial Y}}=$$0,{\mbox{ }}\psi =0,{\mbox{ }}\Pi ={\overline {Nu}}_{h}$

3. Numerical procedure

The governing equations (1) , (2) , (3) , (4) , (5)  and (6) are solved using the control volume method described by Ferziger and Peric [45] . The computation domain is divided into rectangular control volumes with one grid located at the center of the control volume that forms a basic cell. The set of conservation equations are integrated over the control volumes, leading to a balance equation for the fluxes at the interface. In the course of discretization, the power scheme and a blending of second order upwind scheme and central differencing are respectively utilized for the convection and diffusion terms respectively. The system of equations formulated in terms of primitive variables is solved using the strongly implicit procedure (SIP) solver based on lower-upper decomposition (ILU) [46] . The pressure–velocity coupling in the momentum equation needs iterative procedure based on a pressure correction method where SIMPLER algorithm is coupled to the SIMPLEC algorithm, for faster convergence.

Non-uniform grids are implemented in the present investigation, allowing a fine grid spacing especially near the two corrugated sidewalls to capture the rapid changes in the dependent variables. Convergence with mesh size was verified by employing coarser and finer grids on selected test cases of the present problem. The computations reported in this paper have been performed using more than a 141 × 141 grid. The convergence criterion is based on both maximum error of continuity equation and the average quadratic residual over the whole domain for each equation. It is assumed that convergence is achieved when the maximum error is less than 10⁻⁷ .

From the known temperature, concentration and velocity fields, calculated at the obtained permanent solution by solving Equations ((1) , (2) , (3) , (4) , (5)  and (6) ), local entropy generation (S ) is then calculated at any nodal point of the cavity. The total entropy generation for the entire cavity (S_T ) is then obtained by numerical integration. Based on this procedure, the used numerical code written in FORTRAN language to solve all the governing equations have been developed. All the computational cases in the present paper have been done in my personal PC Pentium IV 3.3 Ghz CPU Quad Intel with the CPU time not exceeding 200 s for each one.

4. Numerical results validation

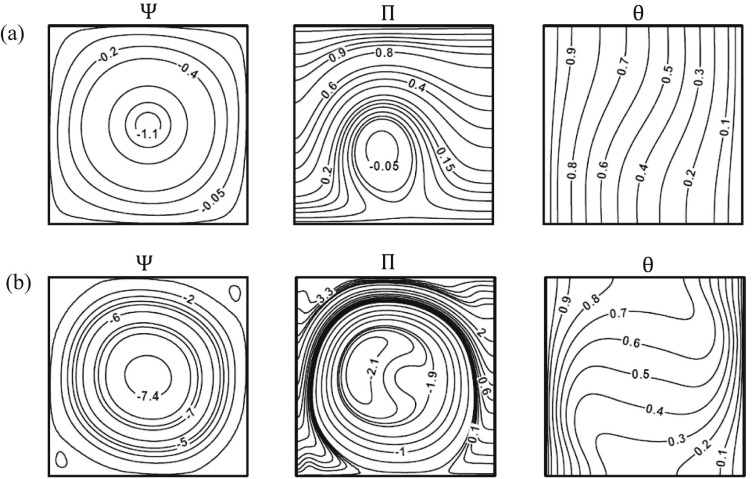
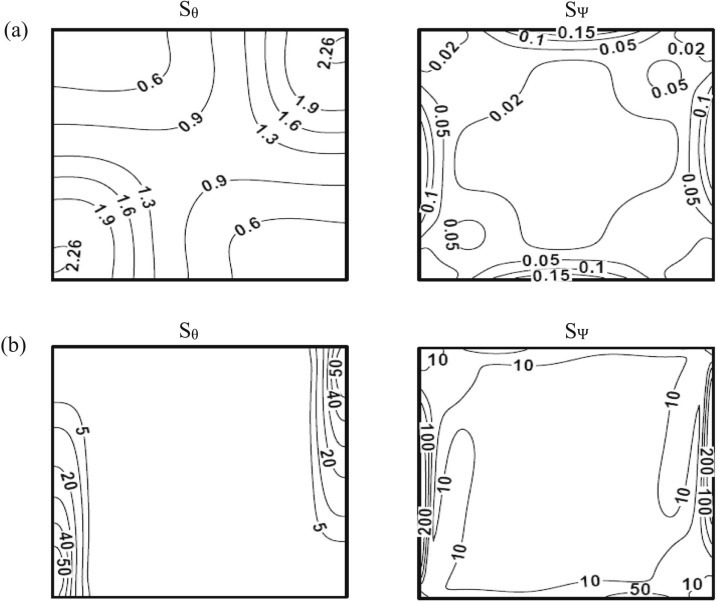
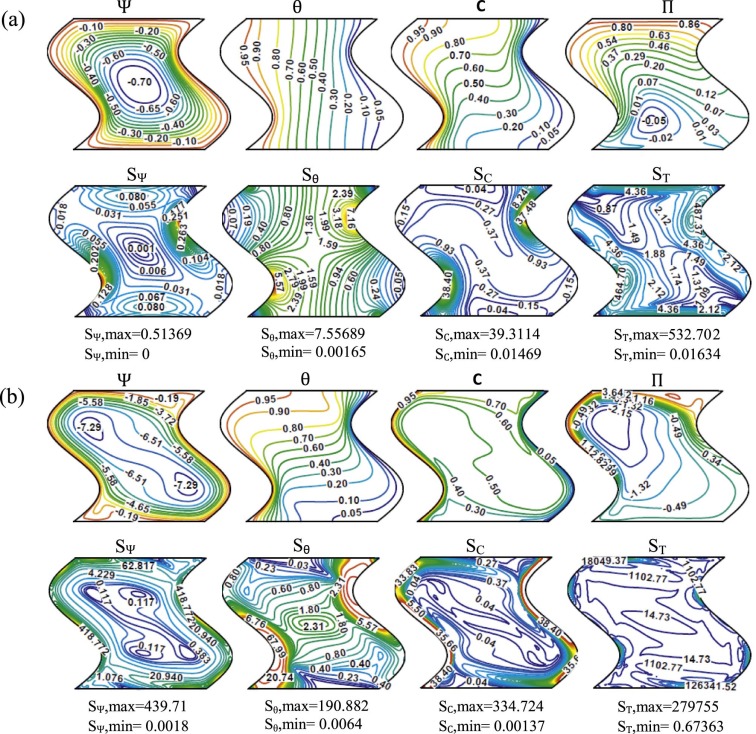
In order to check the accuracy of the computed results, two verification tests are performed. The first test is related with stream function (Ψ), heat function (Π) and temperature (θ) as shown in Fig. 2 . This test is considered for square cavity with hot left sidewall, cold right sidewall and adiabatic top and bottom walls at (a) Ra = 10³ and (b) Ra = 10⁵ respectively for Pr = 0.015. The results are compared with the same problem considered by Ramakrishna et al. [47] . The second test is related with local entropy generations due to heat transfer (S_θ ) and fluid friction (S_Ψ ) as shown in Fig. 3 . Again, the same geometry considered in Fig. 2 is investigated. The only difference is that the Prandtl number in the second test is Pr = 0.7. The results of this test are compared with the results of Ilis et al. [48] and Basak et al. [49] , respectively. Both considered tests show an excellent agreement with the results of Ramakrishna et al. [47] for first test, and Ilis et al. [48] and Basak et al. [49] for second test. Therefore, these verifications give good confidence of our computer code to handle accurately the numerical analysis of the present work.

Fig. 2. Streamfunction (Ψ), heatfunction (Π) and temperature (θ), for square cavity with hot left sidewall and cold right sidewall and adiabatic top and bottom walls at (a) Ra = 103 and (b) Ra = 105 for Pr = 0.015 with benchmark problem [47] .

Fig. 3. Local entropy generation due to heat transfer (Sθ ) and fluid friction (SΨ ) for square cavity with hot left sidewall and cold right sidewall with adiabatic top and bottom walls at (a) Ra = 103 and (b) Ra = 105 for Pr = 0.7 with Ilis et al. [48] and Basak et al. [49] results.

5. Results and discussion

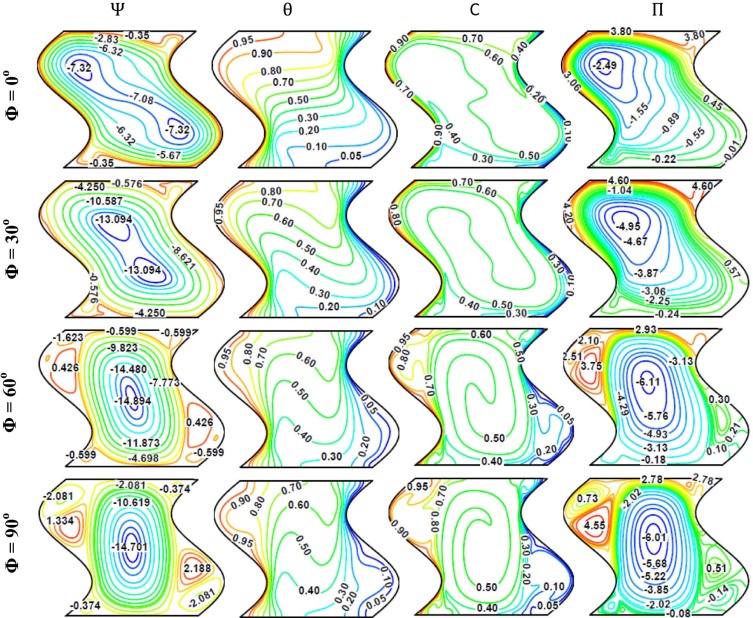
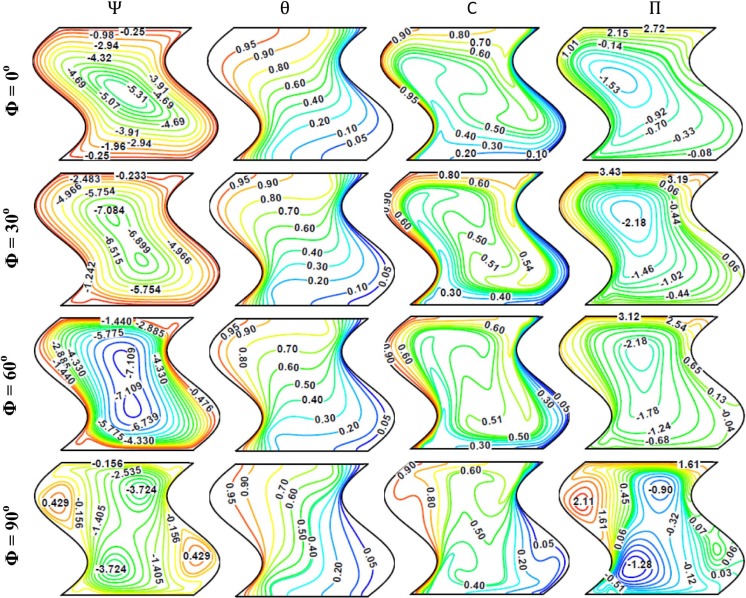
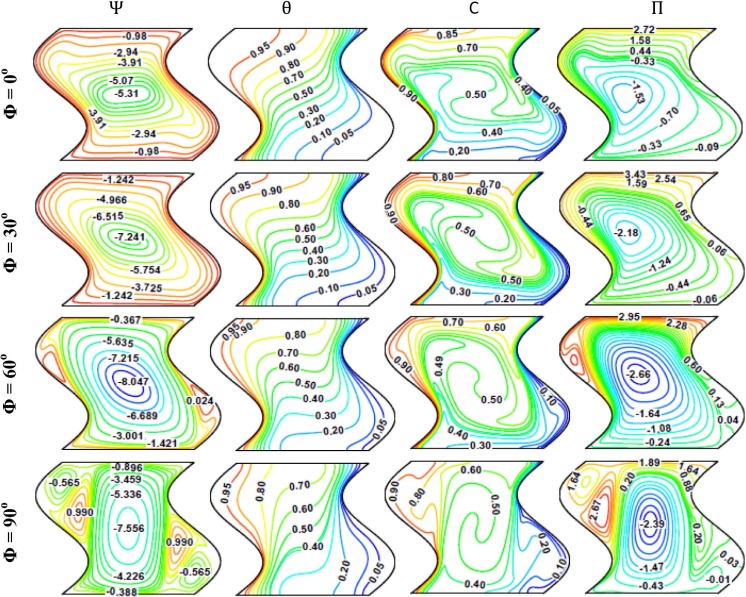
The effects of enclosure inclination angles (Φ) on the flow, thermal and concentration fields are presented in Fig. 4 , which illustrates stream function (Ψ), temperature (θ), concentration (C) and heatfunction (Π) for different inclination angles (Φ) at N = 1, Le =10, Da = 10⁻³ , Ha = 0 and Ra = 10⁶ . It can be observed from the results that when the inclination angle increases from (Φ = 0° or horizontal enclosure) to (Φ = 60°), the stream function values increase from [Ψ = −7.32] to [Ψ = −14.894]. This result ensures that when the inclination angle increases, the strength of natural convection circulation increases inside the corrugated enclosure. At (Φ = 90° or vertical enclosure), the stream function values begin to decrease to [Ψ = −14.701]. Therefore, the effect of buoyancy force decreases slightly for vertical corrugated enclosure. Another interesting result that can be observed from stream function values is that the increase in the inclination angle of the enclosure causes a clear change in the vortices pattern. The distance between core of vortices begins to decrease as the inclination angle increases from (Φ = 0°) to (Φ = 30°) until it merges in one core when the inclination angle increases to (Φ = 60° and 90°) respectively. Also, some minor vortices can be seen in the upper left and lower right edges of the enclosure for high inclination angle (i.e. Φ = 60° and 90°). In general, one can see high values of stream function inside the corrugated enclosure, which indicates a high flow circulation. The reason of this behavior is because the results in Fig. 4 are plotted for high Rayleigh number [i.e. high natural convection effect] and zero Hartmann number [i.e. no magnetic field effect]. For temperature (θ), the isotherm contours match with the behavior of streamlines. When the corrugated enclosure is horizontal (Φ = 0°) the isotherm contours are monotonic and semi-parallel to enclosure horizontal walls. In this case, the heat is transferred by the conduction. But as the inclination angle increases from (Φ = 30° to 90°) a clear disturbance can be seen in isotherm patterns. This disturbance becomes very clear for vertical corrugated enclosure (Φ = 90°). Therefore, one can conclude that as the inclination angle increases from (Φ = 0° to 90°), the heat transfer mode switches from conduction mode to convection one. With respect to concentration (C), the iso-concentrations contours are clustered adjacent the hot left and cold right sidewalls of the corrugated enclosure. A similar behavior to isotherm contours can be seen where the iso-concentrations contours refer that the heat diffuses inside the corrugated enclosure by concentration gradients. Again, as the inclination angle increases from (Φ = 0° to 90°) the activity of iso-concentrations contours increases considerably. Moreover, it can be seen from the results that the concentrations adjacent to the hot left sidewall are greater than their values at the cold right sidewall. This result can be seen for various values of the inclination angle and satisfies indirectly the validity of the problem boundary conditions. The last column in Fig. 4 represents the results of heatfunction (Π). It is presented in our paper to make a good comparison with the classical presentation of temperature results by isotherms. Fig. 4 illustrates heatfunction contours for different inclination angles (Φ). It can be seen that the heatfunction increases as the inclination angle increases from (Φ = 0° to 60°) and then decreases at (Φ = 90°). Therefore, it can be concluded from the results of Fig. 4 , that the inclined enclosures are better than the horizontal and vertical enclosures to enhance the heat transfer inside the corrugated enclosure. Also, the inclination angle has a clear effect on the patterns shape of the heatfunction inside the enclosure. On the other hand, since the Rayleigh number in Fig. 4 is considered high [i.e. Ra = 10⁶ ] and the effect of magnetic field is absent [i.e., Ha = 0]. Therefore, the effect of convection in this case is strong. For this reason it can be seen from heatfunction contours that the heat is transferred from hot left sidewall to the cold right side one, while the heat is transferred inside the enclosure core in a closed path, indicating that its effect on the heat transfer process between the hot left and cold right sidewalls is weak.

Fig. 4. Streamfunction (Ψ), temperature (θ), concentration (C), and heatfunction (Π), for different inclination angles (Φ) at N = 1, Le = 10, Da = 10−3 , Ha = 0 and Ra = 106 .

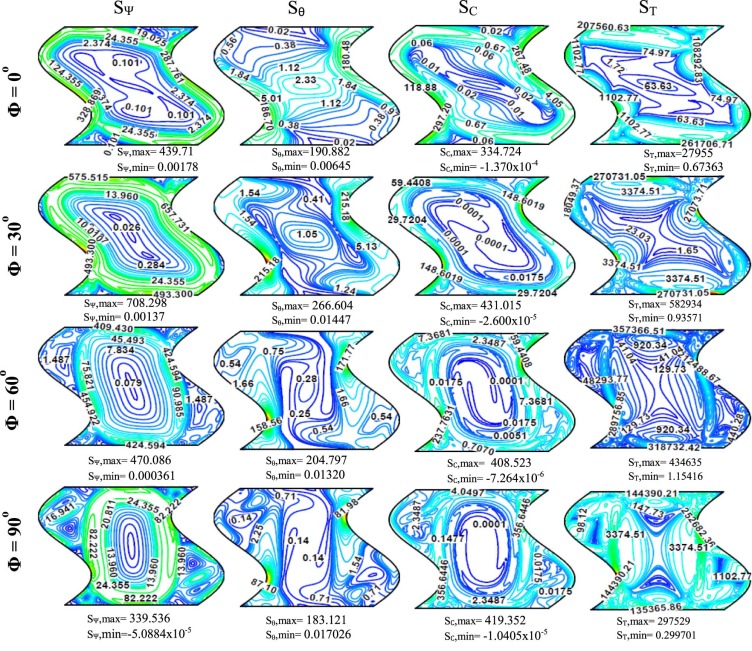
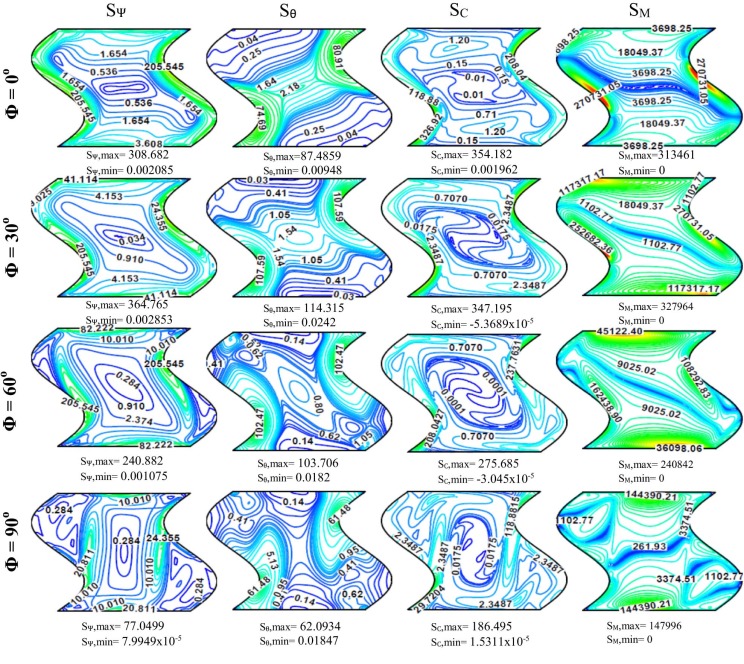
Fig. 5 displays entropy generations due to fluid friction (S_Ψ ), thermal gradients (S_θ ), diffusion (S_C ) and total entropy generation (S_T ) for different inclination angles (Φ) at N = 1, Le = 10, Da = 10⁻³ , Ha = 0 and Ra = 10⁶ . In fact, the main purpose of this figure is to illustrate the effect of enclosure inclination angles (Φ) on different types of entropy generation in the absence of the applied magnetic field [Ha = 0]. It can be seen that the entropy generation due to fluid friction (S_Ψ ) increases from [S_Ψ ,_max  = 439.71] at (Φ = 0° or horizontal enclosure) to [S_Ψ ,_max  = 470.086] at (Φ = 60°). This behavior is due to the increase in the flow velocity as the inclination angle increases from (Φ = 0° or horizontal enclosure) to (Φ = 60°) as illustrated previously in Fig. 4 . But, for vertical corrugated enclosure (Φ = 90°) the entropy generation due to fluid friction decreases to [S_Ψ ,_max  = 339.536] due to the sudden drop in the flow velocity at this position. Therefore, it can be concluded that the inclined corrugated enclosure is better than the horizontal and vertical enclosures to enhance the entropy generation due to fluid friction. For entropy generation due to thermal gradients (S_θ ), the results show that it increases from [S_θ ,_max = 190.882] at (Φ = 0° or horizontal enclosure) to [S_θ ,_max = 204.797] at (Φ = 60°) and then decreases to [S_θ ,_max = 183.121] for vertical corrugated enclosure (Φ = 90°). This behavior is logical, since the natural convection effect becomes more effective as the enclosure inclination angle increases as illustrated previously in Fig. 4 . For entropy generation due to diffusion (S_C ), it can be seen from Fig. 5 , that it increases from [S_C ,_max = 334.724] at (Φ = 0° or horizontal enclosure) to [S_C ,_max = 408.523] at (Φ = 60°) and then increases to [S_C ,_max = 419.352] for vertical corrugated enclosure (Φ = 90°). On the other hand, it can be seen that the enclosure inclination angle has a clear effect on the position of contours of entropy generation due to diffusion (S_C ), since the contours are gradually shifted to the vertical position at (Φ = 90°). With respect to the total entropy generation (S_T ), a similar behavior to both entropy generations due to fluid friction (S_Ψ ) and thermal gradients (S_θ ) can be seen. Since the results of Fig. 5 illustrate that it increases from [S_T ,_max = 27955] at (Φ = 0° or horizontal enclosure) to [S_T ,_max = 434635] at (Φ = 60°) and then decreases to [S_T ,_max  = 297529] for vertical corrugated enclosure (Φ = 90°). This behavior can go back to the increase in both the fluid velocity and heat transfer for inclined enclosure, which leads to increase both friction and thermal entropy generation contributions and leads as a result to increase the total entropy generation (S_T ) for inclined enclosure.

Fig. 5. Entropy generation due to fluid friction (SΨ ), thermal gradients (Sθ ), diffusion (SC ) and total entropy generation (ST ) for different inclination angles (Φ) at N = 1, Le = 10, Da = 10−3 , Ha = 0 and Ra = 106 .

Fig. 6 explains stream function (Ψ), temperature (θ), concentration (C), heat function (Π), entropy generation due to fluid friction (S_Ψ ), thermal gradients (S_θ ), diffusion (S_C ) and total entropy generation (S_T ) at Pr = 0.024, Φ = 0°, Da = 10⁻³ and Ha = 0 for (a) Ra = 10⁴ and (b) Ra = 10⁶ respectively. This figure is devoted to illustrate the effect of the Rayleigh number, when the corrugated enclosure is placed in the horizontal position [Φ = 0°] and the effect of the applied magnetic field is negligible. In general, as described by the stream function (Ψ), the fluid flow inside the corrugated enclosure is represented by the well-known counterclockwise flow vortices. The convection currents start from the hot left sidewall and ends at the cold right sidewall after they pass on the top and bottom adiabatic walls. When the Rayleigh number is low [Ra = 10⁴ ], the values of the stream functions are also low and flow vortices are somewhat symmetrical especially in the core of the corrugated enclosure. When the Rayleigh number increases to [Ra = 10⁶ ], one can see a clear change in the flow field shape. Also, the stream function values jump sharply. For example, the stream function in the core of enclosure increases from [Ψ = −0.7] at [Ra = 10⁴ ] to [Ψ = −6.51] at [Ra = 10⁶ ]. Therefore, as expected when one increases the value of Rayleigh number the stream function value increases and the contribution of the natural convection in the heat transfer process increases. This is due to the increase in the buoyancy force when the Rayleigh number increases. For temperature (θ) and concentration (C) when the Rayleigh number is low [Ra = 10⁴ ], both isotherms and isoconcentration are in general symmetrical in their patterns. The only difference is that the isotherms are more parallel to the hot left and cold right sidewalls of the enclosure than the isoconcentrations. It can be noted that the values of temperatures and concentrations are high at the hot left sidewall and low at the cold right one, which satisfy indirectly the problem boundary conditions. In this case, the thermal energy is transferred inside the corrugated enclosure by the pure conduction. Another important conclusion which can be deduced from the results of Fig. 6 is that the isoconcentrations are more similar to the enclosure geometry than the isotherms. At [Ra = 10⁶ ], a clear deformation occurs in both isotherms and isoconcentrations patterns as a result of dominance of the buoyancy force. Therefore, the natural convection has a significant effect in this case as explained above. In regard to the entropy generation, the results of Fig. 6 explain clearly that the entropy generations due to fluid friction (S_Ψ ), thermal gradients (S_θ ), diffusion (S_C ) and the total entropy generation (S_T ) increase strongly as the Rayleigh number increases from [Ra = 10⁴ ] to [Ra = 10⁶ ]. This increase is very large and can be noticed for various kinds of entropy generation. For example, the entropy generation due to fluid friction (S_Ψ ) jumps from [S_Ψ ,_max  = 0.51369] at [Ra = 10⁴ ] to [S_Ψ ,_max  = 439.71] at [Ra = 10⁶ ], the entropy generation due to thermal gradients (S_θ ) jumps from [S_θ ,_max  = 7.55689] at [Ra = 10⁴ ] to [S_θ ,_max  = 190.882] at [Ra = 10⁶ ]. In the same manner, the entropy generation due to diffusion (S_C ) jumps from [S_C ,_max  = 39.3114] at [Ra = 10⁴ ] to [S_C ,_max  = 334.724] at [Ra = 10⁶ ], while the total entropy generation (S_T ) jumps from [S_T ,_max  = 532.702] at [Ra = 10⁴ ] to [S_T ,_max  = 279755] at [Ra = 10⁶ ]. Therefore, it can be deduced from these results that the Rayleigh number has a significant effect to increase all kinds of entropy generation. Of course, due to the increase in the temperature gradient, concentration gradient and flow velocity as the Rayleigh number increases, which leads to increase in the different kinds of entropy generation. Furthermore, it can be observed that the entropy generation values due to fluid friction (S_Ψ ) near the enclosure walls are greater than the corresponding values at the enclosure core. This is due to the presence of the boundary layer, which increases the entropy generation values due to fluid friction (S_Ψ ) at these regions. Again, the last column in Fig. 6 represents the heatfunction (Π) contours. It can be seen from the results, that the effect of Rayleigh number on heatfunction (Π) contours is very clear. When the Rayleigh number is low [Ra = 10⁴ ], the values of the heatfunction (Π) are also low. This indicates that the conduction effect is dominant. Moreover, there is no closed path of the heat transfer inside the enclosure and the direction of the heatfunction contours is approximately perpendicular to the isotherms (θ) direction. All of these effects are due to the conduction dominance inside the enclosure. When the Rayleigh number increases to [Ra = 10⁶ ], one can see a different behavior of the heatfunction contours. There is a clear increase in the values of the heatfunction which indicating that the convection heat transfer is significant. Furthermore, a closed path of heat transfer can be observed inside the enclosure while the heatfunction contours are not perpendicular to the isotherms (θ) direction. This observation ensures the dominance of convection in the case of [Ra = 10⁶ ]. Therefore, it can be concluded that the heatlines or heatfunction concept gives a better description of the heat transfer process compared with the classical isothermal lines.

Fig. 6. Streamfunction (Ψ), temperature (θ), concentration (C), heatfunction (Π), entropy generation due to fluid friction (SΨ ), thermal gradients (Sθ ), diffusion (SC ) and total entropy generation (ST ) at Pr = 0.024, Φ = 0°, Da = 10−3 , Ha = 0 and λ = 0.02 for (a) Ra = 104 and (b) Ra = 106 .

Fig. 7  and Fig. 9 show stream function (Ψ), temperature (θ), concentration (C) and heatfunction (Π), for different inclination angles (Φ) at N = 1, Le = 10, Da = 10⁻³ and Ra = 10⁶ . These figures are presented when the magnetic field is applied in the horizontal [Hax = 100] (Fig. 7 ) and vertical [Hay = 100] (Fig. 9 ) directions respectively. In fact to understand the results of these figures, one must make a comparison of the results presented in it with the corresponding results presented in Fig. 4 . It can be seen from the results of Fig. 7  and Fig. 9 that when the Hartmann numbers in the horizontal and vertical directions are [Hax = Hay = 100] or in other words that the corrugated enclosure is subjected to a strong magnetic field in the horizontal and vertical directions, the stream function values (Ψ) are reduced, which indicates that the magnetic field can be used to reduce the flow circulation inside the enclosure when applied either horizontally or vertically. For example, the stream function values in the core of enclosure decrease from [Ψ = −7.08] at [Φ = 0°] as shown in Fig. 4 to [Ψ = −5.31] at [Φ = 0] as shown in Fig. 7 for horizontal magnetic field. The same results can be noticed in Fig. 9 for vertical magnetic field. Similar observation is noticed at [Φ = 30°] and [Φ = 60°] respectively for both horizontal and vertical magnetic fields. For vertical corrugated enclosure [Φ = 90°], the results indicated that the reduction in the stream function values become very strong especially for horizontal magnetic field. For example, the stream function values in the core of enclosure decrease from [Ψ = −14.701] as shown in Fig. 4 to [Ψ = −3.724] as shown in Fig. 7 . While for vertical magnetic field, they decrease from [Ψ = −14.701] as shown in Fig. 4 to [Ψ = −7.556] as shown in Fig. 9 . This is because the velocity components decrease rapidly for strong magnetic field due to the effect of the Lorentz force. On the other hand, there is also a clear change in the flow field patterns between the horizontal magnetic field (Fig. 7 ) and vertical magnetic field (Fig. 9 ) cases. This observation is seen for all the considered enclosure inclination angles. Moreover, one can see multi-vortices inside the enclosure when it placed in the vertical direction [Φ = 90°] for both horizontal and vertical magnetic fields. Now, horizontal and vertical magnetic fields on stream function values are compared. The results presented in Fig. 7  and Fig. 9 display that the reduction in stream function values for horizontal magnetic field are greater than the corresponding values for vertical magnetic field. This reduction increases at [Φ = 90°]. Therefore, when the corrugated enclosure is considered vertical [Φ = 90°] and subjected to a horizontal magnetic field, a strong damping in the flow circulation can be captured. For temperature (θ), both horizontal and vertical magnetic fields make the isotherms more similar to the enclosure shape and decreases greatly the disturbance in the isotherms especially when the enclosure inclination angles are [Φ = 60°] and [Φ = 90°] respectively. This behavior ensures the fact that when the enclosure is subjected to a strong magnetic field either horizontally or vertically, the heat transfer mechanism switches from convection (for no magnetic field; Fig. 4 ) to conduction heat transfer mechanism. In general, the isotherms in Fig. 7  and Fig. 9 illustrate that a high temperatures are noticed adjacent to the hot left sidewall while a low temperatures are seen adjacent the cold right one, which satisfy again the boundary conditions. This notation is seen for all values of the enclosure inclination angles. Moreover, the results presented in Fig. 7  and Fig. 9 explain that when the orientation of the magnetic field changes either horizontally or vertically no significant difference occurs in the isotherms patterns.

Fig. 7. Streamfunction (Ψ), temperature (θ), concentration (C), and heatfunction (Π), for different inclination angles (Φ) at N = 1, Le = 10, Da = 10−3 , Hax = 100 and Ra = 106 .

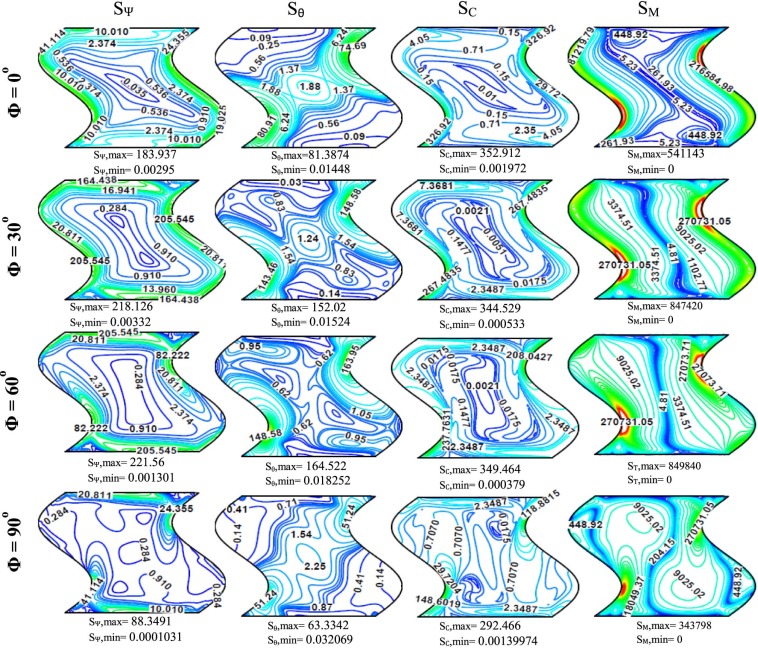
Fig. 8. Entropy generation due to fluid friction (SΨ ), thermal gradients (Sθ ), diffusion (SC ) and magnetic field (SM ) for different inclination angles (Φ) at N = 1, Le = 10, Da = 10−3 , Hax = 100 and Ra = 106 .

With respect to the concentration (C), it can be noticed that the results of Fig. 7  and Fig. 9 are presented when the buoyancy ratio (N) is equal to one. This means that the buoyancy force due to thermal diffusion is equal to its corresponding value due to mass diffusion. The results in both figures show that the iso-concentration contours are affected by the applied horizontal and vertical magnetic fields. This effect becomes more clear if one compares between the iso-concentration contours for no magnetic field (Fig. 4 ) with their corresponding contours in Fig. 7  and Fig. 9 . The horizontal and vertical magnetic fields make the iso-concentration contours more clustered to each other especially in the core of corrugated enclosure. This effect is clearable for all values of the enclosure inclination angles. Again, the horizontal and vertical magnetic fields make the iso-concentration contours less disturbed that the corresponding contours in Fig. 4 . This is because the conduction effect becomes more significant when the enclosure is subjected to a strong magnetic field. Also, the iso-concentration in Fig. 7  and Fig. 9 illustrate that high concentrations are noticed adjacent to the hot left sidewall while a low concentrations are seen adjacent to the cold right one, which satisfy again the boundary conditions. On the other hand, there is a difference between the patterns of iso-concentration when subjected to a horizontal magnetic field (Fig. 7 ) with their patterns when it subjected to a vertical magnetic field (Fig. 9 ). This difference is high for horizontal enclosure [Φ = 0°] and slight for vertical one [Φ = 90°]. Furthermore, the last column in Fig. 7  and Fig. 9 represents the heatfunction (Π) contours. It can be observed from the results that the effect of Hartmann number [or magnetic field effect] on heatfunction (Π) contours is significant. Anyway, when the corrugated enclosure is subjected to a horizontal magnetic field [Hax = 100] (Fig. 7 ) or a vertical magnetic field [Hay = 100] (Fig. 9 ), a decrease in the heatfunction values can be seen. To make this effect clearer, a comparison of the heatfunction results with the corresponding results presented in Fig. 4 [Ha = 0] is necessary in our opinion. It can be seen from the results of Fig. 7  and Fig. 9 that there is a reduction in heatfunction values (Π) inside the enclosure when it subjected to a horizontal or vertical magnetic field. For example, the heatfunction values in the core of enclosure decrease from [Π = −4.95] at [Φ = 30°] as shown in Fig. 4 to [Π = −2.18] at [Φ = 30°] as shown in Fig. 7 for horizontal magnetic field. Similar behavior can be noticed in Fig. 9 for vertical magnetic field. Also, the same results can be seen for other values of enclosure inclination angles. In fact, this result is expected since the conduction effect is dominant inside the enclosure when subjected to a strong magnetic field. This effect of course is considered the main reason of the reduction in heatfunction values.

Fig. 8  and Fig. 10 explain entropy generations due to fluid friction (S_Ψ ), thermal gradients (S_θ ), diffusion (S_C ) and magnetic field (S_M ) for different inclination angles (Φ) at N = 1, Le = 10, Da = 10⁻³ and Ra = 10⁶ . These figures are presented when the magnetic field is applied in the horizontal [Hax = 100] (Fig. 8 ) and vertical [Hay = 100] (Fig. 10 ) directions respectively. Therefore, the main purpose of these figures is to explain the effect of high Hartmann number or strong horizontal and vertical magnetic fields [Hax = Hay = 100] on different kinds of the entropy generation. In order to explain the effect of magnetic field on the entropy generations, a comparison is occurred between the results in Fig. 8  and Fig. 10 with the corresponding results presented in Fig. 5 [i.e. Ha = 0 or with no magnetic field]. It can be seen from the results of Fig. 8  and Fig. 10 that both horizontal and vertical magnetic fields are reduced significantly the entropy generations. This reduction can be seen for horizontal, inclined and vertical enclosures. For example, the entropy generation values due to fluid friction (S_Ψ ) at [Φ = 30°] are reduced from [S_Ψ ,_max  = 708.298] for no magnetic field (Fig. 5 ) to [S_Ψ ,_max  = 218.126] for horizontal magnetic field (Fig. 8 ) and [S_Ψ ,_max  = 364.765] for vertical magnetic field (Fig. 10 ) respectively. This behavior is due to the reduction in the flow circulation inside the enclosure which causes to reduce the entropy generation values due to fluid friction (S_Ψ ). On the other hand, a clear reduction in the entropy generations due to thermal gradients (S_θ ) can be seen for horizontal and vertical magnetic fields. For example, the entropy generation values due to thermal gradients (S_θ ) at [Φ = 30°] are reduced from [S_θ ,_max  = 266.604] for no magnetic field (Fig. 5 ) to [S_θ ,_max  = 152.02] for horizontal magnetic field (Fig. 8 ) and [S_θ ,_max  = 114.315] for vertical magnetic field (Fig. 10 ) respectively. This notation is seen for all values of the enclosure inclination angles. This behavior is due to the reduction in the natural convection effect inside the enclosure when the magnetic field is applied in the horizontal and vertical directions, which causes to reduce the entropy generation values due to thermal gradients (S_θ ). For the entropy generations due to diffusion (S_C ), one can observe also a clear decreasing in their values. For example, the entropy generation values due to diffusion (S_C ) at [Φ = 30°] are decreased from [S_C ,_max  = 431.015] for no magnetic field (Fig. 5 ) to [S_C ,_max  = 344.529] for horizontal magnetic field (Fig. 8 ) and [S_C ,_max  = 347.195] for vertical magnetic field (Fig. 10 ) respectively. This effect is repeated for inclined and vertical enclosures. The reason is due to the reduction in the mass transfer when the enclosure is subjected to a strong horizontal and vertical magnetic field, which leads to reduce the entropy generations due to diffusion (S_C ). With respect to the entropy generations due to magnetic field (S_M ), the results of Fig. 8  and Fig. 10 show that the entropy generation values when the corrugated enclosure is subjected to the horizontal magnetic field (Fig. 8 ) is higher than the corresponding values when it subjected to the vertical magnetic field (Fig. 10 ). This observation can be seen for different values of the enclosure inclination angles. Therefore, the horizontal magnetic field increases the entropy generations more than the vertical magnetic field.

Fig. 9. Streamfunction (Ψ), temperature (θ), concentration (C), and heatfunction (Π), for different inclination angles (Φ) at N = 1, Le = 10, Da = 10−3 , Hay = 100 and Ra = 106 .

Fig. 10. Entropy generation due to fluid friction (SΨ ), thermal gradients (Sθ ), diffusion (SC ) and magnetic field (SM ) for different inclination angles (Φ) at N = 1, Le = 10, Da = 10−3 , Hay = 100 and Ra = 106 .

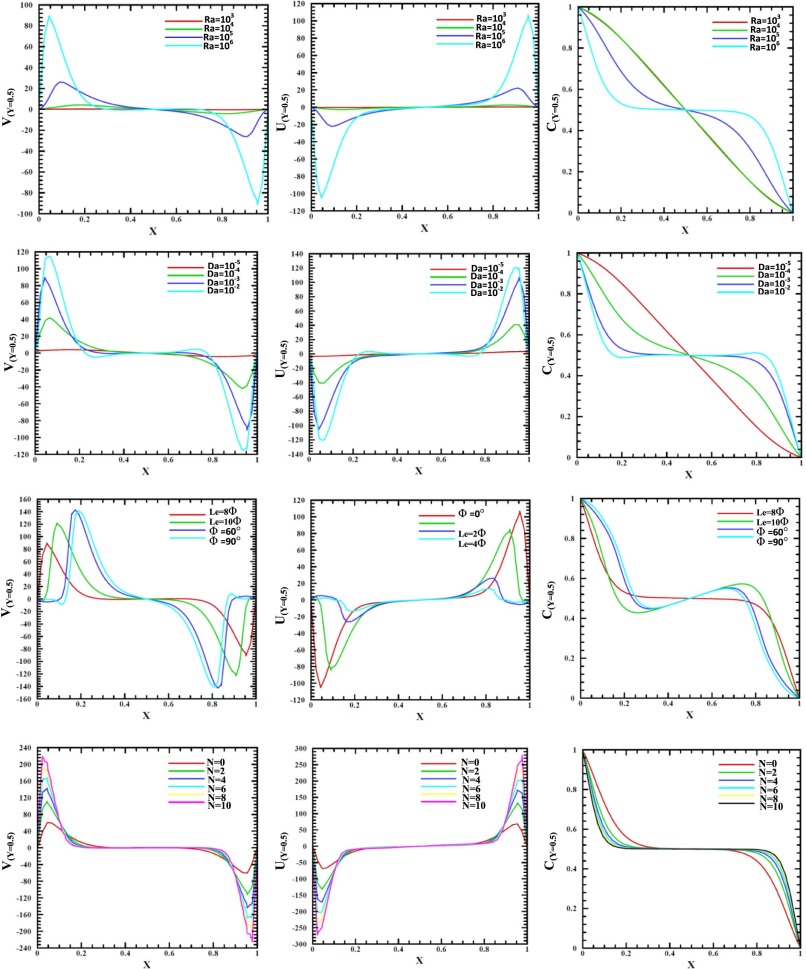
Fig. 11 illustrates profiles of Y-velocity component, X-velocity component and concentration (C) along the vertical mid-section of the enclosure with different Rayleigh (1st row) Darcy (2nd row) numbers, inclination angles (Φ) (3rd row) and buoyancy ratio (N) (4th row) for Ha = 0, Le =1 and φ = 0°. The main purpose of this figure is to explain the effect of Rayleigh number (Ra), Darcy number (Da), inclination angles (Φ) and buoyancy ratio (N) on Y-velocity component, X-velocity component and concentration (C) respectively. With respect to the Rayleigh number effect [1st row], it can be observed that Y-velocity component has a linear behavior for [Ra = 10³ ] and varies slowly for [Ra = 10⁴ ]. But, as the Rayleigh number increases to [Ra = 10⁵ and 10⁶ ], it begins to vary symmetrically along the vertical mid-section of the enclosure. This indicates that the Y-velocity component profiles change their behavior when the Rayleigh number increases due to the improvement in the flow circulation. The results show that a positive velocity profiles can be seen in the region from [0 ≤ X ≤ 0.25], while a negative velocity profiles can be seen in the region from [0.75 ≤ X ≤ 1]. The same observation can be seen for X-velocity component profiles but in the reverse direction. For Darcy number (Da) effect [2nd row], it can be seen again that the Y-velocity component has a linear behavior for [Da =10⁻⁵ ] and changes slowly for [Da =10⁻⁴ ]. While, when the Darcy number (Da) increases to [Da = 10⁻³ and 10⁻² ] a clear variation in the Y-velocity component profiles can be detected. They increase as (X) increases, then become approximately linear in the mid-section at [X = 0.5] and then decrease until they reach zero velocity at [X = 1]. Similar but an opposite behavior can be seen for X-velocity component profiles. Therefore, it can be conclude that both Y and X velocity component profiles affected strongly for high Darcy number. The reason of this behavior is due to the increasing in the natural convection effect at high Darcy number. To study the effect of inclination angle (Φ) [3rd row], the results of Fig. 11 show that the Y-velocity component increases when the inclination angle increases from (Φ = 0° or horizontal enclosure) to (Φ = 60°). At (Φ = 90° or vertical enclosure) it begins to decrease slightly. These results are due to the increase in the stream function values when the inclination angle increases from (Φ = 0°) to (Φ = 60°) and to the decrease in their values at (Φ = 90°) as discussed previously in Fig. 4 . However, the Y-velocity component profiles increase as (X) increases, then become approximately linear in the mid-section at [X = 0.5] and drop until they reach zero velocity at [X = 1]. The same notation is seen for X-velocity component profiles but in the opposite direction. To discuss the effect of buoyancy ratio (N) [4th row], the results of Fig. 11 demonstrate that the Y-velocity component increases when the buoyancy ratio increases. The minimum profile can be seen at [N = 0] or pure thermal convection, while the maximum one can be seen at [N = 10]. This is because the flow circulation increases for high concentration case. Anyway, all profiles reach zero velocity at enclosure mid-section and then begin to decrease to negative values until they reach zero velocity at [X = 1]. It is useful to mention that for high buoyancy ratio, the flow field is strongly affected by buoyancy forces due to temperature and concentration. For X-velocity component, negative velocity profiles can be seen in the region of [X ≤ 0.2] while a positive profiles are seen in the region [0.8 ≤ X]. With respect to profiles of dimensionless concentration (C) along the vertical mid-section [Y = 0.5] of the enclosure. The results show that the profiles are approximately linear for low Rayleigh and Darcy numbers [Ra = 10³ –10⁴ ] and [Da = 10⁻⁵ ]. But, when Rayleigh and Darcy numbers increase a variation in the profiles can be seen. This is due to the increase in the concentration for high Rayleigh and Darcy numbers. On the other hand, the profiles of dimensionless concentration (C) are also affected by enclosure inclination angles, since they convert their shape from uniform variation for (Φ = 0° or horizontal enclosure) to non-uniform one as inclination angles increases. The results of Fig. 11 shows that the profiles of dimensionless concentration (C) are not greatly affected by the variation of buoyancy ratio (N) where an approximately symmetrical profiles can be seen for various values of buoyancy ratio.

Fig. 11. Profiles of Y-velocity component, X-velocity component and concentration (C) along the vertical mid-section of the enclosure with different Rayleigh (1st row) Darcy (2nd row) numbers, inclination angles (Φ) (3rd row) and buoyancy ratio (N) (4th row) for Ha = 0, Le = 1 and φ = 0°.

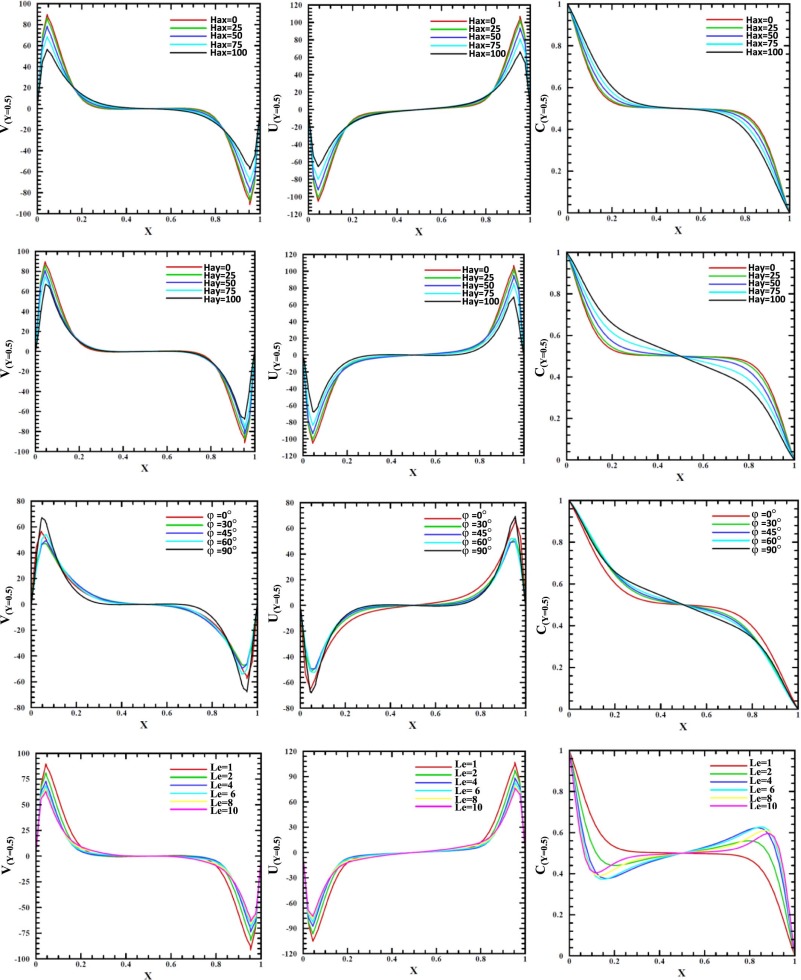
Fig. 12 presents profiles of Y-velocity component, X-velocity component and concentration (C) along the vertical mid-section of the enclosure with different Hartmann numbers at φ = 0° [horizontal magnetic field] (1st row), φ = 90° [vertical magnetic field] (2nd row), magnetic field angles (φ) (3rd row) and Lewis number (Le) (4th row) for Ra = 10⁶ , N = 1,Φ = 0° and Da =10⁻³ . It can be seen from the results that both Y and X velocity components decrease as the Hartmann number increases. This observation can be seen when the enclosure is subjected to a horizontal magnetic field [Hax = 0–100] or when it subjected to a vertical magnetic field [Hay = 0–100]. The velocity profiles are approximately linear in the mid-section of the enclosure. For strong horizontal and vertical magnetic fields [Hax = Hay = 100] at [X = 0.5] the velocity components reach zero velocity. This is a logical result, since the magnetic field reduces flow circulation significantly. Also, it can be seen that the profiles of Y-velocity component and X-velocity component grow in the opposite direction to each other. On the other hand, the effect of magnetic field orientation angle (φ) is also presented in Fig. 12 . For Y-velocity component, the profiles reach their maximum value as the orientation angle increases from [φ = 0°] to [φ = 90°]. However, a significant variation in the velocity components can be seen at the hot left [X = 0] and cold right [X = 1] sidewalls of the enclosure due to the presence of the flow circulation. The fourth row of Fig. 12 explains the effect of Lewis number on profiles of Y-velocity component, X-velocity component and concentration (C) along the vertical mid-section of the enclosure. It can be noticed that Y-velocity component increases as the Lewis number decreases. In fact, when the Lewis number increases, the velocity of the flow circulation decreases due to the increase in the fluid thermal diffusivity. From the other hand, the increasing in the Lewis number causes to increase the thermal boundary layer thickness, which causes to decrease the fluid velocity. Again, at mid-section of the enclosure the velocities approach zero. An opposite behavior can be observed for X-velocity component. With respect to the concentration, it can be seen that concentration reaches its maximum value when the Lewis number is low [Le = 1] and then begins to decrease as the Lewis number increases. This is a logical result since when the Lewis number is low the mass diffusivity is high and as a result the concentration increases. But, when the Lewis number increases, the mass diffusivity decreases and causes the reduction of the concentration. A reverse behavior can be seen at the cold right sidewall.

Fig. 12. Profiles of Y-velocity component, X-velocity component and concentration (C) along the vertical mid-section of the enclosure with different Hartmann numbers at φ = 0° (1st row), φ = 90° (2nd row), magnetic field angles (φ) (3rd row) and Lewis number (Le) (4th row) for Ra = 106 , N = 1,Φ = 0° and Da = 10−3 .

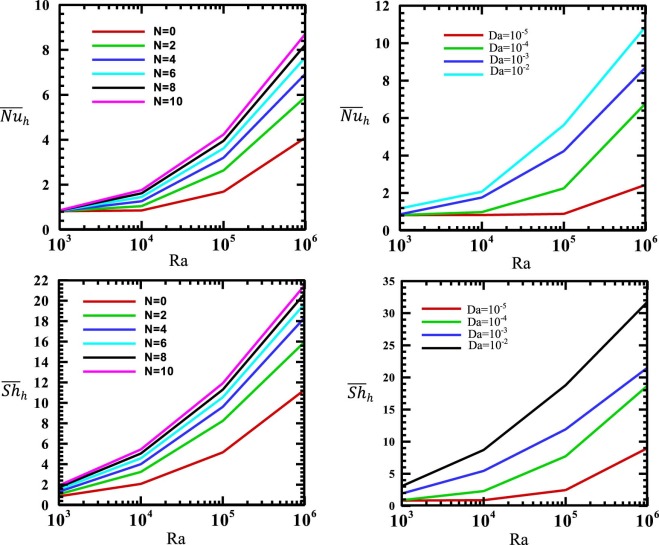
Fig. 13 shows the variation of the average Nusselt and Sherwood numbers along the heated wall with Rayleigh numbers for various buoyancy ratios (N) (on the left when Da = 10⁻³ ) and various Darcy numbers (on the right when N = 10) at Φ = 0°, φ = 0° and Ha = 0 with Le = 1(on the top) and Le = 10 (at the bottom). The results exhibit that as the buoyancy ratio (N) increases, the relationship between the average Nusselt and Sherwood numbers with Rayleigh number increases. For (N = 0), the flow is driven by thermal convection only (or the effect of mass transfer is negligible). But, when the buoyancy ratio increases, the flow inside the enclosure will be driven by mixed effect of thermal and concentration buoyancy forces which cause to a clear increase in the average Nusselt and Sherwood numbers value. With respect to the relationship between the Rayleigh number and average Nusselt and Sherwood numbers for various values of Darcy number. It can be seen that as the Darcy number increases from [Da = 10⁻⁵ ] to [Da = 10⁻² ], an increasing relationship can be seen between the Rayleigh number and average Nusselt and Sherwood numbers at the heated wall. Since, when the Darcy number is low [Da = 10⁻⁵ ], the flow and mass circulations inside the porous media are very weak, which cause a clear reduction in the average Nusselt and Sherwood numbers value. But, as the Darcy number increases to [Da = 10⁻² ], the average Nusselt and Sherwood numbers increase strongly with the Rayleigh number due to the strong flow and mass circulations inside the porous media when the Darcy number is high [i.e. Da = 10⁻² ].

Fig. 13. Variation of the average Nusselt and Sherwood numbers along the heated wall with Rayleigh numbers for various Buoyancy ratios (N) (on the left when Da = 10−3 ) and various Darcy numbers (on the right when N = 10) at Φ = 0°, φ = 0 and Ha = 0 with Le = 1(on the top) and Le = 10 (on the bottom).

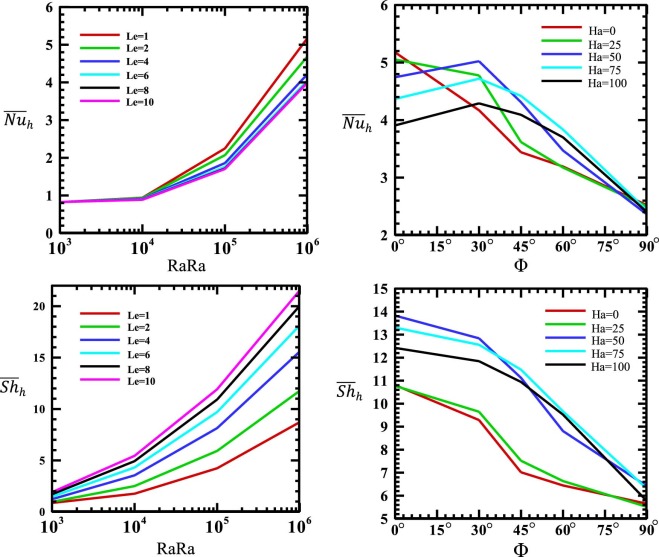
Fig. 14 explains the variation of the average Nusselt and Sherwood numbers along the heated wall with Rayleigh numbers (on the left) for various Lewis numbers (Le) when Φ = 0°, Ha = 0 and with enclosure inclination angles (Φ) (on the right) for various Hartman numbers (Ha) when Ra = 10⁶ at Da = 10⁻³ with Le = 1 (on the top) and Le = 10 (at the bottom) respectively. It can be observed that as the Lewis number increases, the relationship between the average Nusselt number and Rayleigh number decreases. This is due to the increase in the fluid thermal diffusivity, which causes to increase the effect of conduction and as a result decreases the average Nusselt number along the heated wall. While, the relationship between the average Sherwood number and Rayleigh number increases as the Lewis number increases. This is due to the decrease in the fluid mass diffusivity, which causes to increase the mass transfer effect inside the enclosure. From the other side, the results show that for horizontal enclosure [Φ = 0°], the average Nusselt number along the heated wall reaches a maximum value for [Ha = 0 or with no magnetic field] and decreases as the Hartmann number increases. This is because the magnetic force reduces the flow circulation. But, as the enclosure inclination angle increases to (Φ = 30°), a clear improvement on the average Nusselt number values can be seen especially at high values of Hartmann number. This is due to the increase in the flow circulation. But, the average Nusselt number values drop sharply for vertical enclosure (Φ = 90°). Since, the effect of buoyancy force decreases for vertical corrugated enclosure as discussed previously in Fig. 4 . With respect to the average Sherwood number, it can be seen also that as the enclosure inclination angle increases, the average Sherwood number begin to decrease. The maximum value of average Sherwood number can be noticed at (Φ = 0°) and (Ha = 50). Therefore, it can be concluded that the horizontal position of the enclosure is better than the inclined and vertical enclosures to improve the mass transfer inside the corrugated enclosure.

Fig. 14. Variation of the average Nusselt and Sherwood numbers along the heated wall with Rayleigh numbers (on the left) for various Lewis numbers (Le) when Φ = 0°, Ha = 0 and with enclosure inclination angles (Φ) (on the right) for various Hartman numbers (Ha) when Ra = 106 at Da = 10 with Le = 1 (on the top) and Le = 10 (on the bottom).

6. Conclusions

The following conclusions can be drawn from the results of the present work:

• The inclination angle of the corrugated enclosure has an important effect on the flow pattern. When it increases to (Φ = 60° and 90°), the strength of flow circulation increases and some minor vortices begin to appear inside the enclosure.
• The heat transfer mode switches from conduction to convection one, when the enclosure switches from horizontal position (Φ = 0°) to the inclined (Φ = 30° and 60°) or vertical (Φ = 90°) positions.
• Activity of iso-concentrations contours increases as the inclination angle increases from (Φ = 0° to 90°).
• When the Rayleigh number is low, the isotherms and isoconcentrations are uniformly distributed in the corrugated enclosure and the heat conduction is dominant.
• The strength of circulation increases when the Rayleigh number increases. Also, a deformation occurs in the isotherms and isoconcentration indicating that the natural convection has the biggest share in the heat transfer process inside the corrugated enclosure.
• A clear reduction in the flow circulation can be seen when the enclosure is subjected to a strong magnetic field either horizontally or vertically. This reduction becomes very strong at [Φ = 90°] especially for horizontal magnetic field.
• To enhance the flow circulation inside the corrugated enclosure, one must exclude the vertical position of the enclosure and horizontal magnetic field.
• No significant difference occurs in the isotherm patterns when the orientation of the magnetic field changes either horizontally or vertically.
• The horizontal and vertical magnetic fields make the iso-concentration contours less disturbance and increase the effect of heat conduction.
• The inclined corrugated enclosure is better than the horizontal and vertical enclosures to enhance the entropy generation due to fluid friction (S_Ψ ), thermal gradients (S_θ ) and the total entropy generation (S_T ).
• When the Rayleigh number increases, a clear jump in all kinds of entropy generation is noticed.
• The entropy generations due to magnetic field (S_M ) when the enclosure is subjected to the horizontal magnetic field are higher than the corresponding values when subjected to the vertical magnetic field for different values of the enclosure inclination angles.
• The results of heatfunction contours explain that the heat transfer enhancement is better for inclined position of the enclosure than the horizontal and vertical positions of it.
• The values of the heatfunction increases as the Rayleigh number increases. Also, the heatlines or heatfunction concept gives a better description of the heat transfer process compared with the classical isothermal lines.
• Both Y and X velocity component profiles are affected strongly by Rayleigh number, Darcy number, enclosure inclination angle, magnetic field angles, Hartmann number, Lewis number and buoyancy ratio.
• Dimensionless concentration (C) profiles are affected highly by Rayleigh number, Darcy number, enclosure inclination angle, Lewis number and have slight variation with buoyancy ratio.
• The average Nusselt number decreases when the Lewis number increases. While the average Sherwood number increases when the Lewis number increases.
• The average Nusselt and Sherwood numbers increase when the Darcy number and buoyancy ratio increase.
• The enclosure inclination angle has a clear effect on the average Nusselt and Sherwood numbers value.
• Heatline visualization concept is successfully applied to the considered problem.

References

1. [1] Y. Varol, H. Oztop; Free convection in a shallow wavy enclosure; Int. Commun. Heat Mass Transfer, 33 (2006), pp. 764–771
2. [2] P. Das, S. Mahmud; Numerical investigation of natural convection inside a wavy enclosure; Int. J. Therm. Sci, 42 (2003), pp. 397–406
3. [3] R. Mebrouk, B. Abdellah, S. Abdelkader; Effect of wall waviness on heat transfer by natural convection in a horizontal wavy enclosure; Appl. Mech. Rev, 1 (2) (2006), pp. 187–201
4. [4] F. Garoosi, L. Jahanshaloo, M. Rashidi, A. Badakhsh, M. Ali; Numerical simulation of natural convection of the nanofluid in heat exchangers using a Buongiorno model; Appl. Math. Comput, 254 (2015), pp. 183–203
5. [5] F. Garoosi, G. Bagheri, M. Rashidi; Two phase simulation of natural convection and mixed convection of the nanofluid in a square cavity; Powder Technol (2015), pp. 239–256 http://dx.doi.org/10.1016/j.powtec.2015.02.013
6. [6] M. Rashidi, T. Hayat, M. Keimanesh, A. Hendi; New analytical method for the study of natural convection flow of a non-Newtonian fluid; Int. J. of Num. Meth. for Heat and Fluid Flow, 23 (2013), pp. 436–450
7. [7] M. Ali, S. Husain; Effect of corrugation frequencies on natural convective heat transfer and flow characteristics in a square enclosure of vee-corrugated vertical walls; Int. J. Energy Res, 17 (1993), pp. 697–708
8. [8] G. Saha, S. Saha, M. Ali, M. Islam; Natural convection in a vee-corrugated square enclosure with discrete heating from below; J. Eng. Technol, 6 (1) (2007), pp. 15–27
9. [9] N. Hasan, S. Saha, C. Feroz; Natural convection with in an enclosure of sinusoidal corrugated top surface; Proceedings of the 4thBSME-ASME International Conference on Thermal Engineering, 27–29 December, 2008, Dhaka, Bangladesh  (2008)
10. [10] S. Saha, T. Sultana, G. Saha, M. Rahman; Effects of discrete isoflux heat source size and angle of inclination on natural convection heat transfer flow inside a sinusoidal corrugated enclosure; Int. Commun. Heat Mass Transfer, 35 (2008), pp. 1288–1296
11. [11] S. Hussain, A. Hussein, M. Mahdi; Natural convection in a square inclined enclosure with vee-corrugated sidewalls subjected to constant flux heating from below; Nonlinear Anal. Model. Control, 16 (2) (2011), pp. 152–169
12. [12] M. Bakier; Flow in open C-shaped cavities: how far does the change in boundaries affect nanofluid?; Int. J. Eng. Sci. Technol, 17 (2014), pp. 116–130
13. [13] B. Mliki, M. Abbassi, K. Guedri, A. Omri; Lattice Boltzmann simulation of natural convection in an L-shaped enclosure in the presence of nanofluid; Int. J. Eng. Sci. Technol, 18 (2015), pp. 503–511
14. [14] B. Kumar; A study of free convection induced wavy surface with heat flux in a porousenclosure; Numer. Heat Transfer A, 37 (2000), pp. 493–510
15. [15] A. Misirlioglu, A. Baytas, I. Pop; Free convection in a wavy cavity filled with a porous medium; Int. J. Heat Mass Transf, 48 (2005), pp. 1840–1850
16. [16] A. Misirlioglu, A. Baytas, I. Pop; Free convection in a wavy cavity filled with heat-generating porous media; J. Porous Media, 9 (3) (2006), pp. 1–16
17. [17] K. Khanafer, B. Al-Azmi, A. Marafie, I. Pop; Non-Darcian effects on natural convection heat transfer in a wavy porous enclosure; Int. J. Heat Mass Transf, 52 (2009), pp. 1887–1896
18. [18] K. Mushatet; Investigation of natural convection inside an inclined porous square cavity with two wavy walls; Global J. Res. Eng, 10 (6) (2010), pp. 35–46
19. [19] M. Mansour, M. Abd El-Aziz, R. Mohamed, S. Ahmed; Numerical simulation of natural convection in wavy porous cavities under the influence of thermal radiation using a thermal non-equilibrium model; Transp. Porous Media, 86 (2011), pp. 585–600
20. [20] G. Saha; Finite element simulation of magnetoconvection inside a sinusoidal corrugated enclosure with discrete isoflux heating from below; Int. Commun. Heat Mass Transfer, 37 (2010), pp. 393–400
21. [21] S. Hussain, A. Hussein, R. Mohammed; Studying the effects of a longitudinal magnetic field and discrete isoflux heat source size on natural convection inside a tilted sinusoidal corrugated enclosure; Comput. Math. Appl, 64 (2012), pp. 476–488
22. [22] B. Rathish Kumar, S. Krishna Murthy; Soret and Dufour effects on double-diffusive free convection from a corrugated vertical surface in a non-Darcy porous medium; Transp. Porous Media, 85 (1) (2010), pp. 117–130
23. [23] S. Krishna Murthy, B. Rathish Kumar, P. Chandra, V. Sangwan, M. Nigam; A study of double diffusive free convection from a corrugated vertical surface in a Darcy porous medium under Soret and Dufour effects; J. Heat Transfer, 133 (2011), pp. 1–7
24. [24] M. Rahman, R. Saidur, S. Mekhilef, M. BorhanUddin, A. Ahsan; Double-diffusive buoyancy induced flow in a triangular cavity with corrugated bottom wall: effects of geometrical parameters; Int. Commun. Heat Mass Transfer, 45 (2013), pp. 64–74
25. [25] R. Nikbakhti, J. Khodakhah; Numerical investigation of double diffusive buoyancy forces induced natural convection in a cavity partially heated and cooled from sidewalls; Eng. Sci. Technol. Int. J. (2015) http://dx.doi.org/10.1016/j.jestch.2015.08.003 Article in Press
26. [26] S. Mahmud, A. Islam; Laminar free convection and entropy generation inside an inclined wavy enclosure; Int. J. Therm. Sci, 42 (2003), pp. 1003–1012
27. [27] S. Mahmud, R. Fraser; Free convection and entropy generation inside a vertical in-phase wavy cavity; Int. Commun. Heat Mass Transfer, 31 (2004), pp. 455–466
28. [28] S. Mahmud, R. Fraser, I. Pop; Flow, thermal, energy transfer, and entropy generation characteristics inside wavy enclosures filled with microstructures; J. Heat Transfer, 129 (2007), pp. 1564–1575
29. [29] M. Esmaeilpour, M. Abdollahzadeh; Free convection and entropy generation of nanofluid inside an enclosure with different patterns of vertical wavy walls; Int. J. Therm. Sci, 52 (2012), pp. 127–136
30. [30] S. Das, A. Banu, R. Jana, O. Makinde; Entropy analysis on MHD pseudo-plastic nanofluid flow through a vertical porous channel with convective heating; Alexandria Eng. J., 54 (3) (2015), pp. 325–337
31. [31] A. Eegunjobi, O. Makinde; Second law analysis for MHD permeable channel flow with variable electrical conductivity and asymmetric Navier slips; Open Physics, 13 (2015), pp. 100–110
32. [32] M. Mkwizu, O. Makinde; Entropy generation in a variable viscosity channel flow of nanofluids with convective cooling; Comptes Rendus Mécanique, 343 (2015), pp. 38–56
33. [33] M. Rashidi, N. Kavyani, S. Abelman; Investigation of entropy generation in MHD and slip flow over a rotating porous disk with variable properties; Int. J. Heat Mass Transf, 70 (2014), pp. 892–917
34. [34] M. Rashidi, M. Ali, N. Freidoonimehr, F. Nazari; Parametric analysis and optimization of entropy generation in unsteady MHD flow over a stretching rotating disk using artificial neural network and particle swarm optimization algorithm; Energy, 55 (2013), pp. 497–510
35. [35] M. Rashidi, S. Abelman, N. Freidooni Mehr; Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid; Int. J. Heat Mass Transf, 62 (2013), pp. 515–525
36. [36] S. Kimura, A. Bejan; The heatline visualization of convective heat transfer; J. Heat Transfer, 105 (1983), pp. 916–919
37. [37] V. Costa; Bejans heatlines and masslines for convection visualization and analysis; Appl. Mech. Rev, 59 (2006), pp. 126–145
38. [38] A. Dalal, M. Das; Heatline method for the visualization of natural convection in a complicated cavity; Int. J. Heat Mass Transf, 51 (2008), pp. 263–272
39. [39] T. Basak, S. Roy, A. Matta, I. Pop; Analysis of heatlines for natural convection within porous trapezoidal enclosures: effect of uniform and non-uniform heating of bottom wall; Int. J. Heat Mass Transf, 53 (2010), pp. 5947–5961
40. [40] R. Kaluri, T. Basak; Heatline analysis of thermal mixing due to natural convection in discretely heated porous cavities filled with various fluids; Chem. Eng. Sci, 65 (2010), pp. 2132–2152
41. [41] T. Basak, A. Chamkha; Heatline analysis on natural convection for nanofluids confined within square cavities with various thermal boundary conditions; Int. J. Heat Mass Transf, 55 (2012), pp. 5526–5543
42. [42] Y. Varol, H. Oztop, M. Mobedi, I. Pop; Visualization of natural convection heat transport using heatline method in porous non-isothermally heated triangular cavity; Int. J. Heat Mass Transf, 51 (2008), pp. 5040–5051
43. [43] K. Hooman, H. Gurgenci, I. Dincer; Heatline and energy-flux-vector visualization of natural convection in a porous cavity occupied by a fluid with temperature-dependent viscosity; J. Porous Media, 12 (3) (2009), pp. 265–275
44. [44] T. Basak, D. Ramakrishna, S. Roy, A. Matta, I. Pop; A comprehensive heatline based approach for natural convection flows in trapezoidal enclosures: effect of various walls heating; Int. J. Therm. Sci, 50 (2011), pp. 1385–1392
45. [45] J. Ferziger, M. Peric; Computational Methods for Fluid Dynamics; (second ed.)Springer Verlag, Berlin (1999)
46. [46] H.L. Stone; Iterative solution of implicit approximations of multidimensional partial differential equations; SIAM J. Numer. Anal, 5 (1968), pp. 530–558
47. [47] D. Ramakrishna, T. Basak, S. Roy; Analysis of heatlines and entropy generation during free convection within trapezoidal cavities; Int. Commun. Heat Mass Transfer, 45 (2013), pp. 32–40
48. [48] G. Ilis, M. Mobedi, B. Sunden; Effect of aspect ratio on entropy generation in a rectangular cavity with differentially heated vertical walls; Int. Commun. Heat Mass Transfer, 35 (2008), pp. 696–703
49. [49] T. Basak, P. Gunda, R. Anandalakshmi; Analysis of entropy generation during natural convection in porous right-angled triangular cavities with various thermal boundary conditions; Int. J. Heat Mass Transf, 55 (2012), pp. 4521–4535