Abstract
Using non-linear analyses and Monte Carlo simulations, a simplified accidental-torsion design procedure is evaluated. The design procedure does not use an accidental eccentricity like the building codes do. For the evaluation, four reinforced concrete frame building models of four and seven stories are dynamically studied in the nonlinear range. The models are subjected to a set of five firm-soil, bidirectional seismic records. The design procedure is evaluated by comparing the ductility demands of both beams and columns for three conditions of each building model: a) the torsionally balanced model without accidental torsion (model TB), which establishes the reference values of ductility demands; b) the same nominal model but incorporating accidental torsion via the Monte Carlo method; and c) a model with amplified strength (model AS) according to the accidental-torsion design procedure to be evaluated. Results indicate that there is a probability smaller than 2.5% that accidental torsion can cause ductility demands approximately 20% to 25% larger than those of similar building models without accidental torsion. A comparison of ductility demands for the reference models without accidental torsion and those of models with accidental torsion and designed with the procedure that is evaluated, reveals that the design procedure is effective to control the effects of accidental torsion.
Keywords: Seismic accidental torsion, accidental eccentricity, Monte Carlo simulation, nonlinear seismic analysis
1. Introduction
During earthquake ground motions, the response of buildings is essentially horizontal when they are far from the earthquake source. However, when acting inertial lateral forces do not act in the same line of the resistant lateral forces, rotations around a building vertical axis may occur. For this reason, the eccentricities between both acting and resisting forces are associated with building torsion. Torsion of buildings is also present when there are eccentricities between the centers of mass (CM) and centers of stiffness (CS).
Given the association of these eccentricities with the action of torsion, the building codes [1-4] use design eccentricities () as a basic design parameter to estimate the effects of torsion in buildings and to design it accordingly. Typically, the design eccentricity is assumed as the sum of a nominal (or natural) eccentricity and an accidental eccentricity .
The natural eccentricity is the theoretical eccentricity that a building has at each story by virtue of its theoretical distributions of both mass and stiffness. Plausible deviations of these nominal distributions of mass and stiffness during a ground motion may cause an additional eccentricity. Variations on mass, material properties or structural element dimensions can cause these deviations. Moreover, some studies suggest that the torsional component of the ground during an earthquake can contribute to the accidental eccentricity. For most of the building dimensions, however, this torsional component is neglected.
As for the accidental eccentricity, design codes [1-3] recommend that its value can be estimated as a proportion () of the building plan dimension () measured along the perpendicular direction of the seismic action. References [1-3] recommend the use of , i.e., . On the other hand, the design code for the City of México [4] specifies an accidental eccentricity that varies with height, according to the following formulas:
|
(1a) | |
|
|
(1b) |
In these formulas, is the accidental eccentricity at the story , is the number of stories of the building, and is the building plan dimension of the story measured along the perpendicular direction of the seismic action.
Accidental torsion has been studied before. For instance, De la Llera y Chopra [5] corroborated the proposed values of the UBC using one-story building models. De la Colina and Almeida [6] concluded that the probability of exceedance of the ductility demands decrease more than 35% in systems designed to account for accidental torsion, with respect to those systems without an accidental-torsion design. Using an analytical solution, Dimova and Alashki [7] concluded that the accidental eccentricity could lead to structural responses 60% larger than those of systems without accidental torsion. Using dynamics tests in actual buildings, Mendoza [8] evaluated three methods to estimate the accidental eccentricity and concluded that in most of the studied cases, the torsional eccentricity is larger than 0.20.
Other studies suggest that the use of accidental eccentricity in seismic design codes is not required. For example, Stathopoulos and Anagnostopoulos [9] concluded that the inclusion of accidental eccentricity in the design does not cause any substantial reduction of ductility demands, in comparison with cases where accidental eccentricity is not included. Moreover, DeBock et al. [10] concluded that accidental-torsion provisions could be removed from seismic design provisions in some cases. In accordance with their findings, Stathopoulos and Anagnostopoulos [9] suggest that design accidental eccentricities should be eliminated or replaced by more effective design procedures. These studies show that the current torsion design provisions based on design eccentricities should be revised and recommend that new design procedures should be proposed and studied.
The main objective of this work is to verify the effectiveness of the proposed simplified seismic accidental-torsion design procedure, to control the ductility demands of beams and columns in building models. The dynamic nonlinear study considers four frame reinforced concrete building models subjected to five firm-soil ground motions with two horizontal components each one. The accidental-torsion design procedure to be evaluated is based on a simple amplification of the seismic effects computed on the associated torsionally balanced (TB) model, to estimate the design strengths of the structural elements of the building exposed to accidental torsion.
2. Accidental-torsion design procedure to be evaluated
Gálvez [11] presented the design proposal to account for seismic accidental torsion. Although the method was initially studied for building systems with no natural eccentricity, it is assumed that the procedure is applicable to systems with because the basic case with is more affected by accidental torsion than systems with [12]. The design proposal is simple and does not need to incorporate any accidental eccentricity. The proposed design method was initially formulated for frame buildings with no less than two frames along each orthogonal direction. The design procedure under scrutiny is described as follows.
First, the building structural model is assumed without accidental torsion. Since in this stage of evaluation only models with are studied, the model is torsionally balanced (TB). In this evaluation, this TB model is also identified as the reference model. If the model had nonzero natural eccentricity (), the corresponding torsionally unbalanced model with no accidental torsion would be the reference model (RM).
Second, a seismic analysis of the reference model (RM) is carried out to estimate the effects (force elements) that the design ground motion causes. A typical linear elastic seismic spectral analysis suffices to estimate the effects in beams and columns caused by the design seismic action.
The design proposal consists in amplifying the mechanical elements (bending moments, axial forces, etc.) computed from the seismic analysis of the reference model to obtain the design strength of the system to withstand accidental torsion. The following equation estimate the element strengths required to cope with accidental torsion. The design values are the amplified values of the effects of the reference model computed for the design seismic action. This amplified effect provides the strength of each structural element of the building model that will be exposed to accidental torsion
|
|
(2) |
where is any effect in the reference model (or TB model when ) caused by the seismic design action. For the purposes of this work, are the bending moments and axial forces at beams and columns of the reference model subjected to the design spectrum.
is an amplification factor by accidental torsion equal to 1.2 [11].
Currently, the application of accidental torsion provisions of building codes [1-4] implies to carry out several analyses varying the design eccentricities and looking for the more critical response. The application of the equation (2) only requires a seismic analysis of one model.
3. Methodology to evaluate the accidental-torsion design proposal
Gálvez [11] based the accidental-torsion design proposal on an elastic study of reinforced concrete frame-building models subjected to a single bi-directional (2D) earthquake ground motion (El Centro, 1940). The evaluation presented in this work pretends to have an extended view of the design proposal by using non-linear responses of four frame, reinforced concrete models subjected to five bidirectional earthquake firm-soil ground motions. Since the critical case corresponds to systems with , this work is also constrained to models without natural eccentricity (i.e., symmetric models). The original work [11] used live loads typical of offices; likewise, this extended evaluation applies to office buildings.
As indicated before, the evaluation of the accidental-eccentricity design proposal rests on the comparison of ductility demands of beams and columns of the building models. Before describing the evaluation methodology, it is important to bear in mind that the accidental-torsion design is not a determinist problem. The variables that define the accidental torsion in a building are random. The methodology used here to evaluate the design proposal, as well as the assessment of the importance of accidental torsion, are based on the following steps:
- 1) For a ground motion intensity (design spectrum), seismic-action effects and ductility demands of both beams and columns are computed for the torsionally balanced reference models. In this study, the models with result to be symmetrical. This step of the methodology establishes the reference ductility demands when accidental torsion is not considered. These ductility demands will be used later to compare with two conditions. The first comparison will be with corresponding models when they have accidental torsion; and the differences between both conditions will reveal the importance of accidental torsion. The second comparison will be with the corresponding models with amplified strength, according with Eq. (2). This second comparison will indicate how the strengthened models (and the design procedure) cope with accidental torsion. As for the seismic-action effects, these will be used in step 3 to define the strength of the structural elements.
- 2) Since the variables that lead to accidental torsion are random, the Monte Carlo method [13] is used to generate a large number of realizations that can occur during a seismic event. In these simulations, the statistical properties of the random variables are incorporated with appropriate probability density functions. The dynamic nonlinear response of each resulting model and ground motion is computed for each realization that simulates accidental torsion. From this collection of simulation results, statistical values are computed for each model and ground motion. In particular, the parameters of interest are the mean, the maximum values and the coefficient of variation (cov) of ductility demands of beams and columns. As anticipated, the simulation of accidental torsion converts the buildings into torsionally unbalanced models. This second step is not required for the evaluation of the design procedure; but it reveals the impact of accidental torsion on the (no strengthened) models.
- 3) All seismic effects at the structural elements, computed as indicated in step 1, are amplified with the factor , using Eq. (2). These amplified effects are used to design both beams and columns, and the resulting model is identified as the model with amplified strength (or resistant), . It is interesting to see that with this simple design procedure, the amplification defined by Eq. (2) can be computed inside the same analysis/design program by defining a load combination with a “load factor” equal to 1.2 applied to the seismic action. According with the accidental-torsion design procedure, the resulting effects of this combination provide the strengths required to cope with the accidental torsion.
- 4) The Monte Carlo method is used again to simulate accidental torsion. This time, the simulations apply to the model with amplified strength (). The results of the simulations provide the new ductility demands of the model . As part of the methodology to evaluate the design procedure, the mean, the maxima, and the coefficient of variation of these ductility demands are computed for the models with simulated accidental torsion. This step is the numerical experimentation of the models by accidental torsion. As indicated before, these statistical values (mean, maxima and coefficient of variation) of the new computed ductility demands are compared with those of the reference models to evaluate the design procedure by accidental torsion.
Random variables
Specific probability density functions (pdf) give the values of the random variables required by the Monte Carlo method [13] to generate each realization. These variables are used to simulate the variations on the structure stiffness and the mass distribution that lead to accidental torsion.
For the research related to this work, it is assumed that the accidental torsion is due to the following random variables: magnitude of dead load, magnitude and position of live load resultant, as well as flexural stiffness of beams and columns.
The probability density functions (pdf) as well as their parameters provide the information to generate each of the random variables. For instance, the pdf’s of the flexural stiffness of the structural elements ( and ) were based on the work by Ramsay et al. [14]. As for the dead-load magnitude, reference [15] was considered. Finally, for the live-load magnitude and its position, the references [2,16-18] provided the information. Table 1 resumes the information required to generate the random variables.
| Variable ID | Model or Level | Random variable | Mean | Std. Dev. | cov | |
|---|---|---|---|---|---|---|
| At offices | Live-load magnitude | Gamma | 122 kg/m2 (1196.4 N/m2) | 35.62 kg/m2 (359.3 N/m2) | 0.292 | |
| At roofs | Live-load magnitude | Gamma | 100 kg/m2 (980.6 N/m2) | 29.20 kg/m2 (286.3 N/m2) | 0.292 | |
| , | All cases | Live-load position | Normal | 0.5 (m) | 0.037 (m) | 0.074 |
| M4S6 and M4R6 | Dead-load magnitude< | Normal | 450 kg/m2 (4413 N/m2) | 45 kg/m2 (441.3 N/m2) | 0.100 | |
| M7S8 and M7R8 | Dead-load magnitude | Normal | 550 kg/m2 (5393.6 N/m2) | 55 kg/m2 (5393.6 N/m2) | 0.100 | |
| All cases | Beam flexural stiffness | Normal | 0.110 | |||
| All cases | Column flexural stiffness | Normal | 0.110 |
Number of simulations
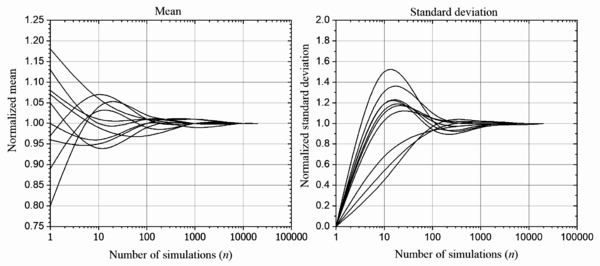
In this work, the number of simulations required to obtain results with a precision required to evaluate the accidental-torsion procedure, was evaluated with a stability analysis of both the mean and the standard deviation of two structural response parameters. Thus, Figure 1 shows both statistical values of the ductility demands of ten beams of the first level of model M4S6, normalized with respect to the corresponding parameters computed for a large number of simulations (). Each line in the figure represents a different beam.
To illustrate this criterion to select the number of simulations, the following steps were carried out. First, the mean and standard deviation of ductility demands for the ten first-level selected beams of model M4S6 were computed. These computations were applied to different groups with sample sizes . Then, the parameters for each group were normalized with respect to the parameters for . These normalized values are shown in Figure 1, as a function of the group size . It is clear that the statistical normalized values become stable as the group size increases. Since for , the variation of the parameters does not change significantly, the number of simulations to use in this study was set equal to 10,000.
The structural-response parameters selected for the evaluation of the accidental-torsion design procedure were the ductility demands (moment-curvature) at the ends of both beams and columns of the structural models described in the following section. The computer program used to perform the nonlinear dynamic analyses was the program Canny-E [19]. This analysis program was combined with a Matlab program to carry out the simulations, according with the Monte Carlo method.
4. Building structural models
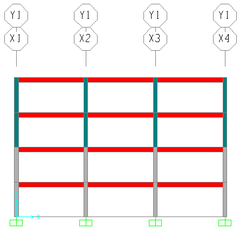
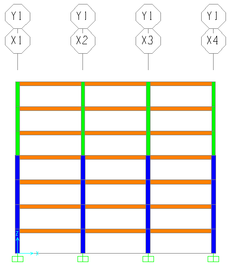
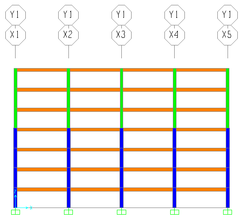
For the evaluation of the design procedure proposed by Gálvez [11], four reinforced concrete frame building models were considered in this study (Figures 2, 3, 4 and 5). These models are representative of office buildings with 4 and 7 stories and story heights equal to 3 m. For all models, the slabs were assumed as in-plane rigid diaphragms. As for the material properties, the following concrete parameters were selected: kg/cm2 (2942 N/cm2) and kg/cm2 (2’377,985 N/cm2). Since the multi-spring model was used for the columns [20], a yield stress value for the steel reinforcement (bars) was required. In this case, the value of kg/cm2 (41,187.9 N/cm2) was used for all columns.
|
|
| Figure 2. Model M4S6 and its frame Y1 | |
|
|
| Figure 3. Model M4R6 and its frame Y1 | |
|
|
| Figure 4. Model M7S8 and its frame Y1 | |
|
|
| Figure 5. Model M7R8 and its frame Y1 | |
Two models had square plan and two rectangular plan with aspect ratio equal to 2:1. For all the four-story models the distance between columns in each frame was equal to 6 m; while for the seven-story models de distance was equal to 8 m. Table 2 summarizes the model plan dimensions, the dimensions of the element cross sections, the nominal dead load values for each model and the initial modal vibration periods. Each model is identified with a four-character label. The first number indicates the number of stories and the third digit indicates a square plan (S) or a rectangular plan (R). The last number indicates the distance in meters between columns for each frame.
| Model and periods | Plan dimensions and bay spans (m) | Column cross sections (m) | Beam cross sections (m) | Dead load |
|---|---|---|---|---|
| M4S6
= 0.85 s. = 0.85 s. = 0.65 s. |
Along direction: 18 Along direction: 18
|
Stories 1-2: 0.40 0.40
|
All levels: 0.20 0.40 | All floors: 450 kg/m2 (4,413 N/m2) |
| M4R6
= 0.81 s. = 0.86 s. = 0.67 s. |
Along direction: 24 Along direction: 12
|
Stories 1-2: 0.40 0.40
| ||
| M7S8
= 1.54 s. = 1.54 s. = 1.19 s. |
Along direction: 24 Along direction: 24
|
Stories 1-4: 0.55 0.55
|
All levels: 0.25 0.50 | All floors: 550 kg/m2 (5,394 N/m2) |
| M7R8
= 1.43 s. = 1.54 s. = 1.22 s. |
Along direction: 32 Along direction: 16
|
Stories 1-4: 0.55 0.55
|
For analysis, all elements of the reference model (RM) (torsionally balanced model when ) were assumed nonlinear. For design, a seismic design spectrum reduced with a response modification coefficient and an overstrength factor was used, as suggested by the ASCE 7-16 [2]. For the design of beams and columns, the earthquake bidirectional effects were taken into account by adding the 100% of the effects of one ground motion direction plus the 30% of the effects of the orthogonal ground motion direction.
The yield bending moment of beams was assumed to be equal to the maximum bending moment of that beam computed with the reduced seismic design spectrum. The non-linear behavior of beams was simulated in the Canny-E program with the concentrated modified Clough model [21] at the element ends. The central part of the beam elements was assumed linear and elastic. It is known that the modified Clough model takes into account the more important features of the non-linear flexural behavior of beams, such as the stiffness reduction [22].
The design forces for columns were computed with a seismic design spectrum with and . Since the reference models have no torsion, the design of columns does not initially include any torsion effect. Moreover, both load and reduction factors were equal to 1.0. As indicated in Table 2, two different column cross-section dimensions were used for each building model. Three different types of columns were designed for a building plan: corner columns, edge columns and central columns. For the four-story models, column sections were equally designed for stories 1 and 2, so that these two stories had 3 different designs. A second group consisted of columns designed for stories 3 and 4. For the seven-story buildings the first group included columns for stories 1-4, while the second group consist of columns designed for stories 5-7.
For the nonlinear analyses, each column was idealized with three longitudinal zones: one elastic zone in the middle and concentrated multi-spring elements at their ends. These elements model the nonlinear behavior of both the concrete and the reinforcement and, therefore, the nonlinear assemblies take into account the interaction of axial load and bending moments at the column ends [22-23]. With the arrangement of reinforcement for each column the multi-spring assemblies were defined.
5. Seismic records
In the work by Gálvez [11], wherein the accidental-torsion design method was proposed, the amplification factor by accidental torsion was obtained using linear analyses and one bi-directional ground motion (1940 El Centro earthquake). In this work such design proposal is revised using five bi-directional firm-soil ground motions along with nonlinear analyses. The seismic records were selected taking into account the recommendations of the Section 2.62 of the FEMA-273 guidelines [24]. Table 3 summarizes the main characteristics of the ground motions and Figure 6 illustrates the acceleration response spectra of each component computed for a damping ratio . Figure 6 also shows both the elastic design spectrum and the reduced design spectrum ( and ). The design spectrum was obtained with the recommendations of Ref. [2] for a firm soil.
| Number | Country | Date (dd/mm/yyyy) | Earthquake | Station | Magnitude |
|---|---|---|---|---|---|
| 1 | USA | 17/10/1989 | Loma Prieta | Corralitos | 7.0 |
| 2 | México | 19/09/1985 | Michoacán | C. U. | 8.1 |
| 3 | México | 19/09/2017 | Morelos | Barros Sierra | 7.1 |
| 4 | Japan | 16/01/1995 | Kobe | Chihaya | 6.9 |
| 5 | Chile | 03/03/1985 | Valparaíso | Valparaíso | 7.8 |
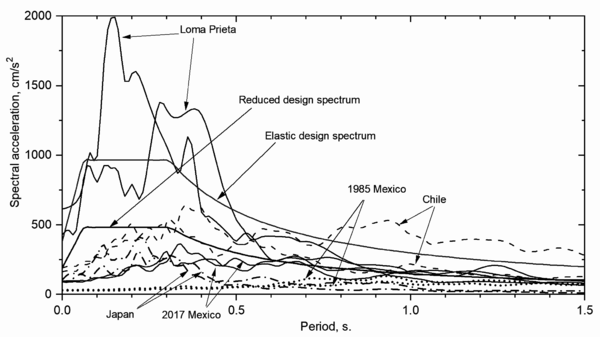
|
| Figure 6. Acceleration response spectra for each ground motion and design spectra |
For the evaluation of the design proposal using only one building design for all ground motions, the earthquake records were scaled. In this work, the ordinate of the larger seismic component (of each ground motion pair) was adjusted to have the same ordinate of the elastic acceleration design spectrum, at the model first period of vibration. The perpendicular horizontal component (the smaller component) was scaled with the same factor used for the larger component. In this way each ground motion pair was scaled with the same scale factor.
Thus, the scale factor for each ground motion pair is given by the following equation, where is the spectral ordinate of the elastic design spectrum and is the acceleration spectral ordinate of the largest horizontal ground motion components. Both ordinates are evaluated at the (initial) fundamental period of vibration T of the analyzed model. This is a simple way to adjust the intensity of the ground motions to that of the elastic design spectrum
|
|
(3) |
This is a practical and simple way of scaling the earthquake records. For the purposes of the work, this scaling procedure seems to be reasonable.
6. Results and discussion
According to the methodology presented above, the building models were analyzed for three different conditions. The first condition corresponds to the reference model (RM), which is torsionally balanced (TB) due to its natural eccentricity is equal to zero (). For this condition, no accidental torsion was included, therefore only one case was analyzed for each model and ground motion. This analysis provides the levels of ductility demands when accidental torsion is not present. This initial condition is identified as the condition a.
The second condition corresponds to similar building models of the previous condition but with accidental torsion simulated with the Monte Carlo method. It is important to realize that the models of this second condition are not strictly equal to the models of condition a. For this second condition (condition b), the mass and stiffness of the models vary with respect to the mean values used for models of condition a because of the random nature of both variables. Since each realization of the simulation process represents a building configuration when the earthquake ground motion occurs, the results consist of N different analysis sets. For a comparison results of condition b with those of condition a, it is convenient a statistical treatment of the results of condition b. It is not possible a simple comparison of the deterministic values of the condition a with the random results of the condition b. Some useful parameters for these comparisons (in terms of ductility demands) are the mean, the maxima, and the coefficient of variation (cov). This comparison allows to compute the models ductility demand increments due to the accidental torsion.
The third condition (condition c) corresponds to models with statistically similar nominal values of stiffness and mass of the previous condition (b) but, with an increasing of the models strength in accordance with the simplified torsion design procedure that is analyzed in this paper. Equation (2) leads to similar structural models with amplified strength (). According to the design proposal that is evaluated in this work, the strength increment will cope with the accidental torsion; therefore, it is expected that the models in this condition c will undergo ductility demands of the same order than those computed for the condition a. Again, a simple comparison between conditions a and c is not simple because in the first case the results consist of a deterministic value for each model and ground motion, while in the condition c, N analysis sets result.
6.1. Condition a: Reference Models (RM)
In this subsection, the ductility demands computed for beams and columns are presented for the reference models described in Section 4. Table 4 shows the ductility demands of eight beams along the direction and eight beams along the direction. For space limit in this work, only beams of levels 1 (L1) and 2 (L2) of models M4S6 (square plan) and M4R6 (rectangular plan) are listed in Table 4. Table 5 lists the ductility demands of beams for levels 1 and 4 of models M7S8 y M7R8. The identification number of each earthquake ground motion is indicated in Table 3.
Table 4 shows that for beams of the four-story models, ductility demands varied between 1.00 and 3.60. As for the ductility-demand averages, taken with respect to the ground motions, the values oscillated between 1.74 and 2.90. These values seems reasonable for the values used to reduce the ordinates of the elastic design spectrum (response modification coefficient and overstrength factor ). Table 5 shows that beam ductility demands for the seven-story models varied in a wider range: between 0.86 and 4.31. However, average values, taken with respect to the ground motions, varied within a similar range as in the case of the four-story models, between 1.78 and 3.23. A value smaller than 1.0 indicates that the element response remained linear.
| Model | Beam type | Location and orientation of beams | Ground motion 1 | Ground motion 2 | Ground motion 3 | Ground motion 4 | Ground motion 5 | Average ductility demand, with respect to ground motions | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L1 | L2 | L1 | L2 | L1 | L2 | L1 | L2 | L1 | L2 | L1 | L2 | |||
| M4S6 | Edge | X1: Y1 - Y2 | 2.72 | 2.60 | 2.90 | 3.27 | 2.09 | 2.36 | 1.70 | 2.57 | 1.70 | 2.57 | 2.22 | 2.67 |
| X1: Y2 - Y3 | 2.93 | 2.86 | 3.23 | 3.57 | 2.31 | 2.57 | 1.94 | 2.74 | 1.94 | 2.74 | 2.47 | 2.90 | ||
| Central | X2: Y1 - Y2 | 2.66 | 2.60 | 2.93 | 3.29 | 2.01 | 2.35 | 1.75 | 2.57 | 1.75 | 2.57 | 2.22 | 2.68 | |
| X2: Y2 - Y3 | 2.84 | 2.86 | 3.23 | 3.60 | 2.32 | 2.55 | 1.97 | 2.74 | 1.97 | 2.74 | 2.47 | 2.90 | ||
| Edge | Y1: X1 - X2 | 3.02 | 2.15 | 2.66 | 2.75 | 2.01 | 2.09 | 1.35 | 1.07 | 1.35 | 1.07 | 2.08 | 1.83 | |
| Y1: X2 - X3 | 3.48 | 2.20 | 2.66 | 2.76 | 1.96 | 2.11 | 1.52 | 1.14 | 1.52 | 1.14 | 2.23 | 1.87 | ||
| Central | Y2: X1 - X2 | 3.10 | 2.10 | 2.67 | 2.73 | 1.88 | 2.10 | 1.33 | 1.05 | 1.33 | 1.05 | 2.06 | 1.81 | |
| Y2: X2 - X3 | 3.55 | 2.24 | 2.68 | 2.74 | 1.95 | 2.08 | 1.50 | 1.13 | 1.50 | 1.13 | 2.24 | 1.86 | ||
| M4R6 | Edge | X1: Y1 - Y2 | 1.85 | 1.42 | 2.85 | 3.32 | 2.09 | 2.35 | 1.66 | 2.44 | 2.62 | 2.92 | 2.21 | 2.49 |
| X1: Y2 - Y3 | 2.08 | 1.73 | 3.14 | 3.57 | 2.30 | 2.57 | 1.78 | 2.67 | 2.58 | 2.86 | 2.38 | 2.68 | ||
| Central | X3: Y1 - Y2 | 1.95 | 1.40 | 2.88 | 3.32 | 2.15 | 2.31 | 1.67 | 2.40 | 2.55 | 2.91 | 2.24 | 2.47 | |
| X3: Y2 - Y3 | 2.16 | 1.75 | 3.11 | 3.57 | 2.34 | 2.65 | 1.82 | 2.69 | 2.55 | 2.77 | 2.40 | 2.69 | ||
| Edge | Y1: X1 - X2 | 2.08 | 2.21 | 2.60 | 2.70 | 1.90 | 1.86 | 1.41 | 1.00 | 1.03 | 1.02 | 1.80 | 1.76 | |
| Y1: X2 - X3 | 2.44 | 2.45 | 2.66 | 2.72 | 1.96 | 1.90 | 1.53 | 1.11 | 1.02 | 1.01 | 1.92 | 1.84 | ||
| Central | Y2: X1 - X2 | 1.99 | 2.12 | 2.63 | 2.67 | 1.90 | 1.87 | 1.40 | 1.00 | 1.06 | 1.06 | 1.80 | 1.74 | |
| Y2: X2 - X3 | 2.46 | 2.43 | 2.72 | 2.74 | 1.92 | 1.90 | 1.51 | 1.11 | 1.05 | 1.04 | 1.93 | 1.84 | ||
| Model | Beam type | Location and orientation of beams | Ground motion 1 | Ground motion 2 | Ground motion 3 | Ground motion 4 | Ground motion 5 | Average ductility demand, with respect to ground motions | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L1 | L4 | L1 | L4 | L1 | L4 | L1 | L4 | L1 | L4 | L1 | L4 | |||
| M7S8 | Edge | X1: Y1 - Y2 | 3.50 | 3.61 | 2.41 | 2.60 | 1.37 | 2.13 | 2.04 | 3.76 | 1.62 | 1.96 | 2.19 | 2.81 |
| X1: Y2 - Y3 | 3.64 | 3.53 | 2.45 | 2.83 | 1.38 | 2.29 | 2.01 | 3.84 | 1.73 | 2.05 | 2.24 | 2.91 | ||
| Central | X2: Y1 - Y2 | 3.52 | 3.53 | 2.44 | 2.59 | 1.34 | 2.12 | 2.00 | 3.72 | 1.61 | 1.93 | 2.18 | 2.78 | |
| X2: Y2 - Y3 | 3.65 | 3.55 | 2.46 | 2.81 | 1.36 | 2.28 | 2.03 | 3.87 | 1.73 | 2.04 | 2.25 | 2.91 | ||
| Edge | Y1: X1 - X2 | 3.24 | 2.54 | 2.75 | 2.95 | 2.13 | 2.27 | 2.15 | 2.09 | 1.11 | 0.97 | 2.28 | 2.16 | |
| Y1: X2 - X3 | 3.28 | 2.64 | 2.89 | 2.97 | 2.24 | 2.46 | 2.19 | 2.17 | 1.10 | 0.96 | 2.34 | 2.24 | ||
| Central | Y2: X1 - X2 | 3.28 | 2.42 | 2.72 | 2.95 | 2.12 | 2.25 | 2.14 | 2.05 | 1.12 | 1.01 | 2.28 | 2.14 | |
| Y2: X2 - X3 | 3.31 | 2.67 | 2.87 | 2.96 | 2.23 | 2.44 | 2.19 | 2.18 | 1.11 | 1.02 | 2.34 | 2.25 | ||
| M7R8 | Edge | X1: Y1 - Y2 | 2.94 | 2.66 | 2.40 | 1.86 | 2.21 | 2.24 | 1.58 | 1.73 | 0.92 | 0.87 | 2.01 | 1.87 |
| X1: Y2 - Y3 | 2.79 | 2.55 | 2.34 | 1.73 | 2.19 | 2.24 | 1.56 | 1.70 | 0.88 | 0.82 | 1.95 | 1.81 | ||
| Central | X3: Y1 - Y2 | 2.96 | 2.61 | 2.39 | 1.82 | 2.21 | 2.26 | 1.51 | 1.75 | 0.93 | 0.91 | 2.00 | 1.87 | |
| X3: Y2 - Y3 | 2.83 | 2.41 | 2.33 | 1.68 | 2.20 | 2.25 | 1.53 | 1.70 | 0.89 | 0.86 | 1.96 | 1.78 | ||
| Edge | Y1: X1 - X2 | 2.97 | 2.63 | 2.38 | 1.81 | 2.30 | 2.46 | 1.60 | 1.88 | 0.92 | 0.89 | 2.03 | 1.93 | |
| Y1: X2 - X3 | 3.22 | 2.77 | 2.58 | 1.94 | 2.56 | 2.75 | 1.76 | 2.11 | 0.99 | 0.98 | 2.22 | 2.11 | ||
| Central | Y2: X1 - X2 | 3.35 | 3.29 | 3.31 | 3.78 | 1.41 | 2.17 | 2.03 | 4.17 | 1.49 | 1.97 | 2.32 | 3.08 | |
| Y2: X2 - X3 | 3.41 | 3.34 | 3.45 | 3.87 | 1.56 | 2.43 | 2.14 | 4.31 | 1.67 | 2.20 | 2.45 | 3.23 | ||
Tables 4 and 5 also suggest that the average ductility demands for beams of square-plan models were similar to those of rectangular-plan models.
As for columns, Table 6 shows ductility demands of six first-story columns of the four-story models (M4S6 and M4R6) subjected to the five ground motions. Similarly, Table 7 shows the information of the first-story columns corresponding to the seven-story models (M7S8 and M7R8). Table 6 shows that ductility demands of the first-story columns for the four-story models varied between 0.75 and 2.50. The ductility-demand averages, taken with respect to the ground motions, oscillated between 1.13 and 1.57. Table 7 shows that ductility demands of the first-story columns for the seven-story models varied within a broader range: between 0.53 and 3.74. The average values, taken with respect to the ground motions, varied between 1.46 and 2.15.
| Model | Column type | Location of columns | Ground motion 1 | Ground motion 2 | Ground motion 3 | Ground motion 4 | Ground motion 5 | Average ductility demand, with respect to ground motions |
|---|---|---|---|---|---|---|---|---|
| M4S6 | Corner | X1 - Y1 | 2.26 | 1.85 | 1.29 | 1.02 | s0.80 | 1.44 |
| X4 - Y4 | 2.15 | 1.82 | 1.49 | 1.03 | s0.78 | 1.45 | ||
| Edge | X1 - Y2 | 2.50 | 1.84 | 1.36 | 1.08 | s0.81 | 1.52 | |
| X2 - Y1 | 2.36 | 2.02 | 1.30 | 1.09 | s0.82 | 1.52 | ||
| Central | X2 - Y2 | 2.33 | 1.96 | 1.53 | 1.20 | s0.84 | 1.57 | |
| X3 - Y3 | 2.33 | 1.94 | 1.50 | 1.19 | >0.85 | 1.56 | ||
| M4R6 | Corner | X1 - Y1 | 1.38 | 1.45 | 1.27 | 0.75 | s0.88 | 1.15 |
| X5 - Y3 | 1.16 | 1.58 | 1.29 | 0.79 | s0.94 | 1.15 | ||
| Edge | X1 - Y2 | 1.53 | 1.37 | 1.27 | 0.77 | s0.87 | 1.16 | |
| X3 - Y1 | 1.42 | 1.62 | 1.44 | 0.87 | s0.93 | 1.26 | ||
| Central | X2 - Y2 | 1.36 | 1.41 | 1.24 | 0.76 | 0.90 | 1.13 | |
| X3 - Y2 | 1.41 | 1.62 | 1.43 | 0.87 | 0.93 | 1.25 |
| Model | Column type | Location of columns | Ground motion 1 | Ground motion 2 | Ground motion 3 | Ground motion 4 | Ground motion 5 | Average ductility demand, with respect to ground motions |
|---|---|---|---|---|---|---|---|---|
| M7S8 | Corner | X1 - Y1 | 3.55 | 2.84 | 1.40 | 1.47 | 0.67 | 1.99 |
| X4 - Y4 | 3.32 | 3.74 | 1.56 | 1.30 | 0.82 | 2.15 | ||
| Edge | X1 - Y2 | 3.58 | 3.08 | 1.64 | 1.42 | 0.67 | 2.08 | |
| X2 - Y1 | 3.44 | 3.05 | 1.37 | 1.46 | 0.73 | 2.01 | ||
| Central | X2 - Y2 | 3.52 | 3.42 | 1.61 | 1.41 | 0.77 | 2.15 | |
| X3 - Y3 | 3.50 | 3.38 | 1.57 | 1.43 | 0.77 | 2.13 | ||
| M7R8 | Corner | X1 - Y1 | 2.55 | 1.57 | 1.64 | 1.02 | 0.53 | 1.46 |
| X5 - Y3 | 2.37 | 1.71 | 1.79 | 1.02 | 0.62 | 1.50 | ||
| Edge | X1 - Y2 | 2.62 | 1.61 | 1.92 | 1.05 | 0.53 | 1.55 | |
| X3 - Y1 | 2.54 | 1.65 | 1.86 | 1.07 | 0.62 | 1.55 | ||
| Central | X2 - Y2 | 2.51 | 1.53 | 1.89 | 1.02 | 0.54 | 1.50 | |
| X3 - Y2 | 2.55 | 1.65 | 1.87 | 1.07 | 0.61 | 1.55 |
A comparison between the reference models indicates that ductility demands of columns resulted smaller than ductility demands of beams. Column ductility demands resulted approximately equal to 0.7 times the beam ductility demands
Tables 6 and 7 also show that, the average ductility demands (with respect to the ground motions) for columns of rectangular-plan models resulted between 20% and 30% smaller than the values for square-plan models.
A statistical analysis of the ductility demands of beams and columns (Tables 4 and 5), taken with respect to the ground motions, show that the coefficient of variation (cov) of these demands resulted approximately between 0.20 and 0.35. This result shows a small effect of the ground motions on the beam ductility demands. For columns, however, the coefficients of variation reached values up to 0.78.
6.2. Condition b: models with accidental torsion
In this condition, the nominal models analyzed in the previous subsection were exposed to accidental torsion by varying both the distribution of mass and the variation of stiffness for beams and columns, according to the probability density functions described in subsection 3.1. A total of 10,000 realizations were computed for each building model. For each model and ground motion, the following statistical parameters for beams and columns are reported: mean, maxima and coefficient of variation. These statistical values were evaluated for each case (model and ground motion), i.e., the statistical values were taken with respect to the number of realizations of each model and earthquake. Therefore, the statistical values reported for each case show the effect of accidental torsion.
Table 8 shows that the average ductility demand in beams at levels 1 and 2 of model M4S6, taken with respect to the number of realizations, oscillated between 0.94 and 3.60. However, the maximum values varied between 1.56 and 5.22. The coefficients of variation stayed between 0.10 and 0.14 for each earthquake. This table shows the results for the same beams listed before for the condition a (table 4); this time however, the ductility demands reflect the effect of the accidental torsion. It is clear that accidental torsion can increase or decrease ductility demands of structural elements; but, the mean value stays close to the ductility demand values of the corresponding elements of models without accidental torsion. Although beam ductility-demand averages are the same for the cases with and without accidental torsion, beam ductility demands caused by accidental torsion can result 50%-75% larger than those for models without accidental torsion, for the same ground motion.
The corresponding statistical parameters of beams computed for the models M4R6, M7S8 and M7R8 (not shown here) displayed similar values as those presented for the model M4S6.
Table 9 shows the same statistical parameters (mean, maxima and coefficient of variation) for the columns of the first story of model M4S6 in the condition a (Table 6); this time however, the results are for the condition b, which reflects the effect of the accidental torsion. This table shows that for the models exposed to accidental torsion, ductility-demand means of the first-story columns oscillated between 0.85 and 2.42. The same table shows that the ductility-demand maxima varied between 1.21 and 3.22. The coefficient of variation, among earthquakes, ranged between 0.07 and 0.16. Again, column ductility-demand averages result the same for the cases with and without accidental torsion; but column ductility demands caused by accidental torsion can result 50%-75% larger than those for models without accidental torsion, computed for the same ground motion.
| Level | Beam type | Beam location | Ground motion 1 | Ground motion 2 | Ground motion 3 | Ground motion 4 | Ground motion 5 | All ground motions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Max | cov | Mean | Max | cov | Mean | Max | cov | Mean | Max | cov | Mean | Max | cov | Mean | Max | |||
| 1 | Edge | X1: Y1 - Y2 | 2.58 | 3.57 | 0.12 | 2.94 | 4.40 | 0.11 | 2.10 | 2.94 | 0.12 | 1.71 | 2.43 | 0.11 | 2.44 | 3.34 | 0.12 | 2.35 | 4.40 |
| X1: Y2 - Y3 | 2.83 | 4.08 | 0.12 | 3.26 | 4.52 | 0.12 | 2.32 | 3.37 | 0.11 | 1.88 | 2.73 | 0.12 | 2.55 | 3.51 | 0.11 | 2.57 | 4.52 | ||
| Central | X2: Y1 - Y2 | 2.53 | 3.46 | 0.12 | 2.96 | 4.25 | 0.12 | 2.10 | 2.93 | 0.11 | 1.72 | 2.44 | 0.12 | 2.44 | 3.49 | 0.11 | 2.35 | 4.25 | |
| X2: Y2 - Y3 | 2.78 | 3.88 | 0.12 | 3.28 | 4.44 | 0.12 | 2.33 | 3.11 | 0.11 | 1.90 | 2.72 | 0.12 | 2.57 | 3.44 | 0.11 | 2.57 | 4.44 | ||
| Edge | Y1: X1 - X2 | 3.11 | 4.35 | 0.13 | 2.63 | 3.90 | 0.11 | 1.98 | 2.77 | 0.12 | 1.47 | 2.16 | 0.13 | 0.94 | 1.56 | 0.11 | 2.03 | 4.35 | |
| Y1: X2 - X3 | 3.45 | 5.22 | 0.13 | 2.69 | 3.75 | 0.11 | 1.99 | 2.82 | 0.12 | 1.55 | 2.24 | 0.13 | 0.96 | 1.66 | 0.12 | 2.13 | 5.22 | ||
| Central | Y2: X1 - X2 | 3.14 | 4.61 | 0.12 | 2.63 | 3.55 | 0.11 | 1.98 | 2.97 | 0.12 | 1.46 | 2.27 | 0.14 | 0.95 | 1.71 | 0.11 | 2.03 | 4.61 | |
| Y2: X2 - X3 | 3.51 | 5.05 | 0.13 | 2.71 | 3.61 | 0.11 | 1.99 | 3.03 | 0.13 | 1.53 | 2.20 | 0.13 | 0.96 | 1.69 | 0.12 | 2.14 | 5.05 | ||
| 2 | Edge | X1: Y1 - Y2 | 2.58 | 3.71 | 0.12 | 3.26 | 4.45 | 0.11 | 2.39 | 3.40 | 0.12 | 2.42 | 3.27 | 0.11 | 2.51 | 3.38 | 0.11 | 2.63 | 4.45 |
| X1: Y2 - Y3 | 2.78 | 4.12 | 0.13 | 3.60 | 4.94 | 0.11 | 2.64 | 3.73 | 0.12 | 2.69 | 3.74 | 0.11 | 2.66 | 3.71 | 0.11 | 2.87 | 4.94 | ||
| Central | X2: Y1 - Y2 | 2.57 | 3.68 | 0.12 | 3.27 | 4.43 | 0.11 | 2.38 | 3.39 | 0.11 | 2.41 | 3.32 | 0.11 | 2.53 | 3.57 | 0.11 | 2.63 | 4.43 | |
| X2: Y2 - Y3 | 2.78 | 3.83 | 0.13 | 3.60 | 4.95 | 0.11 | 2.59 | 3.63 | 0.12 | 2.66 | 3.63 | 0.11 | 2.65 | 3.71 | 0.11 | 2.86 | 4.95 | ||
| Edge | Y1: X1 - X2 | 2.05 | 2.82 | 0.11 | 2.71 | 3.69 | 0.11 | 2.11 | 3.52 | 0.13 | 1.16 | 1.69 | 0.13 | 1.02 | 1.59 | 0.12 | 1.81 | 3.69 | |
| Y1: X2 - X3 | 2.23 | 3.03 | 0.11 | 2.73 | 3.74 | 0.11 | 2.10 | 3.28 | 0.14 | 1.21 | 1.85 | 0.12 | 1.03 | 1.92 | 0.14 | 1.86 | 3.74 | ||
| Central | Y2: X1 - X2 | 2.06 | 3.28 | 0.12 | 2.71 | 3.76 | 0.11 | 2.13 | 3.66 | 0.14 | 1.14 | 1.81 | 0.13 | 1.05 | 1.74 | 0.13 | 1.82 | 3.76 | |
| Y2: X2 - X3 | 2.25 | 3.32 | 0.12 | 2.75 | 3.67 | 0.11 | 2.10 | 3.42 | 0.14 | 1.19 | 1.82 | 0.12 | 1.03 | 1.81 | 0.14 | 1.86 | 3.67 | ||
| Column type | Location | Ground motion 1 | Ground motion 2 | Ground motion 3 | Ground motion 4 | Ground motion 5 | All ground motions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Max | cov | Mean | Max | cov | Mean | Max | cov | Mean | Max | cov | Mean | Max | cov | Mean | Max | ||
| Corner | X1 - Y1 | 2.28 | 2.98 | 0.08 | 1.84 | 2.46 | 0.11 | 1.37 | 2.43 | 0.16 | 1.09 | 1.47 | 0.14 | 0.85 | 1.21 | 0.10 | 1.49 | 2.98 |
| X4 - Y4 | 2.09 | 2.87 | 0.10 | 1.86 | 2.67 | 0.11 | 1.53 | 2.12 | 0.08 | 1.11 | 1.57 | 0.13 | 0.90 | 1.38 | 0.14 | 1.50 | 2.87 | |
| Borde | X1 - Y2 | 2.42 | 3.20 | 0.09 | 1.84 | 2.43 | 0.11 | 1.47 | 2.41 | 0.12 | 1.15 | 1.57 | 0.13 | 0.88 | 1.36 | 0.12 | 1.55 | 3.20 |
| X2 - Y1 | 2.40 | 3.01 | 0.07 | 2.02 | 2.70 | 0.11 | 1.38 | 2.74 | 0.16 | 1.17 | 1.56 | 0.12 | 0.90 | 1.27 | 0.10 | 1.57 | 3.01 | |
| Central | X2 - Y2 | 2.34 | 3.03 | 0.08 | 1.96 | 2.56 | 0.10 | 1.56 | 2.50 | 0.11 | 1.29 | 1.75 | 0.13 | 0.93 | 1.38 | 0.13 | 1.62 | 3.03 |
| X3 - Y3 | 2.33 | 3.22 | 0.08 | 1.95 | 2.65 | 0.10 | 1.54 | 2.53 | 0.12 | 1.28 | 1.75 | 0.13 | 0.93 | 1.32 | 0.12 | 1.61 | 3.22 | |
6.3. Condition c: Models with both accidental torsion and amplified strength ()6.3. Condition c: Models with both accidental torsion and amplified strength (
M
A
R
{\textstyle {\mathit {\boldsymbol {M}}} {\mathit {\boldsymbol {AR}}}}
)
Ductility demands of the same nominal models studied before, but with amplified strength according with Eq. (2), are presented in this subsection. The strengthened models have accidental torsion (Section 3) and they are exposed to the same earthquakes (and with the same intensity) of Section 5. Table 10 shows the statistical ductility-demand parameters (mean, standard deviation and coefficient of variation) described before. Table 10 shows these parameters for the same beams of levels 1 and 2 of the model M4S6. This time, the results also correspond to models with accidental torsion but they have been strengthened according to the design proposal that is evaluated.
Table 10 shows that the average ductility demands for beams of model M4S6 under the condition c varied between 0.78 and 2.95. The ductility-demand maxima oscillated between 1.15 and 4.25. The coefficients of variation ranged between 0.09 and 0.15. It is clear, by comparing beam ductility demands for conditions b (Table 8) and c (Table 10) that the amplification with Eq. (2) reduces both the mean values and the maximum values. This reduction of ductility demands is close to the 20%. of the demands for the elements of systems wherein the design procedure is not applied.
Table 11 shows the ductility-demand statistical parameters of the same first-story columns of model M4S6 (Table 9), this time under condition c (accidental torsion and amplified strength). This table indicates that the ductility-demand averages ranged between 0.78 and 1.87. Similarly, the maxima varied between 1.04 and 2.53 for the columns in condition c. The coefficients of variation varied between 0.08 and 0.18. Again, the application of the accidental-torsion design procedure reduced the ductility demands in about the 20% with respect to the corresponding columns of the same model under condition b.
| Level | Beam type | Beam location | Ground motion 1 | Ground motion 2 | Ground motion 3 | Ground motion 4 | Ground motion 5 | All ground motions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Max | cov | Mean | Max | cov | Mean | Max | cov | Mean | Max | cov | Mean | Max | cov | Mean | Max | |||
| 1 | Edge | X1: Y1 - Y2 | 2.18 | 3.15 | 0.12 | 2.40 | 3.50 | 0.12 | 1.88 | 2.78 | 0.13 | 1.61 | 2.28 | 0.11 | 2.11 | 3.01 | 0.12 | 2.04 | 3.50 |
| X1: Y2 - Y3 | 2.45 | 3.49 | 0.11 | 2.65 | 3.76 | 0.12 | 1.99 | 2.78 | 0.11 | 1.75 | 2.53 | 0.12 | 2.29 | 3.33 | 0.13 | 2.23 | 3.76 | ||
| Central | X2: Y1 - Y2 | 2.17 | 2.94 | 0.12 | 2.41 | 3.63 | 0.12 | 1.89 | 2.81 | 0.14 | 1.61 | 2.39 | 0.12 | 2.12 | 3.02 | 0.12 | 2.04 | 3.63 | |
| X2: Y2 - Y3 | 2.43 | 3.40 | 0.11 | 2.67 | 3.74 | 0.12 | 2.00 | 2.75 | 0.12 | 1.77 | 2.54 | 0.12 | 2.30 | 3.49 | 0.14 | 2.23 | 3.74 | ||
| Edge | Y1: X1 - X2 | 2.15 | 3.18 | 0.14 | 2.17 | 3.12 | 0.12 | 1.70 | 2.45 | 0.12 | 1.31 | 1.82 | 0.12 | 0.78 | 1.15 | 0.10 | 1.62 | 3.18 | |
| Y1: X2 - X3 | 2.35 | 3.82 | 0.15 | 2.20 | 3.02 | 0.12 | 1.69 | 2.39 | 0.12 | 1.42 | 1.97 | 0.11 | 0.80 | 1.29 | 0.10 | 1.69 | 3.82 | ||
| Central | Y2: X1 - X2 | 2.18 | 3.38 | 0.14 | 2.17 | 2.94 | 0.11 | 1.68 | 2.32 | 0.11 | 1.29 | 1.82 | 0.12 | 0.79 | 1.20 | 0.10 | 1.62 | 3.38 | |
| Y2: X2 - X3 | 2.40 | 3.52 | 0.15 | 2.21 | 2.98 | 0.11 | 1.66 | 2.37 | 0.12 | 1.39 | 1.99 | 0.12 | 0.80 | 1.31 | 0.10 | 1.69 | 3.52 | ||
| 2 | Edge | X1: Y1 - Y2 | 2.25 | 3.16 | 0.12 | 2.65 | 3.66 | 0.12 | 2.13 | 3.40 | 0.14 | 2.13 | 2.99 | 0.11 | 2.13 | 3.09 | 0.12 | 2.26 | 3.66 |
| X1: Y2 - Y3 | 2.53 | 3.65 | 0.11 | 2.95 | 4.25 | 0.11 | 2.22 | 3.34 | 0.12 | 2.37 | 3.19 | 0.11 | 2.33 | 3.43 | 0.13 | 2.48 | 4.25 | ||
| Central | X2: Y1 - Y2 | 2.23 | 3.22 | 0.12 | 2.67 | 3.64 | 0.11 | 2.13 | 3.14 | 0.14 | 2.14 | 2.93 | 0.11 | 2.14 | 2.99 | 0.12 | 2.26 | 3.64 | |
| X2: Y2 - Y3 | 2.49 | 3.60 | 0.12 | 2.93 | 4.14 | 0.11 | 2.20 | 3.05 | 0.13 | 2.35 | 3.15 | 0.11 | 2.32 | 3.41 | 0.13 | 2.46 | 4.14 | ||
| Edge | Y1: X1 - X2 | 1.59 | 2.20 | 0.12 | 2.19 | 2.96 | 0.12 | 1.67 | 2.41 | 0.14 | 0.99 | 1.41 | 0.10 | 0.84 | 1.16 | 0.09 | 1.46 | 2.96 | |
| Y1: X2 - X3 | 1.75 | 2.40 | 0.11 | 2.21 | 3.04 | 0.12 | 1.67 | 2.52 | 0.14 | 1.05 | 1.46 | 0.11 | 0.85 | 1.43 | 0.11 | 1.51 | 3.04 | ||
| Central | Y2: X1 - X2 | 1.58 | 2.49 | 0.12 | 2.19 | 3.13 | 0.12 | 1.67 | 2.59 | 0.14 | 0.98 | 1.62 | 0.10 | 0.85 | 1.34 | 0.10 | 1.45 | 3.13 | |
| Y2: X2 - X3 | 1.72 | 2.42 | 0.11 | 2.22 | 3.04 | 0.11 | 1.66 | 2.45 | 0.14 | 1.04 | 1.44 | 0.11 | 0.85 | 1.45 | 0.10 | 1.50 | 3.04 | ||
| Column type | Column location | Ground motion 1 | Ground motion 2 | Ground motion 3 | Ground motion 4 | Ground motion 5 | All ground motions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Max | cov | Mean | Max | cov | Mean | Max | cov | Mean | Max | cov | Mean | Max | cov | Mean | Max | ||
| Corner | X1 - Y1 | 1.71 | 2.45 | 0.10 | 1.40 | 2.10 | 0.13 | 1.44 | 2.25 | 0.18 | 0.92 | 1.44 | 0.16 | 0.78 | 1.04 | 0.09 | 1.25 | 2.45 |
| X4 - Y4 | 1.55 | 2.21 | 0.12 | 1.42 | 2.04 | 0.13 | 1.33 | 1.81 | 0.10 | 0.92 | 1.43 | 0.15 | 0.84 | 1.24 | 0.11 | 1.21 | 2.21 | |
| Borde | X1 - Y2 | 1.87 | 2.53 | 0.10 | 1.42 | 2.06 | 0.12 | 1.45 | 2.18 | 0.16 | 0.98 | 1.47 | 0.15 | 0.80 | 1.14 | 0.10 | 1.30 | 2.53 |
| X2 - Y1 | 1.83 | 2.40 | 0.08 | 1.53 | 2.21 | 0.12 | 1.47 | 2.20 | 0.17 | 1.00 | 1.51 | 0.14 | 0.87 | 1.14 | 0.09 | 1.34 | 2.40 | |
| Central | X2 - Y2 | 1.80 | 2.41 | 0.09 | 1.54 | 2.18 | 0.12 | 1.51 | 2.15 | 0.13 | 1.10 | 1.72 | 0.14 | 0.88 | 1.24 | 0.08 | 1.37 | 2.41 |
| X3 - Y3 | 1.79 | 2.53 | 0.09 | 1.55 | 2.24 | 0.13 | 1.53 | 2.27 | 0.15 | 1.10 | 1.68 | 0.14 | 0.88 | 1.20 | 0.08 | 1.37 | 2.53 | |
6.4. Analysis of ductility demands for the three conditions (a, b and c)
In this subsection, a comparison of ductility demands of both beams and columns for the three conditions is showed. For space limitation in this work, this comparison is carried out for one model (M4S6) under two ground motions (1989 Loma Prieta/Corralitos and 1985 México/CU). The other ground motions and models lead to similar results. These ground motions were selected for the evaluation of the design procedure because they maintain the ratio () in Eq. (3) approximately constant for growing values of the structural periods of vibration.
As mentioned before, the comparison of ductility demands of the reference model (condition a) with the conditions b and c requires the selection of some statistical parameters. As a measure of how large the ductility demand can result with a reasonable low probability of exceedance , the value of the ductility demand associated to the mean () plus two standard deviations () is selected. It is known [25], that this parameter leads to a if a normal distribution is assumed. The ductility demand for this exceedance probability is identified as . This ductility demand is considered a better parameter than the maximum value.
Table 12 shows the comparison of ductility demands for beams of levels 1 and 2 of model M4S6 for the three conditions (a, b and c) under the Loma Prieta earthquake. The ductility demands of the reference model under condition a () are listed in the fourth column. These ductility demands are considered as reference values. The ductility demands corresponding to condition b for are listed in the seventh column identified as (). The comparison of both columns shows that there is a probability equal to 2.5% that accidental torsion can cause ductility demands larger than 25% than the ductility demands of systems without accidental torsion (condition a), as indicated by the quotients (). This result is and simple indicator of how much the accidental torsion can affect the model.
The comparison of the ductility demands for the reference model () with the values of () for the condition c indicates that the design procedure is effective to control the demands when accidental torsion is present. This leads to a 2.5% probability that ductility demands result larger than those of the reference model. An ideal design procedure against accidental torsion should take back the ductility demands (caused by accidental torsion) to this reference values. This can be corroborated for the Loma Prieta/Corralitos ground motion by observing the values of ( for condition c in Table 12, which are close to 1.0.
Table 13 leads to similar results for columns of the same model M4S6 under the Loma Prieta ground motion. A comparison of conditions a and b suggests that there is a 2.5% probability that accidental torsion can cause an increment close to 15% in column ductility demands. A comparison of conditions a and c in Table 13 (Loma Prieta) reveals that the design procedure is effective to control the effects of accidental torsion in columns.
Table 14 lists the corresponding ductility demands for beams of levels 1 and 2 of model M4S6 under the ground motion 2 (1985 México/CU). By the same arguments described before for Tables 12 and 13, in this case the comparison of conditions a and b reveals that the increment of ductility demands of beams is approximately between 20% and 25% with . The comparison of conditions a and c (last column of Table 14) shows that the design procedure seems effective to control accidental torsion in beams.
Table 15 presents the ductility demands for columns of the story 1 of model M4S6, under the México ground motion. Results indicate that accidental torsion increments the column demands in approximately 20-25%, with respect to the values of the reference model. Finally, a comparison of conditions a and c corroborates that the design procedure is effective to control the ductility demands of columns caused by accidental torsion.
| Level | Beam type | Beam location | condition a (reference model) | Condition b | Condition c | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. dev. | Mean | Std. dev. | ||||||||
| 1 | Edge | X1: Y1 - Y2 | 2.72 | 2.58 | 0.30 | 3.18 | 1.17 | 2.18 | 0.26 | 2.71 | 0.99 |
| X1: Y2 - Y3 | 2.93 | 2.83 | 0.33 | 3.48 | 1.19 | 2.45 | 0.27 | 3.00 | 1.02 | ||
| Central | X2: Y1 - Y2 | 2.66 | 2.53 | 0.29 | 3.12 | 1.17 | 2.17 | 0.25 | 2.68 | 1.01 | |
| X2: Y2 - Y3 | 2.84 | 2.78 | 0.32 | 3.43 | 1.21 | 2.43 | 0.27 | 2.97 | 1.05 | ||
| Edge | Y1: X1 - X2 | 3.02 | 3.11 | 0.40 | 3.90 | 1.29 | 2.15 | 0.30 | 2.75 | 0.91 | |
| Y1: X2 - X3 | 3.48 | 3.45 | 0.45 | 4.36 | 1.25 | 2.35 | 0.35 | 3.04 | 0.88 | ||
| Central | Y2: X1 - X2 | 3.10 | 3.14 | 0.39 | 3.92 | 1.27 | 2.18 | 0.30 | 2.78 | 0.90 | |
| Y2: X2 - X3 | 3.55 | 3.51 | 0.46 | 4.44 | 1.25 | 2.40 | 0.35 | 3.10 | 0.87 | ||
| 2 | Edge | X1: Y1 - Y2 | 2.60 | 2.58 | 0.30 | 3.18 | 1.22 | 2.25 | 0.28 | 2.81 | 1.08 |
| X1: Y2 - Y3 | 2.86 | 2.78 | 0.35 | 3.47 | 1.21 | 2.53 | 0.29 | 3.11 | 1.08 | ||
| Central | X3: Y1 - Y2 | 2.60 | 2.57 | 0.30 | 3.16 | 1.21 | 2.23 | 0.27 | 2.77 | 1.06 | |
| X3: Y2 - Y3 | 2.86 | 2.78 | 0.35 | 3.48 | 1.22 | 2.49 | 0.29 | 3.08 | 1.08 | ||
| Edge | Y1: X1 - X2 | 2.15 | 2.05 | 0.23 | 2.51 | 1.17 | 1.59 | 0.19 | 1.96 | 0.91 | |
| Y1: X2 - X3 | 2.20 | 2.23 | 0.26 | 2.74 | 1.25 | 1.75 | 0.20 | 2.15 | 0.98 | ||
| Central | Y2: X1 - X2 | 2.10 | 2.06 | 0.25 | 2.57 | 1.22 | 1.58 | 0.19 | 1.96 | 0.94 | |
| Y2: X2 - X3 | 2.24 | 2.25 | 0.27 | 2.78 | 1.24 | 1.72 | 0.20 | 2.12 | 0.94 | ||
| Column type | Column location | condition a (reference model) | Condition b | Condition c | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. dev. | Mean | Std. dev. | |||||||
| Corner | X1 - Y1 | 2.26 | 2.28 | 0.18 | 2.63 | 1.17 | 1.71 | 0.17 | 2.04 | 0.90 |
| X4 - Y4 | 2.15 | 2.09 | 0.22 | 2.52 | 1.17 | 1.55 | 0.19 | 1.92 | 0.89 | |
| Borde | X1 - Y2 | 2.50 | 2.42 | 0.21 | 2.85 | 1.14 | 1.87 | 0.19 | 2.25 | 0.90 |
| X2 - Y1 | 2.36 | 2.40 | 0.16 | 2.73 | 1.16 | 1.83 | 0.15 | 2.13 | 0.90 | |
| Central | X2 - Y2 | 2.33 | 2.34 | 0.18 | 2.69 | 1.16 | 1.80 | 0.16 | 2.12 | 0.91 |
| X3 - Y3 | 2.33 | 2.33 | 0.18 | 2.68 | 1.15 | 1.79 | 0.16 | 2.10 | 0.90 | |
| Level | Beam type | Beam location | condition a (reference model) | Condition b | Condition c | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. dev. | Mean | Std. dev. | ||||||||
| 1 | Edge | X1: Y1 - Y2 | 2.90 | 2.94 | 0.33 | 3.61 | 1.25 | 2.40 | 0.28 | 2.96 | 1.02 |
| X1: Y2 - Y3 | 3.23 | 3.26 | 0.39 | 4.03 | 1.25 | 2.65 | 0.31 | 3.28 | 1.01 | ||
| Central | X2: Y1 - Y2 | 2.93 | 2.96 | 0.35 | 3.66 | 1.25 | 2.41 | 0.28 | 2.97 | 1.02 | |
| X2: Y2 - Y3 | 3.23 | 3.28 | 0.38 | 4.05 | 1.25 | 2.67 | 0.31 | 3.29 | 1.02 | ||
| Edge | Y1: X1 - X2 | 2.66 | 2.63 | 0.30 | 3.23 | 1.21 | 2.17 | 0.25 | 2.67 | 1.00 | |
| Y1: X2 - X3 | 2.66 | 2.69 | 0.31 | 3.30 | 1.24 | 2.20 | 0.25 | 2.71 | 1.02 | ||
| Central | Y2: X1 - X2 | 2.67 | 2.63 | 0.29 | 3.21 | 1.20 | 2.17 | 0.24 | 2.66 | 1.00 | |
| Y2: X2 - X3 | 2.68 | 2.71 | 0.30 | 3.30 | 1.23 | 2.21 | 0.25 | 2.71 | 1.01 | ||
| 2 | Edge | X1: Y1 - Y2 | 3.27 | 3.26 | 0.36 | 3.98 | 1.22 | 2.65 | 0.31 | 3.27 | 1.00 |
| X1: Y2 - Y3 | 3.57 | 3.60 | 0.38 | 4.37 | 1.22 | 2.95 | 0.33 | 3.61 | 1.01 | ||
| Central | X3: Y1 - Y | 3.29 | 3.27 | 0.35 | 3.97 | 1.21 | 2.67 | 0.29 | 3.26 | 0.99 | |
| X3: Y2 - Y3 | 3.60 | 3.60 | 0.39 | 4.37 | 1.21 | 2.93 | 0.32 | 3.58 | 0.99 | ||
| Edge | Y1: X1 - X2 | 2.75 | 2.71 | 0.30 | 3.30 | 1.20 | 2.19 | 0.25 | 2.69 | 0.98 | |
| Y1: X2 - X3 | 2.76 | 2.73 | 0.31 | 3.35 | 1.21 | 2.21 | 0.26 | 2.74 | 0.99 | ||
| Central | Y2: X1 - X2 | 2.73 | 2.71 | 0.29 | 3.30 | 1.21 | 2.19 | 0.25 | 2.69 | 0.99 | |
| Y2: X2 - X3 | 2.74 | 2.75 | 0.30 | 3.34 | 1.22 | 2.22 | 0.25 | 2.73 | 1.00 | ||
| Column type | Column location | condition a (reference model) | Condition b | Condition c | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. dev. | Mean | Std. dev. | |||||||
| Corner | X1 - Y1 | 1.85 | 1.84 | 0.20 | 2.23 | 1.21 | 1.40 | 0.18 | 1.75 | 0.95 |
| X4 - Y4 | 1.82 | 1.86 | 0.21 | 2.28 | 1.25 | 1.42 | 0.18 | 1.78 | 0.98 | |
| Borde | X1 - Y2 | 1.84 | 1.84 | 0.20 | 2.23 | 1.21 | 1.42 | 0.17 | 1.75 | 0.95 |
| X2 - Y1 | 2.02 | 2.02 | 0.22 | 2.46 | 1.21 | 1.53 | 0.19 | 1.91 | 0.94 | |
| Central | X2 - Y2 | 1.96 | 1.96 | 0.20 | 2.36 | 1.20 | 1.54 | 0.19 | 1.91 | 0.97 |
| X3 - Y3 | 1.94 | 1.95 | 0.20 | 2.35 | 1.21 | 1.55 | 0.19 | 1.93 | 1.00 | |
7. Conclusions
The aim of this work is twofold: 1) to evaluate a simplified accidental-torsion design procedure and 2) to assess the increments of ductility demands caused by accidental torsion in beams and columns of building models. The design procedure does not use an accidental eccentricity. It is based on a simple amplification of the element forces due to the seismic action in the corresponding torsionally balanced model to obtain the design values considering accidental torsion. This is equivalent to an artificial amplification of the acting seismic forces. The evaluation was carried out using four reinforced concrete frame building models and five firm-soil bidirectional ground motions. The evaluation of the design procedure was supported on the dynamic nonlinear response of the models. The accidental torsion was simulated using the Monte Carlo method. The variables that were assumed random were: dead-load magnitude, live-load position and magnitude, and the flexural stiffness of beams and columns.
The conclusions of this work are as follows:
Condition a) – Models without accidental torsion
- 1) In reference models (four- and seven-story models without accidental torsion) subjected to firm-soil ground motions, ductility demands of columns resulted smaller than those of beams (column values resulted approximately equal to 0.7 times the beam values). For a response modification coefficient and an overstrength factor , average ductility demands of beams varied between 1.74 and 3.23. For columns, the average demands varied between 1.13 and 2.15.
- 2) Average ductility demands (taken with respect to the ground motions) for columns of rectangular-plan models (Tables 6 and 7) resulted between 20% and 30% smaller than for columns of square-plan models.
- 3) The variation of ductility demands among ground motions resulted larger for columns than for beams. The coefficients of variation for beams ranged between 0.20 and 0.35, approximately; however, for columns the coefficients of variations reached values up to 0.80.
Condition b) – Models with accidental torsion
- 4) The mean value of ductility demands of beams and columns for models with accidental torsion stays close to the mean ductility demand of the corresponding elements of models without accidental torsion. However, peak ductility demands of beams and columns caused by accidental torsion can result from 50% to 75% larger than those of the corresponding elements for building models without accidental torsion (computed for the same earthquake).
- 5) There is a probability equal to 2.5% that accidental torsion can cause ductility demands 25% larger than the demands of systems without accidental torsion.
Condition c) – Strengthened models with accidental torsion
- 6) The accidental-torsion design procedure evaluated in this work (Eq. 2) reduces both the mean and the maximum values of ductility demands of beams and columns in systems with accidental torsion. This reduction of ductility demands is close to the 20% of the demands for the elements of systems wherein the design procedure is not applied.
- 7) Results indicate that the application of the design procedure evaluated in this work leads approximately to a 2.5% probability that ductility demands would result larger than those of the reference model (without accidental torsion). This suggests that the design procedure seems effective to control the ductility demands caused by accidental torsion.
Glossary
: Spectral ordinate of the elastic design spectrum
: Acceleration spectral ordinate of the largest horizontal ground motion components
: Plan dimension perpendicular to the direction of analysis
cov: Coefficient of variation
: Ductility demands of the reference model under condition a
: The ductility demand associated to the mean () plus two standard deviations ()
: Concrete modulus of elasticity
: Elements amplified by accidental torsion (Eq. (2))
: Beam flexural stiffness
: Column flexural stiffness
: Any effect in the reference model caused by the seismic design action (Eq. (2))
: Design eccentricity
: Natural eccentricity
: Accidental eccentricity
: Amplification factor by accidental torsion equal to 1.2 (Eq. (2))
: Concrete compressive strength
: Yield stress value for the steel reinforcement
: Sample size ()
: Models with amplified strength
Max: Maximum ductility demand
: Number of simulations ()
: Function of the group size
: Exceedance probability
: Probability density function
: Response modification coefficient
RM: Reference model
TB: Torsionally balanced
: Dead-load magnitude
: Live-load magnitude
, : Live-load position
: Coefficient of accidental eccentricity proposed by design codes
: Standard deviation
: Mean
: Damping ratio
: Overstrength factor
References
[1] IBC. International Building Code. International Code Council, Inc., 2018.
[2] ASCE/SEI 7. Minimum design loads and associated criterial for building and others structures. American Society of Civil Engineers, 2016.
[3] EC. Eurocode 8. Design of structures for earthquake resistance. European Committee for Standardization, 2004.
[4] RC-Reglamento de Construcciones de la Ciudad de México. Gaceta Oficial de la Ciudad de México, 2017.
[5] De la Llera J., Chopra A. Evaluation of code-accidental torsion provisions using earthquake records from three nominally symmetric-plan building. Earthquake Engineering and Structural Dynamics, 1-162, 1992.
[6] De la Colina J., Almeida C. Probabilistic study on accidental torsion of low-rise buildings. Earthquake spectral, 20:25-45, 2003.
[7] Dimova S., Alashki I. Seismic desing of symmetric structures for accidental torsion. Bulletin of Earthquake Engineering, 1:303-320, 2003.
[8] Mendoza R. Evaluación de métodos para estimar la excentricidad accidental de estructuras a partir de pruebas dinámicas. Tesis de Maestría, UNAM, 2007.
[9] Anagnostopoulos A., Kyrkos T., Papalymper A., Plevr E. Should accidental eccentricity be eliminated from Eurocode 8?. Earthquakes and Structures, 8:463-484, 2015.
[10] DeBock J., Liel B., Haselton B., Hooper D., Henige Jr R. Importance of seismic design accidental torsion requirements for building collapse capacity. Earthquake Engineering & Structural Dynamics, 6:831-850, 2013.
[11] Gálvez G. Procedimiento para tomar en cuenta los efectos de la excentricidad accidental en el diseño sísmico de edificios. Tesis de Maestría, UAEM, 2017.
[12] De la Llera J., Chopra A. Accidental torsion in buildings due to base rotational excitation. Earthquake Engineering & Structural Dynamics, 23:1-15, 1994.
[13] Metropolis N., Ulam S. The Monte Carlo method. Journal of the American Statistical Association, 43:1-8, 1949.
[14] Ramsay R., Mirza S., MacGregor J. Monte Carlo study for short time deflections of reinforced concrete beams. ACI Journal, 76:897-918, 1979.
[15] Galambos T., MacGregor J. Building code requirements for minimum design loads in buildings and other structures. U.S. Department of Commerce/ National Bureau of Standards, 577, 1980.
[16] Santos M., Ruiz S., Bojórquez J. Metodología para establecer valores de diseño de la carga viva instantánea. Sociedad Mexicana de Ingeniería Estructural, 1-18, 2014.
[17] De la Colina J., Ruiz S., Benítez B. Accidental eccentricity of story shear for low-rise office buildings. Journal of Structural Division, 137:513- 520, 2011.
[18] García V. Análisis de las probabilidades de excedencia de las respuestas de modelos estructurales con torsión sujetos a sismos usando simulación Monte Carlo. Tesis de Maestría, UAEM, 2015.
[19] Li K-N. Canny-E User’s manual, three-dimension nonlinear dynamic structural analysis computer program package. Canny Consultants Pte. Ldt., 1996.
[20] Lai S., Will G., Otani S. Model for inelastic biaxial bending of concrete members. Journal of the Structures Division, 110(11), 1984.
[21] Clough R., Johnston S. Proc. of the Japan Earthquake Engineering Conference, 1966.
[22] Otani S. Hysteresis models of reinforced concrete for earthquake response analysis. Journal of the Faculty of Engineering, 36:125-159, 1981.
[23] Li K-N., Otani S., Aoyama H. Reinforced concrete columns under varying axial load and bi-directional horizontal load reversals. Pacific Conference on Earthquake Engineering, 1987.
[24] FEMA-273. NEHRP guidelines for the seismic rehabilitation of buildings. Building Seismic Safety Council, 1997.
[25] Montgomery D., Runger G., Hubele N. Engineering statistics. 4th ed. Wiley, 2010.
Document information
Published on 12/01/21
Accepted on 22/10/20
Submitted on 13/04/20
Volume 37, Issue 1, 2021
DOI: 10.23967/j.rimni.2020.10.009
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?