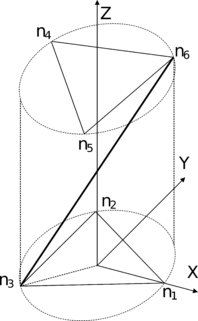Use of the SVD method for the stability analysis of tensegrity structures

Resumen

En este artículo se presenta la aplicación del método de la descomposición en valores singulares SVD al análisis de las estructuras tensegríticas. Para ello se describe primeramente el método SVD de manera general, sin profundizar en las técnicas para su cálculo. Posteriormente se definen las ecuaciones de equilibrio de las estructuras tensegríticas. La solución del sistema homogéneo de equilibrio de estas estructuras es desarrollada utilizando el método SVD y el significado estructural de los valores en las matrices producto de la descomposición es definido. El método es utilizado para la solución de diversas estructuras, algunas de ellas ampliamente estudiadas de forma previa y otras nuevas.

Palabras clave: Tensegridad, estructuras livianas, matriz de equilibrio, SVD, tensegrity

Abstract

In this paper, the application of the singular value decomposition SVD for the analysis of tensegrity structures is presented. For this purpose, the SVD method is described generally, without detailing the calculating method. Next, the equilibrium equations of tensegrity structures are defined. The solution to the homogeneous system of equilibrium of the tensegrity structures is developed using the SVD method, and the meaning of the values in the matrices is presented. The method is used for the solution of several structures, some of them widely studied and some new.

Keywords: Tesnegrity, light structures, balance matrix, SVD

1. Introducción

Las estructuras tensegríticas son sistemas pretensados, compuestos por barras y cables, donde las barras no se encuentran en contacto entre sí. Esta característica le permite a la estructura realizar una distribución de fuerzas únicamente en la dirección de los ejes de cada miembro; es decir, las barras y cables experimentan solamente compresión y tensión, respectivamente. De esta forma, esfuerzos como la torsión, flexión o cortante son descartados en el proceso de diseño.

Entre las principales características de las tensegridades está el ser livianas, compresibles y desplegables, la posibilidad de agregarles sistemas de control para modificar su geometría, y su relativo bajo costo, entre otras. Es por estas razones que, en los últimos años, han sido consideradas como la base para el diseño de diferentes tipos de estructuras en variados campos de la ingeniería, como es el caso de reflectores y antenas satelitales desplegables, sondas de exploración interplanetaria, puentes peatonales, techos de estadios y más.

El análisis de la estabilidad de estas estructuras es un tema de investigación recurrente en revistas y conferencias. Connelly y Back [1] usan la teoría de representación de grupos para proponer que las variaciones simétricas de una estructura estable son también estables; Motro [2] aplicó el método de la relajación dinámica al simular desplazamientos en estructuras hasta encontrar un estado de equilibrio, con y sin amortiguamiento cinemático. Más recientemente, los algoritmos genéticos [3,4] han aparecido como una herramienta en el cálculo de configuraciones estables tanto a nivel estático como dinámico, permitiendo el desarrollo de sistemas de control para el manejo de robots tensegríticos. El método de la densidad de fuerza [2] es ampliamente utilizado por su simplicidad y poca demanda de recursos computacionales. Este método convierte el problema no lineal del equilibrio estático de las estructuras tensegríticas en uno lineal, al sustituir las fuerzas en los elementos por una relación de fuerza por unidad de longitud.

Pellegrino [5] propuso el uso del método de la descomposición en valores singulares para el análisis de conjuntos estructurales en general. Más tarde, Gómez Estrada et al. [6] hicieron uso de este principio para desarrollar un método de búsqueda de topologías estables para estructuras tensegríticas; este método emplea tanto la descomposición en valores singulares de la matriz de equilibrio como la factorización de Schur de la matriz de densidades de fuerza. Tran y Lee [7] presentaron una variante de este método que hace uso del SVD para la descomposición de ambas matrices.

El objetivo de este artículo es describir la importancia de la descomposición en valores singulares SVD en el diseño y análisis de las estructuras tensegríticas. El artículo se distribuye de la siguiente manera: primeramente la Sección 2 menciona la teoría del SVD, la Sección 3 describe la composición de las matrices de equilibrio y de densidad de fuerza de las estructuras tensegríticas mientras que la Sección 4 relaciona su descomposición SVD con las propiedades estructurales; la Sección 5 muestra algunos ejemplos numéricos y reales. Cabe resaltar que aquí no se profundizará en los métodos para el cálculo del SVD, ya que la descomposición puede ser fácilmente obtenida mediante el uso de software.

2. Descomposición en valores singulares

Sea ${\bf {A}}$ una matriz $n\times d$, esta puede ser factorizada en la forma

${\begin{array}{cc}{\boldsymbol {A}}={\boldsymbol {UV}}{\boldsymbol {W}}^{T},&{\boldsymbol {V}}=diag\left(v_{1},v_{2},\ldots ,v_{d}\right)\end{array}}\in {\mathbb {R} }^{n\times d}$

(1)

donde $v_{1}\geq v_{2}\geq \cdots \geq v_{d}$, y son llamados valores singulares de ${\bf {A}}$. Ambas U ${\textstyle (\in {R}^{n\times n})}$ y ${\bf {W}}$ ${\textstyle (\in {R}^{d\times d})}$ son matrices ortogonales que contienen los vectores singulares izquierdos u_i y derechos w_i de ${\bf {A}}$, respectivamente.

La dimensión de la matriz V puede variar dependiendo de las siguientes condiciones [8]

• n ≠ d. La matriz V es n × d y tiene las mismas dimensiones que A.

• m = n. La matriz V es cuadrada.

• m = n = rango (A). La matriz V es cuadrada y reducida.

Como describe Kalman [9], la significancia de este método radica en que el SVD comprende la base para el dominio y el rango de la transformación lineal asociada a la matriz A. El rango r_A de la matriz A corresponde a la cantidad de valores singulares ${\textstyle \left\{{v}_{1},\ldots ,{v}_{r}\right\}}$ diferentes a cero presentes en V, mientras que los restantes ${\textstyle \left\{{v}_{r+1},\ldots ,{v}_{d}\right\}}$ valores en V corresponden al espacio nulo n_A de la matriz A [8]. Por lo tanto, se define entonces que los vectores ${\textstyle \left\{{w}_{r+1},\ldots ,{w}_{d}\right\}}$ componen la base ortonormal de n_A.

Una de las ventajas de la descomposición en valores singulares es que está definida para cualquier matriz. Esto la diferencia de la descomposición en vectores propios, la cual asegura ortogonalidad de los vectores propios solamente para matrices cuadradas, entre otras condiciones. El método SVD ha probado su utilidad en aplicaciones como la solución de problemas de mínimos cuadrados, análisis de componentes principales, estimación del rango de matrices o el cálculo de la inversa generalizada de matrices.

3. Estabilidad de las estructuras tensegríticas

3.1 Descripción de las estructuras tensegríticas

Se puede definir a las estructuras tensegríticas como sistemas estables auto soportados compuestos por nodos en el espacio, conectados entre sí por barras y cables, sin que dos o más barras entren en contacto. Estas estructuras pueden ser diseñadas de numerosas formas y complejidades, pero estas generalmente pueden ser modeladas como el ensamble de dos o más estructuras simples o unitarias, como la mostrada en la Figura 1.

Figura 1. Simplificación de una estructura tensegrítica. La línea gruesa representa una barra conectando dos nodos n₃ y n₆.

La topología de una estructura tensegrítica de m miembros (s cables más b barras), está dada por dos variables, la matriz nodal N ${\textstyle (\in {R}^{n\times 3})}$ que contiene las coordenadas [x y z] de cada uno de los n nodos y la matriz de conectividad C ${\textstyle (\in {R}^{m\times n})}$. Si un miembro m_k conecta los nodos i y j (i ˂ j), las entradas i y j de la fila k de C serán -1 o 1, respectivamente, si

${\boldsymbol {C}}_{\left(k,p\right)}=\left\{{\begin{array}{c}-1\quad {\mbox{para }}\quad p=i\\1\quad \,{\mbox{para }}\quad p=j\\0\quad {\mbox{otros nodos}}\end{array}}\right.$

(2)

3.2 Principio de la densidad de fuerza

La no-linealidad del comportamiento de las estructuras tensegríticas se ve reflejada en algunos de los métodos de análisis. Entre ellos, el método de matrices de rigidez y el método de elementos finitos hacen uso de información estructural, como la elasticidad del material de los miembros, o el área trasversal de los mismos, para los cálculos. Sin embargo, en muchas ocasiones no se cuenta con esta información.

Figura 2. Barra de longitud l que conecta los nodos n_i y n_j, sujeta a una fuerza f.

En este caso, una solución es utilizar el método de la densidad de fuerza, presentado en 1971 por Schek y Linkwitz [10]. De la Figura 2, si se divide la fuerza interna f de cada miembro por su longitud l, se obtiene una densidad de fuerza por unidad de longitud, independiente del área trasversal o de la elasticidad. Estos factores sustituyen las fuerzas en el sistema de ecuaciones para convertir el sistema en lineal.

3.3 Ecuaciones de equilibrio

Si q ${\textstyle (\in {R}^{m\times 1})}$ representa el vector que contiene las densidades de fuerza de los m miembros de la estructura, el problema de la estabilidad de las estructuras tensegríticas se puede reducir a la solución del sistema

${\boldsymbol {Eq}}={\boldsymbol {F}}$

(3)

donde E ${\textstyle (\in {R}^{3n\times m})}$ es la matriz de equilibrio y F ${\textstyle (\in {R}^{3n\times 1})}$ representa el vector de fuerzas externas que actúan sobre los nodos del sistema. La matriz E está definida por

${\boldsymbol {E}}=\left({\begin{array}{c}{\boldsymbol {C}}^{T}diag\left({\boldsymbol {Cx}}\right)\\{\boldsymbol {C}}^{T}diag\left({\boldsymbol {Cy}}\right)\\{\boldsymbol {C}}^{T}diag\left({\boldsymbol {Cz}}\right)\end{array}}\right)$

(4)

donde x, y, z son los correspondientes vectores 1, 2 y 3 de la matriz nodal N. En el caso estático, asumiendo que no hay fuerza externa, el vector F se convierte en nulo y la ecuación (3) se reduce a

${\textstyle {\boldsymbol {Eq}}={\boldsymbol {0}}}$

(5)

El sistema lineal homogéneo de equilibrio puede reescribirse en términos de las densidades de fuerza y las coordenadas nodales como

${\textstyle {\boldsymbol {DN}}={\boldsymbol {0}}}$

(6)

donde D ${\textstyle (\in {R}^{n\times n})}$ es conocida como la matriz de densidad de fuerza, y está definida por

${\textstyle {\boldsymbol {D}}={\boldsymbol {C}}^{T}diag({\boldsymbol {q}}){\boldsymbol {C}}}$

(7)

Esta matriz representa el equilibrio entre las densidades de fuerza que confluyen en cada nodo, sin considerar la ubicación de los mismos. Es de igual importancia que la matriz de equilibrio en el proceso de diseño de estructuras tensegríticas y es por esto que es incluida en este artículo.

4. Significado estructural del SVD

4.1. Matriz de equilibrio

Como es sabido, el set de vectores q que satisfacen el sistema homogéneo de la ecuación (5) reside en el espacio nulo de la matriz E [11]. No obstante, al no ser E una matriz invertible, requiere el uso de métodos matemáticos especiales. Es aquí donde el método de la descomposición en valores singulares encuentra importancia en el campo de las estructuras tensegríticas.

La descomposición en valores singulares de la matriz E se define de acuerdo a la ecuación (1) como

${\boldsymbol {E}}={\left[{\begin{array}{ccc}{\boldsymbol {u}}_{1}&\cdots &{\boldsymbol {u}}_{r_{E}}\end{array}}\vert {\begin{array}{ccc}{\boldsymbol {u}}_{r_{E}+1}&\cdots &{\boldsymbol {u}}_{3n}\end{array}}\right]}_{3n\times 3n}{\left[{\begin{array}{cccc}v_{1}&&&\\&\ddots &&0\\&&v_{r_{E}}&\\&0&&0\end{array}}\right]}_{3n\times m}$ ${\left[{\begin{array}{ccc}{\boldsymbol {w}}_{1}&\cdots &{\boldsymbol {w}}_{r_{E}}\end{array}}\vert {\begin{array}{ccc}{\boldsymbol {w}}_{r_{E}+1}&\cdots &{\boldsymbol {w}}_{m}\end{array}}\right]}^{T}{}_{m\times m}$

(8)

donde r_E es el rango de E y los últimos m-r_E vectores de W ${\textstyle (\in {R}^{m\times m})}$ representan el espacio nulo de E. Estos vectores son conocidos como los estados de auto estrés de la estructura; es decir, las diferentes combinaciones de fuerzas internas para las cuales la estructura es estable por si sola. Como es de suponer, para que una tensegridad sea estable, su nulidad debe ser al menos uno. Motro [2] lo resume con la condición necesaria

$n_{E}=m-r_{E}\geq 1$

(9)

donde n_E es la dimensión del espacio nulo de E.

Conociendo las longitudes de los diferentes miembros de la estructura, y seleccionando uno de estos estados de auto estrés, se pueden determinar las fuerzas netas que actúan sobre cada miembro. Con esta información se puede diseñar la estructura final, pues es posible seleccionar diámetros y materiales acordes a los esfuerzos y tolerancias.

Los últimos 3n-r vectores de la matriz U ${\textstyle (\in {R}^{3n\times 3n})}$ también presentan significado a nivel estructural. Estos representan los mecanismos infinitesimales del sistema tensegrítico; mecanismos que permiten solamente pequeños cambios en la longitud de ciertas barras aún bajo grandes desplazamientos de los nodos [12]. Los mecanismos infinitesimales han probado ser de gran utilidad en el diseño de estructuras desplegables, pues durante los movimientos a lo largo de estos mecanismos no hay pérdida de energía debido al amortiguamiento cinemático lineal de los cables [13].

4.2. Matriz de densidad de fuerza

Utilizando la misma notación que E, la descomposición de D es dada por

${\boldsymbol {D}}={\left[{\begin{array}{ccc}{\boldsymbol {u}}_{1}&\cdots &{\boldsymbol {u}}_{r_{D}}\end{array}}\vert {\begin{array}{ccc}{\boldsymbol {u}}_{r_{D}+1}&\cdots &{\boldsymbol {u}}_{3n}\end{array}}\right]}_{n\times n}{\left[{\begin{array}{cccc}v_{1}&&&\\&\ddots &&0\\&&v_{r_{D}}&\\&0&&0\end{array}}\right]}_{n\times n}$ ${\left[{\begin{array}{ccc}{\boldsymbol {w}}_{1}&\cdots &{\boldsymbol {w}}_{r_{D}}\end{array}}\vert {\begin{array}{ccc}{\boldsymbol {w}}_{r_{D}+1}&\cdots &{\boldsymbol {w}}_{m}\end{array}}\right]}^{T}{}_{n\times n}$

(10)

El espacio nulo de D es de utilidad en el diseño de estructuras tensegríticas cuando se conoce la cantidad de componentes, su tipo y conectividad, pero se requiere averiguar las coordenadas de los nodos para las cuales la estructura es estable. Debido a que la suma de las entradas en una fila o una columna de D es siempre cero, el vector ${\textstyle {\left\{1,1,\ldots ,1\right\}}^{T}}$es una solución de la ecuación (6); sin embargo, este vector degenera la geometría de la estructura.

Es necesario entonces obtener d+1 soluciones particulares para formar un espacio vectorial de dimensión d: las coordenadas [x y z] de la estructura. Por ejemplo, una nulidad de 4 es necesaria para una estructura de 3 dimensiones. Para el caso de la matriz semidefinida D y su rango r_D, la condición de su espacio nulo [2] está dada por

$n_{D}=n-r_{D}\geq d+1$

(11)

4.3. Aplicaciones especiales

La descomposición en valores singulares de la matriz E, en especial las entradas de su matriz diagonal V, son de gran utilidad en el cálculo del rango real de esta matriz. Debido a la pérdida de precisión durante los cálculos por parte de Matlab, o cualquier otro software, ocasiona que, en ciertos casos, el rango calculado por el mismo no sea el verdadero.

Ciertas estructuras construidas en nuestro laboratorio con base en parámetros previamente establecidos para su equilibrio [14], presentan una matriz de equilibrio con rango completo, de acuerdo a Matlab. No obstante, al inspeccionar los valores singulares, se observa que al menos uno es de dimensiones cercanas a ${\textstyle 1\times {10}^{-14}}$ o inferior. Es un valor que Matlab no considera cero, a pesar de ser sumamente pequeño al compararse con los demás valores singulares, por lo que Matlab considera a E como de rango completo. Como afirman Quintana y Quintana [15], esta necesidad de precisión en los datos justifica el relativamente alto coste computacional del método.

5. Ejemplos numéricos

Se presentan a continuación algunos ejemplos numéricos de estructuras tensegríticas. El vector de densidades de fuerza es calculado utilizando el software Matlab y los valores son agrupados por simetrías para reducir la cantidad de información a mostrar en este artículo. Una fotografía de cada estructura real construida en nuestro laboratorio es mostrada junto con el gráfico generado por computadora.

5.1. 3 barras

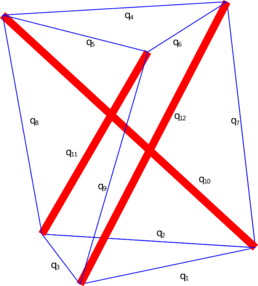
La estructura tensegrítica más simple está compuesta por tres barras y nueve cables, como se muestra en la Figura 3. A pesar de su simplicidad, es utilizada como unidad básica para la construcción de estructuras más complejas.

(a)	(b)

Figura 3. Estructura de 3 barras. (a) Gráfico de Matlab, (b) modelo real.

Definiendo una altura de 200 mm y un radio de 70 mm, de Skelton y De Oliveira [14] se pueden obtener los seis nodos de esta estructura. Utilizando la ecuación (2) para generar la matriz de conectividad C, e introduciendo N y C en la ecuación (4) y posteriormente calculando el SVD de E, se obtiene el vector de densidades de fuerza.

Miembro	Densidad de fuerza
q1	1.0
q2	1.0
q3	1.0
q4	1.0
q5	1.0
q6	1.0
q7	1.7321
q8	1.7321
q9	1.7321
q10	-1.7321
q11	-1.7321
q12	-1.7321

Tabla 1. Densidades de fuerza para estructura de 3 barras.

De la Tabla 1 se observa que, como es de esperarse, los cables del mismo grupo de simetría poseen la misma densidad de fuerza. Para esta estructura, E tiene una nulidad de 1 y la matriz D tiene una nulidad de 4, confirmando la estabilidad de la estructura.

5.2. Octaedro expandido

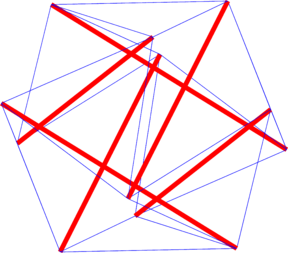
La Figura 4 corresponde a un octaedro expandido, estructura ampliamente estudiada en años recientes por sus propiedades y alta simetría. Esta figura puede ser modelada como el ensamble de dos estructuras de tres barras, o como una esfera.

(a)	(b)

Figura 4. Estructura de 6 barras. (a) Gráfico de Matlab, (b) modelo real.

Si se considera un radio de 105 mm, del SVD de E, en la Tabla 2 se muestra que el valor de la densidad de fuerza de todos los cables es igual (aquí se muestra solamente el valor del tipo de miembro para claridad). Para el octaedro expandido, la nulidad de E es 1 y la nulidad de D es 4.

Miembro	Densidad de fuerza
Cables	1.0
Barras	-1.5

Tabla 2. Densidades de fuerza para el octaedro expandido.

5.3. Esfera con conectividad estrella

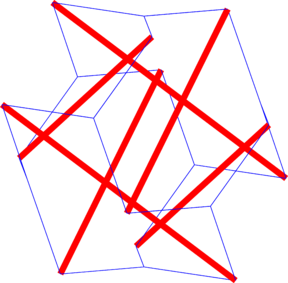
La Figura 5 es una modificación del octaedro expandido mostrado en la figura 4. En esta estructura, cada cable conecta únicamente una de las barras con un nodo ubicado en el centroide de cada uno de los triángulos equiláteros de la figura previa. Esta conectividad es conocida como estrella.

(a)	(b)

Figura 5. Estructura de 6 barras con conectividad estrella. (a) Gráfico de Matlab, (b) modelo real.

La Tabla 3 muestra que el patrón de conectividad influye en la distribución de fuerzas. Mientras que para el octahedro expandido la fuerza en las barras es 1.5 veces mayor que en los cables, con la conectividad estrella la densidad de fuerza en los cables duplica la de los elementos compresivos. De igual forma, la nulidad de las matrices E y D es 1 y 4, respectivamente.

Miembro	Densidad de fuerza
Cables	1.0
Barras	-0.5

Tabla 3. Densidades de fuerza para octaedro con conectividad estrella.

5.4. Domo tensegrítico

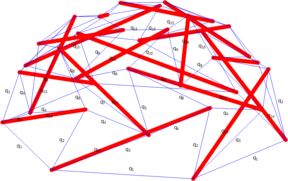
La estructura de la Figura 6 corresponde a un domo auto soportado, diseñado y construido en nuestro laboratorio; su topología puede ser consultada en [16]. Está conformado por 18 barras y 78 cables.

(a)	(b)

Figura 6. Domo de 18 barras. (a) Gráfico de Matlab, (b) modelo real.

Este domo fue generado mediante la modificación del método de Tran y Lee [7] introduciendo de un set inicial de coordenadas. Mediante el método de búsqueda de topología se obtiene una matriz E con nulidad 1 y un set de coordenadas que produce una matriz D con nulidad 4. En la Tabla 4 se muestran las densidades de fuerza para los diferentes grupos de simetría.

Miembros	Densidad de fuerza
q1	0.02724
q2	0.02328
q3	0.09232
q4	0.12494
q5	0.09889
q6	0.04232
q7	0.06705
q8	0.09870
q9	0.14854
q10	0.11530
q11	0.03074
q12	0.18298
q13	0.09209
q14	-0.07564
q15	-0.13213
q16	-0.11831

Tabla 4. Densidades de fuerza para domo tensegrítico.

6. Conclusiones

En el presente artículo se ha explicado el significado estructural de la descomposición en valores singulares de las matrices de equilibrio y de densidad de fuerza de las estructuras tensegríticas. Para ello se han descrito las propiedades teóricas del método de la descomposición en valores singulares SVD, además se ha detallado la topología y construcción de las diferentes matrices. Posteriormente se han relacionado los subespacios fundamentales de estas matrices con conceptos estáticos y cinemáticos de las estructuras tensegríticas. Finalmente se presentan diversos ejemplos de estructuras y los vectores de fuerzas obtenidos con el SVD.

La nulidad de la matriz de equilibrio permite obtener no solo la cantidad de estados de auto estrés de la estructura, sino también los valores de las densidades de fuerza que permiten alcanzar ese estado. Los vectores singulares izquierdos de esta matriz, a su vez, proporcionan información sobre los mecanismos infinitesimales de la estructura. El espacio nulo de la matriz de densidad de fuerza brinda los vectores necesarios para formar el set de coordenadas de una estructura estable.

Así pues, el SVD demuestra ser un método poderoso en el diseño de estructuras tensegríticas, que brinda gran cantidad de información presentada de manera lógica. Trabajo futuro debería considerar su aplicación a la solución de estructuras bajo carga externa.

Agradecimientos

Este artículo está financiado por el Fondo Nacional de Ciencias Naturales de China (NSFC), fondos 51605111, 51675114.

Bibliografía

[1] Connelly R., Back A. Mathematics and Tensegrity. American Scientist, 86:142-151, 1998.

[2] Motro, R. Tensegrity: Structural Systems for the Future. Kogan Page Science, Londres, 2003.

[3] Rieffel J., Valero-Cuevas F. y Lipson H. Automated discovery and optimization of large irregular tensegrity structures. Computers and Structures, 87:368-379, 2009.

[4] Koohestani K. Form-finding of tensegrity structures via genetic algorithm. International Journal of Solids and Structures, 49:739-747, 2012.

[5] Pellegrino S. Structural computations with the singular value decomposition of the equilibrium matrix. Int. J. Solids Struct., 30:3025-3035, 1993.

[6] Gómez-Estrada G., Bungartz H. y Mohrdieck C. Numerical form-finding of tensegrity structures. Int. J. Solids Struct., 43:6855-6868, 2006.

[7] Tran H.C., Lee J. Form-finding of tensegrity structures using double singular value decomposition. Engineering with Computers, 29:71-86, 2013.

[8] Hogben, L. Handbook of Linear Algebra. Chapman and Hall/CRC, New York, 2013.

[9] Kalman D. A Singularly Valuable Decomposition: The SVD of a Matrix. The College Mathematics Journal, 27:2-23, 1996.

[10] Gidak P., Fresl K. Programming the Force Density Method. IASS-APCS 2012, From spatial structures to space structures, Seoul, 2012.

[11] Lay, D., Lay, S. y McDonald, J. Linear Algebra and Its Applications. Pearson, Essex, 2015.

[12] Garcea G., Formica G. y Casciaro R. A numerical analysis of infinitesimal mechanisms. International Journal for Numerical Methods in Engineering, 62:979-1012, 2005.

[13] Sultan C. Tensegrity deployment using infinitesimal mechanisms. Int. J. Solids Struct., 51:3653-3668, 2014.

[14] Skelton, R., de Oliveira, M. Tensegrity Systems. Springer, New York, 2009.

[15] Quintana-Ortí G., Quintana-Ortí E. Descomposiciones ortogonales para el cálculo del rango numérico matricial. Revista internacional de métodos numéricos para cálculo y diseño en ingeniería, 15:461-470, 1999.

[16] González, A., Luo A., y Liu H. Study of a novel design for self-standing tensegrity domes. Proceedings of the IASS Annual Symposium 2017, Hamburg, 2017.