Cuantificación de incertidumbre sobre parámetros en modelos no lineales

1 Introducción

De acuerdo con [1], tradicionalmente se han modelado los problemas de ciencias, ingeniería, medioambiente y otras aplicaciones mediante modelos matemáticos deterministas que describen leyes naturales subyacentes. En la actualidad, se tiende cada vez más a incorporar algún tipo de incertidumbre para representar la falta de conocimiento sobre parámetros y datos físicos relevantes, variaciones aleatorias en las condiciones de operación o pura ignorancia sobre cómo debiera ser el modelo en realidad.

Suponga que se cuenta con observaciones ${\textstyle \mathbf {Y} =(y_{1},\dots ,y_{n}),}$ tomadas en los tiempos ${\textstyle \mathbf {t} =(t_{1},\dots ,t_{n})}$, de un fenómeno representado por medio de un sistema de ecuaciones con la siguiente estructura:

$y_{i}={\mathcal {H}}(X_{\theta }(t_{i}))+\varepsilon _{i},i={\overline {1,n}},$

(1)

donde ${\textstyle {\mathcal {H}}}$ es el funcional de observaciones, es común por ejemplo tener ${\textstyle \varepsilon _{i}\sim _{i.i.d.}{\mathcal {N}}(0,\sigma ^{2})}$ y ${\textstyle X_{\theta }}$ es la solución del siguiente sistema de ecuaciones diferenciales ordinarias, es decir; el regresor o el modelo directo (forward):

${\frac {dX_{\theta }}{dt}}=F(X_{\theta },t,\theta );X_{\theta }(t_{0})=X_{0}.$

(2)

Conociendo el verdadero valor de ${\textstyle \theta }$ y las condiciones iniciales, resolver y conocer a ${\textstyle X_{\theta }}$ se le llama un problema directo.

Sin embargo, en este caso el objetivo es hacer inferencia sobre ${\textstyle \theta }$ a partir de las observaciones ${\textstyle Y,}$ por eso se habla de un problema inverso [2].

Se puede considerar este problema como un mapeo:

${\mathcal {F}}_{\mathbf {t} }(\theta )=({\mathcal {H}}(X_{\theta }(t_{1})),\dots ,{\mathcal {H}}(X_{\theta }(t_{n}))),$

este es el “mapeo del modelo directo”.

El mapeo inverso está, en general; mal planteado y no tiene mucho sentido:

${\mathcal {F}}_{\mathbf {t} }^{-1}(y_{1},\dots ,y_{n})=\theta ,$

por eso es necesario realizar una estrategia de regularización, como la cuantificación de la incertidumbre mediante inferencia bayesiana.

Para resolver el problema de inferencia dado en la ecuación (1) se propone que las entradas de ${\textstyle \theta }$ sean variables aleatorias que siguen alguna distribución de probabilidad. Esto no necesariamente tiene un significado físico o intrínseco, sólo se sabe que se tiene incertidumbre acerca de los valores que pueden tomar estas variables aleatorias, y que la distribución de probabilidad cuantifica su incertidumbre. En este sentido, en el presente trabajo se aborda el problema de cuantificar la incertidumbre desde la perspectiva Bayesiana, en donde se obtiene la distribución a posteriori de los parámetros de interés.

2 Teoría Bayesiana

El trabajo de Thomas Bayes, publicado de manera póstuma en 1763, ha tenido una importante consecuencia en la forma de hacer inferencia estadística, este provee una manera formal de combinar el conocimiento a priori (o inicial) que se tiene sobre un fenómeno, con el nuevo conocimiento que se adquiere a partir de nuevos datos y mediciones sobre el mismo, obteniendo así un conocimiento a posteriori (o final). Es decir, el conocimiento a priori se actualiza con la nueva información, y dicho conocimiento a posteriori se convertirá en el nuevo conocimiento a priori, a la espera, otra vez, de nueva información que lo actualice. En este sección se utilizaron las siguientes bibliografías: [3], [4], [5], [6] y [7].

2.1 Distribución a priori y a posteriori

En estadística bayesiana, el término común para referirse a la información con la que cuenta el investigador es el de información subjetiva, y es importante aclarar, al menos brevemente, qué se entiende en este contexto por el adjetivo “subjetiva”, ya que puede tener una connotación distinta a la que se requiere bajo el enfoque bayesiano.

Al hablar de información subjetiva se refiere a toda aquella información a priori que se tiene en relación al fenómeno aleatorio de interés, antes de recolectar o realizar nuevas mediciones sobre el mismo, y esto incluye: datos históricos, teorías, opiniones y conjeturas de expertos, conclusiones basadas en estudios previos.

El primer paso en la inferencia estadística bayesiana es traducir todo lo anterior en una distribución de probabilidad a priori (o inicial). El segundo paso consiste en recolectar o realizar nuevas mediciones, y actualizar la distribución de probabilidad a priori, para obtener, mediante el teorema de Bayes, una distribución de probabilidad a posteriori (o final).

Será esta última la mejor descripción posible de la incertidumbre, de acuerdo a toda la información disponible, y por tanto, será la herramienta fundamental a partir de la cual se realiza inferencia estadística.

Para referirse a un modelo probabilístico paramétrico general se denota como ${\textstyle p_{X|\Theta }(x|\theta )}$, donde la función ${\textstyle p_{X|\Theta }(\cdot |\theta )}$ puede ser una función de masa de probabilidades de una variable (o vector) aleatoria discreta o bien una función de densidad de una variable aleatoria continua. El escribir dicha función condicional en el parámetro (o vector de parámetros) ${\textstyle \theta }$ se debe al hecho de que, una vez dado un valor específico de ${\textstyle \theta }$, la función de probabilidad queda totalmente determinada.

Para referirse a una muestra aleatoria (m.a.) se utilizará la notación ${\textstyle \mathbf {X} =(X_{1},\ldots ,X_{n})}$ y para referirse a una observación muestral se utilizará ${\textstyle \mathbf {x} =(x_{1},\ldots ,x_{n})}$. Por espacio paramétrico se entenderá como el conjunto ${\textstyle \Theta }$ de todos los valores que puede tomar ${\textstyle \theta }$, y por familia paramétrica se entenderá como un conjunto ${\textstyle P=\{p_{X|\Theta }(x|\theta ):\theta \in \Theta \}}$.

Siguiendo a [7], la estadística bayesiana modela la incertidumbre que se tiene sobre ${\textstyle \theta }$ probabilísticamente. Esto es, considere el valor de ${\textstyle \theta }$ como una variable (o vector) aleatoria con una distribución de probabilidad a priori (o inicial) ${\textstyle p(\theta )}$, de la misma forma se denotará solo como ${\textstyle p(\cdot )}$, sin importar si ${\textstyle \theta }$ es una variable aleatoria discreta o continua. Se trata de una distribución basada en experiencia previa (experiencia de especialistas, datos históricos, etc.) antes de obtener datos. Luego se procede a observar los nuevos datos (obtención de la muestra) ${\textstyle \mathbf {x} =(x_{1},\ldots ,x_{n})}$ y combina esta información con la distribución a priori mediante el teorema de Bayes y se obtiene una distribución de probabilidad a posteriori (o final):

$p_{\Theta |\mathbf {X} }(\theta |\mathbf {x} )={\frac {p_{\mathbf {X} ,\Theta }(\mathbf {x} ,\theta )}{p_{\mathbf {X} }(\mathbf {x} )}}={\frac {p_{\mathbf {X} |\Theta }(\mathbf {x} |\theta )\cdot p_{\Theta }(\theta )}{\int p_{\mathbf {X} |\Theta }(\mathbf {x} |\theta )\cdot p_{\Theta }(\theta )\,d\theta }}.$

(3)

Note que ${\textstyle p_{\Theta |\mathbf {X} }(\theta |\mathbf {x} )}$ es también una distribución de probabilidad de ${\textstyle \theta }$, pero a diferencia de la distribución a priori ${\textstyle p_{\Theta }(\theta )}$ toma en cuenta tanto la información contemplada en ${\textstyle p_{\Theta }(\theta )}$ como la información contenida en los datos observados ${\textstyle \mathbf {x} =(x_{1},\ldots ,x_{n})}$. La distribución a posteriori de la variable aleatoria ${\textstyle \Theta }$ es la base para hacer inferencias sobre ${\textstyle \theta }$.

Tenga presente que, por un lado, la función de verosimilitud ${\textstyle p_{\mathbf {X} |\Theta }(\mathbf {x} |\theta )}$ y ${\textstyle p_{\Theta }(\theta )}$ son distribuciones de probabilidad, y por otro:

$p_{\mathbf {X} }(\mathbf {x} )=\int p_{\mathbf {X} |\Theta }(\mathbf {x} |\theta )\cdot p_{\Theta }(\theta )\,d\theta ,$

es la probabilidad (o densidad) conjunta de la muestra ${\textstyle \mathbf {x} =(x_{1},\ldots ,x_{n})}$ observada a partir del vector aleatorio ${\textstyle \mathbf {X} =(X_{1},\ldots ,X_{n})}$. Pero hay que estar consciente de que ${\textstyle p(\mathbf {x} )}$ es constante respecto a ${\textstyle \theta }$, por lo que se puede escribir:

$p_{\Theta |\mathbf {X} }(\theta |\mathbf {x} )\propto p_{\mathbf {X} |\Theta }(\mathbf {x} |\theta )\cdot p_{\Theta }(\theta ),$

(4)

note que ${\textstyle p_{\mathbf {X} |\Theta }(\mathbf {x} |\theta )=p_{X|\Theta }(x_{1},x_{2},\dots ,x_{n}|\theta )}$, es la probabilidad conjunta de la muestra condicional en ${\textstyle \theta }$, llamada función de verosimilitud, denotada también por ${\textstyle L(\theta |\mathbf {x} )}$. En el caso particular de que los componentes del vector aleatorio ${\textstyle \mathbf {X} =(X_{1},\ldots ,X_{n})}$ resulten ser independientes, se tiene que:

$p_{\mathbf {X} |\Theta }(\mathbf {x} |\theta )=\prod _{j=1}^{n}p_{X|\Theta }(x_{j}|\theta {).}$

Puede proponer como estimador puntual de ${\textstyle \theta }$ alguna medida de tendencia central, por ejemplo la mediana o la esperanza:

${\hat {\theta }}:=E(\theta )=\int \theta \,p_{\Theta |X}(\theta |x)\,d\theta {.}$

(5)

Y aún en el caso de que no se cuente con información muestral se puede calcular ${\textstyle {\hat {\theta }}}$ utilizando ${\textstyle p_{\Theta }(\theta )}$ en lugar de ${\textstyle p_{\Theta |\mathbf {X} }(\theta |\mathbf {x} )}$.

En algunos casos en los que, en vez de conocer el vector de parámetros ${\textstyle \theta }$, lo que interesa es describir el comportamiento de observaciones futuras del fenómeno aleatorio en cuestión, esto es, hacer predicción.

Dado un valor de ${\textstyle \theta }$, la distribución que describe el comportamiento de la observación futura ${\textstyle X_{n}}$ es ${\textstyle p_{X_{n}|\Theta }(x|\theta )}$. El problema es que por lo general el valor de ${\textstyle \theta }$ es desconocido. Por lo regular, la estadística frecuentista aborda este problema estimando puntualmente a ${\textstyle \theta }$ con base en la muestra observada, y dicho estimador ${\textstyle {\hat {\theta }}}$ es sustituido en ${\textstyle p_{X_{n}|\Theta }(x|{\hat {\theta }})}$. Desde la perspectiva bayesiana, el modelo ${\textstyle p_{X_{n}|\Theta }(x|\theta )}$ junto con la distribución a priori ${\textstyle p_{\Theta }(\theta )}$ inducen una distribución conjunta para el vector aleatorio ${\textstyle (X_{n},\Theta )}$ mediante el concepto de probabilidad condicional:

$p_{X_{n},\Theta }(x,\theta )=p_{X_{n}|\Theta }(x|\theta )p_{\Theta }(\theta {).}$

Si se marginaliza la distribución de probabilidad conjunta anterior se obtiene:

$p_{X_{n}}(x)=\int _{\Theta }p_{X_{n},\Theta }(x,\theta )\,d\theta {.}$

De los dos resultados anteriores, se tiene:

$p_{X_{n}}(x)=\int _{\Theta }p_{X_{n}|\Theta }(x|\theta )p_{\Theta }(\theta )\,d\theta {.}$

(6)

A ${\textstyle p_{X_{n}}(x)}$ se le denomina distribución predictiva a priori (o inicial) y describe el conocimiento acerca de una observación futura ${\textstyle X_{n}}$ basado únicamente en la información contenida en ${\textstyle p_{\Theta }(\theta )}$. Nótese que ${\textstyle p_{X_{n}}(x)}$ no depende ya de ${\textstyle \theta }$.

Para hacer estimación por regiones, por ejemplo, si desea calcular la probabilidad de que el vector de parámetros ${\textstyle \theta }$ pertenezca a una región ${\textstyle A\subset \Theta }$:

$P(\theta \in A)=\int _{A}p_{\Theta |\mathbf {X} }(\theta |\mathbf {x} )d\theta ,$

o bien, dado un valor ${\textstyle \delta \in (0,1)}$, se busca un ${\textstyle A\subset \Theta }$ tal que ${\textstyle P(\theta \in A)=\delta }$. Con frecuencia la solución para ${\textstyle A}$ no es única. Cabe aclarar que si ${\textstyle {\hbox{dim}}(\Theta )=1}$ las regiones son subconjuntos de ${\textstyle \mathbb {R} }$ y que un caso particular de estas regiones son los intervalos. En este sentido, la estimación por regiones en estadística bayesiana es más general que la estimación por intervalos de la estadística frecuentista.

Una vez obtenida la muestra, el modelo ${\textstyle p_{X|\Theta }(x|\theta )}$ y la distribución a posteriori ${\textstyle p_{\Theta |\mathbf {X} }(\theta |\mathbf {x} )}$ inducen una distribución conjunta para ${\textstyle (\mathbf {X} ,\Theta )}$ condicional en los valores observados ${\textstyle \mathbf {x} =(x_{1},\dots ,x_{n})}$:

$p_{X,\Theta |\mathbf {X} }(x,\theta |\mathbf {x} )={\frac {p_{X,\Theta ,\mathbf {X} }(x,\theta ,\mathbf {x} )}{p_{\mathbf {X} }(\mathbf {x} )}}$ $={\frac {p_{X|\Theta ,\mathbf {X} }(x|\theta ,\mathbf {x} )p_{\Theta ,\mathbf {X} }(\theta ,\mathbf {x} )}{p_{\mathbf {X} }(\mathbf {x} )}}$ $=p_{X|\Theta ,\mathbf {X} }(x|\theta ,\mathbf {x} )p_{\Theta |\mathbf {X} }(\theta |\mathbf {x} )$ $=p_{X,\Theta }(x|\theta )p_{\Theta |\mathbf {X} }(\theta |\mathbf {x} ).$

En lo anterior, ${\textstyle p_{X|\Theta ,\mathbf {X} }(x|\theta ,\mathbf {x} )=p_{X,\Theta }(x|\theta )}$ se justifica por la independencia condicional de ${\textstyle X}$ y ${\textstyle \mathbf {X} =(X_{1},...,X_{n})}$ dado ${\textstyle \theta }$. Si se marginaliza la distribución conjunta condicional anterior:

$p_{X|\mathbf {X} }(x|\mathbf {x} )=\int p_{X,\Theta |\mathbf {X} }(x,\theta |\mathbf {x} )\,d\theta {.}$

Combinando los dos resultados anteriores:

$p_{X,\mathbf {X} }(x|\mathbf {x} )=\int p_{X|\Theta }(x|\theta )p_{\Theta |\mathbf {X} }(\theta |\mathbf {x} )\,d\theta .$

(7)

A ${\textstyle p_{X|\mathbf {X} }(x|\mathbf {\hbox{x}} )}$ se le llama distribución predictiva a posteriori (o final), y describe el conocimiento acerca de una observación futura ${\textstyle X}$ basado tanto en la información contenida en ${\textstyle p_{\Theta }(\theta )}$ como en la información muestral ${\textstyle \mathbf {x} =(x_{1},...,x_{n})}$. Nótese nuevamente que ${\textstyle p_{X|\mathbf {X} }(x|\mathbf {x} )}$ no depende de ${\textstyle \theta }$.

Así que para hacer predicción sobre observaciones futuras del fenómeno aleatorio que esté modelando se usa ${\textstyle p_{X}(x)}$ o bien ${\textstyle p_{X|\mathbf {X} }(x|\mathbf {x} )}$, según sea el caso. Y de manera análoga a lo mencionado sobre inferencia bayesiana, una manera simple de hacer predicción puntual, por ejemplo, de una observación futura ${\textstyle X}$ podría ser mediante alguna medida de tendencia central, como la mediana o la esperanza:

${\hat {x}}=E(X)=\int _{{\hbox{R}}(X)}x\,p_{X|\mathbf {X} }(x|\mathbf {x} )\,dx,$

donde ${\textstyle {\hbox{R}}(X)}$ es el rango de la v.a. ${\textstyle X}$. También, una manera de calcular la probabilidad de que una observación futura se encuentre en un conjunto ${\textstyle A\subseteq {\hbox{R}}(X)}$ sería:

$P(\{X\in A\})=\int _{A}p_{X|\mathbf {X} }(x|\mathbf {x} )dx.$

Las ecuaciones (3), (6) y (7) constituyen el modelo general de la estadística bayesiana. Cualquier problema estadístico tratado bajo el enfoque bayesiano implica la obtención y utilización de las distribuciones correspondientes.

3 Análisis bayesiano del problema inverso

Una vez conocidas algunas bases sobre probabilidad y estadística, estadística bayesiana, se puede realizar inferencia bayesiana para resolver problemas inversos. El caso particular que se abordará, será el del modelo de crecimiento logístico. Para el desarrollo de este capítulo se utilizaron las siguientes bibliografías: [8], [7], [9], [10] y [11].

3.1 Aproximación bayesiana a inferencia

Se considera un fenómeno representado por medio de un sistema de ecuaciones diferenciales ordinarias. Suponga que se cuenta con observaciones ${\textstyle \mathbf {y} =(y_{1},\dots ,y_{n})}$ tomadas en los tiempos ${\textstyle t=(t_{1},\dots ,t_{n})}$, con la siguiente estructura:

$y_{i}={\mathcal {H}}(X_{\theta }(t_{i}))+\varepsilon _{i},i={\overline {1,n}}$

(8)

Como se mencionó en la introducción, el objetivo es hacer inferencia sobre ${\textstyle \theta }$ a partir de las observaciones. Para resolver el problema de inferencia (8) se propone que las entradas de ${\textstyle \theta }$ sean variables aleatorias que siguen alguna distribución de probabilidad. La incertidumbre se cuantifica con una medida de probabilidad. El agente interesado en conocer el parámetro ${\textstyle \theta }$, establece una variable aleatoria ${\textstyle \Theta }$ con su densidad de probabilidad

$p_{\Theta }(\cdot ),$

Los valores que ${\textstyle \Theta }$ toma son los posibles valores para los parámetros, en este caso ${\textstyle \Phi =(\Theta ,\Sigma )}$ toma valores (${\textstyle \theta ,\sigma }$). Esta medida de probabilidad cuantifica la incertidumbre que tiene el agente respecto a los posibles valores de los parámetros en el modelo, ${\textstyle P_{\Phi }(\theta ,\sigma )}$ es la distribución a priori .

En presencia de datos ${\textstyle \mathbf {Y} =\mathbf {y} }$, y suponiendo un modelo para la distribución conjunta:

$p_{\mathbf {Y} |\Phi }(\mathbf {y} |\theta ,\sigma ),$

para ${\textstyle \mathbf {Y} }$, donde ${\textstyle E(y_{i}\mid \theta ,\sigma )={\mathcal {H}}(X_{\theta }(t_{i}))}$. Al observar los datos ${\textstyle Y}$, interesa inferir el valor de ${\textstyle \theta }$. La teoría bayesiana prescribe que calcular la distribución condicional de las incógnitas de interés dados los datos, se calcula utilizando el teorema de Bayes para variables aleatorias:

$p_{\Phi |\mathbf {Y} }(\theta ,\sigma |\mathbf {y} )={\frac {p_{\mathbf {Y} |\Phi }(\mathbf {y} |\theta ,\sigma )p_{\Phi }(\theta ,\sigma )}{p_{\mathbf {Y} }(\mathbf {y} )}},$

${\textstyle p_{\Phi |\mathbf {Y} }(\theta ,\sigma |\mathbf {y} )}$ es la distribución a posteriori; además ${\textstyle p_{\Phi }(\theta ,\sigma )}$ es la distribución a priori de ${\textstyle (\Theta ,\Sigma )}$ y

$p_{\mathbf {Y} }(\mathbf {y} )=\int p_{\mathbf {Y} ,\Phi }(\mathbf {y} ,\theta ,\sigma )d\theta d\sigma ,$

$p_{\mathbf {Y} }(\mathbf {y} )=\int p_{\mathbf {Y} |\Phi }(\mathbf {y} |\theta ,\sigma )p_{\Phi }(\theta ,\sigma )d\theta d\sigma ,$

es la constante de normalización, también llamada verosimilitud marginal.

En el caso en que el error de cada observación representa un ruido aditivo gaussiano, la función de verosimilitud es:

$p_{Y|\Phi }(\mathbf {y} |\theta ,\sigma )=\sigma ^{-n}(2\pi )^{-n/2}\exp \left(-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(y_{i}-{\mathcal {H}}(X_{\theta }(t_{i})))^{2}\right).$

Note que, cada vez que se evalué ${\textstyle p_{Y|\Phi }(\mathbf {y} |\theta ,\sigma )}$ debe resolverse a ${\textstyle X_{\theta }}$, lo cual se hace de forma aproximada por medio de un método numérico.

Como consecuencia, el sistema de ecuaciones diferenciales ordinarias se resuelve utilizando un método numérico y la inferencia se realiza, no en el modelo exacto anterior, sino en un modelo aproximado, a saber:

$y_{i}={\mathcal {H}}(X_{\theta }^{h}(t_{i}))+\varepsilon _{i},\quad \varepsilon _{i}{\underset {i.i.d}{\sim }}{\mathcal {N}}(0,\sigma ^{2})$

donde ${\textstyle X_{\theta }^{h}}$ denota la solución aproximada proporcionada por el método numérico. La nueva verosimilitud derivada del modelo es:

$p_{\mathbf {Y} |\Phi }^{h}(\mathbf {y} |\theta ,\sigma )=\sigma ^{-n}(2\pi )^{-n/2}\exp \left(-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(y_{i}-{\mathcal {H}}(X_{\theta }^{h}(t_{i})))^{2}\right).$

Para calcular ${\textstyle p_{\Phi |\mathbf {Y} }(\theta ,\sigma |\mathbf {y} )}$ comúnmente se usan métodos tipo Monte Carlo vía cadenas de Markov (MCMC). Este cálculo a su vez va a estar afectado por la precisión del método numérico usado para calcular a ${\textstyle X_{\theta }{.}}$

La distribución a posteriori numérica es:

$p_{\Phi |Y}^{h}(\theta ,\sigma |\mathbf {y} )={\frac {p_{Y|\Phi }^{h}(\mathbf {y} |\theta ,\sigma )p_{\Phi }(\theta ,\sigma )}{p_{\mathbf {Y} }^{h}(\mathbf {y} )}},$

donde ${\textstyle p(\theta ,\sigma )}$ es la distribución a priori en ${\textstyle (\theta ,\sigma )}$ y

$p_{\mathbf {Y} }^{h}(\mathbf {y} )=\int p_{\mathbf {Y} |\Phi }^{h}(\mathbf {y} |\theta ,\sigma )p_{\Phi }(\theta ,\sigma )d\theta d\sigma ,$

es la constante de normalización, también llamada verosimilitud marginal. Note que dado que no hay otra alternativa que utilizar la distribución a posteriori numérica, hay una necesidad real de comprender y controlar el error incurrido al trabajar con ${\textstyle p_{\Phi |\mathbf {Y} }(\theta ,\sigma |\mathbf {y} )}$ y la aproximada numéricamente ${\textstyle p_{\Phi |\mathbf {Y} }^{h}(\theta ,\sigma |\mathbf {y} ).}$

En el anexo A se menciona que un método numérico es de orden ${\textstyle p}$, si ${\textstyle \varepsilon _{h}(\theta )={\mathcal {O}}(h^{p})}$, es decir, ${\textstyle \varepsilon _{h}(\theta )\leq Kh^{p},}$ con K una constante global que no depende de ${\textstyle h}$. [12] demuestran que bajo un tamaño de paso ${\textstyle h,}$ se garantiza que prácticamente no existe diferencia entre la distribución a posteriori teórica ${\textstyle p_{\Phi |\mathbf {Y} }(\theta ,\sigma |\mathbf {y} )}$ y la aproximada numéricamente ${\textstyle p_{\Phi |\mathbf {Y} }^{h}(\theta ,\sigma |\mathbf {y} ).}$ Con lo cual se le da validez al análisis de inferencia que se realice a partir de la distribución a posteriori aproximada numéricamente.

Los métodos estadísticos tradicionales se centran en la estimación puntual. El estimador de máxima a posteriori (MAP) se considera como una versión regularizada del estimador de máxima verosimilitud o el estimador de mínimos cuadrados.

$\log(p_{\Phi |\mathbf {Y} }^{h}(\theta ,\sigma |\mathbf {y} ))=C+\log p_{\mathbf {Y} |\Phi }^{h}(\mathbf {y} |\theta ,\sigma )+\log p_{\Phi }(\theta ,\sigma )$ $=C-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(y_{i}-{\mathcal {H}}(X_{\theta }^{h}(t_{i})))^{2}+\log p_{\Phi }(\theta ,\sigma ),$

donde ${\textstyle C}$ es constante respecto a ${\textstyle \Phi }$. Si se supone que hay independencia entre las variables ${\textstyle \theta }$ y ${\textstyle \sigma ,}$ se tiene que:

$\log(p_{\mathbf {Y} |\Phi }^{h}(\mathbf {y} |\theta ,\sigma ))=C-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(y_{i}-{\mathcal {H}}(X_{\theta }^{h}(t_{i})))^{2}+\log p_{\Theta }(\theta )+\log p_{\Sigma }(\sigma )$

(9)

Esta última ecuación se llamará objetivo, y se utilizará más adelante.

3.2 El modelo logístico

De acuerdo con [9,13], una población es un grupo de organismos vivos (plantas, animales, microorganismos, etc.) que está compuesto por individuos con un comportamiento dinámico similar. Las poblaciones cambian de tamaño (crecen o disminuyen) debido al nacimiento, muerte y migración.

La dinámica de poblaciones estudia las leyes que rigen los cambios de la población en el espacio y el tiempo. Se centra en cómo las poblaciones cambian con el tiempo. Además, una población se describe por su número de individuos.

En 1798, Thomas Robert Malthus, propuso su modelo bajo las siguientes hipótesis:

1. La población es homogénea (todos los individuos son idénticos).
2. El medio es homogéneo, es decir, las características físicas, biológicas, etcétera, son las mismas en el hábitat.
3. No hay limitaciones ni de espacio ni de alimento para el crecimiento de la población (la tasa de cambio de la población en el tiempo ${\textstyle t}$ es proporcional a la población en ese instante de tiempo).
4. La población está aislada (no hay migración).
5. Las tasas de natalidad y de mortalidad son constantes.

Denote por:

• ${\textstyle X(t)}$ el número de individuos en el tiempo ${\textstyle t}$,
• ${\textstyle \beta }$ la tasa de natalidad, y
• ${\textstyle \mu }$ la tasa de mortalidad,

con ${\textstyle \beta }$ y ${\textstyle \mu }$ positivos, entonces, por las hipótesis dadas, se tiene el siguiente modelo:

${\frac {dX(t)}{dt}}=\beta X(t)-\mu X(t),$

o bien,

${\frac {dX(t)}{dt}}=rX(t),$

donde ${\textstyle r=\beta -\mu >0}$ y se le conoce como tasa de crecimiento instantáneo o tasa de crecimiento per cápita.

Cuarenta años más tarde, en 1838, el matemático belga Pierre François Verhulst (1804-1849) modificó el modelo de Malthus, cambiando la hipótesis 3:

• Los recursos (alimentos o tamaño del medio) son finitos.

Con esta nueva hipótesis habrá competencias entre la misma especie, así Verhulst propuso el modelo de crecimiento logístico:

${\frac {dX(t)}{dt}}=rX(t)\left(1-{\frac {X(t)}{K}}\right),$

o bien,

${\frac {dX(t)}{dt}}=LX(t)\left(K-X(t)\right),$

(10)

donde ${\textstyle L={\frac {r}{K}}}$ y se llama capacidad de carga.

Dada una condición inicial ${\textstyle X(0)=X_{0}}$, la ecuación (10) tiene como solución:

$X(t)={\frac {KX_{0}e^{LKt}}{K+X_{0}\left(e^{LKt}-1\right)}},$

(11)

o bien,

$X(t)={\frac {K}{1+\left({\frac {K}{X_{0}}}-1\right)e^{-rt}}}.$

A la ecuación (10) se le llama ecuación logística. A pesar de que el modelo de crecimiento logístico tiene a esta como solución explícita, se utilizará el programa odeint, que se encuentra en la paquetería scipy.integrate implementado en Python; pues realizarlo de esta manera podrá ser replicable para cualquier otro modelo no lineal al que se pueda solucionar con un método numérico.

3.3 Simulación estocástica y aplicación

De acuerdo con [8], las evaluaciones de incertidumbre también pueden adoptar la forma de intervalos o regiones de credibilidad, similares a los intervalos de confianza utilizados en la estadística clásica. En general, para realizar inferencias sobre las incógnitas en el modelo y finalmente responder preguntas relevantes de investigación, se debe ser capaces de analizar la distribución a posteriori.

Conforme a [14], aunque no es prudente intentar analizar directamente las propiedades de la distribución posterior, existen métodos indirectos que puede proporcionarnos información considerable. En lugar de pensar en la distribución posterior como una función, se puede utilizar el hecho de que es una distribución de probabilidad y, por lo tanto, puede analizarse mediante métodos estadísticos, siempre que exista una manera de obtener una muestra.

Para eso, se utilizará un método de Monte Carlo vía Cadenas de Markov (MCMC). Los métodos de MCMC representan un conjunto de algoritmos que permiten obtener muestras aleatorias de una determinada distribución de probabilidad objetivo, de la cual es difícil muestrear directamente. Estos métodos se basan en construir una cadena de Markov cuya distribución de equilibrio, es la distribución objetivo. De esta forma, los estados de la cadena de Markov después de que esta ha alcanzado el estado estacionario representan muestras de la distribución objetivo.

La principal ventaja de los métodos de Monte Carlo es que podemos muestrear de una medida de probabilidad solo conocida hasta una constante de normalización. La principal limitación de este enfoque es que los métodos de Monte Carlo se deterioran con el aumento de la dimensión del parámetro.

El algoritmo base para realizar MCMC, es el algoritmo Metropolis-Hasting, este tiene la siguiente estructura:

Sea ${\textstyle f}$ la distribución de interés. Como pre-proceso se genera el valor incial ${\textstyle X_{(0)}\sim \mu _{0}}$ (con ${\textstyle \mu _{0}}$ una distribución de probabilidad con el mismo soporte que ${\textstyle f}$). Para generar los valores ${\textstyle t=1,2,\dots }$ de la cadena de Markov, se hace: Siendo ${\textstyle X_{t}=x_{t}}$ el estado actual de la cadena de Markov se propone como candidato para el siguiente elemento de la cadena a ${\textstyle y_{t}\sim q(\cdot |x_{t}),}$ con ${\textstyle q}$ una distribución de probabilidad instrumental. Se hace ${\textstyle X_{(t+1)}={\begin{cases}y_{t}&{\hbox{ con probabilidad }}\rho (x_{t},y_{t})\\x_{t}&{\hbox{ con probabilidad }}1-\rho (x_{t},y_{t})\end{cases}}}$ con ${\textstyle \rho (x_{t},y_{t})=\displaystyle \min \left\{1,{\frac {f(y)q(x|y)}{f(x)q(y|x)}}\right\}}$.

Algoritmo. 1 Algoritmo Metropolis -Hasting

En general, los métodos de MCMC son muy complejos, requiriendo una calibración cuidadosa por parte de un experto, tanto para optimizar la velocidad de convergencia , como para identificar cuanto tiempo debe simularse la cadena antes de extraer la muestra. Una solución a este problema es el uso de una biblioteca de Python escrita por [15], llamada el t-walk, disponible en http://www.cimat.mx/ jac/twalk/. El t-walk utiliza un tipo especial de algoritmo Metropolis-Hastings de propósito general que se ajusta automáticamente para muestrear de cualquier distribución cuando se le proporcionan las funciones de soporte y el logaritmo de la función objetivo, en este caso la ecuación (9). Para iniciar el MCMC se debe añadir la cantidad de muestras a obtener y dos puntos iniciales.

Simulando un conjunto de datos sintético con la ecuación (11), con el modelo de error ${\textstyle y_{i}=X(t_{i})+\varepsilon _{i}}$, donde ${\textstyle \varepsilon _{i}\sim N(0,\sigma ^{2})}$, y los siguientes parámetros:

$X(0)=100,\quad L=1/1000,\quad K=1000,\quad \sigma =30.$

Se consideran 26 observaciones en los tiempos ${\textstyle t_{i}}$ distribuidos regularmente entre 0 y 10.

Para realizar la cuantificación de incertidumbre para esta simulación, se tiene:

$y_{i}={\mathcal {H}}(X_{\theta }(t_{i}))+\varepsilon _{i},i\in \{1,2,\dots ,n\},$

donde ${\textstyle {\mathcal {H}}(x)=x}$ y ${\textstyle \varepsilon _{i}\sim {\mathcal {N}}(0,\sigma ^{2})}$, además el modelo directo es,

${\frac {dX_{\theta }}{dt}}=F(X_{\theta },t,\theta ),$

$F(X_{\theta },t,\theta )=LX(K-X),$

donde ${\textstyle \theta =(L,K).}$ Suponiendo independencia a priori sobre los parámetros ${\textstyle K,L}$ y ${\textstyle \sigma }$, las distribuciones a priori propuestas son:

$K\sim Gamma(2,1/0.001),$

$L\sim Gamma(2,1/0.001),$

$\sigma \sim Gamma(2,1/0.001),$

dado que lo único que se “conoce” sobre estos parámetros es que son positivos, por esto se tomarán valores de la distribución gamma, la cual toma solo valores positivos.

(a) Distribución a posteriori del parámetro K.	(b) Distribución a posteriori del parámetro L.
(c) Distribución a posteriori del parámetro $\sigma$.
Figura 1: Distribuciones a posteriori de los parámetros del modelo.

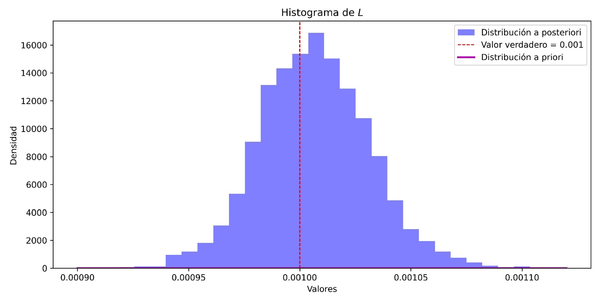
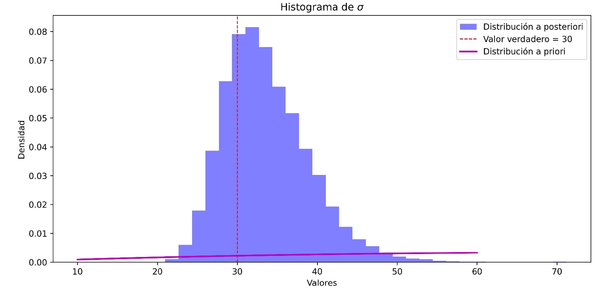
En las Figuras 1a, 1b y 1c, se tienen los histogramas de ${\textstyle 100\,000}$ valores de la distribución a posteriori de ${\textstyle K,L}$ y ${\textstyle \sigma {.}}$ Se puede observar que el valor verdadero, con el que se realizó la simulación está dentro de la distribución a posteriori, además de estar cercano al punto con mayor credibilidad. Además, note que la distribución a priori queda muy por debajo de la distribución a posteriori.

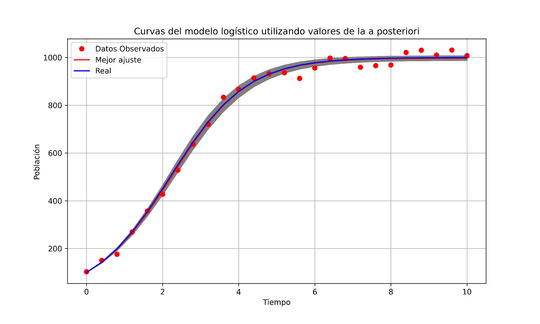
Figura 2: Incertidumbre del ejemplo de simulación.

En la Figura 2 se muestran los datos simulados, la solución del modelo logístico con los parámetros reales, la curva que mejor se ajusta la cual se forma utilizando los valores de mayor credibilidad en cada distribución a posteriori. Note que la curva con los parámetros reales y el mejor ajuste está una encima de la otra, salvo un pequeño error que es provocado por el error del método numérico. Por último, la parte sombreada son curvas solución a partir de valores de las distribución a posteriori para cada parámetro.

3.4 Aplicación: Saccharomyces cerevisiae

Las levaduras son hongos que forman sobre los medios de cultivo colonias pastosas, constituidas en su mayor parte por células aisladas que suelen ser esféricas, ovoideas, elipsoideas o alargadas. Los genetistas [16] realizaron un estudio para comparar la capacidad de sobrevivencia de cepas haploides, diploides y tetraploides de la levadura Saccharomyces cerevisiae al ser expuestas a mutaciones inducidas por metanosulfonato de etilo, evaluando las ventajas del enmascaramiento en niveles altos de ploidía, así como la eliminación de mutaciones en células haploides.

[9] recopilaron los datos del crecimiento de esta población de levaduras en diferentes horas, los datos se muestran en la Tabla 1.

Tabla. 1 Crecimiento de la levadura Saccharomyces cerevisiae.

Tiempo	Tamaño	Tiempo	Tamaño
(hrs)	($\times 10^{6}$/mL)	(hrs)	($\times 10^{6}$/mL)
0	0.200	19	209
1	0.330	20	190
2	0.500	21	210
3	1.10	22	200
4	1.40	23	215
5	3.10	24	220
6	3.50	25	200
7	9.00	26	180
8	10.0	27	213
9	25.4	28	210
10	27.0	29	210
11	55.0	30	220
12	76.0	31	213
13	115	32	200
14	160	33	211
15	162	34	200
16	190	35	208
17	193	36	230
18	190

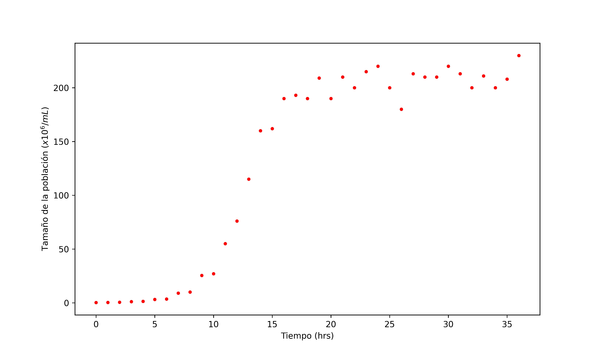
En la figura 3a se puede observar el crecimiento de la levadura durante las primeras 36 horas, donde es claro observar que siguen el comportamiento de un modelo de crecimiento logístico donde su capacidad de carga llega aproximadamente a 250.

(a) Crecimiento de la levadura Saccharomyces cerevisiae.	(b) Crecimiento de Saccharomyces cerevisiae, con el ajuste por mínimos cuadrados.
Figura 3: Análisis del crecimiento de Saccharomyces cerevisiae.

[9] sugieren el modelo logístico y muestran que las estimaciones de los parámetros son:

$K=211.538461,\quad L=0.0026,$

como los mejores para el ajuste de los datos al modelo. Cabe mencionar que no especifican el método utilizado para dichas estimaciones.

[17] presentó las siguientes estimaciones de los mismos parámetros calculados por mínimos cuadrados:

$K=208.855224,\quad L=0.00263224.$

La figura 3b muestra la gráfica del crecimiento y la curva con los parámetros estimados en [17].

Usando estos datos, se realiza el procedimiento de cuantificación de la incertidumbre suponiendo el modelo de crecimiento logístico como el regresor. Este proceso se realiza de manera similar al ejemplo de simulación, es decir, se toman las mismas distribuciones a priori.

Figura 4: Distribución a posteriori del parámetro $K$, Saccharomyces cerevisiae.

Figura 5: Distribución a posteriori del parámetro $L$, Saccharomyces cerevisiae.

Figura 6: Distribución a posteriori del parámetro $\sigma$, Saccharomyces cerevisiae.

En las Figuras 4, 5 y 6, se tienen los histogramas de ${\textstyle 100\,000}$ valores de la distribución a posteriori de ${\textstyle K,L}$ y ${\textstyle \sigma {.}}$ Se puede observar que los valores estimados por [9], [17] están dentro de la distribución a posteriori, además de estar cercanos al punto con mayor credibilidad, puede parecer que los valores estimados son los mismos pero se debe a la escala, estos si difieren un poco. Además, note que la distribución a priori queda muy por debajo de la distribución a posteriori. Por último, se puede ver la distribución a priori, donde hay un gran cambio entre la distribución a priori y la distribución a posteriori.

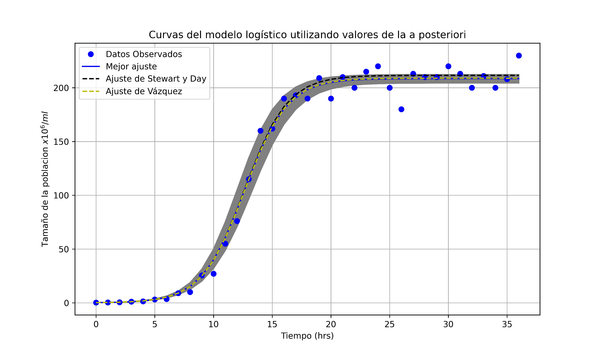
Figura 7: Incertidumbre de Saccharomyces cerevisiae.

En la Figura 7 se muestran los datos recopilados de la Tabla 1, la solución del modelo logístico con los parámetros de [17], [9] y la curva que mejor se ajusta, esta última se realizó utilizando los valores de mayor credibilidad en cada distribución a posteriori. Note que la curva con los parámetros dados por Vázquez se aleja un poco de las otras dos curvas, además la curva de mejor ajuste con la de Stewart y Day coinciden, por ese motivo se colocó de manera punteada, para distinguir entre cada una.

La Figura 7 es un ejemplo de una aplicación de la distribución a posteriori. Además, como se tiene varios valores de esta distribución se pueden encontrar valores de interés como las medidas de localización, medidas de variabilidad, coeficiente de asimetría y coeficiente de curtosis o algún otro cálculo dependiendo del interés del investigador.

El área sombreada se formó tomando curvas solución a partir de valores de las distribución a posteriori para cada parámetro. El uso de un área sombreada alrededor de los parámetros que mejor se ajustan en las gráficas de modelos es una técnica común en el análisis de datos. Esta área sombreada suele representar la incertidumbre o la variabilidad de los parámetros del modelo, en este caso, obtenida de la distribución a posteriori.

Esta área sombreada proporciona una visualización clara de la incertidumbre en las estimaciones de los parámetros del modelo. Muestra cómo varían las predicciones del modelo debido a la variabilidad en los datos. Esto es crucial en el enfoque bayesiano, donde la incertidumbre en los parámetros es una parte integral del análisis, por ejemplo, permite comunicar de manera efectiva la precisión y la confianza en las predicciones del modelo. El investigador puede ver, no sólo una línea de mejor ajuste, sino también cuánto pueden variar las predicciones. Esto es importante en contextos de toma de decisiones, donde entender la variabilidad puede influir en las decisiones basadas en los resultados del modelo. Además, facilita la comparación entre diferentes modelos o ajustes. Al superponer áreas sombreadas de diferentes modelos, se puede ver rápidamente cuál modelo proporciona predicciones más precisas o con menos incertidumbre.

Las áreas sombreadas pueden ayudar a identificar puntos de datos que se encuentran fuera de las predicciones esperadas, señalando posibles anomalías o la necesidad de ajustar el modelo. Por todo esto, es mejor optar en el futuro por resolver problemas inversos utilizando estadística bayesiana, no sólo usar métodos estadísticos y numéricos clasicos.

4 Conclusiones

El análisis de cuantificación de incertidumbre bayesiana de problemas inversos continua siendo un tema de investigación desafiante. El presente artículo es una introducción a realizar inferencia en el aspecto del análisis bayesiano de sistemas de ecuaciones diferenciales ordinarias en el contexto de problemas inversos, en particular el caso del modelo logístico.

Los problemas inversos surgen en una variedad de aplicaciones científicas y de las ingenierías, donde los parámetros del modelo deben ser estimados a partir de datos observacionales. Estos problemas se caracterizan por errores observacionales, errores de modelo y problemas de mal planteamiento que generan incertidumbres en los parámetros del modelo. Los enfoques estadísticos bayesianos permiten realizar simulaciones y predicciones con incertidumbres cuantificadas.

Se ha destacado la dificultad añadida que presentan estos problemas debido a la incapacidad de tratar analíticamente la función del regresor, lo que nos obliga a recurrir a aproximaciones numéricas. A pesar de que comúnmente se pasa por alto la sustitución de la solución teórica por una aproximación numérica. Se ha señalado el trabajo de investigación que [12] ha llevado sobre realizar inferencia sobre la distribución a posteriori númerica, en lugar de la téorica.

Como se mencionó, la distribución a posteriori puede tomar la forma de un área sombreada alrededor de los ajustes del modelo, esta área sombreada muestra la incertidumbre en las estimaciones de los parámetros del modelo. Muestra cómo varían las predicciones del modelo debido a la variabilidad en los datos. El investigador al resolver el problema inverso utilizando este método no solo obtiene los mejores parámetros que se ajustan, sino toda una distribución para ellos, lo que ayuda a ver cuánto pueden variar las predicciones.

Uno de los logros destacables de este trabajo es presentar de manera detallada un código realizado en Python, para la obtención de la distribución a posteriori para los parámetros de un modelo no lineal. Además, que el mismo genera histogramas de esta distribución, lo que ayuda a comprender a la misma y analogizar entre distribuciones más conocidas. Este código no lo muestran en trabajos del mismo tema, con este nivel de detalle. Los códigos se encuentran disponibles en https://github.com/RodGon22/RepositarioTesisRodrigo o escaneando el código QR de la Figura 8.

Por último, la aplicación como la que se mostró en la sección 3 ilustra cómo un enfoque probabilístico para codificar errores en el proceso de modelado puede conducir a simulaciones predictivas con medidas de incertidumbre confiables en problemas del mundo real. Sin embargo, aplicaciones más rigurosas conllevan más desafíos relacionados con la computación de alto rendimiento, alta dimensionalidad en datos y parámetros, predicción y otros que no se abordaron en este trabajo que se pueden considerar problemas a futuro.

Figura 8: QR del repositario, generado con Google.

BIBLIOGRAFÍA

[1] Carpio, Ana. (2023) "Incertidumbre y problemas inversos"

[2] Molina, Muñoz J. D. (2023) "Cuantificación de la Incertidumbre desde el enfoque bayesiano en el contexto de EDO"

[3] Lee, Peter M. (2009) "Bayesian statistics: an introduction. 3rd". Wiley, New York

[4] Bernardo, José M and Smith, Adrian FM. (2009) "Bayesian theory", Volume 405. John Wiley & Sons

[5] Mendoza, Manuel and Regueiro, Pedro. (2011) "Estadística Bayesiana". Instituto Teconológico de México

[6] Correa Morales, Juan Carlos and Barrera Causil, Carlos Javier. (2018) "Introducción a la estadística Bayesiana". Editorial ITM. Textos Académicos

[7] Erdely, Arturo and Gutiérrez-Peña, Eduardo. (2023) "Monografía de Estadística Bayesiana". arXiv preprint arXiv:2309.06601

[8] Christen, J Andrés. (2020) "Cuantificación de Incertidumbre bayesiana (Bayesian UQ)"

[9] Stewart, James and Day, Troy. (2015) "Biocalculus: Calculus for Life Sciences". Cengage Learning

[10] Kuschinski Kathmann, Nicolás Elio. (2014) "Improvements in Chronology Building from 14C Measurements using Bayesian Inference on Autoregressive Gamma Processes". CIMAT

[11] Torres, Maria Luisa Daza. (2018) "Numerical Solution of the Inverse Scattering Problem using High Level Representations"

[12] Capistran, Marcos and Christen, J. and Daza, Maria and Flores Arguedas, Hugo and Montesinos-López, J. (2021) "Error Control of the Numerical Posterior with Bayes Factors in Bayesian Uncertainty Quantification", Volume -1. Bayesian Analysis

[13] Iannelli, Mimmo and Pugliese, Andrea. (2015) "An introduction to mathematical population dynamics: along the trail of volterra and lotka", Volume 79. Springer

[14] Kuschinski Kathmann Nicolás Elio. (2014) "Improvements in Chronology Building from 14C Measurements using Bayesian Inference on Autoregressive Gamma Processes". CIMAT

[15] Christen, J Andrés and Fox, Colin. (2010) "A general purpose sampling algorithm for continuous distributions (the t-walk)"

[16] Mable, Barbara K and Otto, Sarah P. (2001) "Masking and purging mutations following EMS treatment in haploid, diploid and tetraploid yeast (Saccharomyces cerevisiae)", Volume 77. Cambridge University Press. Genetics Research 1 9–26

[17] Virgilio Vázquez. (2023) "Notas de modelación matemática". Universidad Tecnológica de la Mixteca