Resumo
Este trabalho tem como objetivo avaliar o comportamento inelástico de sistemas estruturais metálicos submetidos à flexão em torno do eixo de menor inércia. Consideram‐se seções transversais compactas do tipo I. Nessas seções, a flexão em torno do eixo mais fraco apresenta benefícios importantes como a capacidade de desenvolver toda resistência plástica sem ocorrência de flambagem lateral por torção. Adota‐se uma formulação de elementos finitos reticulados planos, na qual o processo de plastificação do aço é acompanhado através do método da rótula plástica refinado. Nesse método, os efeitos decorrentes do escoamento do material são capturados através de um parâmetro que reduz a rigidez do membro estrutural em função do desenvolvimento de regiões plásticas. Emprega‐se ainda nesse método o módulo tangente para considerar a degradação da rigidez em função das forças internas. Efeitos de segunda ordem, tensões residuais e imperfeições geométricas também são considerados nas análises. Como critério para definir o estado limite último de resistência da seção transversal adotam‐se superfícies de plastificação que descrevem a interação entre esforço normal e momento fletor. Para solução das equações não lineares de equilíbrio estrutural usa‐se o método de Newton‐Raphson acoplado a estratégias de continuação. Colunas isoladas e pórticos planos são analisados e os resultados obtidos são comparados aos encontrados por outros pesquisadores. Essas comparações permitem concluir que as técnicas usadas neste trabalho são eficazes e necessárias para uma melhor previsão do comportamento das estruturas com membros submetidos à flexão em torno do eixo de menor inércia.
Abstract
This work presents an evaluation of the inelastic behavior of steel structures subjected to minor‐axis bending. Profiles type I and compact cross‐sections are considered. In these sections, the bent about weak axis presents important benefits, such as the ability to develop all of their plastic resistance without the occurrence of lateral torsional buckling. A nonlinear beam‐column element formulation is adopted, in which the steel yielding process is accounted by the refined plastic‐hinge method. In this method the effects of material yielding are captured by a parameter that reduces the structural member stiffness with the development of cross‐section plastic regions. The tangent modulus approach is used to consider the stiffness degradation caused by the increase in internal forces. Second–order effects, residual stresses and geometric imperfections are also considered in analysis. To define the cross‐section strength ultimate limit state, the study adopts strength surfaces that describe the interaction between internal forces — axial force and bending moment. The nonlinear equations at the structural system level are solved using the Newton‐Raphson iterative strategy coupled with path‐following methods. Isolated steel columns and portal frames are analyzed, and the results obtained are compared to those of other investigators. The comparison shows that the numerical methodology presented in this work is effective and can be used for predicting the behavior of steel structures with members under minor‐axis bending.
Palavras‐chave
Análise inelástica ; Método dos elementos finitos ; Método da rótula plástica refinado ; Módulo tangente ; Eixo de menor inércia
Keywords
Inelastic analysis ; Finite Element Method ; Refined plastic‐hinge method ; Tangent modulus ; Minor axis bending
1. Introdução
Para melhor prever o comportamento de uma estrutura de aço, os efeitos da inelasticidade do material, de segunda ordem e tensões residuais devem ser considerados. Devido a isso, a análise inelástica avançada, na qual esses efeitos são avaliados, vem sendo tema de muitos estudos nos últimos anos [1] , [2] , [3] , [4] , [5] and [6] .
No contexto do método dos elementos finitos ressaltam‐se 2 métodos de análise inelástica avançada: zona plástica e rótula plástica refinado. No método da zona plástica [1] and [2] a seção transversal de cada elemento finito é discretizada em fibras. Efeitos de segunda ordem e tensões residuais podem ser considerados diretamente na análise. Além disso, o estado de tensão pode ser obtido em cada fibra, o que possibilita o acompanhamento gradual do escoamento na seção transversal. Devido à eficácia desse método, suas soluções são tratadas como «exatas» na literatura [7] . Porém, o método da zona plástica não é usado rotineiramente nos escritórios de engenharia, pois requer um intenso esforço computacional. Por isso sua aplicação é mais restrita à simulação de estruturas simples, que servirão de comparação e/ou calibração para o desenvolvimento de outros modelos e formulações.
No método da rótula plástica refinado [3] and [4] , a consideração da plastificação do material é concentrada nos pontos nodais de cada elemento finito. Nesses nós pode ocorrer formação de rótulas plásticas, caracterizando assim uma seção totalmente plastificada. Esse método é mais eficiente computacionalmente e captura de maneira aproximada o avanço da plastificação nas seções do elemento antes da formação da rótula plástica.
O objetivo deste artigo é possibilitar, através do método da rótula plástica refinado, uma modelagem adequada do comportamento inelástico de colunas de aço com seções compactas do tipo I, submetidas à flexão em torno do eixo de menor inércia. Embora não seja usual, colunas com flexão em torno desse eixo apresentam benefícios importantes como a capacidade de desenvolver toda a sua resistência plástica sem a ocorrência da flambagem lateral por torção [8] and [9] . Além disso, para perfis de abas largas, o fator de forma é aproximadamente 35% maior que o referente ao eixo de maior inércia [10] . Ressalta‐se ainda que a flexão em torno do eixo mais fraco não é alvo de muitos estudos e uma análise inelástica nessa situação requer técnicas adequadas. Este trabalho vem contribuir exatamente com o estudo de tais técnicas.
Para atender ao objetivo proposto, foi implementado no sistema computacional Computational System for Advanced Structural Analysis (CS‐ASA) [11] a equação para o módulo tangente sugerida por Ziemian e McGuire [5] . Nessa equação a degradação da rigidez da seção varia em função do esforço normal e do momento fletor em torno do eixo de menor inércia. Também empregam‐se superfícies de resistência [9] , [12] and [13] que avaliam de maneira adequada a interação entre esforço normal e momento fletor no eixo de menor inércia. A validação dessas estratégias é feita com a análise de colunas isoladas e pórticos com membros fletidos em torno do eixo de menor inércia. Os resultados obtidos são comparados com soluções analíticas ou soluções numéricas encontradas com o método da zona plástica. Neste trabalho, os efeitos de segunda ordem são simulados através de equações desacopladas de rigidez e a metodologia de solução não linear é baseada no emprego do método de Newton‐Raphson acoplado a estratégias de continuação.
2. Método da rótula plástica refinado
O objetivo do método da rótula plástica refinado é capturar o avanço da plastificação na seção transversal desde o início do escoamento até sua plastificação total com a formação da rótula plástica. Para atender esse objetivo, o método possui algumas estratégias fundamentais. As equações das superfícies de resistência, por exemplo, são responsáveis por detectar a formação das rótulas plásticas. O módulo de elasticidade tangente, por sua vez, captura a degradação da rigidez da seção transversal devido ao esforço normal. Destacam‐se também as formulações adotadas para considerar os efeitos de segunda ordem e as tensões residuais. Todas essas estratégias são descritas com mais detalhes nas subseções seguintes.
2.1. Superfícies de resistência
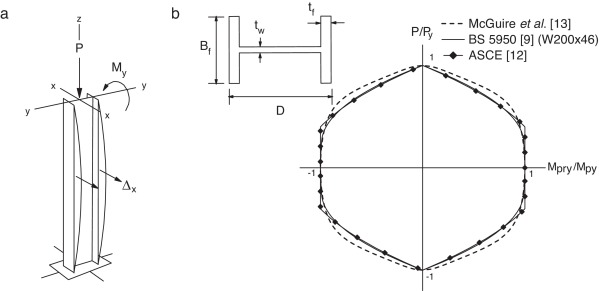
No contexto do método da rótula plástica refinado, as superfícies de resistência são responsáveis por definir o instante em que ocorre a formação da rótula plástica, ou seja, a plastificação total da seção. Essa definição é feita a partir da avaliação da interação entre as forças internas (esforço normal e momento fletor) nas seções transversais. O comportamento do membro estrutural quando o momento fletor atua no eixo de menor inércia é ilustrado na figura 1 a, na qual Δx indica a deformação devido à flexão.
|
|
|
Figura 1. a) Membro estrutural submetido à flexão em torno do eixo de menor inércia; b) superfícies de resistência. |
McGuire et al. [13] propuseram uma superfície válida para perfis padrão americano de peso leve a médio que, particularmente para o eixo de menor inércia, pode ser expressa por:
|
|
( 1) |
sendo Mpry o momento plástico reduzido e Mpy o momento de plastificação, ambos em relação ao eixo de menor inércia. Nessa equação, p é a relação entre o esforço normal atuante e a força normal de escoamento (p = P/Py ).
A ASCE [12] , por sua vez, recomenda a utilização da seguinte expressão:
|
|
( 2) |
Já a norma britânica BS 5950 [9] fornece expressões para o momento plástico reduzido (Mpr ) de perfis compactos do tipo I ou H , e com mesas iguais, na presença de esforço normal. Em relação ao eixo de menor inércia essas equações são dadas por:
|
|
( 3) |
|
|
( 4) |
Nas equações (3) e (4), A é a área da seção do perfil, tw é a espessura da alma, tf é a espessura da mesa, Bf é a largura da mesa e D é a altura da seção do perfil, como mostrado na figura 1 b. O termo Zy é o módulo plástico da seção em relação ao eixo de menor inércia. Na figura 1 b também são ilustradas as superfícies de resistência obtidas conforme as equações apresentadas anteriormente.
2.2. Módulo de elasticidade tangente
O módulo de elasticidade tangente captura, de maneira aproximada, a redução da rigidez da seção do elemento devido ao esforço normal. As equações de resistência para colunas do AISC [8] definem a variação do módulo tangente como:
|
|
( 5) |
em que E é o módulo de elasticidade do material, P é o esforço normal atuante, e Py é o esforço normal de escoamento. Nessas equações estão incluídos os efeitos das imperfeições iniciais e também das tensões residuais. No entanto, só são válidas para esforços normais de compressão (P < 0). Para esforços normais de tração (P > 0) podem‐se utilizar as equações de resistência para colunas propostas pelo CRC [14] , que são dadas por:
|
|
( 6) |
Ressalta‐se que as equações (5) e (6) consideram de forma implícita os efeitos das tensões residuais. Ziemian e McGuire [5] propuseram uma modificação nas equações propostas pelo CRC [14] na qual o módulo de elasticidade tangente varia em função do esforço normal e, também, do momento de flexão em torno do eixo mais fraco. Nesse caso, tem‐se:
|
|
( 7) |
com:
|
|
( 8) |
Nas equações anteriores o termo β é um valor empírico, que em análises inelásticas de segunda ordem é considerado igual a 0,65 para a flexão em torno do eixo de menor inércia, como propõe Ziemian e McGuire [5] . Na equação (8) My e MPy são o momento fletor atuante e o momento plástico, ambos em relação ao eixo de menor inércia.
2.3. Tensões residuais
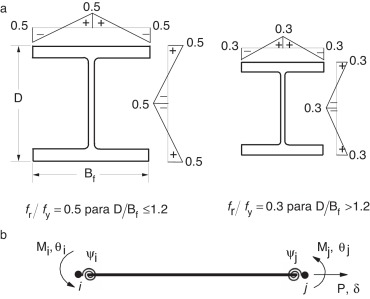
Conforme mencionado na seção anterior, os efeitos causados pelas tensões residuais são considerados de maneira implícita no cálculo do módulo de elasticidade tangente. Porém, essas tensões também podem ser expressas de forma explícita, seguindo recomendações normativas. O European Convention for Construction Steelwork (ECCS) [15] , por exemplo, considera uma variação linear da tensão residual na seção transversal do perfil, como apresentado na figura 2 a, e que seu valor máximo depende da razão entre a altura e a largura da seção. Vale destacar que este trabalho segue as recomendações de [15] , porém, considera que os valores máximos da tensão residual obedeçam as relações fr /fy = 0,5 (D /Bf ≤ 1,2) e fr /fy = 0,3 (D /Bf > 1,2), em que fr é a tensão residual e fy é a tensão de escoamento [3] . Como será mostrado adiante, a tensão residual afetará a determinação do momento de início de escoamento da seção Mer. A norma AISC [8] , por sua vez, recomenda que a tensão residual de compressão nas mesas seja tomada igual a 30% da tensão de escoamento do aço utilizado.
|
|
|
Figura 2. a) Distribuição das tensões residuais nos perfis recomendada pelo ECCS; b) forças e deslocamentos nodais do elemento finito no sistema corrotacional. |
2.4. Efeitos de segunda ordem
Quando ocorrem grandes deslocamentos, a deflexão lateral de um membro pode levar ao aparecimento de momentos fletores adicionais devido à presença de esforço normal, que dão origem aos efeitos de segunda ordem. No presente trabalho, para simular esses efeitos utilizam‐se equações desacopladas de rigidez oriundas da formulação geometricamente não linear proposta por Yang e Kuo [16] . A utilização dessas equações será mostrada na seção seguinte.
3. Modelagem numérica
As análises estruturais realizadas neste trabalho foram feitas através do sistema computacional CS‐ASA [11] . Para atender aos objetivos propostos, o código foi expandido com novas implementações e possibilidades de análise estrutural. Nesta seção apresenta‐se a modelagem numérica para análise inelástica e as principais intervenções propostas nesta pesquisa.
3.1. Hipóteses assumidas
As seguintes hipóteses são consideradas na modelagem das estruturas:
- todos elementos são inicialmente retos e prismáticos, e suas seções transversais permanecem planas após a deformação;
- os perfis são compactos de forma que a seção possa desenvolver capacidade total de rotação plástica sem que haja flambagem local;
- grandes deslocamentos e rotações de corpo rígido são permitidos;
- encurtamento axial devido à curvatura oriunda de flexão no membro é desprezado;
- os efeitos de deformação por cortante serão desprezados.
Utiliza‐se o elemento finito de pórtico plano delimitado pelos pontos nodais i e j , com molas fictícias nas extremidades. Esse elemento é apresentado na figura 2 b considerando o sistema corrotacional. Nessa mesma figura pode ser visto o parâmetro ψ, que está associado com o nível de plastificação nos nós e será detalhado a seguir.
3.1.1. Formulação inelástica
Assume‐se que o desenvolvimento da plasticidade nos membros estruturais seja simulado através de uma pseudomola com rigidez rotacional variável. Para acompanhar a degradação da rigidez da seção transversal nos pontos nodais do elemento utiliza‐se o parâmetro ψ, que assume valor unitário quando o elemento está no regime elástico e se anula quando ocorre a formação de uma rótula plástica. Considerando esse parâmetro, a rigidez da mola denotada por Ss é expressa como:
|
|
( 9) |
em que E é modulo de elasticidade, I é o momento de inércia e L é comprimento do elemento de viga‐coluna.
A expressão usada para definir ψ é [3] :
|
|
( 10) |
sendo Mer o momento de início de escoamento e Mpr o momento de plastificação. O momento de início de escoamento é dado por:
|
|
( 11) |
no qual fy é a tensão de escoamento, fr é a tensão residual, A é a área da seção e W é o módulo elástico da seção. A tensão residual, fr , deve ser adotada seguindo recomendações normativas, conforme foi descrito na subseção 2.3.
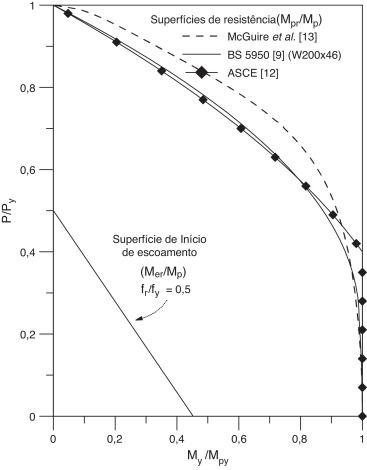
O momento de plastificação é definido conforme a escolha da superfície de resistência a ser utilizada. As superfícies adotadas neste trabalho foram detalhadas na subseção 2.1 e são ilustradas em conjunto com a superfície de início de escoamento na figura 3 .
|
|
|
Figura 3. Superfícies de início de escoamento e de resistência plástica. |
Para o elemento ilustrado na figura 2 b, a relação força‐deslocamento é expressa por:
|
|
( 12) |
sendo β = (Ssi + kii )(Ssj + kjj ) − kjikij . Os subscritos i e j são relacionados às extremidades do elemento e o subscrito c indica o sistema de coordenadas utilizado; A é a área da seção transversal; L é o comprimento do elemento; ΔP e ΔM são, respectivamente, o esforço normal e o momento fletor incrementais; Δδ e Δθ são os incrementos de deformação axial e rotação nodais.
Os termos kii , kij , kji e kjj são responsáveis por simular os efeitos de segunda ordem que, neste trabalho, são definidos como [16] :
|
|
( 13) |
sendo I o momento de inércia. Para atender o objetivo proposto neste trabalho foram utilizadas as equações para o módulo tangente indicadas por Ziemian e McGuire [5] , que dependem do esforço normal e também do momento de flexão em torno do eixo de menor inércia. Como o momento é avaliado nas extremidades i e j do elemento finito ( figura 2 b), os termos provenientes da matriz de rigidez elástica na equação (13) são recalculados considerando que o módulo tangente varia linearmente ao longo do comprimento do elemento finito, ou seja:
|
|
( 14) |
com Et ,i e Et ,j representando o módulo tangente modificado nas extremidades i e j , respectivamente.
Usando funções de interpolação apropriadas, os coeficientes kii, kij , kji e kjj tornam‐se:
|
|
( 15) |
A equação (12) é válida até as forças internas atingirem a resistência plástica da seção. Daí em diante, com a seção já plastificada, o aumento de esforço normal, por exemplo, faz com que a resistência da seção se torne menor que as forças que nela atuam. Assim sendo, uma alteração na relação força‐deslocamento é necessária para que as equações de resistência plástica da seção não sejam violadas. Essa alteração é escrita como:
|
|
( 16) |
na qual K22 = kc (2,2) − kc (2,3) kc (3,2) /kc (3,3) e K33 = kc (3,3) − kc (2,3) kc (3,2) /kc (2,2) , sendo kc (m ,n ) o termo correspondente à linha m e à coluna n na matriz de rigidez Kc (equação 12). O vetor Δfps é o vetor de correção dos esforços internos e os coeficientes C1 , C2 , ζ1 e ζ2 são definidos na tabela 1 de acordo com a extremidade onde se forma a rótula plástica.
| Rótula plástica | Parâmetros | |||
|---|---|---|---|---|
| C1 | C2 | ζ1 | ζ2 | |
| Extremidade i | 0 | 1 | δMpr(i) | δMpr(i) (kc(3,2)/kc(2,2)) |
| Extremidade j | 1 | 0 | δMpr(j) (kc(2,3)/ kc(3,3)) | δMpr(j) |
| Extremidades i e j | 0 | 0 | δMpr(i) | δMpr(j) |
Na tabela 1 δMpr indica a redução necessária no momento fletor M , para que o mesmo retorne à superfície de resistência, mantendo o esforço normal P fixo. A transformação das equações (12) e (16) para o sistema global de coordenadas é detalhada em Silva [11] .
4. Solução numérica
No contexto do método dos elementos finitos, a condição de equilíbrio dos problemas estruturais inelásticos estudados neste trabalho pode ser expressa como:
|
|
( 17) |
em que Fi refere‐se ao vetor de forças internas, que é uma função não linear dos deslocamentos nodais U , e também depende dos esforços normais nos membros, P , e do parâmetro que controla a plastificação da seção, ψ . O lado direito caracteriza o vetor de forças externas, no qual λ é o parâmetro de carga e Fr é o vetor de forças externas de referência.
A solução da equação (17) é obtida neste trabalho através de um processo incremental e iterativo. Esse processo é organizado em 2 etapas fundamentais: primeiramente, a partir da última configuração de equilíbrio da estrutura, monta‐se a matriz de rigidez tangente K e seleciona‐se o incremento inicial de carga Δλ0 , onde se procura satisfazer alguma equação de restrição imposta ao problema. Com o valor de Δλ0 , determina‐se o incremento inicial dos deslocamentos nodais, ΔU0 . Os valores de Δλ0 e ΔU0 caracterizam a chamada solução predita que, a princípio, não satisfaz a equação (17), pois Fi é uma função não linear dos deslocamentos. Por isso, numa segunda etapa, é feita a correção dessa solução predita através do processo iterativo de Newton‐Raphson acoplado às técnicas de continuação, como o comprimento de arco [17] .
5. Exemplos numéricos
Nesta seção avalia‐se a eficácia das estratégias numéricas adotadas na análise inelástica de colunas e pórticos de aço com flexão em torno do eixo de menor inércia. Para facilitar a apresentação dos resultados, usa‐se a notação simplificada indicada na tabela 2 para se referir aos diferentes modelos que descrevem a variação do módulo de elasticidade tangente com as forças internas. O uso do módulo de elasticidade constante é possível, e também está indicado.
| Notação | Descrição/Equação |
|---|---|
| Et0 | Módulo de elasticidade E |
| Et1 | AISC [8] e CRC [14]: equações (5) e (6) |
| Et2 | CRC [14]: equação (6) |
| Et3 | Ziemian e McGuire [5]: equações (7) e (8) |
5.1 Coluna engastada‐livre
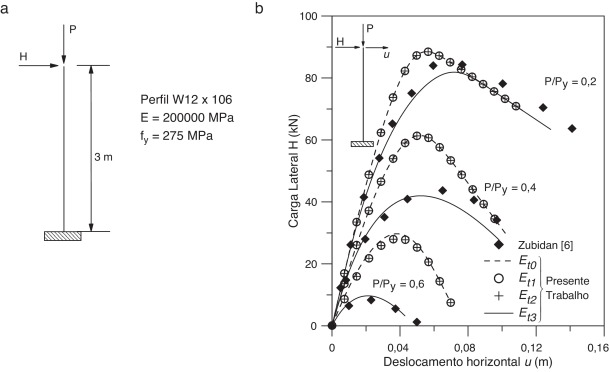
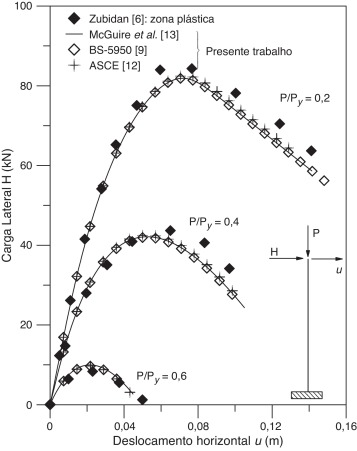
Seja a coluna engastada‐livre submetida a uma carga vertical permanente P e uma carga horizontal variável H aplicada no plano da seção transversal, perpendicularmente ao eixo de menor inércia, conforme ilustra a figura 4 a. Esse exemplo também foi analisado por Zubydan [6] para validar suas formulações numéricas.
|
|
|
Figura 4. a) Coluna engastada‐livre; b) trajetórias de equilíbrio para a coluna engastada‐livre. |
Investigou‐se o comportamento da coluna para 3 níveis do carregamento permanente P : 20%, 40% e 60% da carga axial de escoamento, Py . Controlando o deslocamento horizontal u no topo da coluna foram obtidas as trajetórias de equilíbrio apresentadas na figura 4 b. Os valores obtidos para a carga horizontal de colapso são sumarizados na tabela 3 para os diferentes modelos de módulo tangente e níveis de carregamento.
| Módulo de elasticidade tangente | Carga de colapso H (kN) | ||
|---|---|---|---|
| P/Py = 0,2 | P/Py = 0,4 | P/Py = 0,6 | |
| Et0 | 88,50 | 61,44 | 29,72 |
| Et1 | 88,50 | 61,44 | 28,18 |
| Et2 | 88,50 | 61,44 | 28,18 |
| Et3 | 81,88 | 41,97 | 9,69 |
Para validar os resultados encontrados são empregadas soluções obtidas por Zubydan [6] , que utilizou o método da zona plástica. As tensões residuais foram estabelecidas seguindo o modelo de variação recomendado pelo European Convention for Construction Steelwork (ECCS) [15] . A superfície de resistência proposta por McGuire et al. [13] foi escolhida e os resultados foram obtidos variando o modelo representativo do módulo tangente.
Analisando as trajetórias encontradas e os valores obtidos na tabela 3 , pode‐se concluir que o módulo tangente Et3 é o mais eficaz na previsão da carga limite. Os outros modelos superestimam a carga limite, principalmente para os valores mais elevados da relação P/Py . Sendo assim, mantendo o módulo tangente Et3 foi feita outra análise variando‐se as superfícies de resistência. Os resultados obtidos estão representados na figura 5 . Como pode ser constatado, os resultados são bem próximos para as 3 superfícies de resistência estudadas.
|
|
|
Figura 5. Trajetórias de equilíbrio para diferentes superfícies de resistência. |
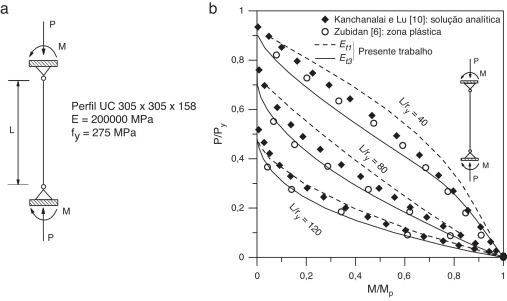
5.2 Coluna biapoiada
Neste exemplo avalia‐se uma coluna biapoiada com uma carga axial permanente P e momento fletor variável atuando nas 2 extremidades, conforme ilustra a figura 6 a. A flexão da coluna ocorre em torno do eixo de menor inércia. Dez elementos finitos são usados na discretização da coluna. Os dados do material e da seção transversal também são mostrados na figura 6 a. Nas análises, utiliza‐se a superfície de resistência recomendada pela norma BS 5950 [9] e é adotada a variação linear da tensão residual indicada no ECCS [15] .
|
|
|
Figura 6. a) Coluna biapoiada; b) curvas de interação da coluna biapoiada com momento nas 2 extremidades. |
As curvas de interação entre momento fletor e esforço normal obtidas para essa coluna são ilustradas na figura 6 b. O estudo foi feito considerando o parâmetro de esbeltez L/ry (sendo L o comprimento da coluna e ry o raio de giração) igual a 40, 80 e 120. São feitas análises adotando os módulos tangentes Et1 e Et3 . Com a finalidade de validar os resultados, empregam‐se soluções analíticas desenvolvidas por Kanchanalai e Lu [10] e soluções numéricas indicadas por Zubidan [6] . Observa‐se que, para L/ry = 120, ao se utilizar o módulo tangente Et1 , obtém‐se uma curva de interação quase coincidente com a solução analítica. Porém, para parâmetros de esbeltez menores, a resistência da coluna é superestimada. Por sua vez, o módulo tangente Et3 , em todas as situações, fornece curvas conservadoras em relação à solução analítica, e mais exatas quando comparadas à solução obtida por Zubidan [6] , que usou o método da zona plástica.
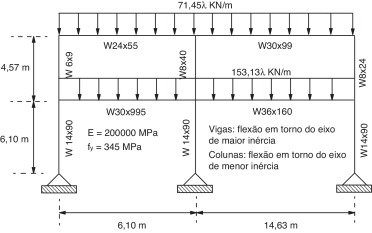
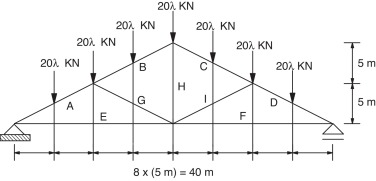
5.3 Pórtico de 2 andares
O pórtico de 2 andares mostrado na figura 7 foi analisado por Ziemian e Miller [18] através dos métodos da rótula plástica e zona plástica. O pórtico está submetido a cargas uniformemente distribuídas que atuam nas vigas. Informações sobre a geometria, o material e os perfis utilizados também são fornecidos na figura indicada. Adotaram‐se 4 elementos finitos em cada membro estrutural.
|
|
|
Figura 7. Pórtico de 2 andares: geometria e carregamento. |
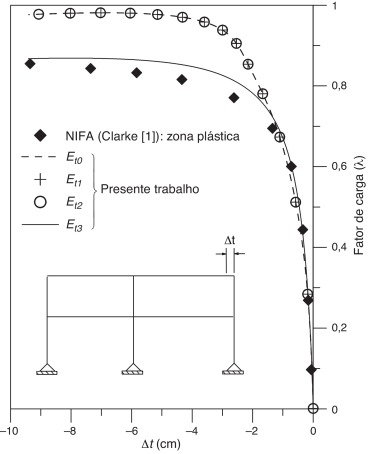
Na figura 8 é mostrada a variação do deslocamento horizontal Δt no topo da terceira coluna à direita com o carregamento. Adotou‐se a superfície da norma BS 5950 [9] . A comparação é feita com os resultados obtidos por Ziemian e Miller [18] com o programa NIFA [1] . Ressalta‐se, mais uma vez, a eficiência do módulo Et3 na simulação do comportamento inelástico do pórtico de 2 andares, produzindo resultados bastante próximos daqueles obtidos com o método da zona plástica. O fator de carga limite encontrado em cada caso analisado é apresentado na tabela 4 .
|
|
|
Figura 8. Trajetórias de equilíbrio do pórtico de 2 andares. |
| Módulo | λlim |
|---|---|
| Et0 | 0,981 |
| Et1 | 0,981 |
| Et2 | 0,981 |
| Et3 | 0,868 |
| Zona plástica [1] | 0,860 |
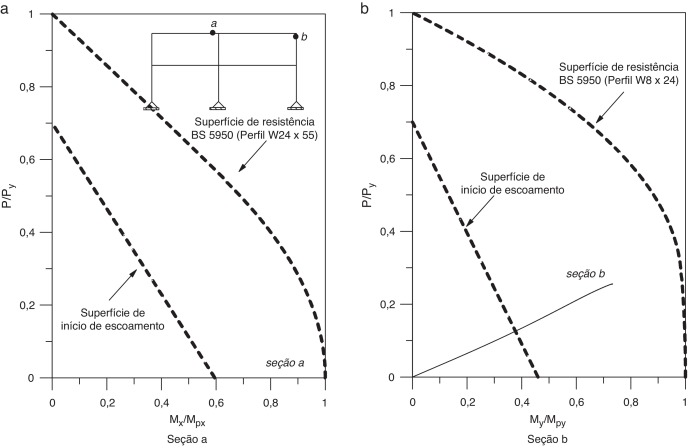
Utilizando o módulo tangente Et3 também se obteve a variação das forças internas (esforço normal e momento fletor) desenvolvidas nas seções transversais da estrutura durante o processo de carregamento, como ilustra a figura 9 . As seções escolhidas são mostradas nessa mesma figura. Analisando os resultados, nota‐se que na seção a (viga) apenas o momento fletor é predominante. Na seção b (coluna) tanto o momento fletor quanto o esforço normal contribuem, evidentemente, para o desenvolvimento da plastificação. Em ambos os casos não há a formação da rótula plástica.
|
|
|
Figura 9. Distribuição de forças internas nas seções a e b do pórtico. |
5.4 Pórtico treliçado
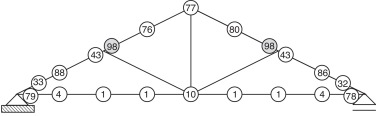
O último problema a ser analisado é ilustrado na figura 10 . Trata‐se de um pórtico treliçado que será referido, aqui, simplesmente como treliça, embora os nós sejam rígidos. O carregamento aplicado e a geometria da estrutura também são mostrados na figura 10 . Todos os membros da treliça estão orientados na direção do eixo de menor inércia. Os perfis que a compõem, bem como a tensão de escoamento em cada um dos membros, são informados na tabela 5 . Assume‐se o módulo de elasticidade igual a 200.000 MPa.
|
|
|
Figura 10. Pórtico treliçado: geometria e carregamento. |
| Membro | Perfil | Tensão de escoamento |
|---|---|---|
| A e D | 250UC 72,9 | 250MPa |
| B e C | 200UC 52,2 | 250MPa |
| E, F e H | 100UC 14,8 | 260MPa |
| G e I | 150UC 23,4 | 260MPa |
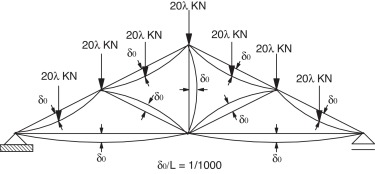
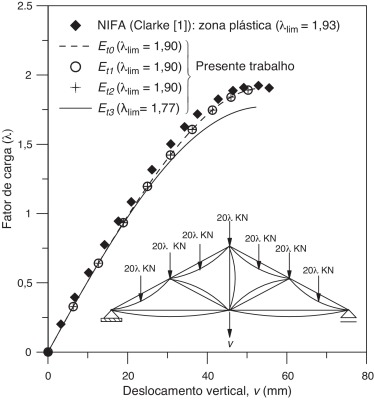
Seguindo o estudo feito por Clarke [1] avalia‐se a treliça geometricamente imperfeita com tensões residuais. A definição da geometria imperfeita desse sistema estrutural treliçado segue o modelo proposto por Clark [1] , em que é assumida uma flecha máxima δ0 = L /1.000 no centro de cada membro estrutural, como ilustra a figura 11 . Destaca‐se, entretanto, que essa definição de imperfeição localizada de cada barra não corresponde o modo crítico de flambagem do sistema estrutural em estudo. Deve‐se também esclarecer que a representação das imperfeições na figura 11 está exagerada para facilitar a sua visualização. Adota‐se a curva de resistência da norma BS 5950 [9] e as tensões residuais seguindo a variação linear recomendada pelo ECCS [15] , citada na subseção 2.3. As trajetórias de equilíbrio encontradas são obtidas controlando o deslocamento vertical v do nó central inferior, como mostra a figura 12 .
|
|
|
Figura 11. Pórtico treliçado com imperfeições geométricas iniciais. |
|
|
|
Figura 12. Trajetórias de equilíbrio do pórtico treliçado. |
Observa‐se que, para fatores de carga inferiores à unidade, as trajetórias obtidas com os 4 modelos do módulo tangente coincidem e estão próximas da curva encontrada por Clarke [1] . Para valores superiores, o resultado obtido com o módulo Et3 começa a divergir, fornecendo um fator de carga mais conservador. Aliás, como os módulos tangentes Et0 , Et1 e Et2 forneceram curvas idênticas, conclui‐se que não houve variação do módulo de elasticidade nessas análises. Assim, creditam‐se os bons resultados obtidos com os mesmos à consideração explícita das tensões residuais.
Para concluir, avaliou‐se o grau de plastificação dos membros da estrutura no instante de colapso, como ilustrado na figura 13 . O grau de plastificação estabelece uma informação útil referente à localização de seções críticas ou regiões com alto grau de plastificação nos sistemas estruturais [11] . Esse índice é calculado pela seguinte relação:
|
|
( 18) |
sendo Mer o momento de início de escoamento e Mpr o momento plástico reduzido, já explicados na subseção 3.2. Na figura 13 , observa‐se que a treliça imperfeita atinge a carga crítica sem o desenvolvimento de rótulas plásticas. Porém, há seções que são indicadas nos círculos hachurados que apresentam alto índice de plastificação.
|
|
|
Figura 13. Plastificação da seção transversal. |
6. Conclusões
No presente trabalho foram apresentadas metodologias que permitem a modelagem do comportamento inelástico de estruturas de aço, com destaque para situações onde ocorre a flexão do membro em torno do eixo de menor inércia. Os efeitos de segunda ordem e das tensões residuais também foram considerados.
Após a análise das estruturas aqui apresentadas, conclui‐se que a utilização de superfícies de resistência específicas para representar o estado limite da seção transversal [9] , [12] and [13] , em combinação com o módulo tangente proposto por Ziemian e McGuire [5] (equação 7), é eficiente e necessária. Essa afirmação se justifica, pois, em geral, os resultados obtidos estiveram em concordância com as soluções analíticas ou numéricas encontradas na literatura.
Os bons resultados obtidos com o módulo tangente supracitado [5] , que varia com a força normal e momento fletor em torno do eixo de menor inércia, ficaram evidentes através da análise das trajetórias de equilíbrio e curvas de interação das estruturas investigadas. Houve uma melhoria considerável na precisão dos resultados em relação às análises feitas com outros modelos para esse módulo, que em geral superestimaram a carga crítica da estrutura.
Por fim, o êxito nos resultados obtidos garante a possibilidade de se realizar uma análise inelástica confiável e realística seguindo os procedimentos numéricos propostos.
Agradecimentos
Os autores agradecem às agências de fomento CNPq, CAPES e FAPEMIG (estado de Minas Gerais) o apoio recebido para a realização deste trabalho.
Bibliografia
- [1] M.J. Clarke; Plastic zone analysis of frames; W.F. Chen, S. Toma (Eds.), Advanced analysis of steel frames: Theory, software, and applications, CRC Press, Boca Raton (1994), pp. 259–319
- [2] A.R. Alvarenga, As Ligações Semirrígidas na Análise Avançada com Zona Plástica de Portais Planos de Aço, Tese de Doutorado, Programa de Pós‐Graduação em Engenharia Civil, Deciv/EM/UFOP, Ouro Preto, MG, Brasil, 2010.
- [3] S.L. Chan, P.P.T. Chui; Non‐linear Static and Cyclic Analysis of Steel Frames with Semi‐Rigid Connections; Elsevier, Oxford (2000)
- [4] J.Y.R. Liew, D.W. White, W.F. Chen; Second‐order refined plastic hinge analysis for frame design: Part 1; J. Struct. Div., 119 (11) (1993), pp. 3196–3216
- [5] R.D. Ziemian, W. McGuire; Modified tangent modulus approach, a contribution to plastic hinge analysis, ASCE; J. Struct. Eng., 128 (10) (2002), pp. 1301–1307
- [6] H.A. Zubydan; Inelastic second order analysis of steel frame elements flexed about minor axis; Eng. Struct., 33 (2011), pp. 1240–1250
- [7] W.F. Chen, S.E. Kim; LRFD Steel Design using Advanced Analysis; CRC Press, Boca Raton Flórida (1997)
- [8] AISC, Specification for Structural Steel Buildings. Chicago, 2005.
- [9] BS 5950, Structural Use of Steelwork in Buildings — Part 1: Code of practice for design — Rolled and welded sections. British Standards Institution, London, England, 2000.
- [10] T. Kanchanalai, L.W. Lu; Analysis and design of framed columns under minor axis bending; AISC Eng. J., 16 (2) (1979), pp. 29–41
- [11] A.R.D. Silva, Sistema Computacional para a Análise Avançada Estática e Dinâmica de Estruturas Metálicas, Tese de Doutorado, Programa de Pós‐Graduação em Engenharia Civil, Deciv/EM/UFOP, Ouro Preto, MG, Brasil, 2009.
- [12] ASCE, Plastic Design in Steel, A Guide and Commentary. ASCE Manual No. 41 New York, 1971.
- [13] W. McGuire, R.H. Gallagher, R.D. Ziemian; Matrix structural analysis; (2nd Ed.)Wiley, New York (2000)
- [14] T.V. Galambos; Guide to stability design criteria for metal structures; Structural Stability Research Council (4th edn.), John Wiley & Sons, Inc, New York (1998)
- [15] ECCS, Ultimate Limit State Calculation of Sway Frames with Rigid Joints, Pub. no. 33, European Convention for Constructional Steelwork, 1983.
- [16] Y.B. Yang, S.B. Kuo; Theory & analysis of nonlinear framed structures; Prentice Hall (1994)
- [17] M. Ritto-Correa, D. Camotim; On the arc‐length and other quadratic control methods: Established, less known and new implementation procedures; Comput. Struct., 86 (2008), pp. 1353–1368
- [18] R.D. Ziemian, A.R. Miller; Inelastic analysis and design: Frames with members in minor‐axis bending; ASCE J. Struct. Eng., 123 (2) (1997), pp. 151–156
Document information
Published on 01/03/16
Accepted on 07/07/14
Submitted on 20/03/14
Volume 32, Issue 1, 2016
DOI: 10.1016/j.rimni.2014.07.002
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?