Resumo
Neste trabalho se apresenta um estudo paramétrico do impacto semifrontal em um ônibus, no qual se avalia independentemente a influência de cada variável envolvida neste tipo acidente. O cenário de impacto semifrontal é sem dúvida um dos mais severos acidentes envolvendo ônibus, pois parte da lateral do ônibus é totalmente danificada, podendo deixar um elevado número de vítimas. A simulação numérica utiliza um modelo de análise explícita formado por elementos de vigas que utiliza uma lei constitutiva elasto‐plástica, a qual leva em conta a influência da taxa de deformação. Com este modelo se realiza um estudo paramétrico das variáveis globais que permitem caracterizar este tipo de cenário. Também são avaliados de forma qualitativa acidentes deste tipo acontecidos nas estradas brasileiras. A discussão dos resultados é finalmente apresentada e serve como um primeiro passo na busca de melhorias a serem introduzidas nas estruturas dos ônibus, objetivando minimizar os danos.
Abstract
This paper presents a parametric study of the offset frontal impact on a bus, in which is assessed independently an influence of each variable involved in this accident type. The scenario of offset frontal impact is surely one of the most severe accidents involving buses, once the same has part of your lateral totally damaged and can leave a large number of victims. The numerical simulation model uses an explicit analysis formed by beams elements which uses elastic‐plastic constitutive law, which takes into account the influence of strain rate. With this model a parametric study of global variables that can characterize this type of scenario is realized. Also are evaluated qualitatively real accidents happened on Brazilian roads. The discussion is finally presented, and serves as a first step in the search for improvements to be made to the structures of the bus, aiming to minimize the damage.
Palavras‐chave
Elementos finitos ; Ônibus ; Modelo de vigas ; Impacto semifrontal
Keywords
Finite Element Method ; Bus ; Beam Models ; Offset Frontal Impact
1. Introdução
O transporte com ônibus no Brasil, país com dimensões continentais, é fundamental para permitir a mobilidade de pessoas. O número de ônibus que circulam nas estradas brasileiras tem aumentado, mas a qualidade das mesmas não acompanhou tal crescimento. Estas condições produziram um aumento considerável no número de acidentes envolvendo ônibus.
Segundo dados fornecidos em pesquisas divulgadas pela Confederação Nacional de Transporte (CNT) [4] , existem no Brasil uma extensão de 1.713.885 km de rodovias, dos quais apenas 202.589 km são pavimentados. As rodovias pesquisadas correspondem a 47,8% (96.714 km) das rodovias pavimentadas, sendo que 88% (85.114 km) da extensão são de pista simples de mão‐dupla. As pistas duplicadas representam apenas 11,7% (11.347 km) do total e 0,3% são de pistas simples de mão única. A segurança nas estradas brasileiras é bastante comprometida, pois grande parte das estradas possui pista dupla de mão simples e também porque 40,5% (39.132 km) da extensão pesquisada não possuem acostamento, o qual possui funções importantes, tal como apoio lateral e área de evasão em situações de emergência. Estes fatos, juntamente com outros problemas como deficiências na sinalização, irregularidades e defeitos na pista e erros humanos, tornam as estradas perigosas, criando um cenário propício para que ocorram acidentes.
Os principais tipos de acidentes envolvendo ônibus são de colisão frontal total ou semifrontal, colisão traseira e tombamento, sendo que os acidentes mais graves registrados são em colisão frontal e semifrontal seguidos de tombamento.
A fim de ilustrar a severidade desses tipos de acidentes, pode‐se citar o acidente de um ônibus contra um caminhão, que deixou 7 mortos e 15 feridos. Este acidente aconteceu na BR 230, ao km 463, no estado da Paraíba, no Brasil, conforme figura 1 (a). Outro exemplo, considerado o pior acidente registrado de trânsito envolvendo ônibus em estradas brasileiras, deixou 32 pessoas mortas e 21 pessoas feridas. Neste caso os 2 veículos colidiram frontalmente num trecho conhecido como «corredor da morte», no estado de São Paulo. O choque foi tão violento que um dos ônibus entrou até à metade do outro veículo. Na figura 1 (b) é apresentada a estrutura do ônibus após o acidente.
|
|
|
Figura 1. a) Acidente de impacto semifrontal na BR 230, KM 463 (PB/BR) e b) acidente de impacto frontal envolvendo ônibus na Av. Raposo Tavares (SP/BR) [8] .
|
Segundo dados fornecidos pelo último anuário estatístico da Agência Nacional de Transportes terrestres (ANTT) [2] , a quantidade de empresas que fornecem transporte com ônibus no Brasil é de 197 e o número de veículos que trafegam nas estradas brasileiras chega a 13.907. A tabela 1 mostra a evolução dos acidentes ocorridos em linhas interestaduais e internacionais de passageiros no Brasil, no período de 2007‐2010.
| Ano | Acidentes envolvendo transporte coletivo |
|---|---|
| 2007 | 8.852 |
| 2008 | 10.185 |
| 2009 | 9.495 |
| 2010 | 9.417 |
Os fabricantes de ônibus, com objetivo de aprimorar os projetos e para aumentar a competitividade, vêm construindo veículos mais leves e duráveis que resultam em estruturas de ônibus que tenham um investimento econômico mais conveniente para seus clientes, as empresas de transporte. No entanto, estas premissas muitas vezes se contrapõem a conceber estruturas mais seguras frente a cenários de impacto e pela falta de normas regulamentadoras adequadas quanto ao desempenho do ônibus frente a impacto frontal ou semifrontal, cenários de acidentes comuns nas estradas brasileiras, resulta que o desempenho das estruturas seja inadequado nestes tipos de acidentes. Muitas vezes para cumprir com estes requisitos de durabilidade e economia esquecem o item de segurança frente a cenários de impacto, o qual deve ser regulamentado de maneira mais efetiva por normas que exijam a avaliação da capacidade de absorção de impacto (CAI) de estruturas de ônibus. A CAI de veículos é regida por 4 conceitos básicos [3] :
- controlar sobre níveis de tolerância as desacelerações que são aplicadas ao ocupante;
- providenciar formas de absorver energia de colisão mantendo, ao mesmo tempo, a segurança dentro do espaço de sobrevivência do ocupante;
- manter o ocupante dentro do espaço de sobrevivência durante a colisão, evitando a ejeção do mesmo;
- proteger o ocupante de riscos após a colisão.
Em geral, normas regulamentadoras exigem que condições mínimas de segurança sejam verificadas com respeito ao tombamento e impacto frontal, sendo apresentado através de normas como a Resolução N.° 316/09 do Conselho Nacional de Trânsito (CONTRAN) [5] . Quanto ao tombamento, essa resolução esclarece de maneira efetiva simulações numéricas ou ensaios para garantir a segurança dos passageiros, mas sem dúvida a regulamentação desta resolução quanto à rigidez mínima ao impacto frontal, baseadas no ensaio do pêndulo, não é suficiente para garantir a segurança dos passageiros. O ensaio do pêndulo, que essencialmente consiste em submeter a frente da estrutura de um ônibus ao impacto de uma massa de 1.000 kg lançada desde uma altura de 4,75 metros, aplica sobre o ônibus uma quantidade de energia 30‐40 vezes menor do que a energia envolvida num acidente de impacto frontal de um ônibus colidindo a 50 km/h contra uma parede rígida, conforme analisado por Dias de Meira Jr. [6] . Neste contexto, é importante que estes tipos de distorções normativas sejam revistas para tornar os ônibus mais seguros.
O arranjo estrutural de uma carroceria de ônibus basicamente é composto de uma estrutura denominada carroceria acoplada em um chassi. Na figura 2 se apresentam as principais partes que compõem a estrutura de um ônibus. Normalmente a resistência estrutural em cenários de impacto era cumprida principalmente pelo chassi do veículo, no entanto, existe uma tendência de alguns fabricantes separarem o chassi e desta forma alcançarem uma maior flexibilidade no projeto do ônibus, com objetivo principal de permitir a ampliação do tamanho do bagageiro. A eliminação da parte central do chassi, caso particular apresentado na figura 2 , leva a diminuição da rigidez do conjunto, sendo que a rigidez da parte central do veículo deve ser garantida pela carroceria. São utilizados diversos materiais na fabricação da carroceria de ônibus, sendo o aço um dos mais utilizados para elementos estruturais. No entanto, outros materiais tais como alumínio e fibra de vidro são utilizados como elementos de vedação do ônibus, ou seja, que não têm função estrutural. A carroceria é basicamente composta por tubos de parede fina [12] .
|
|
|
Figura 2. Chassi e carroceria do ônibus [6] .
|
Um modelo numérico adequado para realizar simulações que reproduzam cenários de acidentes destes tipos de estruturas, a um custo computacional baixo, pode ser obtido empregando modelos unifilares formados por elementos de vigas com comportamento elasto‐plástico, podendo levar em conta a influência da taxa de deformação. No presente trabalho, utilizando este tipo de modelo numérico e considerando a taxa de deformação, é realizado um estudo paramétrico do cenário de impacto semifrontal, no qual geralmente a lateral do ônibus é parcialmente danificada produzindo o que normalmente é chamado efeito «abridor de latas». Apresenta‐se também um estudo qualitativo de alguns acidentes deste tipo acontecidos no Brasil. Uma discussão dos resultados obtidos é finalmente realizada, servindo como um primeiro passo para o desenvolvimento de propostas de mecanismos que minimizem o dano da estrutura do ônibus neste tipo de acidentes.
2. Modelo numérico simplificado
Nesta seção são apresentadas as características e as condições de contorno utilizadas para o desenvolvimento do modelo numérico implementado no software Ls‐Dyna[10] .
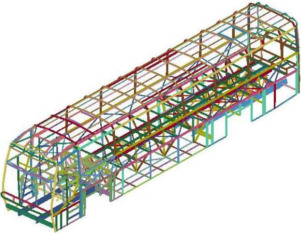
O modelo é composto por 5.502 nós e 2.566 elementos de viga do tipo Hughes_Liu [10] e está apresentado na figura 3 . Este modelo numérico foi desenvolvido e utilizado nas teses de doutorado de Dias de Meira Jr. [6] e Walber [13] , o qual foi baseado em um ônibus rodoviário de um fabricante brasileiro.
|
|
|
Figura 3. Modelo numérico do ônibus.
|
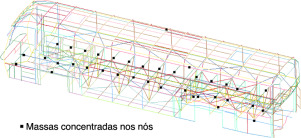
As massas de componentes não estruturais, tais como janelas, elementos de vedação externos, poltronas, eixos dianteiro e traseiro, motor, ar condicionado, portas, portinholas e bagagens foram consideradas como massas concentradas, posicionadas como indicado na figura 4 . Para definição dessas massas, utilizaram‐se as informações fornecidas por uma empresa encarroçadora, sendo adotada uma massa de 5.330 kg para um chassi marca Scania [14] , com 1.030 kg distribuídos na parte dianteira e 4.300 kg na parte traseira. Para a carroceria acoplada ao chassi, ou seja, já considerando a massa de 5.330 kg do chassi, foi adotada uma massa total de 13.020 kg, considerando um ônibus com 44 lugares (12 m de comprimento), com ar condicionado e banheiro. Esta massa considera a carroceria sem passageiros e bagagens (descarregado), sendo 4.520 kg distribuídos na parte dianteira e 8.720 kg na parte traseira. Considerando o veículo com carga máxima de 3.080 kg, o que corresponde a 44 passageiros (70 kg por pessoa em média), mais 1.000 kg de bagagens, se tem uma massa total distribuída de 17.100 kg, conforme apresentado na figura 4 . A massa dos elementos estruturais, os quais são de aço, foi calculada e distribuída pelo software através da densidade do material e pela posição de cada elemento no modelo.
|
|
|
Figura 4. Massas concentradas aplicadas no modelo.
|
O material utilizado no chassi e na carroceria foi o aço estrutural NBR 7008 ZAR 230 [1] , sendo apresentadas suas propriedades mecânicas na tabela 2 . O material foi assumido como elasto‐plástico com endurecimento linear.
| Propriedade | NBR 7008 ZAR 230 |
|---|---|
| σo (MPa) | 230 |
| σu (MPa) | 310 |
| E (GPa) | 210 |
| Et (MPa) | 730 |
| D | 40,4 |
| Q | 5 |
| ν | 0,3 |
| γ (kg/m3) | 7.850 |
O material ZAR 230, especificado na NBR 7008 [1] , é comumente utilizado pelas indústrias de ônibus no Brasil para a fabricação de carrocerias, o qual é sensível à taxa de deformação, ou seja, apresenta uma variação no valor da tensão de escoamento frente a diferentes velocidades de deformação. Para levar em conta este efeito, utilizou‐se a lei constitutiva proposta originalmente por Cowper e Symonds apud Jones [9] , a qual esta apresentada a seguir:
|
|
( 1) |
onde é a tensão de escoamento dinâmico para uma taxa de deformação plástica , σ0 é a tensão de escoamento estático associada e D e q são constantes para um material particular. Para o aço utilizado foi adotado D = 40,4 s‐1 e q = 5 parâmetros que produzem razoável concordância com os dados experimentais [9] .
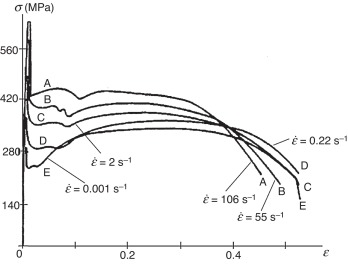
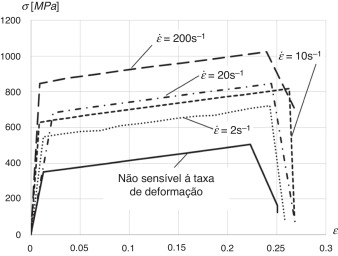
Na figura 5 apresentam‐se os resultados experimentais de Cowper e Symonds apud Jones [9] , podendo‐se observar uma tendência das tensões aumentarem com o incremento da taxa de deformação para todo o espectro de deformações do ensaio. Simular no modelo numérico esse comportamento é crucial para modelar corretamente a dissipação de energia pela deformação plástica dos elementos estruturais do ônibus em cenários de impacto. Como se visualiza na figura 6 , esse comportamento do material foi introduzido na simulação numérica utilizando a lei constitutiva apresentada na Equação 1, com os parâmetros de entrada apresentados na tabela 2 .
|
|
|
Figura 5. Testes dinâmicos uniaxiais de tração para o aço doce para várias taxas de deformação [9] .
|
|
|
|
Figura 6. Simulação numérica do ensaio de tração uniaxial para diferentes taxas de deformação para material elasto‐plástico com endurecimento linear.
|
Na figura 5 apresentam‐se os resultados experimentais de Cowper e Symonds apud Jones [9] , podendo‐se observar uma tendência das tensões aumentarem com o incremento da taxa de deformação para todo o espectro de deformações do ensaio. Simular no modelo numérico esse comportamento é crucial para modelar corretamente a dissipação de energia pela deformação plástica dos elementos estruturais do ônibus em cenários de impacto. Como se visualiza na figura 6 , esse comportamento do material foi introduzido na simulação numérica utilizando a lei constitutiva apresentada na Equação 1, com os parâmetros de entrada apresentados na tabela 2 .
A espessura adotada para as longarinas do chassi é 6,3 mm. Para os tubos que compõem a estrutura do teto foi adotada a espessura de 2,6 mm e para os demais tubos e perfis do casulo uma espessura de 2,0 mm. As dimensões dos tubos quadrados e retangulares, tal como largura e altura da seção transversal, não foram apresentadas devido a grande variedade de perfis utilizados. Maiores informações sobre as seções dos tubos utilizados podem ser encontradas no trabalho de Dias de Meira Jr. [6] .
As informações detalhadas nesta seção serão utilizadas para todos os modelos a serem apresentados a seguir. Condições de contorno específicas, como por exemplo, a velocidade de impacto, ângulo da parede rígida e offset , serão indicadas e estudadas nas seções subsequentes.
Como o modelo numérico do ônibus é construído com vários elementos de viga, sendo que estes durante a simulação colidem entre si e contra uma superfície rígida, o tipo de contato utilizado foi o automático de superfície simples com coeficiente de atrito estático e dinâmico com valores iguais a 0,08. Em simulações de impacto e colisão normalmente utiliza‐se este tipo de contato, pois ele permite que uma superfície entre em contato consigo mesma e também com a superfície de outros corpos.
3. Simulação de impacto semifrontal da estrutura contra uma parede rígida
Nesta seção foram realizadas simulações numéricas para avaliar a sensibilidade dos principais parâmetros envolvidos nos eventos de impacto, efetuando‐se posteriormente uma comparação entre resultados obtidos numericamente com dados coletados de uma série de acidentes reais que aconteceram nas rodovias brasileiras nos últimos anos.
A calibração e validação do modelo de elementos finitos do ônibus utilizado foi realizada comparando‐se as frequências naturais do modelo numérico com as obtidas na medição de um ônibus de características similares, sendo que os resultados desta comparação foram publicados por Walber [13] . Também se realizaram esforços para validar o modelo num cenário de impacto, comparando‐se os resultados numéricos obtidos com informações obtidas em ensaios de crash e acidentes de ônibus, sendo também comparado o modelo de vigas utilizado com modelos numéricos mais simples como o proposto por Riera [11] . Os resultados desta calibração podem ser encontrados em Dias de Meira Jr. [6] .
3.1. Estudo paramétrico das condições de contorno dos cenários de impacto semifrontal estudados
O cenário a ser simulado consiste na colisão de um ônibus rodoviário contra uma parede rígida (impacto semifrontal). Os parâmetros P1 , P2 e P3 que serão estudados para definir o cenário indicado são:
- ângulo da parede rígida (P1 : θp );
- offset da parede rígida (P2 : offset );
- velocidade inicial dos veículos (P3 : Vi ).
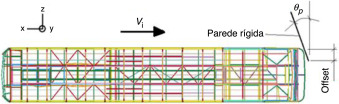
Na figura 7 são apresentados os parâmetros citados, sendo o offset a dimensão frontal do ônibus que impacta contra a parede rígida.
|
|
|
Figura 7. Representação dos parâmetros de entrada definidos para a análise (P1 : θp , P1 :offset e P'''3 : Vi ).
|
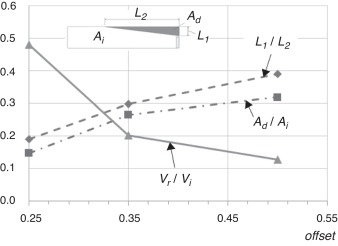
A sensibilidade do cenário frente à variação dos parâmetros definidos (P1 a P3 ) foi medida utilizando‐se índices adimensionais conforme definido a seguir: a relação entre a velocidade inicial (Vi ) e a velocidade residual após o impacto (Vr ) define o índice I1 : Vr /Vi ; a relação entre a área da estrutura deformada devido ao impacto Ad e a área projetada da vista superior do ônibus antes do impacto Aidefine o índice I2 : Ad /Ai ; a relação entre os comprimentos dos lados danificados do ônibus, L1 (lado frontal) e L2 (comprimento lateral), permitem definir o índice I3 : L1 /L2 .
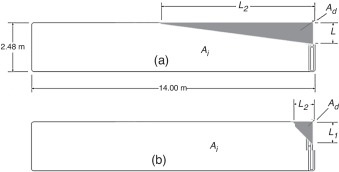
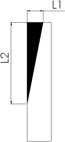
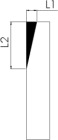
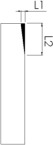
Na figura 8 se apresentam num esquema simplificado os parâmetros que permitem calcular os índices (I1 , I2 e I3 ) para os 2 cenários típicos extremos: (a) acidente onde aparece o chamado efeito «abridor de latas», típico em cenários de impacto semifrontal, chamado neste trabalho de Modo I , e (b) quando acontece um colapso localizado na região frontal do veículo, chamado de Modo II . A ocorrência de um ou outro modo de falha é influenciado pela interação dos parâmetros estudados nessa seção, sendo este um dos objetivos das análises realizadas no estudo paramétrico, procurando identificar qual é influência de cada parâmetro na ocorrência dos modos de falha, principalmente o Modo I , que é o mais severo.
|
|
|
Figura 8. Representação dos parâmetros que permitem definir os índices I1 , I2 e I3 .
|
Quando ocorre o Modo I a parte da lateral da carroceria do ônibus é removida, conforme pode ser observado na representação da figura 8 (a) e no acidente apresentado na figura 1 (a). No Modo I os passageiros que estão sentados no lado do motorista, e principalmente nos primeiros bancos, são atingidos e geralmente são vítimas fatais devido à exposição direta no momento do impacto. Já no Modo II o dano fica confinado à região frontal do ônibus, diminuindo consideravelmente a invasão do espaço de sobrevivência dos passageiros, porém, não evitando a invasão do espaço ocupado pelo motorista. Em acidentes que ocorrem nas estradas brasileiras é muito comum se verificar o Modo I de falha, devido às carrocerias de ônibus comercializadas pelos fabricantes não possuírem sistemas de absorção da energia de impacto, os quais poderiam ajudar a reduzir a invasão da região de sobrevivência dos passageiros, diminuindo o número de vítimas, fazendo com que a deformação devido ao impacto seja mais concentrada na parte frontal (Modo II ).
A seguir os resultados obtidos ao variar os parâmetros de entrada definidos (P1 a P3 ) são apresentados:
- Variação do parâmetro P1 : θp(ângulo da parede rígida)
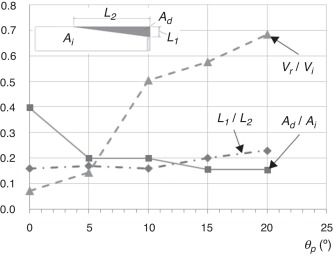
Nesta seção se apresenta o estudo da influência do ângulo da parede rígida com relação aos índices I1 , I2 e I3 . Foram efetuadas 5 análises com auxílio do software LS‐Dyna , variando‐se o ângulo da parede rígida θp de 0° até 20° com passo de 5°. Os resultados obtidos são apresentados na figura 9 e na tabela 3 .
|
|
|
Figura 9. Influência do parâmetro P1 : θp nos valores dos índices I1 , I2 e I3 .
|
| Dados de entrada | P1=θp | 0 a 20° (5° em 5°) | |
| P2=offset | 25% | ||
| P3=Vi | 13,89m/s | ||
| Resultados | θp=0° | θp=20° | |
| I1:Vr/Vi (*δ1=850%) | 0,072 | 0,684 | |
| I2:Ad/Ai (*δ2=156.8%) | 0,398 | 0,155 | |
| I3:L1/L2 (*δ3=43.8%) | 0,160 | 0,230 | |
| Deformada (θp=0°) | |||
| Deformada (θp=20°) | |||
- . δi [%] = [(Ii_max ) − Ii_min )/Ii_min ] × 100
Analisando os resultados obtidos é possível verificar que através do índice I1 : Vr /Vi a velocidade residual do veículo é muito baixa para valores baixos do parâmetro P1 : θp [0° a 5°] e que cresce sensivelmente para valores de ângulo maiores [5‐20°]. O índice I1 mede indiretamente a energia absorvida no impacto. Quanto menor é a energia absorvida na colisão, maior será a velocidade residual, que aumenta juntamente com o aumento do θp , obtendo‐se uma variação de 850% neste parâmetro para os valores extremos analisados.
Analisando‐se o índice I2 : Ad /Ai , o qual mensura o tamanho da área danificada numa vista superior do ônibus, nota‐se que o mesmo sofre uma variação muito grande quando se perde a ortogonalidade entre o ônibus e a parede rígida, ou seja, para θp entre 0‐5°, mantendo‐se aproximadamente constante para θp acima de 5°. Verificando‐se os resultados obtidos para os valores extremos de P1 , contabiliza‐se uma variação de 156,8% neste índice.
Por último é possível observar que a forma da área danificada representada pelo índice I3 : L1 /L2 teve um aumento de 43,8% em seu valor para o intervalo de variação aplicado no parâmetro P1 : θp entre 0‐20°.
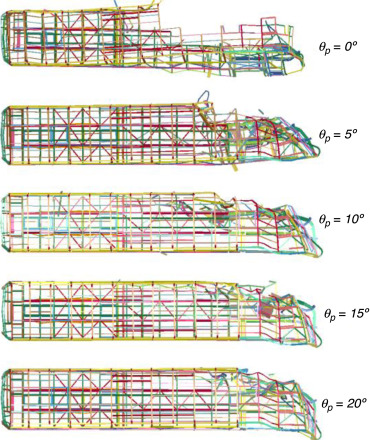
Na figura 10 , são apresentadas as 5 configurações finais das simulações realizadas com diferentes ângulos de inclinação da parede rígida. É importante salientar que se observa uma mudança significativa na forma e tamanho da área danificada quando o ângulo da parede passa de 0° para 5°.
|
|
|
Figura 10. Deformadas para estudos do ângulo da parede rígida.
|
- Variação do parâmetro P2 : offset da parede rígida
O parâmetro P2 , chamado de offset da parede rígida, representa em porcentagem a parte frontal do ônibus que impacta contra a parede rígida. Na figura 11 se apresentam as mudanças dos índices I1 , I2 e I3 definidos em função do parâmetro P2 . Na tabela 4 , os resultados obtidos em termos das configurações finais e valores dos índices máximos e mínimos são mostrados nas condições extremas analisadas. Foram realizadas 3 análises com valores de offset de 25, 35 e 50%.
|
|
|
Figura 11. Influência do parâmetro P2 .
|
| Dados de entrada | P1=θp | 10° | |
| P2=offset | 25%; 35%; 50% | ||
| P3=Vi | 13,89m/s | ||
| Resultados | offset (25%) | offset (50%) | |
| I1:Vr/Vi (*δ1=275%) | 0,480 | 0,128 | |
| I2:Ad/Ai (*δ2=115,5%) | 0,148 | 0,319 | |
| I3:L1/L2 (*δ3=104,2%) | 0,191 | 0,390 | |
| Deformada (offset 25%) | |||
| Deformada (offset 50%) | |||
- . δi [%] = [(Ii_max ) − Ii_min )/Ii_min ] × 100
Os resultados obtidos mostram um aumento gradual nos valores dos índices I2 e I3 , sendo a diferença percentual da ordem de 100% em ambos. No caso do I1 verifica‐se uma queda brusca da ordem de 275%, o que mostra que quanto maior o offset menor será a velocidade residual, ou seja, mais energia é gasta na colisão.
- Variação do parâmetro P3: Vi(velocidade inicial do veículo)
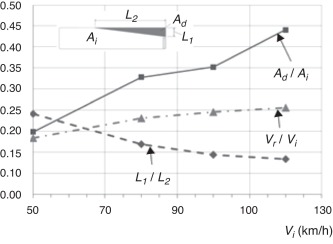
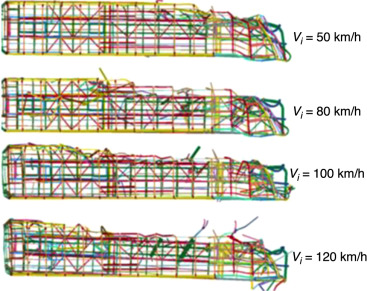
Na figura 12 e na tabela 5 são apresentados os resultados em termos da variação dos 3 índices estudados. A velocidade inicial do veículo para cada análise foi de 13,89 m/s (50 km/h), 22,22 m/s (80 km/h), 27,78 (100 km/h) e 33,33 m/s (120 km/h), totalizando 4 análises. A maior velocidade inicial utilizada nos estudos foi de 33,33 m/s (120 km/h), pois a velocidade máxima permitida na maioria das estradas brasileiras é 22,22 m/s (80 km/h). Avaliaram‐se valores de velocidade acima da permitida, a fim de verificar os efeitos sobre a estrutura, e também para levar em conta a colisão entre 2 veículos, cenário crítico no qual a velocidade dos 2 veículos é somada.
|
|
|
Figura 12. Influência do parâmetro P3 : Vi .
|
| Dados de entrada | P1=θp | 10° | |
| P2=offset | 25% | ||
| P3=Vi | 13,89; 22,22; 27,78; 33,33m/s | ||
| Resultados | Vi=13,89m/s | Vi=33,33m/s | |
| I1:Vr/Vi (*δ1=53,73%) | 0,134 | 0,206 | |
| I2:Ad/Ai (*δ2=164,2%) | 0,148 | 0,391 | |
| I2:Ad/Ai (*δ3=130,1%) | 0,191 | 0,083 | |
| Deformada (Vi=13,89m/s) | |||
| Deformada (Vi=33,33m/s) | |||
- . δi [%] = [(Ii_max ) − Ii_min )/Ii_min ] × 100
Na figura 12 verifica‐se pela curva Ad /Ai , que na medida em que Vi aumenta ocorre um aumento da área danificada da estrutura do ônibus, sendo verificada uma diferença de 164,2% entre as condições extremas estudadas. Nota‐se que se tem a predominância do Modo I (efeito «abridor de latas»), podendo‐se verificar também que a região de sobrevivência dos passageiros com o aumento da velocidade inicial é cada vez mais prejudicada, pois a dimensão L2 aumenta caracterizando efeitos mais nocivos e elevação no número de vítimas fatais devido à exposição durante o período de impacto, pois a lateral da carroceria tem sua estrutura removida até a extensão de L2 . Ainda apresenta‐se na figura 13 as configurações finais para as 4 velocidades iniciais analisadas.
|
|
|
Figura 13. Deformadas finais para análises da velocidade inicial do veículo.
|
Quanto ao índice I1 , através da figura 12 nota‐se que o mesmo aumenta gradualmente quando a velocidade inicial cresce, apresentando uma variação de 53,73% para os valores extremos do parâmetro P3 . Este comportamento evidencia um aumento da velocidade residual com o aumento da velocidade inicial. No entanto, observa‐se também que o gradiente deste índice I1 vai diminuindo para valores de velocidade iniciais maiores que Vi = 90 km/h .
Nota‐se também que o parâmetro I3 diminui gradualmente na medida em que a velocidade inicial aumenta. Isso é evidenciado pois a dimensão L2 aumenta com a velocidade inicial, enquanto a dimensão L1 permanece quase constante (figura 13 ). É importante lembrar que conforme L1 /L2 vai diminuindo, o Modo I de colapso fica mais claro. Com o aumento de Vi , aumenta a Vr e também L2 , consequentemente Ad .
3.2. Estudos de casos reais de acidentes
Nesta seção se apresentam nas Tabela 6 and Tabela 7 os principais dados e a análise paramétrica de acidentes reais acontecidos em estradas brasileiras, avaliando‐se os mesmos índices verificados nas análises numéricas, exceto para o índice I1 : Vr /Vi , pois não se tiveram dados suficientes das velocidades para determiná‐lo. Os valores apresentados foram inferidos a partir de fotografias dos acidentes, através de notícias e informações disponíveis em jornais, avaliando‐se através de escala os valores de L1 , L2 , Ai e Ad .
| Item | Foto do acidente | Local | Mês/Ano |
|---|---|---|---|
| 1 | Paraíba | 01/2012 | |
| 2 | Bahia | 12/2011 | |
| 3 | Goiás | 11/2010 | |
| 4 | Mato Grosso | 04/2011 | |
| 5 | Mato Grosso | 02/2012 |
| Item | L2 | L1 /L2 | Ad /Ai | Mortos | Feridos | Modo de falha |
|---|---|---|---|---|---|---|
| 1 | 7,3 | 0,09 | 0,07 | 7 | 15 | |
| 2 | 9,6 | 0,19 | 0,26 | 36 | 8 | |
| 3 | 3,7 | 0,34 | 0,07 | 5 | 30 | |
| 4 | 5,6 | 0,22 | 0,10 | 0 | 6 | |
| 5* | 3,7 | 0,12 | 0,02 | 0 | 40 |
Obs.: os ônibus avaliados nesta tabela foram considerados iguais ao ônibus desse trabalho, ou seja, comprimento de 14 m e 2,48 m de largura (figura 7 ).
- . Observar que no Caso 5 o efeito «abridor de latas» ocorreu no lado direito da estrutura.
Conforme mencionado na seção 1 e apresentado na tabela 1 , o número de acidentes e vítimas vem crescendo consideravelmente a cada ano nas estradas brasileiras. Os acidentes estudados e que estão apresentados nesta seção são apenas acidentes envolvendo ônibus no cenário de impacto semifrontal, objeto de estudo deste trabalho. Na tabela 6 se mostra uma imagem com o ônibus após o impacto, a fim de verificar os efeitos causados à estrutura. Na tabela 7 é apresentado o número de mortos e feridos, podendo‐se verificar que quanto maior a invasão do espaço de sobrevivência dos passageiros e do motorista, maior é o número de vítimas. É importante salientar que o número de passageiros que estavam no ônibus no instante do acidente é um fator a ser considerado, pois influencia no número de vítimas. No entanto, devido à falta de informações, esse dado não pode ser avaliado.
É importante salientar ainda com relação à tabela 7 que a deformada da estrutura do ônibus quando submetida a impacto semifrontal apresenta à ocorrência do Modo I de falha, sendo que a forma da região deformada é muito semelhante a um triângulo. Com esta verificação, pode‐se concluir que a deformada final obtida numericamente para um ângulo da parede rígida θp = 0 (figura 9 ) não representa a realidade, pois apresentou uma região deformada em forma de retângulo. Desta maneira, pode‐se concluir que para a simulação virtual de impacto da estrutura de um ônibus contra uma parede rígida em offset deve‐se utilizar um ângulo mínimo da parede de θp = 5°.
4. Conclusão
Na seção 3.1 se apresentou um estudo paramétrico das condições de contorno envolvidas em um acidente com impacto semifrontal, tais como ângulo da parede rígida, velocidade inicial do veículo e offset . Neste estudo paramétrico foram realizadas simulações numéricas, nas quais a estrutura do ônibus foi submetida a vários cenários de impacto. Para cada estudo variou‐se apenas um dos parâmetros, mantendo‐se constante os outros, objetivando avaliar separadamente como cada uma das variáveis estudadas influenciava nos resultados.
No desenvolvimento do trabalho foi possível obter as seguintes conclusões:
- Com relação à influência do ângulo de inclinação da parede rígida sobre a qual o ônibus colide na simulação (P1 = θp ):
- Se observa que quanto maior o valor θp maior é a velocidade residual do ônibus, sendo que o crescimento do índice que mede esta influência (I1 : Vr /Vi ) aumenta sensivelmente seu gradiente para θp > 5°, mostrando um grande aumento da velocidade residual com o aumento do θp . Já para os outros índices I2 : Ad /Ai e I3 : L1 /L2 , os mesmos permanecem praticamente constantes para θp > 5°, indicando claramente que o modo de falha e a região deformada da estrutura não são incrementados com o aumento de θp . Observando‐se as Figura 9 and Figura 10 , pode‐se verificar uma grande variação do índice I2 : Ad /Ai para valores de θp < 5°, mostrando que severidade e invasão do espaço de sobrevivência aumentam para pequenos ângulos da parede rígida.
- O índice I1 é uma medida da energia de impacto dissipada na deformação da estrutura, sendo possível observar que o mecanismo de falha por esmagamento parcial da frente do ônibus absorve muita mais energia que o mecanismo onde o efeito «abridor de latas» se manifesta.
- Embasado na evidência experimental verificada através dos acidentes analisados nas Tabela 6 and Tabela 7 , é possível considerar que num cenário de impacto semifrontal o ângulo de incidência entre o ônibus e a parede rígida poderia ser considerado igual a 5°, desta forma simulando o tipo de acidente que mais comumente ocorre com ônibus rodoviários.
- Com relação à influência do offset entre o ônibus e a parede rígida (P2 = offset ):
- Nota‐se que para valores de offset maiores que 0,35 ocorre uma mudança no gradiente de variação de todos os índices. No caso do índice I1 nota‐se que até offset de 0,35 a velocidade residual é bastante influenciada, sendo que a partir deste valor a influência diminui consideravelmente. Já para os índices I2 e I3 , para valor de offset maiores que 0,35 nota‐se uma mudança menor no gradiente, no entanto, verifica‐se pelo índice I3 que conforme aumenta o offset o modo de falha muda de «abridor de latas» para falha frontal concentrada, levando a um aumento da área deformada da estrutura, verificado pelo índice I2 .
- Com relação à influência da velocidade inicial (P3 = Vi ):
- Neste caso se pode observar que a relação entre a velocidade residual e a inicial cresce até uma Vi = 90 km/h, sendo que posteriormente o gradiente de crescimento diminui tendendo a ficar quase constante.
- Por outro lado o índice I2 : Ad /Ai aumenta e o I3 : L1 /L2 diminui, ou seja, o efeito «abridor de latas» aumenta, quase que linearmente, com a velocidade inicial, o que era previsto.
Finalmente algumas considerações de ordem geral:
- O estudo paramétrico realizado permitirá auxiliar na escolha de cenários de impacto que permitam avaliar mecanismos de absorção de energia a ser implementados em estruturas de ônibus.
- O trabalho realizado também deixa em evidencia a insegurança das estruturas de ônibus avaliadas. Cabe salientar que este tipo de acidente vem aumentando consideravelmente, pois a grande maioria das estradas brasileiras são de pistas duplas com mão simples, o que exige a realização da manobra de ultrapassagem invadindo a pista contrária. A melhoria no desempenho dos ônibus frente a este tipo de situações poderia ser induzida criando legislações adequadas que garantam condições mínimas que tenham que ser cumpridas. Como ilustração desta deficiência, é possível mencionar que a legislação brasileira só exige para avaliar a rigidez ao impacto frontal de estruturas de ônibus o chamado ensaio do pêndulo, CONTRAN [5] , o qual segundo a verificação realizada em Dias de Meira Jr.[6] , o ensaio do pêndulo se aplica no ônibus uma energia de impacto 34 vezes menor que a presente quando um ônibus que impacta a 50 kmm contra uma parede rígida. Também é importante salientar que as partes responsáveis pela criação desta norma não se encontram representadas, nem os motoristas dos veículos e nem os passageiros.
Bibliografia
- [1] ABNT ‐ Associação Brasileira de Normas Técnicas. NBR 7008 ‐ Chapas e bobinas de aço revestidas com zinco ou liga zinco‐ferro pelo processo contínuo de imersão a quente Parte 1: Requisitos. Dezembro de 2012.
- [2] ANTT (2007). Agência Nacional de Transportes Terrestres. Ministério dos Transportes [acessado 31 Out 2012]. Disponível em: www.antt.gov.br
- [3] C.A. Aparício Sánchez; Estudo de impacto usando elementos finitos e análise não linear; Dissertação de Mestrado, Escola de Engenharia de São Carlos, Universidade de São Paulo, São Paulo (2001)
- [4] CNT (2013). Confederação Nacional de Transporte [acessado 4 Ago 2012]. Disponível em: www.cnt.org.br
- [5] CONTRAN (2009). «Resolução N° 316/09». Conselho Nacional de Trânsito [acessado 17 Set 2012]. Disponível em: www.denatran.gov.br
- [6] A. Dias de Meira Jr; Avaliação do comportamento da estrutura de ônibus rodoviário solicitado a impacto frontal; Tese de Doutorado. PROMEC – Programa de Pós‐graduação em Engenharia Mecânica, Universidade Federal do Rio Grande do Sul (2010 [acessado 31 Out 2012]) Disponível em http://hdl.handle.net/10183/27932
- [7] DNIT (2010). Departamento Nacional de Infraestrutura de Transporte. Anuário Estatístico de Estradas Federais [acessado 16 Out 2012]. Disponível em: www.dnit.gov.br
- [8] F. Goedel; Aspectos relacionados com o impacto semi‐frontal em ônibus rodoviário; Dissertação de Mestrado. PROMEC – Programa de Pós‐graduação em Engenharia Mecânica, Universidade Federal do Rio Grande do Sul (2013 [acessado 2 Dez 2012]) Disponível em http://hdl.handle.net/10183/75768
- [9] N. Jones; Material strain rate sensitivity; J.A.C. Ambrósio (Ed.), Crashworthiness. Energy management and occupant protection., Springer Wien, New York (2001), pp. 33–47
- [10] LS‐DYNA, User Manual – Non linear Dynamic Analysis of Structures ‐ May 1998 ‐ Version 950‐d Livermore Software Technology Corporation 7374, Las Pocitas Road Livermore.
- [11] J.D. Riera; A critical reapraisal of nuclear power plant safety against accidental aircraft impact; Nucl Eng Des, 57 (1980), pp. 193–206 North Holland
- [12] T.W. Tech, I. Iturrioz; Proposta de metodologia de otimização estrutural de um ônibus em condições de tombamento; Dissertação de Mestrado. PROMEC – Programa de Pós‐graduação em Engenharia Mecânica, Universidade Federal do Rio Grande do Sul (2009 [acessado 8 Dez 2012]) Disponível em http://hdl.handle.net/10183/19042
- [13] M. Walber. Avaliação dos níveis de vibração existentes em passageiros de ônibus rodoviários intermunicipais, análise e modificação projetual. Tese de Doutorado. PROMEC – Programa de Pós‐graduação em Engenharia Mecânica. Universidade Federal do Rio Grande do Sul, 2009 [acessado 9 Dez 2012]. Disponível em: http://hdl.handle.net/10183/16304
- [14] SCANIA. Guia de aplicações para Ônibus [acessado 12 Dez 2012]. Disponivel em: www.scania.com.br
Document information
Published on 01/03/16
Accepted on 15/10/14
Submitted on 26/05/14
Volume 32, Issue 1, 2016
DOI: 10.1016/j.rimni.2014.10.001
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?


![Chassi e carroceria do ônibus [6].](/wd/images/1/18/Draft_Content_506507443-1-s2.0-S0213131514000601-gr2.jpg)