Published in Computers & Fluids, Vol. 141, pp. 90-104, 2016
doi: 10.1016/j.compfluid.2016.04.026
Abstract
In previous works [1,2], the authors have presented a highly efficient extension of the Particle Finite Element Method, called PFEM-2, to solve two-phase flows. The methodology which uses X-IVS [3] to treat convection terms allowing large time-steps was validated for problems where the gravity forces and/or the inertial forces dominate the flow. Although that is the target range of problems to solve with PFEM-2, most of real problems that fall in these categories also includes other flow regimes in certain regions of the domain. Maybe the most common secondary regime is when the surface tension dominates, as an example when drops or bubbles are released from the main flow, and this feature must be taken into account in any complete numerical strategy.
Attending to that, in this work the treatment of the surface tension to PFEM-2 is included. An implicit CSF methodology is employed together with a coupling between the marker function with a Level Set function to obtain a smooth representation of the normal of the interface which allows an accurate curvature calculation. Examples for curvature calculation and isolated bubbles and drops are presented where the accuracy and the computational efficiency are analyzed and contrasted with other numerical methodologies. Finally, a simulation of a jet atomization is analyzed. This case presents the above mentioned features: it is a inertia-dominant flow with a surface tension phenomena on drops and ligaments break up that can not be neglected.
Keywords: PFEM, surface tension, two-phase flows, SCLSVOF
1 Introduction
Solving efficiently multi-phase flows is still an open challenge. Although the dynamics of single phase flows are well understood and can be solved accurately without loss of efficiency, the computational modeling of two or more phases is an underdevelopment field with growing interest. In multi-phase flows the behavior of the fluid at each phase depends on the interface and its shape depends on the flow, then solving this complex coupling is a challenging task.
According to the framework used to derive the formulation, the numerical methods can be split into two main approaches, named Eulerian (fixed framework) and Lagrangian (mobile framework). Former formulations were the first ones to be developed and they provide a natural evolution from single-phase flows since most of Computational Fluid Dynamics (CFD) software are formulated within a fixed framework, while latter formulations offer a more natural choice for simulations in which deformations are not negligible, such as in multi-phase problems.
In the Eulerian strategies, the Finite Element Method (FEM) is a standard tool to solve both structural and fluid problems. In the case of standard FEM, the exact solution cannot be represented in the space spanned by the shape functions, then they will not be able to capture it accurately, but an averaged solution will be obtained. This is particularly important for multi-phase models, since domains composed by different phases usually lead to discontinuities in the properties along the interface, which translates into discontinuities in the unknowns or in their gradients. An alternative to overcome this limitation is to use Enriched Finite Elements [4,5,6,7], which adds degrees of freedom to elements that are cut by the interface in order to capture the part of the solution that escapes from the standard shape function field. Coppola-Owen et al. [8] proposed a simple enrichment functions that is capable of capturing accurately gradient discontinuities (kinks) in the pressure field. Moreover, Ausas et al. [9] proposed a set of three enrichment functions that are able to capture both kinks and jumps in the pressure. Another option in the Eulerian framework is the Finite Volume Method (FVM), which has more followers than the FEM for fluid dynamics. The domain is discretized with cells, and the solution is obtained by calculating fluxes through the faces of each of them. This leads to a formulation that is automatically conservative on the fluxes, unlike FEM.
No matter which Eulerian strategy is used to solve the fluid dynamics, an accurate and efficient simulation of interface evolution is of fundamental importance. For example, in FEM, the use of enriched space is still insufficient to simulate multi-fluids unless it is coupled with a second tool to locate precisely the position of the interface, necessary to build the extra shape functions. It is possible to distinguish two broad classes of computational methods used to describe the evolution of interfaces, namely: interface capturing and interface tracking methods.
Purely Eulerian algorithms, which solve the fluid in a fixed underlying mesh, use capturing methods. In this approach the interface is determined by an implicit function that is advected in the computational domain. Popular methods of this type are the Level Set Method (LSM)[10], which has become widely used when the interface undergoes extreme topological changes, e.g. merging or pinching off; and the Volume of Fluid (VoF) technique[11], which is naturally employed with FVM.
The LSM consists in using a distance function that is convected according to the fluid velocity. This function represents the distance from a point to the interface. By definition, the interface will be located where its value is zero. This level function is variable in the space, but if it has large variations in time, after some time steps it does not represent the distance to the interface anymore, leading to diffusion of the interface and mainly loss of mass. For this reason a reinitialization of the level set must be done to recover a distance function which guarantees that the properties are better conserved. Moreover, an Eulerian advection of the level set function produces large diffusion and requires small time-steps to achieve accurate solutions.
On the other hand, VOF is based on the conservative nature of the FVM, where instead of tracking an interface, it is more natural to save the content of different phases at each cell and define the shape and position from this data later on. The method defines a function that is the fraction occupied by one of the phases in each cell of the domain. Therefore the interface position is not tracked, but the fraction of fluid instead. Once fluids have been convected among cells, the interface position can be reconstructed (accepting some accuracy loss). This exchange between cells, inherited from the conservative nature of the FVM, allows to guarantee mass conservation. This is an important advantage respect to the LSM, in which mass loss is a critical topic which must be addressed and treated. Moreover, the FVM is very robust and is likely to be the most used one in commercial/widespread codes. As an example of application, OpenFOAM®[12] uses this strategy to solve multi-fluid problems.
Formulations clustered in the Lagrangian framework are a more natural choice for simulations where there are large deformations. The original idea, proposed by Monaghan et al. [13] and later works applied to fluid mechanics[14], was a meshless method named Smoothed Particle Hidrodynamics (SPH). Using particles that are advected carrying its own properties over the domain, they are able to almost avoid the numerical diffusion. In the context of incompressible flow, the Lagrangian perspective makes it possible to use a material derivative formulation where the absence of the non-linear convective terms transform the Navier-Stokes system into a transformed linear coupled problem between points and velocities. In the case of multi-phase problems, the calculation of the interface evolution is naturally done using particles [15,16]. However most of Lagrangian formulations have the uncomfortable drawback of requiring a particle position treatment. In the case of meshless methods a constant track of all the moving points must be kept where searching algorithms have to be used to speed up the computational time to calculate the interaction forces. On the other hand, the mesh-based methods must lead with the necessity of constructing or controlling the mesh quality during each time-step of the simulation if the accuracy of the solution has to be maintained. Searching algorithms, evaluation of the mesh distortions or the re-meshing processes are always computationally expensive and it would be interesting to explore the possibility of avoiding those steps.
Alternatives, that combines both Eulerian and Lagrangian tools, have provided to be a good alternative to pure methods. In [17] a pure Eulerian solver for the fluid is used, but Lagrangian marker particles are used to improve the LSM, then the interface tracking. This method proves to be more accurate than the pure Eulerian or pure Lagrangian counterpart in the tracking of the interface. Another option is the named Particle Finite Element Method (PFEM)[18] which consists of using a set of particles that define the nodes of a finite element mesh. Since fluids have no deformation limit, remeshing must be done at each time step. As all Lagrangian methods, the PFEM offers a more natural solution to problems where the particles of the domain can move freely. Unlike LSM, there is no need to recalculate the surface since the location of the interface is obtained trivially; since each particle is associated with a material no extra function is needed. Combining the original idea of Particle in Cell (PIC)[19] where a fixed mesh is used to calculate forces and pressures and moving particles to convect properties, the PFEM method was extended leading to a novel strategy so-called PFEM-2 method[3][20]. This proposal not only tracks material propertiesas density, viscosity, etc., therefore eliminating the need of the non-linear convective term. Also, using an improved explicit integration named X-IVS (eXplicit Integration following the Velocity Streamlines) added to an implicit correction of diffusive terms, there is no limitation in the time step, being the required precision the only bound for the time-step[21]. The enhanced PFEM-2 version to solve multiphase problems, presented in [1] and validated in [2], preserves the large time-step goodnesses of the single-phase strategy, also includes enrichment strategies to capture discontinuities in the pressure gradient, i.e. pressure kinks. However, the range of application of this strategy does not cover an important group of two-phase problems such as those where the surface tension is dominant.
In those problems, a surface tension model must be implemented at the interface being a validated strategy the Continuous Surface Force model (CSF) [22] which is based on an approximation of the interface curvature from the gradient of the marker function. In the case of VoF function, the gradient cannot be calculated accurately since it is a discontinuous step function, and its discrete approximations are known to generate unphysical spurious currents at the interface [23]. Strategies to reduce the spurious currents based on either interface reconstruction or smoothing kernels are available, a literature review can be found in [24], but most of them must be employed only on structured meshes. The coupling achieved by advecting the interface using the conservative VoF function, calculating the interface normal using the smoothed LS function and updating the physical properties from a smoothed Heaviside function is an improved strategy called CLSVOF [25]. In [26], Albadawi et al. present a less expensive option called S-CLSVOF which uses an one-way coupling strategy. This approach was successfully applied on surface tension dominant problems.
The current work proposes a strategy to enlarge the capabilities of PFEM-2 adding the S-CLSVOF method so as to improve the solution of surface tension dominant problems. In Section 1 the governing equations are presented together with the numerical methodology proposed to solve it, doing focus on the interface and surface tension term treatment. Next sections present a set of test properly chosen to show the capabilities of the strategy: starting from pure-convective tests to show the goodness of the Lagrangian framework to transport with neither diffusion nor distortion an arbitrary shape, next surface tension dominant cases where the interface treatment and the method accuracy are quantitatively tested, being PFEM-2 forced to enlarge the time-step where other numerical approaches can not work. Finally, a preliminar simulation of a jet atomization problem is presented. In this type of inertial dominant problem PFEM-2 has demonstrated to be the best numerical option, however a proper treatment of surface tension must be taken into account if an accurate solution of ligaments and droplets formation is searched.
2 Equations and Numerical Formulation
2.1 Governing Equations
The problem to solve is the case of unsteady laminar flow of two immiscible incompressible fluids. Both phases are assumed to be viscous and Newtonian. Isothermal conditions are assumed, and reaction mass transfer and phase transition are not considered. Taking into account all the physical assumptions, both the fluids are then governed by the incompressible Navier-Stokes equation with additional surface tension force along the interface. The governing equations include the continuity, momentum, and interface capturing advection equations which, written in the Eulerian framework, read:
|
|
(1) |
where is the fluid density, the fluid velocity vector, the gravitational acceleration, and with the scalar pressure and the dynamic viscosity of the fluid. The fluid domain is defined for a single mixture where the function is used to distinguish between the two phases. The calculation of the fluid physical properties, the density and viscosity , vary according to the scalar field . The surface tension force is the concentrated load along the interface, defined as
|
|
(2) |
where is the surface tension coefficient between the two phases, is the local curvature of the interface, is the Dirac delta function that localizes the surface tension force to point load on the interface and as the unit normal to the interface.
Employing the material derivative instead of the temporal derivative plus the convective term, the Equation 1 can be reformulated in its Lagrangian version. In this framework, a kinematic problem has to be solved in order to follow the particle trajectories, which leads to a equation system as:
|
|
(3) |
Due to the multiplication of the velocity and its gradient, the convective term in Equation 1 is non-linear. The presence of this non-linear term demands iterative algorithms to converge to the solution including linearisation techniques to solve the system. On the other hand, the Navier Stokes equations written in a Lagrangian framework lead to a system of linear equations due to the absence of the convective term. Moreover, the resulting system changes the non-symmetric equations in the Eulerian frame into a symmetric and positive definite one.
2.2 Discretization Strategy
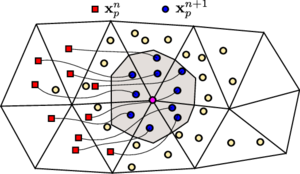
The PFEM-2 algorithm consists of solving the equations presented in Section 2.1 using a mixed Eulerian-Lagrangian discretization. This choice leads to a simplification of complex terms, as the convective one, and to a higher accuracy in the results due to lower error in the approximation comparing with its pure Lagrangian or pure Eulerian counterparts [27]. As it was mentioned, since material points move and the configuration changes continuously in time, it is necessary to couple this set of equations with a strategy that solves for the movement of the material points. This is achieved in PFEM-2 by using a set of Lagrangian particles combined with a fixed FEM mesh as is shown in Figure 1. The main advantage of using the Lagrangian particles is that the convection is obtained by simply moving the particles across the space and therefore the system to be solved does not have the convective term. The remaining set of equations will be calculated on the mesh employing a typical fractional step strategy.
It must be remarked that the particles used in the scheme do not represent a fixed amount of mass but rather material points with certain properties and velocity. This allows for different amount of particles to be used depending on the zone to ensure a better accuracy on those areas. Also, it should be noted that in the algorithm presented in this document, the particles are only used to transport the information (solve convective terms of equations). However, in certain cases where the viscosity is low and there is only one fluid phase, it is possible to solve partially the momentum equation in the particles, as explained by [20]. Although this strategy leads to higher accuracy in the cases analyzed in the article, it lacks the generality that is required for the simulation of two-phase problems. Readers interested in a deep explanation of method basis can read [3,20] and the extension to two-phase problems in [1,2] or to fluid-structure interaction in [28].
2.3 Interface Treatment and Surface Tension
In a PFEM-2 simulation, the Lagrangian particles are integrated following a strategy called X-IVAS [3], where the streamlines fixed at time are employed to update the particle movements and velocities. In order to extend this approach to track the interface, each particle is initially marked with a sign function depending if it belongs to the first or second phase, and this value is preserved over the particle during the entire simulation guaranteeing boundedness. After X-IVS step, the particle data, i.e. velocity and marker function, must be projected to the nodes to continue with next algorithm steps. Although projection strategies are out of scope of this work (a review and recent improvements of this step can be found in [29]), in order to fix ideas the original algorithm used by PFEM-2 [2] to project a given field between nodes using subindices and particles using subindices is presented in this work, which is of the following form:
|
|
(4) |
where the function , associated with the node , can be either the typical kernel functions used in particle methods such as SPH[13] or the linear shape functions elevated to a power (it is ), while is the position of the particle with state and is the number of particles in a region around the node . The region around the node can be selected in different ways, being a possibility choosing the zone colored with grey in Figure 1. Mesh nodes thus obtain real values after the projection which can be different to the integer values that the particles transport. Finally, the interface is defined as the set of points that satisfy the equation .
Once projected over nodes, the function has similar properties to a VoF function: the mass is preserved but the discontinuous shape impossibilities an accurate gradient calculation then a poor curvature is estimated which often lead to unphysical flows around the interface when surface tension is included, resulting in unrealistic interface shapes. As it was mentioned, there are several strategies to overcome this limitation, and in this work the approach called S-CLSVOF [26] is selected. An advantage of this approach is that only the function is needed to advect (in contrast with CLSVOF), then the initial level set-like function is obtained following
|
|
(5) |
The main criterion in choosing this value is to satisfy an initial value of which is close to the mesh step size. This initial function is a signed function since it has a positive value in the denser fluid and a negative value in the lighter. However, in order to obtain a around the interface, the function is then re-distanced by solving the re-initialization equation:
|
|
(6) |
with the initial condition of , being an artificial time discretized with . Because the re-distancing starts from the initial interface and moving towards both fluids, and we are interested only on the zone around the interface, only few iterations are required, with representing the width around the interface, typically .
After solving 6 the is now a continuous smooth function around the interface, which helps in determining accurately the interface normal as usual in LSM, it is
|
|
(7) |
Hence, it provides a more precise and smoother interface curvature
|
|
(8) |
Some details are important to remark when Equations 7 and 8 are solved in the FEM framework. An initial strategy is to replace 7 into 8, and to use weighted residuals with the linear piecewise trial functions solving directly for , it is
|
|
(9) |
However this approach leads to spurious results because is discontinuous between the elements. A further option which obtain better results is first obtain a field with continuous between the elements (linear field in the elements), doing
|
|
(10) |
then, obtain the curvature as usual
|
|
(11) |
with and the normal to the boundary .
One of the most difficult tasks in front-capturing techniques is to accurately identify the interface to directly impose the term . This difficulty can be alleviated by interpreting the surface tension as a continuous body force spread across a transition region of thickness avoiding the need of reconstructing the interface explicitly. In this way, the continuum surface force model (CSF) of Brackbill et al. [22] provides an approach to approximate the term of surface tension force as a force per unit volume as
|
|
(12) |
where is the regularized interface delta function defined as follows
|
|
(13) |
It has been presented [22,30] that if the surface tension term on Equation 12 is discretized explicitly, i.e. the surface tension forces are evaluated on the interface at the previous time step, the stability of the scheme imposes the following restriction on the time step size :
|
|
(14) |
With this restriction the propagation of capillary waves is resolved and their unstable amplification avoided. The Equation 14 can be rather limiting for fine meshes and large surface tension coefficients then is a relevant issue in order to preserve the large time step proposed by PFEM-2. A solution to partially overcome this limitation is to treat the force term 12 implicitly. In this proposal, the surface tension term is included into the implicit calculation of the momentum equation over the mesh using the updated interface position. This helps to extend the time step limitation but is not a fully implicit approach because the interface movement is not coupled with the surface tension imposition. An analysis of the stability of this proposal is presented in Section 4.1.
Finally, the material properties are calculated with the smoothed Heaviside function
|
|
(15) |
|
It must be noticed the relevance of the parameter in this strategy. This parameter, which determines the extent of the interface smearing, has been analyzed in other works [26], concluding on the necessity of using the previously mentioned value that preserves a narrow thickness. There are alternative sharp interface methods such as the Ghost Fluid approach [31] which respects jump discontinuities across the interface and avoids an interface thickness. However, in these type of strategies the extension to unstructured meshes is far from straightforward. A FEM framework strategy to treat surface tension without thickness is employing enriched shape functions to treat pressure jumps as proposed by Ausas[9]. In spite of the possibility of capturing jumps, the curvature calculation still being a difficult task. Height functions [32] seems to be the best option, but its formulation for 3d unstructured meshes is still an open challenge. The Laplace-Beltrami formulation [33] appears as an interesting alternative because the curvature does not appear explicitly. However, this strategy also presents drawbacks: it is only accurate with small surface deformations, and requires the computing of the interfacial mesh leading to expensive computations.
2.4 PFEM-2 with surface tension
In order to decouple the unknown fields: velocity and pressure, the projection method known as fractional step [34] is chosen in PFEM-2. This segregated strategy consist on three main steps: velocity predictor, pressure calculation and velocity corrector. The particularity of this predictor step is that the convective term is decoupled from the rest of the momentum equation: the Lagrangian formulation allows to solve it only transporting the particles, which is done employing X-IVS. Then, the particles states are projected to nodal positions, and the remaining terms (including surface tension) are solved implicitly over the mesh, finishing the predictor step with a predictor velocity that satisfies the boundary conditions. Pressure calculation and velocity correction to obtain (a divergence free field) are done as usual, but the latter step also includes the particle velocity updating.
It is assumed that all fluid variables are known at time for both the particles and the mesh nodes. Subindexes y represent a generic mesh node and a generic particle respectively ( represents the number of particles). Let the finite element linear basis functions. According to this notation, the steps are presented in Algorithm 1, where is a spatial coordinate, , , can be or depending on the pressure restart choice. Also, can be or depending on the necessity or not of an accurate diffusion calculation when large Fourier numbers are employed, , and and are the standard mass and stiffness matrices of any FEM assembling. The computational implementation was done extending the high performing library presented in [21] and each test presented in this work was simulated with that house-made code.
- Convective Stage:
- Projection Stage:
- Momentum Stage:
- Poisson Stage:
- Correction Stage:
Algorithm 1- Time-Step PFEM-2 for two-phase incompressible fluids.
3 Interface evolution Tests
This section will deal with an exhaustive validation of the proposed PFEM-2 method to transport arbitrary shapes with neither interface disturbances or mass loss. It is well known that employing the Lagrangian scheme is relatively easy to solve pure-advective problems as presented in this section, but we consider that it is important for the reader to reach a strong conclusion about the goodness of this framework in contrast with the problems observed with the typical Eulerian schemes. The latter are represented by the suite OpenFOAM®which implements a VoF strategy with interface compression. As will be shown, the larger time step is employed, the more relevant are the differences between the frameworks.
3.1 Rigid Body Rotation of Zalesak's Disk
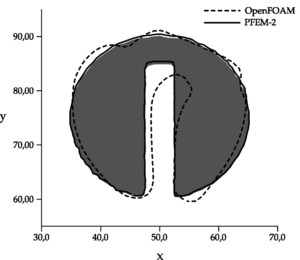
This test consists in the advection of a region composed of a circle with a slot [35]. If the interface tracking is accurate enough, after several revolutions, the shape must remain identical. The computational domain employed is . The advected region is a circle centered at with a radius of and a slot of width and height . The velocity field is a rigid body rotation around the center of the domain with a period of 628 time units:
|
The grid has points in each direction, conforming a cartesian mesh (in the case of PFEM simulations the mesh was split into 20000 triangles). The Courant number used in simulations is aproximately . Both the initial field and the solution after two revolutions are shown on Figure 2. In the case of PFEM simulation, approximately five particles by element were used. Most relevant OpenFOAM®settings are: SuperBee as the divergence scheme for the linear term in volume fraction advection equation, MULES as the time integration scheme, the number of alphaSubCycles is 20 (to guarantee interface Courant number less than 0.5) and the interface-compression factor cAlpha is set to 1.
|
| Figure 2: Zalesak's disk results after two full revolutions with 100 grid point per direction and . The grey region represents the initial condition. |
PFEM evolution shows a good agreement with the expected result (shape preservation). Some small errors, which are more evident when the magnitude of velocity is higher, appear due to approximate a curve with a sequence of straight trajectories. Even though in OpenFOAM®simulation the interface-compression method combined with the advection scheme avoids numerical diffusion, they modify the disk shape excessively, finishing in a poor prediction of the final status.
3.2 Single Vortex Case
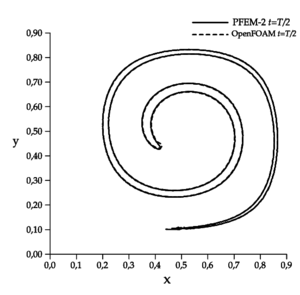
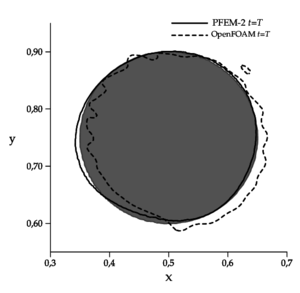
While Zalesak's disk test is a good indicator of numerical diffusion in an interface-capturing method, it does not test the ability to preserve small scale structures of the fluid flow. A well known test to evaluate the ability of the method to solve structures of different sizes and their evolution is given by the vortex-in-a-box problem introduced by Puckett et al. [36]. The difficulty of this tests is that requires the solution of an interface stretching problem. The computational domain is , where the interest region is a circle centered at with a radius of , advected with a velocity field defined by the stream function
|
|
being the velocity components
|
|
The grid has points in each direction, and the Courant number used in simulations is aproximately .
The setting employed for each numerical method in this case is almost equal to the previous test, with the only one difference that in OpenFOAM®the interface-compression factor cAlpha is set to 0.25 to give more stability through relaxing in some level the strong sharpness imposition. Using a larger factor, the simulation turns unstable.
|
|
| Figure 3: Single vortex test using 256 grid points per direction and (). Grey region represents the initial condition. | |
The results presented in Figure 3 show, for PFEM-2, good agreement with the expected result (shape preservation) after the cycle. Although the first half of the evolution is well captured by OpenFOAM®, the reconstruction of the original shape is not good enough.
3.3 LeVeque Deformation Case
LeVeque [37] proposed a three dimensional incompressible flow field which combines a deformation in the plane with one in the plane. This problem can be considered an extension of the previous case, requiring the correct capturing of the stretching phenomenon in three dimensions.
- The computational domain is .
- The advected region is a circle centered at with a radius of .
- The velocity field is given by
|
|
- The grid has points in each direction.
- Courant number used in simulations is aproximately .
Since the flow is reversed for , after one period the function must return to its original shape. Figure 4 shows that PFEM-2 successfully recovers almost the initial shape, which is a very complicated task for other numerical strategies [38,39].

|

|

|
| (a) t = 0 | (b) t = T=2 | (c) t = T |
| Figure 4: Snapshots of 3D deformation field test with PFEM-2. There were used 50 points per direction and . Results were smoothed by post-processing purposes. | ||
4 Surface Tension Test cases
In this section several two-phase incompressible tests are presented. The selected cases are focused in problems where the surface tension play an important role. Therefore, the algorithm 2.4 is exhaustive tested in different situations. The preliminary case analyzes the stability of the surface tension modeling measuring the spurious currents and its dissipation level. Being the advection almost negligible, this case allows to show that the Eulerian parts of the algorithm works as other standard codes. Next case consists in a bubble which rises due to buoyancy force under two different regime, one more rigid where the surface tension is stronger and other more inertial where a skirted shape must be found. An analysis of the parasitic currents and mesh convergence is done for the case where the gravity is neglected. Moreover, the same cases simulated with larger time-steps are stable but with more errors when surface tension increases, in contrast to Eulerian algorithms which tends to turn unstable. The second test is a standing wave dominated by capillarity. Although this problem is not the most indicated to be solved by PFEM-2 due the lack of inertial dominance, the method shows good accuracy even using reasonable large time-steps. Finally, a preliminary simulation of a primary atomization of a liquid jet is done. Being an inertia dominated case, large time-steps can be employed but a proper capture of drops and ligaments depends on the local Weber number.
Herein, the efficient distributed-memory implementation presented in [21] and extended to the free-surface treatment (see Algorithm 2.4) is used to simulate each of next cases presented. Also, the numerical parameter is set to in every case so as to restart the pressure at each time step to allow larger time-steps and iterations of steps 4 and 5 are done to improve the global first order [2]. On the other hand, the parameter is set to except when the Fourier number is greater than where is set to . The latter allows to increase the accuracy of the fractional step strategy for highly diffusive problems.
4.1 Stability Analysis
The most critical numerical artifact introduced by the modeling of the surface tension is the generation of spurious currents which appear in the form of vortices around the interface. The employed method, CSF, is not excepted from that drawback. These flows, also named as parasitic currents, are generated solely due to numerical artifacts through the discrete approximation of the interface which acts as a perturbation on the physically smooth interface.
If the surface tension term is discretized explicitly, i.e. the surface tension forces are evaluated at the interface at the previous time step, the stability of the scheme places a stability condition on a time step [22] as
|
|
(20) |
which results in a limiting for fine meshes and large surface tension coefficients. The implicit treatment of surface tension terms is shown to alleviate this restriction [40]. Instead of evaluating the surface tension with the interface at the previous time-step , the PFEM-2 employs the interface at time . However, the interface movement is not coupled with the surface tension force calculation leading to a sort of semi-implicit scheme. Then, to evaluate the range of stability of this methodology, an analysis similar to that presented by Deshpande et al. [41] is done here.
In order to include the effect of viscosity in the case of low Reynold number, Galusinski and Vigneaux [42] have revisited the time step constrain leading to the following generalized time step criterion
|
|
(21) |
with and two independent time-scales depending on the viscosity and density respectively. The constants and are independent of fluid properties and are only solver specific and in this work are determined experimentally from the simulations.
Following [41], the proposed case has a domain of discretized with a uniform grid of . Centered is a droplet of radius . Both density and viscosity are the same for the fluid inside or outside the drop and their value depend on the time scale considered. The coefficient of surface tension () and simulation time step ( ) are always maintained constant. Gravity is neglected in all simulations. The final simulation time is set to .
![Stability chart for integration times Tf= 10 [s]. Dashed lines represent the boundary between the stable and unstable computations found by Deshpande [39] and by the current work with PFEM-2.](/wd/images/thumb/a/a7/Draft_Samper_638342315-stability_chart_new.png/300px-Draft_Samper_638342315-stability_chart_new.png)
|
| Figure 5: Stability chart for integration times . Dashed lines represent the boundary between the stable and unstable computations found by Deshpande [41] and by the current work with PFEM-2. |
The set of cases simulated covers the values of and desired varying and properly. The Figure 5 presents the stability charts for the behavior of each test. Three categories of simulations are taken into account:
- Stable: kinetic energy calculated over the entire domain decays and center of mass of the droplet remains fixed.
- Unstable type 1: simulation ends, but the center of mass of the droplet finishes displaced more than the size of one element of the mesh and/or the kinetic energy does not decay.
- Unstable type 2: simulation crashes after completion.
From the results, the constants and can be obtained. It should be noted that this set of simulations has an ideal number of Reynolds of which is in the opposite side of a proper application range of Lagrangian strategies. Then, which is actually tested is the performance of the fractional step method employed by PFEM-2 to couple velocity and pressure plus a constant projection/interpolation from/to particles. Comparing with the reference work of Deshpande et al. [41], PFEM-2 is more robust against the density time scale than FVM+VoF, but it is weaker regarding to viscosity time scale. The former is expectable because the density is related to the unsteady and inertia terms. The latter can be understood due to either excessive noise at interface because of the use of particles, which requires more viscosity to dissipate that phenomena than Eulerian strategies and due to failures of the first order fractional step where the iterations do not recompose the solution. Anyway, it has been shown by Deshpande that the generation of spurious currents is only secondary for a moving interface, therefore the time step analysis shown here represents a conservative estimate. It is expected when the convection takes part in the simulation, the advantages of PFEM-2 will be clearer.
4.2 Rising Bubble Case
A widely used surface-tension benchmark is the case of an air bubble rising in a liquid column. Beyond qualitative results, as the bubble shape, Hysing et. al. [43] have presented a set of quantitative results obtained with several CFD multiphase codes solving two cases varying some physical properties. The first one considers a bubble in the ellipsoidal regime which undergoes moderate shape deformation, while in the second one the bubble belongs to the skirted regime and experiences much larger deformation. Both fluids are Newtonian, incompressible and isothermal, with properties listed in Table 1.
| Test | Re | Eo | ||||||
| 1 | 1000 | 100 | 10 | 1 | 0.98 | 24.5 | 35 | 10 |
| 2 | 1000 | 1 | 10 | 0.1 | 0.98 | 1.96 | 35 | 125 |
In the Fig. 6 the case configuration and the boundary conditions are presented. The initial condition is null velocity with the phase marker imposed as shown. In comparison with other reported works, for example [44], where the initial condition had to be relaxed in order to smooth the interface between the two regions, with the current strategy this pre-processing is not necessary because the initial marker field is imposed over particles then projected to the nodes, obtaining a naturally smoothed field over the mesh which diminishes, but not remove, the typical parasitic current of staircase profiles.
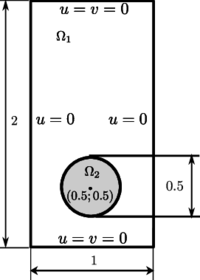
|
| Figure 6: Rising bubble case configuration and boundary conditions. |
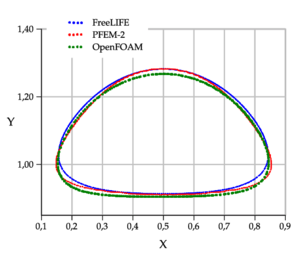
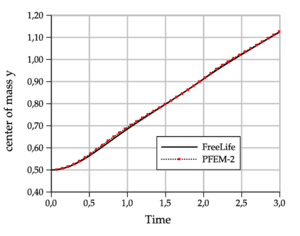
The reference solutions presented in [43] have been run with three different numerical approaches: the TP2D of Turek [45], the FreeLIFE of Parolini & Burman [46], and the MooNMD of Ganesan et al. [47]. They all use the finite element method, but the two first approaches describe the interface with the level set, while the latter tracks it in an arbitrary Lagrangian-Eulerian way. In [44] Klostermann et al. validated the results of the open source library OpenFOAM®, which implements the finite volume method, and particularly for two-phase flows a VoF strategy with interface compression. The following bubble quantities are used to compare the results:
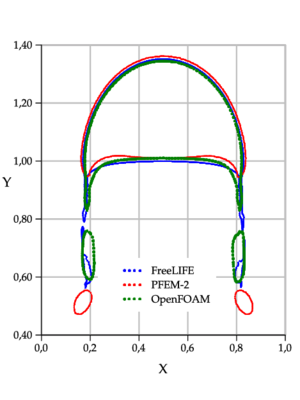
- Shape at the final time
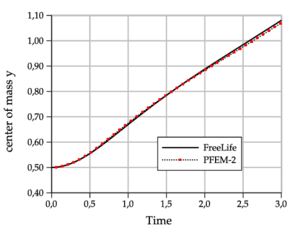
- Center of mass:
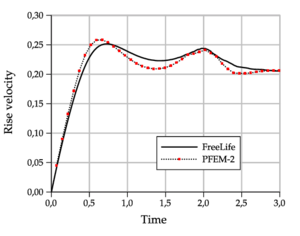
- Rise velocity:
The computations have been performed on structured meshes divided in triangles with element sizes of (levels 1, 2 and 3 respectively), to reach the final simulation time (). During the first group of tests a grid size-dependent time-step of is employed in order to calibrate the simulation to obtain similar results to the reference. Once proved, the time step is increased to analyze the stability and accuracy of the method when it is enforced.
4.2.1 Zero Gravity Condition
In order to estimate some first errors and uncertainties of the numerical model a transient simulation with surface tension but without gravity is carried out. The simulations were done up to reach . The pressure jump over the droplet interface and parasitic velocities are analyzed in the simulation. The value of the pressure jump over the interface due to surface tension in two dimensions can be analytically calculated as
|
|
(22) |
where is the bubble radius. Using the physical conditions of the most surface-tension dominant case (Test 1), it leads to . A normalized pressure can be obtained in the case of a static bubble, it should read in : and in : with a sharp pressure jump at the surface.
Various numerical methods are known to generate spurious artificial numerical flows instead of keeping steady cylindrical drops [48]. The order of magnitude of parasitic velocities can be estimated according to the surface tension coefficient and dynamic viscosity of the bubble:
|
|
(23) |
where is a numerical constant, a characteristic of the quality of the numerical modeling of surface tension forces (a non-dimensional number similar to a capillary number). The optimal value of is zero. Typical values of are found between and .
A set of simulations were done employing different numerical strategies and various meshes in order to calculate the curvature and comparing results. The Table 2 presents the tests and its numerical results, while Figure 7 shows the final pressure field for some simulations. In the set of cases presented, spurious velocities are found on both sides of the interface, which are interpreted as parasitic currents. These observations are in agreement with those found in, for example, [44,48] for a static viscous droplet in equilibrium. The current proposal of PFEM-2 with S-CLSVOF + CSF was tested employing both curvature FEM calculation strategies above cited, i.e. using discontinuous and continuous normals (Equations 9 and 11) showing a clear advantage for the latter option in the parasitic current indicator, i.e. , and similar results about the pressure jump found . On the other hand, the strategy that solves with VoF + interface compression + CSF is also included in the analysis. This approach, employed by the open source library OpenFOAM®and analyzed in [44], shows acceptable accuracy only when grids composed by quads are used. In the case of meshes of triangles, the curvature results are noisy leading to unphysical spikes (overshoots and undershoots) of the pressure and large spurious currents.
So as to completion, the Table 2 also presents the results obtained with PFEM-2+CSF but without smoothing, i.e. calculating the normal and curvature directly with the marker function . As expected, the spurious currents are one order above than the results with smoothing and the pressure jump is over estimated.
The employment of meshes composed by triangles leads to more efficient implementations of the PFEM-2 method, therefore a solution for the curvature in this type of meshes is essential so as not to resign performance. The results presented in this subsection guarantee accurate enough solutions for PFEM-2. However, one of the most important drawbacks of this strategy is that almost no grid convergence was found because the values of and remain almost constant even the mesh is refined. It is known that the integral effect of curvature (i.e. average pressure jump) actually converges to a value that is systematically different from the analytical value [41].
| Method | |||
| PFEM-2 with as Eq. 9 | |||
| PFEM-2 with as Eq. 11 | |||
| PFEM-2 with as Eq. 11 | |||
| PFEM-2 with as Eq. 11 | |||
| VoF quads (ref [42]) | |||
| VoF quads (ref [42]) | |||
| VoF triangles | |||
| PFEM-2 with no smoothing |
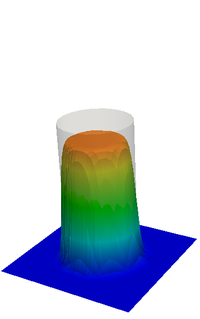
|
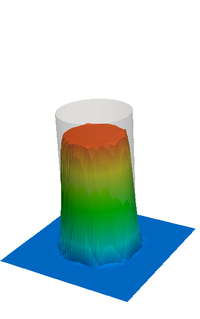
|
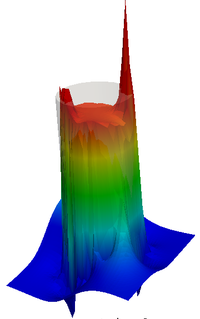
|
| Figure 7: Zero Gravity test with a mesh of . Analytical pressure is shown in grey. | ||
As a footnote comment, in contrast with the set of simulations presented in [42], in our case we did not found the noisy behavior of OpenFOAM®with the quads mesh when finer meshes are used. However, as in that publication, there is not found grid convergence of the method.
4.2.2 Ellipsoidal Regime Test
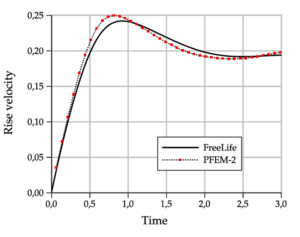
For the Test 1, Figure fg:rising-T1-d shows the PFEM-2 bubble shapes at final time for the meshes , the convergence to the shape of the finest mesh can be observed, which is in good agreement with the OpenFOAM®solution reported in [44] as shown in Figure fg:rising-T1-c. PFEM-2 shape is less similar to FreeLIFE solution, but keeps good agreement. The plots of the bubble rise velocity in Figure fg:rising-T1-a show that our bubble reaches a slightly larger maximum, but the evolution of the center of mass in Figure 8a is again in good agreement.
4.2.3 Skirted Regime Test
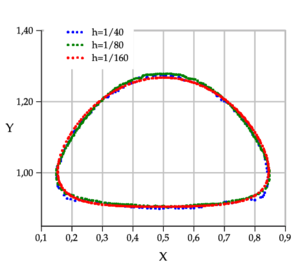
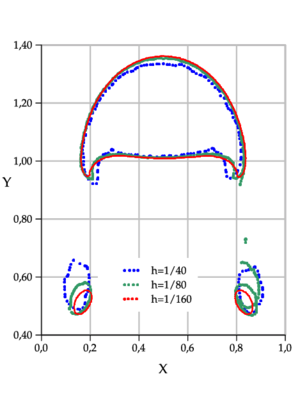
The same type of results are shown for test 2 in Figures fg:rising-T2-c to 9a. Although the bubbles in both test cases rise with similar velocity, the decrease in surface tension as well as higher viscosity and density ratios causes bubble 2 to undergo a much larger deformation and to develop thin filaments. In both FreeLIFE and OpenFOAM solutions these filaments break up, which also happens in PFEM-2 simulation (Figure fg:rising-T2-a). In the physical reality, breakup occurs due to capillary waves present on the interface, which trigger the three-dimensional Plateau-Rayleigh instability when the filament radius is small enough. Thus, capillary waves can cause the skirt filament to fragment during flow, though this response requires very large elongations, typically greater than 20 times the initial bubble radius [30]. The Figure fg:rising-T2-d shows that the PFEM-2 solution converges to the shape of the finest mesh, mainly the size of the two bubbles detached from the filaments (the coarser mesh is employed the larger unphysical satellite bubbles are obtained). The problem here is the use of the interface thickness parameter which is mesh-dependent and introduce several distortions in coarser ones.
4.2.4 Extending Time-Step
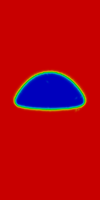
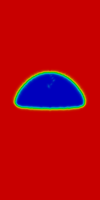
In order to emphasize the capability of the method to manage large time-steps, the current case is also simulated with a range of using the in-house implementation of PFEM-2 and comparing with results obtained by the widely known OpenFOAM®suite which implement, as it was mentioned, VoF with interface compression. The problem setup and domain discretization is the same as presented above. In the case of OpenFOAM®, the solver and the configuration used in [44] is used in this subsection, which ensured good results in the rising bubble case. Compression flux treatment, time schemes and momentum predictor employment are analyzed in the mentioned work, deriving a recommended solver configuration for this case. The time-step employed is , which enforce to obtain number that is critical for Eulerian framework solvers, mainly when it is measured at the interface.
Figure 10 presents PFEM-2 solutions with , and solving the most surface-tension dominant case, i.e. Test 1. Although the solution is stable for each time-step, the higher surface tension relevance respect to Test 2 generates non accurate solutions in the interface zone: unphysical disturbances like Rayleigh-Taylor instabilities are observed showing that the surface tension term is not imposed properly when the largest time-step is used. However, the solution with is good enough and can be used as an accurate initial appearance of the solution. This preliminary and fast solution can not be done with OpenFOAM®, because the solution diverges when is employed, due to the strong interface compression imposition.
|
|

|
| (a) PFEM-2 | (b) PFEM-2 | (c) PFEM-2 |
| Figure 10: Rising bubble Test 1. Comparison of PFEM-2 solutions when the time step is increased. | ||
On the other hand, Figure 11 the solutions obtained at for the Test 2 can be shown. PFEM-2 solution when the time-step is increased is stable and keeps similar shape and quantitative values as rise velocity and center of mass, but loosing some definition of the satellite bubbles. On the other hand, OpenFOAM®(OF) solution with large time-step diverges approximately at because of the disturbance introduced by the interface compression term trying to force a sharp interface. Reducing the interface compression coefficient could preserve the stability, but the final shape is highly diffusive, as presented by [44].

|

|

|

|
| (a) PFEM-2 | (b) PFEM-2 | (c) OpenFOAM® | (d) OpenFOAM® |
| Figure 11: Rising bubble Test 2. Comparison of solutions when the time step is increased. | |||
Figure 12 shows an application of the stability analysis to the case of the rising bubble. Same axis are presented and in this case the simulations presented correspond to the ellipsoidal and skirted regimes with the three time step employed. As it was mentioned before, the stability limits are a conservative estimation due the generation of spurious currents is only secondary for a moving interface. The simulated cases prove this fact: although every test fall into the unstable region (see Figure 5), when convective term is included these numerical artifacts, which are not dissipated in unstable type 1 simulations, does not produce large errors in the results. Therefore, a stronger limit is used here which separates divergent (crashing) and non-divergent (no crashing) simulations.
It should be noted that the region of divergence of PFEM-2 is smaller than the obtained with OpenFOAM®. Therefore, almost every rising bubble simulation falls over the non-divergent region in PFEM-2, but only those that use the smallest time-step do not blow-up with OpenFOAM®. This results is proven experimentally in the cases presented above. Although both large time-step tests theoretically are almost into the unstable region in PFEM-2, only the ellipsoidal test is experimentally unstable. The inclusion of new tests around that region could improve the determination of this limit.
![Rising bubble simulation in the stability chart. Filled line represent the boundary between the non divergent and divergent computations (unstable type 2 simulations) found by Deshpande [39] and by the current work with PFEM-2. Points represent the placement of ellipsoidal and skirted tests employing different time-steps.](/wd/images/thumb/0/03/Draft_Samper_638342315-stability_chart_rising_bubble.png/300px-Draft_Samper_638342315-stability_chart_rising_bubble.png)
|
| Figure 12: Rising bubble simulation in the stability chart. Filled line represent the boundary between the non divergent and divergent computations (unstable type 2 simulations) found by Deshpande [41] and by the current work with PFEM-2. Points represent the placement of ellipsoidal and skirted tests employing different time-steps. |
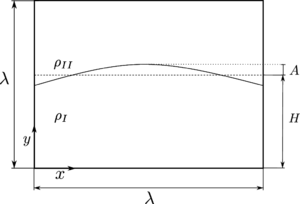
4.3 Standing capillary wave
In previous work [2], authors have presented the results of the PFEM-2 method solving the case of the standing gravity wave. In those simulations, several number of Reynolds were analyzed obtaining good agreement with analytical solutions. The flow were dominated by the gravity force, therefore the enrichment strategy to capture properly the density jump (the pressure gradient) was mandatory.
In the current work, the case to analyze is governed by a totally different force but leading to similar results. In this test the density jump is secondary, instead a good resolution of the surface tension forces, which dominate the flow behavior, is of transcendental relevance.
|
| Figure 13: Configuration setup of standing capillary wave case. |
The setup used is taken from [41] in this simulation is shown in Figure 13. A perturbation of amplitude where is the wavelength width is imposed as initial condition of the phases positioning, which is allowed to evolve under the influence of surface tension alone. The heavier phase (fluid ) has a density of and a kinematic viscosity of , while the lighter phase has and respectively. Regarding to boundary conditions, bottom is set as slip, left and right sides have a symmetry conditions and the top is considered as atmosphere fixing the pressure as .
Lamb [49] presented an analytical solution of this problem when small-amplitude waves are considered. In this regime, the standing wave evolution can be obtained through the linearization of the Navier-Stokes equations for traveling waves. Therefore, the frequency of oscillation in this linear limit is
|
|
(24) |
where . Analytically, the frequency of change in kinetic energy is twice the frequency of oscillation of the free surface. The analytical period of oscillation of kinetic energy is therefore . In addition, the rate of decay of kinetic energy due to viscous effects is given as
|
|
(25) |
where and .
Three different grid densities were tested with , and . In order to obtain a more accurate dissipative forces calculation, the numerical parameter is set to 1. This selection introduces a diffusion term in the equation of the corrector step as proposed Blasco, Codina and Huerta [50]. Under our experience, without that term would not be possible to obtain the proper decay of kinetic energy with the classical fractional step method used due to the large Fourier number involved in this case.
The evolution of kinetic energy for these grids is plotted in Figure 14 along with the exponential decay of kinetic energy due to viscous effects, calculated from Equation 25.
![Comparison of the period of kinetic energy for the configuration in Figure 13, with the analytical solution of [47].](/wd/images/thumb/b/b7/Draft_Samper_638342315-standing_wave_results.png/300px-Draft_Samper_638342315-standing_wave_results.png)
|
| Figure 14: Comparison of the period of kinetic energy for the configuration in Figure 13, with the analytical solution of [49]. |
| Name | calculated | ||
| Test A | |||
| Test B | |||
| Test C |
The numerical parameters employed in each test with its corresponding computed oscillation periods, averaged over 8 cycles, are shown in Table 3. The period of oscillation for the coarsest grid has the largest error and it is reduced employing finer meshes, achieving an error in period with respect to the analytical solution of with the finer grid. The last shows that, in spite of the inaccuracies in curvature, the results show trends of convergence to a value close to the theory. The observed loss in rate of convergence can be explained as a combination of systematic error in curvature, as it was shown in the zero gravity test, and also the fact that the analytical solution also contains a systematic error, since it is based on the linearized version of the equations, whereas PFEM-2 solves the full version of the Navier-Stokes equations.
4.4 Towards a simulation of 3D Jet Atomization
Liquid atomization is an important process which found interest in several engineering applications such as aerospace propulsion systems, automotive engines, food processing, and ink-jet printing. Its numerical simulation allows to investigate physical processes of the atomization because our understanding on physical mechanisms of such phenomena is still not sufficient. Our investigation group is doing its first steps in this research area and we report in this work our early results using the numerical method presented in this work contrasted with the use of the widely validated tool OpenFOAM®[12].
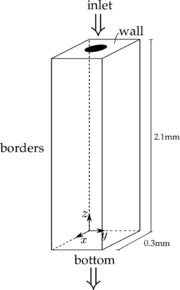
The main properties of the case analyzed are the following: the size of the domain is (, , ), where the first dimension is the streamwise direction and the other two, the spanwise directions. At the injection level, the jet diameter is equal to , while the liquid jet Reynolds number is equal to . A summary of the physical parameters, for this configuration, can be found in Table 4. Also, the geometry and boundary conditions are presented in Figure 15. Boundary condition over borders is slip, over bottom zero gradient velocity and pressure equal to zero. Top boundary has two patches: on inlet a mean inlet of is imposed and over wall no-slip condition is set.
|
| Figure 15: Geometry and boundary conditions for the case of the 3d jet. |
| Parameter | Symbol / Unit | Value |
| Gas density | 25 | |
| Liquid density | 696 | |
| Gas viscosity | ||
| Liquid viscosity | ||
| Surface Tension Coefficient | ||
| Injection Diameter | 100 | |
| Liquid Reynolds | 4659 | |
| Liquid Weber | 7239 | |
| Turbulent Intensity | 0.05 | |
| Turbulent Scale |
As a first reference result, we can cite the work of Ménard et al. [51,52], which employ the LSM to track the interface added to the Ghost Fluid Method (GFM) to describe the interface discontinuites and manage the pressure, density and viscosity jumps. Also, the Level Set method is coupled with the Volume of Fluid method (VoF) to ensure mass conservation. The mesh used by Chesnel and Ménard and co-workers in [52] is a Cartesian grid with regularly spaced nodes (). Liquid surface instabilities close to the injector are visible. Their deformation leads to the formation of ligaments and droplets of various sizes. At the end of the domain, the liquid core has almost disappeared and a dense spray of droplets leaves the computational domain. The key of the quickly drop production is the use of a space-time correlated turbulent flow at the inlet: Ménard uses a syntetized correlated turbulence with a method proposed by Klein et al. [53]. In the work of Desjardins et al. [54], authors employ a forerunner simulation to impose the inlet turbulent boundary condition, obtaining similar results to the above mentioned. Both works have a relevant conclusion: by the end of the computational domain, the liquid core has been fully disintegrated.
Another approach in the numerical characterization of jet atomization is reported by Shinjo et al. in [55,56]. In this work, the authors report that the grid resolution used by Ménard was coarse for the chosen Reynolds and Weber numbers, so this was not a direct numerical simulation in a true sense: the produced ligaments and droplets did not exhibit smooth shapes or wave dynamics driven by surface tension, but the overall liquid jet motion was captured in that simulation. Shinjo solved with a mesh with million of cells (). In contrast to Ménard, the ligament drop is done far from the inlet, being the main responsible the plain velocity front imposed at the inlet by Shinjo instead of using a turbulent-induced flow [57].
Our initial simulations using PFEM-2 and OpenFOAM®employ plain inlet, therefore more similarities with Shinjo results are found. It must be taken into account that in the most refined case simulated with OpenFOAM®, the geometry was meshed with a cartesian base grid of but the solver employed, named interDyMFoam, works with adaptive refinement at interface reaching a minimum grid size of . On the other hand, PFEM simulation has an uniform mesh size of conforming a mesh with 24 millons of tetrahedra, but even far from the refinement degree used in reference works.
Figure 16 shows a comparison at simulation time . The picture shows that the droplet formation and the like-mushroom shape are comparable, but the minimum drop size is better described using a finer mesh. The great advantage of using PFEM-2 is when the computing time is analyzed because simulation was done employing a Courant number at interface CFL while OpenFOAM®crashes when CFL was tried. As it was shown in the rising bubble case, the simulation of drops can not be accurate when these large time-steps are used, however the stability of the method allows to obtain a very approximate solution, mainly of the jet core, even spending of time comparing with Eulerian methodologies.

|

|
| (a) OpenFOAM® with | |

|
|
| (b) PFEM-2 with | |
| Figure 16. Overall shape of the liquid jet atomization. Figures correspond to iso-surfaces of (interface). PFEM-2 simulation with CFL and OpenFOAM®with CFL | |
Future works must enhance the simulation with PFEM-2, preferably employing finer meshes to contrast more adequately with reference works. An analysis of droplet size distribution is a relevant pending task which must be done in a future analysis.
5 Conclusions
In this work, the PFEM-2 methodology for two-phase fluids has been extended to the case of problems with surface tension dominant where the surface tension term is solved with the CSF approach. A strategy, which is based in a simple coupling between Level Set and Volume of Fluid approaches, allows to calculate accurate curvatures then reducing the spurious velocities produced by the surface tension term in the case of sharp interfaces.
Despite obtaining a smooth mesh solution at interface, the primary data set in PFEM-2 are the particles, which advects a sharp interface. This feature makes PFEM-2 a method with several goodness in inertia dominant flows that distinguish it from other numerical alternatives: the interface is moved without diffusion, the mass is automatically conserved and the time-step can be enforced to CFL resigning some accuracy, mainly in zones where the surface tension is relevant, but not losing stability. The results for pure advective, surface tension dominant, and a jet atomization tests presented in the current work, together with the facts mentioned above, locate PFEM-2 as one of the fastest algorithms to solve two-phase flow problems.
Acknowledgments
Authors gratefully thank the help and contributions of Dr. Santiago Márquez Damián and Dr. Pedro Morin. Simulations were done in the cluster Bora at the CIMEC-UNL-Argentina and in the Mendieta cluster of the Centro de Computación de Alto Desempeño CCAD-UNC-Argentina. Also, authors want to thank to CONICET, Universidad Nacional del Litoral and ANPCyT for their financial support (grants PICT 0830 (2013), PIP-2012 GI 11220110100331 and CAI+D 2011 501 201101 00435 LI. J. Gimenez gratefully acknowledges the support of the Argentinian National Scientific and Technical Research Council (CONICET) through a type-II doctoral scholarship and the program ERASMUS MUNDUS action 2 ARCOIRIS project for financial support through a six-month doctoral scholarship. This work was also partially supported by the European Research Council under the Advanced Grant: ERC-2009-AdG ‘‘Real Time Computational Mechanics Techniques for Multi-Fluid Problems’’ and by the ERC Proof of Concept FORECAST (Ref. 664910) under H2020 Programme.
Bibliography
[1] Idelsohn, Sergio R. and Marti, Julio and Becker, Pablo and Oñate, Eugenio. (2014) "Analysis of multifluid flows with large time steps using the particle finite element method", Volume 75. International Journal for Numerical Methods in Fluids 9 621–644
[2] Juan M. Gimenez and Leo M. González. (2015) "An extended validation of the last generation of particle finite element method for free surface flows", Volume 284. Journal of Computational Physics 0 186 - 205
[3] Sergio Idelsohn and N.M. Nigro and A. Limache and E. Oñate. (2012) "Large time-step explicit integration method for solving problems with dominant convection", Volume 217-220. Comp. Meth. in Applied Mechanics and Engineering 168-185
[4] Moës, Nicolas and Dolbow, John and Belytschko, Ted. (1999) "A finite element method for crack growth without remeshing", Volume 46. John Wiley Sons, Ltd. International Journal for Numerical Methods in Engineering 1 131–150
[5] J. Alfaiate. (2003) "New developments in the study of strong embedded discontinuities in finite elements", Volume 251. Advances in Fracture and Damage Mechanics 2 109–114
[6] J. Simo and J. Oliver. (1993) "An analysis of strong discontinuities induced by strain softening in rate-independent inelastic solids", Volume 12. Computational Mechanics 277–296
[7] J. Oliver and A. Huespe. (2004) "Continuum approach to material failure in strong discontinuity settings", Volume 193. Computer Methods in Applied Mechanics and Engineering 3195–3220
[8] A. H. Coppola-Owen and R. Codina. (2005) "Improving Eulerian two-phase on finite element approximation with discontinuous gradient pressure shape functions", Volume 49. International Journal for Numerical Methods in Fluids 1287 - 1304
[9] Ausas, Roberto F. and Buscaglia, Gustavo C. and Idelsohn, Sergio R. (2012) "A new enrichment space for the treatment of discontinuous pressures in multi-fluid flows", Volume 70. John Wiley Sons, Ltd. International Journal for Numerical Methods in Fluids 7 829–850
[10] S.J. Osher and R.P. Fedkiw. (2001) "Level set methods: an overview and some recent results", Volume 169. Journal of Computational Physics 463 - 502
[11] C.W. Hirt and B.D. Nichols. (1981) "Volume of fluid (Vof) method for the dynamics of free boundaries", Volume 39(1). J. Comput. Phys 201-225
[12] Weller, H. G. and Tabor, G. and Jasak, H. and Fureby, C. (1998) "A tensorial approach to computational continuum mechanics using object-oriented techniques", Volume 12. Computers in Physics 6 620-631
[13] R. A. Gingold and J. J. Monaghan. (1977) "Smoothed Particle Hydrodynamics, theory and application to non-spherical stars", Volume 181. Royal Astronomical Society 375–389
[14] J.J. Monaghan. (1988) "An introduction to SPH", Volume 48. Computational Physics Communications 89-96
[15] Harlow, Francis H. and Welch, J. Eddie. (1965) "Numerical Calculation of Time Dependent Viscous Incompressible Flow of Fluid with Free Surface", Volume 8. Physics of Fluids (1958-1988) 12 2182-2189
[16] Simone E. Hieber and Petros Koumoutsakos. (2005) "A Lagrangian particle level set method", Volume 210. Journal of Computational Physics 2 342 - 367
[17] Douglas Enright and Ronald Fedkiw and Joel Ferziger and Ian Mitchell. (2002) "A Hybrid Particle Level Set Method for Improved Interface Capturing", Volume 183. Journal of Computational Physics 1 83 - 116
[18] S.R. Idelsohn and E. Oñate and F. Del Pin. (2004) "The particle finite element method a powerful tool to solve incompressible flows with free-surfaces and breaking waves.", Volume 61. International Journal of Numerical Methods 964–989
[19] M. Evans and F. Harlow and E. Bromberg. (1957) "The particle-in-cell method for hydrodynamic calculations". DTIC Document
[20] S.R. Idelsohn and N.M. Nigro and J.M. Gimenez and R. Rossi and J. Marti. (2013) "A fast and accurate method to solve the incompressible Navier-Stokes equations", Volume 30-Iss:2. Engineering Computations 197-222
[21] J.M. Gimenez and N.M. Nigro and S.R. Idelsohn. (2014) "Evaluating the performance of the Particle Finite Element Method in parallel architectures", Volume 1. Journal of Computational Particle Mechanics 103-116
[22] J.U Brackbill and D.B Kothe and C Zemach. (1992) "A continuum method for modeling surface tension", Volume 100. Journal of Computational Physics 2 335 - 354
[23] Sharen J. Cummins and Marianne M. Francois and Douglas B. Kothe. (2005) "Estimating curvature from volume fractions", Volume 83. Computers and Structures 6–7 425 - 434
[24] K. W. Lam. (2009) "A Numerical Surface Tension Model for Two-Phase Flow Simulations". University of Groningen
[25] Mark Sussman and Elbridge Gerry Puckett. (2000) "A Coupled Level Set and Volume-of-Fluid Method for Computing 3D and Axisymmetric Incompressible Two-Phase Flows", Volume 162. Journal of Computational Physics 2 301 - 337
[26] A. Albadawi and D.B. Donoghue and A.J. Robinson and D.B. Murray and Y.M.C. Delauré. (2013) "Influence of surface tension implementation in Volume of Fluid and coupled Volume of Fluid with Level Set methods for bubble growth and detachment", Volume 53. International Journal of Multiphase Flow 0 11 - 28
[27] Sergio Idelsohn and Eugenio Oñate and Norberto Nigro and Pablo Becker and Juan Gimenez. (2015) "Lagrangian versus Eulerian integration errors", Volume 293. Computer Methods in Applied Mechanics and Engineering 0 191 - 206
[28] Becker, P. and Idelsohn, S.R. and Oñate, E. (2014) "A unified monolithic approach for multi-fluid flows and fluid–structure interaction using the Particle Finite Element Method with fixed mesh". Springer Berlin Heidelberg. Computational Mechanics 1-14
[29] J.M. Gimenez and N. Nigro and P. Morin and S. Idelsohn. (2015) "Numerical comparison of the Particle Finite Element Method against an Eulerian formulation", Volume. AFSI 2014. Springer International Publishing in revision
[30] M. De Mier. (2009) "Numerical Simulation of multi-fluid flows with the particle finite element method"
[31] Ronald P Fedkiw and Tariq Aslam and Barry Merriman and Stanley Osher. (1999) "A Non-oscillatory Eulerian Approach to Interfaces in Multimaterial Flows (the Ghost Fluid Method)", Volume 152. Journal of Computational Physics 2 457 - 492
[32] Lorstad, Daniel and Francois, Marianne and Shyy, Wei and Fuchs, Laszlo. (2004) "Assessment of volume of fluid and immersed boundary methods for droplet computations", Volume 46. John Wiley Sons, Ltd. International Journal for Numerical Methods in Fluids 2 109–125
[33] Bänsch, Eberhard. (2001) "Finite element discretization of the Navier–Stokes equations with a free capillary surface", Volume 88. Springer-Verlag. Numerische Mathematik 2 203-235
[34] J. Donea and A. Huerta. (1983) "Finite Element Method for Flow Problems". Wiley
[35] S. Zalesak, Fully multidimensional flux-corrected transport algorithms for Fluids, J. Comput. Phys. 31(3) (1979) 335–362
[36] E. Puckett, A. Almgren, J. Bell, D. Marcus, W. Rider, A highorder projection method for tracking fluid interfaces in variable density incompressible flows, J. Comput. Phys. 130(2) (1997) 269–282.
[37] R. LeVeque. (1996) "High-resolution conservative algorithms for advection in incompressible flow", Volume 33(2). SIAM J. Numer. Anal. 627–665
[38] Enright, Douglas and Losasso, Frank and Fedkiw, Ronald. (2005) "A Fast and Accurate semi-Lagrangian Particle Level Set Method", Volume 83. Pergamon Press, Inc. Comput. Struct. 6-7 479–490
[39] S. D. Costarelli and M. A. Storti and R. R. Paz and L. Dalcin and S. R. Idelsohn. (2013) "GPGPU implementation of the BFECC algorithm for pure advection equations", Volume accepted. Cluster Computing
[40] Hysing, S. (2006) "A new implicit surface tension implementation for interfacial flows", Volume 51. John Wiley Sons, Ltd. International Journal for Numerical Methods in Fluids 6 659–672
[41] S. Deshpande and L. Anumolu and M. Trujillo. (2012) "Evaluating the performance of the two-phase flow solver interFoam", Volume 5. Comput. Sci. Disc 014016 (36pp)
[42] Cédric Galusinski and Paul Vigneaux. (2008) "On stability condition for bifluid flows with surface tension: Application to microfluidics", Volume 227. Journal of Computational Physics 12 6140 - 6164
[43] Hysing, S. and Turek, S. and Kuzmin, D. and Parolini, N. and Burman, E. and Ganesan, S. and Tobiska, L. (2009) "Quantitative benchmark computations of two-dimensional bubble dynamics", Volume 60. John Wiley Sons, Ltd. International Journal for Numerical Methods in Fluids 11 1259–1288
[44] Klostermann, J. and Schaake, K. and Schwarze, R. (2013) "Numerical simulation of a single rising bubble by VOF with surface compression", Volume 71. John Wiley Sons, Ltd. International Journal for Numerical Methods in Fluids 8 960–982
[45] S. Turek. (1998) "Efficient Solvers for Incompressible Flow Problems". Springer
[46] N. Parolini and E. Burman. (2005) "A finite element level set method for viscous free-surface flows". 7th Conference on Applied and Industrial Mathematics in Italy 416-427
[47] Sashikumaar Ganesan and Gunar Matthies and Lutz Tobiska. (2007) "On spurious velocities in incompressible flow problems with interfaces", Volume 196. Computer Methods in Applied Mechanics and Engineering 7 1193 - 1202
[48] L. Strubelj and I. Tiselj and B. Mavko. (2009) "Simulations of free surface flows with implementation of surface tension and interface sharpening in the two-fluid model", Volume 30. International Journal of Heat and Fluid Flow 4 741 - 750
[49] H. Lamb. (1993) "Hydrodynamics". Cambridge Mathematical Library 6th Edition
[50] J. Blasco and R. Codina and A. Huerta. (1998) "A fractional-step method for the incompressible Navier-Stokes equations related to a predictor-multicorrector algorithm", Volume 28. Int. J. Numer. Methods Fluids 10 1391–1419
[51] T. Ménard and S. Tanguy and A. Berlemont. (2007) "Coupling level set/VOF/ghost fluid methods: Validation and application to 3D simulation of the primary break-up of a liquid jet", Volume 33. International Journal of Multiphase Flow 5 510 - 524
[52] J. Chesnel and Thibaut Ménard and Julien Reveillon and Francois-Xavier Demoulin. (2011) "Subgrid analysis of liquid jet atomization", Volume 21. Atomization and Sprays 1 41-67
[53] M. Klein and A. Sadiki and J. Janicka. (2003) "A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations", Volume 186. Journal of Computational Physics 2 652 - 665
[54] Olivier Desjardins and Vincent Moureau and Heinz Pitsch. (2008) "An accurate conservative level set/ghost fluid method for simulating turbulent atomization", Volume 227. Journal of Computational Physics 18 8395 - 8416
[55] J. Shinjo and A. Umemura. (2010) "Simulation of liquid jet primary breakup: Dynamics of ligament and droplet formation", Volume 36. International Journal of Multiphase Flow 7 513 - 532
[56] J. Shinjo and A. Umemura. (2011) "Surface instability and primary atomization characteristics of straight liquid jet sprays", Volume 37. International Journal of Multiphase Flow 10 1294 - 1304
[57] Huu P. Trinh and C. P. Chen. (2005) "Modeling of Turbulence Effects on Liquid Jet Atomization". 43rd AIAA Aerospace Sciences Meeting and Exhibit
Document information
Published on 01/01/2016
DOI: 10.1016/j.compfluid.2016.04.026
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?