Abstract
In this work, the effects of variables such as initial carded web mass, needle penetration depth, punch density, and the frequency of incident sound wave on transmission of sound through polypropylene needle-punched nonwovens were investigated. Fibrous carded webs using commercially available 17 dtex, 90 mm staple length polypropylene fibers were prepared with different mass per unit area using carding machine. Samples were needled at various punch-densities and needle penetration depths were produced. Design points of experiments were set up using Taguchi experimental design method. Sound transmission loss (STL) of needled samples was measured using an impedance tube equipped with four microphones. Minitab software was used to analyze the sound transmission ability of the samples. Results indicated that all of the considered controllable factor have significant effects on STL values determined for the needled nonwovens. Also, initial carded web mass was found to be the most influential factor affecting sound transmission through the samples. It was concluded that an increase in thickness of the samples as well as mass per unit area of nonwovens results in higher sound transmission loss by the samples.
Keywords
Sound transmission loss; Polypropylene needle-punched nonwoven; Impedance tube with 4 microphones; Taguchi method
1. Introduction
Use of sound insulation in automobiles is of particular importance even in low cost vehicles. Sound insulation in vehicles can be measured by active and passive techniques. The former is based on wave interference phenomenon and the latter uses acoustic materials to dampen the incident sound waves [1]. Textile materials due to their inherent porosity and low-cost are ideal candidate for sound insulation. Nonwoven structures due to their technical and economical merits are currently used to make over 40 various parts of vehicles that include trunk liners, carpets and filters [2] and [3]. Good performance and safety, engineered nonwovens incorporating inherent essential properties, performance and safety provide advanced insulation.
Acoustic properties of nonwoven structures are related to geometry of constituent fibers and their orientation within the fibrous structure [4]. Like other surfaces upon incident of sound wave on surfaces of nonwovens, the incident wave is partly reflected, absorbed and transmitted [5].
Measurement of sound absorption by porous materials can be achieved by following methods [3] and [4]:
- Reverberant field
- Free field
- Impedance tube
The impedance tube method equipped with two microphones is an effective and inexpensive means which is commonly used to measure both sound absorption and sound reflection coefficients of the barrier material [6], [7], [8], [9], [10] and [11].
Most of studies conducted so far have focused on absorption of sound by nonwoven materials using two microphone impedance tube. Research on transmission as well as insulation of sound by nonwovens is scarce. In case of highly porous material with low flow resistivity, four microphone systems are preferred over two microphone system which usually is used for determination of absorbed component of sound wave. The sound insulation ability of materials is generally determined in terms of transmitted component of sound wave. Sound Transmission Loss (STL) represents the amount of sound, in decibels (dB) that is isolated by a material or partition in a particular octave band. It can be measured using impedance tube equipped with four microphones.
Lee and Kim [12] studied sound absorption behavior and sound transmission loss (STL) of composite structures. A composite sheet was fabricated by hot-pressing the sandwiched polypropylene and polyethylene terephthalate nonwovens. The sound transmission loss of a nonwoven composite containing the activated carbon fiber and cotton was studied in another investigation [13]. Sengupta [14] predicted sound transmission loss of jute needle-punched nonwovens in terms of punch density, depth of needle penetration and mass per unit area by developing a statistical model, based on central composite rotatable experimental design.
This study undertakes the effect of different processing parameters such as carded web mass, needle penetration depth, punch density and also sound frequency on the sound transmission loss of needled polypropylene nonwovens, using Taguchi method. Sound transmission loss through the nonwoven samples was measured using impedance tube equipped with four microphones. Using Taguchi experimental design, the effect of the particular controllable parameters on sound transmission loss of the samples was determined.
2. Materials and methods
2.1. Samples preparation
Processing parameters such as initial carded web mass, needle penetration depth and punch density were selected for consideration. Staple 17 dtex, 90 mm melt-spun polypropylene fibers at a crimp frequency of 3 crimp/cm were used to produce the needled samples of nonwovens. Initial carded webs of 200, 300 and 400 g/m2 were prepared using a laboratory carding machine. The laboratory carding specification is listed in Table 1. The carded batts were needled using a laboratory needling machine equipped with 60 × 10 cm needle board and Groz-Backert felting needles type: G, 15 × 18 × 32 × 3. The needle-punched samples were produced at punch densities of 30, 60 and 90 (punch/cm2) at 5, 10 and 15 (mm) needle penetration depth. Nine circular needle-punched samples (Diameter = 113 mm) prepared using Taguchi experimental design are shown in Table 2.
| Parameters | Value |
|---|---|
| Machine width | 100 cm |
| Feeding roller diameter | 5 cm |
| Cylinder diameter | 40 cm |
| Doffer roller diameter | 27 cm |
| Feeding roller linear speed | 0.28 cm/s |
| Take up roller linear speed | 3.97 cm/s |
| Trial | Carded web mass (g/m2) | Punch density (punch/cm2) | Needle depth (mm) | Frequency (Hz) | Measured STL |
|---|---|---|---|---|---|
| 1 | 200 | 30 | 5 | 500 | 0.47 |
| 2 | 200 | 30 | 5 | 1000 | 0.48 |
| 3 | 200 | 30 | 5 | 1600 | 0.6 |
| 4 | 200 | 60 | 10 | 500 | 0.5 |
| 5 | 200 | 60 | 10 | 1000 | 0.51 |
| 6 | 200 | 60 | 10 | 1600 | 0.62 |
| 7 | 200 | 90 | 15 | 500 | 0.4 |
| 8 | 200 | 90 | 15 | 1000 | 0.39 |
| 9 | 200 | 90 | 15 | 1600 | 0.51 |
| 10 | 300 | 30 | 10 | 500 | 0.59 |
| 11 | 300 | 30 | 10 | 1000 | 0.63 |
| 12 | 300 | 30 | 10 | 1600 | 0.81 |
| 13 | 300 | 60 | 15 | 500 | 0.67 |
| 14 | 300 | 60 | 15 | 1000 | 0.71 |
| 15 | 300 | 60 | 15 | 1600 | 0.88 |
| 16 | 300 | 90 | 5 | 500 | 0.49 |
| 17 | 300 | 90 | 5 | 1000 | 0.5 |
| 18 | 300 | 90 | 5 | 1600 | 0.62 |
| 19 | 400 | 30 | 15 | 500 | 0.71 |
| 20 | 400 | 30 | 15 | 1000 | 0.76 |
| 21 | 400 | 30 | 15 | 1600 | 0.96 |
| 22 | 400 | 60 | 5 | 500 | 0.66 |
| 23 | 400 | 60 | 5 | 1000 | 0.71 |
| 24 | 400 | 60 | 5 | 1600 | 0.89 |
| 25 | 400 | 90 | 10 | 500 | 0.72 |
| 26 | 400 | 90 | 10 | 1000 | 0.78 |
| 27 | 400 | 90 | 10 | 1600 | 0.98 |
2.2. Experimental design
Design points of experiments were set up using Taguchi experimental design method [10]. In this method a target value for measuring the process response based on the loss function concepts should be defined. This is followed by selection of design parameters that affect process objective and their specified number of variation levels. According to the number of selected parameters and their variation levels, a proper orthogonal array is determined. The trials as indicated in Taguchi orthogonal array table are performed and data of the process response are collected. Eventually, the effect of the different parameters on the process response is analyzed.
Analysis is based upon ratio of signal to noise (SN), which in fact compares the level of a desired signal with the level of background noise. This ratio refers to the amount of noise in the output of a specified process [10]. Considering the type of response parameters, three general standard SN equations for classification of the objective function including ‘larger the better’, ‘smaller the better’, or ‘nominal the best’ are available. Since the sound transmission loss as the process response is expected to have larger values, the loss function of the larger-the better quality characteristics was determined that can be described as in Eqs. (1) and (2):
|
|
(1) |
|
|
(2) |
where n is the number of tests, yi, the experimental value of the ith quality characteristic, Lj, the overall loss function, and ηj the SN ratio.
In addition to the selected processing parameters, the effect of the frequency of incident sound waves on the STL was investigated. Different variation levels were allocated to the variable parameters individually in which all parameters were given at three levels.
Taguchi orthogonal array L27 as indicated in Table 2 was determined in terms of the selected number of parameters and their variation levels. The table also contains details of variation levels for each controllable parameter.
2.3. Measurement of sound transmission loss
Sound transmission loss (STL) of the samples was measured according to ASTM Work Item E2611 [15]. This standard method uses an impedance tube equipped with four microphones, and a digital frequency analyzer for STL measurement. Brüel and Kjær TL tube Type 4206T which is an extension of Brüel and Kjær impedance tube Type 4206, is a purpose designed apparatus for STL measurement. The design includes an extra pair of microphones and two extended tubes; a large tube (100 mm diameter) was used. Sound transmission loss of samples was measured at frequencies of 500, 1000 and 1600 Hz.
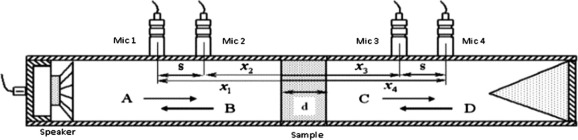
Impedance tubes are used below their lowest cutoff frequency to produce plane waves. Thus, the resulting sound field in the tube consists of one component traveling toward the sample and one reflected component [16]. The impedance tube used for measurement of the STL value is shown in Fig. 1. Two microphones (MP1 and MP2) were mounted in the upstream tube and another two microphones (MP3 and MP4) were placed in the downstream tube so that measurement of both incident and reflected waves could be obtained. The reference position (x = 0) is given as the front surface of a sample: x1, x2, x3 and x4 likewise denote each microphone’s position. The complex sound pressures at the four microphone locations in the tube can be expressed as follows:
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
where k represents the wave number, A and B indicate the incident and the reflected wave components in the upstream tube and C and D indicate the transmitted and the reflected wave components in the downstream tube. Eqs. (3), (4), (5) and (6) can be arranged to solve for the coefficients A to D as follows:
|
|
(7) |
|
|
(8) |
|
|
(9) |
|
|
(10) |
|
|
|
Figure 1. Schematic representation of four microphone impedance tube. |
The solution involves measuring the sample material with various boundary conditions. There are two methods used, the Two-Load method and the One-Load method (also known as the Anechoic Termination Method). The Two-Load Method: By having two different end conditions, for example, with a rigid cap or having no cap (i.e. leaving it open, or using a reference material. Bruel & Kjaer suggest using two different absorptive materials) the two equations can be solved:
|
|
(11) |
where A1, C1, D1 are the wave amplitudes for the first load measurement and A2, C2, D2 are the wave amplitudes for the second load measurement. The transmission loss matrix relates the forward and backward traveling acoustic waves as
|
|
(12) |
The main coefficient of interest is α and this is known as the pressure transmission loss coefficient of the sample determined from the send side of the tube, δ is the pressure transmission loss coefficient of the sample determined from the receiver side of the tube. These parameters should be the same (assuming the sample is acoustically symmetrical). β and γ are parameters determining acoustic impedance of the sample [16]. The transmission loss coefficient (α) is used to calculate sound transmission loss (STL) in dB as follows:
|
|
(13) |
Five specimens were cut from each sample to fit to tube and average of sound transmission loss values was reported.
2.4. Measurement of thickness and porosity
Thickness of samples was measured using a digital fabric thickness gauge in accordance with ISO5084 standard. Average of thickness of five samples cut from each needled fabrics was calculated. The measured sample thickness was in the range of 0.6–2.95 mm. Mass per unit area of the needled specimens was also measured using a digital balance. The measured mass per unit area of the specimen was in the range of 84–314 g/m2.
The following equation was used to calculate the samples porosity (P) which has significant effect on acoustical properties [12] and [13].
|
|
(14) |
In this equation m, A, L and ρ represent sample mass, cross-sectional area, sample thickness, and fiber density respectively. The calculated porosity was in the range of 82–89%.
The appearance characteristics of the nonwoven samples used during the current experimental procedure, are depicted in Fig. 2.
|
|
|
Figure 2. Needle-punched samples. |
Mass per unit area of the needled specimens together with their thickness and porosity is listed in Table 3. The effect of selected controllable factors on STL values of the samples was statistically analyzed using Mini-tab software.
| Samples | Initial carded web mass (g/m2) | Punch density (p/cm2) | Needle penetration depth (mm) | Nonwoven mass per unit area (g/m2) | Thickness (mm) | Porosity % |
|---|---|---|---|---|---|---|
| A1 | 200 | 30 | 5 | 145.16 | 1.15 | 87.2 |
| B1 | 60 | 10 | 165.54 | 0.94 | 82.2 | |
| C1 | 90 | 15 | 84.04 | 0.6 | 85.8 | |
| D1 | 300 | 30 | 10 | 229.21 | 1.4 | 83.4 |
| E1 | 60 | 15 | 268.68 | 1.75 | 84.4 | |
| F1 | 90 | 5 | 146.44 | 0.95 | 84.4 | |
| G1 | 400 | 30 | 15 | 301.79 | 2.3 | 86.7 |
| H1 | 60 | 5 | 280.14 | 2.5 | 88.6 | |
| I1 | 90 | 10 | 314.52 | 2.2 | 85.5 | |
3. Results and discussions
ANOVA analysis was applied to examine the effects of different controllable parameters on the response sound transmission loss. Table 4 presents the ANOVA results of the sound transmission loss of the samples. In this table, DF is the degree of freedom, and SS and MS are the sum of squares and the mean sum of squares due to the source respectively. Also, parameter F means the F-statistic and P means the P-value. Results indicate that the effect of all considered parameters is statistically significant. This is due to the fact that their corresponding P-values are less than 0.05.
| Source | DF | SS | MS | F | P |
|---|---|---|---|---|---|
| Carded web mass | 2 | 76.061 | 38.0306 | 101.65 | 0.0 |
| Punch density | 2 | 9.587 | 4.7936 | 12.81 | 0.0 |
| Needle depth | 2 | 5.338 | 2.6692 | 7.13 | 0.005 |
| Frequency | 2 | 28.794 | 14.3971 | 38.48 | 0.0 |
| Residual error | 18 | 6.734 | 0.3741 | ||
| Total | 26 | 126.515 | |||
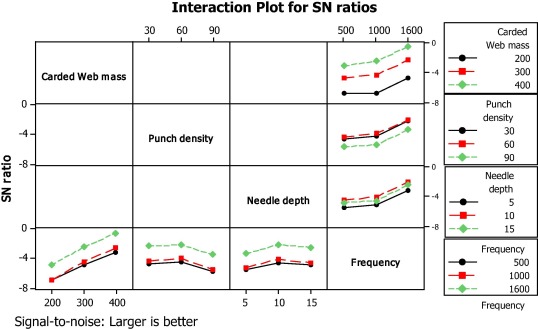
Table 5 shows the SN ratios result in association with considered controllable parameters and their variation levels. Difference between the highest and the lowest SN ratios of each parameter is called Delta. Delta value is an index which indicates the effect of the controllable parameters on STL values of the nonwoven samples. Thus, it can be concluded that the initial carded web mass and needle depth with delta values of 4.09 and 1.078 have the most and least effects on STL, respectively. The variation of STL values in different levels of controllable parameters is separately depicted in Fig. 3. The levels of one factor are indicated on the horizontal axis, while the levels of the other factor are indicated by different colored lines and symbols. Because the lines are parallel to each other, then there is no interaction between the considered controllable factors [17]. When there are no interactions present, it is simpler to interpret the factor effects. Then, the main effects plots and response tables show how changing the level of one factor while holding the other factors steadily affects the response characteristic.
| Source | Level 1 | Level 2 | Level 3 | Delta | Rank |
|---|---|---|---|---|---|
| Carded web mass | −6.153 | −3.818 | −2.055 | 4.098 | 1 |
| Punch density | −3.72 | −3.465 | −4.838 | 1.373 | 3 |
| Needle depth | −4.593 | −3.515 | −3.918 | 1.078 | 4 |
| Frequency | −4.915 | −4.55 | −2.56 | 2.351 | 2 |
|
|
|
Figure 3. Variation of STL values in different levels of controllable parameters and their interactions. |
3.1. Effect of initial carded web mass on STL values
Fig. 3 depicts the linear increasing trend of the STL values of needled samples with corresponded increase in mass of initial carded web.
Tascan and Vaughn [4] stated that upon impact of the incident sound wave on porous materials, sound wave encounters both air and fibers. At air/fibers boundaries, a single sound wave while traveling through the material, branches along many transmitted and reflected paths. This eventually results into reduction in sound wave energy. Thus, an increase in branching of the sound wave after impact within the material causes the sound transmission loss by the fibrous textile material to be increased. The increase in the initial carded web mass effectively results in existence of higher number of within the material which in effect increases the air/fiber boundaries within the nonwoven structure. This in turn offers higher resistance to the incident sound wave by the material and consequently higher sound transmission loss.
3.2. Effect of frequency on STL values
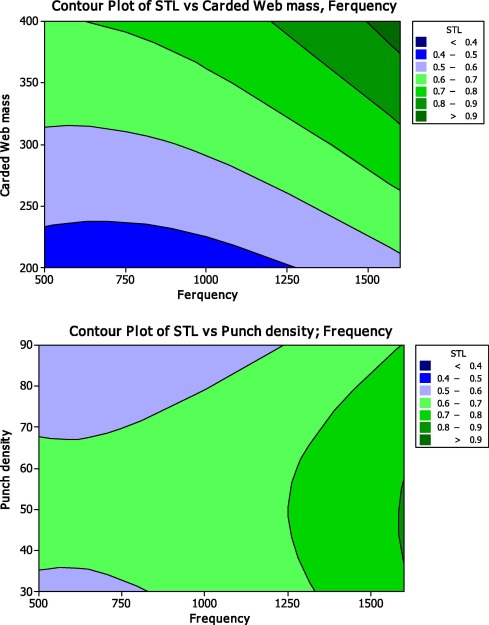
Fig. 3 shows the effect of frequency of sound wave on the STL of the samples. The frequency at which the sound waves are transmitted through a material depends on the density of material. Relations between initial carded web mass, punch density, frequency and ST values (Fig. 4) indicate that nonwoven samples produced using higher carded web mass and punch density exhibit STL values at higher frequency. Higher carded web mass and punch density result in production of denser fibrous structure. Thus it can be concluded that while in denser fibrous structures, sound absorption occurs almost at high frequencies, in less dense fibrous structures, sound tends to be absorbed at relatively low frequencies. These results confirm the previous findings reported by Seddeq [18].
|
|
|
Figure 4. Relation between initial carded web mass, punch density, frequency and STL of the samples. |
3.3. Effect of punch density on STL values
Fiber arrangement is an important factor that affects sound insulation ability of a fibrous structure. Fiber arrangement is important as this governs the number of fiber–fiber contact points within the structure.
Interaction of fibers with sound waves is directly dependent upon fiber–fiber contact points. As far as increase in punch density is concerned, it can be stated that at higher punch density more but smaller pores are formed in the nonwoven structure, which results in increase in the sound insulation ability of the samples. Results depicted in Fig. 3 indicate that punch density in range of 30–60 p/cm2 has enhanced both STL values and sound insulation ability of the nonwoven samples. This may be due to formation of small pores which entrap the sound waves within the fibrous structure. Nevertheless, increasing the needle punch in range of 60–90 p/cm2 decreases the STL values of the nonwoven samples. This can be due to decrease in tortuosity and small pores which can occur at higher punch density.
3.4. Effect of needle penetration depth on STL values
Fig. 3 shows the effect of needle penetration depth on STL of the samples. Increase in needle penetration depth between 5 and 10 mm causes higher sound transmission loss by the samples. More intense fiber entanglement occurs when needle penetration depth increases. Intense fiber entanglement results in formation of numerous but smaller pores which effectively cause an increase in sound/fiber interface within the fibrous structure. This in turn results in changes in the frictional resistance encounter by sound waves which subsequently lead to dissipation of more energy by sound waves and increase in the sound transmission loss [19]. Nevertheless, when the needle penetration depth varies from 10 to 15 mm, the sound transmission loss reduces. This may be due to the fact that intense fiber entanglement leads to reduction in the number of pores formed in the nonwoven structures. This in turn results in lower frictional resistance offered by the samples, and thus the observed reduction in the sound transmission loss by the samples.
3.5. Effect of thickness, mass per unit area of nonwoven and porosity on STL values
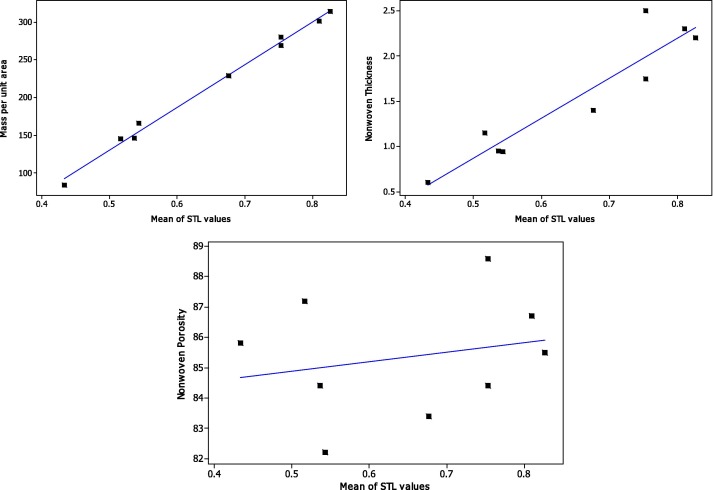
It should be stated that the mean calculated STL values at frequencies of 500, 1000 and 1600 were plotted against variations of thickness, mass per unit area and porosity of nonwovens.
Numerous studies that have been conducted on absorption of sound by porous materials have unanimously concluded that sound absorption is related to nonwoven thickness [10], [11] and [13]. Influence of nonwoven thickness on STL is demonstrated in Fig. 5. The results show higher STL occurs at frequencies of 500–1600 Hz, in thicker material. This can be attributed to both higher resistance to airflow and tortuosity within thicker fibrous layers. This can significantly assist sound energy dissipation and the amount of transmitted sound through the layer.
|
|
|
Figure 5. Correlations between thickness, mass and porosity with STL of the nonwoven. |
Sound absorption coefficient in nonwovens is directly proportional to nonwoven mass per unit area [10]. Correlation between STL and mass per unit area which points to increase in mean STL in relation to increase in mass per unit area of the samples is shown in Fig. 5. This trend can be due to effect of increase in resistance to airflow, higher tortuosity and smaller pore of the samples.
Pore population, size and geometry are the principle factors that must be considered when sound absorption mechanism in porous materials is researched. Determination of pore size and geometry in voluminous nonwoven samples is rather a difficult task. Based on Eq. (1) porosity of the samples was calculated, and plot of porosity versus STL is shown in Fig. 5. The calculated porosities lie in the range of 0.82–0.89. Statistically no significant correlation between STL and porosity exists. The statistical insignificance can be attributed to the fact that the porosity of nonwovens along the thickness is not necessarily uniform. This points to the fact that size of the pores is not constant. In order to establish the real correlation, new porosity measurement technique such as X-ray tomography and large number of data must be employed.
Regression model that represents the relationship between independent variables (frequency, punch density, needle penetration depth and initial carded web mass), and response variable STL was obtained. The regression model can predict the sound insulation ability of polypropylene nonwovens, by considering various controllable factors such as initial carded web mass, needle penetration depth, punch density and sound frequency as the predictor terms. It is indicated that the model can successfully predict the STL values. Using Minitab software [17], the multivariate linear regression equation is as follows:
|
|
(15) |
4. Conclusion
Transmission of sound through needled polypropylene fibers nonwoven in relation to variables such as initial carded web mass, needle penetration depth, punch density and the frequency of incident sound wave was investigated. Results of ANOVA test pointed to significant effect of all considered parameters on sound transmission loss by the samples. Results vividly demonstrated that STL of the samples was most influenced by initial carded web mass on STL. It was shown that STL increased by increase in initial carded web mass.
Results showed not only higher sound transmission loss occurred at higher frequencies but also increase in the amount of needle penetration depth and punch density resulted in higher sound transmission loss by the samples. The findings revealed that there is a high correlation between nonwoven mass per unit area and fabric thickness. An increase in fabric mass and thickness not only resulted to increase in the sound transmission loss by the samples but also improved insulation performance of the nonwoven layers.
References
- [1] T. Dias, R. Monaragala; Sound absorption in knitted structures for interior noise reduction in automobiles; Meas. Sci. Technol., 17 (2006), pp. 2499–2505
- [2] Y. Shoshani, Y. Yakubov; A model for calculating the noise absorption capacity of non-woven fiber webs; Text. Res. J., 69 (1999), pp. 519–526
- [3] Y. Shoshani, Y. Yakubov; Use of nonwovens of variable porosity as noise control elements; Nonwovens J., 10 (2001), pp. 23–28
- [4] M. Tascan, E. Vaughn; Effects of total surface area and fabric density on the acoustical behavior of needle-punched nonwoven fabrics; Text. Res. J., 78 (2008), pp. 289–296
- [5] Y. Chen, N. Jiang; Carbonized and activated non-woven as high performance acoustic materials: part II noise insulation; Text. Res. J., 79 (2009), pp. 213–218
- [6] S. Vasile, L. Van Langenhove; In situ measurements of surface impedance and absorption coefficients of porous materials using two microphones and ambient noise; Appl. Acoust., 66 (2004), pp. 845–865
- [7] Y. Shoshani, Y. Yakubov; A model for calculating the noise absorption capacity of nonwoven fiber webs; Text. Res. J., 69 (1999), pp. 519–526
- [8] B. Castagnede, A. Aknine, B. Brouard, V. Tarnow; Effects of compression on the sound absorption of fibrous materials; Appl. Acoust., 61 (2000), pp. 173–182
- [9] A. Mahmoud Abdelfattah, E. Ibrahim Ghalia, R. Mahmoud Eman; Using nonwoven hollow fibers to improve cars interior acoustic properties; Life Sci. J., 8 (2011), pp. 344–351
- [10] S. Hassanzadeh, M. Zarrebini, H. Hasani; An investigation into acoustic properties of lightly needled Estabragh nonwovens using Taguchi method; J. Eng. Fiber Fabric, 9 (2014), pp. 19–27
- [11] S. Hassanzadeh, H. Hasani, M. Zarrebini; Analysis and prediction of the noise reduction coefficient of lightly needled Estabragh/polypropylene nonwovens using simplex lattice design; J. Text. Inst., 105 (2014), pp. 256–263
- [12] B.C. Lee, S.R. Kim; Effect of structure on sound absorption and sound transmission loss of composite sheet; Adv. Compos. Mater., 23 (2014), pp. 319–325
- [13] N. Jiang, J.Y. Chen, D.V. Parikh; Acoustical evaluation of carbonized and activated cotton nonwovens; Bioresour. Tech., 100 (2009), pp. 6533–6536
- [14] S. Sengupta; Modeling on sound transmission loss of jute needle-punched nonwoven fabrics using central composite rotatable experimental design; Indian J. Fiber Text. Res., 35 (2010), pp. 293–297
- [15] ASTM – E2611-09, Standard Test Method for Measurement of Normal Incidence Sound Transmission of Acoustical Materials Based on the Transfer Matrix Method.
- [16] T. Koizumi, N. Tsujiuchi, A. Adachi; The Development of Sound Absorbing Materials using Natural Bamboo Fibers, High Performance Structure and Composites; WIT Press (2002)
- [17] M. Evans; MINITAB Manual for Introduction to the Practice of Statistics; University of Toronto (2000)
- [18] H.S. Seddeq; Factors influencing acoustic performance of sound absorptive materials; Aust. J. Basic Appl. Sci., 3 (2009), pp. 4610–4617
- [19] P.P. Narang; Material parameter selection in polyester fiber insulation for sound transmission and absorption; Appl. Acoust., 45 (1995), pp. 335–358
Document information
Published on 12/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?