Abstract
Enhancing light absorption within thin film amorphous silicon (a-Si) solar cells should lead to higher efficiency. This improvement is typically done using various light trapping techniques such as utilizing textured back reflectors for pronounced light scattering within the cell thus achieving higher absorption. It is believed that embedding metallic nanoparticles (MNPs) inside the structure could increase light scattering. However, embedding MNPs can also cause significant structure defects and pronounced efficiency drop as well – it has been indicated by many experiments that disproved this belief. In search of ways to improve efficiency, we have investigated the impact of MNPs size, and location within the solar cell, in addition to the effect of defects, and doping levels on the overall efficiency. On the basis of our 3D multiphysics (optical-electric) modeling, we developed a design guideline for embedding these MNPs and reducing the impact of defects created in the embedding process. The results of simulations were compared to relevant measured data, and it showed a good agreement. Subsequently, models were used to predict performance, and over 30% improvement in solar cell efficiency (~13% is predicted); which is beyond the state of the art. This was predicted by optimizing the size and location of the MNPs and tailoring the doping levels to have better forward light trapping and absorption.
Introduction
Remarkable manufacturing cost reduction in solar cells can be achieved using thin film hydrogenate amorphous silicon (A-Si:H) instead of bulk silicon. However, a pronounced efficiency drop could be incurred by utilizing thin film silicon [1]. Typically, any thin film solar cells suffer from a huge reduction in light absorption within absorber layers (semiconductors), and that can cause efficiency drop due to inherent surface reflection.
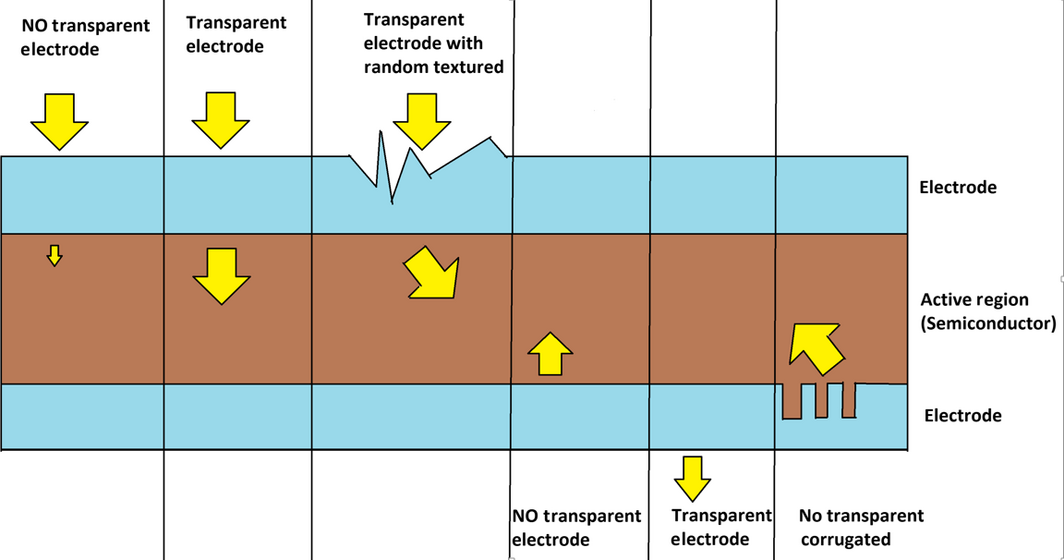
To achieve higher efficiency, some boosting techniques have been developed for better light absorption. These enhancement methods are based on increasing the optical path length and embedding scatterers within cells. They are designed for constructive interference. Random textured or corrugated external/internal interfaces are used to improve scattering [2-8], while transparent conductive oxide (TCO) layers are utilized to minimize reflections at interfaces, additionally highly reflective surfaces are used to enhance back reflections. Figure 1 illustrates such enhancing techniques.
|
|
|
Figure 1. Optical paths inside solar cells for different type of electrodes. |
Alternatively, MNPs are intentionally placed within solar cells. MNPs (few nanometers in diameter) can scatter a wide range of visible light, and also can create high intensity near-fields in their vicinity [10]. However, light can face optical losses for small (few nanometer) MNPs that can supersede scattering. Therefore methods need to be developed to enhance scattering and to improve absorption if possible.
Typically, the optical properties of MNPs are highly controlled by changing size [9], density [10, 15], conductivity [9], location [11, 16], and shape [12-14]. These MNPs can be made out of gold or silver, and both could exhibit great metal/plasmon behavior at optical frequencies and consequently would impact on amorphous silicon thin film solar cells performance [11]. Several studies have utilized nanotechnology to fabricate embedded MNPs within solar cells. Unfortunately, serious parasitic losses and structure defects were incurred and had been associated with these MNPs that led to significant overall solar cell efficiency degradation. So studies are still going on to explore the feasibility of finding an efficient light scattering scheme whenever MNPs are carefully embedded within the structure to increase optical path length and to provide better absorption for light, while minimizing energy loss.
To combat such efficiency drop, we need to address some challenging issues like: optical losses within MNPs, and those due to fabrication defects. The optical loss is manifested by a large fraction of the impinging light energy absorbed by MNPs and converted to phonons, thus reducing the overall efficiency. Add to that, during the fabrication process, gross material defects can occur. Defects would spread around embedded MNPs causing loss that would increase even further with higher defect density. So these issues associated with the design and fabrication, need to be resolved to enhance efficiency. Several investigations have been carried out to understand the role of these embedded nanoparticles and potential to improve performance [9-11]. Further studies are still needed, given that the impact of MNPs has not been experimentally materialized yet and the need has significantly increased to reveal a successful design recipe.
Along these lines, we carried out a detailed 3D multiphysics modeling of plasmon solar cells [17], and we studied the effect of MNPs on performance in search for efficiency enhancement. In this paper, new design rules for embedding MNPs inside thin film amorphous silicon solar cells will be presented that would lead to solar cell efficiency enhancement. A modeling toolbox was successfully developed for 3D solar cells performance analysis [17], and it was validated by previously published experimental data carried out by Ref. [11].
The effect of placing MNPs at alternative locations (front, middle, and back of the P-I-N solar cell) to maximize the photocurrent generation will be discussed in section II. A new design methodology will be recommended in sections III and IV. Conclusion will be given in section V. Finally a methodology for a robust simulation will be presented in the Appendix.
Simulation Analysis
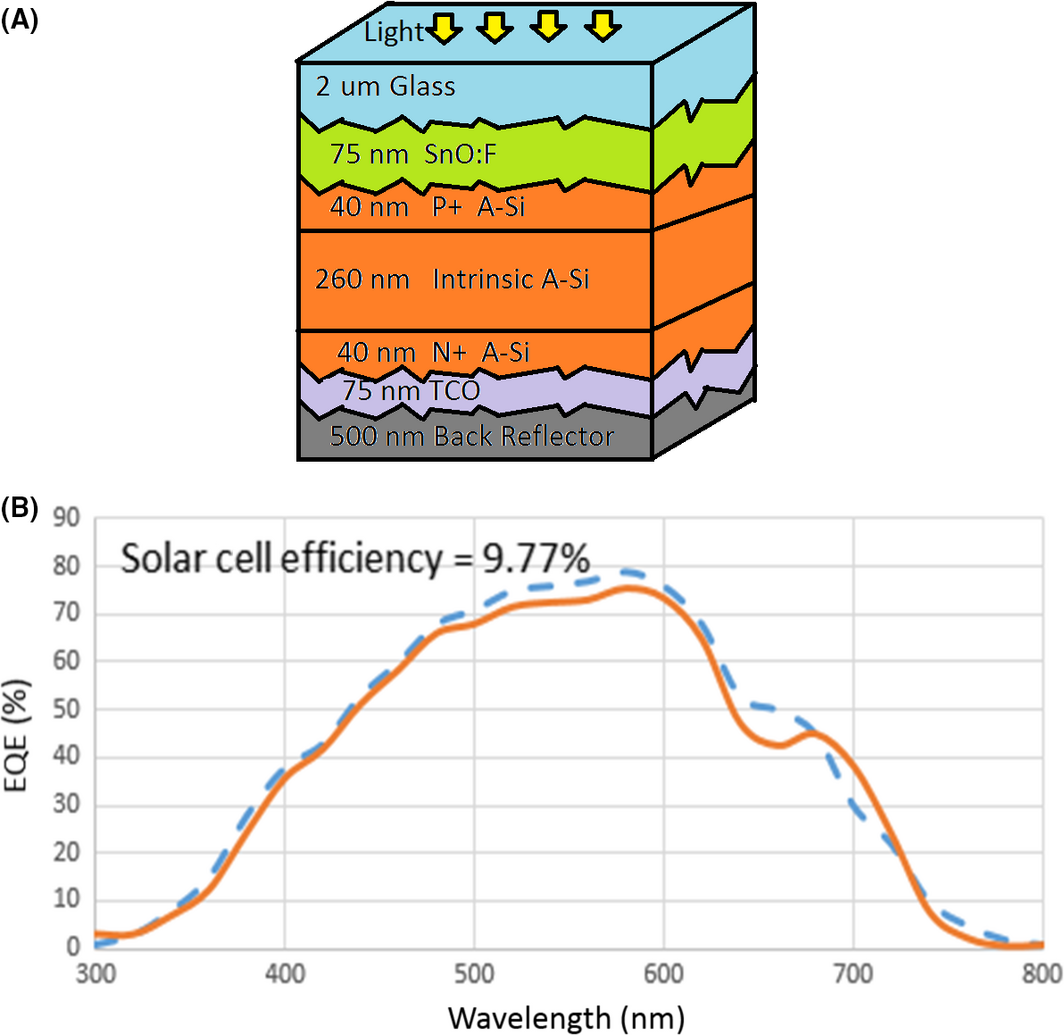
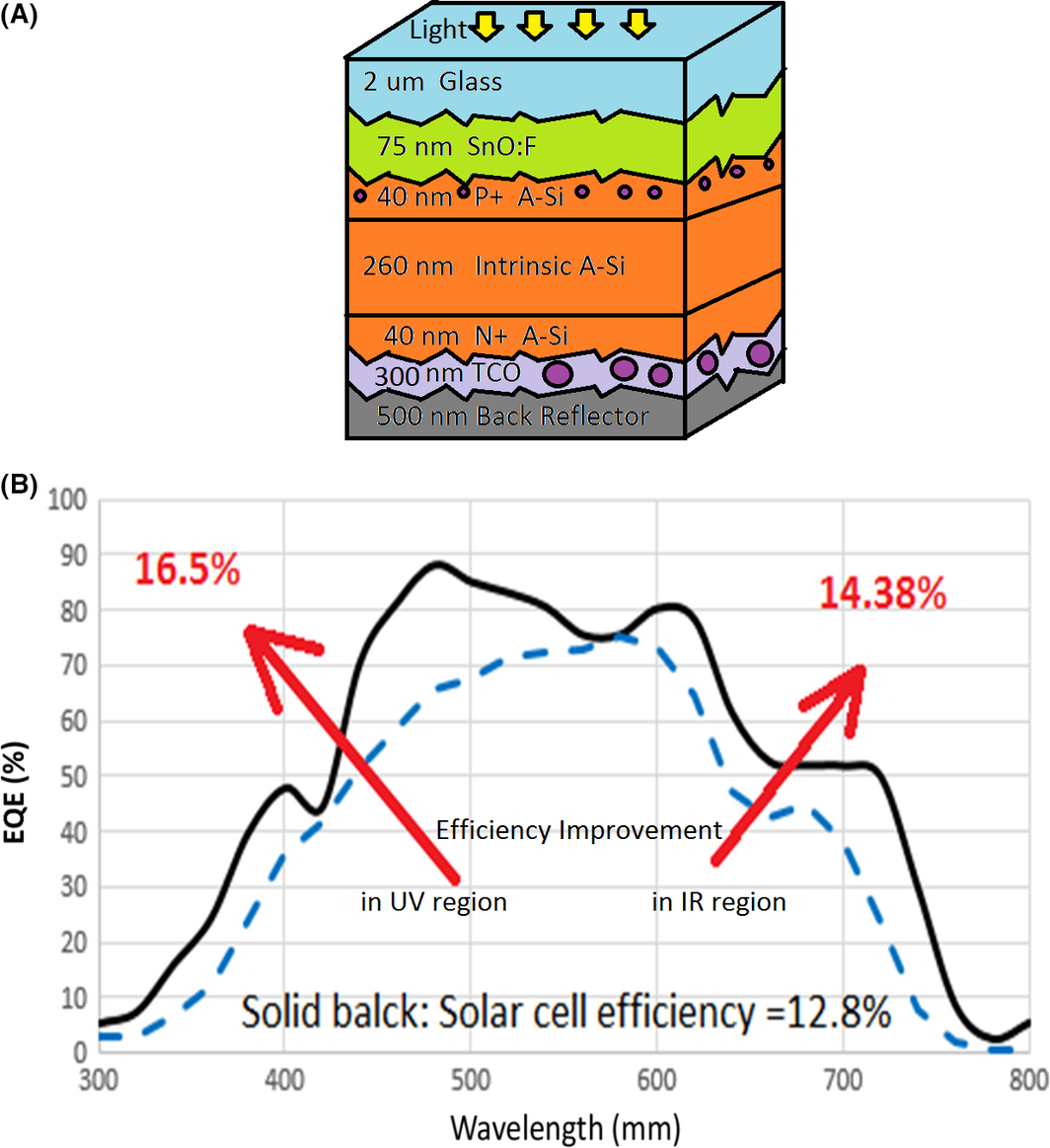
A 3D model of a thin film amorphous silicon solar cell has been developed which accounts for surface roughness as well. A view of the structure is shown in Figure 2A. The surface roughness would impact on the overall performance. Typically, the amount of surface roughness is related to transparent conductive oxide (TCO) type. For instance, using TCO film with large grains would increase the surface roughness [24-26]. At the same time, the size of the grains is correlated with the thickness of the thin film TCO layer, where a thinner film may have less surface roughness [24-26]. For instance, the thickness of the thin film TCO, considered for this model, is 75 nm, and its surface roughness is estimated to be <10 nm.
|
|
|
Figure 2. (A) schematic of the P-I-N device; (B) EQE curve (dash line represents measurement [11]; solid line represents simulation result) [17, 34]. |
In our investigation, to model the solar cell and to take the effect of surface roughness into account, a 3D device model like a trapezoidal grating is assumed [17]. A periodic structure of a trapezoidal shape (like that of [27]) is designed and implemented to the 3D model of [11]. Utilizing our model, a comparison between our results and that measured External Quantum Efficiency (EQE) by [11] is shown in Figure 2B. Only a slight discrepancy is seen – thus validating our models. This success establishes the logistics to extrapolate models that include MNPs effects and the impact of their size, shape, and location of the device layers on solar cell efficiency.
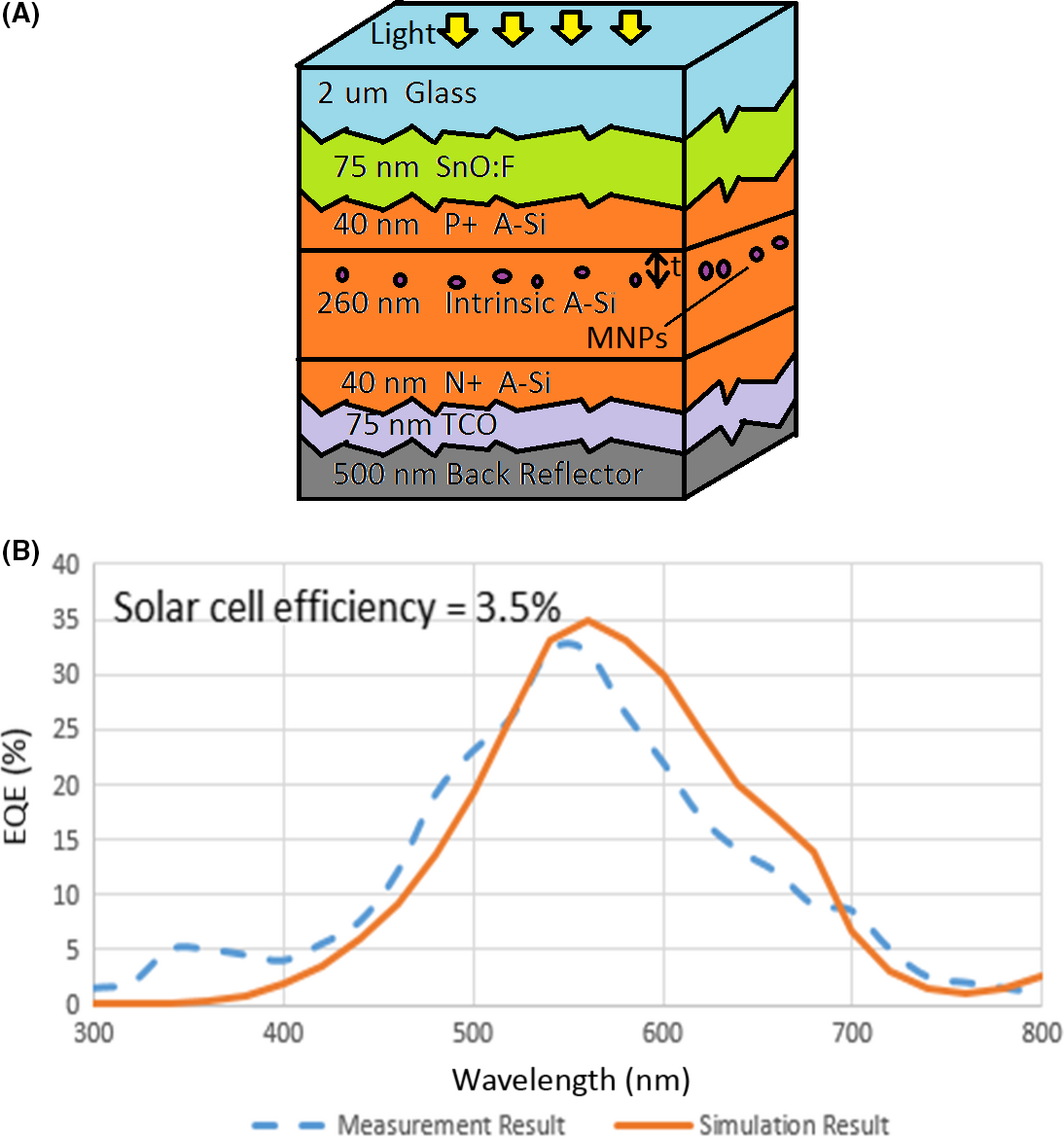
To understand the effect of existing silver nanoparticles, we studied solar cells performance after embedding these MNPs at different layers, one layer at a time. In our model, silver nanoparticles are designed as spheres with 18 nm diameter and placed in a random 2D array with a maximum center-to-center spacing of 36 nm. First, we embedded MNPs inside the absorber region (t = 50 nm as seen in Fig. 3A), and our simulation results (Fig. 3B) rather huge drop in conversion efficiency which is once more consistent with Ref. [11] observations.
|
|
|
Figure 3. (A) Schematic of the P-I-N device; (B) EQE curve (dash line represents measurement [11]; solid line represents simulation result), after considering of defects [34]. |
The agreement seen in Figure 3B between simulation and measurement is good, and it validates our model again. Although surprisingly, the efficiency has dropped to 3.5% in contradiction to the common belief that it should be enhanced upon using MNPs – (however, if no defects exist, the efficiency though would be 9.77% as indicated in Fig. 2B). We have done several modeling for cases of MNPs that were moved from the top of the intrinsic layer to its bottom, however, the solar cell efficiency still dropped even further to 2.55% [17], which is related to effect of defects. In our previous publication [17], we showed that how EQEs can be changed by placing the MNPs at different positions within the layer of the absorber. We also calculated the amount of efficiency, FF, Voc, and Jsc for various scenarios.
Impact of Defects
One of the disadvantages of embedding MNPs inside a semiconductor is increasing the density of defects especially around the MNPs. Presence of defects can cause optical losses. This extra optical loss is due to a large Shockley Read Hall recombination rate – which would mean a huge efficiency drop. For instance, to consider the effect of defects around MNPs (inside the intrinsic region), the recombination rate was considered 100 times higher than normal value estimated when inside intrinsic region.
To demonstrate this effect, a P-I-N structure was analyzed before and after embedding the MNPs [17], and a huge difference between the results with and without accounting for the presence of the defects was seen in our first experiment (efficiency of 9.8% without considering defects, and 3.5% with as seen in Fig. 3).
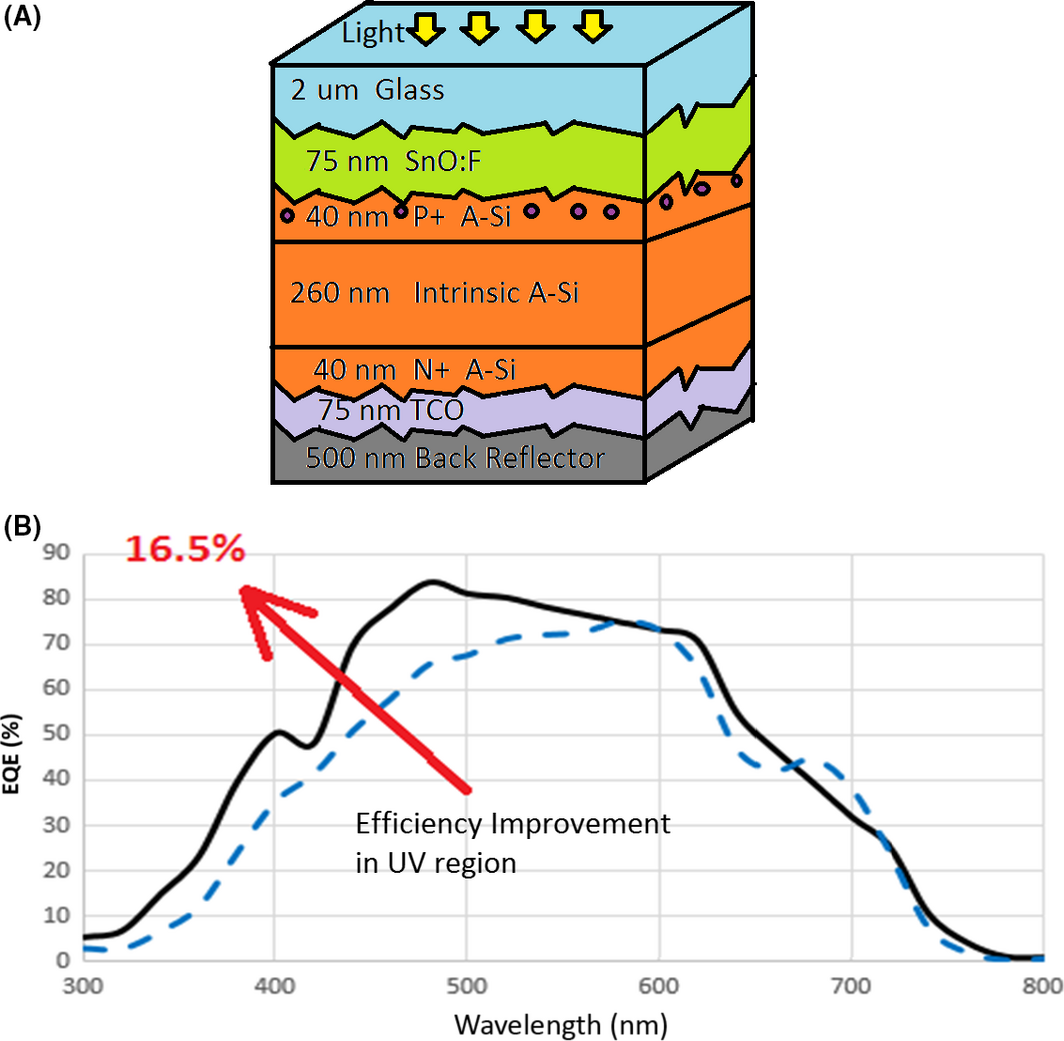
To avoid such a problem, MNPs should be placed in a proper location so they would cause minimal impact on efficiency reduction. It turns out that if defects are placed in a highly doped region, they would not impact on recombination rate in this region, on the other hand the recombination rate would relatively increase if MNPs are placed in a lightly doped region; hence, it is better off placing the MNPs in a highly doped region. In other words, the impact of placing MNPs on recombination rate can be very high if they are placed inside the intrinsic layer compared to being in a highly doped region (P+, or N+) as shown in Figure 4A. Subsequently, the recombination rate should not change much compared to the MNP-free case. [17]. Simulation result shown in Figure 4B, is validating our observation, and indicates pronounced efficiency improvement when placing MNPs only inside the top P+ layer as expected. The improvement happens due to a relatively strong light intensity propagating through the top layer where strong localized fields exist around MNPs close to depleted region of P-I-N.
|
|
|
Figure 4. (A) Schematic of the P-I-N device; (B) Comparison of EQE with and without MNPs; solid line represents MNPs inside the P+ top layer of the a-Si; dash line represents the case with No MNPs [34]. |
To improve the performance even further, the size, and location of MNPs should be optimized as well. Intuitively, the high-frequency spectrum of light is mostly absorbed within the top layers. Hence, if small size MNPs with diameters in the range of 18 nm (i.e., resonating at these high frequencies) are used in the top P+ layer, they would enhance the scattering and absorption of this spectrum. Meanwhile, use of such small MNPs would still allow the relatively low-frequency spectrum to travel through the top layers and reach the bottom ones. However, to have appreciable absorption for the spectrum at low frequencies large MNPs (size around 200 nm in diameter) resonate and enhance absorption. Large MNPs should be placed at the bottom layer (i.e., inside TCO – next to the N+ region, see Fig. 5A). At this point, the intensity of light for the ultraviolet (UV) rays (high frequencies) close to the N-type region (at the back) is very weak, since most of their energies have already been absorbed by the top layers of the absorber (i.e., inside the P+, and intrinsic region), and mostly Infrared (IR) rays exist. In case of placing small MNPs on the top and large MNPs on the bottom, simulation result shows remarkable improvement for solar cell efficiency by roughly 30%, as seen in Figure 5B. This would simply mean an overall efficiency of 13%.
|
|
|
Figure 5. (A) Schematic of the P-I-N device; (B) Using different size of MNPs, in two different locations EQE curve for the simulation (solid line represents after optimization-black; dash line represents No MNPs blue) [34]. |
Optimization of Highly Doped Region
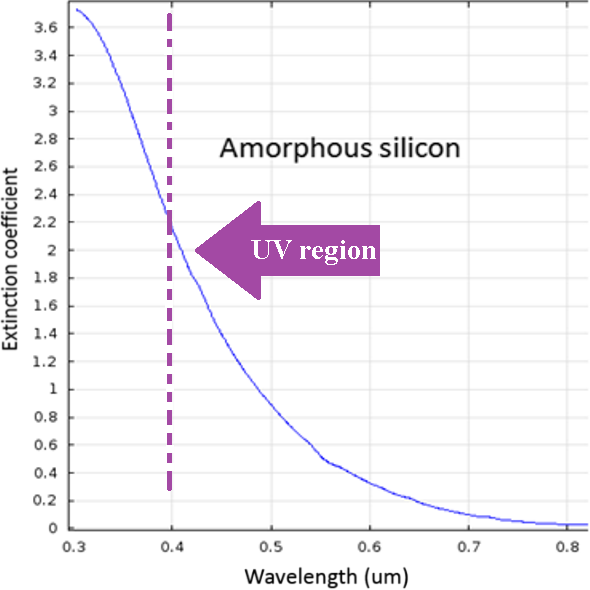
Doped layer thickness and doping level can impact the efficiency of thin film solar cell. At high frequencies (UV region), most of the impinging solar energy on the cell is absorbed at the top of the semiconductor close to the surface (here P+ region), and it happens before approaching UV rays to the junction or depleted region. This is obviously translated to an energy loss [18-21]. Figure 6 shows that the extinction coefficient of amorphous silicon which has exponential growth rate in UV region. It turns out pronounced light absorption happens with very low EQE. In other word UV rays are absorbed dramatically very close to the surface of the semiconductor (free charges will recombine together, because there is no electric field force for separation), and they may not be capable of reaching to the sweet spot inside the device (which is close to the junction called depleted region). So increasing the thickness of intrinsic layer of the semiconductor is not suggested for efficiency improvement at UV range, unless the absorber has low light absorption at this frequency range. However, if UV rays instead of being absorbed mostly in P+ layer (close to the surface) reach to the depleted region, and propagate in a longer path inside the P-I-N device, then more electron–hole pairs will be generated and will be separated (having more separated charges can be expected as more electricity). This would require: first, optimizing the thickness of the highly doped layer; and second, optimizing the level of dopant. Hence, the thickness of P+ layer should be thinned and the level of dopant (here P+) needs to be decreased enough, thus pushing the depleted region closer to the surface of the semiconductor on the top. Therefore, the probability of generating separated charges (electron–hole pairs) by UV rays will increase. The main reason that light trapping of MNPs for a-Si solar cells (in the state of the art) only occurs in long wavelengths (above 500 nm) is that the observation of UV rays inside intrinsic layer or close to the device junction normally happens with very low intensity (regarding to the huge absorption occurs at the surface of the absorber). Also the chance of existing MNPs at the right place (for resonance) is low. It is suggested that small MNPs to be placed between the transparent electrode and the highly doped semiconductor at the top layer side, instead of inside the P+ region for ease of fabrication process. In this case, the near field of those nanoparticles (at resonance) would still have some effects inside the depleted region and could generate more free electron–hole pairs compared to embedding MNPs on the P+ layer.
|
|
|
Figure 6. Extinction coefficient of amorphous silicon. |
Conclusion
Random embedding of MNPs has resulted in a drop of solar cell efficiency. Extensive simulation, based on our 3D combined optical-electric modeling toolbox has led to very promising results for ways to achieve higher efficiency. First, a significant efficiency drop detected after adding the MNPs (related to the substantial number of defects left). Presence of defects has resulted in a considerable optical loss around the MNPs. Second, increasing the recombination rate would reduce the conversion of optical energy to electricity. Hence, better manufacturing techniques need to be developed to reduce both defects and recombination, and to direct more light to the depleted region. Such as strategically locating small MNPs at the highly doped regions (i.e., P+ and N+) rather than inside the intrinsic layer. Additionally, using small MNPs at the top (P+) layer should allow a significant portion of the optical energy to propagate through (it acts like a transparent layer for long wavelengths), meanwhile larger MNPs are placed at the bottom to enhance reflection/scattering. It is certainly not recommended to embed large MNPs inside the active region, because it can cause a large amount of optical loss for the whole system. Optimizing the thickness of the highly doped layers and level of dopant can have a huge effect on solar cells' performance as well. Finally simulation results indicate an impressive efficiency enhancement of up to ~30% which amounts to 13% overall efficiency.
Acknowledgments
This work was supported by the grant from the National Science Foundation of USA (Grant No. NSF EPS-1004083).
Conflict of Interest
None declared.
Appendix
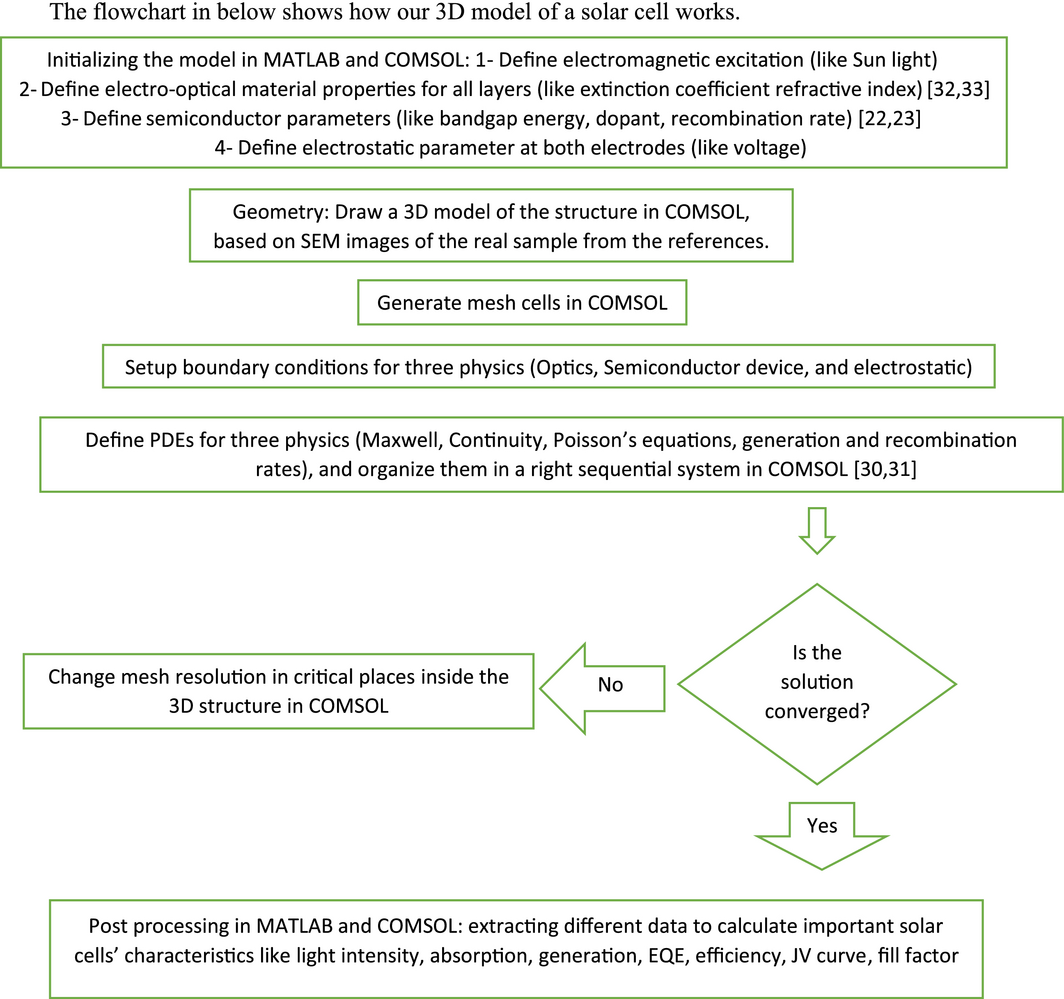
A1. Developing a Methodology for a Robust Simulation
The flowchart in below shows how our 3D model of a solar cell works.
|
|
A2. Initialization, Mesh Generation, and Boundary Conditions
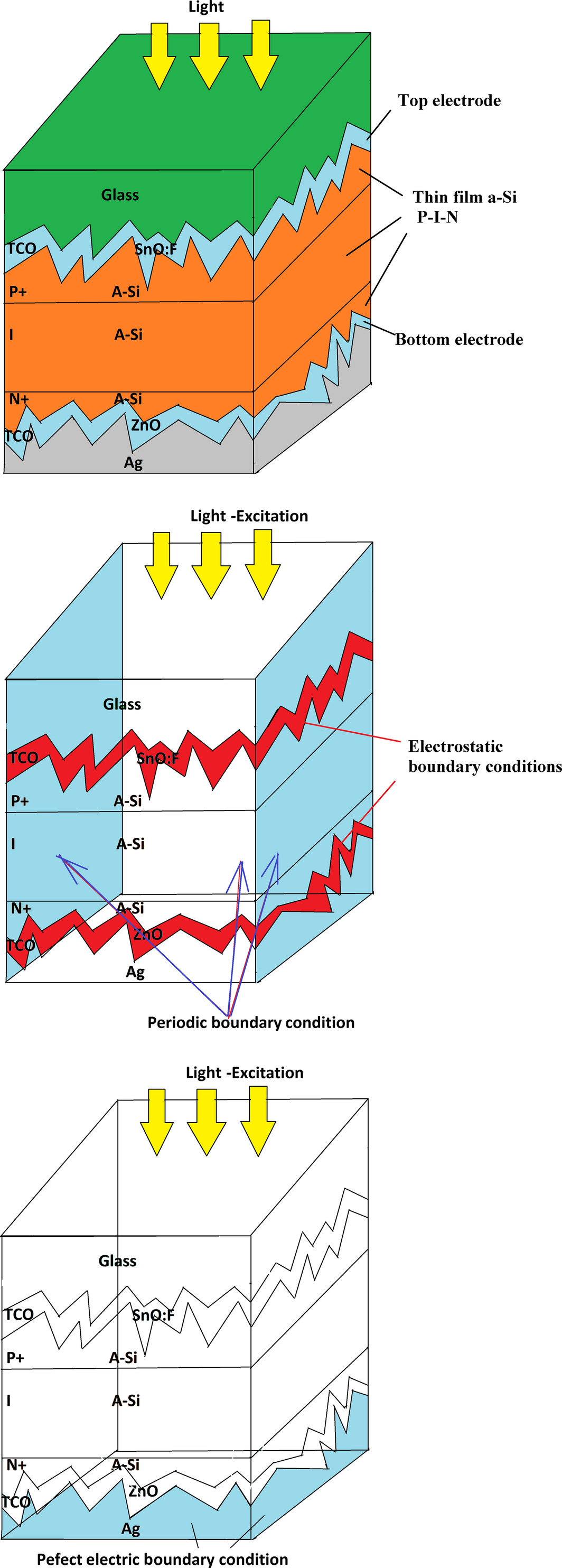
Initialization of the input data is the crucial part of this work. The accuracy of the results is directly related to the input data. For instance using the accurate solar spectrum of energy as an excitation for electromagnetic propagation, applying the right values for electro-optical material properties to solve light intensity inside the structure, and also initializing semiconductor with right amount of carrier density inside P-I-N, and recombination rate to solve continuity equation (in physics device) are some basic steps to start modeling for solar cells. Table 1 shows the list of parameters that are used for initialization of the 3D model. Selecting right type of mesh with right size for each cell is very important challenge (in numerical methods) for converging the matrices for a nonlinear system of Partial Differential Equations (PDEs). Since three physics are solved sequentially with the same structure of mesh cells, converging the solver with accurate result in minimum time of processing is our target. Free Tetrahedral has been selected as a type of mesh. The minimum size of element for critical regions like the junctions inside the semiconductor, electrodes, and around metallic nanoparticles changes between 0.1 and 1 nm. The maximum size of element depends on: 1-the longest side of each single layer 2-operation wavelength. It changes between 10 nm to 100 nm. This cad tool used Finite Element Method (FEM) as a numerical method to solve the nonlinear system of PDEs. Figure 7 shows the geometry of the whole structure in 3D with considering boundary conditions as well.
| Parameter –Name | Value |
|---|---|
| T(temperature) | 300 [K] |
| Ni -Ref[28] | 0.949 × 106 [cm−3] |
| Doping (N+) | 1 × 1020 [cm−3] |
| Doping (P+) | 1021 [cm−3] |
| Thickness (N+, a-Si)-Ref [9] | 40 [nm] |
| Thickness (intrinsic, a-Si)- Ref [9] | 260 [nm] |
| Thickness (P+, a-Si)- Ref [9] | 40 [nm] |
| Thickness (AZO) -(TCO in front)- Ref [9] | 75 [nm] |
| Thickness (glass)- Ref [9] | 200 [μm] |
| Thickness (Air)- Ref [9] | 20 [μm] |
| Thickness -(TCO BACK)- Ref [9] | 75 [nm](AZO) |
| Thickness (Silver) Reflector back- Ref [9] | 500 [nm] |
| Electron mobility, a-Si -intrinsic-Ref [12] | 20 [cm2/(V sec)] |
| Hole mobility, a-Si -intrinsic-Ref [12] | 2 [cm2/(V sec)] |
| Electron mobility, a-Si N+-Ref [12] | 20 [cm2/(V sec)] |
| Hole mobility, a-Si N+-Ref [12] | 2 [cm2/(V sec)] |
| Electron mobility, a-Si P+-Ref [12] | 20 [cm2/(V sec)] |
| Hole mobility, a-Si P+-Ref[12] | 2 [cm2/(V sec)] |
| Electron Life time, a-Si -intrinsic-Ref [27, 28] | 20 [nsec] |
| Hole Life time, a-Si -intrinsic-Ref [27, 28] | 20 [nsec] |
| Electron Life time, a-Si N+-Ref [27, 28] | 0.0001 [nsec] |
| Hole Life time, a-Si N+-Ref [27, 28] | 10 [nsec] |
| Electron Life time, a-Si P+-Ref [20, 21] | 10 [nsec] |
| Hole Life time, a-Si P+-Ref [20, 21] | 0.0001 [nsec] |
| Density Of State Valence band, a-Si –Ref [25] | 2.5 × 1020 [cm−3] |
| Density Of State Conduction band, a-Si –Ref [25] | 2.5 × 1020 [cm−3] |
| Difference between Defect level and intrinsic level N+,P+-Ref [29] | 0.7 |
| Difference between Defect level and intrinsic level intrinsic-Ref [29] | 0.3 |
| Energy Band gap a-Si-Ref [28] | 1.74 |
| Diameter silver NPs-Ref [9] | 20 [nm] |
| Affinity, a-Si (electro affinity)-Ref [12] | 4.00 eV |
| Incident Light Angle | 0 [deg] |
|
|
|
Figure 7. The boundary conditions, and the excitation in a 3D structure of the solar cell. |
A3. Optimization Method
For a common problem in solar cells (no plasmon), some degree of freedoms for optimization are presented in bellow to improve the conversion efficiency.
- Extinction coefficient of semiconductor
- Refractive index of materials (attached to the top and the bottom of the absorber)
- Thickness of each layers
- Doping level of highly doped region
- Surface roughness of the electrodes
- Grating at the back reflectors
- Conductivity of the electrodes
Although the spotlight of this study is based on using plasmon layers (MNPs) to improve the efficiency of thin film amorphous silicon solar cells. For this reason the degree of freedoms to optimize the model are limited by the type and dimension of the original sample has already defined (in case of no MNPs). It means that the only variables that need to be addressed to reach the goal are: 1-shape of MNP 2- size of MNP 3-location of MNP. Since during the fabrication process there is no control on the shape of silver NPs, then only two variables left for tuning thin film plasmon solar cells. Finally we are able to find the sweet spot by tuning the two variables. Although in some cases like placing small MNPs close to the junction inside the semiconductor, it is not easy to get a quick convergence. Therefore, it is a major requirement to define very fine mesh especially around the critical regions. Lack of any control on mesh generation can cause long time of processing, or out of memory due to aggressive computations.
References
- Zeman, M.2006. Advanced amorphous silicon solar cell technology. Pp. 173–236inJ. Poortmans and V. Archipov, eds. Thin film solar cells: fabrication, characterization and applications. Wiley, Wiley, Chichester. ISBN: 978-0-470-09126-5.
- Deckman, H. W., C. B. Roxlo, and E. Yablonovitch. 1983. Maximum statistical increase of optical absorption in textured semiconductor films. Opt. Lett.8:491–493.
- Isabella, O., F. Moll, J. KrC, and M. Zeman. 2010. Modulated surface textures using zinc-oxide films for solar cells application. Phys. Status Solid. A207:642–646. doi:10.1002/pssa.200982828.
- Kambe, M., A. Takahashi, N. Taneda, K. Masumo, T. Oyama, and K. Sato. 2008. Proceedings of the 33rd IEEE PVSC: San Diego. IEEE, New York, Pp. 1–4, doi: 10.1109/PVSC.2008.4922507
- Borri, C., and M. Paggi. 2015. Topological characterization of antireflective and hydrophobic rough surfaces: are random process theory and fractal modeling applicable?J. Phys. D: Appl. Phys.48:045301.
- Haug, F.-J., T. Söderström, O. Cubero, V. Terrazzoni-Daudrix, X. Niquille, S. Perregeaux, et al. 2008. Materials Research Society Symposium Proceedings 1101: KK13-KK. doi: 10.1557/PROC-1101-KK13-01.
- Krc, J., M. Zeman, A. Cˇampa, F. Smole, and M. Topicˇ. 2006. Novel approaches of light management in thin-film silicon solar cells. Materials Research Society Symposium Proceedings 910: A25-A; doi: 10.1557/PROC-0910-A25-01.
- Pahud, C., O. Isabella, A. Naqavi, F.-J. Haug, M. Zeman, H. P. Herzig, et al. 2013. Plasmonic silicon solar cells: impact of material quality and geometry. Opt. Express21:A786–A797. doi:10.1364/OE.21.00A786.
- Stuart, H. R., and D. G. Hall. 1998. Island size effects in nanoparticle-enhanced photodetectors. Appl. Phys. Lett.73:3815.
- Toroghi, S., and P. G. Kik. 2012. Cascaded plasmonic metamaterials for phase-controlled enhancement of nonlinear absorption and refraction. Phys. Rev. B85:045432.
- Santbergen, R., R. Liang, and M. Zeman. 2010. A-Si:H Solar Cells with embedded silver Nanoparticles. Photovoltaic Specialists Conference PVSC, IEEE, doi: 10.1109/PVSC.2010.5617095.
- Chen, Y.-S., W. Frey, S. Kim, K. Homan, P. Kruizinga, K. Sokolov, et al. 2010. 1. Enhanced thermal stability of silica-coated gold nanorods for photoacoustic imaging and image-guided therapy. Opt. Express18:8867–8878. doi:10.1364/OE.18.008867.
- Lu, X., M. Rycenga, S. E. Skrabalak, B. Wiley, and Y. Xia. 2009. Chemical synthesis of novel plasmonic nanoparticlesAnnu. Rev. Phys. Chem.60:167–192.
- Mock, J. J., M. Barbic, D. R. Smith, D. A. Schultz, and S. J. Schultz. 2002. Shape effects in plasmon resonance of individual colloidal silver nanoparticles. Chem. Phys.116:6755–6759.
- Zhang, W., Q. Li, and M. Qiu. 2013. A plasmon ruler based on nanoscale photothermal effect. Opt. Express21:172–181. doi:10.1364/OE.21.000172.
- Sha, W. E. I., H. L. Zhu, L. Chen, W. C. Chew, and W. C. H. Choy. 2015. A general design rule to manipulate photocarrier transport path in solar cells and its realization by the plasmonic-electrical effect. Sci. Rep.5:8525. doi:10.1038/srep08525.
- Ghahremani, A., and A. E. Fathy. 2015. A three-dimensional multiphysics modeling of thin-film amorphous silicon solar cells. Energy Sci. Eng.3(6):520–534. doi:10.1002/ese3.100A.
- Balanis, C. A.1989. Advanced engineering electromagnetics. Wiley, Hoboken, New Jersey, USA.
- Neamen, D. A.2003. Semiconductor physics and devices: basic principles, 3rd ed. McGraw Hill, New York.
- Sze, S.1981. Physics of semiconductor devices, 2nd ed. Interscience, New York.
- Madelung, O.2012. Semiconductors: data handbook. Springer, Verlag Berlin Heidelberg.
- Hall, R. N.1952. Electron-hole recombination in silicon. Phys. Rev.87:387.
- Shockley, W., and W. T. Read. 1952. Statistics of the recombinations of electrons and holes. Phys. Rev.87:835–842.
- Gracia, M., F. Rojas, and G. Gordillo. Morphological and optical characterization of SnO2:F thin films deposited by spray pyrolysis. 20th European Photovoltaic Solar Energy Conference, 6–10 June 2005, Barcelona, Spain.
- Chaaya, A. A., R. Viter, M. Bechelany, Z. Alute, D. Erts, A. Zalesskaya, et al. 2013. Evolution of microstructure and related optical properties of ZnO grown by atomic layer deposition. Beilstein J. Nanotechnol.4:690–698. doi:10.3762/bjnano.4.78.
- Kumar, V., N. Singh, R. M. Mehra, A. Kapoor, L. P. Purohit, and H. C. Swart. 2013. Role of film thickness on the properties of ZnO thin films grown by sol-gel method. Thin Solid Films539:161–165.
- Isabella, O., S. Solntsev, and M. Zeman. 2013. 3-D optical modeling of thin-film silicon solar cells on diffraction gratings. Prog. Photovolt. Res. Appl.21:94108.
- Sakata, I., and Y. Hayashi. 1985. Theoretical analysis of trapping and recombination of photo generated carriers in amorphous silicon solar cells. Appl. Phys. A37:153–164.
- Ihalane, E., M. Meddah, A. Elfanaoui, L. Boulkaddat, E. El hamri, X. Portier, et al. 2011. Numerical simulation of photocurrent in a solar cell based amorphous silicon. Moroccan J. Condens. Matter.13:83–87.
- Piprek, J.2003. Semiconductor optoelectronic devices introduction to physics and simulation. Academic Press; 1 edition (January 21, 2003). ISBN-13: 978-0125571906.
- Weiland, T.1977. A discretization method for the solution of Maxwells equations for six-component fields. Electron. Commun.31:116–120.
- Moharam, M. G., and T. K. Gaylord. 1981. Rigorous coupled-wave analysis of planar-grating diffraction. J. Opt. Soc. Am.71:811–818.
- Bakr, N. A., A. M. Funde, V. S. Waman, M. M. Kamble, R. R. Hawaldar, D. P. Amalnerkar, et al. 2010. Determination of the optical parameters of a-Si:H thin films deposited by hot wire–chemical vapor deposition technique using transmission spectrum only. Pramana J Physics.76:519–531.
- Ghahremani, A., and A. E. Fathy. Strategies for designing high efficient thin-film amorphous silicon solar cells. Photovoltaic Specialist Conference (PVSC), 2015 IEEE 42nd.
Document information
Published on 01/06/17
Submitted on 01/06/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?