Abstract
A study, entitled “Wabamun Lake Sequestration Project” or “WASP,” was performed to evaluate large-scale CO2 storage opportunities in the Wabamun area including potential risks. The project examined the feasibility of storing 20 megatons (Mt) of CO2 per year over 50 years. This scale is one order of magnitude larger than the typical benchmark (1 Mt/year) used in academic research and commercial projects that are currently in place or under review. The study was conducted by a group of researchers from several universities as well as industry consultants. This study presents an overview of the reservoir modeling part of this study, which the authors were responsible for. The main objectives of the reservoir modeling for WASP project were as follows: (1) estimation of storage capacity (traditionally, this value is projected based on the available pore space, but we have an additional practical consideration: the maximum amount one can inject within short period of time [~50 years] and within a localized injection area [~30 km × 90 km]); (2) investigation of CO2 plume movement and pressure distribution during and after injection including the effect of formation dip angle on the plume shape and its migration; (3) investigation of the long-term fate of injection associated with free phase CO2 (risks of leakage) and aquifer pressurization (possible geomechanical changes and related phenomena); (4) investigation of the phase behavior of H2S initially available and dissolved in brine during CO2 sequestration process. The WASP reservoir modeling study mentioned above led to a few important findings. The most important one is that, when CO2 is being injected into a sour aquifer, initially dissolved H2S will release into the expanding CO2 plume and accumulate at the leading edge of the plume. Also, the large-scale injection scheme (20 Mt/year), which requires multi well injectors, provides very different pressure response compared to a one well (1 Mt/year) scenario.
Introduction
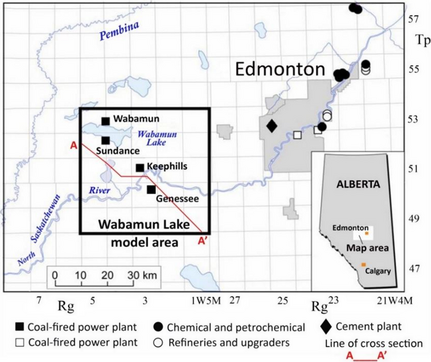
Carbon dioxide emissions from use of fossil fuels are likely to be the dominant drivers of climate change over the coming decades [1]. The use of carbon capture and storage (CCS) technology offers the possibility of maintaining access to fossil energy while reducing emissions of carbon dioxide to the atmosphere. However, for this technology to play a significant role in managing global emissions, it should be carried out at very large scales. Although aquifers offer a large storage potential for CCS, the injection of large volumes to fill up this capacity can be challenging. In this study, we performed a comprehensive numerical simulation of injection into the Nisku aquifer located in Wabamun Lake Area, Alberta, Canada, where large CO2 emitters are present (Fig. 1).
|
|
|
Figure 1. Location of the major CO2 emission sources in Alberta and the location of the Wabamun Lake study (redrafted from ref. [2]). |
Together the four coal-fired power plants in the Wabamun study area emit ~30 Mt CO2 per year. The Alberta Geological Survey has identified this area as a potential storage site with different underground storage targets. Identification of the targets was based on evaluation of a variety of parameters such as stratigraphy and lithology, fluid composition, rock properties, geothermal, geomechanical, and pressure regimes. One of these targets, the Nisku Formation in the Devonian Winterburn Group, was selected for WASP study. The Nisku was deposited at the edge of a carbonate shelf. From southeast to northwest, relatively pure platform carbonates change into interbedded limestone and shale of ramp and ultimately basin slope characteristics. The depth to the top of the Nisku formation, and for its whole areal extension, ranges between 1600 m in the northeast and gradually increases to 2150 m in the southeast at a dip angle of 0.5° [2]. This amount of change in the formation depth can consequently bring about a wide range of variation in fluid properties such as temperature and pressure. However, in the limited area of the injection site considered for this project, these variations are minimal and therefore neglected. Table 1 summarizes the average aquifer and fluid properties used in the study.
| Property | Value |
|---|---|
| Depth, m | 1860 |
| Thickness, m | 70 |
| Initial pressure at aquifer top, MPa | 16 |
| Temperature, °C | 60 |
| Permeability, mD | 30 |
| Ratio of vertical to horizontal permeability | 0.27 |
| Porosity, % | 10 |
| Salinity of formation water, mg/L | 190,000 |
| Density of formation water, kg/m3 | 1155 |
| Viscosity of formation water, cp | 0.84 |
| Rock compressibility, 1/kPa | 4.5 × 10−7 |
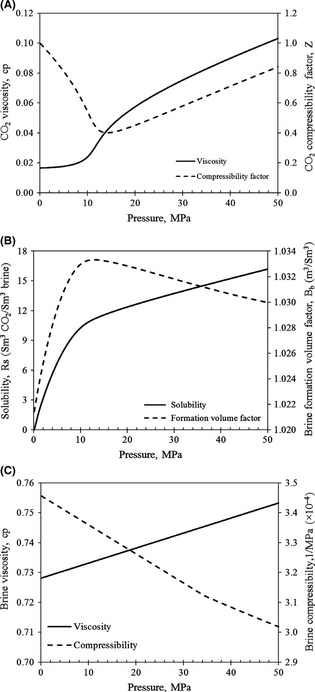
Both compositional and black-oil models have been reported in the literature to capture the interactions between CO2 and brine in storage processes. The compositional modeling relies on equation of state (EOS) flash calculations, and therefore they are usually computationally very expensive and impractical for large simulation models. On the other hand, in the black-oil approach, PVT (pressure–volume–temperature) calculations are facilitated through simple table-look up of properties (e.g., fluids density, viscosity, and compressibility) which change solely as a function of pressure. Therefore, the “black-oil” approach is much faster and less vulnerable to convergence issues, which both are crucial for simulation of large models. Accurate black-oil PVT model for a two-component CO2–brine system have been developed and validated against the experimental data and were adopted in this project. The details of the PVT model and its implications can be found in Hassanzadeh et al. [3, 4]. Figure A1(A–C) in Appendix A1 shows the properties of the fluid system pertinent to this study.
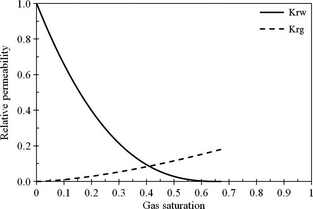
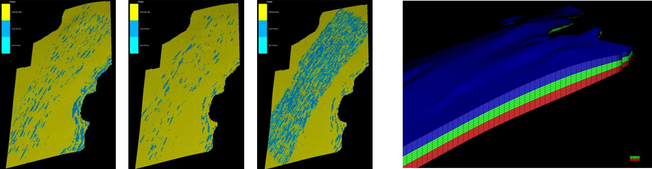
The characteristic relative permeability curves of the Nisku carbonate, which have been measured at in situ conditions of pressure, temperature, and brine salinity are shown in Figure 2 [5].
|
|
|
Figure 2. Nisku relative permeability curves for gas and water. |
Although the presented curves belong to a drainage process, the same curve is assumed for the imbibition process. Nevertheless, one can investigate the effect of relative permeability hysteresis on the residual gas trapping using different curves for imbibition and drainage processes. In addition, the effect of capillary pressure in all simulation models was neglected.
An important rock property, which is crucial to any injection scenario, is the fracture pressure gradient and hence the fracture pressure along the injectors wellbore. Practically, the injection pressure should be limited to 90% of the local fracture pressure to avoid the formation and propagation of fractures from the aquifer into the cap rock [2]. According to Bell et al. [6] the fracture pressure gradient for Wabamun area could be as high as 24 kPa/m; however, Karsten et al. [2] have used a more conservative value of 20 kPa/m. Based on these values, an average base case value of 22 kPa/m was assumed in study which corresponds to 40 MPa of fracture pressure at the average depth considered. The maximum bottom-hole pressure of the injectors in the simulation models are constraint to this value. This constraint will ascertain that the pressure in the aquifer will be remaining in the safe operating window.
In the following sections, the results of reservoir simulation of saturation (plume size) and pressure distributions in a simplified conceptual homogeneous model, as well as full size homogeneous and heterogeneous reservoir models, are presented. Secondly, the effect of reservoir dip on plume evolution is discussed. Thirdly, the long-term fate of average reservoir pressure and CO2 in the free gas phase is investigated. Finally, the phenomena of H2S exsolution during CO2 injection into a sour aquifer are briefly addressed.
Sensitivity of Simulation Results to Grid Size
The numerical simulations in the current project were conducted using IMEX, the CMG commercial black-oil simulator. Since the horizontal extension of the presented models can reach several hundred kilometers, larger grids were used to construct the overall parent grid and local grid refinement (LGR) was applied in the vicinity of the injectors where the maximum changes in flow parameters happen. The LGR option in IMEX is a very practical way to quickly examine the effect of grid block size, especially when the dimensions of the model are very large. In Appendix B, more details about the grid size and grid refinement applied in simulation models are provided.
Preliminary Conceptual Model
To develop a benchmark at the beginning of the project, a simplified conceptual model was developed assuming homogeneous properties (provided in Table 1) and an infinite acting aquifer. A square (200 km × 200 km) simulation domain was chosen to represent the aquifer (the results were not sensitive to an increase in model size to 250 km × 250 km). By setting the model to these dimensions, the aquifer behaves as though it were infinite acting for the injection of the target volume of CO2. Figure 3 shows the model configuration for different numbers of vertical injector wells (1–25).
|
|
|
Figure 3. Configuration of injection wells and element of symmetry (gray area). |
All wells are perforated from the top to the bottom of the aquifer. The number of wells (n) and placement configuration were designed to allow the use of an element of symmetry and hence reduce the total number of grid cells by a factor of four. The distance between the wells in x and y directions are the same and equal to λ. The total cumulative amounts of injected CO2 (denoted as V1, V4, V9, V16, and V25), increase with the number of wells and these amounts are split equally between injectors in each case. For example, in the case of nine wells, the yearly flow rate per each well is V9/(nine wells × 50 years). In all cases, the injection time is chosen as 50 years and injection capacity is defined as the maximum amount, which is possible to inject without exceeding the average reservoir fracture pressure of 40 MPa.
Simulation results demonstrate that, for a single (n = 1) injector completed in the whole formation interval and at the center of the reservoir, the plume radius reaches 4.6 km after 100 years. Most plume propagation takes place during the injection period and virtually stops after 100 years from the start of injection (50 years after injection stops). The injection rate capacity was found to be ~1 Mt/year for this vertical injector (constrained by fracture pressure), while horizontal well 1 km in length and completed open-hole, can improve the injectivity to ~1.5 Mt/year.
For the multiple wells (n > 1) injection scenario, CO2 saturation plumes do not interfere and n individual plumes each having a radius 4–5 km are observed. However, the pressure field behavior is completely different from the saturation field. By the end of CO2 injection period, there are no individual pressure plumes. Instead, different pressure plumes merge into a single large (scale of hundred km) pressure envelope. Injection capacity increases with the number of wells but this effect is rapidly vanishing after n ~ 10. These phenomena will be discussed in detail later, when a full Nisku aquifer geomodel is considered.
Detailed Modeling with Full Aquifer Extent
In this section, simulation results for CO2 injection into the Nisku formation are presented. First, a homogenous model is used to investigate injectivity into a semiinfinite formation. Then, a heterogeneous model is populated with realistic permeability and porosity fields in order to demonstrate the effect of heterogeneity and reservoir dip angle on the evolution of a CO2 plume as well as the impact on reservoir pressure.
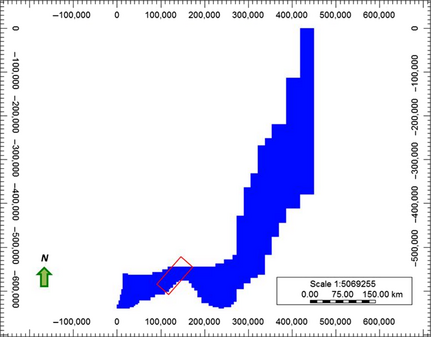
Figure 4 shows a top view of the Nisku aquifer. The illustrated area is approximately 450 km × 640 km while the area outlined in red corresponds to the injection area (1500 km2). The injection site is chosen to be near wells with available core and log data. The base properties used for homogeneous model are the same as for the conceptual model (base case).
|
|
|
Figure 4. Top view of the Nisku formation in the Wabamun Lake area (study area: the location of the proposed injection site is outlined by red box). |
Dependency of Plume Size and Pressure Field on the Number of Injectors
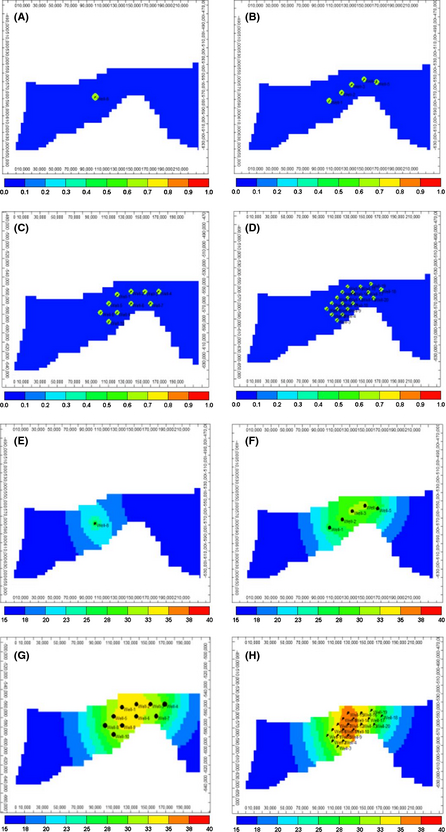
Figure 5 presents the plume extension and pressure distribution after 50 years of injection using base case properties.
|
|
|
Figure 5. (A–D) Saturation and (E–H) pressure (in MPa unit) distribution after 50 years of injection for different numbers of wells in the Nisku study area (wells within the red area in Fig. 4). |
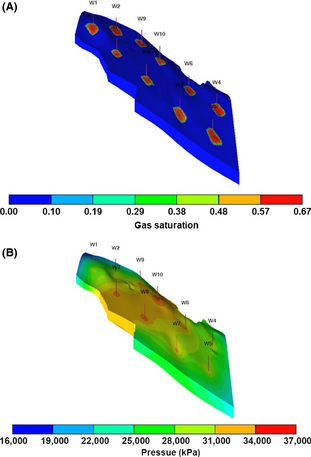
For the case with one well, the plume radius in the top layer is about 4.6 km, which is consistent with the conceptual model as well as analytical solution radius [7]. It is noticeable that the size of “pressure plume” is much larger (about 65 km), even for one well. In the cases of n number of injectors, one can see the existence of n individual plumes for CO2 saturation. As the number of wells increases, the individual injector flow rate decreases (fracture pressure constraint) and consequently the plume radius decreases. For pressure, however, strong interference between injectors occurs leading to pressurization of the total area covered by injectors and far beyond that.
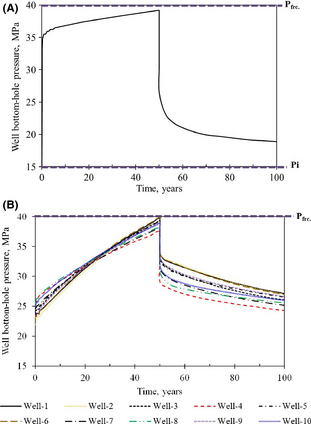
It is very important to mention that the dynamics of the pressure field is very different for one well injection and for multiple injection wells, as depicted in Figure 6. One can see that the pressure fall-off after ending CO2 injection is much quicker for a single well than multiple wells. The pressure fall-off for multiple wells is much slower because of the larger area of pressure influence.
|
|
|
Figure 6. Pressure buildup and drawdown during CO2 injection and after stopping injection for (A) one injector (B) 10 injectors. On this figures, Pi and Pfrc. refer to initial pressure and fracture pressure, respectively. |
Sensitivity study of injection capacity
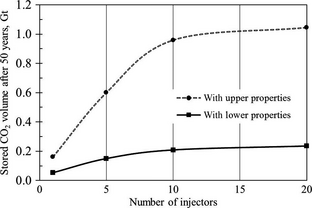
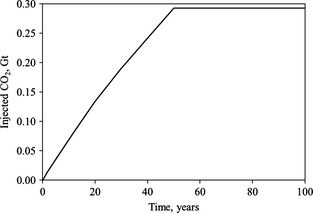
Starting with one well, the maximum achievable rate was determined to be as high as 1.1 Mt CO2/year (matches the results of conceptual modeling), which is equivalent to 0.055 Gt after 50 years. This flow rate causes the bottom-hole pressure to reach 40 MPa (fracture pressure) at the end of the injection period. This value for the formation fracture pressure was assumed by WASP team at the beginning of the project based on some literature data for Alberta reservoirs. Later, midway through the project, the Geomechanical Simulation Group (part of the WASP team) estimated this value to be around 35–37 MPa. Because our original assumption was very close to this estimate, the 40 MPa estimate was kept in our reservoir numerical modeling (a sensitivity of capacity to different fracture pressures within the range of 30–40 MPa is presented later in this section). When the next five wells are placed in the zone, the corresponding flow rate for each well reduces to 0.625 Mt/year per well with cumulative injection of 0.15 Gt. Increasing the number of wells to ten, brings the flow rate to 0.418 Mt/year per well with total injected CO2 of 0.209 Gt. Finally, the values for 20 wells are equal to 0.238 Mt/year and 0.238 Gt, respectively. These results are shown in Figure 7 (solid-line curve). In addition, we estimated the reservoir properties required to achieve the target storage of 1.0 Gt. The dashed-line curve on Figure 7 presents the injection capacity of the focus area with the following aquifer properties: porosity of 20%, horizontal permeability of 90 mD. Although these values cause significant difference in the outcome, the limitation in injectivity improvement for more than 10 wells still exists.
|
|
|
Figure 7. Variation of Nisku capacity with respect to number of wells and formation properties (solid line represents base properties). |
Some options to increase capacity (horizontal injection, fracturing)
In the storage process, the term “capacity” could have two meanings. The apparent capacity is the available and accessible pore volume of the aquifer. However, the injection capacity is the amount of CO2 that can be injected realistically into the formation and is a function of the number of wells and the fracture pressure of the formation. As discussed earlier, for a restricted injection area, such as one in the Nisku study, increasing the number of wells beyond a certain limit (which is controlled by formation properties and injection site area) has a minor effect on the injection capacity. A few methods that could increase injection capacity are discussed below.
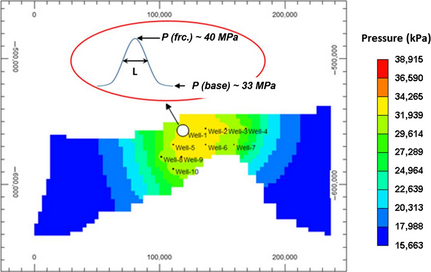
The first method is using horizontal wells instead of vertical wells. For vertical wells, it is preferable to use fully penetrated wells over the whole thickness of the aquifer. To find the minimum length of the horizontal well that would increase the injection capacity over vertical wells, the effective radius of pressure disturbance around the vertical injection well, which is again a function of formation properties, should be determined. After the start of injection through a vertical well, the pressure around the wellbore increases rapidly and causes the development of a narrow width pressure peak in the vicinity of the well (Fig. 8).
|
|
|
Figure 8. Pressure distribution at the end of injection. |
Using horizontal wells with a total length greater than the scale of the vertical injectors pressure peak “L1 ” (Fig. 8) will diminish these high-pressure peaks in the vicinity of the wellbore and cause the injectivity to increase. For the Nisku formation, this minimum required well length was estimated to be 3000 m. The middle points of the horizontal laterals are placed at the same locations of the vertical injectors. They are all in N–S direction and parallel to each other and located in the middle of the model thickness. In Appendix A2, some details of the gridding for simulation of horizontal wells are presented.
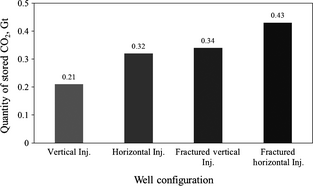
Figure 9 compares the effect of different well configurations on the achievable CO2 injection capacity.
|
|
|
Figure 9. Comparison of the effect of different well configurations and stimulation on the storage capacity of the model. |
While the vertical injectors provide the minimum capacity, their replacement with the horizontal wells will increase storage capacity by ~50%. Application of stimulation techniques such as hydraulic fracturing (HF) can also improve injectivity, with the results depicted as the last two bars in Figure 9. Nevertheless, the technical feasibility of implementing these techniques requires careful geomechanical characterization of the formation. For example, maintenance of the caprock integrity is a major concern in using such techniques for secure underground storage of CO2. The details of simulation for HF can be found somewhere else [8].
Heterogeneity study
Two different heterogeneity models suggested and provided by geo-statistics group were considered in this study: stochastic and object based modeling. The stochastic modeling was based on existing quantitative data (wireline log, acoustic impedance) and geo-statistical tools. It relies on resistivity-derived porosities and permeabilities (nearly 60 wells). For this study, five equi-probable realizations of properties were generated (Fig. 10). Porosity ranges from 1.3% to 28.6% (mean 4.9%) and permeability from 3.1 to 393 mD (mean 22.37 mD). Details of the development of the geo-statistical realizations, generated by a geo-statistics group for the WASP project, are presented in the geomodeling section [9] of WASP report. It should be noted that the presented geomodels only cover the study area (see Fig. 4); however, the pore volume of the boundary grids (far from the well locations) have been modified such that the total pore volume of the complete model is still honored. This is an important consideration for running such a huge model without sacrificing the accuracy of the results.
|
|
|
Figure 10. Geo-statistical realizations for porosity and permeability of WASP study area (from ref. [9]). |
Object-based models use “objects” (of same size) with higher porosity and permeability zones. The geometry and distribution of the objects in this study were constrained by dimensions of existing modern carbonate analogs, conceptual understanding of the Nisku carbonate in the Wabamun area, wireline log data, and seismic data.
Two kinds of objects were used: (1) dark blue (minor width = 500 m, major/minor ratio = 5, and thickness = 5 m) and (2) light blue (minor width = 300 m, major/minor ratio = 5, and thickness = 2 m). These are oriented along dip and distributed in each zone (upper, middle, and lower, Figure 11 left) of the Nisku. Figure 11 right shows the trend in layering of these zones (upper third has 13 layers with average vertical grid size z = 1.72 m; middle third has five layers with z = 4.46 m and lower third has 12 layers with average z = 1.86 m).
|
|
|
Figure 11. Object-based realization for porosity. |
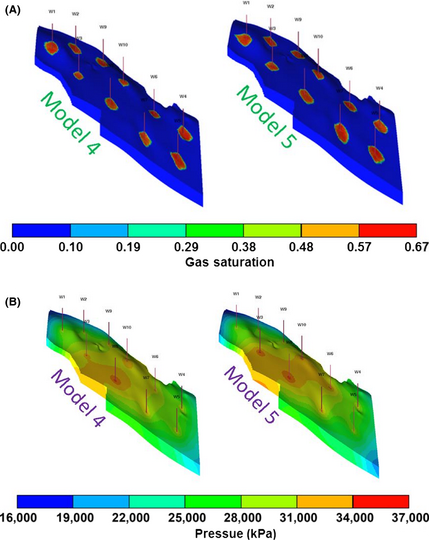
For stochastic modeling examples (realizations 4 and 5), the saturation and pressure fields are shown in Figure 12.
|
|
|
Figure 12. (A) Saturation and (B) pressure fields for stochastic-based geomodels after 50 years of injection. |
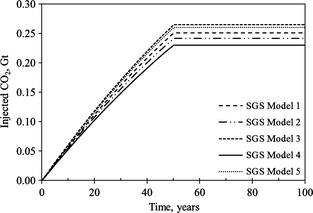
Although one can see some differences on a small scale for saturation and pressure fields of these two models, the injection capacities for all cases are almost identical (Fig. 13) and very close to the homogeneous model (Fig. 7, for 10 wells injection).
|
|
|
Figure 13. Injection capacity for five different realizations. |
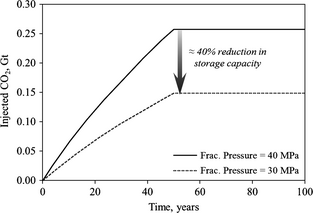
The above results represent the storage capacity when the fracture pressure was set to 40 MPa. To investigate the effect of fracture pressure limit on the storage capacity, simulations were run with sequential Gaussian simulation (SGS) model 1 in Figure 13. Sensitivity of capacity to fracture pressure is shown in Figure 14; a 25% reduction in fracture pressure will reduce the aquifer capacity by 40%, which is significant.
|
|
|
Figure 14. Injection capacity for two different fracture pressures. |
For object modeling, the saturation, and pressure fields are shown in Figure 15.
|
|
|
Figure 15. (A) Saturation and (B) pressure fields for object modeling after 50 years of injection. |
Injection capacity, as in the case of stochastic modeling, is very close to the homogeneous model (Fig. 16).
|
|
|
Figure 16. Injection capacity for object modeling. |
Based on this limited number of realizations, it is tentatively concluded that the small-scale heterogeneity (compared to plume size) considered in this study does not exert a strong control on pressure and saturation fields or on overall capacity of the injection site. However, it is expected that for layered systems, and for objects comparable to plume size, the effect of heterogeneity will be substantial. This heterogeneity will especially affect selective placement of injectors. Such a study would require more detailed knowledge of the property distribution within the aquifer.
Long-term Fate of CO2 Injection
In this section, the long-term fate of CO2 injection is discussed in association with the following phenomena:
- Increased aquifer pressure during and after injection
- Migration of CO2 beyond injection area due to dip
- Buoyancy of CO2 over long period of time (leakage risk)
- H2S issues
Pressure field evolution during and after injection
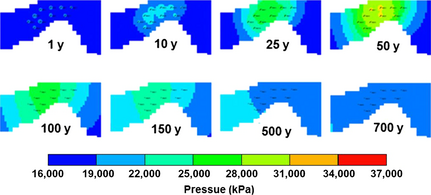
As discussed in the previous sections, the pressure in the aquifer (within and around injection area) increases rapidly during the injection period and then gradually decreases toward the initial pressure distribution after injection stops, due to the very large volume of the Nisku aquifer. It is important to know how long it will take for a substantial pressure disturbance to dissipate. The simulation results of a 10-well scenario are presented in Figure 17.
|
|
|
Figure 17. Pressure buildup (top row) during injection and pressure fall-off (bottom row) after injection stops for an injection scenario with 10 wells each injecting at 0.5 Mt/year for 50 years. |
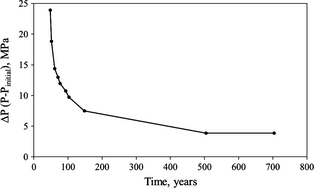
One can see that pressure does not reach initial reservoir pressure (Pi = 16 MPa) even 650 years after injection stops, although the difference in ΔP = P − Pinitial is small compared to the maximum difference (ΔPmax = Pfinal − Pinitial = 24 MPa at the end of injection). The graph of ΔP versus time is presented in Figure 18, which allows estimation of the time scale of pressure decay. From this graph, it can be inferred that ΔP falls e (~2.7) times at ~120 years, when the pressure fall-off curve starts to level off and thereby providing the time scale for the fate of pressure under injection design.
|
|
|
Figure 18. Progression of pressure fall-off after the injection stops |
Effect of aquifer dip on plume movement and its size
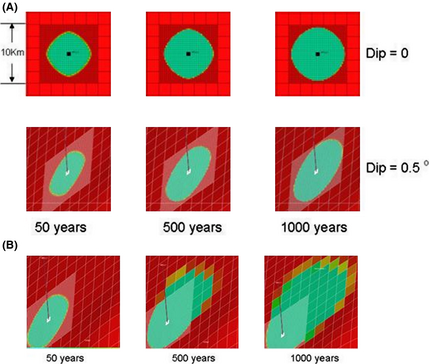
The effect of aquifer dip was evaluated with simulation runs using the base Nisku properties (Table 1) and a single well injection rate of 1 Mt/year for 50 years. Simulations were run up to 1000 years after injection started, and two cases were considered for comparison: (1) dip angle = 0° and (2) dip angle = 0.5°. The second case corresponds to the average dip angle of Nisku formation. The results of CO2 saturation at the top layer versus time are shown in Figure 19. One can see that at base conditions the effect of dip angle on the plume movement is marginal (Fig. 19A), although when permeability was increased (while all other parameters remained the same) noticeable plume migration along dip was observed (Fig. 19B).
|
|
|
Figure 19. Saturation field for a single injector: (A) base properties; (B) permeability is increased to 150 mD. |
The above results suggest that if the plume reaches regions with higher permeability, it will migrate upwards, and this should be taken into consideration for management of leakage risk.
Estimation of onset of convection for free phase CO2
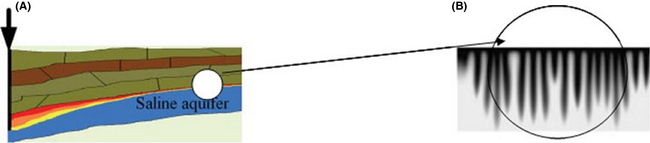
The CO2 injected into a deep aquifer is typically 10–40% less dense than the resident brine. Driven by density contrasts, CO2 will flow vertically first and then horizontally spreading under the caprock. If there are breaches in the caprock, leakage could occur through these high permeability zones or through artificial penetrations such as abandoned wells. It is very important to know how long the CO2 remains as a free phase beneath the caprock and how long complete dissolution of CO2 into the brine phase will take because this determines the time scale over which free phase CO2 has a chance to leak out. After injection, free-phase CO2 (gas or supercritical fluid) will be partially trapped as residual saturation and the rest will slowly dissolve in the brine [10]. Depending on reservoir properties, different mechanisms may be responsible for dissolution. Here, we estimate the dissolution mechanisms at Nisku conditions and the associated time scales of dissolution. In the short term (Fig. 20A), during and after injection, some amount of CO2 is residually trapped and the remainder may be dissolved by natural convection (Fig. 20B). The amount of trapped CO2 depends on rock fluid properties (relative permeability curves), and in the Nisku case, is about 30%. The amount of dissolved CO2 depends on reservoir pressure and temperature as well as brine salinity, and in the Nisku case, is about 3–5%. The remaining amount of free CO2 (~65%) will slowly dissolving into the brine by a combination of diffusion or natural convection.
|
|
|
Figure 20. (A) Accumulation of free CO2 below the caprock (short-term) and (B) combination of diffusion and natural convention (long-term processes) involved in geological storage of CO2 in saline aquifers (source of figure: [11]). |
The important parameter to describe convection is the porous medium Rayleigh number, defined as Ra = kgh∆ρ/(μφD), where k is the permeability, φ is the porosity, g is the acceleration due to gravity, h is the aquifer thickness, μ is the viscosity, ∆ρ is the density difference (CO2 saturated and fresh brine), and finally D is the molecular diffusion coefficient. If Ra > 49 then natural convection occurs. At Nisku conditions, Ra ~ 400, from which we estimated the onset of convection at these conditions (tonset ~ 80 years) and time scale of convective dissolution (tdis ~ 3000 years). Estimations are made based on Hassanzadehs model [11]. One can see that the time scale for possible leakage is very long and this can be a serious obstacle for implementation of an injection project due to regulatory and monitoring issues. Active reservoir engineering might be needed (for example, see ref. [12]) to reduce the dissolution time to the scales of hundreds years.
H2S issue
While working on the WASP project, we discovered that when CO2 is injected into a sour saline aquifer, the H2S initially dissolved in the brine will be exsolved and released into an expanding CO2 plume. A comprehensive study of this phenomenon has been made and all detailed results are presented elsewhere [13].
Summary
In this study we performed numerical modeling of injection of large volumes of CO2 (1 Gt target over 50 years) into the Nisku Formation located in Alberta. Injection modeling was performed within localized injection area of 30 km × 60 km. The main objectives of the study were to:
- Estimate the injection capacity and CO2 plume movement and pressure distribution during and after injection;
- estimate the time scale of pressure relief upon injection, time scale of CO2 dissolution, effect of dip angle on plume shape, and its migration; and
- assess the possible H2S evolution in the CO2 plume over time and space.
The following observations were made in this study:
- The capacity of injection is limited not by available pore space but by ability to inject without exceeding the fracture pressure of the formation. The capacity increases with the number of injectors but increasing the number of wells has a limit even considering a large well spacing. Very strong interference between pressure plumes was observed with no substantial benefits beyond 10 wells. Horizontal injection wells and aquifer fracturing may be considered as alternative options to increase the capacity. Sensitivity of capacity to reservoir permeability, rock compressibility, and well placement was investigated.
- For multiple injection scenarios (n wells), CO2 saturation plumes have no interference; we see n individual plumes of radius 4–5 km for each injector. The pressure field behavior is totally different from the saturation field. There are no individual pressure plumes but a single large (scale of hundred km) pressure envelope.
- The dip in the Nisku formation does not affect the results (i.e., no substantial plume movement) although free-phase CO2 may migrate along the dip if it reaches a zone with higher permeability above 100 mD. We estimated that at Nisku conditions, the time scale for pressure relief is 120 years and time scale for free phase CO2 dissolution is ˜3000 years where the mechanism of dissolution is natural convection.
- H2S dissolved in aquifer brine will be released into the CO2 plume during injection and will reach a high mole fraction at the outer edge of the CO2 front.
Acknowledgments
Financial support for this work was provided by NSERC Strategic Grant and AERI with additional funding from industry partners through Wabamun Area CO2 Sequestration Project (WASP) led by the University of Calgary. Simulation software (CMG) was donated by Computer Modeling Group. This support is gratefully acknowledged. We also wish to thank Long Neighem and Vijay Shrivastava for their help with the new version of GEM and for useful discussions of its applications to this study.
Conflict of Interest
None declared.
Note
- 1 L is determined based on the concept of FWHM (full-width at half maximum).
Appendix 1: “Black-oil” PVT properties pertinent to WASP
The model presented by Hassanzadeh et al. [3] was used to generate the PVT tables required for black-oil simulation of WASP project in CMG-IMEX [15]. Figure A1 depicts graphical representation of PVT behavior of the CO2–brine system as a function of pressure at constant temperature of 60°C and brine salinity of 190,000 ppm.
|
|
|
Figure A1. (A) CO2 and (B and C) brine black-oil PVT and transport properties used in the simulations. |
Appendix 2: Details of Grid Size and Associated Refinement in Simulation Models
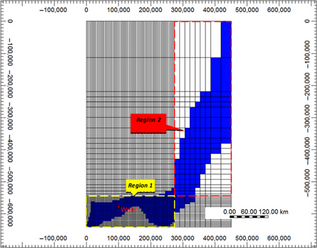
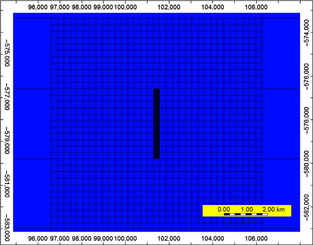
Sensitivity of the result to the grid size is a common approach to validate a simulation model. In this project, since the models are very large in horizontal directions, it was inevitable to use coarse grid size to create the global model. However, LGR was used to obtain a suitable level of refinement around the wells. Figure A2 displays the variation of grid resolution for the global model of the Nisku formation (with homogenous properties). The model uses smaller grids in “Region 1,” where it is enclosing the injection site and becomes coarser in “Region 2” and away from the injectors (see the map scale on the figure).
|
|
|
Figure A2. Grid resolution used in construction of the global model for the Nisku formation with homogenous properties. |
The horizontal dimensions of the parent grids in Region 1 are 3220 m × 3220 m. In the following the refinement procedure and the way that different levels of refinement was applied to each well is demonstrated.
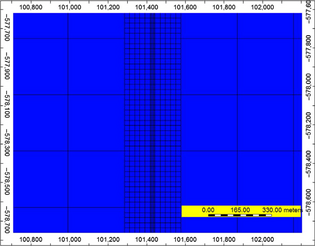
A square-shape area around each vertical well with three blocks on each side (area ~ 8000 m × 8000 m) is considered as the area for the first level of refinement (Fig. A3).
|
|
|
Figure A3. First level of refinement encloses nine parent blocks with the vertical well located at the central block. |
At this stage, each parent block is divided into 121 blocks with 11 divisions on each side. The central block in the refined area is then selected and further refined into 121 blocks (called nested refinement) to achieve the level 2 of refinement. Finally, the very central block from the previous refinement task is divided into 25 blocks to complete the refinement at level 3 (Fig. A4).
|
|
|
Figure A4. Second and third levels of refinement are achieved by further refinement of the center block from the previous stages. |
Table A1 shows the dimensions of the blocks at different levels of refinement.
| Grid block | Horizontal dimensions |
|---|---|
| Parent block (Region 1) | 3220 m × 3220 m |
| Refined blocks – Level 1 | 293 m × 293 m |
| Refined blocks – Level 2 | 27 m × 27 m |
| Refined blocks – Level 3 | 5.3 m × 5.3 m |
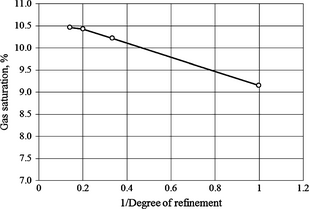
It should be noted that in all the conducted simulations with LGR, the same properties as those of the parent grid block are assigned to all the refined grid blocks. Also, the proper level of refinement is determined by studying the convergence behavior of the solution. For example, in the case of CO2 sequestration, the amount of free gas at the end of the injection scenario could serve as a worthy criterion to consider. As such, to obtain the required number of divisions at level 3, we plot the average free CO2 gas saturation in the whole refined area versus the reciprocal of degree of refinement. At the same time, proper refinement in the vertical direction is also required to capture the buoyancy effect of free CO2 movement in the upward direction. Figure A5 shows the free gas saturation in the refined area at the end of a scenario in which the CO2 injection happens continuously at constant injection rate of 1.0 Mt/year and for 50 years.
|
|
|
Figure A5. Convergence behavior of the simulation runs based on the degree of refinement in the horizontal direction at third level of refinement. |
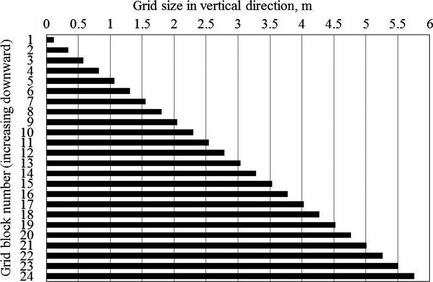
According to this figure, the parent block of refined area should be divided into five blocks in each x, and y directions with equal length and width of 5.3 m. This degree of refinement is corresponding to the refinement level at which the gas saturations starts to level off. It should be noted that the level of refinement in the horizontal direction should be considered combined with grid size gradient in the z direction. Figure A6 shows the final results of the applied grid size in the vertical direction.
|
|
|
Figure A6. Gradual increase in the grid size for the blocks in the z direction obtained as a results of grid size sensitivity analysis. |
Similar steps were performed to obtain a refined model for simulation of horizontal wells. The first level of refinement was applied exactly the same way it was performed for vertical wells. At the second level, the central column of the refined blocks in center block is divided into 121 blocks each. Finally, the central columns of the refined blocks are divvied into five blocks in the perpendicular direction to the horizontal well trajectory (here E–W). Figures A7 and A8 show the refinements details for levels 2 and 3, respectively.
|
|
|
Figure A7. Second level of refinement for horizontal wells is obtained by refinement of all blocks of the central column of the center grid. |
|
|
|
Figure A8. Third level of refinement for horizontal wells is obtained by refinement of all blocks of the central column of the center grid from the second level into five division in perpendicular direction to well trajectory. |
References
- Climate Change2007: Synthesis Report, Contribution of Working Groups I, II and III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, R. K. Pachauri and A. Reisinger (Eds.), IPCC , Geneva,Switzerland.
- M.Karsten, S. Bachu, and B. E. Buschkuehle. 2007. Assessment of a carbonate aquifer for CO2 geological storage in the Wabamun lake area. CSPG/CSEG Convention, May 14–17, Calgary, Canada.
- Hassanzadeh, H., M. Pooladi-Darvish, A. M. Elsharkawy, D. W. Keith, and Y. Leonenko. 2008. Predicting PVT data for CO2-brine mixtures for black-oil simulation of CO2 geological storage. Int. J. Greenhouse Gas Control2:65–77.
- Hassanzadeh, H., M. Pooladi-Darvish, and D. W. Keith. 2009. Accelerating CO2 dissolution in saline aquifers for geological storage – mechanistic and sensitivity studies. Energy Fuels23:3328–3336.
- Bennion, B., and S. Bachu. 2008. Drainage and imbibition relative permeability relationships for supercritical CO2/brine and H2S/brine systems in intergranular sandstone, carbonate, shale, and anhydrite rocks. SPE Reservoir Eval. Eng.11:487–496.
- Bell, J. S., P. R. Price, and P. J. McLellan. 1994. In-situ stress in the western Canada sedimentary basin, Chapter 29. Geological Atlas of the Western Canada Sedimentary Basin. Alberta Geological Survey, Edmonton, Canada.
- Nordbotten, J. M., M. A. Celia, and S. Bachu. 2005. Injection and storage of CO2 in deep saline aquifers: analytical solution for CO2 plume evolution during injection. Transp. Porous Media58:339–360.
- Ghaderi, S. M., D. W. Keith, and Y. Leonenko. 2009. Feasibility of injecting large volumes of CO2 into aquifers. Energy Procedia1:3113–3120.
- Eisinger, C. L., and J. L. Jensen. 2010. Data integration, petrophysics, and geomodeling, in wabamun area CO2 sequestration project. Report Available at http://www.ucalgary.ca/wasp/Geology%20and%20Geomodeling.pdf (accessed 07 Feb 2014).
- Hassanzadeh, H., M. Pooladi-Darvish, and D. W. Keith. 2006. Stability of a fluid in a horizontal saturated porous layer: effect of non-linear concentration profile, initial, and boundary conditions. Trans. Porous Media65:193–211.
- Hassanzadeh, H., M. Pooladi-Darvish, and D. W. Keith. 2007. Scaling behavior of convective mixing, with application to geological storage of CO2. AIChE J.53:1121–1131.
- Leonenko, Y., and D. W. Keith. 2008. Reservoir engineering to accelerate the dissolution of CO2 stored in aquifers. Environ. Sci. Technol.42:2742–2747.
- Ghaderi, S. M., D. W. Keith, R. Lavoie, and Y. Leonenko. 2011. Evolution of hydrogen sulfide in sour saline aquifers during carbon dioxide sequestration. Int. J. Greenhouse Gas Control5:347–355.
- Hitchon, B.1996. Aquifer disposal of carbon dioxide, hydrodynamic and mineral trapping: proof of concept. Geoscience Publishing Ltd., Sherwood Park, Alberta, Canada.
- Computer Modeling Group (CMG). 2008. Users Guide-IMEX, Version 2008.12. Computer Modeling Group Ltd., Calgary, AB, Canada.
Document information
Published on 01/06/17
Submitted on 01/06/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?