Resumen
El objetivo de este trabajo es el análisis comparativo de los cambios hemodinámicos locales producidos en una bifurcación coronaria por el implante de stents mediante 3 técnicas diferentes: stent simple en la arteria principal, stent simple en la arteria principal con orificio de comunicación con la arteria secundaria para el paso de un balón de inflado («kissing») y «culotte» . Para ello se ha utilizado la geometría ideal de una bifurcación coronaria a 45 y 90°.
En primer lugar se simularon los modelos en régimen estacionario mediante el código comercial ANSYS Fluent, y a continuación se validaron con las medidas experimentales tomadas en el laboratorio mediante velocimetría de imagen de partículas (particle image velocimetry [PIV]). Una vez obtenida una buena concordancia de resultados entre ambos estudios en régimen permanente, se abordó el flujo pulsátil. Los parámetros que se consideraron para comparar las diferentes técnicas en este régimen fueron los esfuerzos cortantes y la caída de presión promediados en el tiempo, así como el índice de esfuerzos cortantes oscilatorios (oscillatory shear index [OSI]). Las conclusiones finales fueron que el stent simple presenta los peores resultados, en términos de caída de presión, y la técnica «kissing» , los mejores. Esto sería aplicable a los stents liberadores de fármacos, donde la reestenosis no es tan crucial como el restablecimiento del flujo sanguíneo. En cuanto al criterio basado en el valor menor de los esfuerzos cortantes (< 0,4 Pa) y un OSI elevado (> 0,1), la técnica «culotte» presenta el peor comportamiento. Esto sería aplicable a los stents sin recubrimiento, en que la mejor opción sería el stent simple.
Abstract
The objective of this work is to analyze the local hemodynamic changes caused in a coronary bifurcation by three different stenting techniques: simple stenting of the main vessel, simple stenting of the main vessel with kissing balloon in the side branch and culotte. To carry out this study an idealized geometry of a coronary bifurcation is used, and two bifurcation angles, 45° and 90°, are chosen as representative of the wide variety of real configurations. Both numerical simulations and experimental measurements are performed. First, steady simulations are carried out with the commercial code ANSYS Fluent, then, experimental measurements with PIV (Particle Image Velocimetry), obtained in the laboratory, are used to validate the numerical simulations. The steady computational simulations show a good overall agreement with the experimental data. Second, pulsatile flow is considered to take into account the transient effects. The time averaged wall shear stress, oscillatory shear index (OSI) and pressure drop obtained numerically are used to compare the behavior of the stenting techniques. As conclusions obtained, simple stenting technique shows the worst results in terms of pressure drop, and kissing the best ones. This criterion could be applied for DES (Drug Eluting Stents) where the restenosis is not as critical as the reestablishment of the blood flow. But considering the regions of low wall shear stress (< 0.4 Pa) and elevated OSI (> 0.1), the culotte procedure shows the worst performance and the simple stent, the best. This could be applied to BMS (Bare Metal Stents).
Palabras clave
Stent ; Bifurcación coronaria ; Dinámica de fluidos computacional ; Esfuerzo cortante
Keywords
Stent ; Coronary bifurcation ; Computational fluid dynamics ; Wall shear stress
1. Introducción
El flujo sanguíneo a través de las arterias que presentan aterosclerosis es un tema de gran interés hoy en día, debido al desarrollo creciente de episodios cardiacos y al mayor número de accidentes cardiovasculares que se están sucediendo en las últimas décadas. Las enfermedades arteriales se caracterizan por la aterosclerosis, que es un proceso crónico de degeneración que evoluciona hacia la obstrucción de la luz arterial. La pared de la arteria se va engrosando al depositarse en ella elementos grasos tales como el colesterol. Este estrechamiento de los vasos, también denominado estenosis , puede reducir el flujo de forma severa y ocasionar graves consecuencias para la salud, como demuestran las cifras que sitúan esta patología como una de las principales causas de mortalidad en el mundo industrializado. Existen estudios experimentales sobre las consecuencias que producen las variaciones locales en el flujo [1] . La mayoría de ellos señalan que existe una correlación entre el valor bajo de los esfuerzos cortantes en la pared y el engrosamiento de la misma, aunque hay una cierta discrepancia en los resultados [2] , [3] and [4] . Numerosos estudios han observado una relación inversa entre el esfuerzo cortante y el espesor neointimal en las arterias coronarias [5] . Por otro lado, no solo los esfuerzos cortantes bajos, sino también los oscilatorios parecen coincidir con el engrosamiento temprano de la pared de la arteria carótida [6] y de la aorta abdominal [7] . Estos efectos locales tienen su origen en la distribución preferente de la placa aterosclerótica en ubicaciones específicas tales como las bifurcaciones y las arterias curvadas, razón por la cual se ha llevado a cabo este estudio.
Los stents intraluminales son diminutas estructuras tubulares autoexpandibles de malla de metal que se colocan dentro de la arteria coronaria después de una angioplastia con balón para prevenir el cierre de dicha arteria. El uso de stents coronarios contribuye a hacer decrecer la incidencia de este fenómeno. Pero, lamentablemente, la reestenosis dentro del stent sigue ocurriendo en el 20-30% de los casos tras el implante coronario. A pesar de estar diseñados para ser compatibles con el tejido humano, a menudo se produce una reacción en cadena de consecuencias no deseadas. Se habla de una incidencia global del 28%, y la causa principal de su aparición es la proliferación neointimal a través de una compleja cascada de sucesos que pueden tardar meses en desarrollarse. Una de las reacciones más importantes es la trombosis o formación de una fina capa de coágulo como respuesta a la presencia de un material extraño. Se ha propuesto un modelo simplificado para el crecimiento neointimal y el cambio en los parámetros dinámicos del fluido en el tiempo tras el implante del stent , así como un criterio para la reestenosis basado en el signo de la segunda derivada de la velocidad cerca de la pared [8] . Existen también numerosos estudios que demuestran la relación entre el diseño del stent y la estrategia de su implante con el valor de los esfuerzos cortantes y la formación de trombosis neointimal, reendotelización y reestenosis. Se plantea una situación crítica cuando las lesiones ateroscleróticas aparecen en la bifurcación coronaria, ya que, en estos casos, la técnica de implante del stent no es única. Aunque muchos trabajos clínicos se han centrado en el estudio de bifurcaciones coronarias, existen pocas referencias numéricas o experimentales sobre las arterias con stents . Algunos estudios tratan de la geometría ideal de una bifurcación con doble implante de stent[9] . También existen análisis de los cambios hemodinámicos producidos por el implante de un stent en la rama principal de una bifurcación coronaria representativa, con o sin angioplastia de balón en la rama secundaria [10] . También se han estudiado los esfuerzos mecánicos en la pared arterial antes y después del inflado de un balón en el uso de la técnica «kissing»[11] . Asimismo, existe un estudio comparativo de los diferentes patrones de liberación de medicamentos de un stent en una bifurcación coronaria [12] . Aunque existen numerosas referencias sobre estudios de técnicas de stents[12] , [13] , [14] , [15] , [16] , [17] , [18] , [19] and [20] , ninguno de ellos contiene un estudio comparativo teórico y experimental de las diferentes técnicas de implante de stent en una bifurcación con diferentes ángulos de apertura.
Numerosas técnicas son susceptibles de ser utilizadas para tratar lesiones en una bifurcación. En este trabajo se consideraron 3: stent simple en la rama principal; stent en la rama principal con orificio de comunicación con la rama secundaria, que puede dar libertad de paso a un alambre guía de balón, de gran utilidad si se quiere realizar un inflado poststent («kissing») , y la técnica «culotte» . En esta última, tras desplegar el stent en la rama principal, un segundo stent avanza parcialmente a través de la rama lateral y se expande en ella, de tal manera que la parte proximal de este segundo stent se despliega en la rama principal, mientras que la porción distal del mismo queda en la rama lateral.
Estas técnicas de implante se han evaluado para bifurcaciones coronarias de 45 y 90°, con una ratio de diámetro de rama secundaria a principal de 1,0 como caso más desfavorable de las diferentes configuraciones existentes. Esta última decisión se ha basado en un estudio sobre el efecto hemodinámico producido en una bifurcación con 3 diferentes ratios: 1,0, 0,8 y 0,6, que llegó a la conclusión de que, cuanto mayor era la ratio, mayores eran las pérdidas de carga en la rama secundaria [21] .
Inicialmente se desarrollaron las simulaciones numéricas en régimen estacionario utilizando el código comercial ANSYS Fluent, y los resultados obtenidos se compararon con las medidas experimentales desarrolladas con el equipo particle image velocimetry (PIV) en el laboratorio, con el fin de validar el proceso computacional. A continuación, una vez obtenida una concordancia satisfactoria entre ambos estudios, se analizaron las mismas configuraciones, esta vez en régimen no estacionario, para tener en cuenta la pulsatilidad inherente al flujo sanguíneo. Los parámetros utilizados para evaluar el comportamiento de las diferentes configuraciones de stent fueron los esfuerzos cortantes, el índice de esfuerzos cortantes oscilatorios (oscillatory shear index [OSI]) y la caída de presión en la bifurcación.
En la sección 2 se expone el procedimiento experimental, y en la sección 3 se describe la simulación numérica. Los resultados obtenidos se discuten en la sección 4, y las conclusiones se resumen en la sección 5.
2. Estudio experimental
Para realizar las medidas experimentales en el laboratorio en régimen estacionario se diseñó un circuito hidráulico que representaba un modelo de una bifurcación coronaria fabricado en metacrilato. El procedimiento para evaluar el flujo fue un equipo de PIV, que proporciona medidas de la velocidad instantánea en la sección transversal del flujo con micropartículas reflectoras. Las partículas fluorescentes de polímero que se introdujeron en el fluido eran de 1-20 μm y el equipo de PIV utilizado era un modelo Dantec FlowMap con láser Nd:YAG. Se construyeron 4 modelos para cada uno de los 2 ángulos de bifurcación estudiados, de 45 y 90°. Tres de ellos tenían uno o 2 stents implantados, dependiendo de la técnica analizada. El cuarto no constaba de stent y se utilizó como caso base representativo de una bifurcación coronaria sana. Las arterias consistieron en cilindros rectos de 8 mm de diámetro interior. Aunque este diámetro es grande para una arteria coronaria, facilita el manejo de los modelos y proporciona una mejor resolución experimental sin restar rigor al estudio, pues permite validar el modelo numérico mediante la aplicación de la semejanza parcial de Reynolds, en la cual, para obtener una simulación precisa del flujo computacional, solo hay que forzar la igualdad de los números de Reynolds (Re = ρvD/μ) , donde v y D son la velocidad característica y el diámetro del vaso, respectivamente; ρ, la densidad, y μ, la viscosidad dinámica del fluido. La figura 1 muestra los modelos experimentales para 45 y 90°.
|
|
|
Figura 1. Técnicas de implante de stent en la bifurcación coronaria contempladas en este estudio. a) Stent simple en la rama principal. b) Stent simple en la rama principal con «kissing» a través de la rama lateral. c) Técnica «culotte» .
|
El fluido de trabajo es una mezcla de glicerina (60%) y agua (40%) de propiedades similares a la de la sangre (viscosidad cinemática ν = 3,72 × 10−6 m2 /s, densidad ρ = 1.099,3 kg/m3 ). Se escaló el flujo volumétrico para mantener el mismo número de Reynolds que el utilizado en las simulaciones numéricas, en que el diámetro de las arterias era de 3,2 mm. Solamente se consideraron en el laboratorio los casos en régimen estacionario.
3. Simulación numérica
3.1. Régimen estacionario
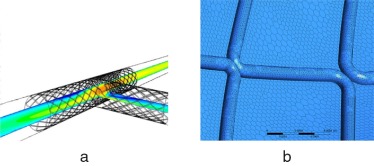
El programa ANSYS Fluent resolvió numéricamente las mismas configuraciones estudiadas con PIV en el laboratorio. Se consideró un diámetro interior de 3,2 mm, con una longitud del stent de 54,28 mm para la rama principal y de 42,8 mm para la secundaria. El stent consta de alambres o struts de 0,045 mm de espesor y 0,838 mm de longitud, que se unen formando celdas abiertas con un ángulo de apertura de 36°. La figura 2 a muestra la reconstrucción geométrica de la técnica «culotte» de implante de stent en una bifurcación de 90° y un mapa de velocidades en el plano medio. Se utilizó una malla de poliedros refinada cerca de los struts o alambres del stent , como se puede apreciar en la figura 2 b, para obtener más información del flujo en estas regiones de contacto del sólido con el fluido. Se llevó a cabo un estudio de sensibilidad de los resultados al tamaño de la celda y, finalmente, se optó por el tamaño de 3 a 5 millones, en función de la técnica de stent utilizada. En cuanto al coste computacional, se realizó el cálculo en un clúster con 32 procesadores, con un tiempo aproximado de media hora para cada caso. Se utilizó un esquema de cálculo upwind de segundo orden para los términos convectivos. Se supuso que la pared arterial era rígida, hipótesis razonable si se considera que la arteria presenta una estenosis con necesidad de angioplastia reparadora y stent a modo de andamiaje. Por tanto, el ateroma que recubre la íntima confiere características de rigidez a las ramas objeto de estudio, así como los struts metálicos que la recubren. Además, recientemente Chiastra et al. (2014) [22] han realizado un estudio comparativo entre la pared flexible y la pared rígida de una arteria en que se había colocado un stent . Los resultados muestran una tendencia similar en términos de esfuerzos cortantes en la pared, tanto instantáneos como promediados en el tiempo. Particularmente, la diferencia obtenida en porcentaje para los esfuerzos cortantes promediados en el tiempo inferiores a 0,4 Pa oscilaba entre el 1 y el 1,5%, dependiendo del tipo de stent . Todas estas conclusiones indicaban que la hipótesis de pared rígida era adecuada si el objetivo a estudiar eran los esfuerzos cortantes cerca de la pared.
|
|
|
Figura 2. a) Reconstrucción de un mapa de contorno de velocidad en el plano medio para la técnica «culotte» en una bifurcación a 90°. b) Detalle de la malla del stent .
|
El fluido se consideró newtoniano, con una viscosidad cinemática ν = 3,72 × 10−6 m2 /s y una densidad ρ = 1.099,3 kg/m3 (número de Reynolds = 172). Se impusieron condiciones de contorno equivalentes a las que tenían los experimentos para el régimen estacionario, y se utilizó un perfil de velocidad tipo Womersley, con una velocidad media de 0,2 m/s a la entrada de la arteria principal. Con el fin de evitar que la solución se viera afectada por las condiciones de contorno en la salida, se amplió el dominio computacional en las simulaciones. En estas configuraciones, las salidas se ubicaron 35 diámetros aguas abajo de la bifurcación, una distancia equivalente a la empleada en los ensayos, donde se fijó una presión manométrica nula. En esta ampliación del dominio las celdas son de mayor tamaño que en el resto de la arteria, especialmente en las zonas de contacto stent -fluido.
3.2. Régimen no estacionario
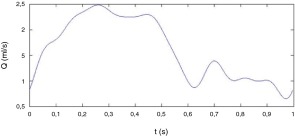
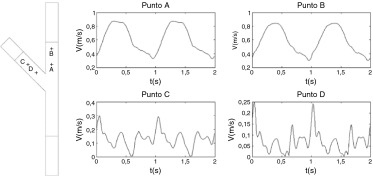
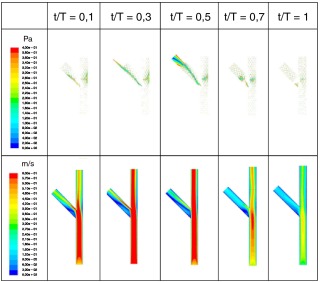
Para el régimen no estacionario se impuso un perfil de velocidades parabólico variable en el tiempo a la entrada de la arteria principal. La onda de velocidad del flujo sanguíneo a la entrada se tomó de [10] . La figura 3 muestra la evolución temporal del caudal en un ciclo cardiaco. Se consideraron solamente los 10 primeros términos de Fourier en este análisis para su representación analítica como condición de contorno. El número de Womersley correspondiente a este flujo es igual a 2,2. En cuanto a las salidas, se impusieron las ratios de caudal de la salida principal a la secundaria obtenidas en régimen estacionario para las diferentes bifurcaciones arteriales y técnicas de stent utilizadas ( tabla 1 ). Se simularon 4 ciclos cardiacos con el fin de obtener una solución estable. La figura 4 muestra la evolución temporal de la velocidad para el tercer y el cuarto ciclos en la técnica «culotte» para un ángulo de 45° en los puntos indicados. En los demás casos, la tendencia fue la misma, es decir, se alcanzó la estabilidad en el cuarto ciclo, razón por la cual todos los resultados están referidos a este último.
|
|
|
Figura 3. Evolución del caudal frente al tiempo adimensionalizado usado en las simulaciones en régimen no estacionario.Fuente: Williams et al. [10] (material suplementario disponible on line).
|
| Sin stent | Con stent simple | «Kissing» | «Culotte» | |
|---|---|---|---|---|
| 45° | 1,203 | 1,285 | 1,215 | 1,172 |
| 90° | 1,217 | 1,395 | 1,305 | 1,309 |
|
|
|
Figura 4. Evolución temporal de la velocidad para el tercer y cuarto ciclo en la técnica «culotte» en los puntos indicados en la figura.
|
4. Resultados
4.1. Régimen estacionario. Resultados numéricos y experimentales
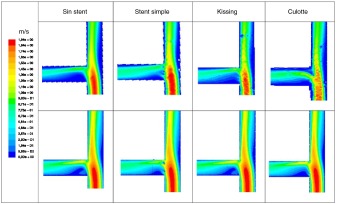
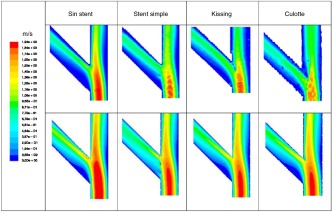
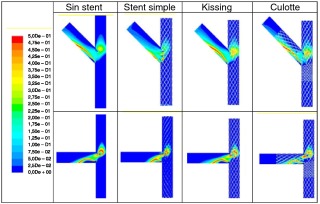
Los resultados que se muestran en esta sección se refieren a la región ocupada por el stent en las diferentes configuraciones y técnicas o, para el caso de la arteria sana exenta de stent , a la región equivalente. Las Figura 5 and Figura 6 muestran los contornos de velocidad en el plano medio obtenidos de forma numérica y experimental. Puede observarse que el patrón de flujo está más perturbado en la técnica del stent simple, en la cual el flujo en la rama lateral aparece distribuido más uniformemente aguas abajo gracias a la presencia de los struts . Este comportamiento se muestra de manera más evidente en el resultado numérico de la bifurcación a 45° ( fig. 6 ), donde se observa una pequeña recirculación y una región de estancamiento en la rama lateral y, por consiguiente, áreas en que el valor del esfuerzo cortante es bajo (v. también fig. 7 ). Esta tendencia también puede observarse en las simulaciones en régimen no estacionario. La comparación de las Figura 5 and Figura 6 permite concluir que el patrón de flujo depende principalmente de la configuración geométrica de la bifurcación y no tanto de la técnica de implante de stent adoptada, especialmente para el ángulo de bifurcación de 90°. Esto último era esperable, ya que las diferencias de flujo entre técnicas para dicho ángulo son menos relevantes.
|
|
|
Figura 5. Contornos de velocidad obtenidos experimentalmente con PIV (imágenes superiores) y simulados numéricamente (imágenes inferiores) para el caso base sin stent , stent simple, «kissing» y «culotte» en una bifurcación a 90°.
|
|
|
|
Figura 6. Contornos de velocidad obtenidos experimentalmente con PIV (imágenes superiores) y simulados numéricamente (imágenes inferiores) para el caso base sin stent , stent simple, «kissing» y «culotte» en una bifurcación a 45°.
|
|
|
|
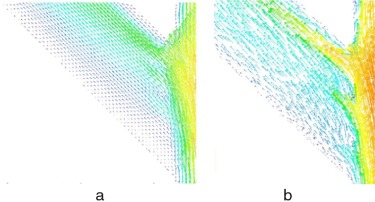
Figura 7. Vectores velocidad en el plano medio en una bifurcación a 45° sometida a la técnica de implante de stent simple. a) Resultados experimentales obtenidos con PIV. b) Resultados numéricos.
|
En la técnica de «culotte» , el stent a través de la rama lateral puede no ajustarse completamente a la pared arterial en la zona del divisor de flujo de la bifurcación, lo cual origina una zona de baja velocidad. Este efecto se reproduce más difícilmente en las simulaciones numéricas, debido a las pequeñas diferencias en la reconstrucción geométrica de los struts distorsionados en dicha zona. Sin embargo, la concordancia entre el estudio numérico y el experimental es razonablemente buena, lo cual puede interpretarse como una validación preliminar de los resultados en régimen no estacionario.
4.2. Simulaciones numéricas en régimen no estacionario y comparación de las diferentes técnicas de implante de stent
Los parámetros que se consideraron para evaluar el comportamiento de las diferentes estrategias de implante de stent en los cálculos en régimen no estacionario fueron los siguientes:
- Caída de presión en la bifurcación.
- Áreas con esfuerzo cortante promediado en el tiempo inferior a 0,4 Pa.
- Índice de esfuerzos cortantes oscilatorios (OSI) superior a 0,1.
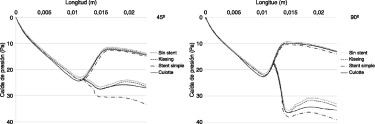
La figura 8 representa la caída de presión promediada en el tiempo en la región recubierta por el stent . Las pérdidas de presión son mayores en la bifurcación a 90° que a 45°, como cabía esperar. También puede apreciarse que, en ambos casos (45 y 90°), las diferencias en la pérdida de presión son pequeñas en la rama principal en todas las configuraciones. Las discrepancias aparecen en la rama lateral, donde la técnica del stent simple presenta el peor comportamiento, particularmente para 45°, donde la pérdida de presión es mayor, aproximadamente en un 10 %, que la que se da en las otras técnicas. Finalmente, la técnica «kissing» es la mejor, en cuanto a pérdida de carga, en ambos casos.
|
|
|
Figura 8. Caída de presión promediada en el tiempo en las diferentes técnicas de implante de stent para una configuración a 45° (izquierda) y 90° (derecha) obtenida en la simulación numérica en régimen no estacionario.
|
Este criterio de la caída de presión podría considerarse decisivo para los stents liberadores de fármacos (drug eluting stents [DES]), en que la reestenosis quedaría mitigada por la acción de dichos medicamentos, mientras que el restablecimiento del flujo sanguíneo a través de la estenosis sería el objetivo fundamental que habría que alcanzar.
La tabla 2 indica las áreas (en mm2 ) en que el valor de los esfuerzos cortantes en la pared es inferior a 0,4 Pa, siendo este el 20% del valor correspondiente a la solución de Poiseuille en la región proximal. Estas regiones de bajo esfuerzo cortante serían, en principio, más susceptibles a presentar reestenosis. Así pues, según este resultado la técnica «culotte» sería la peor, mientras que la técnica de stent simple presentaría un mejor funcionamiento global. Las áreas de bajo esfuerzo cortante están localizadas en el exterior de la bifurcación, donde se pueden apreciar 2 zonas de recirculación ( fig. 9 ). Parece obvio que un mayor contenido metálico en la pared arterial —como se da en la técnica «culotte» , en que hay 2 stents en vez de uno, a diferencia de los demás casos— produce mayores áreas de recirculación detrás de los struts . Este efecto podría explicar la mayor extensión de zonas de esfuerzo cortante bajo que presenta esta técnica.
| Sin stent | Con stent simple | «Kissing» | «Culotte» | |
|---|---|---|---|---|
| 45° | 25,73 | 16,65 | 29,09 | 44,68 |
| 90° | 16,55 | 13,08 | 17,98 | 39,75 |
|
|
|
Figura 9. Zonas sometidas a tensiones tangenciales en la pared, promediados en el tiempo, inferiores a 0,4 Pa para las diferentes técnicas de implante de stent .
|
Por otro lado, los struts que cubren el orificio de comunicación con la rama lateral en la técnica del stent simple reducen el tamaño de la burbuja de recirculación.
En la figura 10 se puede ver la evolución temporal de las zonas afectadas por los esfuerzos cortantes bajos, junto con un mapa de contornos de velocidad en el plano medio. El tiempo se normalizó con el período del ciclo cardiaco de valor 1 s.
|
|
|
Figura 10. Evolución temporal de las tensiones tangenciales en la pared (imágenes superiores) y contornos de velocidades en el plano medio (imágenes inferiores) para la técnica «culotte» en bifurcación a 45°.
|
Finalmente, el parámetro OSI se ha utilizado para cuantificar los esfuerzos cortantes oscilatorios inherentes al flujo sanguíneo de naturaleza pulsátil. Se define de la manera siguiente:
|
|
( 1) |
donde T es el período del pulso cardiaco y es el esfuerzo cortante en la pared proyectado en la dirección principal del flujo.
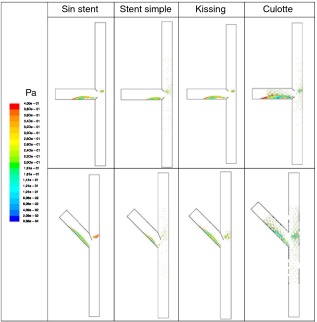
Es bien sabido de investigaciones clínicas que la reestenosis puede ocurrir no solo en regiones de bajo esfuerzo cortante, sino en aquellas zonas donde se propicia el flujo inverso. Estas regiones se caracterizan por las oscilaciones temporales en la dirección de los esfuerzos cortantes. La tabla 3 muestra las áreas con un OSI elevado (> 0,1). La localización de un stent en la rama lateral produce una pequeña zona de recirculación del flujo y un OSI elevado ( fig. 11 ). Esto puede explicar por qué las áreas con OSI > 0,1 son mayores en la técnica «culotte» que en la de implante de un stent simple. Esta tendencia parece más marcada para el ángulo de 45°. La mejor técnica resulta ser, de nuevo, la del stent simple, porque reduce la burbuja de separación del flujo de la pared en la rama lateral.
| Sin stent | Con stent simple | «Kissing» | «Culotte» | |
|---|---|---|---|---|
| 45° | 73,87 | 46,17 | 62,83 | 79,9 |
| 90° | 38,51 | 29,69 | 35,04 | 42,01 |
|
|
|
Figura 11. Índice OSI (oscillatory shear index) para las diferentes configuraciones.
|
5. Conclusiones
Se ha realizado un estudio numérico y experimental sobre la influencia de 3 técnicas de implante de stent en una bifurcación coronaria simplificada. Los resultados experimentales obtenidos con PIV en el laboratorio para los casos en régimen estacionario muestran una concordancia razonable con las simulaciones numéricas en ANSYS Fluent, lo que ha permitido validar el método computacional, el cual ha quedado como único método de evaluación para el régimen no estacionario.
La primera conclusión que cabe destacar es que se observa que el ángulo de la bifurcación tiene una gran influencia sobre el comportamiento hemodinámico en los resultados obtenidos de las diferentes técnicas de implante de stents . La técnica del stent simple presenta los peores resultados en términos de caída de presión, y la de «kissing» , los mejores. Este criterio podría aplicarse a los stents liberadores de fármacos (DES), donde la reestenosis no es tan crucial como el restablecimiento del flujo sanguíneo. En cuanto al criterio que se basa en evaluar las regiones de bajo esfuerzo cortante (< 0,4 Pa) y OSI elevado (> 0,1), la técnica «culotte» , que cuenta con un mayor número de struts , presenta el peor comportamiento y, por consiguiente, incrementa el riesgo de sufrir reestenosis. La mejor opción, en este caso, sería la técnica de stent simple.
Por tanto, se puede decir que las recomendaciones son opuestas en función del tipo de stent elegido. Debido a la presencia de struts en la entrada de la rama lateral, la técnica del stent simple crea vorticidad adicional, lo que provoca una mayor caída de la presión, mientras que las regiones de bajo esfuerzo cortante y recirculación de flujo se reducen en la pared proximal de la rama lateral.
Gao et al. [23] han analizado el comportamiento de los stents liberadores de fármacos (SLF) a través de 2 modalidades: un único stent con un inflado posterior mediante la técnica «kissing» y una técnica más compleja con el uso de 2 stents . Y los resultados obtenidos apuntan a la utilización de un único stent liberador de fármaco en vez de 2, ya que, si bien no se han observado diferencias apreciables en la reestenosis, hay más probabilidades de que aparezca trombosis tardía con la técnica compleja del uso de 2 stents . Una forma de prevenir la trombosis sería evitar al máximo el flujo lento mediante un restablecimiento adecuado del mismo minimizando la pérdida de carga. Ello podría corroborar que el uso de un único stent con inflado posterior mediante la técnica «kissing» es la mejor opción para los stents liberadores de fármacos. García Tejada y Albarrán [24] llegan a una conclusión similar.
Por su parte, Erglis et al. [25] informan de un amplio registro de resultados clínicos a corto y a largo plazo de pacientes que han sido sometidos al implante de stents convencionales (SC) y SLF a través de diferentes técnicas. Destacan los episodios cardiacos adversos en el caso de SC debido al proceso de reestenosis que suele seguir a la utilización de los mismos, frente a los SLF, en particular cuando la técnica utilizada involucra 2 stents , lo cual confirma que la técnica «culotte» es responsable de un mayor índice de reestenosis en los stents sin recubrimiento de medicamento o convencionales. Así pues, en el caso de los SC parece que la recomendación es utilizar un stent simple o «kissing» , pero no «culotte» , ya que produce esfuerzos cortantes más bajos y ello parece ocasionar un mayor depósito de ateroma.
Obviamente, las simulaciones que se han llevado a cabo en este estudio centran su interés en los aspectos hemodinámicos, pero también deberían tenerse en cuenta otros factores antes de elegir la técnica adecuada. Además, este estudio debería hacerse extensivo a configuraciones más realistas. Este podría ser el paso siguiente en esta línea de trabajo.
Agradecimientos
Esta investigación ha sido financiada por el Ministerio de Economía y Competitividad del Gobierno de España, a través del proyecto DPI2012-35524, y con una ayuda de la Junta de Castilla y León (GR57).
Bibliografía
- [1] N. Benard, D. Coisne, E. Donal, R. Perrault; Experimental study of laminar blood flow through an artery treated by a stent implantation: characterization of intra-stent wall shear stress; J. Biomech., 36 (2003), pp. 991–998
- [2] C.K. Zarins, D.P. Giddens, B.K. Bharadvaj, V.S. Sottiurai, R.F. Mabon, S. Glagov; Carotid bifurcation atherosclerosis. Quantitative correlation of plaque localization with flow velocity profiles and wall shear stress; Circ. Res., 53 (4) (1983), pp. 502–514
- [3] A. Gnasso, C. Irace, C. Carallo, M.S. de Franceschi, C. Motti, P.L. Mattioli, et al.; In vivo association between low wall shear stress and plaque in subjects with asymmetrical carotid atherosclerosis; Stroke., 28 (5) (1987), pp. 993–998
- [4] A.M. Shaaban, A.J. Duerinckx; Wall shear stress and early atherosclerosis: a review; AJR Am. J. Roentgenol., 174 (6) (2000), pp. 1657–1665
- [5] J.J. Wentzel, F.J.H. Gijsen, N. Stergiopulos, P.W. Serruys, C.J. Slager, R. Krams; Shear stress, vascular remodeling and neointimal formation; J. Biomech., 36 (2003), pp. 681–688
- [6] D.N. Ku, D.P. Giddens, C.K. Zarins, S. Glagov; Pulsatile flow and atherosclerosis in the human carotid bifurcation: Positive correlation between plaque location and low and oscillating shear stress; Atherosclerosis., 5 (3) (1985), pp. 293–302
- [7] J.E. Moore, C. Xu, S. Glagov, C.K. Zarins, D.N. Ku; Fluid wall shear stress measurements in a model of the human abdominal aorta: Oscillatory behavior and the relationship to atherosclerosis; Atherosclerosis., 110 (1994), pp. 225–240
- [8] J. Garcia, A. Crespo, J. Goicolea, M. Sanmartín, C. García; Study of the evolution of the shear stress on the restenosis after coronary angioplasty; J. Biomech., 39 (2006), pp. 799–805
- [9] V. Deplano, C. Bertolotti, C. Barragan; Three-dimensional numerical simulations of physiological flows in a stented coronary bifurcation; Med. Biol. Eng. Comput., 42 (2004), pp. 650–659
- [10] A.R. Williams, B.K. Koo, T.J. Gundert, P.J. Fitzgerald, J.F. LaDisa; Local hemodynamic changes caused by main branch stent implantation and subsequent virtual side branch balloon angioplasty in a representative coronary bifurcation; J. Appl. Physiol., 109 (2010), pp. 532–540
- [11] S. Morlacchi, C. Chiastra, D. Gastaldi, G. Pennati, G. Dubini, F. Migliavacca; Sequential structural and fluid dynamic numerical simulations of a stented bifurcated coronary artery; J. Biomech. Eng., 133 (12) (2011)
- [12] E. Cutri, P. Zunino, S. Morlacchi, C. Chiastra, F. Migliavacca; Drug delivery patterns for different stenting techniques in coronary bifurcations: A comparative computational study; Biomech. Model. Mechanobiol., 12 (2013), pp. 657–669
- [13] J. Al Suwaidi, P.B. Berger, C.S. Rihal, K.N. Garratt, M.R. Bell, H.H. Ting, et al.; Immediate and long-term outcome of intracoronary stent implantation for true bifurcation lesions; J. Am. Coll. Cardiol., 35 (2000), pp. 929–936
- [14] J.L. Berry, A. Santamarina, J.E. Moore Jr., S. Roychowdhury, W.D. Routh; Experimental and computational flow evaluation of coronary stents; Ann. Biomed. Eng., 28 (2000), pp. 386–398
- [15] R. Balossino, F. Gervaso, F. Migliavacca, G. Dubini; Effects of different stent designs on local hemodynamics in stented arteries; J. Biomech., 41 (2008), pp. 1053–1061
- [16] J. Charonko, S. Karry, J. Schmieg, S. Prabhu, P. Vlachos; In vitro, time-resolved PIV comparison of the effect of stent design on wall shear stress; Ann. Biomed. Eng., 37 (2009), pp. 1310–1321
- [17] S.L. Chen, B. Xu, Y.L. Han, I. Sheiban, J.J. Zhang, F. Ye, et al.; Comparison of double kissing crush versus Culotte stenting for unprotected distal left main bifurcation lesions: Results from a multicenter, randomized, prospective DKCRUSH-III study; J Am Coll Cardiol., 61 (14) (2013), pp. 1482–1488
- [18] R.J. Ruiz-Salmerón, L.F. Valenzuela, I. Pérez, M. Fuentes, S. Rodríguez-Leiras, M. Vizcaíno, et al.; Approach to coronary bifurcation lesions using the everolimus-eluting stent: Comparison between a simple strategy and a complex strategy with T-stenting; Rev. Esp. Cardiol., 66 (2013), pp. 636–643
- [19] W.J. Kim, Y.H. Kim, D.W. Park, S.C. Yun, J.Y. Lee, S.J. Kang; Comparison of single- versus two-stent techniques in treatment of unprotected left main coronary bifurcation disease; Catheter. Cardiovasc. Interv., 77 (6) (2011), pp. 775–782
- [20] N. Foin, A. Mattesini, M. Ghione, G. dall’Ara, S. Sen, S. Nijjer, et al.; Tools & techniques clinical: Optimising stenting strategy in bifurcation lesions with insights from in vitro bifurcation models; EuroIntervention., 9 (2013), pp. 885–887
- [21] S.-S. Yoo, S.-H. Suh, H.-W. Roh; Numerical simulation of flows of non-Newtonian fluids in the stenotic and bifurcated tubes; KSME J., 10 (1996), pp. 223–234
- [22] C. Chiastra, F. Migliavacca, M.Á. Martínez, M. Malvè; On the necessity of modelling fluid-structure interaction for stented coronary arteries; J. Mech. Behav. Biomed. Mater., 34 (2014), pp. 217–230
- [23] Z. Gao, Y.J. Yang, R.L. Gao; Comparative study of simple versus complex stenting of coronary artery bifurcation lesions in daily practice in Chinese patients; Clin. Cardiol., 31 (7) (2008), pp. 317–322
- [24] J. García Tejada, A. Albarrán González-Trevilla; Stents y trombosis; Med. Clin., 130 (5) (2008), pp. 175–176
- [25] A. Erglis, I. Narbute, D. Juhnevica, I. Kumsars, S. Jegere; Lessons for the treatment of bifurcation lesions: From nowadays to the future; J. Interv. Cardiol., 3 (2011), pp. 55–65
Document information
Published on 01/09/16
Accepted on 16/04/15
Submitted on 13/01/15
Volume 32, Issue 3, 2016
DOI: 10.1016/j.rimni.2015.04.003
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?