Thermomechanical simulation of an industrial quenching process applied to a centrifugal pump impeller

Resumen

En este trabajo se estudia el comportamiento termomecánico durante el tratamiento térmico de templado de un rodete de una bomba centrífuga fabricada en fundición blanca. El análisis se realiza mediante una formulación termomecánica acoplada discretizada mediante el método de elementos finitos. La respuesta del material se describe por medio de un modelo termoplástico que incorpora efectos de cambio de fase. En particular, se presenta el proceso de templado desde la austenización hasta el enfriamiento del rodete con la finalidad de evaluar la ocurrencia de falla en la pieza al final del proceso. Para la determinación del daño mecánico se comparan 3 criterios diferentes escritos en función de las tensiones y de las deformaciones plásticas desarrolladas durante el proceso. El estudio se enfoca en 2 tipos de configuración de rodetes, con 4 y 5 álabes, donde la primera de ellas experimenta fractura en el proceso industrial de producción. Los resultados numéricos obtenidos en este trabajo confirman que la metodología propuesta permite predecir de manera realista las posibilidades de falla para los 2 casos analizados.

Abstract

The thermomechanical behaviour during the quenching process of a centrifugal pump impeller made of white iron is studied in this work. The analysis is carried out using a coupled thermomechanical formulation that is discretized within the context of the finite element method. The material response is described by means of a thermoplastic model that includes phase-change effects. In particular, a heat treatment consisting in cooling from the austenizing temperature is presented with the aim of assessing the failure occurrence of the part at the end of the process. Three different criteria written in terms of the stresses and plastic deformations developed during the cooling stage are specifically compared to evaluate the final mechanical damage. The study is focused on two impeller configurations, with 4 and 5 blades, where fracture occurs in the former during its industrial production. The numerical results obtained in this work for these two cases confirm that the proposed methodology realistically predicts their failure possibilities.

Palabras clave

Proceso de templado ; Simulación termomecánica ; Criterios de falla

Keywords

Quenching process ; Thermomechanical simulation ; Failure criteria

1. Introducción

El proceso de templado es un tratamiento térmico muy utilizado en la industria para mejorar las propiedades mecánicas de piezas fundidas tales como la tensión admisible, la tenacidad y la dureza. En la actualidad, la evolución del comportamiento del material durante dicho proceso se analiza mediante simulación numérica debido a la complejidad de las transformaciones físicas involucradas [1] , [2] , [3] , [4]  and [5] . Tal como se comenta a continuación, la mayor parte de los estudios dedicados a este tema se realizaron en distintos tipos de aceros considerando modelos simplificados de laboratorio con geometrías relativamente sencillas como, por ejemplo, discos, placas y cilindros. Sin embargo, la documentación con respecto a la validación de estos modelos en piezas de carácter industrial es escasa, por lo que es difícil evitar el alto costo que significa la prueba experimental de variadas formas y diseños presentes en una cadena de producción masiva.

Cuando se templan piezas de acero o fundición, la etapa inicial del proceso es la austenización. Diversos autores han estudiado los mecanismos de cambio de fase asociados a dicha etapa, en la que la velocidad de enfriamiento juega un rol fundamental en el desarrollo de microestructuras y tensiones internas [1] , [2] , [3] , [4] , [5] , [6] , [7] , [8] , [9] , [10] , [11] , [12] , [13] , [14] , [15] , [16] , [17] , [18] , [19] , [20]  and [21] . En este contexto, en el que es necesario cuantificar de manera adecuada la liberación de calor latente que ocurre durante la transformación, se incluyó en el análisis el acoplamiento mecánico-microestructural con especial énfasis en el efecto de la transformación plástica inducida en el comportamiento de las tensiones durante el cambio de fase [6] , [7] , [8] , [9] , [10] , [11] , [12] , [13] , [14] , [15] , [16]  and [17] . Dicho análisis se realizó en piezas cilíndricas de diferentes aceros por medio de los siguientes modelos: termoelastoplástico incluyendo deformación debida a la transformación de fase [9] , multifase para la predicción de las microestructuras ferrita, cementita, perlita, bainita y martensita [10]  and [13] , termoelastoplástico con transformaciones difusiva (ley de Johnson-Mehl-Avrami-Kolmogorov junto con la regla aditiva de Scheil) y no difusiva (leyes de Koistinenr-Marburger y Yu) [11] y, además, cinético de conversión de la deformación de transformación a fracciones de fase [12] .

Por otro lado, se han realizado estudios para la determinación de esfuerzos residuales producto del templado en tuberías y piezas cilíndricas [14] , [15] , [16] , [17] , [18] , [19] , [20]  and [21] . Diversos autores revisaron los esfuerzos asociados al cambio de fase y sus transformaciones y, a partir de ello, propusieron algunos principios básicos involucrados en la generación de tensiones internas durante el proceso [14] , [15] , [16]  and [17] . En particular, se ha analizado exhaustivamente mediante simulación numérica la influencia del efecto de la transformación de fase austenita-martensita en el desarrollo de tensiones residuales en aceros suponiendo un modelo de comportamiento termoelastoplástico del material [16] . Los resultados numéricos de este tipo de modelos solo se han podido validar experimentalmente con mediciones de tensiones residuales obtenidas con la técnica de difracción de rayos X en cilindros de acero [17]  and [19] . También se ha estudiado la sensibilidad de ciertas propiedades termomecánicas (por ejemplo, la densidad, el calor específico, la conductividad térmica, los módulos volumétrico y de corte, el límite elástico y el módulo de endurecimiento) y metalúrgicas (por ejemplo, la temperatura y el coeficiente de la transformación martensítica) del material en la distorsión y el nivel de tensiones residuales en una pieza de acero [20] .

Es bien sabido que el proceso de templado afecta a algunas de las propiedades mecánicas del material. Específicamente, se ha predicho la distribución de la dureza final a partir de un modelo basado en la ley de mezclas que tiene en cuenta la composición del material, la distribución final de cada fase y la tasa de enfriamiento local [21] y, más recientemente, se ha propuesto y validado experimentalmente a partir de mediciones obtenidas del ensayo Jominy, un modelo de predicción de dureza y resistencia a la fatiga en aceros [22] . Por último, se han analizado, por medio de la técnica numérica conocida como XFEM, la generación de fisuras durante el proceso de templado en laboratorio de una placa gruesa y su influencia en las tensiones residuales resultantes [23] .

En el presente estudio se simula el proceso industrial de templado de rodetes de fundición blanca por medio de una formulación termomecánica que incorpora efectos de cambio de fase. Dicha formulación, previamente validada en situaciones de laboratorio [24] , se utiliza y extiende en el presente trabajo para predecir fallas en la pieza al final del proceso. Con esa finalidad, se propone evaluar el daño mecánico en régimen no isotérmico aplicando 3 criterios diferentes previamente utilizados en problemas isotérmicos de conformado plástico [25] . Los resultados calculados con estos criterios se comparan para 2 configuraciones distintas de rodetes de bomba centrífuga, con 4 y 5 álabes, obteniendo en la primera de ellas índices mayores de daño, lo que confirma en este caso el hecho observado experimentalmente de presencia de fractura al finalizar el proceso. En la sección 2 se describe de manera sucinta el proceso de templado estudiado. La formulación termomecánica utilizada en el análisis se presenta en la sección 3. Dicha formulación se resuelve en el contexto del método de elementos finitos. La sección 4 detalla los aspectos relacionados con la simulación numérica de dicho proceso. En la sección 5 se presentan y discuten los resultados numéricos obtenidos. Por último, en la sección 6 se resumen las principales conclusiones de este trabajo.

2. Descripción del proceso de templado

El procedimiento industrial de templado seguido por la empresa proveedora del rodete en estudio se inicia austenizando la pieza en un horno especial de aleación Kanthal A1. Para esto, el rodete se lleva a una temperatura de 1.060 °C y se lo mantiene en este estado por un tiempo suficiente (se recomiendan al menos 4 horas de horno), de manera que permita homogeneizar todas las zonas del rodete a dicha temperatura.

A partir del estado homogéneo del material austenizado, se inicia el proceso de templado inyectando aire a presión a través del orificio que se aprecia en la figura 1 durante 10 min hasta alcanzar temperaturas de entre 550 °C y 600 °C. Algunas veces es necesario llevar la pieza nuevamente al horno para homogeneizar la temperatura a esos valores. Posteriormente, el rodete se enfría lentamente al aire por convección natural para finalmente obtener una estructura martensítica al final del proceso.

Figura 1. Rodete preparado para ser templado

La empresa fabricante reportó que el rodete de 4 álabes sufrió fractura por tensiones de origen termomecánico presentando grietas y distorsiones mayores que las admisibles. Esta situación no se vio mejorada al ensayar otras configuraciones para realizar el tratamiento térmico con el objetivo de evitar la fractura de la pieza. En la figura 1 se muestra una de tales configuraciones donde es posible apreciar el aislante (de color blanco) colocado para obtener tasas de enfriamiento diferenciadas en las distintas zonas del rodete. Sin embargo, es importante destacar que el rodete de 5 álabes pudo ser templado sin inconvenientes. Esta diferencia en el comportamiento termomecánico de la pieza fundida motiva el presente estudio.

3. Formulación termomecánica

Una descripción detallada de las ecuaciones básicas y de las relaciones constitutivas de la formulación termomecánica empleada en este trabajo pueden consultarse en [24] . Por otro lado, los criterios de falla adoptados en este estudio, que únicamente fueron utilizados para la evaluación del daño mecánico en problemas isotérmicos de conformado plástico, se basan en los desarrollos reportados en [25] . Por lo tanto, a continuación solo se presentan los aspectos más relevantes de la formulación propuesta para el análisis.

3.1. Ecuaciones fundamentales

Las ecuaciones que gobiernan la evolución de un proceso termomecánico son las ecuaciones de cantidad de movimiento lineal y de balance de energía (en este trabajo se adopta la hipótesis de pequeñas deformaciones, por lo que la ecuación de conservación de masa se satisface idénticamente). Despreciando efectos de inercia y de calor debido a trabajo mecánico, dichas ecuaciones se escriben como:

$\nabla \cdot {\boldsymbol {\sigma }}+\rho {\boldsymbol {b}}_{f}=$${\boldsymbol {0}}$

( 1)

$\rho c{\dot {T}}+\rho L{\dot {f}}_{pc}-\nabla (k\nabla T)=$$0$

( 2)

donde σ es el tensor de tensiones de Cauchy, ρ es la densidad, b_f es la fuerza de volumen específica, c es el calor específico, T es la temperatura, L es el calor latente específico, f_pc es la función de cambio de fase y k es el coeficiente de conductividad térmica. El punto sobre las variables indica derivada temporal y ∇ es el operador gradiente. A estas ecuaciones se le añaden condiciones de contorno termomecánicas, condiciones iniciales para el campo de temperatura y relaciones constitutivas para σ y f_pc . Estas últimas se describen brevemente a continuación.

3.2. Relaciones constitutivas

3.2.1. Modelo termoplástico

Se considera que el comportamiento termoelastoplástico asociado del material es isótropo. Las variables internas adoptadas son la componente plástica del tensor de deformaciones ϵ^p y la función de endurecimiento plástico C^p con las respectivas leyes de evolución:

${\dot {{\boldsymbol {\epsilon }}^{p}}}={\dot {\lambda }}{\frac {\partial F}{\partial {\boldsymbol {\sigma }}}}$

( 3)

${\dot {C}}^{p}=H{\dot {{\overline {\epsilon }}^{p}}}$

( 4)

donde F   es la función de cedencia, ${\textstyle {\dot {\lambda }}}$ es el multiplicador plástico (que se obtiene de la condición de consistencia plástica ${\textstyle {\dot {F}}=0}$ ), H (T   ) es el coeficiente de endurecimiento y ${\textstyle {\overline {\epsilon }}^{p}}$ es la deformación plástica efectiva cuya tasa se define como: ${\textstyle {\dot {{\overline {\epsilon }}^{p}}}={\sqrt {{\frac {2}{3}}{\dot {\boldsymbol {\epsilon }}}^{p}:{\dot {\boldsymbol {\epsilon }}}^{p}}}}$ . Para F se adopta la función de von Mises:

$F={\sqrt {3J_{2}}}-C_{y}-C^{p}$

( 5)

donde J₂ es el segundo invariante del tensor de tensiones desviadoras y C_y (T ) es la tensión de cedencia o límite elástico del material.

En este contexto, la ley constitutiva tensión-deformación secante se escribe como:

${\boldsymbol {\sigma }}=\mathbb {C} :({\boldsymbol {\epsilon }}-$${\boldsymbol {\epsilon }}^{p}-{\boldsymbol {\epsilon }}^{th})$

( 6)

donde ${\textstyle \mathbb {C} }$ es el tensor constitutivo elástico isótropo y ϵ^th es la deformación térmica definida como:

${\boldsymbol {\epsilon }}^{th}=[\alpha (T)(T-T_{ref})-$$\alpha (T_{ref})(T_{0}-T_{ref})]{\boldsymbol {1}}$

( 7)

siendo α el coeficiente de dilatación térmica, T_ref la temperatura de referencia, T₀ la temperatura inicial y 1 el tensor identidad.

3.2.2. Función de cambio de fase

Existen distintos modelos para estudiar el cambio de fase de un material. El material analizado en este trabajo es una aleación, por lo que se considera que el cambio de fase es no isotérmico y puede ser representado por:

$f_{pc}={\begin{array}{ll}0&T<T_{s1}\\{\frac {T-T_{s1}}{T_{s2}-T_{s1}}}&T_{s1}<T<T_{s2}\\1&T>T_{s2}\end{array}}$

( 8)

donde T_{s 1} es la temperatura de «solidus 1»y T_{s 2} es la temperatura de «solidus 2».

3.3. Criterios de falla

Para el presente estudio se utilizan y comparan los siguientes 3 criterios de daño mecánico dúctil:

${\int }_{0}^{{\epsilon }_{f}}{\overline {\sigma }}d{\overline {\epsilon }}^{p}=$$C_{1}$

( 9)

${\int }_{0}^{{\epsilon }_{f}}{\sigma }^{\ast }d{\overline {\epsilon }}^{p}=$$C_{2}$

( 10)

${\int }_{0}^{{\epsilon }_{f}}{\frac {{\sigma }^{\ast }}{\overline {\sigma }}}d{\overline {\epsilon }}^{p}=$$C_{3}$

( 11)

donde ${\textstyle {\overline {\sigma }}={\sqrt {3J_{2}}}}$ es la tensión equivalente o de von Mises y σ^* es la tensión principal máxima. Se aprecia claramente que estos criterios predicen que la falla ocurre para ciertos niveles de trabajo plástico (ecuación 9), de una medida de trabajo plástico realizado por la tensión principal máxima (ecuación 10) y de una medida de deformación plástica (ecuación 11) respectivamente expresados por los parámetros del material C₁ , C₂ y C₃ , los cuales se obtienen, usualmente, por medio de ensayos de tracción uniaxial hasta la deformación a rotura ϵ_f de la probeta.

4. Simulación del proceso de templado

Las geometrías de las piezas a estudiar, que corresponden a las configuraciones de rodetes con 4 y 5 álabes, se obtienen a partir de un modelo CAD 3D. Las dimensiones básicas del rodete se muestran en la figura 2 .

Figura 2. Dimensiones (en m) del rodete.

El material empleado en el rodete industrial corresponde a una fundición blanca de alto contenido en cromo ASTM A532 clase IIIa [26] , perteneciente al grupo de las comúnmente denominadas fundiciones blancas resistentes a la abrasión. En la composición química del material destaca el contenido de cromo, entre 23 y 30%, lo que privilegia la formación de carburos de cromo que brindan alta resistencia al desgaste. Las propiedades mecánicas y térmicas de estas fundiciones dependen de la temperatura y de la composición. En este estudio se adoptan las propiedades recopiladas de [18]  and [19] y que se resumen en las tablas 1 y 2 .

Tabla 1. Propiedades mecánicas de la fundición blanca utilizadas en la simulación computacional del templado

Coeficiente de expansión térmica
T [°C]	α   [${\textstyle {\frac {\mu m}{m\quad {\mbox{°}}C}}}$ ]
20	9.7
45	9.7
200	9.1
300	10.4
400	11.6
500	12.7
Coeficiente de endurecimiento y módulo de Young
T [°C]	H [GPa ]	T [°C]	E [GPa ]
25	35.409	0	180
200	28.472	200	160
675	8.785	667	49
815	4.270	828	25
1135	3.342	1172	3.1
Tensión de cedencia y tensión última a la tracción
T [°C]	Cy [MPa ]	σu [MPa ]
25	225	247.5
200	220	242
675	145	159.5
815	45	49.5
1135	15	16.5
Relación de
Poisson ν	0.3
Densidad ρ   [${\textstyle {\frac {kg}{m^{3}}}}$ ]	7400

Tabla 2. Propiedades térmicas de la fundición blanca utilizadas en la simulación computacional del templado

Calor específico
T [°C]	c   [${\textstyle {\frac {J}{kg\quad {\mbox{°}}C}}}$ ]
20	550
600	778
700	850
740	978
750	700
800	700
1000	978
Conductividad térmica
T [°C]	k   [${\textstyle {\frac {W}{m\quad {\mbox{°}}C}}}$ ]
140	25.3
280	26.3
420	24.4
560	20.6
700	16.9
980	16.9
1175	18.8
Temperatura de referencia Tref [°C]	20
Calor latente específico L   [${\textstyle {\frac {kJ}{kg}}}$ ]	86
Temperaturas solidus Ts 1 , Ts 2 [°C]	760.777

En las simulaciones del proceso de templado de ambos rodetes se considera que la temperatura inicial es uniforme en toda la pieza e igual a la temperatura de austenización reportada por la empresa fabricante de 1060 °C. A partir de esta condición se inicia el proceso de templado que se lleva a cabo en 2 etapas: en primera instancia, por convección forzada provocada por un ventilador de alto flujo con el que se enfría rápidamente el rodete durante 10 min seguida, en segunda instancia, por un proceso de enfriamiento por convección natural durante 32 min. Más específicamente, en la tapa lisa del rodete se supone que solo se produce convección natural durante todo el intervalo de tiempo de análisis (42 min) mientras que en toda su zona interior, que está en contacto con el aire que entra inyectado al rodete durante los primeros 10 min del proceso, se considera la condición de convección forzada. Para modelar esta situación, en las simulaciones se utilizan coeficientes convectivos variables de acuerdo con los modelos de chorro de choque y MacAdams, para los fenómenos de convección forzada y convección natural, respectivamente, incluyendo en ambos casos los efectos de radiación a través de la ley de Stefan-Boltzmann [28] (véase la tabla 3 ).

Tabla 3. Coeficientes peliculares de convección–radiación considerados en la simulación

T [°C]	h   [${\textstyle {\frac {W}{m^{2}\quad {\mbox{°}}C}}]}$ (convección natural)
600	22
860	47
1060	71
h  ${\textstyle [{\frac {W}{m^{2}\quad {\mbox{°}}C}}]}$ (convección forzada)
250

La formulación termomecánica presentada en la sección 3 se resuelve en el contexto del método de elementos finitos. Los detalles de la correspondiente formulación discretizada del problema se pueden consultar en [24] . Las ecuaciones acopladas (1) y (2) se resuelven por medio de un esquema alternado isotérmico que garantiza la estabilidad de la solución.

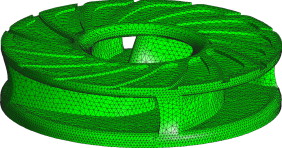
Para la discretización espacial se utilizan elementos tetraédricos isoparamétricos estándar (con 3 puntos de integración) resultando mallas de 109.349 elementos (27.723 nodos) para el rodete de 4 álabes y de 113.792 elementos (28.498 nodos) para la geometría de 5 álabes. Es importante mencionar que el uso de este tipo de elementos se justifica en el hecho de que, tal como se reporta en [24] , estos no presentan, para la formulación termomecánica descrita en la sección 2, el problema de bloqueo de la solución numérica debido al efecto de la incompresibilidad del flujo plástico. De manera ilustrativa, en la figura 3 se muestra el mallado para el rodete de 4 álabes.

Figura 3. Malla de elementos finitos para el rodete de 4 álabes.

La discretización temporal de las ecuaciones (2), (3) y (4) se realiza utilizando el método implícito de Euler con pasos de tiempo variables (una alternativa a este método es el propuesto en [27] ): Δt  = 20 s para el intervalo de tiempo 0 min <t  < 10 min en el que se inyecta el chorro de aire y Δt  = 60 s para 10 min<t < 42 min para el enfriamiento final.

5. Presentación y discusión de resultados

Para la evaluación del estado termomecánico y su consecuencia sobre las posibles causas de defectos en los rodetes estudiados, se analiza la sección correspondiente al plano, medio del rodete para las configuraciones de 4 y 5 álabes (fig. 2 ). Se grafica, en particular, la evolución de temperatura, la tensión de von Mises y la deformación plástica efectiva en un punto ubicado en el extremo de los álabes de dicho plano ya que en las cercanías del mismo se observaron, tal como se comentó anteriormente, grietas al final del proceso de templado para la configuración de 4 álabes. Estas curvas se muestran para ambas configuraciones en las figuras Figura 4  and Figura 5 y 6 , respectivamente.

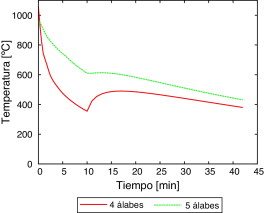
En los resultados de la figura 4 se aprecian claramente las 2 etapas de enfriamiento, por convección forzada (los primeros 10 min) y por convección natural (los últimos 32 min), a las que se somete a la pieza durante el proceso de templado. Las curvas muestran que el rodete de 4 álabes se enfría más rápidamente que el de 5 debido a que en este último la inercia térmica es mayor por poseer más masa que el primero. Además, se observa al inicio de la segunda etapa que la conducción prevalece sobre la convección logrando, de esta manera, una distribución más homegénea de temperatura en la pieza a medida que avanza el proceso.

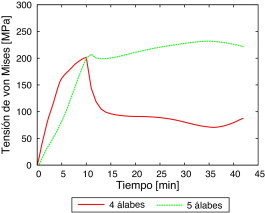
En la figura 5 se ve que los niveles de tensión alcanzados en la primera etapa del templado son similares para los 2 rodetes, mientras que en la segunda etapa, por el contrario, las respuestas tensionales son completamente diferentes, siendo la configuración de 5 álabes la que presenta mayores valores de ${\textstyle {\overline {\sigma }}}$ . Sin embargo, es importante notar que, de acuerdo a los criterios de falla descritos en la sección 3.3, esta variable por sí sola no es buen indicador del daño ya que, cuanto mayor sea la temperatura, más disminuye la tensión de cedencia (a este efecto se lo conoce habitualmente como ablandamiento térmico), por lo que zonas a altas temperaturas plastifican a niveles de esfuerzos muy inferiores al máximo. Por esta razón, para la evaluación del daño deben analizarse en forma conjunta tanto la evolución de T   como la de ${\textstyle {\overline {\sigma }}}$ . Esto es especialmente acentuado en las zonas centrales de los álabes donde, tal como se mostrará más adelante, se produce menor disipación de calor en comparación con los bordes en contacto con el ambiente.

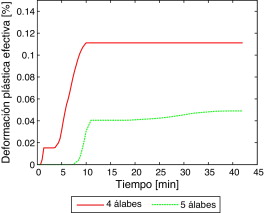
Las curvas graficadas en la figura 6 muestran claramente que la deformación plástica solo evoluciona de manera importante en la primera etapa del proceso de enfriamiento y, más específicamente, al final de la misma donde, aun para temperaturas altas (fig. 4 ), los valores de la tensión de von Mises son los mayores (fig. 5 ), producto de la contracción térmica que sufre la pieza. Se aprecia que en el rodete de 4 álabes se generan mayores deformaciones que en el de 5 álabes donde este último presenta, a diferencia del anterior, un pequeño aumento de esta variable al final del proceso.

Figura 6. Evolución de la deformación plástica efectiva en el plano medio del rodete en el extremo externo de un álabe para las configuraciones de 4 y 5 álabes.

Figura 4. Evolución de la temperatura en el plano medio del rodete en el extremo externo de un álabe para las configuraciones de 4 y 5 álabes.

Figura 5. Evolución de la tensión de von Mises en el plano medio del rodete en el extremo externo de un álabe para las configuraciones de 4 y 5 álabes.

Las distribuciones de temperatura, tensión de von Mises y deformación plástica efectiva para el tiempo final del análisis en el plano medio del rodete para ambas configuraciones de álabes se presentan en las figuras 7 , 8 y 9 , respectivamente.

La figura 7 muestra que en los álabes la distribución de la temperatura es no homogénea en las zonas centrales donde se registran los puntos más calientes. Si bien el rodete de 4 álabes, como se comentó, presenta menores temperaturas en los bordes que el rodete de 5 álabes, en su interior se produce la tendencia contraria. El efecto de alcanzar mayores temperaturas en la configuración de 4 álabes tiene como consecuencias una disminución de la tensión de fluencia y una mayor suceptibilidad a la falla.

Figura 7. Distribución de temperatura [°C] para el tiempo final del análisis (42 min) en el plano medio del rodete para las configuraciones de: a) 4 y b) 5 álabes.

En la figura 8 se ve que los valores altos de la tensión de von Mises solo se sitúan en los extremos externos de los álabes. Dichos valores son mayores, tal como también se ilustra en la figura 5 , en el caso del rodete de 5 álabes. Sin embargo, en este último caso el valor de la tensión de cedencia es más alto ya que el rodete experimenta menores temperaturas.

Figura 8. Distribución de tensiones de von Mises [MPa ] para el tiempo final del análisis (42 min) en el plano medio del rodete para las configuraciones de: a) 4 y b) 5 álabes.

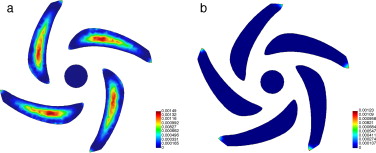
La figura 9 muestra que la distribución de la deformación plástica efectiva es bien diferente para ambas configuraciones: no homogénea y uniforme para los rodetes de 4 y 5 álabes, respectivamente. La uniformidad de la deformación plástica es consecuencia de que las zonas más calientes del rodete de 5 álabes están sometidas a menores esfuerzos (véanse las figs. 7 y 8 ).

Figura 9. Distribución de deformación plástica efectiva para el tiempo final del análisis (42 min) en el plano medio del rodete para las configuraciones de: a) 4 y b) 5 álabes.

Para evaluar la criticidad de falla en el plano medio del rodete se calculan, de acuerdo con los criterios presentados en la sección 3.3, las tensiones y deformaciones plásticas en el extremo externo de un álabe para ambas configuraciones de rodetes. Para los 3 criterios utilizados, se aprecia en la tabla 4 que la configuración de 4 álabes es la más propensa a fallar. Esto está de acuerdo, tal como se comentó anteriormente, con las observaciones realizadas por el fabricante al final del proceso industrial de templado. Cabe destacar que estos criterios de falla predicen de manera más realista la probabilidad de daño mecánico que un criterio basado exclusivamente en el nivel de deformación plástica efectiva que, para este material, predeciría una potencial fractura para niveles de deformación del orden de 1 % [26] , valor que, como se observa en la figura 6 , es muy superior a los alcanzados en los puntos críticos analizados. Es importante destacar, por último, que los criterios de daño empleados en este trabajo constituyen una herramienta de predicción de las zonas con alta probabilidad de falla que permitiría analizar y eventualmente rediseñar el tratamiento térmico con el objeto de producir una pieza sana que opere adecuadamente en condiciones de servicio.

Tabla 4. Valores de los criterios de daño en el plano medio del rodete en el extremo externo de un álabe para las configuraciones de 4 y 5 álabes

	C1 [MJ /m3 ]	C2 [MJ /m3 ]	C3
4 álabes	0,1783	0,2336	0,1458
5 álabes	0,0961	0,1002	0,0005

6. Conclusiones

En este trabajo se analizó el proceso de templado de 2 configuraciones de álabes de un rodete de una bomba centrífuga industrial fabricada en fundición blanca con la finalidad de predecir las condiciones de ocurrencia de falla en la pieza al final del proceso. La respuesta termoplástica del material durante dicho tratamiento térmico se describió mediante una formulación termomecánica acoplada cuya discretización se realizó en el contexto del método de elementos finitos. Se compararon 3 criterios diferentes para la determinación del daño mecánico. Los resultados numéricos obtenidos en este trabajo proporcionaron una predicción realista de las posibilidades de falla para los 2 casos estudiados.

Agradecimientos

Los autores agradecen el apoyo de CONICYT (Comisión Nacional de Investigación Científica y Tecnológica de Chile) a través del Proyecto Fondecyt No. 1130404 y a la empresa Fundición y Maestranza Neptuno.

References

1. [1] S. Denis, E. Gautier, A. Simon, G. Beck; Stress-phase-transformation interactions-basic principles, modelling, and calculation of internal stresses; Mater. Sci. Technol., 1 (10) (1985), pp. 805–814
2. [2] J. Mackerle; Finite element analysis and simulation of quenching and other heat treatment processes: A bibliography (1976-2001); Comput. Mater. Sci., 27 (3) (2003), pp. 313–332
3. [3] L. Huiping, Z. Guoqun, N. Shanting, H. Chuanzhen; FEM simulation of quenching process and experimental verification of simulation results; Mater. Sci. Eng., A, 452 (2007), pp. 705–714
4. [4] V. Srinivasan, K.M. Moon, D. Greif, D.M. Wang, M.H. Kim; Numerical simulation of immersion quenching process of an engine cylinder head; Appl. Math. Modell., 34 (8) (2010), pp. 2111–2128
5. [5] C. Agelet de Saracibar, R. López, B. Ducoeur, M. Chiumenti, B. de Meester; Un modelo numérico para la simulación de disolución de precipitados en aleaciones de aluminio con endurecimiento utilizando redes neuronales; Rev. Int. Métodos Numér. Cálc. Diseño Ing., 29 (1) (2013), pp. 29–37
6. [6] F.M.B. Fernandes, S. Denis, A. Simon; Mathematical model coupling phase transformation and temperature evolution during quenching of steels; Mater. Sci. Technol., 1 (10) (1985), pp. 838–844
7. [7] J.B. Leblond; Mathematical-modeling of transformation plasticity in steels. 2: Coupling with strain-hardening phenomena; Int. J. Plast., 5 (6) (1989), pp. 573–591
8. [8] E. Prieto Silva, P.M.C. Lopes Pacheco, M.A. Savi; On the thermo-mechanical coupling in austenite-martensite phase transformation related to the quenching process; Int. J. Solids Struct., 41 (3) (2004), pp. 1139–1155
9. [9] S.H. Kang, Y.T. Im; Three-dimensional thermo-elastic-plastic finite element modeling of quenching process of plain-carbon steel in couple with phase transformation; Int. J. Mech. Sci., 49 (4) (2007), pp. 423–439
10. [10] W. Porto de Oliveira, M.A. Savi, P.C.M. Lopes Pacheco, L.F. Guimarães de Souza; Thermomechanical analysis of steel cylinders quenching using a constitutive model with diffusional and non-diffusional phase transformations; Mech. Mater., 42 (1) (2010), pp. 31–43
11. [11] P. Carlone, G.S. Palazzo; Development and validation of a thermo-mechanical finite element model of the steel quenching process including solid-solid phase changes; Int. Appl. Mech., 46 (8) (2011), pp. 955–971
12. [12] M. Jung, M. Kang, Y.K. Lee; Finite-element simulation of quenching incorporating improved transformation kinetics in a plain medium-carbon steel; Acta Mater., 60 (2) (2012), pp. 525–536
13. [13] W. Porto de Oliveira, M.A. Savi, P.M.C. Lopes Pacheco; Finite element method applied to the quenching of steel cylinders using a multi-phase constitutive model; Arch. Appl. Mech. (2013), pp. 1–25
14. [14] T. Ericsson, S. Sjostrom, M. Knuuttila, B. Hildenwall; Predicting residual stresses in cases - Case-hardened steels: microstructural and residual stress effects; D.E. Diesburg (Ed.), TMS/AIME (1984), pp. 113–139
15. [15] D. Maijer, S. Cockcroft, A. Jacot; Modeling of microstructure and residual stress in cast iron calender rolls; Metall. Mater. Trans. A, 31 (4) (2000), pp. 1201–1211
16. [16] E. Prieto Silva, P.M.C. Lopes Pacheco, M.A. Savi; Finite element analysis of the phase transformation effect in residual stresses generated by quenching in notched steel cylinders; J. Strain Anal. Eng. Des., 40 (2) (2005), pp. 151–160
17. [17] C. Şimşir, C.H. Gür; A simulation of the quenching process for predicting temperature, microstructure and residual stresses; Stroj. Vestn-J. Mech. E., 56 (2) (2010), pp. 93–103
18. [18] E. Macherauch, H.J. Yu, U. Wolfsteig; Calculation of residual stresses with a special finite element program; Arch. Eisenhüttenw., 49 (1978), pp. 499–552
19. [19] C. Şimşir, C.H. Gür; 3D FEM simulation of steel quenching and investigation of the effect of asymmetric geometry on residual stress distribution; J. Mater. Process. Technol., 207 (1) (2008), pp. 211–221
20. [20] A.K. Nallathambi, Y. Kaymak, E. Specht, A. Bertram; Sensitivity of material properties on distortion and residual stresses during metal quenching processes; J. Mater. Process. Technol., 210 (2) (2010), pp. 204–211
21. [21] P. Carlone, G.S. Palazzo, R. Pasquino; Finite element analysis of the steel quenching process: Temperature field and solid-solid phase change; Comput. Math. Appl., 59 (1) (2010), pp. 585–594
22. [22] B. Smoljan, D. Iljkić, L. Pomenić; Mathematical modelling and computer simulation of mechanical properties of quenched and tempered steel; Int. J. Microstruct. Mater. Prop., 8 (1) (2013), pp. 97–112
23. [23] E. Feulvarch, M. Fontaine, J.M. Bergheau; XFEM investigation of a crack path in residual stresses resulting from quenching; Finite Elem. Anal. Des., 75 (2013), pp. 62–70
24. [24] D. Celentano, D. Gunasegaram, T. Nguyen; A thermomechanical model for the analysis of light alloy solidification in a composite mould; Int. J. Solids Struct., 36 (16) (1999), pp. 2341–2378
25. [25] F. Ozturk, D. Lee; Analysis of forming limits using ductile fracture criteria; J. Mater. Process. Technol., 147 (2004), pp. 397–404
26. [26] AS.M. Handbook; Properties and selection: irons, steels, and high performance alloys; ASM international, 1 (1990), pp. 140–194
27. [27] P. Becker, N. Nigro, S. Idelsohn; Integración temporal explícita con grandes pasos de tiempo de la ecuación de transmisión del calor; Rev. Int. Métodos Numér. Cálc. Diseño Ing., 28 (4) (2012), pp. 187–197
28. [28] F.P. Incropera, D.P. DeWitt, R. Cruz; Fundamentos de transferencia de calor; Prentice Hall, México (1999)