Summary
Derived from simplifications of the Saint-Venant equations, the kinematic wave model has the ability to describe the behavior of surface runoff in watersheds. This paper aims to obtain the numerical simulation of the flow routing in a natural watershed, by using lattice Boltzmann method. In the computational model, the surface of the basin will be represented by a V-shaped segmented in two lateral planes and one main channel. The simulation considers the effective precipitation flowing on the watershed per unit of width at the exit of each of the planes that represent the surface of the basin. The water flowing from the planes enters the main channel in the form of lateral contribution. Hydrograms of two rain events are obtained, which present the volume drained in the outlet corresponding to the whole basin in each event. Two equilibrium distribution functions were developed by Chapmann-Enskog expansion at time scales and model D1Q3, one suitable for flow on the basin surface and another for the main channel, in order to obtain the variables of interest in each case. The numerical results obtained were compared with the KINEROS2 hydrological model.
1 Introduction
The use of numerical methods in hydrodynamics problems enables simulating the runoff behavior of a fluid, obtaining results that are sufficiently close to those observed. The phenomena related to fluid movement may be very complex. Besides theoretical analyses and experimental methods, a third alternative to analyze fluid dynamics is numerical simulation [1]. In this sense, LBM is effective and flexible to simulate flows, especially when they are complex geometries The method is characterized by involving simple calculations, it presents intrinsic characteristics of parallel processing and is easily applied to boundary conditions. Originating in cellular automata, of the type with a gas network (LGCA- Lattice Gas Cellular Automata), the method describes the microscopic movement of particles and, at the macroscopic level it gives a correct average description of a fluid [2]. LBM takes a different approach compared to traditional numerical methods (finite volumes [3], finite differences [4], method of characteristics [5], finite elements [6]), LBM is an indirect way to solve the governing equations of the runoff. LBM does not use discretization of the macroscopic equations, it is based on microscopic models and equations that govern kinetics at a mesoscopic level. In LBM the macrosocopic dynamic of a fluid is the result of the collective behavior of microscopic articles and does not change with the underlying details referring to molecular interactions of fluid [7]. In recent years, the method has been studied by many researchers and became a field of research with a great potential for computer fluid dynamics. Runoffs involving shallow waters and the kinematic wave model were covered by LBM and the simulations presented good results [8,9,10,11,12,13,14,15].
Runoff on a free surface is governed by the Saint-Venant equations. However, elaborate numerical techniques and a large amount of hydraulic information are necessary to solve them. In an attempt to reduce the quantity of data needed and the numerical difficulty in solving the differential equations, simplifications of the Saint Venant equations are used, such as the kinematic wave model which is also called hydraulic model of flood wave routing [16].
The kinematic wave model is applied to describe surface runoffs in river basins and natural watercourses. The focus of interest in this work, river basins are a natural system that requires monitoring to forecast their behavior in actions such as extreme precipitations, floods, droughts and others. Analyzing these events, it is possible to manage the water and energy resources, avoid soil degradation, thus offering adequate planning for the rural, urban and industrial space [17].
LBM is used to simulate surface runoff in a natural river basin that is governed by the equations of the kinematic wave model. The contribution of the present paper lies in the use of two equilibrium functions, one appropriate to runoff on planes that represent the surface of the basin, and the other for the channel segment that represents the main channel. Each equilibrium distribution function was constructed in such a way as to recover the equations of the kinematic wave model adapted to flow in the channel and on the planes, and they were obtained by means of a Chapmann-Enskog expansion on time scales. The boundary conditions are established in such a way that initially there is no runoff in the basin. After precipitation begins, the water that runs off on the lateral planes generates hydrographs that are used for the lateral inflow of water to the main channel.
The work is structured as follows. Section 2 presents the equations governing runoff. Then in section 3, is the numerical method that will be used to simulate the case study presented in section 4. The numerical simulations are detailed in section 5 and the conclusions are in section 6.
2 Runoff Equations
The Saint-Venant equations govern runoff where there is a free surface, under the assumption that the vertical and cross-sectional component of runoff velocity can be neglected regarding the longitudinal components [18]. This description is appropriate for long wave systems, in which the length of the wave is much greater than the depth. The one-dimensional Saint Venant equations form a system of non-linear equations composed by the continuity equations 1 and quantity of momentum 2,
|
where is discharge, is the cross-section area, is the acceleration of gravity, is time, is the spatial coordinate, is the bottom slope and represents the energy line slope.
A large quantity of hydraulic data and elaborate numerical techniques are required to solve complete Saint-Venant equations, especially if they are applied to surface runoff in river basins or in natural rivers [16].
In flow in river basins, the kinematic wave model is used as a simplification of the Saint Venant equations. This model considers the continuity equation and the equation of quantity of momentum, neglecting the terms of pressure and inertia. This results in the equation of quantity of momentum [19],
|
|
(3) |
The kinematic wave model is based mainly on the continuity equation, and there is an approach to the equation of quantity of momentum using a uniform flow formula. Defining the slope of the energy line , with a uniform flow formula, equation 3 can be represented for runoff in a channel or surface runoff using a relationship of power of the form [20],
|
|
(4) |
in which and are coefficients determined by the flow characteristics. This non-linear model considers the variability of the parameters according to flow. Thus flow in reaches of the basin channels is given by the equations,
|
|
(5) |
where is the lateral contribution, e are parameters to be determined.
The inital and boundary conditions in the channels are determined by flow hydrographs resulting from runoff on the surface and in channel reaches upstream.
The basin surface is approached by planes. Thus, considering that the continuity equation 1 describes runoff in a prismatic and rectangular channel, the runoff equations for the planes that describe the basin surface are,
|
|
(6) |
where is discharge per unit of width, is depth, is the effective precipitation, and are parameters to be determined.
The initial and boundary conditions are represented by,
|
|
(7) |
where is slope length.
Applying the kinematic wave model in surface runoff is different from applying it in rivers only as regards the medium where runoff occurs. As to roughness, Manning's hydraulic resistance is used. In the case of equation (6), and , where is surface slope and is Manning's roughness coefficient.
3 Lattice Boltzmann Method
LBM considers molecular dynamics of fictitious particles in which space, time and velocities are discrete. The fictitious particles travel from point to point in the grid in discrete times, and meet at these points at the end of each time step and exchange quantities of movement and energy. As regards the velocity modules, they assume continuous values. On the other hand LBM can be seen as a simplified form of the Boltzmann kinetic equation in which only the essential molecular details to recover correct macroscopic behavior are maintained [21].
Four main elements characterize LBM: the governing equation, the collision operator, the lattice and the equilibrium distribution function [8].
3.1 LBM Equation and BGK Operator
Initially the governing equation of LBM (8) is presented with a BGK collision operator. This form for the collision operator had already been used by Bhatnagar, Gross and Krook [22] to simplify the Boltzmann kinetic equation. Equation (8) has two phases: transmission and collision. During the transmission phase, the particles move from a node in the mesh to one of the neighboring nodes, and the direction is given by velocity. During the collision phase the particles which arrive at the same node interact with each other and change their directions according to the guidelines of the collision operator [23],
|
|
(8) |
where is the distribution function of particles and represents the probability of a particle going in a given direction, is the equilibrium distribution function, is the position of the node in the mesh, is the instant in time, is the mesh spacing, is the increment in time, are the possible directions of movement in the mesh, is the force term, is the collision term and is the relaxation parameter.
3.2 Lattice D1Q3
In LBM the lattice has the function of repesenting the points on the mesh and determining the directions of particle movement. The finite directions and those determined for the movement of the particles define a microscopic model for molecular dynamics. When choosing the lattice to be used, it is essential to observe its symmetry. The lattice must be able to represent the macroscopic equations [8].
In the work by Qian et al. [24], a family of lattices can be found called , where indicates the -dimensional space and the directions of movement of the particle distributions.
According to Liu et al. [13], model has a one-dimensional structure with a null velocity and two velocities in opposite directions; it has two directions for the movement of fluid particles, which move to the neighboring nodes to the left or to the right. The figure 1 shows the lattice with velocities , and , where is the velocity in the lattice.
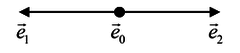
|
| Figure 1: Lattice D1Q3. |
3.3 C. Multi-scale Expansion
A multi-scale expansion must be applied to make the connection between mesoscopic scale, in which LBM is inserted, and the macroscopic scale of the governing equations. The expansion most used is the Chapmann-Enskog expansion [25], which considers time and space scales so that the governing equation of runoff will be derived from the LBE.
In order not to have negative distribution functions associated with the kinematic wave equation, which is against the laws of physics, only the time coordinate should be attributed to multi-scale expansion [11]. Thus, applying three scales to the time coordinate, the differential forms for the space and time coordinate are as follows,
|
|
(9) |
where e are time scales and is the Knudsen number. The Knudsen number is a non-dimensional measure defined as the ratio between the molecular mean free path length and a physically representative scale of length.
Expanding around the equilibrium distribution function with a small we have,
|
|
(10) |
where and is the non-equilibrium distribution function.
The expansion in equation 8 in a second order Taylor series, and considering , results in,
|
|
(11) |
where,
|
|
(12) |
Based on the time scales and on the expansion , equations 9 and 10, respectively, and comparing all orders of , lattice Boltzmann equations are determined with different orders of magnitude
|
Equations 13, 14 and 15 will be used to obtain the moments of the equilibrium distribution function.
3.4 Equilibrium Distribution Function
The equilibrium distribution function, together with the Lattice Boltzmann equation 8 perform an essential role which is to recover the macroscopic equation of fluid. Then the one-dimensional kinematic wave equation 5 is recovered and its equilibrium distribution function is determined. All calculations will be presented to obtain the equilibrium distribution function for the channel. The calculations for obtaining the equilibrium distribution function for the plane are analogous.
Assuming that the distribution function is close to equilibrium in the local sphere, we have that,
|
|
(16) |
in this way, applying the sum total on both sides of the equation 10 and considering 16, we obtain,
|
|
(17) |
Substituting equation 14 into equation 15 results in,
|
|
(18) |
Taking the sum on the directions of the lattice in equations 14 and 18 we have, respectively,
|
|
(19) |
|
|
(20) |
The kinematic wave equation is a special case of Burgers' equation. Burgers' equation is a non-linear convection-diffusion equation [26]. It is an important equation in fluid mechanics which represents phenomena described by and equilibrium between the evaluation of time, the non-linearity and the diffusion, and it appears in various physical problems.
The one-dimensional Burgers' equation can be written as follows [26,11],
|
|
(21) |
where is a function that may represent a real quantity, such as height, flow or cross-section area, is the diffusion coefficient, and are the parameters to be determined, and represents the external effect or external force.
Comparing equation 19 to equation 21 we have,
|
|
(22) |
|
|
(23) |
The substitution of equations 22 and 23, respectively into 19 and 20 results in,
|
|
(24) |
|
|
(25) |
By substituting equation 24 into equation 25 and comparing the modified equation 25 with equation 21 we have,
|
|
(26) |
Burgers' equation with the force term 21 is recovered restoring the time scales and for the time scale . For this we have 14 15,
|
|
(27) |
Substituting equations 19, 23, 24 and 25 into equation 27 and organizing the terms, we obtain,
|
|
(28) |
Comparing equation 28 with 21, the force term is determined,
|
|
(29) |
Taking the mean value in each direction of velocity of lattice , the force term is recovered,
|
|
(30) |
Assuming that the external force is the liquid rate of inflow per unit width of the channel, we obtain,
|
|
(31) |
Equation 28 is also different from equation 21 because of the multiplication of in . In order to eliminate equation 26 is altered to the form,
|
|
(32) |
in which,
|
|
(33) |
Thus, Burgers' equation 21 with a second order truncation error is recovered.
Assuming that in Burgers' equation, we have the kinematic wave equation since in the kinematic wave model there is no diffusion. The equilibrium distribution function is determined by the resolution of the system of equations formed by moments 22, 23 and 32. Taking into account the velocity directions of model , and substituting by the channel cross-section area , the equilibrium distribution function associated with equation 5 is obtained,
|
The same development can be applied to determining the equilibrium distribution function for equation 6 of the basin surface and external force [11],
|
|
|
(36) |
3.5 Boundary Conditions
The adequate representation of the physical characteristics of the problem, by means of initial and contour conditions, is a crucial factor for simulation stability and precision. Figure 2 illustrates a mesh to discretize the problem domain, which defines the entry and exit from a channel and the lattice velocity directions.
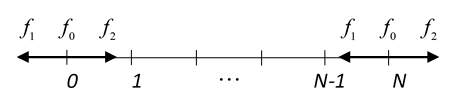
|
| Figure 2: Computational mesh |
The macroscopic boundary conditions for both surface flow and channel flow are known at the left border but unknown at the right border. The macroscopic behavior at the borders is achieved by the correct application of the particle distribution functions. For this purpose, the equilibrium distribution functions are determined by extrapolation [11]. The distribution functions in the left border nodes are given by,
|
and, para os for the right border nodes we have,
|
where is the velocity distribution function of the particles after transmission, is the velocity distribution function of the particles before transmission, is the macroscopic variable at the border, which may be substituted by or and represents the node of the computational mesh at the right border.
3.6 Estability
According to Sterling and Chen [27], it is not possible to ensure the stability of LBM and this is due to the large quantity of parameters that prevent its complete characterization. However, Zhou [8] states that for flows governed by the equations of Saint-Venant, in general, the LBM is stable if the following conditions are satisfied.
In the LBM, the kinematic viscosity , is related to the relaxation parameter by the equation,
|
|
(39) |
The kinematic viscosity is a property of the fluid with positive value, so the relaxation parameter must satisfy,
|
|
(40) |
The magnitude of the physical velocity resulting from the fluid must be smaller than the velocity in the lattice,
|
|
(41) |
For celerity , it is restricted,
|
|
(42) |
Finally, the LBM is applicable to subcritical flows, which can be expressed by the inequality,
|
|
(43) |
where is the number of Froude.
Because the kinematic wave model is a simplification of the Saint-Venant equations, the presented stability conditions were also fulfilled in the simulation of flow in the watershed. The only change made was for celerity, since while in the flow in channels with the equations of Saint-Venant the celerity is represented by , in the flow in rectangular channel by the kinematic wave model, with the Manning's formula, the celerity is described by [16],
|
|
(44) |
4 Case Study: Flow in a Natural Watershed
The watershed consists of a well-defined area that is a catchment for water from precipitation that makes flows converge to a watercourse. In the river basin, flow is divided into surface runoff and channel flow. In surface runoff the water runs on the river basin surface until it finds a watercourse. This displacement occurs as the result of precipitated water that was not intercepted by the plant cover and by the part that did not infiltrate into the soil. Due to the great spatial heterogeneity, the river basin surface is represented by planes where shallow surface runoff takes place. The lateral contribution to the channels is given mainly by precipitation that occurs over each plane [19].
This study looks at the natural basin shown in Figure 3 with a 0.834 area. The main watercourse is long and divides the basin more or less in half. There are other smaller waterways but most of the catchment flow is formed by the surface runoff that reaches the main channel. In this way, the basin is approached by a V-shaped and segmented by two equally sized planes and a channel segment, as illustrated in Figure 4. The Manning's coefficients, slopes and dimensions of the segments are listed in Table 1.
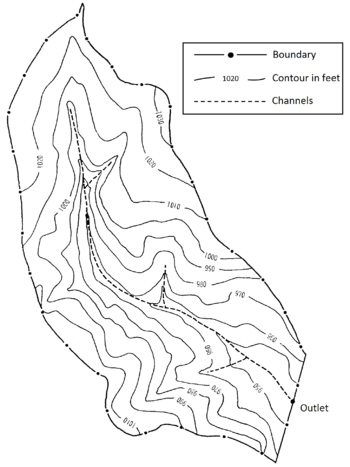
|
| Figure 3: Natural watershed |
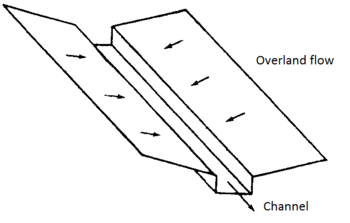
|
| Figure 4: Watershed segmentation |
|
Segment |
Lenght L(m) |
Width b(m) |
Manning's |
Slope |
|
Plane 1 |
308.9 |
1,350 |
0.15 |
0.05 |
|
Plane 2 |
308.9 |
1,350 |
0.15 |
0.05 |
|
Channel |
1,350 |
3 |
0.15 |
0.012 |
Two rainfall events, called event and event were considered to simulate the surface runoff in a river basin using LBM. For this records of excess precipitation that occurred in the river basin shown in Figure 3 at an interval of five years of measurements were utilized. These data are presented by Stephenson and Meadows [28]. In the first event only rainfall intensity is used, 12.7 with a time duration of 1.2 , which is the same event described by Stephenson and Meadows [28], in which the authors apply graphic methods to obtain the hydrographs at the outlet of the river basin. In the second event data of four intervals of excess precipitation are used. These values are shown in Table 2.
|
Event |
Rainfall duration |
Excess rainfall |
|
1 |
1.2 |
12.70 |
|
1.0 |
13.99 | |
|
2 |
0.6 |
17.55 |
|
1.2 |
12.70 | |
|
1.4 |
11.63 |
5 Results and Discussion
In both the rainfall events, the parameters used in LBM are the same and are summarized in Table 3, being the number of lattices that discretize each plan and the channel segment.
| Segment | ||||||
| Plane 1 | 308.9 | 62 | 5 | 0.95 | 5 | 1 |
| Plane 2 | 308.9 | 62 | 5 | 0.95 | 5 | 1 |
| Channel | 1,350 | 270 |
The number of iterations performed in event was , which corresponds to a time of hours. For event the number of iterations performed was corresponding to a time of hours. Compiler GNU Fortran (GCC) was used in a computer with a , processor and of RAM memory, and the operational system Windows 10. The processing time used for each event was less than minute.
The results obtained by LBM are compared to the KINEROS2 model (Kinematic Runoff and Erosion Model) which was developed at the end of the 1960s by the USDA (United States Department of Agriculture). KINEROS2 is a distributed kinematic rainfall-runoff-erosion model with a physical base that can be applied to river basins where surface runoff is predominant. The basin is represented by a cascade of planes and channels on which the flow is routed from top to bottom using a solution of finite differences of the one-dimensional kinematic wave equations [29].
The hydrographs in Figure 5 and Figure 6 show the volume of outflow corresponding to the entire basin at each event simulated. The results obtained by LBM and KINEROS2 (KIN) are illutrated in Table 4, which supplies, for each event , the values of the peak discharge and the time when the peak occurs , the expected discharge and the discharge calculated at the outlet , and the relative error among these flows.
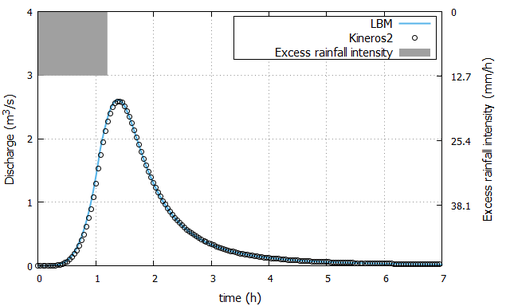
|
| Figure 5: Hidrograph of event 1. |
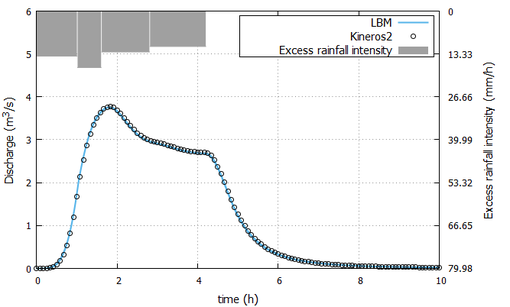
|
| Figure 6: Hidrograph of event 2. |
| Model | (%) | |||||
| 1 |
LBM |
2.61 |
82.93 |
12710.17 |
12340.93 |
2.99 |
|
KIN |
2.59 |
83.92 |
12710.17 |
12162.45 |
4.50 | |
| 2 |
LBM |
3.76 |
108.20 |
46739.04 |
46169.90 |
1.23 |
|
KIN |
3.78 |
109.17 |
46739.04 |
46174.68 |
1.22 |
The peak flow values shown in Table 4 corresponding to event 1 are smaller than that calculated by Stephenson and Meadows [28] which is 2.70 . This difference is attributed to the fact that the authors use graphic methods to calculate the hydrograph.
The hydrographs shown in figures 5 and 6 and the results listed in Table 4 show that LBM and KINEROS present excellent concordance in the simulation of the surface runoff in the river basin shown in this paper.
6 Conclusion
A model based on LBM was proposed, in which two equilibrium distribution functions are used, one appropriate for runoff on planes that represent the basin surface, and the other for the channel segment that represents the main channel. Each equilibrium distribution function was constructed so as to recover the equations of the kinematic wave model adapted to flow in the channel and on the planes, and they were obtained by means of a Chapmann-Enskog expansion in time scales. The equilibrium distribution function constructed for the channel allowed obtaining the area of the cross-section of the channel and, based on the area the flow was obtained by equation 5 with the Manning's formula. The equilibrium distribution function constructed for the planes supplied water depth and, based on depth, flow per unit of width was obtained by equation 6, also with Manning's formula. As a result, we have the hydrograph of a hydrographic basin for the two events chosen.
The simulations obtained from the model proposed in this paper show excellent concordance with the hydrological model KINEROS2 as to peak flow, the temporal distribution of the flows and also the total volume of outflow. Therefore, the model proposed proved adequate and precise to simulate surface runoff in a river basin. It is observed that the calculated values of the volume at watershed outlet are less than the volume expected. This is due to the numerical diffusion present in simulation. The study performed in this paper can be extended to larger basins and it is necessary to consider a larger quantity of segments of planes and channels in order to improve the representation of the basin characteristics.
Bibliography
[1] A. de O. Fortuna, Técnicas Computacionais para Dinâmica de Fluidos. Edusp, São Paulo, Brasil, 2012.
[2] J. G. Zhou, A lattice Boltzmann model for the shallow water equations, Computer Methods in Applied Mechanics and Engineering 191 (2002) 3527-3539.
[3] E. Bladéa, L. Cea, G. Coresteina, E. Escolanoc, J. Puertas, E. Vázquez-Cendónd, J. Dolz, A. Coll, Iber: herramienta de simulación numérica del flujo en ríos, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería 30 (1) (2014) 1-10.
[4] F. U. Prieto, J. J. B. Muñoz, L. G. Corvinos, E. S. Casino, A. C. Acevedo, Estudio de la estabilidad y dispersión del problema de propagación de ondas sísmicas en 2-d utilizando el método de diferencias finitas generalizadas, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería 27 (4) (2011) 269-277.
[5] A. M. Lobeiro, Solução das Equações de Saint-Venant em Uma e Duas Dimensões Usando o Método das Características, Ph.D. thesis, Universidade Federal do Paraná, Curitiba, Brasil (2012).
[6] M. Dourado, J. Meireles, Obtenção de um modelo de elementos finitos simplificado para representação de juntas rebitadas em análise dinâmica de estruturas usando uma ferramenta de updating,, Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 32 (3) (2016) 173-180.
[7] S. Chen, G. D. Doolen. Lattice Boltzmann Method for fluid flows, Annual Review of Fluid Mechanics, vol. 30, no. 1, pp. 329-364, 1998.
[8] J. G. Zhou, Lattice Boltzmann Method for Shallow Water Flows, Springer, New York, 2004.
[9] P. van Thang, B. Chopard, L. Lefèvre, D. A. Ondo, E. Mendes, Study of the 1D Lattice Boltzmann Shallow Water Equation and Its Coupling to Build a Canal Network, Journal of Computational Physics 229 (19) (2010) 7373-7400.
[10] J. G. Zhou, H. Liu, S. Shafiai, Y. Peng, R. Burrows, Lattice Boltzmann Method for Open-channel Flows, Engineering and Computational Mechanics 163 (2010) 243-249.
[11] X. Zhang, J. Feng, T. Yang, Lattice Boltzmann Method for Overland Flow Studies and its Experimental Validation, Journal of Hydraulic Research 53 (5) (2015) 561-575.
[12] N. Liu, The numerical simulation of one-dimensional overland flow by Lattice Boltzmann Method, in: 5th International Conference on Advanced Design and Manufacturing Engineeringe, China, 2015.
[13] H. Liu, H. Wang, S. Liu, C. Hu, Y. Ding, J. Zhang, Lattice Boltzmann Method for the Saint?Venant Equations, Journal of Hydrology 524 (2015) 411-416.
[14] Y. Peng, J. M. Zhang, J. G. Zhou, Lattice boltzmann model using two relaxation times for shallow-water equations, Journal of Hydraulic Engineering 142 (2) (2016).
[15] Z.-m. Zhao, P. Huang, S.-t. Li, Lattice boltzmann model for shallow water in curvilinear coordinate grid, Journal of Hydrodynamics 29 (2) (2017) 251?260.
[16] R. M. Porto, Hidráulica Básica, 4th Edition, EESC-USP, São Carlos, 2006.
[17] J. E. Gribbin, Introduction to Hydraulics and Hydrology with Applications for Stormwater Management, 3rd Edition, Cengage Learning, USA, 2008.
[18] M. H. Chaudhry, Open-Channel Flow, Springer, New York, USA, 2008.
[19] C. E. M. Tucci, Hidrologia: Ciência e Aplicação, 2th Edition, Editora da Universidade Federal do Rio Grande do Sul. Porto Alegre, RS - Brasil, 1998.
[20] J. E. Miller, Basic Concepts of Kinematic-Wave Models, United States Government Printing Office, Washington, 1984.
[21] D. R. Golbert, Método de Lattice Boltzmann em Hemodinâmica Computacional: interações fluido-estrutura e modelos acoplados 1D-3D, Ph.D. thesis, Laboratório Nacional de Computação Científica, Petrópolis, RJ - Brasil.
[22] P. L. Bhatnagar, E. P. Gross, M. Krook, A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems, Physical Review 94 (3) (1954) 511-525.
[23] Z. Guo, C. Zheng, B. Shi, Discrete Lattice Effects on the Forcing Term in the Lattice Boltzmann Method, Physical Review E 65 (2002) 1-6.
[24] Y. H. Qian, D. D'Humières, P. Lallemand, Lattice bgk models for navier-stokes equation, Europhysics Letters 17 (6) (1992) 479-484.
[25] S. Chapman, T. G. Cowling, The Mathematical Theory of Non-uniform Gases. An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases, 3rd Edition, Cambridge University Press, London, 1970.
[26] J. Zhang, G. Yan, A lattice Boltzmann model for the Burgers-Fisher equation, Chaos: An Interdisciplinary Journal of Nonlinear Science 20 (2010) 023129.
[27] J. Sterling, S. Chen, Stability Analysis of Lattice Boltzmann Methods, Journal of Computational Physics, 123 (1) (1996) 196-206.
[28] D. Stephenson, M. E. Meadowns, Kinematic Hidrology and Modelling (Developments in water science), Elsevier, Amsterdam, 1986.
[29] D. A. Woolhier, R. E. Smith, D. C. Goodrich, KINEROS, A Kinematic Runoff and Erosion Model: Documentation and User Manual U. S. Department of Agriculture, Agricultural Research Service, ARS-77. Disponível em: http://www.tucson.ars.ag.gov/kineros. Acesso em: 15/11/2016.
Document information
Published on 03/01/18
Accepted on 08/05/17
Submitted on 24/04/17
Volume 34, Issue 1, 2018
DOI: 10.23967/j.rimni.2017.6.001
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?