FATIGUE FAILURE ANALYSIS OF VIBRATING SCREEN SPRING BY MEANS OF FINITE ELEMENT SIMULATION: A CASE STUDY
Key words: Fatigue Analysis, High-cycle Loading, Non-proportional Loading.
Abstract. Vibrating screens are often used in the mining industry to separate mineral particles by size. In many designs, spring arrays are used to provide the system with the necessary stiffness for screens to vibrate in a controlled manner. Naturally, these springs are subjected to varying loading cycles, which can cause their premature fatigue failure. This behavior has been studied by means of finite element analysis and compared with data obtained from a real case scenario, in which a helical spring failed. The 3D computational model was developed using the geometric characteristics and material properties of a fractured spring, as well as the loading characteristics of a specific vibrating screen. The meshing and the simulation tasks were performed in the general purpose software ANSYS Mechanical. Given the nature of the helical springs and the high-cycle loading conditions, for the fatigue analysis it was determined that a stress-life approach with constant amplitude and non-proportional loading best fit the investigated phenomenon. In solving the non-proportional loading case, stress values of two static scenarios were required to determine the upper and lower limits. Then, to perform the fatigue calculations a solution combination was used. In addition, in order to correct the effect of mean stress and calculate the stresses component respectively the Goodman and Von Mises theories were employed. Simulation results showed that spring would present failure below the second turn of the coil when working with the full nominal load during nearly forty million cycles. These results strongly agreed with the data extracted from a vibrating screen where fractured spring had been working. Fatigue analysis also predicted that the nominal load should be reduced to 90% in order for the spring to meet the minimum life requirements before failure occur.
1 INTRODUCTION
In the mining industry, vibrating screens play an important role, as they allow the adequate sorting of minerals by their size. Complexity in the design of these machines make numerical techniques a proper tool to study their dynamic behaviour, which could include modal or harmonic response analysis [1].
The operational characteristics of a vibrating screen imply that its components support loading and unloading cycles, which could often activate fatigue mechanisms. As it is well known, these mechanisms could lead to the component failure, even though the stress levels that they support are below the yield stress of the material.
The springs that are located in the vibrating screen structure are not exempt from these effects, which is why it becomes important to examine the loads that they support. The type of loading in these springs and their geometry, cause the principal stress directions to change over time. This phenomenon is the cause of non-proportional fatigue, which could have great influence over the strength of a material, diminishing it up to 10 times its original value [2].
A general case of non-proportional fatigue, which includes not only change in the principal stress directions, but also a non-constant load amplitude, has been studied in [3]. There, expected life of compression helical springs was predicted based on critical sliding planes on the fracture surface (Fatemi-Socie and Wang-Brown), as well as with methods based on angular strains (Coffin-Manson). A finite element model that simulated the conditions of the experiment later confirmed these results.
An even more detailed analysis on the characteristics of the steel from which compression springs are usually made can be found in [4]. In contrast with the former analysis, these experiments were carried out by bringing test specimens under loading and unloading cycles with varying alternating stress values. The Wöhler curves that were obtain through these tests showed that not only the type of loading has influence on the fatigue stress limits, but it is affected also by the surface finish and environmental conditions in which the material works. As a supplement to these analysis, [5] describes mathematical crack propagation models as functions of the number of cycles that correspond to the results of the experiments. Moreover, [6] introduces changes in the microstructure to such models, as to evaluate their influence on the fatigue stress limits and on crack propagation.
Even though the experiments mentioned up to this point have been useful to determine mechanical properties in helical springs, all of them have been carried out under controlled laboratory conditions. In contrast, [7] presents the analysis of a helical compression spring that belonged to the suspension system of an automobile, which had failed due to fatigue during normal operation. It was confirmed by a FEM analysis that contact stress between the first turn of the spring (where the failure occurred) and the base, as well as the presence of corrosion, were the cause of nucleation and propagation of cracks that ultimately led to the failure.
Similarly to the latter, the analysis in the present article is based on the failure of a spring during normal operation of a vibrating screen. The geometry was modeled after a spring taking its dimensions directly from the fractured specimen. A FEM analysis was then performed using ANSYS Mechanical. In order to consider the weight of the components and the load of the vibrating screen, a static scenario was first evaluated to obtain the mean deformation during operation. Later, the maximum and minimum vibration amplitudes were taken from field data and were added or subtracted from the static deformation, respectively. Together with the spring geometry, they caused the principal stresses to vary over time, which implied a case of non-proportional fatigue that was analyzed using the software Fatigue Tool, considering an adequate correction on the mean stress to predict the life and safety factor of the spring.
2 ANALYSIS METHODOLOGY
The vibrating screen from which the springs were taken presents two types of loading over them: the first, a static load due to the weight of its components and the material it processes; the second, a dynamic load due to the exciters that produce the screen vibration. The combined effect of both types of loading causes the stress amplitude to oscillate symmetrically around the static stress (pulse loading).
As the dynamic load in terms of force was not directly known, field data concerning the maximum and minimum values of the vibration amplitude were taken. The numerical simulation was based in three scenarios: a first one, considering the static load due to the weight of the screen and its nominal load, which allowed the calculation of the static deformation (and thus, the static force). The second scenario considered the vibration amplitude as contributing to the static load (in the same direction), which gave as result the state of maximum compression over the spring. The last scenario considered the vibration amplitude in the opposite direction of the static load, which gave as result the minimum compression value over the spring.
The results of the static scenarios were finally combined in a single fatigue scenario, which considered the non-proportional effects due to the varying principal stress directions.
3 ANALYSIS PROCEDURE
The following lines contain information about the preprocessing stage of the simulation: geometry, material model and properties, meshing and boundary conditions.
3.1 Geometry
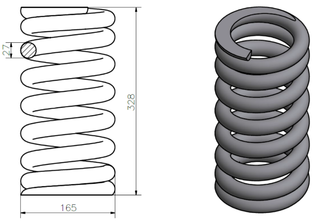
The geometric model was made based on the spring dimensions that operated in the vibrating screen. The shape, as some of the most important dimensions and the 3D model can be observed in figure 1.
3.2 Meshing
Meshing of the 3D model was performed using tetrahedral, second-order elements that allowed a good adaptation of the numerical model to the existing geometry, as well as a better interpolation between the nodal results. It was also considered convenient a mesh refinement in the coil planar faces. The final mesh had 274124 elements, together with a mean element quality of 0.83 and a mean aspect ratio of 1.89. Figure 2 shows the final mesh together with the mesh refinement zone.
3.3 Material properties
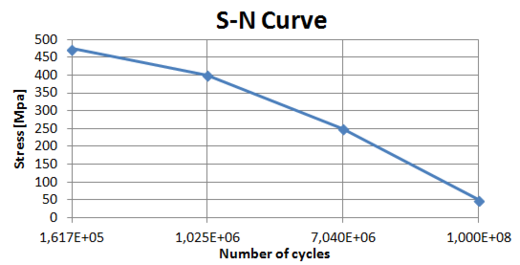
For the present analysis, a SAE 5160 steel was considered [8]. Table 1 shows some physical and mechanical properties that were taken into account during the simulation. Also, figure 3 shows the S-N curve for this steel, which is necessary to perform the fatigue analysis [9].
| Density (kg/m3) |
Elastic Modulus (GPa) |
Ultimate Stress (MPa) | Yield Stress (MPa) | Poisson’s ratio |
| 7850 | 210 | 1400 | 1200 | 0.3 |
3.4 Boundary conditions
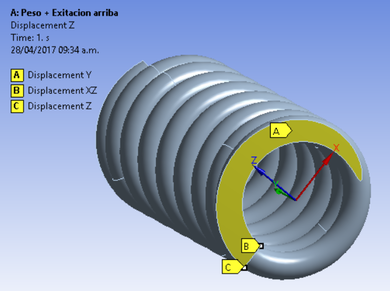
As the dynamic forces are unknown, displacement boundary conditions over the planar faces of the spring were applied instead. On its base, three displacement restrictions were imposed: null displacement in the normal direction of the planar face, null displacement in the radial and tangent direction of the inner vertex in the planar face and null displacement in the tangent direction of the outer vertex in the planar face. Such displacements can be observed in figure 4.
To impose the spring load, a displacement was used on the upper planar face of the spring in its normal direction. This displacement value changed according to the scenarios describe in the analysis methodology. Figure 5 shows this boundary condition for one of the analyzed scenarios.
3.4.1 Static scenario due to the weight of the components
The first simulation scenario only considered the weight of the vibrating screen components on the springs. Available field data showed that each spring supported 9810 N. This load was imposed on the upper planar face of the spring in order for the total static deformation to be calculated.
3.4.2 Static scenario for the maximum compression on the spring
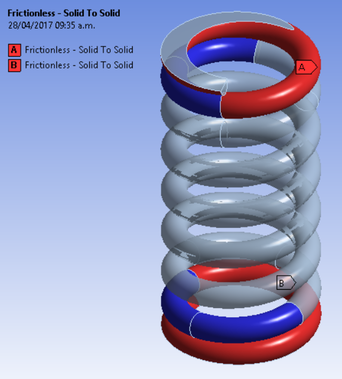
In this scenario, the vibration amplitude (4.9 mm) was subtracted to the already negative deformation due to the weight of the components (calculated in the previous scenario). Frictionless contact conditions were also stablished between the first upper and lower turns fo the coil, in order to prevent self-penetration during the simulation. These conditions are shown in figure 6.
3.4.2 Static scenario for the minimum compression on the spring
This time, the vibrating amplitude was added to the negative deformation due to the static load, resulting in a lower state of compression. The rest of boundary conditions were similar to the previous scenario.
3.4.2 Fatigue analysis scenario
In this scenario, loads from the previous scenarios were considered cycling and varying over time with constant amplitude. Due to the facts exposed in the first part of the article, the fatigue analysis was defined as non-proportional. Taking into account that vibrating screens usually work at high frequencies, a stress-based approach was used to predict the life of the springs. Goodman theory for mean stress correction was used together with the von Mises equivalent stress. Finally, the highest cycle number in the S-N curve defined infinite life (109 cycles).
4 RESULTS
Results of each of the static scenarios were used as inputs to the final fatigue scenario. The results obtained in this last scenario were compared with the actual fractured spring with very good similarities between the numerical model and the component. Also, predicted life had a remarkable correlation with the actual life on which the spring was operational.
4.1 Minimum compression scenario
As previously described, in this scenario the highest displacement was applied (34 mm) and thus, higher equivalent stress values were expected. The higher stresses were obtained from the second upper turn of the coil down to the second lower turn. The stress value in the middle turns was approximately constant. The maximum stress value was 466 MPa. Figure 7 shows the equivalent stress distribution for this scenario.
4.2 Maximum compression scenario
The imposed displacement was 24 mm. In this case, a very similar stress distribution was obtained compared to the previous scenario. The maximum equivalent stress was 336.6 MPa. The equivalent stress distribution can be observed in figure 8.
4.3 Fatigue analysis scenario
Based on the conditions stablished in the analysis methodology, the results of non-proportional fatigue concluded that the spring would have a predicted life of 3.99 107 loading cycles before failure. The predicted life for the entire spring can be observed in figure 9.
If it is taken that the spring should have had a working life of 109 cycles, its fatigue safety factor was calculated to be 0.25, as shown in figure 10.
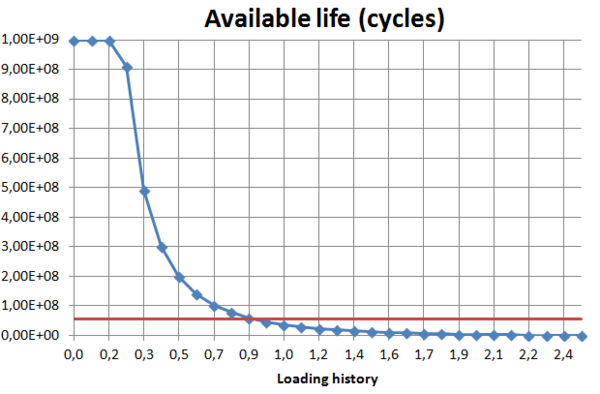
A fatigue sensibility study to the load value showed that, for 109 cycles, only 20% of the nominal load should be applied. In figure 11, it is shown that if the nominal load is lowered by 10%, the spring can achieve 40 working days.
5 CONCLUSIONS
- The different loading scenarios and the spring geometry when the vibrating screen is working with nominal load create the conditions for the spring to be analyzed via a non-proportional fatigue analysis.
- Results obtained through numerical simulation suggest that, when the vibrating screen worked under nominal load, expected life of the springs was about 40 working days, which strongly agreed with actual experience with the fractured specimen.
- The latter also indicates that the stress levels and fatigue life prediction was correct, as the spring presented failure on the turn of the coil in which the numerical simulation showed the highest level of equivalent stress.
REFERENCES
[1] Z. Yue-min, L. Chu-sheng, H. Xiao-mei, Z. Cheng-yong, W. Yi-bin, R. Zi-ting. Dynamic design theory and application of large vibrating screen. The 6th International Conference on Mining Science & Technology. Elsevier (2009).
[2] D. Skibicki. Phenomena and Computational Models of Non-Proportional Fatigue of Materials. Springer (2014).
[3] L. Del Llano-Vizcaya, C. Rubio-González, G. Mesmacque, T. Cervantes-Hernández. Multiaxial fatigue and failure analysis of helical compression springs. Engineering Failure Analysis 13 1303-1313. Elsevier (2006).
[4] D. Angelova, R. Yordanova, T. Lazarova, S. Yankova. On fatigue behavior of two spring steels. Part I: Wöhler curves and fractured surfaces. Frattura ed Integrità Strutturale 37 249-257. Gruppo Italiano Frattura (2016).
[5] D. Angelova, R. Yordanova, T. Lazarova, S. Yankova. On fatigue behavior of two spring steels. Part II: Mathematical models. Frattura ed Integrità Strutturale 37 258-264. Gruppo Italiano Frattura (2016).
[6] B. Žužek, M. Sedlaček, B. Podgornik. Effects of segregations on mechanical properties and crack propagation in spring steel. Frattura ed Integrità Strutturale 34 160-168. Gruppo Italiano Frattura (2015).
[7] Y. Zhu, Y. Wang, Y. Huang. Failure analysis of a helical compression spring for a heavy
vehicle’s suspension system. Case Studies in Engineering Failure Analysis 2 169-173. Elsevier (2014).
[8] L. Pantoja. Determinación de parámetros óptimos del proceso de temple y revenido del acero SAE 6150 como alternativa para la manufactura de resortes de ballesta. Universidad Autónoma de Occidente (2006).
[9] F. Cánticus. Estudio de la resistencia de fatiga del acero SAE 5160 antes y después de proceso shot peening. Universidad Autónoma de Occidente (2010).
Document information
Published on 02/05/17
Submitted on 29/04/17
Licence: Other