Guide to multi-objective optimization for the green vehicle routing problem

Abstract

This article aims to present research conducted on the literature regarding Multi-objective Optimization (MOO) for routing problems with environmental considerations (EC), referred to here as Multi-objective Optimization for the Green Vehicle Routing Problem (MOOGVRP). A Brazilian database, CAPES (Coordination for the Improvement of Higher Education Personnel), was used to collect articles of general application, case studies and reviews in English starting from, since 2012. The terms “green vehicle routing problem” (GVRP), “pollution routing problem” (PRP), “vehicle routing problem in reverse logistics” (VRPRL) and “multi-objective” were used in the research protocol. Consequently, this study obtained 1,744 research results that, following the application of the filtering criterion, resulted in a sample of 76 articles from 38 journals, for which a bibliometric data (bibliometric review) survey was conducted. When dealing with the bibliometric data of the sample, it was possible to identify information such as the number of publications per year and types of published works. Information was also identified regarding the most frequently used journals and the countries and institutions that published the most articles on the proposed theme. It was also possible to analyze the frequency of the protocol terms in the title, abstracts and keywords, the relationship between taxonomies, vehicle fleet types, multi-objective procedures, and VRP procedures. Information was also found regarding solution procedures, number of objectives, and programming languages for computational implementation, the frequency of the most used objectives, and the most cited articles in the sample. The originality of this article lies in how the research is presented, highlighting the results and particular details obtained through the survey, which may be considered of great academic importance in the sense of guiding the trends for future research.

Keywords: Innovative survey, Green Vehicle Routing Problem, pollution routing problem, vehicle routing problem in reverse logistic, multi-objective optimization

1. Introduction

In 2015, the UN proposed an agenda with 17 sustainable development goals to be implemented by all countries by the year 2030. The present study especially focuses on Goals 12 and 13. It addresses Goal 12 (“ensure sustainable consumption and production patterns”) by seeking an intelligent and optimized alternative to perform activities, and 13 (“take urgent action to combat climate change and its impacts”) by seeking to reduce greenhouse gas emissions [1].

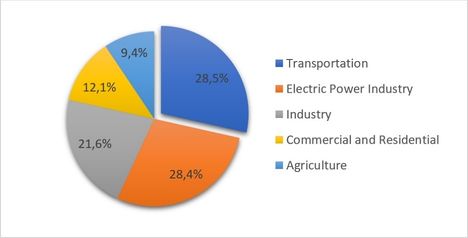
According to the report published by the United States Environmental Protection Agency [2], the sources of greenhouse gas (GHG) emissions include five main sectors: Transportation; Electricity; Industry; Commercial and Residential; and Agriculture, as shown in Figure 1, which presents their respective percentages. In this study, the emphasis will be on the “share” related to Transportation (28.5%). Regarding this “share”, we found the following results: CO$_{2}$ from Fossil Fuel Combustion (27.4%), Substitution of Ozone Depleting Substances (0.7%), Mobile Combustion (0.3%) and Non-Energy Use of Fuels (0.1%). Of these, this study will address the issues related to CO$_{2}$ from Fossil Fuel Combustion and Mobile Combustion.

Figure 1. Emission sources according to the Inventory of U.S. Greenhouse Gas Emissions and Sinks in 2016. Source: US EPA [2]

The Vehicle Routing Problem (VRP), proposed by Dantzing and Ramser [3], is highly significant for an efficient logistic distribution [4,5]. The Green Vehicle Routing Problem (GVRP) directs routing activities through a perspective with environmental considerations [6,7]. Thus, a Multi-objective approach aids this process of complex decision-making in order to meet the objectives to be achieved [8,9,10].

In this context, we identified several works in the literature that address the optimization of fuel consumption [5,11], CO$_{2}$ emission [12,13], both cases simultaneously [14,15] and other approaches [16,17] applied to the Vehicle Routing Problem (VRP).

The aim of this study is to present research conducted on the literature regarding Multi-objective optimization (MOO) for vehicle routing problems with EC, referred to here as MOO for the Green Vehicle Routing Problem (MOOGVRP). Thus, this work aims to detect gaps in the literature for development and advances in this field of knowledge. This has been recognized as an important theme in a wide range of previous literature reviews, such as that of [18].

The originality of this article lies in present an innovative research, showing the results and peculiarities obtained through the content analysis (systematic review), with the bibliometric data collection (bibliometric review) regarding the published articles related to MOOGVRP from 2012 to 2018. Highlights of paper are structured overview of recent studies of VRP with multi-objective approaches and environmental considerations, more specifically, Pollution Routing Problem, Green Vehicle Routing Problem and VRP in Reverse Logistics.The main objectives addressed are cost, fuel consumption and CO$_{2}$ emission minimization. It has research opportunities regarding electric vehicles, social issues and others.

The present work is organized as follows. After this introductory section, the methodological procedures are presented in Section 2. Section 3 contains a brief presentation of the Multi-objective approach (the VRP approach) and its variations, as well as the VRP with EC. In Section 4, the results are explained and discussed. The conclusions of the study are summarized in Section 5.

2. Methodological procedures

For the methodology of this research, the following steps were established as a search protocol:

1. First, the timeline cut, covering the period between 2012 and 2018, in order to identify the recent discussions analyzed by academia. To the protocol used was not found papers before 2012.
2. Database selection: the study used the Brazilian database of CAPES (Coordination for Improvement of Higher Education Personnel), which gathers and makes available international scientific content for educational and research institutions in Brazil, composed of 38,000 journals, 532 reference databases including Cambridge Journals Online, Emerald Insight Emerald, IEEE Xplore, Scopus (Elsevier), Science Direct, SpringerLink, Taylor & Francis, as well as books, encyclopedias, technical standards, statistics and audiovisual content [19].
3. The English language was adopted to select the articles.
4. Only journals (articles) were searched.
5. The keywords, as well as the logical operators used were: “green vehicle routing problem” OR “pollution routing problem” OR “vehicle routing problem in reverse logistics”, which were necessarily linked to “multiobjective” OR “multi-objective” OR “bi-objective”. The possible suffix variations in the terms used were also considered. The terms related to routing with EC (environmental considerations) were obtained from the literature review proposed by [20].
6. As an acceptance criterion, it was established that: (i) the research result should present the “green vehicle routing problem”, “pollution routing problem” or “vehicle routing problem in reverse logistics”, all of them being “multi-objective”; (ii) they could be literature “review”, “general” application (mathematical modeling and/or algorithm improvement articles), as well as “case” studies related to the proposed theme. As exclusion criteria, it was established that the results would be excluded if: (i) they were not related to the proposed theme; (ii) did not have full text available; or (iii) were duplicate articles.

From the protocol presented, we obtained 1,744 research results that, after the protocol filter, resulted in 76 articles for the research sample, from 38 journals. From this selection of articles, this study conducted a critical analysis of the research scope and sought to answer two questions:

1. What are the most relevant studies regarding MOOGVRP?
   
2. What are the trends regarding MOOGVRP that may guide future research?

3. Theoretical framework

In this section, we briefly present the problems of MOO, the VRP and its variations, as well as the VRP with EC, which will be subdivided into the Green Vehicle Routing Problem, Pollution Routing Problem and Vehicle Routing Problem in Reverse Logistics.

3.1 Multi-objective optimization

MOO addresses the process of simultaneously optimizing two or more conflicting objectives subject to restrictions [10,15]. Its mathematical representation is presented using the objective function in Eq. (1) and restrictions in (2)

$min\left(f_{1}(x),f_{2}(x),\cdots ,f_{k}(x)\right)$ (1)

${\hbox{subject to }}x\in X$ (2)

where $k\geq 2$ defines the number of objectives to be optimized and X represents a set of non-empty decision vectors (solution). When we optimize a MOO problem, we arrive at an x-optimal solution for a given objective and, when trying to improve it, the other objectives are affected. In other words, given two x and y solutions, so that $f_{i}(x)\leq f_{i}(y)\,\forall \,i$, $i\in \{1,2,\cdots ,K\}$ and $f_{j}(x)<f_{j}(y)$ for at least one objective $j\in \{1,2,\cdots ,K\}$. In this case, it is said that x is a non-dominated solution, i.e., that it belongs to the optimal Pareto frontier. Therefore, a solution will be considered Pareto efficient (Pareto optimal or non-dominated) if it cannot be eliminated from consideration due to another solution that improves one of the objectives without worsening the others. Thus, the goal of an MOO problem is to find non-dominated solutions and quantify trades-offs to meet the different objectives established [9,21].

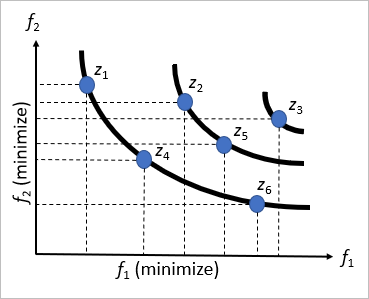
Figure 2 presents a bi-objective academic example about the concept of domination through the Pareto front for the case of minimizing the objective functions 1 and 2. It is observed that z4 dominates z2, z5 and z3. Note that, z4 and z6 are non-dominated solutions, because z4 is worse than z6 in f2 but z6 is worse than z4 in f1. In this context the solutions z1, z4 and z6 are non-dominated by any other solution presented in the population. Thus, these solutions belong to the Pareto front.

Figure 2. Example of Pareto front

MOO methods can be classified into generative methods and preference-based methods. The generative methods seek to generate one or more Pareto optimal points and can take into account the “non-use” for preferences, a scale approach or a multi-objective approach. The preference-based methods use information provided by the decision maker a priori or iteratively, as part of their solution process.

The classic methods commonly used for solving MOO problems can be organized into four categories. The first addresses the methods that do not articulate the given information of preference, such as the Method of Global Criterion. In the second one, we have “a priori” preferences, such as the Methods for Cardinal Information Given (Utility Function and Bounded Objective) and the Methods for Mixed Ordinal and Cardinal Information Given (Lexicographic Method and Goal Programing). In the third category, we have the methods for progressive articulation, most notably the Methods for Explicit Trade-Off Information Given (iterative methods) and implicit methods. Finally, we have “a posteriori” methods, among which we find the Parametric Method, є-constraint, Multi-objective Linear Programming (MOLP) and Adaptative Search [15,18].

According to Heilig et al. [22], the most frequently used Multi-objective techniques are: weighted sum scalarization, the є-constraint method, goal programming, lexicographic ordering and Pareto optimization. In relation to weighted sum scalarization, we must assign weights and treat the problem as a linear combination of established objectives. In the case of the є-constraint method, only one objective must be optimized, and the others must be considered as problem restrictions. In goal programming, the purpose is to meet all objectives, taking account of the goals established for each criterion. Lexicographic ordering considers an order of importance from the sequence in which the proposed objectives were listed. Finally, in Pareto optimization, an “a posteriori” approach provides the Pareto frontier with the intention of performing the trade-off of the solutions of the different objectives.

3.2 Vehicle Routing Problem

VRPs have many variations in the literature, and some of them are presented in Table 1 (in alphabetical order), as proposed by [20,23], followed by reference paper and brief description. It is worth mentioning that two or more of these variations can be combined, generating new variations for the VRP.

Table 1. Some VRP variations

VRP variations	Introduced by	Brief Description
Capacitated VRP	Dantzig and Ramser [3]	Considers the capacity of the vehicle.
Dynamic VRP	Speidel [24]	This is a dynamic procedure where customer orders are organized during planning and assigned to the appropriate vehicle in real time.
Fleet Size and Mix VRP	Golden et al. [25]	Determines the economic combination of vehicles in the fleet by considering the trade-offs between the vehicle’s fixed costs and the proportional variable costs.
Fuzzy VRP	Cheng et al. [26]	Formulates the subjective, uncertain, vague and ambiguous elements.
Generalized VRP	Tsiligirides [27]	Each customer has a different score (or profit) and is divided into unit groupings.
Inventory Routing Problem	Bell et al. [28]	Ensures that there are no stocks on each customer.
Location Routing Problem	Watson-Gandy and Dohm [29]	Addresses a single or a set of deposits and, subsequently, a series of routes to the respective open deposits to minimize the total cost.
Multi-compartment VRP	Christophides [30]	In this case, the problem involves heterogeneous and qualified vehicles. A customer's demand for a particular product cannot be divided.
Multi-depot VRP	Tillman [31]	Has more than one deposit. Each script starts and ends in the same deposit.
Multi-echelon VRP	Crainic et al. [32]	Easily applied to true needs, aims to minimize the total cost of transportation of the vehicles involved at all levels, i.e., freight delivery covers the entire chain and is required to be carried out through an intermediary deposit; therefore, several stages are performed.
Open VRP	Sariklis and Powell [33]	Each route is a Hamiltonian path instead of a Hamiltonian cycle. The vehicles are not required to return to the depot after finalizing their activities.
Periodic VRP	Beltrami and Bodin [34]	Seeks feasible routing so that the cost associated with the time horizon is minimized.
Pickup and Delivery Problem	Wilson and Weissberg [35]	Considers the collection and/or delivery of goods. Large variations are available in the literature.
Site-dependent VRP	Nag [36]	There is compatible independence between clients (sites) and types of vehicles. Each customer can be visited by only a predefined group of vehicle types.
Split-delivery VRP	Dror and Trudeau [37]	Each customer can be served by one or more vehicle.
Stochastic VRP	Tillman [31]	Occurs in non-randomness of elements such as travel times, customer demand or customer groups.
Time-dependent VRP	Cooke and Halsey [38]	The travel time between any pair of deposits and customers depends on the distance between the points or alternatively the time of day.
VRP with Loading Constraints	Iori et al. [39]	Simultaneously determines (as a set) the routes and the packaging standards (loading restrictions).
VRP with Time Windows	Russell [40]	This problem can be of two types: hard or soft time windows. For Hard Time Windows, the vehicle cannot delay, must arrive on time or early. For Soft Time Windows, there may be a violation if there is a penalty.

3.3 VRP with environmental considerations

When addressing the VRP with EC, the classification proposed by Lin et al. [20] was used here, which sticks to the Pollution Routing Problem, Green VRP and VRP in Reverse Logistics. The Pollution Routing Problem (PRP) search vehicle routing plan produces a lesser amount of pollution, in particular with a reduction in greenhouse gases (GHG) and may include broader objectives that reflect the environmental cost. The Green VRP considers the optimization of energy consumption in transport and reduction of fuel consumption.The objective of the VRP in Reverse Logistics (VRPRL) focuses on aspects of reverse logistics distribution. The latter category, VRPRL, can be divided into sub-categories: Selective Pickups with Pricing, Waste Collection, End-of-life Goods Collection and Simultaneous Distribution and Collection.

Selective Pickups with Pricing selects only profitable collection points to visit. Waste Collection (waste management) includes waste reuse, prevention and recycling. End-of-life Goods Collection is useful for remanufacturing. Finally, the Simultaneous Distribution and Collection addresses applied modeling in the context of reverse logistics [7,20,41].

Additionally, Demir et al. [18], in their review article, present, systematize and compare techniques for measuring GHG emission and fuel consumption applied to the road transportation of green loads.

Environmental considerations (EC) can be addressed in one or more Objective Functions (OF) subject to restraints through mathematical modeling, be it a linear, non-linear, integer, mixed or dynamic programming model or other approach. In this study, emphasis will be placed on the OFs focusing on the environmental, social and economic contexts, reverse logistics, fuel consumption and CO₂ emissions.

Thus, it can be said that many authors are concerned with minimizing costs, be they operational, general, financial or for transport [11,42,43] or maximizing revenues or profit [44,45], as well as minimizing the number of vehicles [46,47]. Regarding the social aspect, a point in question is maximizing work opportunities [48], in addition to working hours [8] and social responsibility [49,50]. When it comes to reverse logistics, this is more difficult to measure, as not all problems found are clearly attributed to an OF, but rather to the consequent stratifications of its results [51,52]. On the other hand, GHG emissions and fuel consumption are easily measurable [18,53,54].

4. Results and discussion

In this section, we present the bibliometric data. This study identified information such as the quantity of publications per year, type of works published in the sample and percentage of journals that focus on environmental considerations. The study also identified the countries and institutions that published the most works on the proposed theme, a frequency analysis of protocol terms in the title, abstracts and keywords and the relation between the taxonomies employed. Other information includes the fleets that are used and the most commonly used Multi-objective procedures, VRP procedures, solution procedures, number of objectives and most frequently used metaheuristic methods. The software and programming languages for computational implementation and the frequency of the most used objectives were also identified. The study also includes the works related to the theme in question and a table summarizing the most frequently cited articles in the sample.

As presented in Section 2 (Methodology), this research sample was composed of 76 articles. Figure 3 shows that the number of articles on the proposed theme has increased over the years. It should be highlighted that the sample of 76 articles was collected from 2012 to 2018.

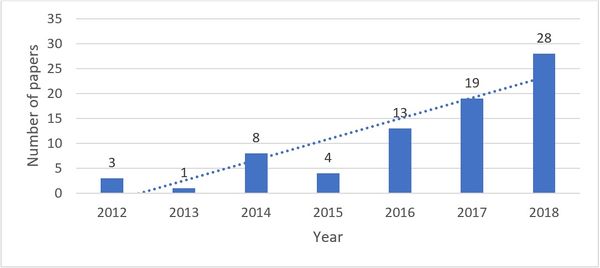
Figure 3. Distribution per year of the 76 publications in the sample on MOOGVRP

According to Figure 4(a), the articles with two, three and four authors correspond to 65 papers in the sample, demonstrating the existence of research groups or works developed in academic environments. As shown in Figure 4(b), the articles were classified as General (27 articles), Case studies (43 articles) and Reviews (6 articles). As also shown in Figure 4(c), it was verified that only 10 of the 38 journals in the sample articles focus on issues related to environmental considerations (more specifically, they show interest in environmental aspects, sustainability, ecology, green manufacturing, the environment and related contexts), namely: Applied Energy, Computers & Operations Research, Decision Science Letters, Ecological Indicators, International Energy & Environment, Journal of Cleaner Production, Journal of Manufacturing Systems, Journal of Manufacturing Technology Management, Sustainability and Transportation Research Part D.

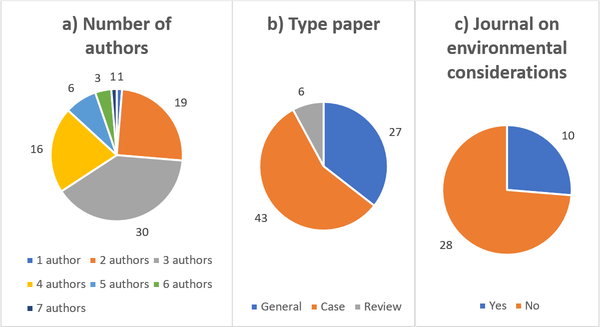
Figure 4. (a) Number of authors. (b) Number of article types. (c) Number of articles on environmental considerations among the 76 articles in the sample on MOOGVRP

Figure 5 shows the publication frequency of the 32 participating countries in the sample of 76 articles. It is worth noting that China and Iran contributed with 19 articles each.

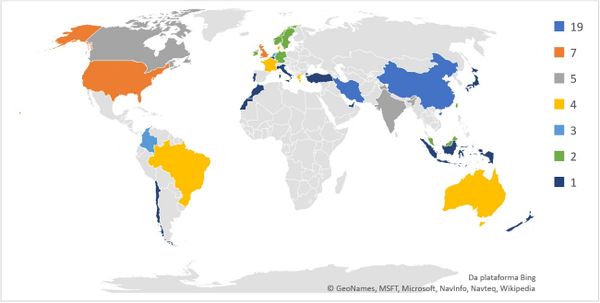
Figure 5. Countries that have contributed to the MOOGVRP Where China and Iran (19); the United Kingdom and United States of America (7); Canada and India (5); Australia, Brazil, Denmark, France and Greece (4); Colombia, Hong Kong and the Netherlands (3); Germany, Ireland, Malaysia, Norway, Sweden and Taiwan (2); Belgium, Chile, Indonesia, Italy, Japan, Morocco, New Zealand, Portugal, Singapore, Turkey and the United Arab Emirates (1).

Table 2 contains a list of affiliations related to the research sample, considering the institutions, research centers and companies with which the authors are associated. Note that several articles cover more than one affiliation. We can particularly highlight three universities in Iran, Iran University of Science and Technology [51,52,53,55,56,57], Islamic Azad University [7,11,16,44,45] and University of Tehran [13,51,56,58,59], with 6, 5 and 5 articles, respectively.

Table 2 Institutions that contributed most to MOOGVRP

Affiliation	Quantity
Iran University of Science and Technology	6
Islamic Azad University and University of Tehran	5
University of Southern Denmark	4
Aristotle University of Thessaloniki, Hubei University, Tongji University and Universidade Federal de Minas Gerais	3
Aalborg University, Amirkabir University of Technology, China University of Mining and Technology, Chongqing Jiaotong University, Eindhoven University of Technology, Emlyon Business School, Oregon State University, The University of Hong Kong, Universidad Tecnológica de Pereira, Universidade Estadual Paulista Júlio de Mesquita Filho, University of Electronic Science and Technology, University of Southampton, University of Washington and Vienna University of Economics and Business	2
Others	96

---

Others: 2CRRC Zhuzhou Institute Co., Ltd.; Allame Tabataba'i University Business School; Arts et Metiers Paris Tech; Athens University of Economics and Business; Beijing Jiaotong University; Beijing University of Aeronautics and Astronautics; Canada Research Chair in Distribution Management, Interuniversity Research Centre on Enterprise Networks, Logistics, and Transportation; Chang’an University; Chung Yuan Christian University; Dalian Maritime University; Democritus University of Thrace; Dongbei University of Finance and Economics; Dublin City University; Dublin City University Business School; Ecole de Technologie Superieure; École Polytechnique de Montréal and GERAD; Erasmus University Rotterdam; ESC Rennes School of Business; Faculty of Economics and Business; Faculty of Engineering (Turkey); Fujian Agriculture and Forestry University; Fuzhou University; Grupo da Causa Humana; HEC Montréal; Hefei University of Technology; Huanggang Normal University; Hunan University of Science and Technology; Ibn Zohr University; IEAv – Institute for Advanced Studies; Indian Institute of Management; Indian Institute of Technology; Institución Universitaria CEIPA; Instituto de Pesquisa e Desenvolvimento de Tecnologias; Instituto Universitário de Lisboa; Isfahan University of Technology; Jeppesen Manager Government and Military Aviation; K. N. Toosi University; K. N. Toosi University of Technology; Karlsruher Institut für Technologie; Kharazmi University; KTH Royal Institute of Technology; Lancaster University Management School; Liverpool John Moores University; Luleå University of Technology; Missouri University of Science and Technology; Monash University Malaysia; Nagoya University; Nanyang Technological University; Narvik University College; National China University; National Institute of Industrial Engineering; North Carolina A&T State University; Petra Christian University; Pontificia Universidad Católica de Valparaíso; PSG College of Technology; Rayalaseema University; SK University; Shandong University of Finance and Economics; Shandong University of Science and Technology; Shanghai Jiao Tong University; Shanghai Maritime University; Sichuan University; Singapore Institute of Manufacturing Technology; Southwest Jiaotong University; Swinburne University of Technology; Tarbiat Modares University; Technical University of Crete; Technische Universität Dresden; The Arctic University of Norway; The Fuzhou University of Management; The Hong Kong Polytechnic University; The Southeast University of Economics and Management; The University of Auckland; UAE University; Universidad de San Buenaventura; Universidad Nacional de Colombia; Universidade de Lisboa; Universidade do Estado do Rio de Janeiro; Universidade Federal da Paraíba; Universidade Federal de Ouro Preto; Universidade Federal Fluminense; Universidade Nova de Lisboa; Università degli Studi di Modena e Reggio Emilia; Université de Lyon; Université Paris; Universiti Tunku Abdul Rahman; University of British; University of Connecticut; University of Delhi; University of East Anglia; University of Hamburg; University of Huddersfield; University of Memphis; University of New South Wales; University of Science and Technology of Mazandaran; University of Sheffield; University of Sussex; University of Vienna Oskar-Morgenstern-Platz; University of Wisconsin–Madison; Wageningen University; Wuchang University of Technology; Zhejiang Gongshang University; Zhejiang University of Technology and Zhongnan University of Economics and Law.

---

Figure 6 presents the numerical frequency of the terms of the research protocol in the titles, abstracts, keywords and the three previous ones (All). This relationship is made clearer in Figure 7. This analysis is extremely important to the study because it is through these terms that the researchers achieved the sample for their works. It can be seen that the greater frequency of terms is concentrated in the abstract of articles and that there are few works that contain the search terms in the three fields.

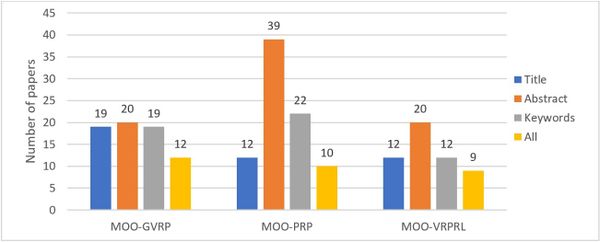
Figure 6. Frequency of the terms of the research protocol in the titles, abstracts and keywords of the 76 articles

Figure 7 shows the relationship between the taxonomies of the MOO-VRP with the EC presented here. We can observe (yellow circle on the left) that 12 articles in the sample address the MOO-GVRP [5,11,41,43,54,58,60,61,62,63,64,65]. Ten articles address the MOO-GVRP in conjunction with MOO-PRP [6,14,15,45,66,67,68,69,70,71]. Five articles address the MOO-GVRP in conjunction with the MOO-PRP and with the MOO-VRPRL [7,20,52,72,73]. Finally, 1 article addresses the MOO-GVRP together with the MOO-VRPRL [74]. Thus, a total of 28 articles are related to the MOO-GVRP. Likewise, we can interpret the other circles (left and right). It should be highlighted that the goal of the GVRP is different from that of the PRP, since the objective of the former is to reduce fuel or energy consumption (or the battery, alternatively) and the latter seeks to minimize GHG emissions, mainly CO₂. It was observed that in some articles the authors implicitly used their own taxonomy, as in [13,22,75,76], generalizing the MOO-PRP as the MOO-GVRP. Furthermore, the opposite occurred in [41], who referred to the MOO-GVRP as the MOO-PRP.

Figure 7. Representation of the research sample on MOO-VRP taxonomies with EC

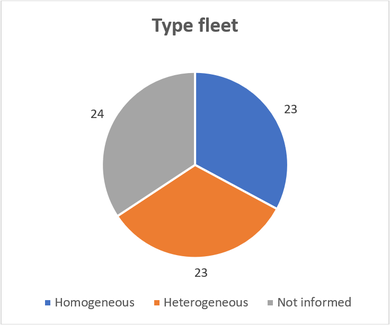
Figures 8 to 13 are related to articles classified as General and Case Studies (70 articles). The review articles (6 articles) will not be considered in these figures because of their wide coverage. Figure 8 shows the fleet classification (homogeneous or heterogeneous) through the sample articles.

Figure 8. Fleet type used by the sample of 70 articles

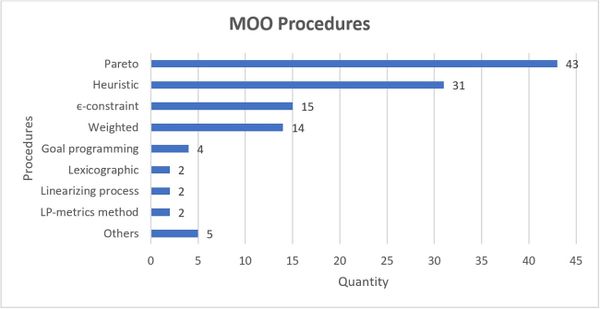
Regarding the MOO procedures presented in Figure 9, we can verify the predominance of the Pareto to analyze the dominance or non-dominance of the obtained solutions. We then have the classification of the use of heuristic, є-constraint and weighted procedures. It is worth noting that several articles include more than one procedure. A subtle description of the techniques Pareto, є-constraint, weighted, goal programing and lexicographic were presented at the end of Section 3.1. In the case of Heuristic, a heuristic or metaheuristic procedure such as NSGA-II was performed. The linearization process deals with the case of a nonlinear model that is converted to linear [7]. Finally, the L-P metrics method, the difference between any present solutions and the optimal solution, is minimized [55].

Figure 9. Most frequently used multi-objective approaches MOOGVRP in the sample of 70 articles

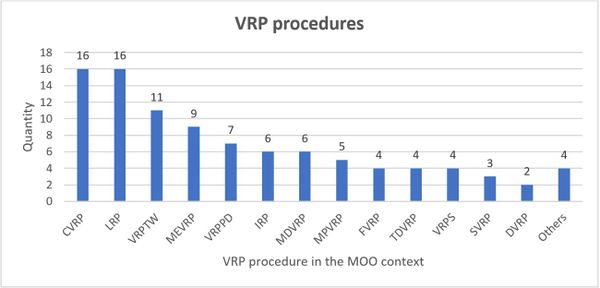
As for the VRP procedures shown in Figure 10, it must be taken into account that the same problem may contain more than one variant, in accordance with the works conducted by [8,16,49,59]. The Location Routing Problem (LRP) and the classical case (Capacitated VRP) were the most frequently used in the sample, followed by Time Windows, Multi-echelon, and Pickup and Delivery.

Figure 10. Solution procedures most used in the MOOGVRP Legend: CVRP (Capacitated VRP), DVRP (Dynamic VRP), FVRP (Fuzzy VRP), IRP (Inventory Routing Problem), LRP (Location Routing Problem), MDVRP (Multi-depot VRP), MPVRP (Multi-period VRP), MEVRP (Multi-echelon VRP), SVRP (Scheduling in VRP), TDVRP (Time-dependent VRP), VRPPD (VRP with Pickup and Delivery), VRPS (VRP Stochastic) and VRPTW (VRP with Time Windows)

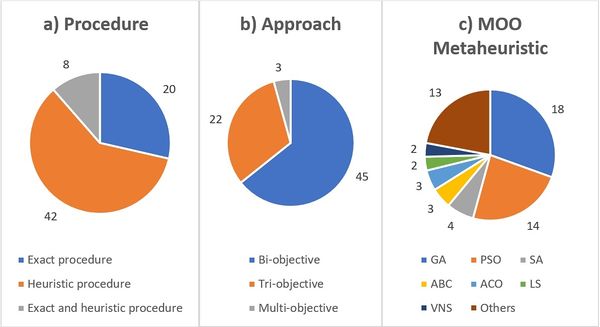
Figure 11(a) presents the use and quantity of exact and heuristic procedure, or both, for the 70 articles. It should be noted that 42 (60%) of the articles only used heuristic procedures. Figure 11(b) shows that 45 (64%) of the articles analyzed presented an approach with only two objectives and 22 (31%) are tri-objective. Figure 11(c) shows the use proportion of heuristic procedures in the MOO context. We can observe that the techniques derived from population algorithms are predominant, where GA and PSO correspond to 54%.

Figure 11. (a) Solution approaches. (b) Approach. (c) Meta-heuristics used Legend: ABC (Artificial Bee Colony), ACO (Ant Colony Optimization), CW (Clarke and Wright Heuristic), GA (Genetic Algorithm), LS (Local Search), PSO (Particle Swarm Optimization), SA (Simulated Annealing), VNS (Variable Neighborhood Search)

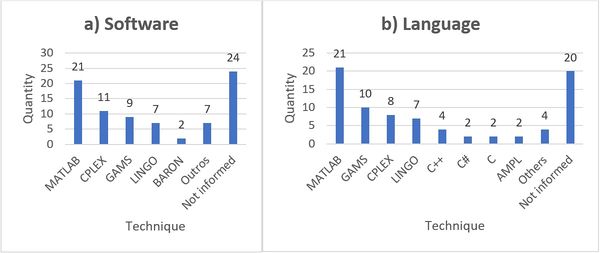
Figure 12 presents the most frequently used software and the respective programming languages for the 70 articles. It should be mentioned that an article may have used more than one software or language, and that some software accepts different languages. Some authors reported only the software, others only the programming language, and there were some works lacking this information.

Figure 12. (a) Software. (b) Most frequently used programming languages Legend: AMPL (A Mathematical Programming Language), CPLEX (Simplex method as implemented in the C programming language), GAMS (General Algebraic Modeling System), LINGO (Language for Interactive General Optimizer) and MATLAB (MATrix LABoratory)

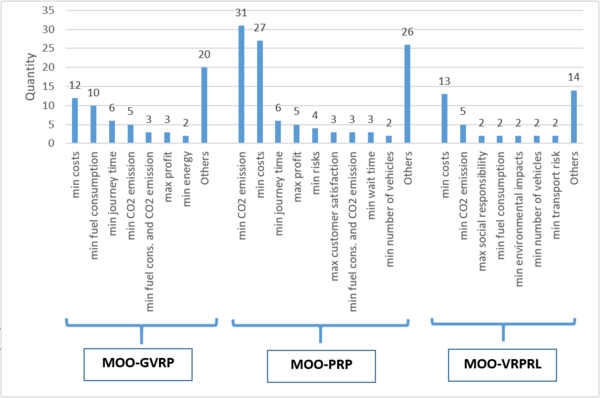
Figure 13 presents the main objective used in the 70 analyzed works. They were grouped into GVRP, PRP and VRPRL, with all of them being multi-objective. We can observe that all prioritize the minimization of costs among the main objectives. In the case of the GVRP, the minimization of fuel consumption is also among the main objectives. The same occurs with the PRP with CO₂ minimization.

Figure 13. Most frequent objectives in MOO problems, applied to the GVRP, PRP

We now present brief reports of the sample of 76 articles in this study and a description of the most frequently cited works in the MOO context.

A summary of the 76 articles related to MMGVRP is presented in Table 3. This Table is organized by references, presented in alphabetical and chronological order. The type of research was classified as a case study (c), general application (g) and review (r). The fleet was classified as homogeneous (ho), heterogeneous (he) or not informed (ni). The VRP with EC was classified by the taxonomy used in this study: GVRP, PRP and VRPRL. It was determined whether the procedures used were exact, heuristic or, alternatively, both approaches. The number of objectives was organized as bi-objective (bi), tri-objective (tri) or multi-objective (multi). The desired outcomes of the study, the proposed application of the work, the solution techniques and number of citations were then specified (May 2019 through SCOPUS).

As an example, one can see [77] and [21]. Thus, [77] is a review article that addresses the PRP with the objective of integration of environmental aspects in logistics, applied to green logistics and with 353 citations. Ehrgott et al. [21], the case study type, with homogeneous fleet, which also addresses the PRP, used heuristic procedure with bi-objective mathematical modeling that proposed minimized journey time and maximized adaptation to the routes used; applied in cyclist route, used the technique bi-objective shortest path problem and had 36 citations.

Table 3. Summary of the 76 articles related to MOOGVRP

Reference	Type	Fleet	EC			Procedure		Objective	Goals	Applications	Techniques	No. of Citations
			GVRP	PRP	VRPRL	Exact	Heuristic
Dekker et al. [77]	r	-		x		-	-	-	Integration of environmental aspects in logistics	Green logistics	Review	353
Ehrgott et al. [21]	c	ho		x			x	bi	Min journey time; Max adaptation to the routes used	Cyclist route	Bi-objective shortest path problem	36
Liu et al. [78]	g	ni			x		x	bi	Min costs; Min number of vehicles	Reverse logistics	MOPSO	1
Chen et al. [79]	c	he		x			x	bi	Min number of truck arrivals; Min waiting time	Queue of trucks	PFGA	53
Demir et al. [18]	r	-	x	x		-	-	-	Survey on road transport of green loads	Green loads	Review	260
Demir et al. [41]	c	ho	x				x	bi	Min fuel consumption; Min journey time	Logistical distributions	ALNS; weighting method; ε-constraint method	156
Govindan et al. [80]	c	he		x			x	bi	Min costs; Min environmental impact	Distribution of perishable food	AMOVNS; MOPSO	201
Khoo and Teoh [66]	c	he	x	x		x		bi	Max operational profit; Min Green Fleet Index (fuel, pollution and noise)	Commercial evaluation	Dynamic Programming	9
Lin et al. [20]	r	-	x	x	x	-	-	-	Survey on environmental consideration applied to VRP	Past and future trends	Review	314
Long et al. [81]	c	ni		x			x	bi	Min traffic congestion; Min environmental pollution	Urban road networks	Modified ABC	28
Ramos et al. [8]	c	he			x	x		tri	Min costs; Min CO2 emissions; Max working hours	Recyclable waste collection system	ε-constraint method	73
Validi et al. [82]	c	he		x			x	bi	Min costs; Min CO2 emissions	Milk distribution	MOGA-II; NSGA-II; Sequential Quadratic Programming.	92
Alexiou and Katsavounis [83]	g	ni		x		x		tri	Min costs; Min pollution; Min risk	Logistic distribution	DPH Procedure	5
Schaefer and Konur [84]	g	ho		x		x		bi	Min costs; Min CO2 emissions	Logistic distribution	Pareto Front approximation	19
Yang et al. [85]	g	he		x			x	tri	Min distribution cost; Max customer satisfaction; Min environmental pollution	Logistic distribution	Hybrid MOGA	14
Yu et al. [86]	c	ni			x	x		bi	Min costs; Min pollution	Garbage collection	Dynamic Programming	8
Amer et al. [14]	c	ni	x	x			x	tri	Min journey time; Min fuel consumption; Min CO2 emissions	Traffic congestion	Improved Simulated Annealing TOPSIS	9
Baykasoglu and Subulan [67]	c	ni	x	x		x		tri	Min total cost; Min journey time; Min CO2 emissions	Logistic distribution	Goal programming	20
Entezaminia et al. [55]	c	ho			x	x		bi	Min the supply chain cost; Max environmental criteria	Reverse logistics	LP-metrics method	35
Ghezavati and Beigi [16]	g	ho			x	x	x	bi	Min costs; Min journey time	Reverse logistics	NSGA-II	10
Govindan et al. [49]	c	ni			x	x	x	multi	Min costs; Min environmental impacts; Max social responsibility	Recycling of medical syringes	MOPSO; ε-constraint method	50
Niknamfar and Niaki [45]	g	he	x	x		x		bi	Max profit of all carriers; Max operational profit	Logistic distribution	Lexicographic	10
Psychas et al. [60]	g	ho	x				x	tri	Min route; Min journey time; Min fuel consumption	Logistic distribution	PMS-NSDEs	4
Rabbani et al. [51]	g	ho			x		x	bi	Min costs; Max social aspects	Waste collection	Hybrid NSGA-II	10
Rao et al. [61]	g	ho	x				x	bi	Min costs; Min fuel consumption	Logistic distribution	MOLS	7
Yin et al. [87]	c	he		x			x	bi	Min costs; Min makespan	Scheduling	Hyper heuristic AOC	14
Zeng et al. [88]	c	ni		x		x		bi	Min CO2 emissions; Min journey time	Navigation system	Linear programing	18
Zohal and Soleimani [44]	c	ho		x	x	x	x	tri	Max revenue; Min costs; Min CO2 emissions	Gold industry	MOACO	31
Al-e-hashem et al. [53]	g	ho		x			x	bi	Min costs; Min GHG emissions	Logistic distribution	Hybrid L-shaped method	3
Androutsopoulos and Zografos [54]	g	ho	x				x	bi	Min time; Min fuel consumption	Logistic distribution	MOACO	9
Coelho et al. [62]	c	he	x				x	multi	Min distance; Min time Min no. of drones (vehicles); Max speed; Min quantity to complete battery charge; Min registration time for collection; Min registration time for delivery	Drone use	Black-box dynamic search algorithm; MOSPOOLS	10
Fu et al. [17]	c	ni			x		x	bi	Min proportion of disposal waste; Min costs	Reverse logistics	MOPSO	3
Govindan et al. [42]	c	ho		x		x		tri	Min cost; Max supplier performance; Min CO2	Closed loop supply chain	MIP Fuzzy	13
Guo et al. [46]	g	ni		x			x	tri	Min CO2 emissions; Min waiting time; Min no. of vehicles	Logistic distribution	MOPSO	2
Gupta et al. [72]	c	he	x	x	x		x	tri	Min route costs; Max service quality; Min vehicular emissions	Eco logistics	MOSPEA	4
Hammad et al. [89]	c	ho		x		x		bi	Min noise; Min journey time	Noise pollution	MILP	9
Hassanzadeh and Rasti-Barzoki [63]	g	ni	x				x	bi	Min total delay cost; Min energy	Logistic distribution	VNSGA-II; NSGA-II	8
Heilig et al. [22]	c	ni		x			x	tri	Min costs; Min journey time; Min CO2 emissions	Inter-terminal transport	AMOSA	6
Kumar et al. [15]	c	ho	x	x			x	bi	Min costs; Min fuel consumption and consequent CO2 emissions	Logistic distribution	SLPSO	36
Norouzi et al. [58]	g	ni	x				x	bi	Min costs; Min fuel consumption	Logistic distribution	MOPSO	13
Ouhader and Kyal [48]	c	ho		x		x		tri	Min costs; Min CO2 emissions; Max work opportunities	Logistic distribution	ε-constraint method	6
Rabbani et al. [56]	g	he			x		x	tri	Min costs; Max response capacity (satisfaction); Min CO2 emissions	Reverse logistics	NSGA-II; MOPSO	3
Rahimi et al. [90]	c	he		x			x	tri	Max profit; Min delays; Min CO2 emissions	Perishable product	NSGA-II	16
Rani and Reddy [64]	g	ni	x				x	bi	Min “sharp values”; Min fuzzy	Logistic distribution	MOSPP	0
Toro et al. [6]	g	ho	x	x		x		bi	Min costs; Min GHG emission	Logistic distribution	ε-constraint method	15
Toro et al. [68]	g	he	x	x		x		bi	Min costs; Min fuel consumption and CO2 emissions	Logistic distribution	ε-constraint method	5
Tricoire and Parragh [75]	c	he		x		x	x	bi	Min costs; Min CO2 emissions	Logistic distribution	BIOBAB; 2-opt	6
Zhu and Hu [50]	g	he			x		x	tri	Min costs; Min environmental impacts; Max social responsibility	Reverse logistics	AUGMENCON	1
Abad et al. [11]	c	ho	x				x	bi	Min costs; Min fuel consumption	Cross docking	NRGA; MOPSO	6
Asadi et al. [57]	c	ni		x		x	x	bi	Min costs; Min CO2 emissions	Logistic distribution	NSGA-II; MOPSO	1
Chen et al. [91]	c	ho		x			x	bi	Min costs; Min CO2 emissions	Fleet of trucks	NSGA-II-TS (with Tabu Search)	2
Costa et al. [92]	g	ho		x			x	bi	Min CO2 emissions; Min wage costs	Logistic distribution	MOLS	0
Das and Jharkharia [69]	r	-		x		-	-	-	Review the relevant literature on low carbon supply chain management	Low carbon supply chain	Review	15
Ebrahimi [12]	c	he		x		x		tri	Min costs; Min CO2 emissions; Max response capacity of the integrated network	Closed supply chain (tires	ε-constraint method	4
Engeland et al. [93]	r	-			x	-	-	-	Integration of reverse supply chain and waste management literature	Waste Reverse Supply Chains	Review	0
FarrokhiAsl et al. [52]	g	he	x	x	x		x	tri	Min general costs, CO2 and fuel; Min transport risk; Min journey risk (site)	Reverse logistics	CA; MOPSO; NSGA-II; SPAE-II; MOSA	0
Fathollahi-Fard et al. [13]	c	he		x			x	bi	Min transport costs and distances; Min CO2 emissions	Home Health Care	MOSSA; MOSA	10
Gong et al. [74]	c	he	x		x		x	tri	Min fuel consumption; Min waiting time; Min distance for delivery	Logistic distribution	BEG-NSGA-II	0
Guo et al. [94]	c	ho		x			x	bi	Min costs; Min CO2 emissions	Transportation scheduling	ESMPO	7
Guo et al. [46]	g	ni		x			x	tri	Min CO2 emissions; Min waiting time (time window); Min number of vehicles	Logistic distribution	MOPSO	2
Liu et al. [76]	g	ni		x			x	bi	Min costs; Min CO2 emissions’	Logistic distribution	HQIA	4
Malladi e Sowlati [73]	r	-	x	x	x	-	-	-	Aspects of sustainability applied to the Inventory Routing Problem	Inventory Routing Problem	Review	2
Poonthalir and Nadarajan [5]	g	ho	x			x	x	bi	Min costs; Min fuel consumption	Logistic distribution	MOPSO	14
Rabbani et al. [59]	c	he		x		x	x	multi	Min costs; Min CO2 emissions; Min dissatisfaction; Max vehicle reliability	Logistic distribution	MOSA	4
Rad and Nahavandi [71]	c	he	x	x		x		tri	Min costs; Min CO2 emissions; Max customer satisfaction	Closed-loop green supply chain network	LP-metrics	5
Rau et al. [65]	c	ho	x				x	bi	Min costs; Min fuel, handling and energy	Logistic management	MOPSO	1
Shui and Szeto [70]	c	ni	x	x			x	bi	Min unmet demand; Min CO2 emission cost and fuel consumption	Bicycle replacement	EABC	10
Soleimani et al. [7]	c	ni	x	x	x	x		bi	Min costs; Min energy consumed (fuel)	Logistic distribution	Linear programming	11
Sun et al. [95]	c	ni		x		x		bi	Min costs; Min CO2 emissions	Multi-modal logistics	MNIP	6
Teoh et al. [96]	g	ni		x			x	bi	Min CO2 emissions; Min risks	Logistic distribution	MODE	0
Validi et al. [97]	c	he		x			x	bi	Min CO2 emissions; Min costs	Logistic distribution	MOGA-II	1
Wang et al. [47]	g	ho	x			x	x	bi	Min costs; Min number of vehicles	Reverse logistics	CW_NSGA-II	2
Wang et al. [43]	c	ni			x		x	bi	Min energy consumption; Min dissatisfaction	Logistic distribution	NSGA-II	0
Yu and Solvang [98]	g	he		x	x	x		bi	Max profit; Min environmental impact (CO2 emissions)	Reverse logistics	Weighting method; ε-constraint method	1
Zapata-Cortes et al. [99]	c	ni		x		x		tri	Min costs; Min inventory; Min CO2 emissions	Logistic distribution	Linear programming	0
Zhang et al. [100]	c	ni		x			x	tri	Min time; Min costs; Min CO2 emission	Medical emergencies	MOGA	2

---

Legend: ABC (artificial bee colony); ALNS (adaptive large neighborhood search algorithm); AMOSA (achieved multi-objective simulated annealing); AMOVNS (adapted multi-objective variable neighborhood search); AUGMENCON (augment constraint algorithm); BEG-NSGA-II (bee evolutionary algorithm guiding nondominated sorting genetic algorithm II); BIOBAB (bi-objective branch-and-bound); CA (Cultural algorithm); CW_NSGA-II (Clarke and Wright savings method and the non-dominated sorting genetic algorithm-II); EABC (enhanced artificial bee colony); ESMPO (evolution-strategy-based memetic pareto optimization); HQIA (hybrid quantum immune algorithm); MIP (mixed integer programming); MILP (mixed integer linear programming); MNIP (mixed non-linear integer programming); MOACO (multi-objective ant colony optimization); MODE (multi-objective differential evolution); MOGA (multi-objective genetic algorithm); MOGA-II (multi-objective genetic algorithm of kind II); MOLS (multi-objective Local Search); MOPSO (multi-objective particle swarm optimization); MOSPEA (metaheuristic optimization algorithm); MOSPOOLS (multi-objective smart pool search metaheuristic); MOSPP (multi objective shortest path problem); MOSSA (multi-objective salp swarm algorithm); NRGA (non-dominated ranking genetic algorithm); NSGA-II (non-dominated sorting genetic algorithm II); PFGA (pareto front genetic algorithms); PMS-NSDEs (parallel multi-start non-dominated sorting differential evolution algorithms); SLPSO (hybrid self-learning particle swarm optimization); TOPSIS (technique for order preference by similarity to ideal solution); VNSGA-II (multi-objective variable neighborhood search with non-dominated sorting genetic algorithm II).

---

The most cited works in the sample are presented in Table 4. The table is structured by references, journals, article type and number of citations obtained through SCOPUS. A description of these works, listed according to their number of citations, is given below.

Table 4 The 11 most cited articles in the sample to MOOGVRP

References	Journals	Types	No. of Citations
Dekker et al., [77]	European Journal of Operational Research	Review	353
Lin et al., [20]	Expert Systems with Applications	Review	314
Demir et al., [18]	European Journal of Operational Research	Review	260
Govindan et al., [80]	International Journal of Production Economics	Case	201
Demir et al., [41]	European Journal of Operational Research	Case	156
Validi et al., [82]	International Journal of Production Economics	Case	92
Ramos et al., [8]	Omega (United Kingdom)	Case	73
Chen et al., [79]	Transportation Research Part E	Case	53
Govindan et al., [49]	Ecological Indicators	Case	50
Ehrgott et al., [21]	Transportation Research Part A	Case	36
Kumar et al., [15]	Computers and Industrial Engineering	Case	36

The three most frequently cited works were literature reviews, conducted by Dekker et al. [77], Lin et al. [20] and Demir et al. [18]. Dekker et al. [77] proposed a contribution to the green logistic, promoting the integration of environmental aspects into the logistic. They addressed facilities, transport and inventory, considering the decision process through design, planning and control. Lin et al. [20] listed the main variations of the VRP, solution procedures (algorithms) and a proposed taxonomy for the VRP with environmental considerations (GVRP, PRP and VRPRL). A study on green road freight transportation was presented by Demir et al. [18], making use of different ways to measure CO₂ emissions and fuel consumption. They identified the criticality of factors to explain consumption, type of vehicle, freight, speed and road gradient, among others.

A case study addressing perishable food distribution was conducted by [80]. For this purpose, the authors used multi-objective particle swarm optimization (MOPSO), adapted multi-objective variable neighborhood search (AMOVNS) and the multi-objective hybrid approach (MHPV), comparatively. Seeking to optimize fuel consumption and journey time, Demir et al. [41] used the є-constraint together with the weighting method for the adaptive large neighborhood search algorithm (ALNS), in addition to a hybrid method (HM). With a view to obtaining a sustainable distribution by minimizing costs and CO₂ emission for milk transportation in Ireland, Validi et al. [82] presented a mixed integer linear programming (MILP) model and solved the problem through procedures derived from the GA: multi-objective GA of kind II (MOGA-II), NSGA-II (non-dominated sorting GA) and a Hybrid combining GA and sequential quadratic programming.

Ramos et al. [8] resolved a case study on a recyclable waste collection system in Portugal, more specifically, in 19 rural municipalities. This reverse logistics problem was modeled as a multi-depot periodic vehicle routing problem with inter-depot routes (MDPVRPI), using the є-constraint technique to solve it. The authors wished to comply with the triple bottom line of sustainability, considering minimizing costs and CO₂ emissions and maximizing working hours. Chen et al. [79] proposed a case involving a bi-objective model based on queues to reduce long lines of trucks at ports. The authors sought to minimize the number of truck arrivals and waiting time. For this purpose, they used the Pareto front genetic algorithms based heuristic (PFGA) and compared it with the NSGA type II. A fuzzy multi-objective model was proposed by Govindan et al. [49] to address the multi-echelon VRP and multi-period reverse logistics. The authors compared a PSO approach with the є-constraint. They applied the model to a case of medical syringe recycling for the purpose of minimizing costs and environmental impact and maximizing social responsibility.

Ehrgott et al. [21] presented a case study on the routing of bicycles in New Zealand, seeking to minimize journey time and maximize the adequacy of the routes that were used. Finally, Kumar et al. [15] presented production and pollution routing problems with time windows (PPRP-TW), in which they implemented the hybrid Self-Learning Particle Swarm Optimization (SLPSO). The authors sought to minimize costs and fuel consumption.

5. Final considerations and suggestions for future works

This study presented bibliometric data involving MOO for the Green Vehicle Routing Problem (MOOGVRP) from 2012 to 2018. This study adopted a protocol that resulted in 1,744 articles that, after a filtering definition, provided a sample of 76 articles from 38 journals. Its main contribution that it highlights the synergy between the VRP, MOO and the approach with EC, which is a relatively new trend that has grown in recent years. The bibliometric analysis was essential to understanding the profiles of published works.

To answer the first question of this survey (What are the most relevant studies regarding MOOGVRP?) the most relevant studies during the analyzed period were presented in Table 4, in which the three most frequently cited articles were reviews. Dekker et al. [77] and Demir et al. [18] addressed aspects related to logistics, while Lin et al. [20] sought to demonstrate the evolution and relationship of the VRP with environmental considerations. The other most frequently cited articles sought to improve techniques and apply them to real contexts.

To answer the second question (What are the trends regarding MOOGVRP that may guide future research?) the stratifications of Section 4 are of great importance. In this context, Table 3 summarized the proposal of the 76 articles focused on reviews, general application and case studies. The sample authors are associated with 96 institutions, research centers and companies, and the largest contributions, so far, have come from Iran, China, the USA and the UK. Figure 7 proved to be very interesting, as it shows the amount of work developed considering GVRP, PRP and VRPRL, as well as their interactions in the analyzed sample.

It was possible to verify the dominance of bi-objective models, which have been solved through heuristic, є-constraint and weighted procedures, with “a posteriori” Pareto optimization, based on Genetic Algorithm (GA) and Particle Swarm Optimization (PSO). The most used VRP procedures in the analyzed sample were the Location Routing Problem (LRP) and the Capacitated VRP (CVRP). As shown in Figure 13, the main objectives addressed in the problems were to minimize costs, fuel consumption and CO₂ emissions. There was great concern over improving the studies related to the reduction of GHG emission and the considerations of reverse logistics.

Many opportunities to explore applications and techniques related to MOOGVRP remain. We hope that the information presented here can aid those interested in their future research. Thus, by “going against the grain” of the most frequently researched themes, there is a great opportunity to make unprecedented contributions, of which the following may be mentioned:

1. Seeking heuristic procedures that have not often been used for multi-objective problems, duly adapted to the contexts in question, such as open, pickup time, multi-product and multi-modal (variations of the MOO-VRP least used in the sample of this study);
2. Although already widespread, seeking hybrid heuristic procedures to improve algorithms used in the context of the MOO-VRP;
3. Exploring applications that involve 4 or more objectives due to the serious lack of such applications in the literature;
4. Developing studies with large instances given the computational difficulty;
5. Presenting works that address the relationships between the MOO-GVRP, MOO-PRP and MOO-VRPRL or all of them simultaneously;
6. Use other types of documents, such as conference papers, book, dissertation or thesis;
7. Use other types of vehicles;
8. Use other databases to compare and complement the sample;
9. Other bibliometric (or review) techniques to expand the analysis;
10. Evaluate the relationship with the triple bottom line.

Acknowledgements

This study was financed in part by PUCPR and the Coordination for the Improvement of Higher Education Personnel - Brazil (CAPES; 1st author), Finance code 001 and by the National Council for Scientific and Technological Development – Brazil (CNPq; 2nd and 3rd authors).

References

[1] Conheça os novos 17 Objetivos de desenvolvimento sustentável da ONU. ONUBR, September 25th, 2015. Available in: [<https://nacoesunidas.org/conheca-os-novos-17-objetivos-de-desenvolvimento-sustentavel-da-onu/amp/>.] Access in: February 15th, 2019.

[2] US EPA. Inventory of U.S. Greenhouse gas emissions and sinks: 1990-2016. EPA 430-R-2018-003, 2018.

[3] Dantzing G.B., Ramser J.H. The truck dispatching problem. Manage. Sci., 6:80–91, 1959.

[4] Validi S., Bhattacharya A., Byrne P.J. A solution method for a two-layer sustainable supply chain distribution model. Comput. Oper. Res., 54:204–217, 2015.

[5] Poonthalir G., Nadarajan R. A Fuel Efficient Green Vehicle Routing Problem with varying speed constraint (F-GVRP). Expert Survey of Green Vehicle Routing Problem: Past and future trends Syst. Appl., 100:131–144, 2018.

[6] Toro E.M., Franco J.F., Echeverri M.G., Guimarães F.G. A multi-objective model for the green capacitated location-routing problem considering environmental impact. Comput. Ind. Eng., 110:114–125, 2017a.

[7] Soleimani H., Chaharlang Y., Ghaderi H. Collection and distribution of returned-remanufactured products in a vehicle routing problem with pickup and delivery considering sustainable and green criteria. J. Clean Prod., 172:960–970, 2018.

[8] Ramos T.R.P., Gomes M.I., Barbosa-Póvoa A.P. Planning a sustainable reverse logistics system: Balancing costs with environmental and social concerns. Omega (United Kingdom), 48:60–74, 2014.

[9] Steiner M.T.A., Datta D., Steiner Neto P.J., Scarpin C.T., Figueira J.R. Multi-objective optimization in partitioning the healthcare system of parana state in brazil. Omega (United Kingdom), 52:53–64, 2015.

[10] Steiner Neto P.J., Datta D., Steiner M.T.A., Canciglieri Júnior O., Figueira J.R., Detro S.P., Scarpin C.T. A multi-objective genetic algorithm based approach for location of grain silos in Paraná State of Brazil. Comput. Ind. Eng., 111:381–390, 2017.

[11] Abad H.K.E.A., Vahdani B., Sharifi M., Etebari F. A bi-objective model for pickup and delivery pollution-routing problem with integration and consolidation shipments in cross-docking system. J. Clean Prod., 193:784–801, 2018.

[12] Ebrahimi S.B. A stochastic multi-objective location-allocation-routing problem for tire supply chain considering sustainability aspects and quantity discounts. J. Clean Prod., 198:704–720, 2018.

[13] Fathollahi-Fard A.M., Hajiaghaei-Keshteli M.H-K., Tavakkoli-Moghaddam R. A Bi-objective green home health care routing problem. J. Clean Prod., 200:423–443, 2018.

[14] Amer H., Salman N., Hawes M., Chaqfeh M., Mihaylova L., Mayfield M. An improved simulated annealing technique for enhanced mobility in smart cities. Sensors (Switzerland), 16:1–23, 2016.

[15] Kumar R.S., Kondapaneni K., Dixit V., Goswami A., Thakur L.S., Tiwari M.K. Multi-objective modeling of production and pollution routing problem with time window: A self-learning particle swarm optimization approach. Comput. Ind. Eng., 99:29–40, 2016.

[16] Ghezavati V.R., Beigi M. Solving a bi-objective mathematical model for location-routing problem with time windows in multi-echelon reverse logistics using metaheuristic procedure. J. Ind. Eng. Int., 12:469–483, 2016.

[17] Fu P., Li H., Wang X., Luo J., Zhan S.L., Zuo C. Multiobjective Location Model Design Based on Government Subsidy in the Recycling of CDW. Math Probl Eng, 2017. https://doi.org/10.1155/2017/9081628

[18] Demir E., Bektaş T., Laporte G. The bi-objective Pollution-Routing Problem. Eur. J. Oper. Res., 232:464–478, 2014a.

[19] Szejka A.L., Canciglieri O., Panetto H., Loures E.R., Aubry A. Semantic interoperability for an integrated product development process: A systematic literature review. Int. J. Prod. Res., 55:6691–6709, 2017.

[20] Lin C., Choy K.L., Ho G.T.S., Chung S.H., Lam H.Y. Survey of Green Vehicle Routing Problem: Past and future trends. Expert Syst. Appl., 41:1118–1138, 2014.

[21] Ehrgott M., Wang J.Y.T., Raith A., Van Houtte C. A bi-objective cyclist route choice model. Transp. Res. Part A: Policy Pract., 46:652–663, 2012.

[22] Heilig L., Lalla-Ruiz E., Voß S. Multi-objective inter-terminal truck routing. Transp. Res. Part E: Logist. Transp. Rev., 106:178–202, 2017.

[23] Braekers K., Ramaekers K., Van Nieuwenhuyse I. The vehicle routing problem: State of the art classification and review. Comput. Ind. Eng., 99:300–313, 2016.

[24] Speidel, V. EDP-assisted fleet scheduling in tramp and coastal shipping. In Proceedings of the 2nd international ship operation automation symposium, 1976.

[25] Golden, B.L., Assad, A., Dahl, R. Analysis of a large scale vehicle routing problem with an inventory component. Large Scale Systems, 7: 181–190, 1984.

[26] Cheng, R., Gen, M., Tozawa, T. Vehicle routing problem with fuzzy duetime using genetic algorithms. Japan Society for Fuzzy Theory and Systems, 7:1050–1061, 1995.

[27] Tsiligirides, T. Heuristic methods applied to orienteering. Journal of the Operational Research Society, 35:797–809, 1984.

[28] Bell, W.J., Dalberto, L.M., Fisher, M.L., Greenfield, A.J., Jaikumar, R., Kedia, P. (1983). Improving the distribution of industrial gases with an on-line computerized routing and scheduling optimizer. Interfaces, 13(6), 4–23.

[29] Watson-Gandy, C., Dohm, P. Depot location with van salesmen – a practical approach. Omega, 1:321–329, 1973.

[30] Christophides, N. Vehicle routing. In E. L. Lawler, J. K. Lenstra, A. H. G. Rinnooy Kan, D. B Shmoys (Eds.), The traveling salesman problem: a guided tour of combinatorial optimization. John Wiley and Sons Ltd, 1985.

[31] Tillman, F. A. The multiple terminal delivery problem with probabilistic demands. Transportation Science, 3:192–204, 1969.

[32] Crainic, T.G., Ricciardi, N., Storchi, G. Models for evaluating and planning city logistics systems. Transportation Science, 43:432–454, 2009.

[33] Sariklis, D., Powell, S. A heuristic method for the open vehicle routing problem. Journal of the Operational Research Society, 51:564–573, 2000.

[34] Beltrami, E.J., Bodin, L.D. Networks and vehicle routing for municipal waste collection. Networks, 4:65–94, 1974.

[35] Wilson, H., Weissberg, H. Advanced dial-a-ride algorithms research project: final report. Technical Report. R76-20, Department of Civil Engineering, MIT, Cambridge, MA, 1967.

[36] Nag, B. Vehicle routing in the presence of site/vehicle dependency constraints. Ph.D. Dissertation, College of Business and Management, University of Maryland at College Park, 1986.

[37] Dror, M., Trudeau, P. Savings by split delivery routing. Transportation Science, 23(2):141–149, 1989.

[38] Cooke, K.L., Halsey, E. The shortest route through a network with timedependent internodal transit times. Journal of Mathematical Analysis and Applications, 14(3):493–498, 1966.

[39] Iori, M., Salazar-González, J.J., Vigo, D. An exact approach for the symmetric capacitated vehicle routing problem with two dimensional loading constraints. Technical Report OR/03/04, DEIS, Università di Bologna, Bologna, Italy, 2003.

[40] Russell, R. An effective heuristic for the M-Tour traveling salesman problem with some side conditions. Operations Research, 25:517–524, 1977.

[41] Demir E., Bektaş T., Laporte G. A review of recent research on green road freight transportation. Eur. J. Oper. Res., 237:775–793, 2014b.

[42] Govindan K., Darbari J.D., Agarwal V., Jha P.C. Fuzzy multi-objective approach for optimal selection of suppliers and transportation decisions in an eco-efficient closed loop supply chain network. J. Clean Prod., 165:1598–1619, 2017.

[43] Wang S., Wang X., Liu X., Yu J. A bi-objective vehicle-routing problem with soft time windows and multiple depots to minimize the total energy consumption and customer dissatisfaction. Sustain, 10:1-21, 2018b.

[44] Zohal M., Soleimani H. Developing an ant colony approach for green closed-loop supply chain network design: a case study in gold industry. J. Clean Prod., 133:314–337, 2016.

[45] Niknamfar A.H., Niaki S.T.A. Fair profit contract for a carrier collaboration framework in a green hub network under soft time-windows: Dual lexicographic max-min approach. Transp. Res. Part E: Logist. Transp. Rev., 91:129–151, 2016.

[46] Guo Y., Cheng J., Luo S., Gong D. Robust Dynamic multi-objective vehicle routing optimization method. IEEE/ACM Trans. Comput. Biol. Bioinforma, 5963:1–13, 2017.

[47] Wang Y., Peng S., Assogba K., Liu Y., Wang H., Xu M., Wang Y. Implementation of cooperation for recycling vehicle routing optimization in two-echelon reverse logistics networks. Sustain, 10:1-27, 2018a.

[48] Ouhader H., El kyal M. Combining Facility Location and Routing Decisions in Sustainable Urban Freight Distribution under Horizontal Collaboration: How Can Shippers Be Benefited? Math. Probl. Eng., 2017:1-18, 2017.

[49] Govindan K., Paam P., Abtahi A.R. A fuzzy multi-objective optimization model for sustainable reverse logistics network design. Ecol. Indic., 67:753–768, 2016.

[50] Zhu L., Hu D. Sustainable Logistics Network Modeling for Enterprise Supply Chain. Math. Probl. Eng., 1-11, 2017.

[51] Rabbani M., Farrokhi-Asl H., Asgarian B. Solving a bi-objective location routing problem by a NSGA-II combined with clustering approach: application in waste collection problem. J. Ind. Eng. Int., 13:13–27, 2016.

[52] Farrokhi-Asl H., Makui A., Jabbarzadeh A., Barzinpour F. Solving a multi-objective sustainable waste collection problem considering a new collection network. Oper. Res., 2018. https://doi.org/10.1007/s12351-018-0415-0

[53] Al-e-hashem S.M.J.M., Rekik Y., Hoseinhajlou E.M. A hybrid L-shaped method to solve a bi-objective stochastic transshipment-enabled inventory routing problem. Int. J. Prod. Econ., 1–18, 2017.

[54] Androutsopoulos K.N., Zografos K.G. An integrated modelling approach for the bicriterion vehicle routing and scheduling problem with environmental considerations. Transp. Res. Part C: Emerg. Technol., 82:180–209, 2017.

[55] Entezaminia A., Heydari M., Rahmani D. A multi-objective model for multi-product multi-site aggregate production planning in a green supply chain: Considering collection and recycling centers. J. Manuf. Syst., 40:63–75, 2016.

[56] Rabbani M., Saravi N.A., Farrokhi-Asl H. Design of a forward/reverse logistics network with environmental considerations. Int. J. Supply Oper. Manag., 4:115–132, 2017.

[57] Asadi E., Habibi F., Nickel S., Sahebi H. A bi-objective stochastic location-inventory-routing model for microalgae-based biofuel supply chain. Appl. Energy, 228:2235–2261, 2018.

[58] Norouzi N., Sadegh-Amalnick M., Tavakkoli-Moghaddam R. Modified particle swarm optimization in a time-dependent vehicle routing problem: minimizing fuel consumption. Optim Lett, 11:121-134, 2017.

[59] Rabbani M., Aghamohammadi Bosjin S., Yazdanparast R., Akbarian Saravi N. A stochastic time-dependent green capacitated vehicle routing and scheduling problem with time window, resiliency and reliability: a case study. Decis. Sci. Lett., 7:381–394, 2018.

[60] Psychas I.D., Marinaki M., Marinakis Y., Migdalas A. Non-dominated sorting differential evolution algorithm for the minimization of route based fuel consumption multiobjective vehicle routing problems. Energy Syst., 8:785–814, 2016.

[61] Rao W., Liu F., Wang S. An Efficient Two-objective hybrid local search algorithm for solving the fuel consumption Vehicle Routing Problem. Appl. Comput. Intell. Soft. Comput., 2016:1–16, 2016.

[62] Coelho B.N., Coelho V.N., Coelho I.M., Ochi L.S., Haghnazar K.R., Zuidema D., Lima M.S.F., da Costa A.R. A multi-objective green UAV routing problem. Comput. Oper. Res., 88:306–315, 2017.

[63] Hassanzadeh A., Rasti-Barzoki M. Minimizing total resource consumption and total tardiness penalty in a resource allocation supply chain scheduling and vehicle routing problem. Appl. Soft. Comput. J., 58:307–323, 2017.

[64] Rani G.V., Reddy B. Multi-objective fuzzy shortest path selection for green routing and scheduling problems. Int. J. Adv. Res. Comput. Sci., 8:470–475, 2017.

[65] Rau H., Budiman S.D., Widyadana G.A. Optimization of the multi-objective green cyclical inventory routing problem using discrete multi-swarm PSO method. Transp. Res. Part E: Logist. Transp. Rev., 120:51–75, 2018.

[66] Khoo H.L., Teoh L.E. A bi-objective dynamic programming approach for airline green fleet planning. Transp. Res. Part D: Transp. Environ., 33:166–185, 2014.

[67] Baykasoğlu A., Subulan K. A multi-objective sustainable load planning model for intermodal transportation networks with a real-life application. Transp. Res. Part E: Logist. Transp. Rev., 95:207–247, 2016.

[68] Toro E.M., Franco J.F., Echeverri M.G., Guimarães F.G., Gallego Rendón R.A. Green open location-routing problem considering economic and environmental costs. Int. J. Ind. Eng. Comput., 8:203–216, 2017b.

[69] Das C., Jharkharia S. Low carbon supply chain: A state-of-the-art literature review. J. Manuf. Technol. Manag., 29:398–428, 2018.

[70] Shui C.S., Szeto W.Y. Dynamic green bike repositioning problem – A hybrid rolling horizon artificial bee colony algorithm approach. Transp. Res. Part D: Transp. Environ., 60:119–136, 2018.

[71] Rad R.S., Nahavandi N. A novel multi-objective optimization model for integrated problem of green closed loop supply chain network design and quantity discount. J. Clean Prod., 196:1549–1565, 2018.

[72] Gupta A., Heng C.K., Ong Y.S., Tan P.S., Zhang A.N. A generic framework for multi-criteria decision support in eco-friendly urban logistics systems. Expert Syst. Appl., 71:288–300, 2017.

[73] Malladi K.T., Sowlati T. Sustainability aspects in Inventory Routing Problem: A review of new trends in the literature. J. Clean Prod., 197:804–814, 2018.

[74] Gong X., Deng Q., Gong X., Zhang L., Wang H., Xie H. A Bee Evolutionary Algorithm for multiobjective Vehicle Routing Problem with Simultaneous Pickup and Delivery. Math. Probl. Eng., 2018:1–21, 2018.

[75] Tricoire F., Parragh S.N. Investing in logistics facilities today to reduce routing emissions tomorrow. Transp. Res. Part B: Methodol., 103:56–67, 2017.

[76] Liu X.H., Shan M.Y., Zhang R.L., Zhang L.H. Green Vehicle Routing Optimization Based on Carbon Emission and Multiobjective Hybrid Quantum Immune Algorithm. Math. Probl. Eng., 2018:1–9, 2018.

[77] Dekker R., Bloemhof J., Mallidis I. Operations Research for green logistics - An overview of aspects, issues, contributions and challenges. Eur. J. Oper. Res., 219:671–679, 2012.

[78] Liu H., Wang W., Zhang Q. Multi-objective location-routing problem of reverse logistics based on GRA with entropy weight. Grey Syst. Theory Appl., 2:249–258, 2012.

[79] Chen G., Govindan K., Golias M.M. Reducing truck emissions at container terminals in a low carbon economy: Proposal of a queueing-based bi-objective model for optimizing truck arrival pattern. Transp. Res. Part E: Logist. Transp. Rev., 55:3–22, 2013.

[80] Govindan K., Jafarian A., Khodaverdi R., Devika K. Two-echelon multiple-vehicle location-routing problem with time windows for optimization of sustainable supply chain network of perishable food. Int. J. Prod. Econ., 152:9–28, 2014.

[81] Long J., Szeto W.Y., Huang H.J. A bi-objective turning restriction design problem in urban road networks. Eur. J. Oper Res., 237:426–439, 2014.

[82] Validi S., Bhattacharya A., Byrne P.J. A case analysis of a sustainable food supply chain distribution system - A multi-objective approach. Int. J. Prod. Econ., 152:71–87, 2014.

[83] Alexiou D., Katsavounis S. A multi-objective transportation routing problem. Oper. Res., 15:199–211, 2015.

[84] Schaefer B., Konur D. Economic and environmental considerations in a continuous review inventory control system with integrated transportation decisions. Transp. Res. Part E: Logist. Transp. Rev., 80:142–165, 2015.

[85] Yang B., Hu Z.H., Wei C., Li S.Q., Zhao L., Jia S. Routing with time-windows for multiple environmental vehicle types. Comput. Ind. Eng., 89:150–161, 2015.

[86] Yu H., Solvang W.D., Li S. Optimization of long-term performance of municipal solid waste management system: A bi-objective mathematical model. Int. J. Energy Environ., 6:153–164, 2015.

[87] Yin P.Y., Lyu S.R., Chuang Y.L. Cooperative coevolutionary approach for integrated vehicle routing and scheduling using cross-dock buffering. Eng. Appl. Artif. Intell., 52:40–53, 2016.

[88] Zeng W., Miwa T., Morikawa T. Prediction of vehicle CO2emission and its application to eco-routing navigation. Transp. Res. Part C: Emerg. Technol., 68:194–214, 2016.

[89] Hammad A.W.A., Akbarnezhad A., Rey D. Sustainable urban facility location: Minimising noise pollution and network congestion. Transp. Res. Part E: Logist. Transp. Rev., 107:38–59, 2017.

[90] Rahimi M., Baboli A., Rekik Y. Multi-objective inventory routing problem: A stochastic model to consider profit, service level and green criteria. Transp. Res. Part E: Logist. Transp Rev., 101:59–83, 2017.

[91] Chen C., Qiu R., Hu X. The Location-Routing Problem with Full Truckloads in Low-Carbon Supply Chain Network Designing. Math. Probl. Eng., 2018:1-13, 2018.

[92] Costa L., Lust T., Kramer R., Subramanian A. A two-phase Pareto local search heuristic for the bi-objective pollution-routing problem. Networks, 72:311–336, 2018.

[93] Engeland J.V., Beliën J., De Boeck L., De Jaeger S. Literature review: Strategic network optimization models in waste reverse supply chains. Omega (United Kingdom), 2018. https://doi.org/10.1016/j.omega.2018.12.001

[94] Guo Z., Zhang D., Liu H., He Z., Shi L. Green transportation scheduling with pickup time and transport mode selections using a novel multi-objective memetic optimization approach. Transp. Res. Part D: Transp. Environ., 60:137–152, 2018.

[95] Sun Y., Hrušovský M., Zhang C., Lang M. A Time-dependent fuzzy programming approach for the green multimodal routing problem with rail service capacity uncertainty and road traffic congestion. Complexity, 2018:1–22, 2018.

[96] Teoh B.E., Ponnambalam S.G., Subramanian N. Data driven safe vehicle routing analytics: a differential evolution algorithm to reduce CO 2 emissions and hazardous risks. Ann. Oper. Res., 270:515–538, 2018.

[97] Validi S., Bhattacharya A., Byrne P.J. Sustainable distribution system design: a two-phase DoE-guided meta-heuristic solution approach for a three-echelon bi-objective AHP-integrated location-routing model. Ann. Oper. Res., 1–32, 2018.

[98] Yu H., Solvang W.D. Incorporating flexible capacity in the planning of a multi-product multi-echelon sustainable reverse logistics network under uncertainty. J. Clean Prod., 198:285–303, 2018.

[99] Zapata-cortes J.A., Arango-serna M.D., Serna-urán C.A. Comparison of three IRP-based models to reduce logistics costs and greenhouse gas emissions. Dyna, 85:199–204, 2018.

[100] Zhang B., Li H., Li S., Peng J. Sustainable multi-depot emergency facilities location-routing problem with uncertain information. Appl. Math. Comput., 333:506–520, 2018.