Experimental characterisation of the translaminar fracture toughness of an additive manufacturing c-CFRP composite

1. Introducción

Los laminados de material compuesto y las estructuras fabricadas con ellos experimentan diversos mecanismos de daño antes de llegar a un completo fallo estructural. La evaluación adecuada de estos mecanismos de iniciación y propagación de la fractura, así como la caracterización de la tenacidad a la fractura asociada a ellos, son factores clave para el desarrollo de estructuras de materiales compuestos reforzados con fibra. En particular, la falla translaminar ocurre cuando una grieta se propaga a través de todas las capas que forman un laminado, causando un daño catastrófico. Este tipo de fractura involucra varios mecanismos de daño, como la rotura de fibras, grietas en la matriz, “fibre-bridging” i “pull-outs” de fibra, que disipan altas cantidades energía [1,2]. Por lo tanto, la evaluación de la tenacidad a la fractura translaminar es determinante para una caracterización adecuada del material y unas predicciones numéricas precisas del comportamiento de estructuras compuestas.

Los mecanismos de daño involucrados en laminados compuestos de fabricación aditiva reforzados con fibra continua son los mismos que se pueden encontrar en estructuras de materiales compuestos tradicionales. Sin embargo, las propiedades relacionadas con la fractura de estos materiales de fabricación aditiva aún no se han evaluado profundamente, en parte, debido a la relativamente reciente aparición de esta tecnología de fabricación. La impresora 3D Markforged® Mark Two™ [3] fue una de las primeras disponibles en el mercado para la fabricación de materiales compuestos con refuerzo de fibra continua, utilizando tecnología de fabricación por filamento fundido (FFF). Hasta la fecha, varios estudios han caracterizado las propiedades mecánicas en el plano de polímeros reforzados con fibra continua de carbono (c-CFRP) fabricados con la Mark Two™ [4-7], así como su tenacidad a la fractura interlaminar [6-11]. En cambio, la tenacidad a la fractura translaminar en este tipo de materiales no ha sido prácticamente objeto de estudio. Recientemente, Huang y Joosten [12] investigaron la tenacidad a la fractura translaminar en laminados de c-CFRP impresos en 3D usando ensayos experimentales “compact tension” (CT). Estudiaron dos tipos de estructuras, una con una arquitectura de capas semi-tejida y otra con capas (0°/90°). Obtuvieron una tenacidad a la fractura translaminar más baja en comparación con un laminado preimpregnado de carbono-epoxi, principalmente debido al menor porcentaje de fibra y al propio proceso de fabricación. En ambos casos la tenacidad a la fractura fue similar, pero en este último caso, se observaron restos de fibra (“pull-outs”) más largos para el laminado 0/90. Aun así, no analizaron la presencia de otros mecanismos de daño durante los ensayos, factor que puede influir en la correcta caracterización de la tenacidad a la fractura. Asimismo, tampoco determinaron el valor de la tenacidad translaminar asociado a la rotura de fibra.

Generalmente, la tenacidad a la fractura translaminar en compuestos se ha obtenido con ensayos experimentales de CT [13-17] basados en el estándar ASTM E399-90 [18], desarrollado inicialmente para materiales metálicos e isotrópicos. Sin embargo, algunos autores demostraron que esta geometría puede no ser válida para materiales compuestos en ciertos casos debido a la aparición de pandeo o daño por compresión en el extremo opuesto a la aplicación de la carga [19,20]. Blanco et al. [21] propusieron una geometría con doble biselado (2TCT), especialmente indicada para materiales con tenacidad a la fractura translaminar relativamente alta, pero con rigidez y resistencia a la compresión relativamente bajas. La geometría propuesta demostró ser adecuada por prevenir otros mecanismos de daño durante el ensayo de CT, a parte de la propia propagación de la grieta translaminar.

Este estudio evalúa la tenacidad a la fractura translaminar de laminados c-CFRP de fabricación aditiva utilizando probetas con doble biselado (2TCT) para los ensayos de “compact tension”. Además, se ha determinado la fractura translaminar asociada a la rotura de la fibra a tensión. Con el objetivo de descartar la presencia de cualquier daño no deseado fuera del plano de fractura, las probetas han sido inspeccionadas con rayos X posteriormente a los ensayos experimentales.

2. Diseño paramétrico

2.1 Definición de propiedades

Para la fabricación aditiva de las probetas ensayadas en este estudio se utilizó la impresora 3D Mark Two™ de Markforged® [3]. Las probetas se fabricaron con filamento termoplástico reforzado con fibra continua de carbono (c-CFRP). Este filamento está compuesto por aproximadamente mil fibras de carbono T300, impregnadas en una matriz de poliamida (PA6), con un porcentaje de fibra en volumen del 35% [22,23]. El porcentaje de porosidad en las piezas fabricadas es relativamente alto, reportando valores de entre el 8% y el 12% [23-25].

Las propiedades mecánicas del material consideradas en este estudio se muestran resumidas en la Tabla 1 [6,7]. Todas las probetas se fabricaron con una arquitectura [90/0]_ns (considerando la carga aplicada en la dirección 0°), usando una densidad de relleno del 100% y un grosor de capa de 0,125 mm. El resto de los parámetros de impresión son fijos y predeterminados por el sistema de la impresora. Las dimensiones definitivas, así como los agujeros de carga y la pre-grieta se mecanizaron posteriormente a la impresión de las probetas según la geometría definida en la Sección 2.3.

Tabla 1. Propiedades mecánicas en el plano del c-CFRP de fabricación aditiva suministrado por Markforged® [6,7].

Modulo elástico longitudinal, ${\textstyle {E}_{12}}$	66500 MPa
Modulo elástico transversal, ${\textstyle {E}_{22}}$	3500 MPa
Modulo elástico cortante, ${\textstyle {G}_{12}}$	1910 MPa
Coeficiente de Poisson, ${\textstyle {\upsilon }_{12}}$	0,39
Resistencia longitudinal a tracción, ${\textstyle {X}^{t}}$	752 MPa
Resistencia longitudinal a compresión, ${\textstyle {X}^{c}}$	426 MPa
Resistencia transversal a tracción, ${\textstyle {Y}^{t}}$	18 MPa
Resistencia transversal a compresión, ${\textstyle {Y}^{c}}$	66 MPa
Resistencia a cortante, ${\textstyle S}$	49 MPa

2.2 Determinación de la geometría de probeta más apropiada

En una fase inicial, se consideró la geometría CT estandarizada (ASTM E399-90) y distintas variaciones geométricas de ésta para determinar la tenacidad a la fractura translaminar del c-CFRP de Markforged®. Sin embargo, mediante un análisis paramétrico preliminar por elementos finitos se pudo comprobar que no es adecuada para la caracterización de la tenacidad a la fractura translaminar de este material. Así pues, se consideró la geometría 2TCT propuesta por Blanco et al. [21], con el principal propósito de reducir las tensiones de compresión en la parte superior, inferior y trasera de la probeta.

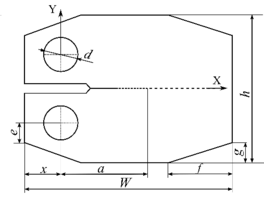
Se establecieron diferentes parámetros geométricos para la probeta 2TCT (Figura 1) y se realizó un análisis paramétrico, basado en el estudio de Blanco et al. [21], para determinar su efecto en los diferentes mecanismos de daño. Durante el análisis paramétrico, se varió un único parámetro a la vez. También se tuvo en cuenta el efecto de la longitud de la grieta para asegurar la determinación experimental de la tenacidad a la fractura translaminar para la propagación. El rango considerado para la longitud de la grieta fue entre 20 y 70 mm. Finalmente, una vez determinada la geometría definitiva de la probeta también se analizó el efecto del espesor del laminado para evitar el pandeo en la parte trasera de la probeta debido a las altas tensiones de compresión, considerando un rango de espesores entre 3 y 5 mm.

Figura 1. Esquema con los respectivos parámetros geométricos de la geometria 2TCT. La orientación a 0° esta orientada siguiendo el eje Y.

En el análisis paramétrico se consideraron los mismos mecanismos de daño que los considerados previamente en otros estudios [21,26]: (FM₁) fractura de fibras por compresión longitudinal ( ${\textstyle {\sigma }_{yy}}$) en el extremo posterior, (FM₂) fractura de fibras por compresión longitudinal ( ${\textstyle {\sigma }_{xx}}$) en los extremos inferior y superior, (FM₃) fallo en la matriz por cortante ( ${\textstyle {\sigma }_{xy}}$), (FM₄) aplastamiento en los agujeros de carga por compresión, (FM₅) fractura por cortante en los agujeros i (FM₆) pandeo en el extremo posterior, i sus correspondientes índices de fallo (FI_i)

El análisis paramétrico se realizó con elementos finitos utilizando Abaqus, modelando cada geometría por completo. Las simulaciones se combinaron con VCCT [27] para calcular la tasa de liberación de energía, ${\textstyle G}$, asociada a la propagación de la grieta translaminar. En todos los modelos se utilizaron elementos S8R5, con un tamaño de malla de 1 × 1 mm, y se aplicó una carga vertical unitaria en el agujero de carga. Los valores obtenidos de ${\textstyle G}$ se compararon con la energía de fractura translaminar, ${\textstyle {G}_{Ic}}$, aproximada como 37,5 N/mm para este mismo material y configuración del laminado [12]. Los índices de daño se calcularon a partir de la proporcionalidad establecida entre la raíz cuadrada de ${\textstyle G}$ y la tensión, ${\textstyle \sigma }$ .

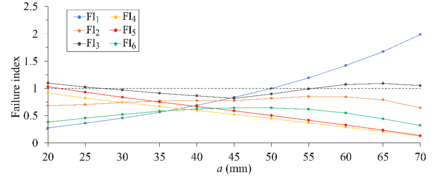
Los resultados del análisis paramétrico de la probeta 2TCT se presentan en la Figura 2. Por claridad y concreción solo se reporta la variación de los índices de fallo con la longitud de grieta para la geometría más adecuada. En la figura se puede observar que el índice FI₁ es el más crítico, alcanzando valores superiores a 1 en longitudes de grieta superiores a 50 mm, lo que correspondería a una eventual falla de la probeta por compresión longitudinal ( ${\textstyle {\sigma }_{yy}}$) en el extremo posterior después de 30 mm de propagación. Aunque FI₃ también es superior al valor crítico para ciertos valores de grieta, no fue posible determinar una combinación de parámetros geométricos con mejores resultados que los mostrados en la Figura 2. Además, el valor máximo de FI₃ es 1.1, ocurriendo esto al principio de la propagación o para grandes longitudes de grieta, una vez la probeta ya habría fallado por compresión en la cara posterior. Por estos motivos, se considera que en este caso el posible efecto en la determinación experimental de la tenacidad a la fractura translaminar del material es poco importante. El resto de los índices de fallo se mantienen inferiores a 1.

Figura 2. Variación de los índices de fallo obtenidos con el análisis paramétrico para la geometría más adecuada de la probeta 2TCT

A partir de estos resultados, la geometría 2TCT óptima considerada para la fabricación de las probetas corresponde a: ${\textstyle W}$ = 92, ${\textstyle h}$ = 50, ${\textstyle e}$ = 12, ${\textstyle x\,}$ = 11, ${\textstyle d}$ = 12, ${\textstyle \,f}$ = 35, ${\textstyle g}$ = 2. El espesor de la probeta se ha considerado de 4,5 mm para reducir FI₆ y evitar cualquier posible efecto de pandeo.

3. Metodología experimental

La campaña experimental se realizó con una máquina universal electromecánica MTS, equipada con una célula de carga de 5 kN. Los ensayos se realizaron con desplazamiento controlado a 0,5 mm/min. Se ensayaron un total de seis cupones 2TCT con la geometría definida en la Sección 2.2. Para un correcto seguimiento de la propagación de la grieta, se empleó una cámara de alta resolución a 3,3 fps sincronizada con la máquina de ensayo. La apertura de la grieta se determinó usando un extensómetro para la medición de apertura de grieta (COD) modelo 3541 de Epsilon, colocado en el eje de aplicación de carga. Para cada ensayo, se relacionó la carga con la correspondiente apertura y longitud de la grieta. El montaje experimental se muestra en la Figura 3.

Figura 3. Equipamiento y montaje empleados para los ensayos 2TCT.

Después del ensayo, algunas de las probetas se usaron para observar las superficies de fractura mediante microscopia. El resto de las probetas se reservaron para observaciones por rayos X para descartar cualquier generación de daño fuera del plano de propagación de la grieta. Para aumentar el contraste en las imágenes de rayos X y detectar adecuadamente cualquier daño o delaminación, las probetas se sumergieron en líquido de contraste antes de la inspección. El equipo de rayos X empleado en este caso dispone de una fuente de 20 W de potencia con un punto focal de 5 μm, con un detector de 2400 x 2400 píxeles. Para las inspecciones de las probetas con radiografias se usó un voltaje de 45 V y una intensidad de 120 μA, con una resolución de 27 μm/px y 3 integraciones por imagen.

4. Discusión de resultados

4.1 Evaluación del daño

La propagación de la grieta se rastreó durante el ensayo sin problema y no se observó ningún otro mecanismo de daño. La grieta se propagó en el plano inicial perpendicularmente a la dirección de la carga sin presencia de pandeo o torsión. Observando la superficie de fractura, puede verse que la superficie presenta “pull-outs” de fibras distribuidos regularmente a lo largo del plano de la grieta (Figura 4a). El tamaño de estos está en un rango de 0,5 – 1 mm, como se muestra en la imagen ampliada de la Figura 4a. Las fibras más largas, de aproximadamente 1 mm, se concentran en las capas internas.

Figura 4. a) Inspección visual de la superficie de fractura. b) Inspección de las probetas con rayos X para la detección de daño interno.

Para descartar la presencia de cualquier otro mecanismo de daño, las probetas se inspeccionaron con rayos X después del ensayo. En la imagen de rayos X de la Figura 4b se puede observar el daño generado por la propagación de la grieta (línea horizontal central negra) en una de las probetas 2TCT ensayadas. El daño aparece limitado al plano de propagación de la grieta. También se pueden observar zonas oscuras cerca de los biseles de la probeta y los agujeros de carga. Estas áreas más oscuras pueden atribuirse a la perforación y mecanizado de las probetas y al líquido de contraste que penetra en estas zonas entre los filamentos, ya que el material presenta una porosidad relativamente alta. De hecho, la orientación de las capas (0°/90°) puede apreciarse en la imagen de rayos X. De este modo, se asegura la ausencia de mecanismos de daño adicionales y una correcta determinación de la energía de fractura translaminar a partir de los ensayos experimentales.

4.2 Resultados experimentales y obtención de la energía de fractura

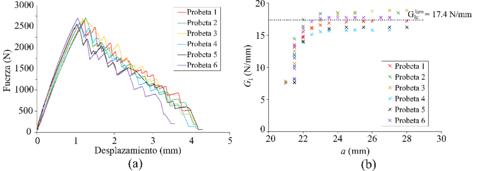
Las curvas fuerza vs. apertura de grieta obtenidas para las seis probetas 2TCT no muestran una propagación progresiva de la grieta. Por el contrario, la grieta de propaga de forma repentina y escalonadamente, como se puede ver en la Figura 5a. Todas las probetas siguen el mismo patrón, dando un comportamiento global consistente y con una rigidez en el tramo elástico similar para todas ellas. El valor medio obtenido para la carga máxima es de 2651 N (±2,46%).

Los valores de carga y de apertura de grieta se relacionaron con los valores correspondientes de la longitud de grieta, previamente al crecimiento repentino de la grieta. De esta forma, se pudo obtener la flexibilidad de la probeta para cada longitud de grieta y, posteriormente, realizar la correspondiente normalización por su respectivo grosor y modulo elástico. Con estos datos experimentales y usando la reducción de datos mediante la solución inversa propuesta por Ortega et al. [28], se puede obtener el valor de la energía de fractura translaminar del laminado, ${\textstyle {G}_{Ic}^{lam}}$.

Las respectivas ${\textstyle R}$-curves (i.e., ${\textstyle {G}_{Ic}}$ vs. ${\textstyle a}$) para cada probeta se obtuvieron a partir del método de solución inversa [12], relacionando la apertura con el crecimiento de la grieta (Figura 5b). El valor medio obtenido para ${\textstyle {G}_{Ic}^{lam}}$ una vez que la zona de proceso de fractura (FPZ) está completamente desarrollada es de 17,4 N/mm (CoV = 7%).

Figura 5. Resultados experimentales de los ensayos 2TCT. a) Curvas fuerza vs. apertura de grieta y b) ${\textstyle R}$-curves con el valor promedio de ${\textstyle {G}_{Ic}^{lam}}$.

4.3 Energía de fractura asociada a la rotura de fibra sometida a tensión

La tenacidad a la fractura por tracción de las capas a 0°, ${\textstyle {G}_{Ic}^{0},}$ se puede derivar de la tenacidad a la fractura del laminado obtenida previamente utilizando el procedimiento basado en la ley de mezclas, teniendo en cuenta que la mitad de las capas están a 0° y la otra mitad a 90°: ${\textstyle {G}_{Ic}^{0}{=2G}_{Ic}^{lam}-}$${G}_{Ic}^{90}$. En este caso, se consideró que la tenacidad a la fractura intralaminar de la matriz, ${\textstyle {G}_{Ic}^{90},}$ es igual a la tenacidad interlaminar entre las capas a 0° [13], obtenido por Santos et al. [7] para el mismo material como ${\textstyle {G}_{Ic}^{90}}$ = 1,72 N/mm. Así, el valor de la tenacidad a la fractura por tracción en la capa a 0° resulta ser ${\textstyle {G}_{Ic}^{0}}$ = 33,11 N/mm.

5. Conclusiones

En este estudio se caracteriza experimentalmente la tenacidad a la fractura translaminar de un laminado c-CFRP de fabricación aditiva. Los ensayos se realizaron utilizando una probeta 2TCT, diseñada mediante un análisis paramétrico para prevenir la aparición de mecanismos de daño no deseados que pudieran influir en la correcta determinación del valor de la tenacidad a fractura. Mediante la inspección de las probetas ensayadas mediante imágenes de rayos X se pudo descartar la presencia de mecanismos de daño adicionales, demostrando que la geometría 2TCT es adecuada para compuestos reforzados con fibra continua de carbono de fabricación aditiva con matriz de poliamida. La tenacidad a la fractura translaminar del laminado se caracterizó utilizando la reducción de datos basada en el método inverso, con un valor promedio de ${\textstyle {G}_{Ic}^{lam}}$ = 17,4 N/mm. También se ha determinado la tenacidad a la fractura asociada con la fractura a tracción de la fibra, obteniendo un valor de 33,11 N/mm.

6. Bibliografía

[1] J. H. Underwood, M. Kortschot, W. Lloyd, N. Eidinoff, D. Wilson, y N. Ashbaugh, «Translaminar fracture toughness test methods and results from interlaboratory tests of carbon/epoxy laminates.», en Fracture mechanics: ASTM STP 1256, vol. 26, 1995.

[2] S. T. Pinho, P. Robinson, y L. Iannucci, «Fracture toughness of the tensile and compressive fibre failure modes in laminated composites», Composites Science and Technology, vol. 66, n.^o 13, pp. 2069-2079, oct. 2006, doi: 10.1016/j.compscitech.2005.12.023.

[3] «Markforged, Inc.», Markforged. Accedido: 12 de diciembre de 2024. [En línea]. Disponible en: https://markforged.com/es/materials/continuous-fibers/continuous-carbon-fiber

[4] L. G. Blok, M. L. Longana, H. Yu, y B. K. S. Woods, «An investigation into 3D printing of fibre reinforced thermoplastic composites», Additive Manufacturing, vol. 22, pp. 176-186, ago. 2018, doi: 10.1016/j.addma.2018.04.039.

[5] J. Justo, L. Távara, L. García-Guzmán, y F. París, «Characterization of 3D printed long fibre reinforced composites», Composite Structures, vol. 185, pp. 537-548, feb. 2018, doi: 10.1016/J.COMPSTRUCT.2017.11.052.

[6] M. Iragi, C. Pascual-González, A. Esnaola, C. S. Lopes, y L. Aretxabaleta, «Ply and interlaminar behaviours of 3D printed continuous carbon fibre-reinforced thermoplastic laminates; effects of processing conditions and microstructure», Additive Manufacturing, vol. 30, p. 100884, dic. 2019, doi: 10.1016/J.ADDMA.2019.100884.

[7] J. D. Santos, A. Fernández, L. Ripoll, y N. Blanco, «Experimental Characterization and Analysis of the In-Plane Elastic Properties and Interlaminar Fracture Toughness of a 3D-Printed Continuous Carbon Fiber-Reinforced Composite», Polymers 2022, Vol. 14, Page 506, vol. 14, n.^o 3, p. 506, ene. 2022, doi: 10.3390/POLYM14030506.

[8] J. D. Santos, J. M. Guerrero, N. Blanco, J. I. Fajardo, y C. A. Paltán, «Numerical and Experimental Analysis of the Mode I Interlaminar Fracture Toughness in Multidirectional 3D-Printed Thermoplastic Composites Reinforced with Continuous Carbon Fiber», Polymers, vol. 15, n.^o 10, Art. n.^o 10, ene. 2023, doi: 10.3390/polym15102403.

[9] Z. Dang, J. Cao, A. Pagani, y C. Zhang, «Fracture toughness determination and mechanism for mode-I interlaminar failure of 3D-printed carbon-Kevlar composites», Composites Communications, vol. 39, p. 101532, abr. 2023, doi: 10.1016/j.coco.2023.101532.

[10] E. Polyzos, A. Katalagarianakis, D. Van Hemelrijck, y L. Pyl, «Delamination analysis of 3D-printed nylon reinforced with continuous carbon fibers», Additive Manufacturing, vol. 46, p. 102144, oct. 2021, doi: 10.1016/j.addma.2021.102144.

[11] J. D. Santos, S. Fotouhi, J. M. Guerrero, y N. Blanco, «Characterization of the mixed-mode interlaminar fracture toughness of an Additive Manufacturing continuous carbon fiber reinforced-thermoplastic composite.», Polymer Composites, vol. In press, doi: 10.1002/pc.29943.

[12] C. Huang y M. W. Joosten, «Investigating the translaminar fracture toughness of 3D printed semi-woven and non-woven continuous carbon fibre composites», Composite Structures, vol. 306, p. 116605, feb. 2023, doi: 10.1016/j.compstruct.2022.116605.

[13] R. Reber, J. de Haan, J. Mayer, M. Petitmermet, y E. Wintermatnel, «Intralaminar fracture of weft-knitted carbon fiber reinforced peek», en European Structural Integrity Society, vol. 27, J. G. Williams y A. Pavan, Eds., en Fracture of Polymers, Composites and Adhesives, vol. 27. , Elsevier, 2000, pp. 123-133. doi: 10.1016/S1566-1369(00)80013-8.

[14] G. Catalanotti, P. P. Camanho, J. Xavier, C. G. Dávila, y A. T. Marques, «Measurement of resistance curves in the longitudinal failure of composites using digital image correlation», Composites Science and Technology, vol. 70, n.^o 13, pp. 1986-1993, nov. 2010, doi: 10.1016/j.compscitech.2010.07.022.

[15] M. W. Czabaj y J. G. Ratcliffe, «Comparison of intralaminar and interlaminar mode I fracture toughnesses of a unidirectional IM7/8552 carbon/epoxy composite», Composites Science and Technology, vol. 89, pp. 15-23, dic. 2013, doi: 10.1016/j.compscitech.2013.09.008.

[16] R. W. Truss, P. J. Hine, y R. A. Duckett, «Interlaminar and intralaminar fracture toughness of uniaxial continuous and discontinuous carbon fibre/epoxy composites», Composites Part A: Applied Science and Manufacturing, vol. 28, n.^o 7, pp. 627-636, ene. 1997, doi: 10.1016/S1359-835X(97)00019-5.

[17] M. J. Laffan, S. T. Pinho, P. Robinson, y A. J. McMillan, «Translaminar fracture toughness testing of composites: A review», Polymer Testing, vol. 31, n.^o 3, pp. 481-489, may 2012, doi: 10.1016/j.polymertesting.2012.01.002.

[18] ASTM E399-22. Test Method for Linear-Elastic Plane-Strain Fracture Toughness of Metallic Materials.

[19] J. Llobet et al., «A continuum damage model for composite laminates: Part IV- Experimental and numerical tests», Mechanics of Materials, vol. 154, p. 103686, mar. 2021, doi: 10.1016/j.mechmat.2020.103686.

[20] C. C. Poe, J. R. Reeder, y F. G. Yuan, «Fracture Behavior of a Stitched Warp-Knit Carbon Fabric Composite», L-18080, may 2001. Accedido: 16 de octubre de 2024. [En línea]. Disponible en: https://ntrs.nasa.gov/citations/20010060618

[21] N. Blanco, D. Trias, S. T. Pinho, y P. Robinson, «Intralaminar fracture toughness characterisation of woven composite laminates. Part I: Design and analysis of a compact tension (CT) specimen», Engineering Fracture Mechanics, vol. 131, pp. 349-360, nov. 2014, doi: 10.1016/j.engfracmech.2014.08.012.

[22] G. D. Goh et al., «Characterization of mechanical properties and fracture mode of additively manufactured carbon fiber and glass fiber reinforced thermoplastics», Materials & Design, vol. 137, pp. 79-89, ene. 2018, doi: 10.1016/j.matdes.2017.10.021.

[23] G. Chabaud, M. Castro, C. Denoual, y A. Le Duigou, «Hygromechanical properties of 3D printed continuous carbon and glass fibre reinforced polyamide composite for outdoor structural applications», Additive Manufacturing, vol. 26, pp. 94-105, mar. 2019, doi: 10.1016/j.addma.2019.01.005.

[24] Q. He, H. Wang, K. Fu, y L. Ye, «3D printed continuous CF/PA6 composites: Effect of microscopic voids on mechanical performance», Composites Science and Technology, vol. 191, p. 108077, may 2020, doi: 10.1016/j.compscitech.2020.108077.

[25] A. Fernández, N. Blanco, D. Trias, y N. Gascons, «Assessment of damage sequence in additive manufactured composite laminates under quasi-static out-of-plane loading», Composites Part A: Applied Science and Manufacturing, vol. 184, p. 108263, sep. 2024, doi: 10.1016/j.compositesa.2024.108263.

[26] W. Cher, «Development of a test to measure energy absorption in fibre failure modes of woven composite laminates», Tech. Rep. Final Year Project Report, 2006.

[27] R. Krueger, «Virtual crack closure technique: History, approach, and applications», Applied Mechanics Reviews, vol. 57, n.^o 2, pp. 109-143, abr. 2004, doi: 10.1115/1.1595677.

[28] A. Ortega, P. Maimí, E. V. González, y D. Trias, «Characterization of the translaminar fracture Cohesive Law», Composites Part A: Applied Science and Manufacturing, vol. 91, pp. 501-509, dic. 2016, doi: 10.1016/j.compositesa.2016.01.019.