Development of a global optimization algorithm in ant colonies with feasible region selection for continuous search spaces

Resumen

En este estudio se introduce un nuevo algoritmo para la metaheurística de optimización de colonias de hormigas (ACO) que se ha desarrollado para resolver problemas de optimización global con variables de decisión continuas. El algoritmo propuesto, denominado ACO-FRS, comprende una estrategia para la selección de regiones factibles para el proceso de optimización y realiza la exploración del espacio de solución de forma similar al proceso que realizan las hormigas para la búsqueda de alimento. Se han evaluado 4 variantes de este algoritmo empleando varios problemas clásicos de optimización global, y los resultados obtenidos se han comparado con los informados en la literatura para otros algoritmos del tipo ACO para espacios continuos. En general, los resultados obtenidos indican que la inclusión de una selección de regiones factibles permite realizar una búsqueda global mediante la eventual exploración de regiones con bajos niveles de feromonas, aumentando así la viabilidad del método para la localización de la solución del problema de optimización.

Abstract

This study introduces a new algorithm for the ant colony optimization (ACO) method, which has been proposed to solve global optimization problems with continuous decision variables. This algorithm, namely ACO-FRS, involves a strategy for the selection of feasible regions during optimization search and it performs the exploration of the search space using a similar approach to that used by the ants during the search of food. Four variants of this algorithm have been tested in several benchmark problems and the results of this study have been compared with those reported in literature for other ACO-type methods for continuous spaces. Overall, the results show that the incorporation of the selection of feasible regions allows the performing of a global search to explore those regions with low level of pheromone, thus increasing the feasibility of ACO for finding the global optimal solution.

Palabras clave

Optimización global ; Métodos estocásticos ; Colonia de hormigas

Keywords

Global optimization ; Stochastic method ; Ant colony

1. Introducción

La mejora de las capacidades de cómputo y la formulación rigurosa de los problemas con modelos precisos ha abierto la posibilidad de plantear diversos problemas de ingeniería altamente no lineales y complejos como problemas de optimización. En ingeniería química, como ejemplo de los diversos campos de aplicación, la optimización es clave para la calendarización de actividades y la operación de reactores, los procesos de separación, el análisis de redes de intercambiadores de calor y el diseño de plantas completas [1] . Sin el uso de técnicas de optimización, los procesos industriales no serían tan eficientes como ahora. En varias aplicaciones es necesario encontrar el óptimo global, y no solo un óptimo local, ya que el primero es obviamente mejor que el segundo en términos del valor de la función objetivo planteada. Incluso en algunas aplicaciones, el óptimo global es la única solución correcta y con significado físico para el sistema analizado.

Los métodos de optimización global se pueden clasificar en 2 grandes grupos: técnicas deterministas y estocásticas (o probabilísticas). Los métodos actuales de optimización global deterministas pueden ser demasiado costosos (en términos de esfuerzo computacional), sobre todo para problemas multivariables, y en algunos casos requieren reformulaciones del problema dependiendo de las características del modelo utilizado. En el caso de las técnicas estocásticas de optimización global (SGO, por sus siglas en inglés) intervienen elementos probabilísticos y, por consiguiente, se utilizan números aleatorios durante la búsqueda del óptimo global. Las técnicas SGO tienen diferentes características que son atractivas para el campo de la ingeniería: son simples y fáciles de implementar, no requieren estimaciones previas, pueden resolver una gran variedad de problemas, tienen la capacidad de proveer resultados robustos para problemas altamente no lineales con múltiples variables de decisión y generalmente presentan una rápida convergencia hacia la solución óptima [1] , [2]  and [3] . Estos métodos explotan diversas estrategias numéricas basadas en conceptos heurísticos para diversificar e intensificar la búsqueda en algunas áreas promisorias durante la localización del óptimo global, escapando así de los mínimos locales de la función objetivo.

En particular, las técnicas SGO que adaptan ideas de comportamientos naturales de poblaciones de individuos se catalogan como métodos de inteligencia de enjambre, y estos métodos de optimización normalmente se consideran efectivos para la resolución de diferentes tipos de problemas. En particular, el algoritmo de optimización con colonias de hormigas (ACO, por sus siglas en inglés) está inspirado en la capacidad de las hormigas (en una colonia) para interactuar de manera eficaz en el proceso de búsqueda de alimento [4] . Hasta la fecha se han probado diferentes algoritmos de optimización del tipo ACO en problemas diversos, y los resultados indican que estos poseen un desempeño destacado, especialmente en problemas con múltiples variables y espacios discretos [5]  and [6] . En particular, ACO ha encontrado aplicaciones en la resolución de problemas reales de las ciencias básicas y aplicadas. Concretamente, este método se ha probado con éxito en problemas clásicos tales como el problema del vendedor viajero [4] , [7]  and [8] , el problema de asignación cuadrática [6] , [9]  and [10] , la determinación de rutas de vehículos [11] , [12]  and [13] , aplicaciones industriales de problemas de calendarización [14]  and [15] , la optimización dinámica de procesos químicos [16] , entre otros. Es conveniente indicar que los algoritmos del tipo ACO inicialmente se diseñaron para aplicaciones en optimización combinatoria, es decir, problemas de optimización discretos [6] .

Es necesario señalar que la mayor parte de los problemas de optimización asociados a aplicaciones de ingeniería y diseño se catalogan como problemas de optimización continuos, puesto que las variables de optimización pueden tomar cualquier valor numérico real dentro de los límites establecidos. Generalmente, estos problemas presentan un número significativo de variables de optimización y las funciones objetivo son altamente no lineales y, por tanto, para su resolución se requieren métodos robustos y preferiblemente con una rápida convergencia. Bajo esta perspectiva, los métodos de optimización estocásticos basados en la metaheurística de ACO son una opción atractiva para la resolución efectiva de este tipo de problemas.

La primera aplicación de colonias artificiales de hormigas para la resolución de funciones continuas la realizaron Bilchev y Pramee [17]  and [18] . Estos trabajos solo utilizaron procedimientos de búsqueda local como parte del algoritmo ACO. Posteriormente, Wodrich y Bilchev [19] extendieron estas estrategias para la resolución de problemas de optimización global mediante la inclusión del concepto de hormigas «locales y globales». Las hormigas «globales» usan mecanismos de caminata aleatoria y difusión de rastro de feromonas , mientras que las hormigas «locales» tienen la capacidad de percibir el rastro de feromonas que han depositado las hormigas «globales». El algoritmo descrito se conoce como ACO-continuo (CACO), y su desempeño numérico fue mejorado posteriormente en otros estudios mediante la implementación de nuevos conceptos en la etapa de búsqueda global [14] , [20]  and [21] . Por otra parte, API es otro algoritmo basado en el comportamiento de hormigas enfocado a espacios continuos [22] . El mecanismo base de API imita el comportamiento particular de la especie Pachycondyla apicalis en el proceso de caza de presas. En API, cada hormiga busca de forma independiente una solución mejor, aunque todas las hormigas empiezan desde el mismo punto, es decir, el nido. La exploración global se lleva a cabo mediante una caminata en tándem , en la que toda la colonia cambia su posición para cazar en otras regiones. Este algoritmo también utiliza una estrategia de reclutamiento para refinar la búsqueda; a dicha búsqueda local se la conoce como captura de presas , donde las hormigas utilizan mecanismos de comunicación directa y poseen una memoria limitada. En otro estudio, Dréo y Siarry [23] propusieron el algoritmo continuo de colonia de hormigas cooperativas (CIAC), en el cual se demuestra que es posible llevar a cabo la tarea de reclutamiento sin tener en cuenta los rastros de feromonas típicos de las estrategias ACO y el proceso de búsqueda se basa en relaciones entre individuos. Pourtakdoust y Nobahari [24] propusieron el algoritmo CACS, donde la función probabilística discreta basada en feromonas se reemplaza por una función de densidad de probabilidad del tipo gaussiana (normal) cuyos parámetros de media y varianza adaptan las hormigas de manera dinámica en cada iteración. Recientemente, Socha y Dorigo [25] propusieron un nuevo algoritmo ACO para espacios continuos, identificado como ACO_R , que mantiene un archivo de las soluciones generadas en iteraciones previas. Las soluciones en el archivo se ordenan considerando el valor de la función objetivo y posteriormente se clasifican para asignar un factor de peso a cada solución. Dicho peso corresponde al rastro de feromonas y, al igual que en CACS, las hormigas usan distribuciones de probabilidad en cada paso de construcción de una solución. Finalmente, De França et al. [26] reportaron otro algoritmo tipo ACO para espacios continuos que está basado en una modificación de las funciones gaussianas para adaptar simultáneamente todas las dimensiones de la distribución aleatoria y generar nuevos individuos en cada iteración.

Cabe mencionar que los resultados de estudios comparativos reportados en la literatura [25] indican que los algoritmos ACO existentes para espacios continuos aún pueden presentar problemas de convergencia prematura para la localización del óptimo global. A pesar de que existen estrategias del tipo ACO que se han aplicado a la resolución de problemas continuos, todavía existen áreas de oportunidad para mejorar el desempeño numérico de los algoritmos ACO para la resolución de problemas multivariables. Hasta la fecha, una posibilidad inexplorada para mejorar el desempeño numérico de ACO consiste en almacenar la información del rastro de feromonas en cada dimensión del archivo de soluciones y adaptar el concepto de regiones factibles propio de los problemas combinatoriales que inicialmente fueron el campo de aplicación de las estrategias ACO. Teniendo en cuenta lo anterior, en este estudio se ha propuesto un algoritmo de optimización alternativo, referido como ACO con selección de región factible (ACO-FRS), con el propósito de fortalecer el desempeño de dicha metaheurística en la resolución de problemas multivariables con espacios continuos. Específicamente, ACO-FRS realiza la exploración del espacio de solución de forma similar al proceso que realizan las hormigas para buscar y recolectar alimento, explorando diferentes regiones y siendo capaces de encontrar el camino más corto después de un determinado tiempo. El desempeño de este algoritmo alternativo se ilustra con diferentes funciones objetivo clásicas del área de optimización global. Además, los resultados obtenidos con ACO-FRS se han comparado con el desempeño numérico de los algoritmos CACS [24] , ACO_R[25] y MACACO [26] .

2. Descripción de la metaheurística de colonias de hormigas

Los estudios del desempeño colectivo de las hormigas abarcan el análisis de su comportamiento cuando buscan y transportan forraje (alimento), la división de labores , la organización de sus cementerios y el envío de ayuda . En particular, la búsqueda de forraje es el comportamiento que más se ha modelado debido a que genera un mecanismo complejo y eficiente con individuos no tan sofisticados [27] . En la literatura, Deneubourg et al. [28] describieron un ejemplo particular de comunicación indirecta entre individuos basada en deposiciones de químicos (feromonas) en la región por la que la hormiga ha explorado y encontrado alimento. Con base en dicho mecanismo de comunicación, Dorigo [4] propuso el primer algoritmo que modelaba la tarea de recolección de forraje como una estrategia colectiva, cuyas primeras implementaciones representaron el surgimiento de los algoritmos de optimización del tipo colonia de hormigas.

En la figura 1 a se presenta el pseudocódigo para la modelación del proceso decisivo de una hormiga real, que se describe como la serie de pasos que una hormiga artificial realiza cuando pretende elegir entre NR rutas potenciales. La probabilidad de selección p(z) es proporcional a la concentración de feromonas de la ruta z con respecto a las demás. Cuando el proceso de decisión mostrado en la figura 1 a lo realiza un conjunto de hormigas (agentes), y este forma parte de un mecanismo de búsqueda de rutas más cortas, dicho proceso se conoce como construcción de la solución y es una de las 3 actividades básicas de la metaheurística ACO [29]  and [30] . Dichas actividades se presentan en la metaheurística mostrada en la figura 1 b, donde se modela el comportamiento de búsqueda y transporte de forraje que ha sido la base para la codificación de la mayor parte de los algoritmos de ACO reportados en la literatura.

Figura 1. a) Proceso de decisión de una hormiga artificial. b) Metaheurística de colonia de hormigas.

Dorigo y Stützle [31] desarrollaron el algoritmo simple de optimización con colonia de hormigas (SACO) como una propuesta sencilla para analizar las propiedades de la metaheurística ACO. En el presente estudio se toma como base la estructura conceptual de dicho algoritmo y se adapta a espacios continuos. A continuación se presenta una breve descripción del mecanismo de optimización de SACO considerando el problema clásico de optimización combinatoria donde se requiere encontrar el camino más corto entre 2 nodos de una gráfica G  = (V ,E ), donde V es el conjunto de vértices (nodos) y E es la matriz de conexiones entre los nodos. La longitud L^k del camino construido, en una etapa (k) de un proceso iterativo, se calcula como el número de saltos entre nodos desde el inicio hasta el destino. Como parte de la primera actividad en SACO, se asocia una concentración inicial (valor aleatorio pequeño) de feromonas o rastro de feromonas τ_ij a cada posible conexión entre dos nodos (i,j) . Un determinado número de hormigas k  = 1,2, …, NA , que corresponde a una etapa del proceso iterativo, se ubica en el nodo de inicio. Usando la lógica de decisión de la figura 1 a, cada hormiga construye un camino (solución) hacia el nodo destino. Si una hormiga k se localiza temporalmente en el nodo i   , esta seleccionará el nodo ${\textstyle j\in N_{i}^{k}}$ considerando la siguiente probabilidad de transición [31] :

$p_{ij}^{k}(t)={\begin{array}{ll}{\frac {{\tau }_{ij}^{a}(t)}{{\Sigma }_{i\in n{\frac {k}{i}}{\tau }_{ij}^{a}(t)}}}&{\boldsymbol {\mbox{IF}}}{\mbox{ }}j\in N_{i}^{k}\\0&{\boldsymbol {\mbox{IF}}}{\mbox{ }}j\not \in N_{i}^{k}\end{array}}$

( 1)

donde ${\textstyle N_{i}^{k}}$ es el conjunto de nodos factibles conectados a i para la hormiga k. Dicha probabilidad varía conforme se realiza el proceso de minimización o, en otras palabras, en función del tiempo t. La constante α toma valores positivos y se utiliza para amplificar la influencia de la concentración de feromonas. Si, para algún nodo i , una hormiga k   encuentra ${\textstyle N_{i}^{k}=}$$0$ , entonces el nodo predecesor de i   se incluye en ${\textstyle N_{i}^{k}}$ . Esta situación puede causar que se generen lazos internos mientras se construye la solución. Una vez que todas las hormigas han construido un camino completo desde el nodo de origen hasta el nodo destino, se eliminan todos los lazos internos (en caso de presentarse) y cada hormiga recorre nuevamente el camino construido hasta el nodo de origen de manera determinista. En este proceso se deposita una cantidad específica de feromonas ${\textstyle \Delta {\tau }_{ij}^{k}(t)}$ en cada conexión. Las conexiones actualizan su concentración de feromonas mediante la siguiente expresión [31] :

${\tau }_{ij}(t)\leftarrow {\tau }_{ij}(t)+\Delta {\tau }^{k}(t)$

( 2)

La intensificación del rastro de feromonas para el camino recorrido es el resultado de la cantidad depositada por cada hormiga en cada conexión, y para la evaluación de dicha cantidad se pueden considerar cualquiera de las siguientes estrategias [27] :

a) Evaluación explícita. El incremento en la concentración o intensidad del rastro contiene información sobre la calidad de la solución generada. Para SACO, la calidad de la solución (del camino construido) se expresa simplemente como el inverso de la longitud del camino, es decir:

$\Delta {\tau }^{k}(t)={\frac {1}{L^{K}}}$

( 3)

b) Evaluación implícita. Las hormigas hacen uso del efecto de longitud diferencial de camino a través de la búsqueda que realizan otros agentes [31] . Con esta evaluación, la selección del camino más corto es el resultado del mecanismo de retroalimentación positiva que caracteriza el comportamiento de las hormigas en una colonia, que describen Deneubourg et al. [28] . Es decir, el incremento ${\textstyle \Delta {\tau }_{ij}^{k}(t)}$ es independiente de la calidad de la solución y todas las hormigas exitosas depositan la misma cantidad de feromonas, donde:

$\Delta {\tau }^{1}=\Delta {\tau }^{2}=\cdots =\Delta {\tau }^{NA}$

( 4)

En SACO, el proceso natural de evaporación del rastro de feromonas se realiza mediante la siguiente expresión:

${\boldsymbol {\tau }}\leftarrow \left(1-\rho \right).{\boldsymbol {\tau }}$

( 5)

donde ρ  ∈ [0, 1] y la matriz τ contienen el valor del rastro de feromonas en cada conexión. La constante ρ determina la tasa de evaporación de las feromonas, provocando que las hormigas «olviden» sus decisiones previas. Este proceso iterativo se detiene hasta cumplir con algún criterio de paro. Para SACO, y en general para la metaheurística de ACO, se pueden aplicar criterios de paro simples. Así, el algoritmo puede terminar la búsqueda cuando, por ejemplo, se ha excedido el número máximo de iteraciones (Iter_MAX) , o cuando se ha encontrado una solución aceptable, considerando que f (x^k (t )) ≤ ɛ , donde x^k (t ) representa una solución en el tiempo t , o alternativamente cuando todas las hormigas (o la mayor parte de ellas) siguen el mismo camino.

3. Descripción del algoritmo ACO-FRS para optimización en espacios continuos

En este estudio se ha propuesto un algoritmo alternativo para ACO, denominado ACO con selección de región factible (ACO-FRS), para incrementar el desempeño de esta metaheurística en la resolución de problemas de optimización con variables de decisión continuas. Específicamente, el primer paso en ACO-FRS es la generación de un archivo de regiones r , donde cada región representa un punto o solución r_i (i  = 1, … NR ). Es conveniente indicar que este concepto se utiliza en la mayoría de los algoritmos ACO para espacios continuos. Sin embargo, la manera en que se almacena la información correspondiente a los niveles de feromonas en ACO-FRS es ampliamente diferente, por ejemplo, al correspondiente para el método CACO [32] . Es decir, si hay un total de n_var variables de decisión, se deposita una cantidad de feromona en todos los componentes ${\textstyle r_{i}^{j}(j=}$$1,\ldots ,n_{var})$ de dichas regiones, mientras que en CACO esta información se almacena solo por región. Los niveles de feromonas se almacenan en la matriz τ , de dimensión NR  × n_var , donde cada elemento ${\textstyle {\tau }_{i}^{j}}$ indica la concentración de feromonas de la i-ésima región para la j-ésima variable de decisión. El parámetro NR es sintonizable y puede considerarse similar al número de individuos para los algoritmos basados en población donde su valor generalmente depende del número de variables de optimización (n_var ) y el tipo de problema. En la figura 2 se presenta el algoritmo base de ACO-FRS que se utilizó como estructura general para el desarrollo y la evaluación de las variantes analizadas en este estudio. La inicialización de las regiones se realiza mediante una generación aleatoria de puntos en el dominio de solución, identificándose la mejor solución, que se almacena en un vector utilizado como comparación (r_B ). En este primer paso se deben establecer los valores de los parámetros del algoritmo, que se describen en la tabla 1 .

Figura 2. Algoritmo base de ACO-FRS.

Tabla 1. Condiciones para la evaluación del algoritmo propuesto ACO-FRS

Parámetro	Valor sugerido	Tipo	Descripción
NR	10 * nvar	Sintonizable	Número de regiones almacenadas
NA	NR	Fijo	Número de hormigas (o regiones recorridas) por iteración
τ0	NR	Fijo	Rastro inicial de feromonas
NSR	2 * nvar	Sintonizable	Número de regiones factibles preseleccionadas
SP	0,5	Sintonizable	Probabilidad de búsqueda de camino
Δτinten	1	Fijo	Depósito de rastro de feromonas por componente
${\textstyle \Delta {\tau }_{evep}}$	1	Fijo	Decremento en la concentración del rastro de feromonas

En el proceso iterativo, una hormiga k solo observará un número limitado de regiones mediante el proceso de selección de regiones factibles (N^k)   . Aquí, ${\textstyle N^{k}=}$$r_{a}^{k},r_{\beta }^{k},\ldots ,r_{NSR}^{k}$ es un conjunto aleatorio de NSR elementos de la matriz de regiones (con al menos 2 elementos diferentes: α  ≠ β ). El parámetro sintonizable NSR determina el grado de influencia que tendrá el rastro de feromonas, y su límite máximo es NR . Con esta preselección de la información disponible, el algoritmo es capaz de realizar una búsqueda global debido a que, ocasionalmente, se tendrán en cuenta regiones con baja concentración de feromonas. Uno de los componentes clave de la metaheurística ACO es la actividad de construcción del vector de solución. Como se observa en el proceso iterativo del pseudocódigo de la figura 2 , en ACO-FRS el paso de construcción del vector de solución se realiza por dimensión. Cada componente dimensional de cada región ${\textstyle \left(r_{i}^{j}\right)}$ posee una probabilidad de selección p cuando una hormiga k explora, en un momento dado, (t). Por tanto, considerando la ecuación (1), el proceso de selección está dado por la siguiente expresión:

$p_{r_{i}^{j}}^{k}(t)={\begin{array}{ll}{\frac {{\tau }_{i}^{j}(t)}{{\sum }_{i\in N^{k}}{\tau }_{i}^{j}(t)}}&{\boldsymbol {\mbox{IF}}}{\mbox{ }}i\in N^{k}\\0&{\boldsymbol {\mbox{IF}}}{\mbox{ }}i\not \in N^{k}\end{array}}$

( 6)

donde las regiones factibles N^k son diferentes para cada hormiga k.

Una vez realizadas todas las selecciones, estas forman parte del subconjunto M^k  ∈ N^k , que contiene los elementos ${\textstyle r_{s^{j}}^{j,k}{\mbox{ }}{\mbox{con}}{\mbox{ }}j=}$$1,\ldots ,{\mbox{n}}_{var}$ . Cada hormiga definirá su componente dimensional x^j , igual al valor del componente seleccionado, o realizará una búsqueda de camino con una probabilidad dada SP , donde SP ∈ [0,1]. La desviación de la región seleccionada puede interpretarse como un mecanismo de exploración, y en la tabla 2 se presentan los operadores sugeridos. Especialmente, se utilizan algunas regiones almacenadas en el archivo r para definir la magnitud de la desviación, y esta acción es el principal mecanismo con el que ACO-FRS realiza la exploración de espacios continuos. Por ejemplo, el operador «A» para la búsqueda de camino está dado por:

$r_{s^{j}}^{j,k}+U[-1,1]{_{\ast }}abs(r_{s^{j}}^{j,k}-r_{a}^{j,k})$

( 7)

donde la magnitud de la desviación del elemento ${\textstyle r_{s}^{j,k}}$ está limitada por la diferencia entre dicho elemento y el elemento aleatorio α que pertenece al conjunto de regiones factibles. Como se puede observar, la desviación puede tomar diferentes direcciones, ya que el número aleatorio generado para la ponderación tiene límites ∈ (−1, 1).

Tabla 2. Variantes ACO-FRS analizadas

Código	Operador de búsqueda de camino		Intensificación − τ
ACO-FRS (1)	A.	${\textstyle r_{s^{j}}^{j,k}+U[-1,1]{_{\ast }}abs(r_{s^{j}}^{j,k}-}$$r_{\alpha }^{j,k})$	A.	${\textstyle {\tau }_{s^{j}}^{j,k}\leftarrow {\tau }_{s^{j}}^{j,k}+}$$1$
ACO-FRS (2)	B.	${\textstyle r_{s^{j}}^{j,k}+U[0,1]{_{\ast }}(r_{\alpha }^{j,k}-}$$r_{\beta }^{j,k})$	A.	${\textstyle {\tau }_{s^{j}}^{j,k}\leftarrow {\tau }_{s^{j}}^{j,k}+}$$1$
ACO-FRS (3)	A.	${\textstyle r_{s^{j}}^{j,k}+U[-1,1]{_{\ast }}abs(r_{s^{j}}^{j,k}-}$$r_{\alpha }^{j,k})$	B.	${\textstyle {\begin{array}{l}{\tau }_{s^{j}}^{j,k}\leftarrow {\tau }_{s^{j}}^{j,k}+1\\{\tau }_{s^{co}}^{j,k}{\leftarrow }_{s^{j}}^{j,k}\end{array}}}$
ACO-FRS (4)	B.	${\textstyle r_{s^{j}}^{j,k}+U[0,1]{_{\ast }}(r_{\alpha }^{j,k}-}$$r_{\beta }^{j,k})$	B.	${\textstyle {\begin{array}{l}{\tau }_{s^{j}}^{j,k}\leftarrow {\tau }_{s^{j}}^{j,k}+1\\{\tau }_{s^{co}}^{j,k}{\leftarrow }_{s^{j}}^{j,k}\end{array}}}$

Cuando una hormiga ha definido los valores de todas las dimensiones, se dice que la hormiga ha construido una solución, es decir, ha creado una nueva región o punto de prueba x^k . Para dicho punto, se examina el valor de la función objetivo y este remplazará una región existente CO solo si f (x^k) es menor que f (r_sco ); es decir, para cada dimensión j se tiene que:

$r_{s^{CO}}^{j.k}\leftarrow x^{j,k}$

( 8)

Es conveniente indicar que CO   es una región de comparación y puede ser cualquiera de las regiones correspondientes a los componentes seleccionados mediante el rastro de feromona ${\textstyle (M^{k}=}$$r_{S^{1}}^{1,k},r_{S^{2}}^{2,k},\ldots ,r_{n_{var}}^{n_{var}k})$ . Si la región generada mejora el valor de la función objetivo de la mejor región r_B en la iteración t , dicha región será actualizada mediante:

$r_{B}(t)\leftarrow X^{k}$

( 9)

La intensificación del rastro de feromonas se realiza con la siguiente ecuación:

${\tau }_{i}^{j}(t)\leftarrow {\tau }_{i}^{j}(t)+\Delta {\tau }_{int}$

( 10)

donde Δτ_int es un valor constante, como se puede ver en la tabla 1 . Las estrategias de intensificación sugeridas para las variantes del algoritmo ACO-FRS se muestran en la tabla 2 . La ecuación (10) es una adaptación de la ecuación (2) y permite que el algoritmo realice una evaluación implícita en los depósitos de feromonas. Se puede observar que, después del proceso de inicialización, se realiza una iteración t hasta que todas las hormigas k  = 1, …, NA han explorado una región. Entonces, el número de hormigas es el número de ocasiones en que se evalúa una nueva región por iteración. Finalmente, cuando todas las hormigas de la colonia han explorado el espacio de búsqueda se lleva a cabo la evaporación de feromonas de la siguiente manera:

${\boldsymbol {\tau }}\leftarrow {\boldsymbol {\tau }}-\Delta {\tau }_{evap}$

( 11)

donde ${\textstyle \Delta {\tau }_{evap}}$ es un valor constante. El mecanismo de evaporación anterior permite una reducción homogénea de la intensidad del rastro de feromonas para todas las regiones y concuerda con el proceso de intensificación implícito presentado en la ecuación (10). En la implementación del algoritmo mostrado en la figura 2 se incluyeron 3 posibles criterios de paro para finalizar el proceso de optimización. El primer criterio corresponde al máximo número de iteraciones (Iter_MAX ), un segundo criterio corresponde al máximo número de funciones que evaluar (NFE_MAX ), mientras que el último criterio finaliza la búsqueda cuando se ha realizado un determinado número de iteraciones sin mejora en la mejor solución encontrada (SC_MAX ). En este último criterio de paro se contabilizan las iteraciones donde no ha cambiado el mejor valor de la función objetivo encontrado por el algoritmo, es decir, si f (r_B (t )) = f (r_B (t  − 1)) para el caso de un problema de minimización.

A diferencia del método CACO [32] , en el algoritmo propuesto ACO-FRS cada hormiga puede realizar una búsqueda eficiente sin ser catalogada como «local» o «global». Concretamente, en ACO-FRS se omiten las edades de las regiones, que se utilizan en CACO para redirigir la búsqueda. Ninguna de las 2 situaciones se observa en los algoritmos de ACO discretos, y esta característica garantiza una mayor similitud del mecanismo de ACO-FRS con la metaheurística básica de ACO. Por otra parte, la estrategia con la que se aborda la exploración en problemas con espacios continuos (es decir, operador de búsqueda de camino) difiere de las implementaciones con funciones de densidad de probabilidad de los métodos CACS, ACO_R y MACACO. Finalmente, el proceso de búsqueda de ACO-FRS difiere de los algoritmos basados en población, ya que es posible que un miembro de la población (un vector de la matriz r ) no cambie, no se utilice o no se compare al terminar una iteración.

4. Resultados y discusión

4.1. Comparación de las variantes propuestas para ACO-FRS

En primera instancia, se desarrollaron e implementaron 4 variantes del método propuesto ACO-FRS para evaluar 2 operadores de búsqueda de camino para la generación de una nueva región y 2 estrategias de actualización de feromonas para las regiones exitosas. Dichas variantes se describen en la tabla 2 . Para la estrategia A de generación o desviación de la región seleccionada ${\textstyle r_{S^{j}}^{j,k}}$ se elige un componente dimensional de una región aleatoria B para definir la distancia que se moverá la hormiga, mientras que en la estrategia B se intercambia información mediante la selección de 2 regiones diferentes (r_α y r_β ) del conjunto N^k . El operador de búsqueda de camino puede generar valores fuera de los límites de la variable de optimización ${\textstyle \left(x_{min}^{j}{\mbox{ }}{\mbox{y}}{\mbox{ }}x_{max}^{j}\right)}$ ; por tanto, se deben verificar dichos valores, tal como se muestra en la figura 2 . Por otro lado, el rastro de feromonas se actualiza con aumentos unitarios en las estrategias de intensificación de τ , situación que concuerda con el proceso de evaporación propuesto. En la estrategia A de actualización del rastro de feromonas solo se intensifican los valores de las feromonas de las regiones seleccionadas ${\textstyle {\tau }_{s^{j}}^{j}}$ , mientras que en la estrategia B se actualiza el rastro de la región de comparación ${\textstyle {\tau }_{s^{co}}^{j}}$ . Para realizar la evaluación de los algoritmos propuestos se ha considerado un valor τ^o  = NR   y, con objeto de evitar valores indefinidos de probabilidad de selección (cuando ${\textstyle {\tau }_{i}^{j}=}$$0$ ), se realiza un ajuste de valores posterior a la evaporación que restringe la intensidad del rastro a valores positivos iguales o mayores que 1. Finalmente, a pesar de que NA es independiente de NR , el uso de valores distintos para estos 2 parámetros modifica el proceso de intensificación del rastro de feromonas y, como consecuencia, se ha considerado NA  = NR . En general, las condiciones de evaluación de las 4 variantes de ACO-FRS analizadas en este estudio se presentan en la tabla 1 y los 4 códigos mostrados en la tabla 2 se implementaron en Matlab^® .

La tabla 3 proporciona los detalles de las funciones seleccionadas para evaluar el desempeño del método de optimización propuesto. La primer columna de dicha tabla, con el encabezado ID, proporciona las etiquetas para identificar las diferentes funciones evaluadas. Es conveniente indicar que estos problemas se han utilizado para evaluar el desempeño numérico de diferentes métodos estocásticos de optimización, puesto que contienen algunas características y dificultades asociadas a diferentes problemas de optimización en ingeniería y diseño. Dichas funciones corresponden a problemas continuos de optimización global sin restricciones cuyas dimensiones varían entre 2 y 20 y que presentan diferente número de óptimos locales. Los problemas seleccionados se utilizaron como punto de partida para comparar las diferentes variantes propuestas para el código base de ACO-FRS, además de entender el comportamiento general del algoritmo y analizar su desempeño en el proceso de resolución de estas funciones objetivo clásicas del área. Por tanto, los resultados de las pruebas con estos problemas son útiles para identificar las debilidades y fortalezas del código propuesto y permiten comparar los resultados obtenidos con estudios previos.

Tabla 3. Problemas de optimización clásicos utilizados para la evaluación de las estrategias propuestas para ACO-FRS

ID	Nombre de la función, Fobj	Variables de decisión, nvar	Mínimo global y vector de posición
B1-B4	Zakharov	nvar  = 2,5,10 y 20	0
	${\textstyle F_{obj}=\left(\sum _{i=1}^{n_{var}}u_{i}^{2}\right)+}$${\left(\sum _{i=1}^{n_{var}}0.5iu_{i}\right)}^{2}+{\left(\sum _{i=1}^{n_{var}}0.5iu_{i}\right)}^{4}$	−5 ≤ ui  ≤ 10	u = (0,…,0)
B5-B8	Rosenbrock	nvar  = 2,5,10 y 20	0
	${\textstyle Fobj=\sum _{i=1}^{n_{var}}\left[100{\left(u_{i}^{2}-u_{i+1}\right)}^{2}+\right.}$$\left.{\left(u_{i}-1\right)}^{2}\right]$	−5 ≤ ui  ≤ 10	u = (1,…,1)
B9	Goldstein y Price	nvar  = 2	3
	${\textstyle F_{obj}=[1+{\left(u_{1}+u_{2}+1\right)}^{2}(19-14u_{1}+3u_{1}^{2}-}$$14u_{2}+6u_{1}u_{2}+3u_{2}^{2})]{_{\ast }}[30+{\left(2u_{1}-3u_{2}^{2}\right)}^{2}(18-$$32u_{1}+12u_{1}^{2}+48u_{2}-36u_{1}u_{2}+27u_{2}^{2})]$	−2 ≤ ui  ≤ 2	u = (0,-1)
B10	Modificada de Himmelblau	nvar  = 0	0
	${\textstyle F_{obj}={\left(u_{1}^{2}+u_{2}-11\right)}^{2}+{\left(u_{1}+u_{2}^{2}-7\right)}^{2}+}$$0.1({\left(u_{1}-3\right)}^{2}+{\left(u_{2}-2\right)}^{2})$	−6 ≤ ui  ≤ 6	u = (3,2)
B11	Rastrigin	nvar  = 20	0
	${\textstyle F_{obj}=10D+\sum _{i=1}^{n_{var}}\left(u_{i}^{2}-\right.}$$\left.10cos(2\pi u_{i})\right)$	−600 ≤ ui  ≤ 600	u = (0,…,0)
B12	Griewank	nvar  = 20	0
	${\textstyle F_{obj}=\sum _{i=1}^{n_{var}}u_{i}^{2}/d-}$$\prod _{i=1}^{n_{var}}cos(u_{i}/{\sqrt {i}})$	−600 ≤ ui  ≤ 600 (d  = D )	u = (0,…,0)
B13-B14	Hartman	nvar  = 3 y 6	Para ηvar  = 3, -3.862782
	${\textstyle F_{obj}=\sum _{i=1}^{4}c_{i}exp\left[-\right.}$$\left.\sum _{j=1}^{n_{var}}a_{ji}{\left(u_{j}-p_{ij}\right)}^{2}\right]$	0 ≤ ui  ≤ 1	u = (0.114614,0.555649,0.852547) Para ηvar  = 6, -3.322368 u = (0.201690,0.150011,0.476874,0.275332,0.311652,0.657301)
B15-B17	Shekel	nvar  = 4	Para m = 5, -10.15
	${\textstyle F_{obj}=-\sum _{i=1}^{m}{\frac {1}{{\sum }_{j=1}^{n_{var}}{\left(u_{j}-a_{ij}\right)}^{2}-c_{i}}}}$	0 ≤ ui  ≤ 10 (m  = 5, 7 y  10)	u = (4,4,4,4) Para m = 7, -10.40 u = (4,4,4,4) Para m = 10, -10.53 u = (4,4,4,4)

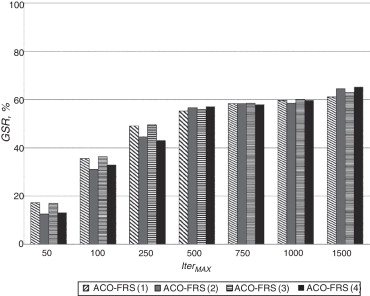
Se evaluó el desempeño numérico de las variantes propuestas para ACO-FRS considerando la confiabilidad del método para localizar el óptimo global, la cual se mide en términos del número de ocasiones en que el algoritmo localizó el óptimo global para 100 pruebas numéricas con estimaciones iniciales aleatorias. Esta métrica se conoce como tasa de éxito (SR). Adicionalmente, se evaluó la eficiencia computacional del método estocástico en términos del número de funciones evaluadas (NFE). El promedio de funciones evaluadas se analizó usando solamente las pruebas exitosas. Es decir, una prueba se consideró exitosa si se obtenía el óptimo global con un error absoluto de 10 × 10^–5 o menor con respecto al valor de la función objetivo. Los resultados obtenidos para el conjunto de funciones reportado en la tabla 3 empleando las diferentes estrategias para ACO-FRS se presentan en la figura 3 . Para el análisis de esta información, se presenta la tasa de éxito global (GSR) de cada estrategia probada. La tasa de éxito global está definida por la siguiente expresión:

$GSR={\sum }_{i=1}^{nb}\left(SR_{i}/nb\right)$

( 12)

donde SR_i es la tasa de éxito del problema i y nb es el total de problemas utilizados para la evaluación del desempeño numérico del método estocástico, respectivamente. Hay que señalar que los resultados del método de optimización de la figura 3 se reportan utilizando Iter_MAX como único criterio de paro. En dicha figura se puede apreciar que los algoritmos ACO-FRS (1) y (3) presentan mayores tasas de éxito para bajas iteraciones (Iter_MAX  < 250) en comparación con los algoritmos restantes. Sin embargo, para un número mayor de iteraciones (Iter_MAX  > 1.500) los algoritmos ACO-FRS (2) y (4) presentan un mejor desempeño. Estos resultados indican que la tasa de éxito global y el desempeño numérico de las variantes propuestas para ACO-FRS son dependientes del esfuerzo cómputo, como se muestra en la figura 3 . En particular, ningún algoritmo superó el 50% de GSR empleando Iter_MAX  < 250 y ACO-FRS (4) presenta la mejor GSR = 71% para Iter_MAX  > 1.500. Estos resultados son consistentes con otros estudios reportados en la literatura en que se ha evaluado el desempeño numérico de diferentes métodos estocásticos y se ha determinado la dependencia entre el esfuerzo numérico y la eficacia del algoritmo para localizar el óptimo global [33]  and [34] . En general, las estrategias de intensificación y diversificación de los métodos estocásticos dependen del esfuerzo numérico del algoritmo y de las características de los problemas de optimización; como consecuencia, las tasas de convergencia de los métodos estocásticos varían en función del número de funciones evaluadas. Con fines ilustrativos, en la tabla 4 se presentan las tasas de convergencia de los algoritmos ACO-FRS (3) y ACO-FRS (4) para todos los problemas de optimización considerados en este estudio. Como se puede observar en esta tabla, ambos métodos de optimización presentan una baja tasa de convergencia para localizar el óptimo global de la función de Rosenbrock. De acuerdo con la literatura [35] , la localización del óptimo global de esta función es difícil y normalmente los métodos de optimización estocásticos presentan problemas de convergencia, especialmente cuando el número de variables de optimización es mayor a 5, debido a que el número de óptimos locales de la función objetivo se incrementa con respecto a la dimensión del problema. Al igual que otros métodos de optimización estocásticos, el método ACO-FRS es inefectivo para escapar de los óptimos locales de esta función objetivo y, por tanto, las tasas de convergencia al óptimo global son bajas.

Figura 3. Comparación de estrategias ACO-FRS para la resolución de problemas de optimización global sin restricciones y con variables continuas.

Tabla 4. Comportamiento numérico de los métodos ACO-FRS (3) y ACO-FRS (4) en la minimización global de problemas multivariables con espacios continuos

Problema	Algoritmo	IterMAX
ID		50	100	250	500	750	1.000	1.500
B1	ACO-FRS (4)	0	0	0	0	0	0	0
	ACO-FRS (3)	0	0	0	0	0	0	17
B2	ACO-FRS (4)	0	0	0	96	100	100	100
	ACO-FRS (3)	0	0	0	100	100	100	100
B3	ACO-FRS (4)	0	3	100	100	100	100	100
	ACO-FRS (3)	0	25	100	100	100	100	100
B4	ACO-FRS (4)	98	100	100	100	100	100	100
	ACO-FRS (3)	99	100	100	100	100	100	100
B5	ACO-FRS (4)	0	0	0	0	0	0	0
	ACO-FRS (3)	0	0	0	0	0	0	0
B6	ACO-FRS (4)	0	0	0	0	0	0	1
	ACO-FRS (3)	0	0	0	0	0	0	0
B7	ACO-FRS (4)	0	0	0	1	0	0	0
	ACO-FRS (3)	0	0	0	1	0	0	1
B8	ACO-FRS (4)	0	0	1	3	19	33	78
	ACO-FRS (3)	0	0	1	4	16	35	54
B9	ACO-FRS (4)	10	84	100	100	100	99	99
	ACO-FRS (3)	13	84	97	97	99	99	100
B10	ACO-FRS (4)	13	62	92	99	99	100	97
	ACO-FRS (3)	29	68	86	93	96	97	94
B11	ACO-FRS (4)	0	0	0	0	0	0	47
	ACO-FRS (3)	0	0	0	1	27	35	33
B12	ACO-FRS (4)	0	0	0	100	100	100	100
	ACO-FRS (3)	0	0	100	100	100	100	100
B13	ACO-FRS (4)	100	100	100	100	100	100	100
	ACO-FRS (3)	100	100	100	100	99	99	100
B14	ACO-FRS (4)	3	91	89	84	86	93	93
	ACO-FRS (3)	44	86	92	88	90	94	87
B15	ACO-FRS (4)	0	22	28	44	48	42	48
	ACO-FRS (3)	1	32	44	39	39	34	47
B16	ACO-FRS (4)	0	45	55	72	61	64	71
	ACO-FRS (3)	1	61	51	60	53	57	62
B17	ACO-FRS (4)	0	54	67	72	72	84	75
	ACO-FRS (3)	3	63	71	67	75	70	73

En la tabla 5 se muestran los promedios de funciones evaluadas para las 100 pruebas numéricas realizadas en cada función objetivo empleando SC_MAX como criterio de paro y fijando Iter_MAX (sin incluir NFE_MAX como criterio de paro). Al examinar los resultados para los problemas individuales, se puede apreciar que los algoritmos ACO-FRS (1) y (3) son capaces de encontrar el óptimo global en el problema de Zakharov (D = 20), a diferencia de los restantes algoritmos. En el problema de Rosenbrock (D = 20), solamente ACO-FRS (4) localizó el óptimo global bajo la tolerancia establecida. Es importante mencionar que la tolerancia establecida supone un esfuerzo numérico significativo para la resolución de los problemas B5 a B8. Para la función objetivo de Zakharov (D = 10), prácticamente todos los algoritmos finalizaron su proceso iterativo tras haber acumulado el máximo número de iteraciones establecido sin cumplir con el criterio SC_MAX; una situación similar se presentó en la función de Rastrigin, pero solo para los algoritmos ACO-FRS (2) y (4). Por otra parte, los resultados obtenidos muestran que los algoritmos ACO-FRS (2) y (4) presentan un mayor NFE cuando se utiliza el criterio de convergencia SC_MAX. Ambos algoritmos poseen el mismo mecanismo de aproximación a la región seleccionada (estrategia de generación B) y solo difieren en la estrategia de actualización de feromonas. La estrategia de generación B utiliza mayor información del archivo o matriz de regiones r (al incluir la región r_β  ≠ r_α ), factor que puede explicar el mejor desempeño de los algoritmos que la poseen.

Tabla 5. Eficiencia de las variantes de ACO-FRS en los problemas de optimización global sin restricción empleando SC_MAX como criterio de paro

Problema			NFE para
ID	Nombre de la función		ACO-FRS (1)	ACO-FRS (2)	ACO-FRS (3)	ACO-FRS (4)
B1	Zakharov (nvar  =  20)	SCMAX   =  6nvar	300.200	–	300.200	–
		SCMAX  = 12nvar	300.200	–	300.200	–
B2	Zakharov (nvar  = 10)	SCMAX  = 6nvar	150.100	150.100	149.690	150.100
		SCMAX  = 12nvar	150.100	150.100	150.100	150.100
B3	Zakharov (nvar  = 5)	SCMAX  = 6nvar	67.197	73.058	70.052	72.725
		SCMAX  = 12nvar	74.709	75.050	74.786	75.050
B4	Zakharov (nvar  = 2)	SCMAX  = 6nvar	4.501	4.286	4.156	3.727
		SCMAX  = 12nvar	26.967	27.012	26.060	27.231
B5	Rosenbrock (nvar  = 20)	SCMAX  = 6nvar	–	–	–	–
		SCMAX  = 12nvar	–	–	–	–
B6	Rosenbrock (nvar  = 10)	SCMAX  = 6nvar	–	–	–	–
		SCMAX  = 12nvar	–	–	–	–
B7	Rosenbrock (nvar  = 5)	SCMAX  = 6nvar	–	–	–	–
		SCMAX  = 12nvar	–	–	–	–
B8	Rosenbrock (nvar  = 2)	SCMAX  = 6nvar	–	–	–	–
		SCMAX  = 12nvar	–	–	–	1.060
B9	Goldstein and Price	SCMAX  = 6nvar	2.523	2.602	2.503	2.638
		SCMAX  = 12nvar	3.566	3.836	3.438	3.764
B10	Modificada de Himmelblau	SCMAX  = 6nvar	3.170	2.651	2.863	2.527
		SCMAX  = 12nvar	5.141	5.425	5.106	4.952
B11	Rastrigin	SCMAX  = 6nvar	230.897	300.200	223.556	300.200
		SCMAX  = 12nvar	252.656	300.200	249.275	300.200
B12	Griewank	SCMAX  = 6nvar	130.086	239.800	127.216	226.722
		SCMAX  = 12nvar	155.256	262.452	151.382	250.562
B13	Hartman (nvar  = 3)	SCMAX  = 6nvar	3.653	4.002	3.573	3.845
		SCMAX  = 12nvar	4.505	4.751	4.332	4.497
B14	Hartman (nvar  = 6)	SCMAX  = 6nvar	12.959	15.232	12.581	14.909
		SCMAX  = 12nvar	15.690	18.323	15.671	17.895
B15	Shekel (M  = 5)	SCMAX  = 6D	7.957	9.055	7.669	8.996
		SCMAX  = 12D	9.361	10.202	9.011	9.741
B16	Shekel (M  = 7)	SCMAX  = 6D	8.036	9.188	7.636	8.984
		SCMAX  = 12D	9.065	10.682	9.174	10.666
B17	Shekel (M  = 10)	SCMAX  = 6D	8.118	9.115	7.742	8.870
		SCMAX  = 12D	9.123	11.006	8.964	10.528

El símbolo «–» indica que NFE no es reportado dado que el método estocástico presenta 0% de SR

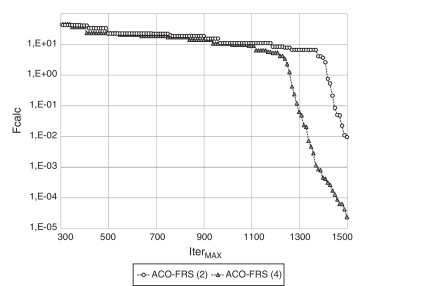
Con fines ilustrativos, en la figura 4 se presentan los historiales de convergencia de las estrategias ACO-FRS (2) y (4) en el proceso de minimización del problema B11. En este problema se minimiza la función de Rastrigin para 20 variables, cuyo mínimo global es cero, y esta gráfica solamente presenta el mejor valor para la función objetivo encontrado en cada iteración (f^calc) . Se observa que para la mayor parte del proceso de minimización, ACO-FRS (4) genera mejores f^calc . Además, se puede apreciar que ACO-FRS (2) requiere más iteraciones para mejorar significativamente f^calc , lo que se puede verificar en la forma del perfil de convergencia del método. En el valor máximo de iteraciones permitidas, ACO-FRS (4) generó una solución con mejor precisión.

Figura 4. Historiales de convergencia en la minimización global del problema B11 empleando los algoritmos ACO-FRS (2) y (4).

En síntesis, los resultados de las 4 variantes de ACO-FRS para la resolución de los problemas de optimización global seleccionados indican que la estrategia de generación B utilizada en los algoritmos ACO-FRS (2) y (4) proporciona un mejor desempeño, especialmente cuando se utiliza un esfuerzo numérico Iter_MAX  > 500. Una vez realizadas pruebas en problemas particulares (p. ej., los resultados de la figura 4 para la función de Rastrigin) se ha identificado la estrategia ACO-FRS (4) como el algoritmo propuesto y sugerido para la resolución de los problemas de optimización multivariables y con varios óptimos locales en espacios continuos. Con este algoritmo se pueden obtener tasas de convergencia superiores al 70% si se utiliza un esfuerzo numérico apropiado.

Con fines ilustrativos, se comparó el desempeño numérico del algoritmo ACO-FRS (4) con los resultados obtenidos para otros algoritmos del tipo ACO para espacios continuos. Los métodos utilizados para la comparación fueron CACS [24] , ACO_R[25] y MACACO [26] . En particular, se evaluó el desempeño numérico de este conjunto de métodos estocásticos en la resolución de 6 problemas con 30 variables de optimización, que se describen en la tabla 6 . En esta comparación se utilizó NFE_MAX como criterio de paro y se empleó un valor de 1 × 10⁶ para cada problema y algoritmo de optimización, con excepción de la función de Rosenbrock, donde el número máximo de funciones evaluadas fue 6 × 10⁶ . Los resultados numéricos de CACS, ACO_R y MACACO se obtuvieron de la literatura [26] , donde dichos algoritmos se implementaron con las condiciones ya mencionadas. Es importante indicar que los parámetros de ACO-FRS (4) utilizados en esta evaluación corresponden a los valores reportados en la tabla 1 . En la tabla 7 se presentan los valores de la media y la desviación estándar de las funciones objetivo utilizadas en el comparativo de los métodos del tipo ACO. Los resultados obtenidos indican que ACO-FRS (4) ofrece el mejor desempeño numérico y es más robusto en la mayoría de los problemas seleccionados. Los valores de las desviaciones estándar para el conjunto de problemas de optimización que se obtuvieron con ACO-FRS (4) son significativamente inferiores a los valores reportados para los otros métodos estocásticos (tabla 7 ). Solamente MACACO muestra una superioridad numérica a ACO-FRS (4) en el problema de Rastrigin (n_var  = 30). En general, los desempeños numéricos de ACO-FRS (4) y MACACO son superiores a los desempeños de los métodos ACO_R y CACS en la resolución de estos problemas de optimización multivariables.

Tabla 6. Problemas de optimización multivariables utilizados para la comparación de ACO-FRS con otros métodos del tipo ACO para espacios continuos

ID	Nombre de la función, Fobj	Variables de decisión, nvar y rango	Mínimo global y vector de posición
B18	Sphere	nvar  = 30	0
	${\textstyle F_{obj}=\sum _{i=1}^{n_{var}}u_{i}^{2}}$	−100 ≤ ui  ≤ 100	u=(0,…,0)
B19	Rosenbrock	nvar  = 30	0
	${\textstyle F_{obj}=\sum _{i=1}^{n_{var}-1}100{\left(u_{i+1}-u_{i}^{2}\right)}^{2}+}$${\left(u_{i}-1\right)}^{2}$	−30 ≤ ui  ≤ 30	u = (1,…,1)
B20	Rastrigin	nvar  = 30	0
	${\textstyle F_{obj}=10n_{var}+\sum _{i=1}^{n_{var}}\left[u_{i}^{2}-\right.}$$\left.10cos\left(2\pi u_{i}\right)\right]$	−5.12 ≤ ui  ≤ 5.12	u = (0,…,0)
B21	Griewank	nvar  = 30	0
	${\textstyle F_{obj}=1+0.00025\sum _{i=1}^{n_{var}}u_{i}-}$$\prod _{i=1}^{n_{var}}cos{\frac {u_{i}}{\sqrt {i}}}$	−500 ≤ ui  ≤ 500	u = (0,…,0)
B22	Schwefel	nvar  = 30	−12569.4866
	${\textstyle F_{obj}=-\sum _{i=1}^{n_{var}}u_{i}sin{\sqrt {\left|u_{i}\right|}}}$	−500 ≤ ui  ≤ 500	u  = (420.968,..., 420.968)
B23	Salomon	nvar  = 30	0
	${\textstyle F_{obj}=1-cos\left(2\pi {\sqrt {\sum _{i=1}^{n_{var}}u_{i}^{2}}}\right)+}$$0.1{\sqrt {\sum _{i=1}^{n_{var}}u_{i}^{2}}}$	−100 ≤ ui  ≤ 100	u = (0,…,0)

Tabla 7. Media y desviación estándar de la mejor solución obtenida por ACO_R ,, CACS, MACACO y ACO-FRS en problemas de optimización multivariables

ID	Nombre de la función	ACOR	CACS	MACACO	ACOFRS
		Valor promedio y desviación estándar de la función objetivoa
B18	Sphere	0  ±  0,00	0  ±  0,00	0  ±  0,00	0  ±  0,00
B19	Rosenbrock	29,93 ± 35,14	1,23 ± 1,91	7,48 ± 11,68	0,01434  ±  0,00061
B20	Rastrigin	101,65 ± 21,01	57,17 ± 14,14	0,00058  ±  0,00009	27,25 ± 3,63
B21	Griewank	0,09 ± 0,18	0,02 ± 0,02	0  ±  0,00	0  ±  0,00
B22	Schwefel	−8.703,26 ± 721,53	−8.934,57 ± 633,78	−12.569,49 ± 0,01	−12.569,49  ±  0,00
B23	Salomon	3,05 ± 1,43	0,33 ± 0,05	0,15 ± 0,05	0,12  ±  0,03

En negrita se indica el método con mejor desempeño.

a. Los valores correspondientes a ACO_R , CACS y MACACO fueron tomados de las referencias [24] , [25]  and [26] .

5. Conclusiones

Los métodos estocásticos basados en la metaheurística de colonia de hormigas son capaces de abordar problemas en espacios continuos sin requerir modificaciones mayores en su estructura básica. Para el caso del algoritmo ACO-FRS propuesto en este trabajo, la inclusión de una selección de regiones factibles permite realizar una búsqueda global mediante la eventual exploración de regiones con bajos niveles de feromonas, aumentando así la confiabilidad del método para la localización de la solución del problema de optimización. De las 4 versiones de ACO-FRS evaluadas en los problemas clásicos de optimización global, los resultados obtenidos indicaron que se consiguieron mejores desempeños mediante la aplicación del operador de búsqueda de camino en el que se combina la información de 2 regiones diferentes para definir la magnitud de desviación de la región seleccionada, en combinación con la estrategia de intensificación de feromonas que aumenta la probabilidad de selección de la región de comparación. Al realizar la comparación de la estrategia de optimización desarrollada con otros algoritmos del tipo ACO se observa un desempeño destacable y se demuestra la capacidad de ACO-FRS en la resolución de problemas multimodales con un número significativo de variables de decisión. Es conveniente indicar que en futuras implementaciones de ACO-FRS se puede considerar una evaluación explícita para el incremento en el nivel de feromonas para mejorar el desempeño numérico del algoritmo. Además, la estrategia de optimización desarrollada se puede adaptar fácilmente para la resolución de problemas con variables mixtas (enteras y continuas) con el objeto de convertirlo en un algoritmo de uso general. Los autores del presente trabajo analizarán estos temas en posteriores estudios.

Agradecimientos

Los autores agradecen las facilidades y el financiamiento otorgado por el Instituto Tecnológico de Aguascalientes y la Universidad de Guanajuato para la realización del presente estudio.

Bibliografía

1. [1] G.P. Rangaiah; Stochastic Global Optimization: Techniques and Applications in Chemical Engineering; World Scientific, Singapore (2010)
2. [2] J.J. Ródenas, G. Bugeda, J. Albelda, E. Oñate, E. Nadal; Sobre la necesidad de controlar el error de discretización de elementos finitos en optimización de forma estructural con algoritmos evolutivos; Rev. Int. Métodos Numér. Cálc. Diseño Ing., 28 (2012), pp. 1–11
3. [3] J. Pons-Prats, G. Bugeda, F. Zárate, E. Oñate; Optimización robusta en aplicaciones aeronáuticas con la combinación de cálculo estocástico y algoritmos evolutivos; Rev. Int. Métodos Numér. Cálc. Diseño Ing., 28 (2012), pp. 18–32
4. [4] M. Dorigo; Optimization Learning and Natural Algorithms [PhD thesis]; Politecnico di Milano, Milano, Italy (1992)
5. [5] E. Bonabeau, M. Dorigo, G. Theraulaz; Inspiration for optimization from social insect behavior; Nature, 406 (2000), pp. 39–42
6. [6] C. Blum; Ant colony optimization: Introduction and recent trends; Phys. Life Rev., 2 (2005), pp. 353–373
7. [7] M. Dorigo, V. Maniezzo, A. Colorni; Ant system: Optimization by a colony of cooperating agents; IEEE Trans. Syst. Man Cybern. Part A Syst. Humans, 26 (1996), pp. 29–41
8. [8] M. Dorigo, L.M. Gambardella; Ant colony system: A cooperative learning approach to the traveling salesman problem; IEEE Trans. Evol. Comput., 1 (1997), pp. 53–66
9. [9] T. Stützle, M. Dorigo; ACO algorithms for the quadratic assignment problem; D. Corne, M. Dorigo, F. Glover (Eds.), New Ideas in Optimization, McGraw-Hill, New York (1999)
10. [10] L.M. Gambardella, E. Taillard, M. Dorigo; Ant colonies for the quadratic assignment problem; J. Oper. Res. Soc., 50 (1999), pp. 167–176
11. [11] A.V. Donati, R. Montemanni, L.M. Gambardella, A.E. Rizzoli; Integration of a robust shortest path algorithm with a time dependent vehicle routing model and applications; Proceedings of International Symposium on Computational Intelligence for Measurement Systems and Applications (2003), pp. 26–31
12. [12] M. Reimann, K. Doerner, R. Hartl; D-ants: Savings based ants divide and conquer the vehicle routing problems; Comp. Oper. Res., 31 (2004), pp. 563–591
13. [13] B. Yu, Z.Z. Yang, B. Yao; An improved ant colony optimization for vehicle routing problem; Eur. J. Oper. Res., 196 (2009), pp. 171–176
14. [14] V.K. Jayaraman, B.D. Kulkarni, S. Karale, P. Shelokar; Ant colony framework for optimal design and scheduling of batch plants; Comp. Chem. Eng., 24 (2000), pp. 1901–1912
15. [15] C. Gagné, W.L. Price, M. Gravel; Comparing an ACO algorithm with other heuristics for the single machine scheduling problem with sequence-dependent setup times; J. Oper. Res. Soc., 53 (2002), pp. 895–906
16. [16] B. Zhang, D. Chena, W. Zhao; Iterative ant-colony algorithm and its application to dynamic optimization of chemical process; Comp. Chem. Eng., 29 (2005), pp. 2078–2086
17. [17] G. Bilchev, I.C. Parmee; The ant colony metaphor for searching continuous design spaces; T. Fogarty (Ed.), Lecture Notes in Computer Science 993, Springer-Verlag, U.K. (1995), pp. 25–39
18. [18] G. Bilchev, I.C. Parmee; Constrained optimization with an ant colony search model; Proceedings of Adaptive Computing in Engineering Design and Control (1996), pp. 145–151
19. [19] M. Wodrich, C. Bilchev; Cooperative distributed search: The ants way; Control Cybern., 26 (1997), p. 413
20. [20] M. Mathur, S.B. Karale, S. Priye, V.K. Jayaraman, B.D. Kulkarni; Ant colony approach to continuous function optimization; Ind. Eng. Chem. Res., 39 (2000), pp. 3814–3822
21. [21] J. Rajesh, K. Gupta, H.S. Kusumakari, V.K. Jayaraman, B.D. Kulkarni; Dynamic optimization of chemical processes using ant colony framework; Comp. Chem. Eng., 25 (2001), pp. 559–583
22. [22] N. Monmarché, G. Venturini, M. Slimane; On how Pachycondyla apicalis ants suggest a new search algorithm  ; Future Gener. Comp. Sy., 16 (2000), pp. 937–946
23. [23] J. Dréo, P. Siarry; A new ant colony algorithm using the heterarchical concept aimed at optimization of multiminima continuous functions; Future Gener. Comp. Sy., 20 (2004), pp. 841–856
24. [24] S.H. Pourtakdoust, H. Nobahari; An extension of ant colony system to continuous optimization problems; M. Dorigo, Birattari M., Blum C., Gambardella L.M., Mondada F., Stützle T. (Eds.), ANTS Workshop, Lecture Notes in Computer Science 3172, Springer, Berlin (2004), pp. 294–301
25. [25] K. Socha, M. Dorigo; Ant colony optimization for continuous domains; Eur. J. Oper. Res., 185 (2008), pp. 1155–1173
26. [26] F.O. De França, G.P. Coelho, F.J. von Zuben; Multivariate Ant Colony Optimization in Continuous Search Spaces; Proceedings of the 10th Annual Conference on Genetic and Evolutionary Computation, Atlanta, Georgia, USA (2008), pp. 9–16
27. [27] A.P. Engelbrecht; Computational Intelligence. An Introduction; John Wiley & Sons, England (2007)
28. [28] J.L. Deneubourg, S. Aron, S. Goss, J.-M. Pasteels; The self-organizing exploratory pattern of the argentine ant; J. Insect Behav., 3 (1990), pp. 159–168
29. [29] M. Dorigo, G. di Caro; Ant colony optimization: A new meta-heuristic; Proceedings of IEEE Congress on Evolutionary Computation (1999), pp. 1470–1477
30. [30] M. Dorigo, G. di Caro, L.M. Gambardella; Ant algorithms for discrete optimization; Artif. Life, 5 (1999), pp. 137–172
31. [31] M. Dorigo, T. Stützle; An experimental study of the simple ant colony optimization algorithm; Proceedings of International Conference on Evolutionary Computation (2001), pp. 253–258
32. [32] K. Socha; Ant colony optimization for continuous and mixed-variable domains [PhD thesis]; IRIDIA Université Libre de Bruxelles, Bruxelles, Belgium (2008)
33. [33] A. Bonilla-Petriciolet, S.E.K. Fateen, G.P. Rangaiah; Assessment of capabilities and limitations of stochastic global optimization methods for modeling mean activity coefficients of ionic liquids; Fluid Phase Equilib., 340 (2013), pp. 15–26
34. [34] S.E. Fateen, A. Bonilla-Petriciolet, G.P. Rangaiah; Evaluation of covariance matrix adaptation evolution strategy shuffled complex evolution and firefly algorithms for phase stability, phase equilibrium and chemical equilibrium problems,; Chem. Eng. Res. Des., 90 (2012), pp. 2051–2071
35. [35] Y.W. Shang, Y.H. Qiu; A note on the extended Rosenbrock function; Evol. Comput., 14 (2006), pp. 126–199