Resumo
Materiais compósitos vêm sendo largamente utilizados no projeto de estruturas aeronáuticas devido ao seu baixo peso e alta resistência mecânica. Porém, estruturas compósitas são expostas a perturbações estáticas e/ou dinâmicas. Assim, um grande esforço de pesquisa é empreendido no desenvolvimento de ferramentas numéricas para a análise e projeto de estruturas compósitas amortecidas. Neste sentido, este artigo apresenta a formulação numérica, via Método dos Elementos Finitos (MEF), de estruturas compósitas não amortecidas e amortecidas por tratamentos internos. Materiais viscoelásticos são os dispositivos utilizados como tratamento interno e são aplicados na forma de uma camada contínua inserida internamente ao estratificado. O amortecimento intrínseco do material compósito é considerado nos estudos realizados. São implementadas numericamente as teorias da Deformação Cisalhante de Primeira Ordem (FSDT) e Alta Ordem (HSDT). Elas se distinguem pela ordem das funções utilizadas na aproximação matemática do campo de deslocamentos mecânicos. Ambas as teorias são implementadas computacionalmente utilizando o elemento finito de placa, chamado Serendipity, dotado de 8 nós, 5 ou 11 graus de liberdade por nó, conforme a teoria utilizada, ou seja, FSDT ou HSDT respectivamente. Os resultados são comparados com os disponíveis na literatura científica, discutindo‐se as vantagens e desvantagens da utilização de cada teoria na modelagem de estruturas compósitas e sanduíches amortecidas.
Abstract
Composite materials have been used in the design of the aircrafts structures because their low weight and high mechanical strength. However, structures made in composite material are exposed to dynamical and/or static loading environments. Therefore, a major research effort is undertaken in the development of tools numerical for analysis and design of composite structures. This paper presents a numerical formulation of the composite structures using the Finite Element Method (FEM ). The damped composite structures, using inserted viscoelastic devices, and undamped composite structures are formulated by FEM . Viscoelastic materials are applied as continuous layers inserted on composite structures. The intrinsic damping of the composite material is included in the studies, too. The First‐order (FSDT ) and Higher‐order Shear Deformation (HSDT ) theories are formulated. They are distinguished by order of the approximation functions used in the mechanical displacements field. Both theories are computationally implemented using the Serendipity finite element. This is a rectangular finite element with 8 nodes, 5 or 11 degrees of freedom per node. The results are compared with papers predictions. The advantages and disadvantages of using each theory in the modeling of composite (thin or thick) and thick sandwiches structures, including the intrinsic and the viscoelastic damping, are discusses.
Palavras‐chave
Materiais compósitos ; Viscoelásticos ; Elementos finitos ; Teorias da Deformação Cisalhante de Primeira Ordem e Alta Ordem
Keywords
Composite materials ; Viscoelastic ; Finite element ; First‐order Shear Deformation Theory ; Higher‐order Shear Deformation Theory
1. Introdução
Materiais compósitos, laminados e sanduíches vêm sendo largamente empregados em numerosos produtos industriais, em virtude de sua elevada relação resistência/peso [1] . Sua estrutura estratificada, resultante da superposição de camadas com diferentes orientações de fibras, permite projetar tais materiais com vistas a um desempenho otimizado em condições de trabalho específicas.
No estado atual do desenvolvimento tecnológico, materiais compósitos estão integrados em diversos produtos de alta tecnologia, notadamente no setor aeroespacial. Normalmente, nestes tipos de aplicações aeronáuticas, as estruturas compósitas estão frequentemente expostas a perturbações estáticas, quase estáticas ou dinâmicas, além de estarem sujeitas a intempéries ambientais tais como a radiação solar, a chuva e o vento. Essas perturbações podem afetar as características mecânicas e comprometer a integridade estrutural dos materiais compósitos, alterando as suas respostas estáticas (deformações, distribuição de tensões, etc.) e dinâmicas (frequências naturais, amortecimento estrutural, etc.), podendo levar à degradação imediata ou após decorrido um grande período de exposição a essas perturbações. Em vista disso, estudos que integram os materiais compósitos a dispositivos de atenuação ativa e/ou passiva mobilizam um grande número de pesquisadores, tais como Chee [2] e Oliveira e Greus [3] . No tocante a atenuação passiva, os materiais viscoelásticos dissipam parcialmente a energia mecânica indesejável na forma de calor e tem suas propriedades mecânicas fortemente dependentes da frequência de excitação e da temperatura de trabalho sob o qual estão sujeitos [4] .
Dentre as diferentes técnicas numéricas de modelagem de estruturas compósitas amortecidas, o Método dos Elementos Finitos (MEF) tem se mostrado o mais adequado, principalmente em virtude de suas características vantajosas de flexibilidade de modelagem e relativa facilidade de implementação numérica. Particularmente, observa‐se na literatura uma grande diversidade de teorias utilizadas na formulação de elementos finitos aplicados ao estudo de estruturas compósitas, cada uma delas apresentando características favoráveis e desfavoráveis próprias, notadamente no que diz respeito à precisão, ao domínio de aplicação e ao esforço computacional envolvido na sua implementação numérica [1] , [5] and [6] . A Teoria da Deformação Cisalhante de Terceira Ordem , também conhecida como Teoria da Deformação Cisalhante de Ordem Superior – Higher‐order Shear Deformation Theory (HSDT) , aproxima as variáveis mecânicas por uma função polinomial de terceira ordem e é considerada a teoria que melhor se aproxima dos valores das tensões e das deformações obtidas pela Teoria da Elasticidade 3D. Outra teoria, a First‐order Shear Deformation Theory (FSDT) , também é largamente utilizada na modelagem de estruturas compósitas devido ao seu baixo custo computacional. Ambas as teorias, FSDT e HSDT , são classificadas na literatura como teorias em Camada Simples Equivalente (Equivalent Single Layer Theory ). Além dessa família de teorias existe também a família das teorias em Camadas Equivalentes Discretas (Layerwise Theory ). Nesta família de teorias os deslocamentos são funções contínuas ao longo da coordenada da espessura do estratificado. Segundo Reddy [1] , quando o interesse é o estudo de efeitos localizados em materiais compósitos, tais como mecanismos de delaminação entre camadas adjacentes, rompimento de fibras e efeitos de borda, as teorias em Camadas Equivalentes Discretas são mais apropriadas que as teorias formuladas em Camada Simples Equivalente , que por sua vez são mais recomendadas nos estudos envolvendo comportamentos globais do estratificado compósito, tais como determinação das frequências naturais, dos modos de vibração e dos deslocamentos, o que justifica a escolha das teorias em FSDT e HSDT neste artigo.
O principal objetivo deste artigo é a implementação e confrontação numérica das teorias FSDT e HSDT implementadas via MEF , e a validação numérica de ambas através da confrontação de artigos científicos para o estudo de estruturas compósitas amortecidas por tratamentos internos viscoelásticos, sem desprezar o amortecimento inerente (intrínseco ou natural) do material compósito. O Módulo Complexo , normalmente utilizado na modelagem do amortecimento viscoelástico, também é empregado neste artigo na aproximação matemática do amortecimento intrínseco das lâminas compósitas, permitindo a inclusão da influência da temperatura e da frequência de excitação no comportamento final da estrutura compósita amortecida. Esta é uma das originalidades deste artigo, além, é claro, da confrontação numérica das teorias FSDT e HSDT utilizadas na modelagem, via MEF , de estruturas compósitas amortecidas pelo uso de tratamentos internos viscoelásticos, pouco difundida na literatura científica.
A formulação das teorias FSDT e HSDT , via MEF , incorporando os amortecimentos inerente e viscoelástico, é sumarizada na próxima seção.
2. Formulação via Método dos Elementos Finitos das teorias da Deformação Cisalhante de Primeira Ordem e Alta Ordem
2.1. Campo de deslocamentos mecânicos
Especificadamente, no caso da teoria HSDT , o comportamento mecânico da estrutura compósita é aproximado matematicamente por um campo de deslocamentos de terceira ordem, expresso como:
|
|
( 1) |
sendo: , , , e ; uo , vo e wo são deslocamentos nas direções coordenadas (x, y, z ) de um ponto material do plano médio de referência (x, y , 0) da estrutura compósita; θx , θy e θz são respectivamente rotações dos segmentos normais à superfície de referência em torno dos eixos elementares y , x e z . Já na teoria FSDT tem‐se que i = 0 a 1 e a componente θz é negligenciada. As funções ζx , ζy , ζz , Γx e Γy são funções que não apresentam significado físico evidente, mas podem ser vistas como rotações de ordem superior [5] .
Usando as definições da Teoria da Elasticidade 3D[1] e a equação (1) , as deformações na teoria HSDT são expressas sob a forma:
|
|
( 2) |
sendo: . Já na teoria FSDT, i = 0 a 1 e as componentes θz , ζx , ζy e ζz são negligenciadas.
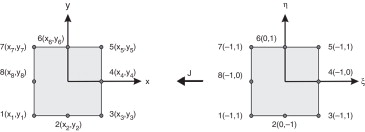
As variáveis mecânicas apresentadas nas equações (1) e (2) são convertidas neste artigo para sua formulação em elementos finitos usando as funções de forma apropriadas do elemento finito Serendipity ( fig. 1 ). Esse elemento finito trata‐se de um elemento de placa, dotado de um total de 8 nós, sendo 3 por aresta [1] .
|
|
|
Figura 1. Elemento finito Serendipity com 8 nós em coordenadas elementares (x ,y ) e locais . |
As variáveis mecânicas do campo de deslocamentos das teorias FSDT e HSDT , fornecidas na equação (1) , são expressas respectivamente nos vetores e . Na formulação via elementos finitos, essas variáveis mecânicas são expressas em termos das variáveis mecânicas nodais e , respectivamente, conforme a equação que se segue:
|
|
( 3) |
sendo n o número de variáveis mecânicas da teoria utilizada, ou seja, 5 para a teoria FSDT e 11 para a HSDT .
Utilizando a equação (3) , o campo de deslocamentos mecânicos das teorias FSDT e HSDT pode ser expresso, em coordenadas elementares, sob a forma:
|
|
( 4) |
As 8 funções de forma do elemento finito Serendipity , fornecidas em Reddy [1] , são incluídas na matriz Ntheory das funções de forma, de acordo com a teoria utilizada.
Substituindo a equação (4) na (2) , as deformações mecânicas podem ser escritas em termos das funções de forma do elemento Serendipity e dos deslocamentos nodais de acordo com a expressão [6] :
|
|
( 5) |
com:
|
|
( 6) |
2.2. Matrizes de massa e rigidez elementares
A formulação das matrizes elementares é feita via Princípio Variacional de Hamilton (PVH) , que permite a incorporação de todas as contribuições energéticas presentes na estrutura. A seguir, são apresentadas as expressões das matrizes de massa e de rigidez, em nível elementar e em coordenadas locais , obtidas via PVH :
|
|
( 7) |
|
|
( 8) |
onde: é a matriz de massa elementar ( ou ) de ordem n × 8; é a matriz de rigidez elementar ( ou ) de ordem n × 8; nk é o número total de camadas k ao longo da espessura z do estratificado; ρk é a densidade do material de cada camada k ; C é a matriz das constantes de elasticidade (dependente da camada k do laminado, da frequência de excitação ω e da temperatura T de trabalho) e J é o Jacobiano da transformação das coordenadas locais para as elementares .
Para o caso particular de um material ortotrópico que apresenta 9 coeficientes de elasticidade independentes, a matriz Cl , escrita no sistema de referência do material (1,2,3), segue a forma:
|
|
( 9) |
onde: ; ; ; ; ; ; ; e . No caso particular dos materiais isotrópicos (como os viscoelásticos) a matriz Cl da eq. (9) contém 2 coeficientes independentes, que são o módulo de Young E e o módulo de Cisalhamento G .
Quando o interesse é a formulação da teoria FSDT via MEF , a eq. (9) deve ser modificada adicionando coeficientes de correção apropriados para a correção dos valores das tensões (e das deformações) cisalhantes transversais (σxz , σyz ) ao longo da espessura do estratificado, tal como indicado em Reddy [1] .
Para a transformação das constantes de elasticidade do sistema de referência material (1,2,3) para o sistema de referência elementar (x ,y ,z ) utiliza‐se uma matriz de transformaçãoT (θ ), dada sob a forma matricial:
|
|
( 10) |
sendo que a matriz de transformação T é função do ângulo θ (das fibras) formado entre o sistema material de referência (1,2,3) em relação ao sistema elementar (x ,y ,z ) [5] .
2.3. Amortecimento inerente e passivo
Os materiais compósitos reforçados com fibras apresentam mecanismos de amortecimento natural (inerente) associados ao comportamento viscoelástico de suas matrizes poliméricas [7] .
A introdução do amortecimento inerente em uma dada camada k do estratificado é feita considerando os coeficientes de elasticidade da matriz C , fornecidos na eq. (9) , como dependentes da temperatura de trabalho e da frequência de excitação.
No caso particular de utilização de um material ortotrópico, os módulos de elasticidade longitudinal , transversal ( ) e plano (gp = G12 ) são funções complexas do tipo:
|
|
( 11) |
sendo: ; o vetor módulo de armazenamento ; o vetor módulo de perda ; o vetor que contém os fatores de perda do material; Id um vetor identidade de ordem 6 × 1 e .
Os fatores de perda do vetor η são fornecidos pela micro‐mecânica para diferentes modelos teóricos, tais como os de Hashin, Tsai, Zhao‐Weng, Mori‐Tanaka, entre outros, e são fornecidos em diversas publicações, tais como em Fisher et al. [8] .
Assume‐se neste artigo que os coeficientes da matriz C , eq. (10) , e que os fatores de perda do vetor η , eq. (11) , dos materiais laminados são independentes da temperatura e da frequência de excitação do material, devido à ausência de publicações experimentais que forneçam esta dependência para altas frequências, sendo obtidos somente para frequências menores que 10 Hz, tal como no trabalho de Melo et al. [9] .
Outro tipo de amortecimento de interesse neste artigo é o proveniente do uso de tratamentos internos viscoelásticos, inseridos ao longo da espessura do estratificado laminado na forma de camada, em vista ao aumento do amortecimento final da estrutura sanduíche resultante.
Os materiais viscoelásticos são geralmente elementos de natureza isotrópica, cujas propriedades mecânicas são fortemente dependentes da temperatura de trabalho e da frequência de excitação [4] . Baseado no conceito de Módulo Complexo[4] , o módulo de cisalhamento do material viscoelástico poder ser expresso pela equação:
|
|
( 12) |
Utilizando a equação (12), a matriz C (ω , T ) da eq. (9) (reescrita no caso particular de material isotrópico) pode ser expressa em termos do: módulo de armazenamento , do fator de perda η (ω , T ) e do coeficiente de Poisson ν do material viscoelástico. Além disso, o módulo pode ser facilmente fatorado da matriz e consequentemente da matriz de rigidez elementar , uma vez que v é constante [6] .
O Princípio da Equivalência Frequência‐Temperatura (PEFT) é utilizado para a obtenção do módulo de armazenamento e do fator de perda dos materiais viscoelásticos termo‐reologicamente simples. Segundo Nashif et al. [4] , a relação inversa entre os efeitos da frequência e da temperatura é a base do PEFT , segundo o qual as propriedades do material viscoelástico em função da frequência, coletadas em diferentes temperaturas, podem ser geradas em uma curva mestre (monograma ) utilizando‐se um fator de deslocamento apropriado, dependente da temperatura. Assim, a frequência de excitação ω pode ser escrita em função de uma frequência reduzida ωr e de um fator de deslocamento αT apropriado, ou seja, [4] . De Lima et al. [6] sugerem em seu trabalho expressões analíticas, obtidas por ajuste de curvas, para o módulo complexo e para o fator de deslocamento para vários materiais viscoelásticos comerciais, e dentre eles o ISD112 da 3 M adotado neste artigo.
2.4. Forças em nível elementar
As contribuições das forças V de corpo, S de superfície e P pontuais em nível elementar são obtidas formulando o trabalho virtual em termos das funções de forma e variáveis nodais, resultando na seguinte expressão:
|
|
( 13) |
na qual: é o vetor de forças elementares de acordo com a teoria utilizada; ve e se são respectivamente o volume e a área elementar.
Levando‐se em conta a conectividade entre nós e utilizando o procedimento padrão de montagem das matrizes globais [10] , o modelo matemático da equação global do movimento do sistema amortecido, para as teorias FSDT e HSDT , pode ser expresso pela equação geral:
|
|
( 14) |
onde: M é a matriz de massa global da estrutura compósita amortecida, de ordem Nn x n (sendo Nn o número total de nós da estrutura modelada), simétrica e definida positiva; é a matriz de rigidez global de ordem Nn x n, simétrica e semi‐definida positiva, sendo que Ko e Kv são respectivamente as matrizes de rigidez da subestrutura laminada e viscoelástica; f (t ) é o vetor de carregamentos externos, de ordem Nn x1.
O procedimento descrito pela equação (14) refere‐se à aplicação de um tratamento viscoelástico disposto como camada única e contínua ao longo da espessura da estrutura compósita analisada. De Lima et al. [6] descrevem o procedimento de modelagem via MEF quando são utilizadas pastilhas viscoelásticas discretas ao longo da superfície da estrutura compósita.
A imposição das condições de contorno nas teorias FSDT e HSDT segue as orientações fornecidas em Correia et al. [11] . Após a imposição das condições de contorno, as variáveis mecânicas prescritas são eliminadas dentre as incógnitas nodais, o que leva a uma diminuição da ordem dos vetores e matrizes da equação (14) .
3. Análise sob vibrações livres para um sistema amortecido
Para realizar análises sob vibrações livres, a equação (14) é manipulada, adotando uma solução periódica sob a forma e assumindo que o vetor de forças globais f (t ) é um vetor nulo [12] . Assim, a equação (14) pode ser reduzida na seguinte equação geral:
|
|
( 15) |
em que: λ = ω2 e são respectivamente os auto‐valores e auto‐vetores complexos , soluções do sistema (15) .
Uma vez que os coeficientes das matrizes Ko e Kv são dependentes da frequência ω e da temperatura T , a equação (15) deve ser resolvida através de um procedimento numérico iterativo [13] . Para tal, a equação (15) é resolvida considerando que, inicialmente, as matrizes Ko e Kv são independentes da frequência de excitação e temperatura de trabalho. Assim, uma frequência teste , de um determinado modo de vibração i de interesse, é obtida através do cálculo dos autovetores. Essa frequência inicial de teste é adotada para o cálculo dos novos coeficientes da matriz , eq. (9) , e do , eq. (12). A nova matriz de rigidez obtida fornecerá uma nova frequência teste . Adotando um critério de convergência apropriado, a frequência final ωi é obtida. Após a convergência da frequência de interesse, o autovalor final no modo de vibração i de interesse pode ser calculado pela expressão [13] :
|
|
( 16) |
Além disso, e segundo Meunier e Shenoi [13] , o fator de amortecimento ηi , do modo de vibração i , da estrutura compósita amortecida pode ser calculado através da expressão:
|
|
( 17) |
Neste artigo as matrizes M e Ko , das eqs. (14) e (15) , são adotadas independentes de ω e T .
4. Função resposta em frequência do sistema amortecido
Considerando que as estruturas compósitas amortecidas são sujeitas a uma força de excitação harmônica variável com o tempo, do tipo , e que a resposta induzida por esta excitação é do tipo harmônica, [12] , a equação (14) escrita no domínio do tempo por ser transformada para o domínio da frequência através da Função Resposta em Frequência (FRF ):
|
|
( 18) |
sendo: b o vetor que permite escolher, entre todos os graus de liberdade (g.d.l .) dos MEFs, FSDT ou HSDT , onde são aplicadas as forças de excitação na estrutura; c o vetor que fornece o local onde as respostas do sistema são captadas e a matriz de rigidez dinâmica do sistema amortecido.
A equação (18) é utilizada para a obtenção das amplitudes de vibração das estruturas compósitas amortecidas, via tratamento interno viscoelástico e amortecimento natural do laminado, submetidas a um sistema de forças de excitação qualquer. Neste tipo de sistema amortecido, a matriz deve ser calculada e invertida para cada valor de frequência de excitação ω e de temperatura T de trabalho na banda de frequência de interesse.
5. Aplicações numéricas
Três diferentes aplicações numéricas são implementadas em ambiente Matlab® . A primeira para a confrontação e validação experimental, com base em artigos científicos, das teorias FSDT e HSDT no cálculo das frequências naturais e dos modos de vibração de estruturas compósitas laminadas finas . A segunda aplicação para demonstrar a precisão numérica de ambas as teorias na obtenção do fator de amortecimento e da frequência natural fundamental de estruturas sanduíche espessas amortecidas, variando as condições de contorno das placas sanduíche. E a terceira aplicação numérica procura demonstrar a influência da temperatura e da frequência na amplitude das vibrações em uma estrutura sanduíche fina amortecida.
Na primeira aplicação considera‐se uma placa compósita fabricada em material laminado não amortecido. A placa compósita é considerada fina (a /h > 20, sendo a o lado maior da placa e h a espessura total da placa), de dimensões 0,290 m × 0,234 m × 0,005 m, constituída por 8 camadas, orientadas a (90°/0°)2s e com condições de contorno livre‐livre.
Os resultados experimentais e numéricos de Cugnoni et al. [14] , obtidos no estudo desta mesma placa compósita, são usados neste artigo para verificar a acuracidade de ambas as teorias FSDT e HSDT formuladas via MEF .
Para a obtenção dos resultados numéricos empregando as teorias FSDT* e HSDT* de Cugnoni et al. [14] , este utiliza um elemento finito de casca de dupla curvatura, dotado de 8 nós, da família C0 e obtido da degeneração de um elemento sólido multicamada. Em ambas as teorias o número de g.d.l . por nó é 3(p + 1), onde p denota a ordem do polinômio utilizado na aproximação do campo de deslocamentos mecânicos das teorias de primeira e alta ordem formuladas por Cugnoni et al. [14] . Os resultados numéricos apresentados nesta seção adotam p = 3 para a teoria HSDT* , ou seja, cada elemento finito de casca apresenta um total de 96 g.d.l . e p = 1 para a teoria FSDT* , ou seja, 48 g.d.l ./EF . Além disso, a teoria FSDT* de Cugnoni et al. [14] inclui a rotação normal (θz ) em sua formulação.
Os valores das propriedades físicas das camadas do material laminado são: E1 = 23,5 GPa, E2 = E3 = 9,4 GPa, G12 = G13 = 2,5 GPa, G23 = 1,8 GPa, ν12 = 0,08, ν13 = 0,35, ν32 = 0,38 e ρ = 1463 kg/m3 .
Após estudo de convergência de malha, a placa compósita analisada é discretizada em 8 × 8 elementos finitos, utilizando os MEFs FSDT e HSDT implementados neste artigo.
A formulação do MEF ‐FSDT adota 5/6 como fator de correção do cisalhamento transversal, proposto por Reddy [1] para materiais compósitos laminados e homogêneos.
A tabela 1 compara os valores das 7 frequências naturais obtidas via MEFs FSDT e HSDT com os resultados experimentais e numéricos de Cugnoni et al. [14] empregando as teorias FSDT* e HSDT* .
| Modos | Experimental* (Hz) fExp | HSDT* (Hz) | FSDT* (Hz) | HSDT (Hz) | FSDT (Hz) | Erro (%) | Erro (%) | Erro (%) | Erro (%) |
|---|---|---|---|---|---|---|---|---|---|
| M ‐ 1 | 101,7 | 101,5 | 101,5 | 102,1 | 102,4 | 0,2 | 0,2 | 0,4 | 0,7 |
| M ‐ 2 | 190,1 | 188,8 | 187,3 | 188,4 | 198,1 | 0,7 | 1,5 | 0,9 | 4,2 |
| M ‐ 3 | 273,9 | 277,9 | 277,0 | 279,3 | 287,6 | 1,5 | 1,1 | 2,0 | 5,0 |
| M ‐ 4 | 340,9 | 340,2 | 338,3 | 339,5 | 354,1 | 0,2 | 0,8 | 0,4 | 3,9 |
| M ‐ 5 | 389,7 | 394,7 | 393,1 | 395,1 | 406,6 | 1,3 | 0,9 | 1,4 | 4,3 |
| M ‐ 6 | 524,5 | 519,5 | 515,6 | 525,0 | 556,0 | 1,0 | 1,7 | 0,1 | 6,0 |
| M ‐ 7 | 558,2 | 563,5 | 562,4 | 567,5 | 585,6 | 0,9 | 0,8 | 1,7 | 4,9 |
Na tabela 1 , fExp indica as frequências experimentais obtidas por Cugnoni et al. [14] para a placa sanduíche em questão, e são respectivamente as frequências analíticas obtidas por Cugnoni et al. [14] utilizando as teorias HSDT* e FSDT* , e são as frequências numéricas obtidas com as teorias HSDT e FSDT implementadas neste artigo, e são respectivamente os erros relativos entre as frequências experimentais e analíticas de Cugnoni et al. [14] , e, finalmente, e são os erros relativos entre as frequências experimentais de Cugnoni et al. [14] com as numéricas obtidas segundo os MEF HSDT e FSDT deste artigo.
Comparando os resultados numéricos das frequências naturais obtidos pelas teorias FSDT e HSDT com os experimentais de Cugnoni et al. [14] , a teoria HSDT proporciona resultados numéricos mais próximos dos experimentais do que os obtidos via FSDT . Agora, comparando os valores numéricos das frequências naturais obtidas pelas diferentes formulações numéricas em relação aos dados experimentais de Cugnoni et al. [14] nota‐se, através da tabela 1 , que os valores numéricos fornecidos por Cugnoni et al. [14] são mais satisfatórios para ambas as formulações FSDT* e HSDT* , em comparação aos resultados obtidos via teorias FSDT e HSDT . No entanto, deve ser notado que as teorias FSDT* e HSDT* requerem um custo computacional bem superior ao requerido pelas teorias FSDT e HSDT , visto que, enquanto as teorias HSDT* e FSDT * apresentam respectivamente um total de 96 e 48 g.d.l. /EF , as teorias HSDT e FSDT apresentam respectivamente 88 e 40 g.d.l. /EF. Além disso, a teoria FSDT* inclui em sua formulação a rotação normal θz . A rotação normal pode explicar a discrepância, já citada, entre os resultados numéricos obtidos pelo MEF ‐FSDT na obtenção das frequências naturais em relação aos demais modelos, uma vez que ele não inclui em sua formulação a rotação normal θz e que se revela influente nos resultados obtidos.
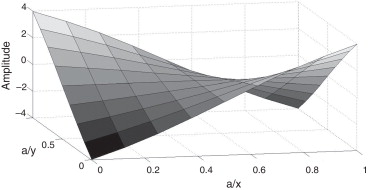
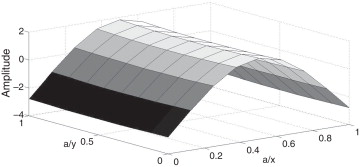
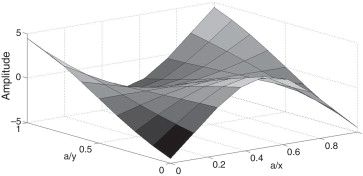
As Figura 2 , Figura 3 , Figura 4 and Figura 5 ilustram os 4 primeiros modos de vibração da placa compósita formulada pelo MEF‐HSDT e que são normalizados através da matriz de massa modal[12] .
|
|
|
Figura 2. 1.° modo de vibração ω1 = 102,1 Hz. |
|
|
|
Figura 3. 2.° modo de vibração ω2 = 188,4 Hz. |
|
|
|
Figura 4. 3.° modo de vibração ω3 = 279,3 Hz. |
|
|
|
Figura 5. 4.° modo de vibração ω4 = 339,5 Hz. |
A próxima aplicação numérica é baseada nos resultados analíticos apresentados por Meunier e Shenoi [13] e que utiliza a teoria HSDT simplificada de Reddy (HSDT *). Nesta teoria, apenas 5 funções incógnitas: u0, v0, w0, ψx e ψy são adotadas na formulação do campo de deslocamentos mecânicos do material compósito, que é a mesma quantidade de incógnitas utilizadas pela teoria FSDT , o que a torna uma teoria bastante atrativa em termos de redução do custo computacional e precisão numérica. Porém, como o termo z3 envolve derivadas de w0 , as deformações envolvem também derivadas de w0 , exigindo o uso de funções com primeiras derivadas contínuas, pertencentes ao espaço C1 . Além disso, a tensão normal σzz que ocorre ao longo da espessura do estratificado não é considerada na formulação analítica formulada por Meunier e Shenoi [13] .
Duas diferentes placas sanduíche espessas (a /h < 20) são analisadas nesta aplicação numérica e se diferenciam pelos tipos de condições de contorno aplicadas em suas bordas, sendo uma apoiada‐apoiada (Placa I ) e a outra engastada‐engastada (Placa II ). Ambas as placas são formadas por duas faces em Fibre Reinforced Plastic (FRP ), cada uma orientada a 0o /90o /0o , e coladas a um núcleo interno de material viscoelástico.
Para a temperatura em estudo de 90 °C, o amortecimento inerente das faces compósitas laminadas é assumido constante com a frequência de excitação, já as propriedades do núcleo viscoelástico variam com a frequência de excitação e temperatura de trabalho. Os modos de armazenamento e os fatores de perda do núcleo viscoelástico HEREX C70.130 são, segundo Meunier e Shenoi [13] , em MPa: , , e . A densidade do núcleo viscoelástico é de 130 kg/m3 e as propriedades mecânicas das faces em FRP são: , , , ν12 = ν23 = ν13 = 0,3, η12 = η13 = η23 = 1,0998 × 10‐2 e ρ = 1813,9 kg/m3 .
Nas estruturas sanduíches analisadas a relação entre a espessura do núcleo viscoelástico (hc ) e a espessura total da placa (h ) compósita é variada (0, 01 ≤ hc /h ≤ 0, 97), sendo mantida a relação entre o lado maior da placa sanduíche e sua espessura total igual a 10, ou seja a/h = 10.
Ambas as placas sanduíches, (I) e (II) , formuladas via MEF FSDT e HSDT são discretizadas com uma malha composta por 4 × 4 elementos finitos, obtida após estudo de convergência de malha.
As frequências fundamentais e os fatores de amortecimento tabelados a seguir são obtidos considerando o processo iterativo de convergência da frequência fundamental para cada uma das duas estruturas sanduíche analisadas proposto por Meunier e Shenoi [13] .
Por meio dos resultados numéricos fornecidos na tabela 2 para as Placas (I)* e (I) , constata‐se que a teoria HSDT , comparada com a FSDT , foi a que melhor se aproximou dos resultados analíticos de Meunier e Shenoi [13] empregando a teoria HSDT* . Esses resultados já eram esperados, visto que a teoria HSDT promove melhores resultados do que a FSDT para a modelagem de estruturas compósitas espessas, sendo a teoria FSDT mais apropriada para a modelagem de estruturas compósitas finas [1] . Além disso, sugere‐se que a discrepância dos resultados apresentados pela teoria FSDT , comparados com a HSDT* de Meunier e Shenoi [13] , pode também estar relacionada a utilização de fatores de correção do cisalhamento transversal, iguais a 5/6, apropriados para a modelagem de estruturas compósitas homogêneas, que não é o caso com a utilização de um núcleo viscoelástico. Outro aspecto importante a ser considerado para explicar a diferença encontrada entre os resultados numéricos, obtidos via MEF‐HSDT , com os analíticos de Meunier e Shenoi [13] , pode ser associado à ausência da deformação normal ɛzz e da tensão σzz normal na teoria HSDT* , que, segundo Mendonça [5] , pode afetar o balanço de forças e impedir a correta satisfação das equações de equilíbrio, gerando descontinuidades das tensões σyz e σxz , além de afetar os deslocamentos transversais. Como já é bem conhecido na literatura, as tensões cisalhantes transversais são importantes na capacidade de amortecimento dos materiais viscoelásticos [4] . Já o MEF ‐HSDT formulado neste artigo não negligencia nem as tensões σzz e nem as deformações ɛzz normais.
| Placa (I)* | Placa (I) | Placa (II) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HSDT* | HSDT | FSDT | HSDT | FSDT | ||||||
| η | η | η | η | η | ||||||
| 0,01 | – | – | 28,37 | 0,006 | 29,48 | 0,006 | 52,14 | 0,006 | 52,77 | 0,006 |
| 0,03 | – | – | 28,54 | 0,006 | 29,67 | 0,006 | 52,33 | 0,006 | 53,03 | 0,006 |
| 0,05 | – | – | 28,82 | 0,006 | 29,99 | 0,006 | 52,65 | 0,006 | 53,47 | 0,006 |
| 0,10 | – | – | 29,39 | 0,006 | 30,65 | 0,006 | 53,22 | 0,006 | 54,37 | 0,006 |
| 0,20 | – | – | 30,49 | 0,006 | 32,05 | 0,006 | 54,00 | 0,007 | 56,22 | 0,007 |
| 0,30 | – | – | 31,40 | 0,007 | 33,51 | 0,006 | 53,93 | 0,007 | 58,05 | 0,007 |
| 0,40 | – | – | 31,86 | 0,007 | 34,95 | 0,007 | 52,49 | 0,008 | 59,78 | 0,007 |
| 0,58 | 32,23 | 0,009 | 30,06 | 0,009 | 37,28 | 0,007 | 44,56 | 0,011 | 62,21 | 0,007 |
| 0,64 | 31,37 | 0,010 | 28,15 | 0,012 | 37,87 | 0,007 | 40,06 | 0,014 | 62,66 | 0,007 |
| 0,70 | 29,77 | 0,012 | 25,32 | 0,017 | 38,27 | 0,007 | 34,69 | 0,019 | 62,78 | 0,008 |
| 0,76 | 27,13 | 0,016 | 21,58 | 0,028 | 38,36 | 0,007 | 28,68 | 0,030 | 62,39 | 0,008 |
| 0,82 | 23,11 | 0,026 | 17,20 | 0,059 | 37,89 | 0,007 | 22,53 | 0,058 | 61,11 | 0,008 |
| 0,88 | 17,68 | 0,065 | 13,13 | 0,143 | 36,29 | 0,007 | 17,24 | 0,130 | 58,02 | 0,009 |
| 0,91 | 14,81 | 0,116 | 11,79 | 0,216 | 34,59 | 0,008 | 15,50 | 0,193 | 55,08 | 0,009 |
| 0,94 | 12,56 | 0,204 | 11,35 | 0,283 | 31,62 | 0,008 | 14,77 | 0,259 | 50,15 | 0,010 |
| 0,97 | 11,78 | 0,270 | 11,75 | 0,292 | 25,70 | 0,010 | 15,11 | 0,296 | 40,65 | 0,013 |
Os dados da tabela 2 também demonstram que a variação das condições de contorno tem pouca influência no fator de amortecimento e grande influência sobre as frequências fundamentais da placa sanduíche, ou seja, para a condição de contorno engastada‐engastada (Placa II ) a rigidez final da estrutura aumentou, o que era esperado, no entanto, o fator de amortecimento aumentou de maneira menos pronunciável. Além disso, observando os dados fornecidos na tabela 2 para essas duas placas sanduíche, quando menor a relação hc /h menor a discrepância entre os valores das frequências naturais e dos fatores de amortecimento obtidos pelos MEFs FSDT e HSDT .
Na terceira e última aplicação numérica, uma placa sanduíche fina (a /h > 20) simplesmente apoiada nas quatro bordas, é estudada. A placa sanduíche, de dimensões 0,30 m × 0,30 m × 0,01 m, é constituída por um núcleo viscoelástico embutido entre duas faces laminadas orientadas a 90°.
O núcleo viscoelástico tem suas propriedades mecânicas variáveis com a frequência de excitação e temperatura de trabalho e o amortecimento inerente das duas faces laminadas é considerado. O material viscoelástico utilizado é o ISD112 e suas propriedades mecânicas são fornecidas por De Lima et al. [6] . Já as propriedades das duas faces laminadas são iguais a: , , , ν12 = ν23 = ν13 = 0,30, η1 = 4,5 × 10‐3 , η2 = 4,22 × 10‐2 , η12 = η13 = η23 = 7,05 × 10‐2 e ρ = 1813,9 kg/m3 .
A placa sanduíche amortecida é modelada via MEF ‐HSDT , sendo discretizada por uma malha formada por 8 × 8 elementos finitos, obtida após estudo de convergência de malha.
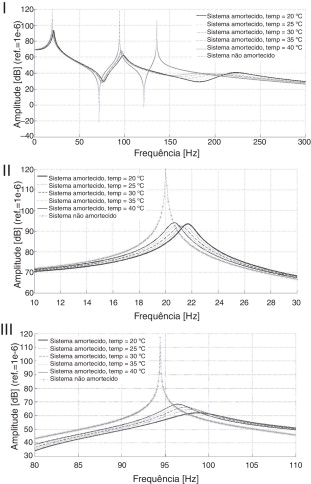
As FRF ilustradas na figura seguir em (I), são obtidas para uma excitação unitária aplicada e captada no centro da placa sanduíche, variando a temperatura em 5 em 5 °C entre 20 a 40 °C e considerando a banda de frequência entre 0 a 300 Hz.
A figura 6 também ilustra em (II) e (III) as amplitudes das FRF na faixa de frequência incluindo as duas primeiras frequências naturais da placa sanduíche para os diferentes valores de temperatura analisados.
|
|
|
Figura 6. FRF da placa sanduíche entre 0‐300 Hz para diferentes temperaturas, I, e FRF em torno da primeira (II ) e da segunda (III ) frequência natural. |
Comparando os resultados ilustrados na figura 6 , nota‐se a forte influência da temperatura sobre as amplitudes de vibração da placa sanduíche amortecida por tratamento interno viscoelástico. Nota‐se que quanto menor a temperatura, maior a rigidez do material viscoelástico e maiores são os valores das frequências naturais. Por outro lado, não se observa, para a primeira frequência, uma tendência monotônica de variação da amplitude de ressonância em função da temperatura, tendência esta que é observada para a segunda frequência.
6. Conclusões
A validação experimental dos procedimentos de modelagem numérica, via MEF utilizando as teorias FSDT e HSDT , de materiais compósitos laminados é um aspecto importante deste artigo. Com base nos resultados numéricos apresentados, pode‐se concluir que a modelagem via MEF ‐FSDT e HSDT , permite prever satisfatoriamente o comportamento dinâmico de estruturas compósitas laminadas finas não amortecidas. Particularmente, o MEF ‐FSDT é mais apropriado para a modelagem numérica de estruturas compósitas laminadas finas e o MEF‐HSDT de estruturas compósitas laminadas finas e espessas. A dificuldade apresentada na obtenção dos fatores de correção do cisalhamento transversal da teoria FSDT , conjuntamente com a crescente potência de cálculo dos computadores e a melhor aproximação verificada dos modelos numéricos que utilizam a formulação HSDT em relação aos modelos que utilizam a formulação FSDT , torna atrativo o uso da teoria HSDT na formulação numérica via MEF de estruturas compósitas, finas ou espessas.
A formulação numérica do amortecimento viscoelástico e inerente do laminado, formulados via Módulo Complexo , também é apresentada neste artigo. Por meio de simulações numéricas é demonstrado que as propriedades dinâmicas (amortecimento estrutural e frequência natural) de estruturas sanduíche tratadas por núcleo viscoelástico recebem influência direta da espessura do núcleo, da temperatura de trabalho e da frequência de excitação. Além disso, a teoria HSDT , em detrimento da FSDT , aproxima melhor a capacidade dissipativa dos materiais viscoelásticos aplicados como tratamentos internos em estruturas sanduíche espessas. Quanto maior a espessura do tratamento interno, maior o fator de amortecimento final da estrutura. Entretanto, atenção especial deve ser voltada ao aumento do peso final da estrutura tratada e sua resistência mecânica.
Bibliografia
- [1] J.N. Reddy; Mechanics of laminated composite plates: theory and analysis; (2nd ed.)CRC Press, New York (1997)
- [2] C.Y.K. Chee; Static shape control of laminated composite plate smart structure using Piezoelectric Actuator, Ph. D. thesis; University of Sydney, Sydney (2000)
- [3] B.F. Oliveira, G.J. Greus; Viscoelastic failure analysis of composite plates and shells; J. Composite Materials., 49 (2000), pp. 369–384
- [4] A.D. Nashif, D.I.G. Jones, J.P. Henderson; Vibration Damping; John Wiley & Sons, N.Y (1985)
- [5] P.T.R. Mendonça; Materiais compostos & estruturas ‐ sanduíches: projeto e análise; Manole, SP (2005)
- [6] A.M.G. de Lima, A.W. Faria, D.A. Rade; Sensitivity analysis of frequency response functions of composite sandwich plates containing viscoelastic layers; J. Composite Structures., 92 (2010), pp. 364–376
- [7] M.F.S.F. Moura, A.B. Morais, A.G. Magalhães; Materiais compósitos: materiais, fabrico e comportamento mecânico; Publindústria, Porto (2005)
- [8] F.T. Fisher, L.C. Brinson; Viscoelastic interphases in polymer‐matrix composites: theoretical models and finite‐element analysis; J. Composites Science and Technology., 61 (2001), pp. 731–748
- [9] J.D.D. Melo, D.W. Radford; Time and temperature dependence of the viscoelastic properties of CFRP by dynamic mechanical analysis; J. Composite Structures., 70 (2005), pp. 240–253
- [10] K.-J. Bathe; Finite element procedures in engineering analysis; Prentice Hall, New Jersey (1996)
- [11] V.M.F. Correia, M.A.A. Gomes, A. Suleman, C.M.M. Soares, C.A.M. Soares; Modeling and design of adaptive composite structures; J. Computer Methods in Applied Mechanics and Engineering., 185 (2000), pp. 325–346
- [12] L. Meirovitch; Fundamentals of vibrations: mechanical engineering series; McGraw‐Hill (2001)
- [13] M. Meunier, R.A. Shenoi; Dynamic analysis of composite sandwich plates with damping modelled using high‐order shear deformation theory; J. Composite Structures., 54 (2001), pp. 243–254
- [14] J. Cugnoni, T. Gmür, A. Schorderet; Identification by modal analysis of composite structures modeled with FSDT e HSDT laminated shell finite elements; J. Composites: Part A., 35 (2004), pp. 977–987
Document information
Published on 01/06/14
Accepted on 08/11/12
Submitted on 06/01/12
Volume 30, Issue 2, 2014
DOI: 10.1016/j.rimni.2012.11.004
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?