Estimating the Macroeconomic Costs of CO2 Emission Reduction in China Based on Multi-objective Programming

Abstract

This paper estimates the macroeconomic costs of CO₂ emission reduction in China employing the input-output analysis with the multi-objective programming approach. The results show that the effect of reducing CO₂ emissions on China’s economy is significant. Under the present conditions, the estimated macroeconomic costs of CO₂ emission reduction in 2010 for China are approximately 3,100–4,024 RMB t ^- 1 . The stronger the abatement actions, the higher the macroeconomic costs of per unit emission reduction would be. Excavation industry, oil industry, chemical industry, and metal smelting industry have high potential to abate their CO₂ emissions.

Keywords

CO2 emission reduction ; macroeconomic cost ; multi-objective programming ; input-output analysis

1. Introduction

Global warming has been posed widespread concern on international level. In order to mitigate climate change, some developed countries have begun to promote emission reduction of greenhouse gases in terms of agreements. However, the emission reduction can sacrifice economic costs which may be different in various countries for their diversity in many aspects such as stage of development, economic industry structure and energy consumption structure. China is currently in the process of industrialization and urbanization. The proportion of heavy and chemical industry is rather high, resulting in rapid increasing in energy consumption. Thus mandatory emission reduction will have serious impacts on China’s economy. Given these situations, it is important to estimate the macroeconomic costs of emission reduction in China through objective and reasonable assessment of the impact on its economy. This may provide a scientific foundation for countries at different development levels to participate actively in international climate change negotiations and to take actions to reduce CO₂ emissions in a reasonable way.

In order to quantitatively model the effects of CO₂ emission reduction on a country’s economy, many researchers have employed various methodologies to study the complex system of economy-resource-environment and the relevant issues of CO₂ emission reduction. Manne and Richels [1991] presented the Global 2100 model, a non-linear programming model for evaluating the costs and benefits of controlling CO₂ emission. They analyze the impacts of CO₂ emission reduction on the economy of the U. S., and believe that under the scenario of limiting emissions by OECD (Organization for Economic Cooperation and Development), the annual GDP loss for CO₂ emission reduction will rise from 2% in the year 2000 to above 4% in 2020. Rose and Steven [1993] established a non-linear programming model to simulate and estimate the net welfare loss due to CO₂ emission reduction strategies. The results indicate that the strategy of integrated emission reduction would be better than the strategy of non-elastic emission reduction in each country by 20%. Hafkamp and Nijkamp [1982] discussed the effects of resource allocation policies and showed the disadvantages of single-objective models in the assessment of changes in social welfare. Hsu and Chou [2000] analyzed the integrated planning for CO₂ emission reduction of Taiwan and estimated the macroeconomic costs based on multi-objective programming. The macroeconomic costs of CO₂ emission reduction were estimated about 345–404 US$ t^- 1 . Yang [2000] also used the multi-objective programming method to estimate macroeconomic costs of CO₂ emission reduction in Taiwan, which were 7,512–8,202 TWD t^- 1 (about 263–287 US$ t ^- 1 ). Chen [2001] presents an integrated analysis on the effects of emission reduction on Taiwan’s economic growth through multi-objective programming. The results show that if Taiwan’s emissions in 2000 were limited to 128% of the level in 1990, the average annual economic growth rate would reduce to 5.4%, compared with the targeted GDP growth rate. These studies provide useful references for the estimation of macroeconomic costs of China’s CO₂ emission reduction in this paper.

Similar to the studies of Hsu and Chou [2000] and Yang [2000], in this paper the macroeconomic costs of mandatory CO₂ emission reduction are defined in short as the GDP losses due to the adjustment of industrial structures or limiting the development of high-emission sectors to achieve emission reduction at the current economic development stage and without taking into account the changes in technology advancement, energy consumption level, and emission factors. This is different from the common definition of CO₂ emission reduction costs, which usually considers the technology or capital investment that is needed to reduce CO₂ emissions (through improving energy efficiency or utilizing new technologies to cut emissions) and is generally a measure of direct costs to enterprises.

In this paper, a model based on multi-objective programming is established to balance and simulate the two objectives of optimizing economic growth and reducing CO₂ emissions. An input-output model is employed to reflect the relations in economy. Thus the macroeconomic losses of CO₂ emission reduction (i.e., the macroeconomic costs of mitigation) are studied in this paper.

2. Multi-objective programming model

Reducing CO₂ emissions through adjusting the industrial structure or limiting the development of high-emission sectors will constrain the development of some industries, which to some extent will result in the country’s macroeconomic losses. The conflict between economic development and reducing CO₂ emissions is in need of being balanced by policy-makers. In this paper, a multi-objective programming model based on input-output analysis is developed to study the relationship between the development of China’s economy and the CO₂ emission reductions in different scenarios. Through comparing these results, the macroeconomic costs of CO₂ emission reduction in China are estimated.

Considering the availability of data on energy consumption, water utilization coefficients, input-output tables, etc., we combined 42 sectors in the input-output table to 24 sectors for the sake of avoiding non-consistency in sector classification. The developed model has 24 decision variables (the output of each sector), 2 objective functions, and 97 constraints.

2.1. Objective functions

Two objective functions in the model represent the maximized GDP ( Z_GDP , the sum of added value over sectors) and the minimized CO₂ emission (${\textstyle Z_{{CO}_{2}}}$ , the sum of CO₂ emission over sectors) respectively.

$Z_{GDP}=\sum _{i=1}^{n}V_{i}\cdot X_{i}$

( 1)

$Z_{{CO}_{2}}=\sum _{i=1}^{n}P_{i}\cdot X_{i}$

( 2)

Here, X_i is the output of sector i ; V_i is the added value coefficient of sector i ; P_i is the emission coefficient of sector i ; n = 24, which is the number of sectors.

2.2. Constrains

Mainly 97 constraints can be included into four groups in the model, the general equilibrium constraints, water resource constraints, sector expansion constraints and non-negative constraints. The general equilibrium constraints mean that the sum of output and import for each sector must equal to the sum of its final consumption demand and intermediate demand from other sectors, while the final demand for the planning year should not be lower than that in 2005. This is consistent with other researches [ Hsu and Chou, 2000  ;  Chen, 2001 ]. Water resource constraints require that the sum of water utilization in all sectors can not be larger than the maximum supply of water resource. Constraints on the industry sector expansion put limits on industry adjustment. And non-negative constraints are required for the practical significance of the decision variables.

General equilibrium constraints

$F=\left(I-A+M\right)\quad \cdot \quad X\geq F_{2005}$

( 3)

Water resource constraints

$\sum _{i=1}^{n}r_{i}\cdot x_{i}\leq W_{\mbox{max}}$

( 4)

Sector expansion constraints

$X_{i}^{L}\leq X_{i}\leq X_{i}^{U}\quad \left(i=1,2,\ldots ,n\right)$

( 5)

Non-negative constraints

$X_{i}\geq 0\quad \left(i=1,2,\ldots ,n\right)$

( 6)

In the constrains above, F is the final demand for all sectors (n×1 matrix); I is an identity matrix; A is a n × n matrix of intermediate consumption coefficients; M is the n × n import coefficient diagonal matrix; X is the output vector for the n sectors (n × 1 matrix); F₂₀₀₅ is the final consumption demand for all sectors in year 2005 (n × 1 matrix); r_i is the water utilization coefficient for sector i ; W_max is the upper bound for water resource supply; X_i^L and X_i^U are the lower and upper bounds for the output expansion of sector i .

3. Data sources and preconditioning

The data used in the model include the data from input-output table and the balance tables of energy consumption in 2005 [ NBSC and NEA, 2008 ], CO₂ emission factors estimated on basis of IPCC [ Gomez et al., 2006 ], water utilization coefficients from the Researching Group of Chinese Input-Output Association [ RGCIOA, 2007 ], the water supply data from the Macroeconomic Research Institute of National Development and Reform Commission [ MRINDRC, 2004 ], CO₂ emissions data from the International Energy Agency (IEA) [ IEA , 2008 ], and GDP data from National Bureau of Statistics of China [ NBSC , 2008 ]. The planning year in the model is set to 2010.

We estimate the CO₂ emission in the production process by each sector through multiplying its consumption of various energy sources by the emission factors. From the China energy statistical yearbook, we obtained the consumption of each energy source, including coal, coke, crude oil, gasoline, kerosene, diesel, fuel oil, natural gas and electricity. Afterwards the CO₂ emissions of each sector are calculated based on the carbon emission factors provided by IPCC.

As electricity produced by power sector is mainly consumed by other sectors, the large amount of CO₂ emissions produced in the process of generating electricity from fossil fuels should not be put on power sector alone. Referring to various studies, for example Hsu and Chou [2000], we allocated the CO₂ emission from power sector among all sectors according to their electricity consumption. Then the CO₂ emission coefficient of each sector is obtained based on CO₂ emissions and outputs for each sector.

4. Structure and implementation of the model

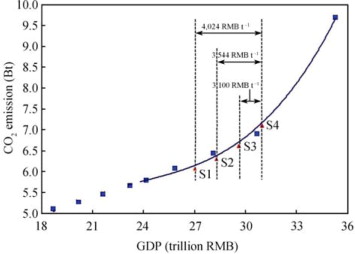
The two objective functions represent the maximized GDP and the minimized CO₂ emission, respectively, and compose a two-dimensional space ( S objective) ( Fig. 1 ). The constrains in the model form the constrains-set R. This paper aims to roughly estimate the macroeconomic costs of emission reduction in China through examining the trade-off relationship between GDP growth and CO₂ emissions, i.e. the potential GDP loss when reducing a certain amount of CO₂ emissions. Therefore we employ the “compromise method” [ Zeleny, 1982 ] which is described stepwise in the following to obtain the non-inferior solutions of the multi-objective programming model.

Figure 1. Several non-inferior solutions for the multi-objective programming model and their curve fitting in two-dimensional objective space

In the first step, the optimal values for the two objectives under the constrains-set are derived. The value for the maximized GDP is ${\textstyle Z_{\mbox{GDP}}^{\ast }=35.30}$ trillion RMB, while the value for the minimized CO₂ emission is ${\textstyle Z_{{\mbox{CO}}_{\mbox{2}}}^{\mbox{*}}=5.1\quad {\mbox{Bt}}}$ . The two optimal values can not be reached simultaneously, i.e., there is not such a solution that can satisfy the maximized GDP and minimized CO₂ emission at the same time. The main attempt is to approach the two optimal values as close as possible.

For the second step, with the optimal values of the objectives ${\textstyle \left(Z_{\mbox{GDP}}^{\mbox{*}}\quad {\mbox{and}}\quad Z_{{\mbox{CO}}_{\mbox{2}}}^{\mbox{*}}\right)}$ being defined as the ideal values for GDP and CO₂ emissions, respectively, we try to minimize the Euclidean distance (d ) from the two objectives to their ideal values under the constrains-set (R ) of the model. Following this, the non-inferior solutions for the original multi-objective programming model can be obtained by solving the non-linear programming problem.

${\underset {x\in R}{mind}}={\left[W_{1}\cdot {\left(Z_{GDP}-{Z^{\ast }}_{GDP}\right)}^{2}+W_{2}\cdot \left(Z_{{CO}_{2}}-{Z^{\ast }}_{{CO}_{2}}\right)\right]}^{1/2}$ $=\left[W_{1}\cdot \left(\sum _{i=1}^{n}V_{i}\cdot X_{i}-{35.30}^{2}\right)\right]+$$W_{2}\cdot {\left(\sum _{i=1}^{n}P_{i}\cdot X_{i}-51.10\right)}^{2}]{}^{1/2}$

( 7)

With W₁ and W₂ being defined as the weights for two objectives, ${\textstyle W_{1}={\frac {W_{1}}{W_{1}+W_{2}}}}$ and ${\textstyle W_{2}={\frac {W_{2}}{W_{1}+W_{2}}}}$ can represent the relative weights of two objectives — GDP (w₁ ) and CO₂ emissions (w₂ ) respectively, and w₁ + w₂ = 1 . By changing the relative values of w₁ and w₂ , several groups of non-inferior solutions for the multi-objective programming model can be estimated.

If w₁ = 1, it means that the policy makers consider only the single objective of maximizing GDP and do not consider CO₂ emissions reduction, which results in a maximum GDP of 35.3 trillion RMB, which is the same to the ideal value of GDP obtained above. The corresponding CO₂ emissions will be 9.7 Bt. If the value of w₁ is changed to 0.875, 0.75, 0.625, 0.5, 0.375, 0.25 and 0.125, respectively, it implies that the policy makers gradually relax the objective of maximizing GDP, and pay more attention to reducing the CO₂ emissions. We obtain the following non-inferior solutions of ${\textstyle Z_{\mbox{GDP}},\quad Z_{{\mbox{CO}}_{\mbox{2}}}}$  : (30.67, 6.9), (28.09, 6.4), (25.85, 6.1), (24.16, 5.8), (23.19, 5.7), (21.60, 5.5), and (20.18, 5.3). Here, the unit is trillion RMB for GDP and billion tons for CO₂ emission. If w₁ = 0 (i.e., w₂ = 1), it is implying that at this time the policy makers only consider the CO₂ emission reduction and have no concern on the GDP growth. The minimized CO₂ emissions are 5.1 Bt, while the corresponding GDP is 18.69 trillion RMB. The relative positions of the groups of non-inferior solutions in the objective space are shown in Figure 1 . We used a polynomial curve, which was chosen as it fit the calculated points relatively well, so as to obtain the estimated relation between GDP and CO₂ emissions.

$Z_{{CO}_{2}}=0.0173\cdot {Z^{3}}_{GDP}-1.2281\cdot {Z^{2}}_{GDP}+$$29.996\cdot Z_{GDP}-194.39$

( 8)

The fitting degree of the function above for the nine planning points is 0.9968, and when Z_GDP > 23.66, this function is convex. So it can be seen as an estimation of the trade-off relationship between macroeconomic growth and CO₂ emissions.

We consider 4 scenarios of the average annual GDP growth rate for China from the base year (2005) to the planning year (2010) (denoted as S1, S2, S3, and S4): 8%, 9%, 10% and 11% respectively. The GDP of 2010 would be 27.02, 28.29, 29.61, and 30.98 trillion RMB, respectively. According to the curve in Figure 1 , the corresponding CO₂ emissions are 6.1, 6.3, 6.6, and 7.1 Bt, respectively.

It can be seen that different CO₂ emission levels correspond to different GDP growth rates, in other words, the restrictions on CO₂ emissions may lead to decrease in the rate of GDP growth. Considering the actual growth rates in recent years and the national economic plan, the scenario S4 is set to be the base case. When the GDP growth rate is reduced from 11% (S4) to 10% (S3), CO₂ emission will be reduced by 442 million tons, implying that the macroeconomic loss would be 1.37 trillion RMB, that is, an average macroeconomic cost of 3,100 RMB per ton CO₂ . With reducing the GDP growth rate to 9% (S2), the CO₂ emission reduction will reach 759 million tons, implying that the macroeconomic losses would be 2.69 trillion RMB, i.e., an average macroeconomic cost of 3,544 RMB per ton CO₂ . When the GDP growth rate is decreased to 8% (S1), CO₂ emissions will be reduced by 984 million tons, and the macroeconomic costs would be 3.96 trillion RMB, implying an average macroeconomic cost of 4,024 RMB per ton CO₂ .

In Table 1 it is obvious that the stronger the abatement actions, the greater the macroeconomic losses due to emission reduction will be, and the higher the corresponding macroeconomic costs for per unit CO₂ emission reduction will be. When the emission reduction changes from 442 million to 759 million tons (increase by 72%), the corresponding macroeconomic cost rises by 14% (from 3,100 RMB t ^- 1 to 3,544 RMB t ^- 1 CO₂ ), implying that in average a 1% increase in emission reduction will lead to about 0.2% increment of macroeconomic cost. When the emission reduction increases from 759 million to 984 million tons (increase by 29.6%), the corresponding macroeconomic cost would go up from 3,544 RMB t ^- 1 to 4,024 RMB t ^- 1 ( increase by 13.5%), implying that a 1% increase in reductions would result in about 0.46% increment of macroeconomic cost in average in this interval. It can be observed that the magnitude of the rise in macroeconomic costs will increase with the magnitude of emission reduction efforts.

Table 1. Amounts of CO₂ emission reduction and the macroeconomic cost for per unit emission reduction for China in 2010

CO2 emission reductiona (million tons)	Macroeconomic loss (trillion RMB)	GDP growth rate (%)	Macroeconomic cost for per unit emission reduction (RMB per ton CO2 )	The decrease of carbon intensityb (take 2005 as the base year) (%)
442	1.37	10	3 100	18
759	2.69	9	3 544	20
984	3.96	8	4 024	20

Notes:

a. Calculated with setting 11% as the base case of GDP annual growth rate

b. CO₂ emission is based on the estimation by IEA

Looking at different sectors, the effects of increasing magnitudes of emission reductions show that mining industry, oil industry, chemical industry, and metal smelting industry are high CO₂ emission industries, and have more potential to abate their CO₂ emissions. For example, the possible reduction in the chemical industry’s emission with increasing the magnitude of emission reduction can theoretically reach 43%, while for other high-emission sectors, such as mining and metal smelting, the possible reduction magnitude in CO₂ emissions can reach more than 50%. In contrast, the construction industry has much less CO₂ emissions (about 50 million tons in average), and has not much potential for reducing emissions.

5. Conclusions and suggestions

The results in this paper indicate that CO₂ emission reduction has a significant effect on China’s economy. It is estimated that the macroeconomic cost of China’s CO₂ emission reduction in 2010 will be 3,100–4,024 RMB per ton CO₂ (about 456–592 US$ per ton), which is higher than estimated for Taiwan through multi-objective programming [ Hsu and Chou, 2000  ;  Yang, 2000 ]. Therefore, the impact of CO₂ emission reduction on China’s economy may be higher compared with that on the economy of Taiwan.

In this study, the macroeconomic costs of emission reduction include not only the direct costs of emission reduction through investing in green or advanced technologies, but also the national macroeconomic losses due to limiting the development of high-emission sectors. Mandatory emission reduction may have more significant effects on the economy of developing countries and regions, i.e. their macroeconomic costs may be higher due to their economic development stage and energy-economy characteristics. As has been pointed out by Yang [2000], high dependency of economy on mass energy inputs and high-carbon energy consumption may result in higher macroeconomic costs of emission reduction. Currently, China’s economy has high dependency on fossil fuels and high-emission sectors. Mandatory emission reduction in China would have a significant macroeconomic impact, i.e., relatively high macroeconomic costs of CO₂ emissions. Therefore, the commitment to reduce CO₂ emissions is very cost intensive in China, but is an important contribution to global climate change mitigation.

Mining industry, oil industry, chemical industry, and metal smelting industry have high potential to abate their CO₂ emissions. China should increase the investment to improve the technology in the energy-intensive industries, such as oil and chemical industries, and accelerate the technology and equipment reconstruction to decrease energy consumption and improve the energy usage efficiency, and thus to reduce their CO₂ emissions.

With an increasing magnitude of emission reduction effort, the corresponding macroeconomic costs of reducing CO₂ emissions increase too. Therefore, when setting the targets of controlling CO₂ emissions, the effects of CO₂ emission reduction on economy must be taken into account. Reasonable targets should be set based on the principles of “common but differentiated responsibilities” established by the Kyoto Protocol [ UN, 1997 ] and the real potential or endurance. Emission reduction should depend on technological advances in the long term.

Estimating the macroeconomic costs of CO₂ emission reduction in countries at different economic development stages can give insights to the macroeconomic impact of mandatory CO₂ emissions on different countries. This is also of significance regarding the allocation of responsibility at international level. This study on China’s macroeconomic costs of CO₂ emission reduction will help to increase the understanding of impacts of emission reduction on China’s economy. To create a uniform modeling framework and uniform data specifications, so as to estimate and compare macroeconomic costs of CO₂ emission reductions in different countries and regions, is an interesting task for further research.

Acknowledgements

This paper is supported by the National Natural Science Foundation of China under Grant Nos. 70825001 and 70941039.

References

1. Chen, 2001 T.Y. Chen; The impact of mitigating CO₂ emissions on Taiwan’s economy  ; Energy Economics, 23 (2001), pp. 141–151
2. Gomez et al., 2006 D.R. Gomez, J.D. Watterson, B.B. Americano, et al.; Stationary combustion; 2006 IPCC Guidelines for National Greenhouse Gas Inventories, IPCC National Greenhouse Gas Inventory Programme, IGES (2006), pp. 2.1–2.45
3. Hafkamp and Nijkamp, 1982 W.A. Hafkamp, P. Nijkamp; An integrated interregional model for pollution control; T.R. Lakshmanan (Ed.), et al. , Economic Environmental Interactions Modeling and Policy Analysis, Martinus Nijhof (1982), pp. 149–170
4. Hsu and Chou, 2000 G.J.Y. Hsu, F.Y. Chou; Integrated planning for mitigating CO₂ emissions in Taiwan: a multi-objective programming approach  ; Energy Policy, 28 (2000), pp. 519–523
5. IEA, 2008 IEA (International Energy Agency); CO₂ Emissions from Fuel Combustion 1972–2006, OECD/IEA (2008), p. 391
6. Manne and Richels, 1991 A.S. Manne, R.G. Richels; Global CO₂ emissions reduction: the impact of rising energy costs  ; The Energy Journal, 12 (1) (1991), pp. 87–107
7. MRINDRC, 2004 MRINDRC (Macroeconomic Research Institute of National Development and Reform Commission); Analysis of safety factors of water resources in China in 2020 and strategic suggestions; Macroeconomic Research (in Chinese), 6 (2004), pp. 3–6
8. NBSC, 2008 NBSC (National Bureau of Statistics of China); China Statistical Yearbook 2008 (in Chinese), China Statistical Press (2008), p. 1026
9. NBSC and NEA, 2008 NBSC (National Bureau of Statistics of China), NEA (National Energy Administration); China Energy Statistical Yearbook 2008 (in Chinese), China Statistical Press (2008), p. 284
10. RGCIOA, 2007 RGCIOA (Researching Group of Chinese Input-Output Association); Input-output analysis of water resources consumption and water input coefficient in national economic sectors: the fifth of researching report series on input-output tables of 2002; Statistical Research (in Chinese), 24 (3) (2007), pp. 20–25
11. Rose and Steven, 1993 A. Rose, B. Steven; The efficiency and equity of marketable permits for CO₂ emissions  ; Resource and Energy Economics, 15 (1993), pp. 117–146
12. UN, 1997 UN (United Nations); Kyoto Protocol to the United Nations Framework Convention on Climate Change; FCCC/CP/1997/L.7/Add.1 (1997), pp. 10–11
13. Yang, 2000 H. Yang; On the estimation of mitigating costs for CO₂ emissions due to energy use in the Taiwan economy: a multi-objective programming approach  ; Journal of Social Sciences and Philosophy (in Chinese), 12 (3) (2000), pp. 459–494
14. Zeleny, 1982 M. Zeleny; Multiple Criteria Decision Making, McGraw Hill (1982), p. 563