Advanced thermal control of VARI process with self-heating mold

1. Introducción

Es bien conocida la importancia que un riguroso control térmico tiene en todo proceso afectado térmicamente, como es el caso de los procesos de fabricación fuera de autoclave en vía líquida de materiales compuestos termoestables. En la fase de impregnación, las diferencias de temperatura en el molde pueden modificar localmente la viscosidad de la resina afectando el patrón de llenado. Por otra parte, la evolución de la temperatura durante el proceso de curado posterior afecta fuertemente a la calidad final de la pieza, tanto a la distorsión que puede producirse como a las propiedades mecánicas finales de la misma.

Para el control térmico de moldes, es posible encontrar soluciones comerciales [1], que son desarrollos generales y normalmente se basan en compensadores PID estándar, aunque, dada su importancia técnica, también se pueden encontrar soluciones más avanzadas en la bibliografía científica. Estos enfoques tratan de añadir el conocimiento del sistema en el propio controlador para mejorar su rendimiento, por ejemplo, mediante el uso de controles difusos [2][3] o redes neuronales (NN) [4], aunque más aplicados en las industrias de transformación de termoplásticos. Este tipo de aproximaciones suelen obtener buenos resultados en los puntos de control donde se ubican los sensores de temperatura, pero tiene un control más deficiente sobre el resto de las zonas.

Como antecedente al presente trabajo, ITA ya desarrolló y presentó en MATCOMP17 una arquitectura optimizada de control predictivo basado en modelos (MPC) para un proceso de RTM de un molde rectangular sencillo [5]. El algoritmo calculaba las acciones de control a partir de las predicciones de un modelo de orden reducido (MOR) generado mediante el método de identificación ARX en base a datos virtuales recogidos de un modelo de elementos finitos (MEF) validado experimentalmente.

En la presente contribución se desarrolla el control térmico de un molde geométricamente más complejo y en este caso para infusión por vacío (VARI), que aporta unas condiciones de contorno térmicas disimilares en la pieza entre el lado del molde y el lado de los consumibles de infusión. Además, se ha empleado una aproximación diferente para la obtención del modelo reducido, lo que ha mejorado la precisión del control de temperatura y ha permitido introducir fácilmente sensores virtuales en puntos no medibles del sistema.

El apartado 2 describe dicho sistema físico, tanto el hardware como el software que incluye. El apartado 3 presenta el modelo térmico detallado que aporta la información basada en la física del sistema, junto con la obtención del modelo reducido a partir de él que es utilizado en tiempo real para las acciones de control. El apartado 4 muestra la arquitectura de control desarrollada, cuya validación experimental se incluye en el apartado 5. En el apartado 6 se indican las principales conclusiones que se extraen del estudio.

2. Descripción del sistema

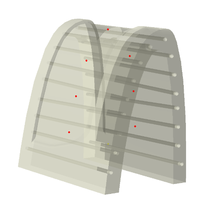
El sistema prototipo físico (Figura 1) está constituido por un molde de aluminio cuya forma exterior replica un tramo de borde de ataque de un estabilizador horizontal aeronáutico. En su superficie se colocan las distintas capas de tejido de carbono correspondientes al laminado utilizado y se disponen los consumibles para realizar el proceso de infusión por vacío, básicamente un tejido pelable, sangrador, malla distribuidora y la bolsa de vacío, además de tubos, válvulas, frenos y sellos necesarios.

Figura 1. Sistema prototipo físico

Dicho molde dispone de un sistema de calentamiento mediante resistencias eléctricas en su interior, constituido por 16 cartuchos, junto con un elemento calefactor superficial (manta flexible) con dos zonas de calentamiento independientes, que cubre externamente todo el montaje de infusión. El molde cuenta con siete termopares fijos en diferentes ubicaciones para el control del sistema (Figura 2). Un termopar adicional monitorizará la temperatura ambiente. El armario de control recoge las lecturas de los termopares y puede modular individualmente la potencia aportada a cada resistencia. Adicionalmente se cuenta con un sistema de adquisición externo que permitirá añadir ocho termopares provisionales durante las pruebas de puesta en marcha y ajustes.

Figura 2. Ubicación de los cartuchos y de los sensores de temperatura en el molde

El programa de control desarrollado en entorno LabVIEW permite establecer las consignas de temperatura necesaria en cada etapa del proceso (infusión y curado) y las velocidades o rampas de calentamiento deseadas entre dichas etapas, además de monitorizar las potencias aportadas por cada resistencia y las temperaturas en los termopares fijos. En dicho entorno se integra el controlador de temperatura desarrollado, que es explicado en mayor detalle en el apartado 4.

3. Modelo térmico del sistema

3.1 Modelo detallado

El modelo detallado térmico del molde está compuesto por un modelo de elementos finitos (MEF) que incluye la representación de los distintos componentes del sistema: el molde de aluminio calefactado, el laminado, la bolsa de vacío y la manta térmica (Figura 3). Todas ellas están representadas mediante elementos sólidos cuya interacción viene definida por un contacto de tipo térmico. El modelo térmico completo contiene 21,235 nodos y 38,074 elementos.

Figura 3. Componentes del modelo MEF

En el caso de la bolsa se han asignado las propiedades térmicas equivalentes del conjunto de capas que componen los consumibles de infusión (bolsa, malla, sangrador y pelable), estimada a partir de las propiedades térmicas y espesores individuales de dichos elementos. En el caso del laminado se consideran las propiedades del tejido seco, o del conjunto de tejido y resina, dependiendo de la fase del proceso, llenado o curado respectivamente. Las propiedades térmicas de la manta calefactora se han ajustado mediante la realización y simulación de varios ensayos de calentamiento de este elemento aisladamente.

Los mecanismos de transferencia de calor considerados en el modelo son la conducción y la convección. Ésta última se introduce mediante coeficientes de convección en las superficies exteriores del sistema de calentamiento. Dichos coeficientes se han ajustado experimentalmente mediante la simulación de una serie de ensayos en situaciones estacionarias a distintos niveles de temperatura con el molde vacío. Para ello se ha registrado la temperatura en diferentes localizaciones del sistema de calentamiento.

Finalmente, el modelo ha sido validado comparando los resultados de simulación con ensayos experimentales de calentamiento de carácter transitorio. A continuación, se han extraído las matrices del modelo térmico desarrollado en el software comercial Abaqus/Standard.

3.2 Modelo reducido (MOR)

Se ha obtenido una representación reducida del sistema térmico para ser posteriormente implementada en el algoritmo de control. Para construir dicho modelo se ha partido de las matrices de rigidez y capacidad térmicas, así como de los vectores de carga extraídos del modelo MEF. Con estos datos, se ha construido un modelo dinámico lineal, donde los estados son las temperaturas nodales y las entradas son las potencias de las fuentes de calor. El procedimiento seguido consiste en la discretización de la ecuación de conducción de un sistema térmico mediante un esquema de Euler [6]. Específicamente se han obtenido tres modelos dinámicos de alto orden (21,235 estados) a partir del MEF linealizado para tres puntos de temperatura (20ºC, 100ºC y 180ºC).

Para la reducción de orden se aplica el método POD (Proper Orthogonal Decomposition) [7]. Para ello, se realiza una simulación de entrenamiento sobre el modelo de alto orden con señales de entrada a escalones aleatorios en amplitud y frecuencia. A partir de una matriz con los datos de temperatura a lo largo del tiempo obtenida de dicha simulación, se aplica una descomposición en valores singulares (SVD) y se obtiene la matriz de transformación truncada hasta los n valores singulares de mayor peso, que permite construir el modelo reducido a partir del modelo de alto orden. Se ha realizado dicho procedimiento para la reducción de orden de los tres modelos linealizados (20ºC, 100ºC y 180ºC) y discretizados con un paso de tiempo de 100 segundos. Se consideran n=50 estados para la reducción lo que supone la obtención de errores medios entre modelos de alto orden y modelos reducidos inferiores a 0.01ºC durante el entrenamiento.

A continuación, se ha obtenido la correlación entre los tres modelos reducidos linealizados y el MEF para una señal de validación. Se consiguen porcentajes de error RMSE frente al MEF del 13% para el modelo linealizado a 20ºC, 9% a 100ºC y 4% a 180ºC. Se ha seleccionado el modelo reducido linealizado a 180ºC para el algoritmo de control al obtener el menor error entre los tres modelos.

4. Arquitectura de control

Se ha diseñado un controlador MPC con la finalidad de obtener un seguimiento preciso de la temperatura en los sensores del molde. Además, se han considerado sensores virtuales asociados a la pieza para asegurar homogeneidad térmica en la cavidad del molde donde no es posible colocar sensores físicos. Tras analizar varias disposiciones por simulación, se selecciona una configuración de 15 sensores virtuales que es combinación de dos tipos: sensores tipo media que evalúan la temperatura media por zonas de la pieza, de los cuales se consideran 4 (superficie exterior-izquierda, exterior-derecha, interior-izquierda e interior-derecha); y sensores puntuales que evalúan la temperatura de puntos concretos de la pieza. Se consideran 11 sensores virtuales puntuales, de los cuales 7 corresponden a las posiciones equivalentes de los sensores físicos en la superficie exterior de la pieza y 4 corresponden a posiciones en los extremos de la pieza en su base (2 en la superficie exterior y 2 en la superficie interior), tal como se muestra en la Figura 4.

Figura 4. Esquema de sensores virtuales en la pieza

Adicionalmente, para predecir y compensar los comportamientos no recogidos por el modelo reducido linealizado a 180ºC descrito en el apartado anterior, se implementa un estimador de estado y de perturbaciones basado en filtro de Kalman. Se considera que las perturbaciones son los efectos térmicos que difieren con respecto a la linealización en este punto de temperatura, principalmente relacionados con la variación del coeficiente de convección con la temperatura. Tras la implementación del filtro de Kalman y el ajuste de las incertidumbres asociadas al modelo de estimación y a los sensores de medida [8], se valida el algoritmo de predicción y compensación de las perturbaciones por simulación. Se consiguen errores de temperatura inferiores a 0.15% de media e inferiores al 2% de máxima con respecto al MEF para una señal de validación.

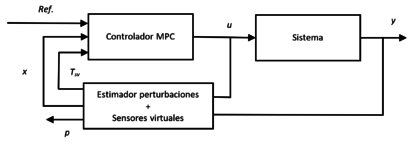
El esquema de la arquitectura de control se muestra en la Figura 5, donde el controlador MPC obtiene las potencias a suministrar a las fuentes de calor de forma independiente a partir de la estimación de la evolución del sistema basada en el modelo reducido hasta un determinado horizonte temporal. Las entradas del controlador son, por una parte, las temperaturas de consigna y, por otra, la estimación del estado del sistema y la temperatura de los sensores virtuales predichas por el filtro de Kalman.

Figura 5. Arquitectura de control

La implementación y resolución de la arquitectura de control se realiza de forma equivalente a la mostrada en [5], cuyo planteamiento inicial se basa en la teoría de control desarrollada en [9]. Dicha implementación se realiza en MATLAB/Simulink.

5. Validación experimental

El esquema de control descrito previamente se ha implementado sobre el molde prototipo mediante su adaptación al software LabVIEW. Con la finalidad de verificar la homogeneidad de temperatura en la cavidad, se ha realizado un ensayo sin infusión de resina donde se introduce una pieza previamente fabricada en la cavidad del molde colocando termopares provisionales, que no son utilizados en el lazo de control, en 8 puntos representativos de las diferentes zonas de la pieza, tanto en su superficie interior y exterior como en su lado derecho e izquierdo. La Figura 6 muestra dicha configuración en la superficie exterior de la pieza.

Figura 6. Disposición de sensores provisionales sobre la superficie exterior de la pieza

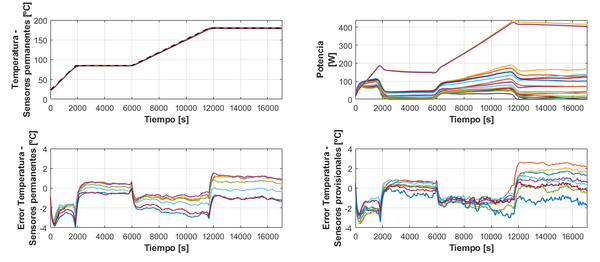
La consigna de temperaturas que se ha empleado para el ensayo corresponde a un perfil característico para el procesado con la resina que se emplearía en la fabricación de la pieza. En la Figura 7 se muestran los resultados más representativos del ensayo. Para los sensores permanentes, se obtienen errores RMSE (error durante el ensayo completo) de 1.3ºC como valor medio entre sensores y 1.9ºC como valor máximo; mientras que para los sensores provisionales el error RMSE es de 1.3ºC como valor medio y 1.8ºC como valor máximo; lo que implica que el seguimiento de la temperatura es preciso, no solamente en los puntos de medida del molde, sino también en la cavidad interna donde se alberga la pieza.

Figura 7. Resultados del ensayo experimental sin infusión de resina

Posteriormente, se ha realizado un ensayo de fabricación de la pieza de material compuesto donde se comprueba que la presencia del material, el proceso de infusión de la resina y el calor generado durante el curado han tenido un efecto bajo sobre el control térmico del molde, que ha compensado correctamente estos efectos manteniendo un error bajo en el seguimiento de la trayectoria de temperaturas predefinida.

6. Conclusiones

Se ha desarrollado un esquema MPC para el control térmico durante el proceso de fabricación de piezas de material compuesto que, adicionalmente al seguimiento de perfiles de temperatura en los sensores del molde, cuenta con sensores virtuales que permiten mantener una temperatura homogénea en la cavidad del molde donde se alberga la pieza. La técnica de reducción de orden empleada para el modelo de control permite obtener una representación completa del dominio térmico con una precisión alta respecto al MEF, que se ha modelado considerando la geometría real y las características térmicas del sistema, y que ha sido previamente ajustado en base a ensayos experimentales. Adicionalmente, la implementación de un estimador de estado y perturbaciones basado en filtro de Kalman ha permitido detectar y compensar los efectos no recogidos por el modelo de control, y filtrar el ruido de los sensores de medida. Los algoritmos se han ajustado por simulación y verificado experimentalmente obteniendo como resultado un error medio durante el ensayo inferior a 2ºC considerando los sensores permanentes y los sensores provisionales colocados en diferentes posiciones de la pieza, lo que indica un seguimiento preciso de temperatura en el sistema térmico completo. Finalmente, se ha llevado a cabo satisfactoriamente el proceso de infusión y curado de la resina para la fabricación de la pieza usando el algoritmo de control implementado. La metodología desarrollada que se ha aplicado en este estudio puede extrapolarse con facilidad permitiendo la generación de controladores de temperatura precisos para otros diseños de moldes.

7. Agradecimientos

La parte metodológica para generación del MOR térmico y una parte del desarrollo y de la validación del algoritmo de control, así como la escritura del presente artículo, han sido realizados como una actividad de investigación interna del ITA, y de su difusión, con el soporte del Fondo Europeo de Desarrollo Regional (FEDER) para Aragón (España).

8. Bibliografía

[1] Watlow, consultado el 6 de febrero de 2019. Catálogo de sistemas térmicos y técnicas de medición y control. http://www.watlow.es/common/catalogs/files/esplc0604.pdf

[2] Wang, Y.-T., and Wu, S.-L.. “Modeling and control for a thermal barrel in plastic molding processes”. Tamkang Journal of Science and Engineering, 9(2), (2006), pp. 129–140.

[3] Muñoz-Barron et al. FPGA-based multiprocessor system for injection molding control. Sensors, 12(10), (2012), pp. 14068–14083.

[4] Deng, J. et al. Heuristically optimized RBF neural model for the control of section weights in stretch blow moulding. In Control (CONTROL), 2012 UKACC International Conference on, IEEE, pp. 24–29.

[5] Escolano, M., et al. "Modelado y control predictivo de un molde de RTM." Materiales Compuestos 2.3 (2018): 56-62.

[6] Thompson, M. K., & Thompson, J. M. (2017). ANSYS mechanical APDL for finite element analysis. Butterworth-Heinemann.

[7] Pinnau, R. (2008). Model reduction via proper orthogonal decomposition. In Model order reduction: theory, research aspects and applications (pp. 95-109). Berlin, Heidelberg: Springer Berlin Heidelberg.

[8] Grewal, M. S., & Andrews, A. P. (2014). Kalman filtering: Theory and Practice with MATLAB. John Wiley & Sons.

[9] Wang, L. (2009). Model predictive control system design and implementation using MATLAB (Vol. 3). London: springer.