Tip speed ratio control of a 200 kW VAWT with synchronous generator and variable DC voltage

Abstract

A novel control method for a fixed-pitch variable speed wind turbine is introduced and experimental results are presented. The measured absorbed power and rotational speed, together with a look-up table for the aerodynamic efficiency, are used to estimate the wind speed reaching the turbine as well as the tip speed ratio. Thereby, the control is independent on wind speed measurements and the wind turbine itself is used as an anemometer. Tip speed ratio control is implemented by comparing the estimated tip speed ratio to a reference value and adjusting the DC voltage level accordingly. Tip speed ratio control benefits from that the aerodynamic efficiency hardly varies with changing tip speed ratio when close to its optimum value. Experimental results from a 200 kW vertical axis wind turbine are presented. The voltage from the permanent magnet generator is passively rectified and the alternating DC voltage is then inverted, filtered, transformed, and grid connected. The estimated wind speed is compared with the measured wind speed. The absorbed power when tip speed ratio control has been implemented is shown. It is concluded that the presented control method works and some future improvements are discussed.

Introduction

The use of vertical axis wind turbines (VAWTs) has increased during the last years, especially for small-scale turbines in urban environments [1]. It is also possible to scale the turbines to MW-scale to compete with the more common horizontal axis wind turbines [2, 3]. In this article, experimental results from control of a 200 kW test turbine, erected in 2010 and designed as a scaled prototype of a MW-turbine, are presented. The presented variable speed vertical axis wind turbine has a direct-driven permanent magnet generator and a full converter enabling grid connection. A first turbine prototype of 12 kW was built in 2006 and has been tested since then [4, 5].

In conventional horizontal axis wind turbines, the gearbox, pitch, and yaw systems stand for a substantial part of the downtime [6], parts that are omitted in the presented design. The turbine is controlled electrically by controlling the power output and rotational speed of the generator, that is, no mechanical control as described in [7] is needed. The generator can be designed for robustness and efficiency in the absence of weight and volume constraints, as it is placed on ground level. The direct-driven generator has been tested in the laboratory before being installed in the turbine [8].

The 200 kW wind turbine has electrically controlled passive stall control substituting pitch control [9]. The passive stall control regulates the power at high wind speeds above rated speed. This article treats the speed control to accommodate for optimum variable speed operation. This innovative control strategy aims to keep the tip speed ratio at an optimum value at normal operation between start-up and rated wind speed.

The presented wind energy converter system has some unique features with respect to control. It has fixed pitch and it delivers a variable DC voltage to the inverter as it is a full variable speed turbine. The inverter is used to control the DC voltage and thereby the rotational speed of the turbine, substituting the commonly used active rectifier or DC/DC converter. The DC voltage span is large as the variable speed generator has a permanent magnet rotor and passive diode rectification.

This article demonstrates the electrical system and control strategy for the wind turbine. On-site experience has indicated differences between the wind speed measured by an anemometer, placed at hub height 100 m from the turbine, and the corresponding absorbed power by the wind turbine, even in days with a wind direction perpendicular to the line between turbine and anemometer, when it theoretically should be correlated. This was one of the reasons for implementing a control strategy that estimates the wind speed using the turbine itself, as presented in this article. The operational range during the experiments has been limited as the purpose only was to demonstrate and test the operation of the control system. The control method has been developed by analyzing experimental data and using experience from operation and aerodynamic simulations. This article presents the theory behind the control and experimental results from measurements on a wind turbine prototype.

Method

The wind turbine system

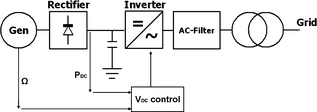
The 200 kW vertical axis wind turbine is 40 m high and has three straight blades connected to a hub by support arms, see Figure 1 and Table 1. The turbine is rated at 200 kW at a nominal wind speed of 11.7 m/sec and at a rotational speed of 33 rpm. The turbine is not self-starting. It is instead started by running the generator as a motor as demonstrated in [10]. A drive shaft connects the turbine to the direct-driven ground-based generator. The direct-driven permanent magnet synchronous generator has characteristics presented in Table 2 [8]. The generator has a high overload capacity and operates with a small load angle to enable electrically controlled braking at all times as well as passive rectification. The turbine operates with variable speed and therefore a full converter is needed to connect to the grid. The generator is connected to a DC bus through a passive rectifier. From the DC bus, an inverter controls the power flow to the grid. The output from the inverter is filtered and a transformer steps up the voltage before grid connection. The layout of the electric system is shown in Figure 2.

Table 1. Turbine characteristics

Power (kW)	200
Wind speed (m/sec)	11.7
Number of blades	3
Rotational speed (rpm)	33
Projected area (m2)	624
Hub height (m)	40
Turbine radius (m)	13
Blade length (m)	24
Aerodynamic control	Passive stall

Table 2. Generator characteristics at rated conditions [8]

Rated power (kW)	225
No load L-L voltage (V) rms	839
Load L-L voltage (V) rms	810
Current (A) rms	160
Number of phases	3
Electrical efficiency (%)	96.7
Rotational speed (rpm)	33
Torque (kNm)	67
Maximum torque (p.u.)	3.3
X (p.u.)	0.17
Load angle (°)	9.9

Figure 1. The 200 kW VAWT.

Figure 2. Layout of the electric system for the 200 kW VAWT with PM generator and DC voltage control in the inverter.

Control strategy

For a variable speed wind turbine with a direct-driven synchronous generator, the voltage varies with the rotational speed of the turbine. The voltage in one of the phases, V_a , can be described as

$V_{a}={\omega }_{el}{\lambda }_{m}cos\left({\theta }_{el}\right)-$$I_{a}R_{a}-L_{a}{\frac {dI_{a}}{dt}}$

(1)

where ω_el is the electrical angular frequency, λ_m is the peak strength of the flux linkage, θ_el , is the electrical angle, I_a is the current, R_a is the phase resistance, and L_a is the phase inductance. The generator voltage is passively rectified in a six-pole diode bridge; by controlling the DC voltage, the rotational speed of the turbine can be controlled. The control of DC voltage is commonly done by either a DC/DC converter as in [11] or by an active IGBT (insulated-gate bipolar transistor) rectifier as in [12]. Thus, the goal is to control the generator voltage and at the same time boost the DC voltage to a constant level before entering the inverter. Another approach to control the DC voltage is to design a generator with a higher voltage than the grid-side voltage and thus remove the need to boost the voltage before the inverter. If the inverter modulation is used to lower the DC voltage, DC/DC and active rectifier becomes unnecessary from a control system point of view. The 200 kW VAWT considered in this article has a generator voltage that is higher than the grid voltage in the whole operating range and an in-house designed inverter control. Hence, the inverter can handle the varying DC voltage delivered from the generator.

The DC voltage set point can be calculated to run the turbine in an optimal way if the wind speed as well as the relationship between the aerodynamic power coefficient, C_P , and the tip speed ratio, λ; the C_P – λ dependency, of the turbine are known. However, accurate wind measurements are difficult and costly to achieve. At the site of the 200 kW VAWT, a measurement tower with anemometers is placed 100 m from the turbine according to the international standard for C_P measurements [13]. Operational experience indicates that this distance is too long to use for accurate regulation of the turbine. An error in wind speed has a large influence on the control as the relationship between power and wind speed is cubic. To circumvent this problem, an MPPT (maximum power point tracking) algorithm can be used to find the optimal operating point by iteration as done in [14]. Another solution is to use the turbine as an anemometer which has the advantage that it measures the wind speed reaching the turbine, but requires more knowledge about the aerodynamic properties of the turbine [15]. For these two methods, the anemometer in the control system is replaced by measurements of DC power and rotational speed. However, an anemometer might still be used to indicate cut-in and cut-out wind speed, but it can be less accurate than an anemometer used for regulation. A control method combining MPPT with tip speed ratio control, but using the measured wind speed, is presented in [16]. The method of combined MPPT and tip speed ratio control is compared with a proposed method of optimal current given MPPT control in [17]. In [18], several alternatives for control are reviewed with focus on dampening of vibrations. The method proposed here is not an MPPT, but focuses on keeping the tip speed ratio on a given level comparing rotational speed to estimated wind speed. Keeping the tip speed ratio at a fixed value should be an easier control strategy than torque control, which is based on a look-up table to match torque with speed.

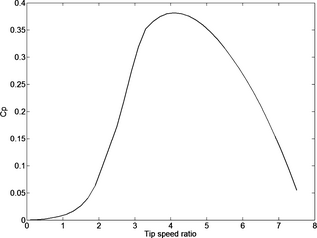
For the 200 kW turbine, the dependence between C_P and tip speed ratio has been estimated with the aerodynamic models described in [19], see Figure 3. This curve has not been verified and therefore the exact power-wind speed dependency, that is, the power curve, is not known. Hence, the anemometer independent method has been considered to be a good solution, as otherwise both an error in wind speed and an error in C_P might affect the control and alter the results. Tip speed ratio control takes advantage of the fact that the C_P  - λ curve is quite flat close to its optimum value, so small errors in the estimated tip speed ratio should not influence the results too much.

Figure 3. The CP − λ dependency for the turbine based on simulations.

The control method used here is based on that the power absorbed by the turbine, P, can be calculated as

$P={\frac {1}{2}}\rho {\mbox{AU}}^{3}C_{P}$

(2)

where ρ is the air density, A is the projected turbine area, and U is the wind speed. The tip speed ratio λ can be calculated as

$\lambda ={\frac {\Omega r}{U}}$

(3)

where Ω is the rotational speed of the turbine and r is the radius. The efficiency of the system from the power absorbed by the turbine to the DC bus is denoted η, that is,

$P_{DC}=\eta P$

(4)

where P_DC is the power measured on the DC bus (see Fig. 2). The efficiency, η, takes into account the mechanical losses in couplings and bearings in the wind turbine, generator losses, and rectification losses. The generator losses for this specific generator are discussed in [8]. The efficiency is dependent on rotational speed and current, but does not change much for the operational range considered here. Here, the efficiency is assumed to be fairly constant. However, the decreasing generator efficiency at low wind speeds might influence results slightly, see Figures 6, 7, and 8 in Results and Discussion section.

The estimation of the tip speed ratio is based on equations (2), (3), and (4) as

${\lambda }_{t}=3{\sqrt {\frac {0.5\rho Ar^{3}\eta C_{P}\left({\lambda }_{t-1}\right){\Omega }^{3}}{P_{DC}}}}$

(5)

and uses the turbine as an anemometer through measurements of absorbed DC power and rotational speed, see Figure 2. In this work, η has been set to the constant value of 0.90 for simplicity. This value is lower than expected for normal operation, but is considered reasonable for the limited operational range in this study, as the generator efficiency decreases at low wind speed. However, a sensitivity analysis shows that the results are not influenced much by a small error in the estimated efficiency, see 'Sensitivity analysis' section. The value of C_P is taken from a look-up table based on aerodynamic simulations, see Figure 3. The key to search the look-up table is the tip speed ratio calculated in the previous iteration, λ_t−1. This method is similar to the one used in [15], but instead of controlling the optimal torque the control is focused toward finding the optimal tip speed ratio by measuring the absorbed power. The error, e(t), between the optimal tip speed ratio, λ_opt, and the result from equation (5) is calculated as

$e\left(t\right)={\lambda }_{opt}-{\lambda }_{t}$

(6)

and is used in a PID (proportional-integral-derivative) regulator described as

$u\left(t\right)=K_{p}e\left(t\right)+K_{i}\int _{0}^{t}e\left(T\right)dT+$$K_{d}{\frac {d}{dt}}e\left(t\right)$

(7)

where K_p , K_i , and K_d are constants regulating the proportional, integral, and derivative parts of the regulator, respectively. A new set point for the DC voltage, U_DC, is calculated as

$U_{DC}\left(t\right)=U_{DC}\left(t-1\right)\left[1+\right.$$\left.u\left(t\right)\right]$

(8)

There are two reasons for using a regulator controlled by the error in tip speed ratio to set the DC voltage; a rapid step in voltage is avoided at gusty wind conditions and the influence of the current-dependent voltage drop across the generator (−I_aR_a − L_a dI_a/dt in eq. (1)) can be avoided. The inverter is used to control the DC voltage based on the output from the tip speed ratio regulator. Hence, when the wind speed fluctuates, the absorbed power is changed, through the generator current, giving a new regulator set point in DC voltage (for large enough wind speed fluctuations).

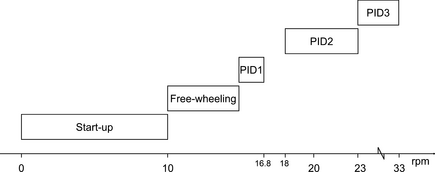
The control strategy can be divided into different parts, see Figure 4. The start-up system accelerates the wind turbine up to about 10 rpm from where it can self-start. The turbine is then allowed to freewheel up to a rotational speed of about 15 rpm. The DC voltage is set at 520 V and at a rotational speed of about 15 rpm, the turbine can start to deliver power. The PID regulator is activated when a DC power level of 20 kW is reached and the turbine is operated at optimal tip speed ratio up to 16.8 rpm (PID 1). The present tower configuration has a critical speed around 17.5 rpm, which is avoided by implementing a jump in rotational speed in the control system across the speeds 16.8–18 rpm. Hysteresis is implemented to avoid too many jumps at wind speeds corresponding to operation around 17.5 rpm. At DC power levels below 20 kW, the turbine is operated with a constant DC voltage level of 520 V due to decreased accuracy in tip speed ratio estimation at low power level. The change in control method goes smoothly, as the tip speed ratio based control is operating at a DC voltage close to 520 V around this operating point. This smooth change from freewheeling to tip speed ratio control is not included in Figure 4 as it only represents operation around 15 rpm.

Figure 4. The control strategy at different rotational speed.

The operation of the PID regulator is divided into three regions for different power levels with slightly different parameters due to the turbines more rapid behavior at high power. The first region (PID 1) represents low power and rotational speed between 15 and 16.8 rpm. The second region (PID 2) is for medium speed, from 18 to 23 rpm, and medium power. The third region (PID 3) is activated for DC power levels above 70 kW. The different PID parameters, used in equation (7), for the three regions can be seen in Table 3.

Table 3. PID parameters for the three operating modes

	Kp	Ki	Kd
PID 1	0.02	0	0
PID 2	0.012	0.001	0.03
PID 3	0.006	0	0.03

Above rated rotational speed, 33 rpm, a speed limitation is activated, keeping the rotational speed below 33 rpm. For the study presented in this article, the rotational speed limit has been set to 21 rpm, see 'Experiments' section. The rotational speed is kept constant by keeping the DC voltage constant or, when needed, decreasing the DC voltage. When rated power is reached, the control will change from tip speed ratio control to power control, keeping the power constant until cut-out wind speed, accommodated by passive stall control. The passive stall control for this turbine is demonstrated in [9]. As the wind speed increases, the turbine will vary slightly in rotational speed depending on the shape of the C_P - λ curve, that is, the effectiveness of the stall control. At cut-out wind speed a dump-load is connected directly at the generator terminals, braking the turbine efficiently [8]. Around the cut-out wind speed some hysteresis is implemented to avoid starting and stopping the turbine continuously at wind speeds fluctuating around cut-out wind speed. For cut-in and cut-out wind speed, 10-min sliding average values of the wind speed measured by the anemometer were used.

Experiments

The measurements, the estimation of tip speed ratio, as well as the tip speed ratio control loop were run at a NI cRIO9074 at 1 Hz, together with other control functions of the wind turbine. The anemometer (Thies Clima 4.3351.00.161, Adolf Thies GmBH & Co. KG, Göttingen, Germany) was placed in a measurement tower 100 m from the turbine at a height of 42 m. The air density used in data treatment was set at a constant value of 1.2775 kg/m³ which is calculated from the estimated mean values of air pressure and temperature during the measurement campaign. The rotational speed of the turbine was measured by a 10-bit rotational encoder placed on the drive shaft. The DC power was measured through a current transducer (SSET CEIZ04-55E4-1.0/0-400A) and a voltage transducer (Tektronix P5200).

During the experiment, limitations of the operational range was set to be able to thoroughly test the behavior of the control system close to the limits of allowed rotational speed and wind speed. The limits were based on the wind climate at the site and are set quite low as the annual mean wind speed at the site is quite low. The goal with the experiment was to test the control strategy at variable speed and to test the operation with variable DC voltage; not to test the turbine for its full operational range. The tip speed ratio set point was set to 3.8. The limitation in rotational speed was set to 21 rpm, corresponding to a wind speed of 7.3 m/sec and a DC power of 53 kW, and the cut-out wind speed was set to 8 m/sec for the measured mean wind speed. If the rotational speed is increased above 21 rpm, the DC voltage is forced down by 4 V/sec until 20.5 rpm is reached. This is to protect the turbine from over speeding and implement some hysteresis into the control. At cut-out wind speed, the dump-load is connected. According to this operational limit, only PID 1 and PID 2 in Figure 4 are used. Cut-in wind speed was set to 3.5 m/sec and the wind turbine can start to deliver energy when the rotational speed has increased past 15 rpm.

The wind speed estimated by the turbine is calculated from the estimated tip speed ratio and the measured rotational speed according to equation (3). The wind speed estimation is started at a measured DC power above 20 kW as it is difficult to get a proper estimation of wind speed at lower power. The wind speed is not continuously calculated and logged by the measurement system. However, the rotational speed and the DC power are logged which makes it possible to calculate the wind speed afterward.

Sensitivity analysis

A sensitivity analysis was performed in order to analyze how sensitive the control system is for changes in the value for ηC_P (λ_t−1) from the maximum values for optimum tip speed ratio operation used here of η at 0.90 and C_P at 0.38, see Table 4. The analysis was done by varying both the efficiency, η, and the maximum C_P value. The results show that even if the generator efficiency and/or the C_P has been estimated wrong, the resulting error in tip speed ratio will be small, as the tip speed ratio only is affected by the error to the power of 1/3. The generator electromagnetic efficiency increases from about 94% at about 4.5 m/sec to 96% at higher wind speeds.

Table 4. Sensitivity analysis for changes in ηC_P (λ_t−1). λ_new denotes the tip speed ratio with η and C_P from the table and λ_est denotes the tip speed ratio for η = 0.90 and C_P  = 0.38

η	CP	λnew/λest = (ηCP/(0.09 × 0.38))1/3
0.87	0.38	0.99
0.90	0.38	1
0.93	0.38	1.01
0.96	0.38	1.02
0.90	0.35	0.97
0.93	0.35	0.98
0.90	0.41	1.03

Results and Discussion

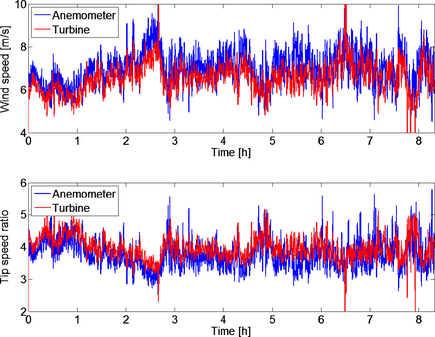
From the measured DC power and rotational speed, the tip speed ratio is estimated according to equation (5). The estimated wind speed at the turbine can be found from equation (3) and (5) and is used in Figures 5, 6, and 7. The estimated wind speed is compared with wind speed measurements from the anemometer for 8 h in Figure 5 (top figure). The results are shown as 25-sec moving average values to increase visibility and to compensate for the distance between turbine and anemometer. The time it takes for a gust of 4 m/sec to travel the distance between anemometer and turbine corresponds to 25 sec. The estimated wind speed follows the variations in measured wind speed closely. However, the estimated wind speed is roughly 7% lower than the wind speed measured by the anemometer. The spikes in the estimated wind speed are from occasions when the absorbed power is too low for an accurate estimation or from periods when the regulator is overridden by the limit in rotational speed which releases stored kinetic energy from the turbine to the grid. Thus, a large difference between numerator and denominator in equation (5), gives a divergent behavior in the estimated tip speed ratio.

Figure 5. The top figure shows a comparison of measured and estimated wind speeds. The figure below shows the tip speed ratio for the same time interval. Wind speed and tip speed ratio are from the same 8 h of data and the data are shown as 25 sec sliding averages. The reference value for the tip speed ratio is 3.8.

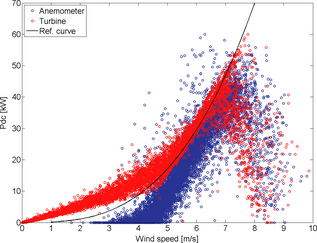
Figure 6. Power as a function of wind speed. The black curve shows the theoretical curve based on a simulated CP of 0.38 and a system efficiency of 0.90. The blue curve is based on wind speed from the anemometer and the red curve is based on turbine-estimated wind speed.

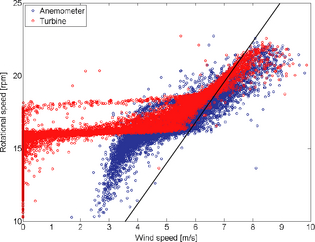
Figure 7. Rotational speed as a function of wind speed. The black line represents the reference value for the tip speed ratio of 3.8.

The tip speed ratio during the same 8 h of operation as above is shown in Figure 5 (lower figure). The set point for tip speed ratio in the control system was 3.8, which is slightly lower than optimal tip speed ratio, enabling more stable operation, as we would rather operate on the left side than on the right side of the optimum operating point [9], see Figure 3. The mean value of anemometer measured tip speed ratio was 3.76, with a median value of 3.70 and a standard deviation of 0.57. The tip speed ratio estimated by the turbine had a higher mean value of 3.96. The standard deviation for the estimated tip speed ratio was 0.41, which is lower than if measured by the anemometer. The results show that the control system is able to control the tip speed ratio of the turbine in a satisfying way, that is, we operate at the top of the C_P (λ) curve in Figure 3, also demonstrated in Figure 6, which is the goal of this control strategy.

The estimation of tip speed ratio from equation (5) includes the term ηC_P (λ_t−1), where the efficiency, η, is set to the constant value of 0.90. The efficiency is expected to be roughly constant for the tested interval apart from at low power, where the generator efficiency decreases due to dominating iron losses [8]. Furthermore, the value for the aerodynamic power coefficient used in equation (5), taken from the simulated C_P curve in Figure 3, might differ from the C_P achieved during these experiments.

Figures 6, 7, and 8 show 10-min average values for 1488 h of operational data. The estimated wind speed was not calculated for power levels below 20 kW. For those measurement points, the estimated wind speed was set to 0 m/sec and these points were included in the calculated 10-min moving average values, resulting in some average values at low wind speeds.

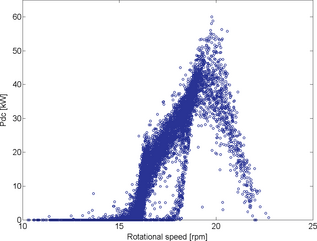
Figure 8. Power as a function of rotational speed.

The behavior of absorbed power at different wind speeds is shown in Figure 6 together with the power curve based on the theoretical C_P curve. Also here, a small difference is seen between the estimated and measured wind speed. The measured power curve, P_DC, follows the power curve based on the theoretical C_P well, as would be expected since the wind speed estimation is based on this curve. However, if the estimation would have been very wrong, it would be difficult to stay on the P_DC curve and we would have larger fluctuations in absorbed power.

The differences in measured and estimated wind speed could have several reasons. First, the value for ηC_P (λ_t−1) might not be correct. However, the sensitivity analyze in Sensitivity analysis section showed that this would only have a small impact on the results. However, at low power we expect the calculated wind speed to be underestimated, as the generator efficiency decreases rapidly at low power, which is visible in the red curve for low power levels in Figure 6. Second, we might have an error in the wind speed measured by the anemometer. This would explain and confirm the good power curve fit in Figure 6. An error in wind speed measurements could be caused by wind shear, erroneous hub height estimation, or the anemometer not being correctly calibrated. However, the constant density is not expected to be the reason as it would not give a constant error in the wind speed, as we have here.

The rotational speed is fairly proportional to the wind speed for higher wind speeds with this control strategy, see Figure 7, which corresponds to equation (3). The tip speed ratio regulation starts at wind speeds above 5.3 m/sec. At low wind speeds the decreased efficiency, which has not been accounted for, might lead to an underestimation of the wind speed. This might be one of the reasons to why the curves do not follow the reference line corresponding to a tip speed ratio of 3.8 at low wind speeds. The jump in rotational speed to bypass the critical speed is clearly visible in this figure and it can be seen that a hysteresis is implemented. The same phenomena can be seen in Figure 8, showing the power as a function of rotational speed.

In Figures 6 and 8, it is shown that the power decreases at high rotational speeds. This is an artifact caused by hysteresis behavior around the point of maximum rotational speed, see 'Experiments' section. At this point, the turbine is stalling at increasing wind speeds during a slow, forced deceleration of the turbine, followed by the turbine freewheeling up to the maximum rotational speed as the wind speed decreases again. The rotational energy stored in the turbine might influence the results, especially around the lower and upper limits in rotational speed [4].

The theoretical C_P curve, showed in Figure 3 and included in Figure 6, shows the aerodynamic C_P . In Figure 6, the theoretical DC power at the turbine is compared with the measured power at the DC bus, P_DC. The problem of using wind speed measurements in the control system is that a measurement error and/or effect of the large distance between turbine and anemometer will be cubic. The rpm and P_DC, from equation (5), are measured directly at the turbine and is only expected to have small errors. However, in this study, a constant density has been assumed, which might influence the results slightly.

The presented control method can be improved to work even better by measuring C_P . The theoretical C_P (λ) graph is quite wide with an optimum tip speed ratio between 3.5 and 4.2, as seen in Figure 3. An even more wide and flat curve was measured for a 12 kW turbine of the same features [5]. By aiming at a tip speed ratio of 3.8, it can be assumed that the turbine is operated at, or close to, optimum tip speed ratio. However, the optimum C_P is not known and it is therefore considered that C_P has a constant error. When the exact C_P curve have been measured, the values for C_P (λ_t−1) in equation (5) can be set exactly. The suggested control strategy will then be even more exact than a control based on wind speed measurements. Furthermore, this control strategy enables a faster regulation as the wind speed is estimated instantly. The maximum power coefficient for this turbine can be found according to IEC 61400-12-1 [13], by running the turbine at fixed rotational speeds at varying wind speeds. An alternative method could be to use the control method proposed here, including the speed- and load-dependent system efficiency, and varying C_P until the power curve is maximized (Fig. 6).

During the experiments, the DC voltage was allowed to vary between 510 and 720 V, that is, the inverter was subject to a variable DC voltage. The results show that it works to run a turbine with variable DC voltage to the inverter.

Conclusions

It has been demonstrated that the optimum tip speed ratio regulation independent of wind speed measurements works and that the tip speed ratio is controlled and kept at a desired level. The control method is independent on wind speed measurements and the wind turbine itself is used as an anemometer, measuring the actual wind speed reaching the turbine. With a measured C_P , this control method could be an interesting alternative to a wind speed measurement based control method. Furthermore, the results verify that it works to run a turbine with variable DC voltage to the inverter. The estimated wind speed is slightly lower than the measured wind speed and we believe this is attributed to a small constant error in the wind speed measurements.

A long-time measurement campaign to find C_P for all different tip speed ratios should be performed. Future work also includes implementing the speed- and load-dependent system efficiency curve in the control system.

An alternative to the standard method, with wind speed measured at a distance [13], to find the turbines power curve has been proposed, where different C_P values would be included in the tip speed ratio control method and the turbine run until the maximum power curve is found.

Acknowledgments

Acknowledgments are given to Vertical Wind, E.ON, Falkenberg Energy, and the Swedish Energy Agency. In addition, Elias Björkelund de Faire is acknowledged for valuable contribution.

Conflict of Interest

None declared.

References

1. Eriksson, S., H. Bernhoff, and M. Leijon. 2008. Evaluation of different turbine concepts for wind power. Renew. Sustain. Energy Rev.12:1419–1434.
2. Paquette, J., and M. Barone. 2012. Innovative offshore vertical-axis wind turbine rotor project. Proceedings of EWEA 2012 Annual Event, 16–19 April, Copenhagen, Denmark.
3. Schmidt Paulsen, U., T. Friis Pedersen, H. Aagaard Madsen, K. Enevoldsen, P. H. Nielsen, J. H. Hattel, et al. 2011. Deepwind – an innovative wind turbine concept for offshore. Proceedings of EWEA Annual Event, 14–17 March, Brussels, Belgium.
4. Deglaire, P., S. Eriksson, J. Kjellin, and H. Bernhoff. 2007. Experimental results from a 12 kW vertical axis wind turbine with a direct driven PM synchronous generator. Proceedings of European Wind Energy Conference EWEC, 7–10 May, Milan, Italy.
5. Kjellin, J., F. Bülow, S. Eriksson, P. Deglaire, M. Leijon, and H. Bernhoff. 2011. Power coefficient measurement on a 12 kW straight bladed vertical axis wind turbine. Renewable Energy36:3050–3053.
6. Ribrant, J., and L. M. Bertling. 2007. Survey of failures in wind power systems with focus on Swedish wind power plants during 1997-2005. IEEE Trans. Energy Convers.22:167–173.
7. Samsonov, V., and P. Baklushin. 1992. Comparison of different ways for VAWT aerodynamic control. J. Wind Eng. Ind. Aerodyn.39:427–433.
8. Eriksson, S., H. Bernhoff, and M. Leijon. 2011. A 225 kW direct driven PM generator adapted to a vertical axis wind turbine. Adv. Power Electronics 2011. article ID 239061, 7 pages
9. Kjellin, J., S. Eriksson, and H. Bernhoff. 2013. Electric control substituting pitch control for large wind turbines. J. Wind Energy 2013. Article ID 342061, 4 pages.
10. Kjellin, J., and H. Bernhoff. 2011. Electrical starter system for an H-Rotor Type VAWT with PM-generator and auxiliary winding. Wind Eng.35:85–92.
11. Molina, M. G., and P.E. Mercado. 2008. A new control strategy of variable speed wind turbine generator for three-phase grid-connected applications. Pp. 1–8in Transmission and Distribution Conference and Exposition: Latin America, 2008 IEEE/PES, Bogota, Colombia, 13–15 August 2008.
12. Senjyu, T., S. Tamaki, N. Urasaki, K. Uezato, T. Funabashi, and H. Fujita. 2003Wind velocity and position sensorless operation for PMSG wind generator. Pp. 787–792in Power Electronics and Drive Systems, PEDS 2003. The Fifth International Conference on, Singapore, Vol. 1, 17–20 November 2003.
13. International Electrotechnical Commission. 2005. International standard IEC 61400-12-1, Power performance measurements of electricity producing wind turbines. 1st ed. International Electrotechnical Commission, Geneva, Switzerland.
14. Thongam, J. S., P. Bouchard, H. Ezzaidi, and M. Ouhrouche. 2009. Wind speed sensorless maximum power point tracking control of variable speed wind energy conversion systems. Pp. 1832–1837in Electric Machines and Drives Conference, IEMDC ‘09, IEEE International, Miami, FL 3–6 May.
15. Haque, M.E., M. Negnevitsky, and K. M. Muttaqi. 2008. A novel control strategy for a variable speed wind turbine with a permanent magnet synchronous generator. Pp. 1–8in Industry Applications Society Annual Meeting, IAS ‘08. IEEE, Edmonton, Alberta, Canada, 5–9 October.
16. Jeong, H. G., R. H. Seung, and K. B. Lee. 2012. An improved maximum power point tracking method for wind power systems. Energies5:1339–1354.
17. Zhu, Y., M. Cheng, W. Hua, and W. Wang. 2012. A novel maximum power point tracking control for permanent magnet direct drive wind energy conversion systems. Energies5:1398–1412.
18. Bossanyi, E. A.2000. The Design of closed loop controllers for wind turbines. Wind Energy3:149–163.
19. Deglaire, P. 2010. Analytical aerodynamic simulation tools for vertical axis wind turbines. Doctoral dissertation, Uppsala University [Acta Universitatis Upsaliensis], Uppsala, Sweden. ISSN 1651-6214; 774.