Abstract
In this paper, a new perturbation technique is employed to solve strongly nonlinear Duffing oscillators, in which a new parameter is defined such that the value of α is always small regardless of the magnitude of the original parameter . Therefore, the strongly nonlinear Duffing oscillators with large parameter ε are transformed into a small parameter system with respect to . Approximate solution obtained by the present method is compared with the solution of energy balance method, homotopy perturbation method, global error minimization method and lastly numerical solution. We observe from the results that this method is very simple, easy to apply, and gives a very good accuracy not only for small parameter εbut also for large values of ε.
Keywords
Analytical solution; Perturbation technique; Strongly nonlinear Duffing oscillators
1. Introduction
Duffing oscillators are described by nonlinear differential equations that modeled the behavior of many practical problems that arise in engineering, physics, and in many real world applications [1], [2], [3], [4] and [5]. It is well known that Duffing oscillators can be found in the modeling of free vibrations of a restrained uniform beam with intermediate lumped mass, the nonlinear dynamics of slender elastica, the generalized Pochhammer–Chree (PC) equation, the generalized compound KdV equation in nonlinear wave systems, among others [6].
The study of Duffing oscillators has received considerable attention in recent years due to a variety of engineering applications. Several approaches have been proposed so far dealing with the nonlinear Duffing oscillators. Variational iteration method [7], homotopy perturbation method [8], He’s energy balance method [9], He’s parameter-expanding method [10], He’s max–min approach [11] and global error minimization method [12] are some examples.
In this paper, we will apply He’s modified perturbation technique [13] and [14] to solve nonlinear Duffing oscillators of fifth order in two cases first, without forced term and second with forced term, which hold for all the values of amplitude of the oscillator [15], [16] and [17].
2. Basic idea of the method
To illustrate the basic idea of the present note, we will consider the following nonlinear Duffing equation with nonlinearity of fifth order:
|
|
(1) |
Re-write Eq. (1) in the form
|
|
(2) |
where
|
|
(3) |
Here β is the angular frequency which is unknown to be further determined and ε is a large parameter.
Now define a new parameter
|
|
(4) |
such that
|
|
(5) |
Then , when , so ε can be written as follows:
|
|
(6) |
Assume that η and u can be written as follows:
|
|
(7) |
|
|
(8) |
Substituting Eqs. (6), (7) and (8) into Eq. (2) and equating coefficients of like powers of α yield the following equations:
|
|
(9) |
|
|
(10) |
|
|
(11) |
Solving Eqs. (9), (10) and (11), we obtain,
|
|
(12) |
|
|
(13) |
|
|
(14) |
Substituting and into Eq. (3), we have
|
|
(15) |
Then, the second approximate solution to Eq. (1) becomes,
|
|
(16) |
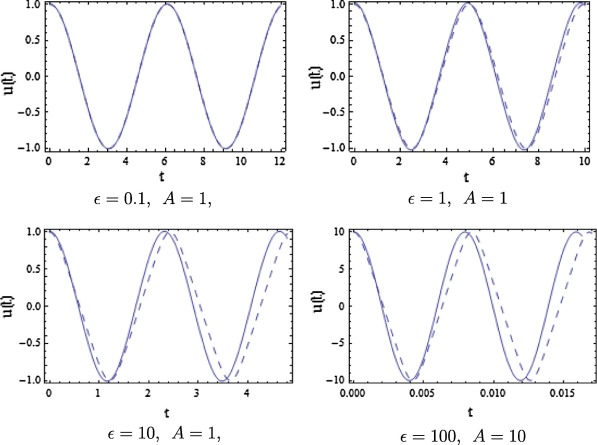
To show the remarkable accuracy of the obtained result, the approximate solution with the energy balance method [18], homotopy perturbation method [19], global error minimization method [20] and numerical solution are compared at in Table 1 (see Fig. 1).
| A | EBM [18] | HPM [19] | GEMM [20] | Present | Numerical |
|---|---|---|---|---|---|
| 0.1 | 1.00003 | 1.00003 | 1.00003 | 1.00003 | 1.00003 |
| 0.2 | 1.00047 | 1.00050 | 1.00050 | 1.00050 | 1.00050 |
| 0.3 | 1.00236 | 1.00253 | 1.00254 | 1.00253 | 1.00253 |
| 0.5 | 1.01807 | 1.01934 | 1.01941 | 1.01940 | 1.01940 |
| 1 | 1.25831 | 1.27475 | 1.28082 | 1.28211 | 1.28079 |
| 5 | 19.1202 | 19.7895 | 20.3919 | 20.5027 | 19.9719 |
| 10 | 76.3828 | 79.0633 | 81.4807 | 81.9253 | 80.0801 |
|
|
|
Figure 1. Comparison of the approximate solution (solid line) with the numerical solution (dashed line). |
3. Forced Duffing equation of fifth power nonlinear function
We consider next an oscillator with fifth power nonlinearity in the form
|
|
(17) |
which represents a forced Duffing equation. Changing Eq. (17) into another case by using Eq. (3) to obtain
|
|
(18) |
Substituting Eqs. (6) and (8) into Eq. (18), and setting the coefficients of the powers of α equal to zero, resulting in
|
|
(19) |
|
|
(20) |
Solving Eq. (19), results in
|
|
(21) |
Substituting Eq. (21) into Eq. (20), to obtain
|
|
(22) |
and
|
|
(23) |
Using Eq. (8) the perturbation solution can be expressed as follows:
|
|
(24) |
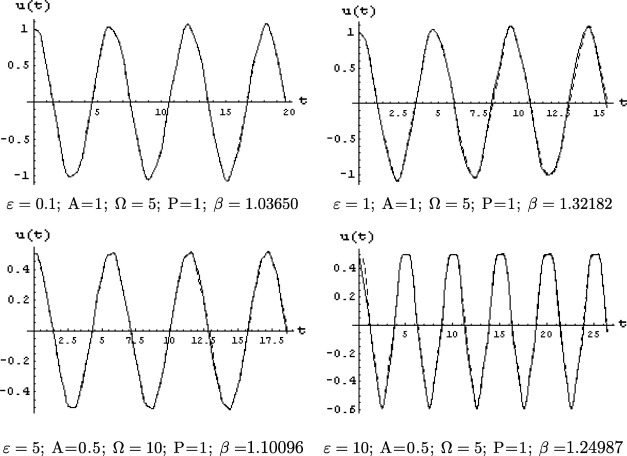
where and are given by Eqs. (21) and (23). As we did before we check numerically the validity of Eq. (17) by calculating the solution of Eq. (24) and also, a good agreement is found for different values of A and ε as shown in Fig. 2.
|
|
|
Figure 2. Comparison of the approximate solution (solid line) with the numerical solution (dashed line). |
4. Conclusion
A new perturbation technique valid for large parameter is employed in the present paper. It is an effective method to determine analytical solution for strongly nonlinear Duffing oscillators. All analytical solutions computed in the present paper are in pretty good agreement with those obtained by the numerical solutions. It is worthy to mention that the present method is an extremely simple and leads to high accuracy of the obtained results.
References
- [1] A.H. Nayfeh, D.T. Mook; Nonlinear Oscillators; John Wiley, New York (1973)
- [2] A.L. Maimistov; Propagation of an ultimately short electromagnetic in a nonlinear medium described by the fifth-order Duffing model; Opt. Spectrosc., 94 (2003), pp. 251–257
- [3] A.E. Zuniga; Exact solution of the cubic-quintic Duffing oscillator; Appl. Math. Model., 37 (2013), pp. 2574–2579
- [4] T. Öziş, A. Yildirim; Determination of limit cycles by modified straightforward expansion for nonlinear oscillators; Chaos Soliton Fract., 32 (2007), pp. 445–448
- [5] W.U. Baisheng, L.I. Pengongli; A method for obtaining approximate analytic periods for a class of nonlinear oscillators; Meccanica, 36 (2001), pp. 167–176
- [6] B.S. Wu, W.P. Sun, C.W. Lim; An analytical approximate technique for a class of strongly non-linear oscillators; Int. J. Non-Linear Mech., 41 (2006), pp. 766–774
- [7] J.H. He; Variational iteration method – a kind of nonlinear analytical technique: some examples; Int. J. Non-Linear Mech., 34 (1999), pp. 699–704
- [8] J.H. He; Homotopy perturbation method: a new nonlinear analytical technique; Appl. Math. Comput., 135 (2003), pp. 73–79
- [9] H. Babazadeh, D.D. Ganji, M. Akbarzade; He’s energy balance method to evaluate the effect of amplitude on the nonlinear frequency in nonlinear vibration systems; Prog. Electromag. Res. M, 4 (2008), pp. 143–154
- [10] F. Ozen Zengin, M.O. Kaya, S.A. Demirbag; Approximate period calculation for some strongly nonlinear oscillation by He’s parameter-expanding methods; Nonlinear Anal.: Real World Appl., 10 (2009), pp. 2177–2182
- [11] L.B. Ibsen, A. Barari, A. Kimiaeifar; Analysis of highly nonlinear oscillation systems using He’s max–min method and comparison with homotopy analysis and energy balance methods; Sādhanā, 35 (2010), pp. 433–448
- [12] M. Akbarzade, J. Langari; Solutions of nonlinear oscillators using global error minimization method; Adv. Stud. Theor. Phys., 5 (2011), pp. 349–356
- [13] J.H. He; Analytical solution of a nonlinear oscillator by the linearized perturbation technique; Commun. Nonlinear Sci. Numer. Simul., 4 (1999), pp. 109–113
- [14] J.H. He; Modified straightforward expansion; Meccanica, 34 (1999), pp. 287–289
- [15] J.H. He; A new perturbation technique which is also valid for large parameters; J. Sound Vib., 229 (2000), pp. 1257–1263
- [16] J.H. He; Iteration perturbation method for strongly nonlinear oscillations; J. Vib. Control, 7 (2001), pp. 631–642
- [17] J.H. He; A modified perturbation technique depending upon an artificial parameter; Meccanica, 35 (2000), pp. 299–311
- [18] H. Babazadeh, D.D. Ganji, M. Akbarzade; He’s energy balance method to evolute the effect of amplitude on the natural frequency in nonlinear vibration systems; Prog. Electromag. Res. M, 4 (2008), pp. 143–154
- [19] J.H. He; Homotopy perturbation method: a new nonlinear analytical technique; Appl. Math. Comput., 135 (2003), pp. 73–79
- [20] M. Akbarzade, J. Langari; Solution of nonlinear oscillator using global error minimization method; Adv. Stud. Theor. Phys., 5 (2011), pp. 349–356
Document information
Published on 12/04/17
Licence: Other
Share this document
claim authorship
Are you one of the authors of this document?