Abstract
Spatial evolution in ancient Chinese villages is always one of the most interesting research topics in the field of architectural design, urban planning and history of architecture. Xi-di village exemplifies traditional settlements in ancient China. For many years, numerous researchers have explored its built form, origin and evolution process from different perspectives. This paper attempts to position the spatial evolution process of this village in the context of complex system theory, which views the process of space self-organization as a form of disequilibrium and non-linear development process. Through analyzing the mechanism of village space changes, we develop the dynamic evolution modeling based on the theory of cellular automata. The purpose of the paper is to provide a new perspective for the conventional architectural research of space self-organization.
Keywords
Complex system ; Self-organization ; Cellular Automata ; REPAST ; Spatial evolution
1. Introduction
Over the past 50 years, complexity has been regarded as a metaphor that boosts the argument on the issues of cities. Many informal descriptions of complex systems related to the concept of self-organization and evolution exist, including, “highly structured system which shows the structure with variations” (Goldenfeld and Kadanoff), “systems in process that constantly evolve and unfold over time” (Author, 1999 ) or “the system featuring a large number of interacting components whose aggregate activity is nonlinear and typically exhibits hierarchical self-organization under selective pressure (Rocha, 1999 ). Self-organization is the centrality of the theory of complex system that provides common language, and conceptual and methodological framework in studying cities and urbanism (Portugali, 1999 ). The complex system is characterized by its unpredictable outcomes. None of the traditional analyzing methods can predict the behavior of a complex system because of its unpredictable outcomes. Simulation is the only option (Batty, 2004 ). This paper attempts to simulate the spatial evolution of Xi-di village in Anhui province according to the principles of complex system. In this setting, we define the simple rules or interactions that give rise to spatial evolution based on the theory of cellular automata.
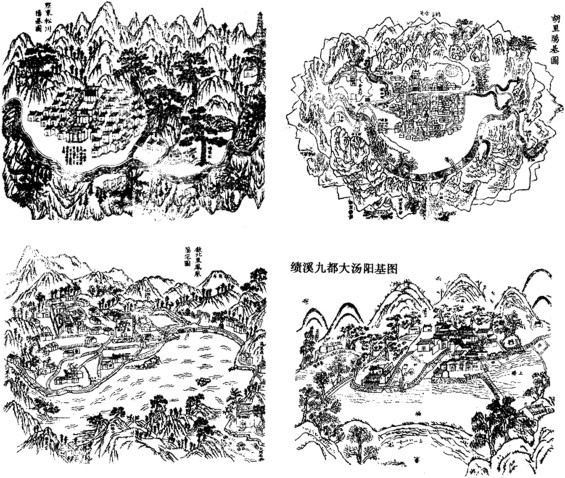
Xi-di is one of the most famous ancient villages (Figure 1) in China, with a long history tracing back to the Song dynasty (A.D. 960–1279). The development of the village occurred during the period of the Ming dynasty, followed by prosperity in early Qing dynasty and downfall afterwards. More recently, the village experienced repetitious demolitions between 1950s and 1970s, with many historic buildings ruined. Despite continuous destruction, the fundamental space structure and morphology of this ancient village survived. In 2000, Xi-di, along with Hongcun, another ancient village 12 miles away, was listed as World Heritage Sites by UNESCO. One year later, Xi-di was included in the Cultural Relics of National Importance under the Protection of the State, fascinating researchers across the country and tourists as well. For many years, numerous architectural researchers have explored its built form, origin and evolution process from different perspectives (Duan, 2006 ). (Figure 2)
|
|
|
Figure 1. Ancient paintings of Xi-di village (Duan, 2006 ).
|
|
|
|
Figure 2. Aerial photo of Xi-di village (Duan, 2006 ).
|
2. Cell-space modeling
The theory of cellular automata (CA) has been clearly propounded in the early works of Wolfram (1984, 1994) (Wolfram, 2002 ). Early attempts at CA simulation of cities were typically more in the nature of metaphors of urban growth, with little explicit relation with the underlying behavioral theory (Couclelis, 1985 ).
The strict CA method appears not appropriate to be immediately applied to real systems, where the definition of states, neighborhoods, and transition rules is much more specific than the theory suggests. Various approaches to rule definition have been undertaken in an attempt to enrich the theoretical basis of simulation. The cell-space modeling, for example, in contrast to strict CA, has relaxed the definition of local neighborhood and transition rules. Other significant features of this method involve the relation with GIS software, the extent to which multiple states are dealt with, and the starting points for simulations based on a limited numbers of seeds or already developed landscapes (Batty, 2004 ).
2.1. Cellular space
In conventional CA, the cell space is homogeneous. However, in the modeling for Xi-di village, it is useful to work on a heterogeneous cellular space. Each cell may have intrinsic qualities, representing real geographical space such as topography, slope or other attributes. The cellular space is not regular because it corresponds to polygons of the space.
In the Xi-di modeling, the life cycle model for the cellular space is set, where for every supposed time step of the iteration, the developed cellular space will be re-converted to an undeveloped cellular space, similar to the process in which old buildings are torn down after a period of time and the land is vacant again. The purpose of life cycle modeling is to simulate the metabolism process of land use in Xi-di village; otherwise the village space will be filled with the developed land with the step iteration going on.
2.2. Cellular states
In the Xi-di cell-space modeling, cellular states refer to land use. The two kinds of cell states are developed land and undeveloped land. However, the states of some of the cellular space are fixed, such as river, mountain, etc., and are not subject to changes (Figure 3) .
|
|
|
Figure 3. Northeast part of the Xi-di village model and the life cycle.
|
2.3. Initial conditions and neighborhood
A set of initial conditions is defined by seed cells, (Figure 4 ) which are determined by locating various original settlements identified from historical maps and other sources and dating their foundations. The seed cells include important ancestral temples, such as Jing-ai Tang, and Chang-chun Tang, among others, which became significant cores of the village during the period of space diffusion.
|
|
|
Figure 4. Seed cells of initial condition.
|
We cannot use the strict CA neighborhood, such as that of Von Neumann or Moore, because the cell space in this case is not regular. Alternatively, we use GeoDa1 to generate the polygon neighborhood. If the neighborhood radius is 1, under the pattern of Rook Contiguity, the surrounding polygons which have common boundaries with the central polygon will be selected. Under the pattern of Queen Contiguity, the neighborhood polygons will include all those with common points, boundaries and vertices. If neighborhoods larger than a Moore neighborhood are required, the radius of adjacency is subject to increase in order to take into account the “action at a distance”.
2.4. Transition rules
The transition rules of the space are integrated with a multi-criteria evaluation, which is selected for the special purpose for the current study. Conventionally, the studies of spatial evolution process, which lasts nearly one thousand years, depend on the analysis of historic materials. However, our study is an attempt to investigate the implications of different self-organization modes for generic growth patterns. Multi-criteria evaluation also provides an interface for conducting what a simulation runs in a more sophisticated, transparent, and reliable manner than in heuristic-driven CA. The state of land use at t +1 is determined by the state of land and the development situation of its neighborhood at time t in accordance with a set of transition rules. The state of land use is expressed as ( Wu and Webster, 1998 ):
|
|
where and are the states of land use at location ij at the time t+ 1 and t , respectively; is the development situation in the neighborhood space of the location ij , and Tt is a set of transition rules.
The probabilistic approach allows a flexible translation from context and local dependencies into the rules of transition, so the state at time t+ 1 becomes:
|
|
where pijs is the probability of transition to the state s at the location ij :
|
|
rijs rates the suitability of conversion s at the location ij ; Fijk is the score of development factor k at the location ij ; Wk is the vector of weights that gives relative importance to each development factor; ω is the combination function which sums the score of the weighted development factors, and ϕ is the function which translates the composite suitability score into the probability. A nonlinear transformation is required to depress the probability away from rmax in order to achieve greater discrimination between cellular cells in any one simulation, such as
|
|
|
|
In the Xi-di model, the land use of river or mountain cannot be converted to the developed land, which is represented as follows:
|
|
where β1 –β4 are the weight parameters acquired from the historical materials analysis, and the mountain , river , road , and neighbors are development factors. There are several phases in the spatial development of Xi-di village according to historic materials (refer to Section 4.1). In the first phase of the village development, there were no tangible road systems, with dwelling houses stochastically distributed. Ancient dwellers preferred to live at the foot of the mountain in the north of the village in order to escape the insect attack. rijs will be influenced by β1 and β5 ; thus β1 =β5 =0.5. In the second phase, people selected to live near the river due to increasing improvement of productivity. rijs will be influenced by β2 and β5 accordingly, thus β2 =β5 =0.5. In the third phase, people began to aggregate their dwellings near the road developed in the second phase owing to flourishing of trade, making the center of the village an important factor in the process of spatial evolution. Therefore, rijs will be influenced by β3 , β4 and β5 ; thus β3 =β5 =0.3, while β4 =0.4.
2.5. Simulation of random process
Although we can roughly analyze the process of spatial evolution of Xi-di village according to the historic maps, the real process of spatial evolution will undoubtedly be full of randomness, especially in the early stage of development. In complex systems, random behavior is also an important characteristic factor influencing the pattern of global structure. Randomness is a condition implying arbitrary decision making. In the computer simulation, randomness pertains to the addition of a degree of “noise” to decision making, implying some variety or heterogeneity of preferences on the part of those making decisions (Batty, 2004 ).
In the cell-space modeling, the Monte Carlo algorithm is used to simulate the random processes of conversion. RePast has automated Monte Carlo simulation framework.2 It can produce a random number between 0 and 1. The random number can be compared with the transition probability of the cellular space, which is also between 0 and 1. If the random number is smaller than the probability, the cellular space is converted to developed land; otherwise, another cellular space is selected randomly. The Monte Carlo algorithm may imply that developers respond to land supply opportunities that follow a random pattern and consider the local and global suitability of opportunities as they arise (Wu and Webster, 1998 ).
3. Simulation platform of the spatial evolution
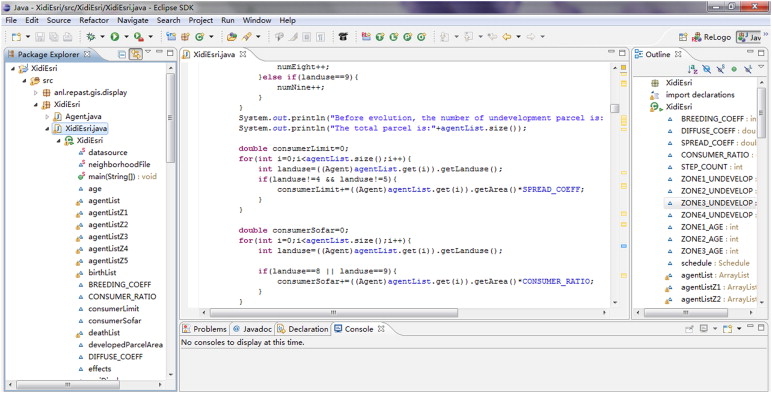
In the simulation of spatial evolution of this village, we build the cell-space model integrated with GIS on the RePast platform.2 RePast is a popular platform of agent-based modeling. It is an extensible framework for agent simulation created by the Social Science Research Computing at the University of Chicago. RePast with GIS support is based on the geography projection. A geography is essentially a space where agents are associated with a spatial geometry (polygon, point, etc). The agents are stored by type in layers within the geography, and agents of the same type must have the same geometry. The geography can be queried spatially to return a result with all the agents within some particular area. When a geography is displayed, the agents are likewise displayed in a typical GIS fashion and represented by their associated geometries. It uses Geotools and the Java Topology Suite extensively for its GIS support. The RePast actions tab will show the model parameters in the running processes of simulation. The three programming languages supported by RePast are JAVA, PYTHON and NET. For this study, JAVA, which can edit the code in Eclipse Figure 5 ; Figure 6 , is selected as the programming language.
|
|
|
Figure 5. RePast programming environment of Eclipse.
|
|
|
|
Figure 6. Display window of the programming run.
|
4. The fruits of simulation
4.1. Phases of development based on historic materials
In order to build the spatial evolution model of Xi-di village, we have to know its development history from historic maps or relative materials, which can be divided into four phases covering nearly one thousand years. The first phase (A.D. 1100–1300) is the establishment phase of the village, characterized by its ancient residents living around the Chengjiali Mountain as well as stochastic distribution of settlements without any tangible road system. The second phase (A.D. 1300–1600) is the development phase of the village, with the spatial evolution feature of people living near the Qianbian River running through the village from north to south and at the same time abandoning their dwellings around the mountain. The main road of the village was also developed during this period. The third phase (A.D. 1600–1900) witnessed the flourishing of the village, with its space form gradually developed as a “boat” shape. The population also grew rapidly in this phase. The fourth phase (after 1900 till 2000) is the decline and revival period of the village. Important buildings were demolished or razed because of the declining trend of trading business. Many villagers left the village for a living, leading to a prompt population decrease. Beginning in the 1980s, the emerging development of tourism propelled population and economic growth, signaling the revival phase of the village.
4.2. Integration with the regional model
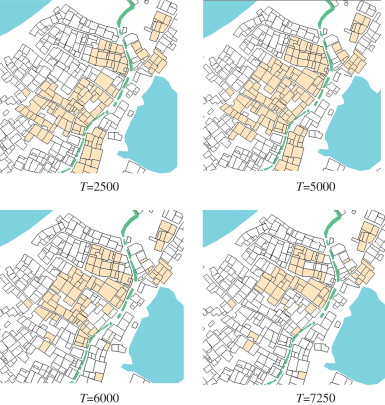
The cell-space model can be used to explain urban development according to the principles of self-organization, in which large-scale urban structure evolves from local decision making processes (Couclelis, 1985 ). However, the global pattern of urban form is unlikely to result only from local decision making processes alone. Ward (2003) suggests that a regional scale optimization model can be integrated into a local scale CA model (Ward et al., 2003 ). From historic materials relating Xi-di village, it can be seen that, to a large extent, its space structure was determined by the social and consanguineous patterns (Figure 7) . Our model aims to be characterized by and capable of transformation from one phase to another when the growth rate of the system exceeds a critical high or drops below a critical low value. The method refers to the Clarke case (1997), which is a successful model for the historical development of the San Francisco Bay and Washington, DC, areas (Clarke et al., 1997 ).
|
|
|
Figure 7. Pictures of simulation every 100 iterations.
|
We define four different types of space growth in the modeling. The critical value controls the transformation of the different types. The parameter of the critical value can be modified to allow specialists to test the results of space transformation in the simulation process.
- Mod1: spontaneous local growth
Spontaneous local growth occurs when the land use falls close enough to the seed cells, simulating the influence of urban area on their surroundings;
- Mod2: mountain-influenced growth
Mountain-influenced growth occurs when land use is near the mountain, simulating the influence of the ancient residents who lived around the mountain in order to avoid flooding and insect/pest infestation during the early stage;
- Mod3: river-influenced growth
River-influenced growth encourages undeveloped cells to develop along the river, simulating the development period of this ancient village;
- Mod4: road-influenced growth
Road-influenced growth encourages undeveloped cells to develop along the road, simulating the period of trade booming phase.
4.3. Calibration of the model
Firstly, the digital topographic map of Xi-di village produced in 2004 is exported from AutoCAD to ArcGIS9.3. Then, the data of properties are encoded as the polygons of geometry. Finally, we use GeoDa to generate the neighborhood list of polygons, and run the program in Eclipse. In the simulation, the calibration of the model is a necessary step. In the beginning, the control parameter is set from the initial conditions and is undetermined, the result of which is tested through the running of the program. If it can represent the land use transformation consistently in accordance with the historic maps, the parameter can be determined. If not, we will adjust it until it fits the model. Since the remotely sensed imagery of the village is not available, and the aerial photograph is the only imagery resource, the simulation of the processes of spatial evolution has to be built on the historic maps and materials. Defining the parameter accurately will be difficult and the determination of control parameters inexplicit.
5. Conclusions
Xi-di village is one of the significant representatives of traditional settlements in China. The process of its spatial evolution is from the bottom up and influenced by the sense of identity of traditional clan. The kin is another factor affecting the distribution of its residences. All the factors forming simple rules in selecting the residential sites are considered. The CA modeling is suitable for simulating the process of space development because the process is diffused gradually from the center of the village, in which no top-down planning or steering of local government is involved. The CA is the type of model that can simulate processes where local action generates global order, and the global or centralized order “emerges” as a consequence of applying local or decentralized rules embodied in local processes. The space morphology is the result of this emergence. From this case, we know that the coherence of urban form can be understood from the perspective of the theory of complex interacting systems. Complex large-scale wholes are assembled from tightly interacting subunits on many different levels of scale, in a hierarchy following the natural structure of materials (Salingaros, 2000 ).
The weak point of our modeling is the lack of relevant materials, especially the remotely sensed imagery of the village every several years. Thus, the model cannot be calibrated accurately. In future, if more information or real maps of its space development become available, the model will serve as an effective tool for forecasting space changes, which are always unanticipated spatial outcomes, through computer simulation.
Acknowledgments
This research was sponsored by the National Natural Science Foundation of China (Grant no.50878044 ). We greatly acknowledge the support from Prof. Jiyue Chen, the well-known specialist on ancient architecture in Anhui province, who provided us with valuable advice and historic materials about the ancient Xi-di village.
References
- Author, 1999 W.B. Author; Complexity and the economy; Science, 284 (1999), pp. 107–109
- Batty, 2004 M. Batty; Cities and Complexity; The MIT Press, Cambridge, Massachusetts, London, England (2004)
- Clarke et al., 1997 K.C. Clarke, S. Hoppen, L. Gaydos; A self-modifying cellular automaton model of historical urbanization in the San Francisco Bay area; Environment and Planning B: Planning and Design, 24 (1997), pp. 247–261
- Couclelis, 1985 H. Couclelis; Cellular worlds: a framework for modeling micro-macro dynamics; Environment and Planning A, 17 (1985), pp. 585–596
- Duan, 2006 J. Duan; Urban Space, The SEU Press, Nanjing (2006) p. 42, p. 248
- Portugali, 1999 J. Portugali; Self-Organization and the City; Springer (1999)
- Rocha, 1999 Rocha, Luis M., 1999. BITS: Complex Systems Modeling: Using Metaphors from Nature in Simulation and Scientific Models.
- Salingaros, 2000 N.A. Salingaros; Complexity and urban coherence; Journal of Urban Design, 5 (2000), pp. 291–316
- Ward et al., 2003 D.P. Ward, A.T. Murray, S.R. Phinn; Integrating spatial optimization and cellular automata for evaluating urban change; The Annals of Regional Science, 37 (2003), pp. 131–148
- Wolfram, 2002 S. Wolfram; A New Kind of Science; Wolfram Media. Inc (2002)
- Wu and Webster, 1998 F. Wu, C.J. Webster; Simulation of land development through the integration of cellular automata and multicriteria evaluation; Environment and Planning B, 25 (1998), pp. 103–126
Notes
1. Refer to http://www.csiss.org/clearinghouse/GeoDa/ .
2. Refer to http://repast.sourceforge.net/ .
Document information
Published on 12/05/17
Submitted on 12/05/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?