Probabilistic dynamic analysis of steel buildings with long duration earthquakes

Resumen

El análisis probabilista del comportamiento sísmico de una estructura requiere cuantificar las incertidumbres de las variables y parámetros involucrados, incluyendo la acción sísmica y las propiedades mecánicas de sus elementos. En este artículo se analiza el comportamiento sísmico de edificios de acero bajos, medianos y altos, sometidos a las acciones sísmicas de larga duración probables de la Ciudad de México. El análisis se efectúa bajo una perspectiva probabilista. Las acciones sísmicas se han seleccionado de forma que sean compatibles con los espectros de diseño, para suelos blandos y sismos de larga duración de esta área. Los análisis dinámicos, se llevan a cabo usando simulaciones Monte Carlo. La resistencia y la ductilidad de vigas y columnas se consideran como variables aleatorias; las acciones sísmicas también se consideran de forma probabilista. El daño esperado es evaluado con el índice de Park y Ang. Los resultados muestran que las incertidumbres esperadas en la respuesta son significativas, siendo la aleatoriedad de la acción sísmica la principal causa. De la comparación entre los valores medianos del enfoque probabilista con los del caso determinista se observa una buena consistencia de los resultados correspondientes a edificios de baja y mediana altura, siendo menor en el comportamiento no lineal de los edificios altos. Los edificios bajos y medianos analizados tienen un comportamiento adecuado antes las acciones sísmicas de la zona de estudio, pero los edificios altos tienen un mayor riesgo sísmico y podrían tener daños leves o moderados. Se concluye que el enfoque probabilista proporciona información más rica sobre la respuesta estructural.

Palabras clave: Análisis dinámico no lineal; edificios de acero; índice de daño de Park y Ang; Método Monte Carlo; incertidumbre.

Abstract

The probabilistic analysis of the seismic performance of a structure requires quantifying the uncertainties of the involved variables and parameters, including the seismic action and mechanical properties of its elements. In this article, the seismic performance of high-rise, mid-rise and low-rise of steel buildings, subjected to long duration seismic actions like those of Mexico City, is analyzed. The analysis is conducted by using a probabilistic approach. The seismic actions are selected to be compatible with the design spectra of the Mexican seismic code for soft soils and long duration earthquakes, characteristic for this region. The dynamic analyses are performed by using Monte Carlo simulations. The strength and ductility of the beams and columns are considered random variables; the seismic actions are also modelled in a probabilistic way. The damage index of Park and Ang is used. The results show that the uncertainties expected in the response are significant, being the randomness of the seismic action the main cause. From the comparison between the mean values of the probabilistic approach and those corresponding to the deterministic case, a good consistency of the result obtained for low-rise and mid-rise buildings is observed. Nevertheless, the consistency is lower in the case of high-rise buildings. The analyzed low-rise and mid-rise buildings show a good seismic performance to seismic actions, but the high-rise buildings show slight or moderate damage. It is concluded that the probabilistic approach provides a more complete information on the structural response.

1. Introducción

Para la evaluación del daño y riesgo sísmico en una estructura, el método del análisis dinámico no lineal (ADNL) ha mostrado ser el que proporciona resultados más parecidos con el comportamiento real. En el ADNL, las acciones sísmicas son descritas mediante acelerogramas reales o sintéticos. Además, a partir de la respuesta no lineal del sistema, es posible calcular el grado de daño en los elementos considerando la degradación de la resistencia y la energía disipada, entre otras variables. Si el cálculo dinámico se hace de forma incremental (Incremental Dynamic Analysis, IDA) [1], es posible obtener curvas de daño que relacionan el daño con la variable incrementada que, generalmente, es la intensidad de la acción sísmica como, por ejemplo, la aceleración máxima del suelo (PGA). El IDA ha mostrado ser la herramienta que mejor representa el comportamiento de la estructura sometida a acciones sísmicas conllevando, como contrapartida, un coste computacional alto.

El análisis estructural debe tener en cuenta que las variables que intervienen tienen grandes incertidumbres que pueden ser de dos tipos: aleatorias y epistémicas [2,3]. Las incertidumbres epistémicas se deben a la falta de conocimiento sobre el modelo o parámetro; las incertidumbres aleatorias provienen de las imprecisiones en las medidas. En cuanto a las acciones sísmicas, las incertidumbres aleatorias están asociadas a los movimientos esperados del terreno y, por lo tanto, no se pueden controlar; pero, sin duda, su influencia en la respuesta puede ser estimada mediante enfoques probabilistas. En cuanto a las estructuras, las incertidumbres aleatorias se deben a la falta de conocimiento preciso de sus propiedades mecánicas y geométricas. La respuesta no lineal de las estructuras sometidas a terremotos, que también tiene grandes incertidumbres, depende del comportamiento de los elementos estructurales, así como de la acción. Las incertidumbres en las propiedades de los materiales pueden reducirse realizando pruebas para determinar sus propiedades. Las normas de diseño sísmico consideran las incertidumbres recomendando realizar cálculos deterministas con valores reducidos de la resistencia de los materiales y aumentando las acciones mediante factores de seguridad. Sin embargo, en los procesos no lineales, los niveles de confianza asociados a la respuesta pueden ser diferentes de los asociados a las variables de entrada [4,5]. En la última década se ha hecho énfasis en la importancia de hacer uso del IDA desde una perspectiva probabilística [3]. Este enfoque ha sido utilizado en estudios recientes mediante el uso del método de Monte Carlo [6–11], lo que permite obtener una visión global del desempeño esperado de las estructuras y proporcionar resultados controlando la fiabilidad. Sin embargo, conviene recordar que para estos análisis es necesario llevar a cabo un número significativo de ADNL, lo que supone un alto coste computacional.

El comportamiento de estructuras de acero sometidas a acciones dinámicas ha sido estudiado por Vamvatsikos y Fragiadakis [12] que investigaron el efecto de las incertidumbres en los pórticos de acero concluyendo que las incertidumbres de los parámetros tienen una importante contribución a la dispersión de la respuesta estructural. Ibarra y Krawinkler [13] establecieron que el efecto del deterioro en el modelo histérico tiene un impacto significativo en la predicción del colapso para sistemas de un grado de libertad. Por esta razón es recomendable abordar el estudio del comportamiento desempeño de las estructuras de acero desde un enfoque probabilista, usando modelos histéricos que permitan incorporar las incertidumbres en la capacidad de los elementos. En este sentido es de mucho interés el modelo Ibarra-Medina-Krawinkler (IMK) modificado [14–18] que detalla las relaciones necesarias para modelizar el deterioro cíclico de la resistencia a flexión y de la rigidez de elementos estructurales de acero. Estas relaciones quedan definidas por ecuaciones empíricas multi-variables desarrolladas con base en un estudio experimental de 300 vigas de acero de alas anchas [15]. La evaluación del daño y riesgo sísmico de edificios, encuentran una aplicación en los estudios de riesgo a nivel urbano [19–22].

En este artículo se propone evaluar el comportamiento sísmico de edificios acero, sometidas a acciones sísmicas similares a las esperadas en la Ciudad de México y considerando las incertidumbres en las propiedades mecánicas de las vigas y columnas. Las acciones sísmicas también son abordadas desde un enfoque probabilista. Para la evaluación de la vulnerabilidad y daño, se utiliza el análisis dinámico incremental, IDA, con el enfoque probabilístico proporcionado por el método de Monte Carlo. También se utiliza el algoritmo de simulación Latin Hypercube Sampling (LHS), que permite optimizar el número de muestras usadas. Los resultados se comparan con los obtenidos mediante un enfoque determinista clásico, para analizar y cuantificar los niveles de incertidumbre cuando un fenómeno altamente aleatorio se reduce a uno determinista.

2. Modelos estructurales

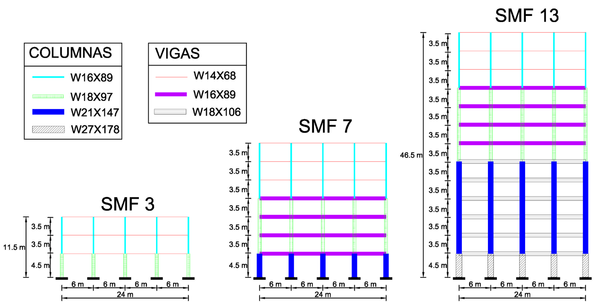
El estudio de la vulnerabilidad de los edificios de acero bajo una perspectiva probabilista se realiza considerando 3 tipos de edificios: de gran altura (13 pisos), de mediana altura (7 pisos) y de baja altura (3 pisos). Todos tienen estructuras con pórticos especiales resistentes a momento (SMF, abreviatura usada en el ANSI/AISC 341-10 para estas tipologías), con vigas y columnas de secciones tipo W del ANSI/AISC 341-10 (Sección tipo I) con conexiones totalmente rígidas (FR) precalificas [23]. Los edificios se han diseñado para uso de oficinas utilizando NTC-DF [24] y ANSI/AISC 341-10 [25] para la zona sísmica IIIb (suelos blandos) de la Ciudad de México y satisfacen el criterio ANSI/AISC 341-10 de columna fuerte-viga débil. Tienen una planta rectangular de 3 vanos de 5 m en la dirección transversal y 4 vanos de 6 m en la dirección longitudinal. En los análisis realizados se han considerado los pórticos centrales en la dirección longitudinal de los edificios. Sus 3 modelos 2-D (SMF 3, SMF 7 y SMF 13) se muestran en la Figura 1.

Figura 1. Modelos 2D de los edificios arquetipo estudiados

Los ADNL se realizaron con el software Ruaumoko 2D [26]. El peso de la estructura, así como el de los acabados arquitectónicos e instalaciones fueron considerados como cargas muertas (CM), mientras que la carga viva (CV) es la establecida en NTC-DF [24] para uso de oficinas. La carga gravitacional considerada en los análisis no lineales queda establecida como 1.0 CM + 0.2 CV [27]. Las vigas y columnas se modelizan con elementos de barra con rotulas plásticas en sus extremos. Las rotulas plásticas siguen la ley de histéresis bi-lineal con endurecimiento y degradación de la resistencia con base a la ductilidad (Appendix A - Ruaumoko 2D) [26]. Para esta tipología de edificios, los mayores daños son debidos a los efectos de los momentos y cortantes en los extremos de los elementos. Por esta razón, las limitaciones del modelo analítico adoptado, que sólo es capaz de reproducir el fallo por momentos y cortante y que no considera la interacción entre el momento flector y la fuerza axial, no afecta los resultados. La interacción de la superficie de fluencia se define para las columnas y vigas por el diagrama momento flector - rotación. Los edificios se suponen empotradas en la base y las losas se consideran rígidas en la dirección del análisis. El efecto P-Δ fue incluido. Las zonas panel fueron modeladas con la rigidez rotacional en las conexiones, obtenida con el modelo propuesto por Krawinkler [28] y presentado en FEMA 355C [29]. En todos los casos se consideró un 2% de amortiguamiento Rayleigh [30] para el primero y último modo de vibración considerado. Los periodos fundamentales, Ts, de los modelos fueron de 0.63 s para el edificio SMF3, 1.22 s para SMF7 y 1.92 s para SMF13.

3. Relación resistencia-ductilidad

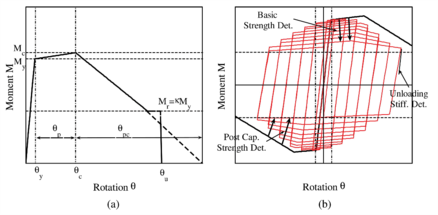
El diagrama de momento flector – rotación (M-) en las vigas y columnas fue definido con base en la relación resistencia ductilidad del modelo IMK modificado [17,18]. Este modelo establece límites de resistencia basados en su curva envolvente (Figura 2a) y define las características del comportamiento histerético considerando el endurecimiento y la degradación de los elementos (Figura 2b). De este modo, el desempeño de los elementos queda definido por 3 parámetros de resistencia (M_y=momento de fluencia efectivo, M_c=momento límite máximo o relación post-fluencia, M_c/M_y, y momento residual M_r=k•M_y) y por 4 parámetros de deformación (_y=rotación de fluencia, _p=pre-límite de rotación plástica, _pc= post-límite de rotación plástica y _u=rotación última).

La resistencia de las secciones estructurales es definida por los parámetros de fuerzas del modelo IMK, las cuales pueden ser obtenidas con sólo dos propiedades: el módulo plástico, Z, y la resistencia a fluencia efectiva, f_y. Los 3 parámetros son obtenidos, de acuerdo a Lignos y Krawinkler [16], mediante las siguientes ecuaciones:

${\textstyle {M}_{y}=1.17\cdot Z\cdot {f}_{y}}$	(1)
${\textstyle {M}_{c}=1.11\cdot {M}_{y}}$	(2)
${\textstyle {M}_{r}=0.4\cdot {M}_{y}}$	(3)

Figura 2. Modelo modificado IMK; (a) curva envolvente; (b) definición de modos básicos de deterioro cíclico [17]

La ductilidad en las secciones estructurales se define mediante las variables de deformación del modelo IMK. _y se determina con la ecuación (4), _p y _pc se define con las ecuaciones empíricas multi-varibles (5) y (6) desarrolladas por Lignos & Krawinkler [15] para secciones W y, finalmente, _u se define mediante la ecuación (7), de acuerdo a la recomendación del PEER/ATC 72-1 [27]

${\theta }_{y}={\frac {{(M}_{y}}{{k}_{o})/L}}={\frac {({M}_{y}}{6\cdot E\cdot I)/L}}$	(4)
${\theta }_{p}=0.0865\cdot {\left({\frac {h}{{t}_{w}}}\right)}^{-0.365}\cdot {\left({\frac {{b}_{f}}{2\cdot {t}_{f}}}\right)}^{-0.140}\cdot {\left({\frac {L}{d}}\right)}^{0.340}\cdot {\left({\frac {{c}_{unit}^{1}\cdot d}{533}}\right)}^{-0.721}\cdot {\left({\frac {{c}_{unit}^{2}\cdot {f}_{y}}{355}}\right)}^{-0.721}\,\,{\sigma }_{In}=$$0.32$	(5)
${\theta }_{pc}=5.63\cdot {\left({\frac {h}{{t}_{w}}}\right)}^{-0.565}\cdot {\left({\frac {{b}_{f}}{2\cdot {t}_{f}}}\right)}^{-0.800}\cdot {\left({\frac {{c}_{unit}^{1}\cdot d}{533}}\right)}^{-0.280}\cdot {\left({\frac {{c}_{unit}^{2}\cdot {f}_{y}}{355}}\right)}^{-0.430}\quad {\sigma }_{In}=$$0.25$	(6)
${\theta }_{u}=1.5\cdot \left({\theta }_{y}+{\theta }_{p}\right)$	(7)

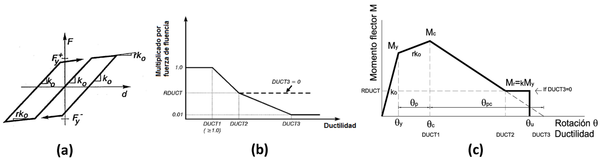
donde k_o es la rigidez elástica inicial; E es el módulo de elasticidad; I es la inercia; c¹_unit y c²_unit son factores de conversión de unidades; h/t_w es la relación de altura y espesor del alma de la sección; L/d es la relación de vano con la altura de la sección; b_f/2t_f es la relación de anchura y espesor de las alas de la sección y σ_In es la desviación estándar del ajuste lognormal de los datos experimentales. Mediante los parámetros del modelo IMK modificado, se define la ley de histéresis bi-lineal con endurecimiento (Figura 3a) y degradación de la resistencia con base en la ductilidad (Figura 3b) utilizada en la modelación de los elementos estructurales con Ruaumoko 2D

$r={\frac {\left[{\frac {{M}_{c}-{M}_{y}}{{\theta }_{p}}}\,\right]}{{k}_{o}}}$	(8)
$DUCT1={\frac {{\theta }_{y}+{\theta }_{p}}{{\theta }_{y}}}$	(9)
$DUCT2={\frac {{\theta }_{y}+{\theta }_{p}+\left[{\frac {{\theta }_{pc}({M}_{c}-{M}_{r})}{{M}_{c}}}\right]}{{\theta }_{y}}}$	(10)
$DUCT3={\frac {{\theta }_{y}+{\theta }_{p}+{\theta }_{pc}}{{\theta }_{y}}}$	(11)

En estas ecuaciones, r define el endurecimiento post-fluencia; DUCT1, la ductilidad donde inicia la degradación de la fuerza; DUCT2, la ductilidad donde acaba la degradación de la fuerza y DUCT3, la ductilidad donde la fuerza máxima se ha degradado hasta su 1%. DUCT3 puede tomar el valor cero, lo que indica que la fuerza se debe mantener constante desde DUCT2; es decir cuando el elemento tenga una ductilidad mayor a DUCT2, se considerará que, para esa rotación el elemento tendrá un valor de resistencia igual a M_r en la regla de histéresis. Es necesario definir la constante RDUCT, que representa el valor de k del modelo IMK modificado que, para este estudio, se considera de 0.4. En la Figura 3c se muestra el modelo de fuerza-deformación utilizado con base en los parámetros del modelo IMK modificado.

Figura 3. (a) Ley de histéresis bilineal con endurecimiento; (b) modelo de degradación de la regla de histéresis con base de la ductilidad usado por Ruaumoko 2D [26]; (c) modelo de momento flector - rotación utilizado con base en el modelo IMK modificado

4. Variables probabilistas

Se considera que la masa y el amortiguamiento son deterministas y que sólo la relación resistencia y la ductilidad en los elementos estructurarles tienen incertidumbres que requieren un tratamiento probabilista. En el caso de la resistencia, el módulo plástico, Z, y la inercia, I, se consideran de forma determinista, ya que sus variaciones son muy pequeñas, menores que el 2%, y su influencia no tiene un impacto importante en la respuesta final [31]. Solo la fuerza de fluencia, f_y, fue usada como una variable aleatoria en las simulaciones LHS considerándose una distribución normal. Es importante mencionar que la variación del módulo de elasticidad, E, está relacionada directamente con la variación en el f_y. En el caso de la ductilidad, el parámetro _y es considerado dependiente del f_y, por lo que sólo los parámetros _p y _pc son considerados como variables aleatorias en las simulaciones, con una distribución lognormal. El parámetro _u depende directamente de _y y _p. El valor medio, μ, la desviación estándar, σ, o el coeficiente de variación, COV, y las distribuciones de probabilidades supuestas para las variables de resistencia y ductilidad, se muestran en la Tabla 1. Para las simulaciones realizadas utilizando el LHS, tanto la distribución normal de f_y como la distribución lognormal de _p y _pc fueron truncadas en ambos extremos, estableciéndose los limites inferior y superior por el valor medio ± 2 veces su desviación estándar ( ${\textstyle \mu }$ ±2 ${\textstyle \sigma }$ ). El propósito de este truncamiento es evitar una subestimación o sobreestimación de las capacidades de los elementos, es decir, evitar obtener muestras sin significado físico.

Tabla 1. Propiedades probabilistas de las variables de resistencia y ductilidad.

Tipo	Variable	Media (${\textstyle \mu }$)	Desviación estándar (${\textstyle \sigma }$)	Función	Límite superior	Límite inferior
Resistencia	${\textstyle f_{y}}$	375.76 Mpa*	26.68 (COV=0.071*)	Distribución normal	429.14 Mpa	322.4 Mpa
Rotación	${\textstyle \theta _{p}}$	${\textstyle \theta _{pEc.2}}$	0.32+	Distribución Lognormal	${\textstyle \theta _{pEc.2}+2\sigma }$	${\textstyle \theta _{pEc.2}-2\sigma }$
Rotación	${\textstyle \theta _{pc}}$	${\textstyle \theta _{pcEc.3}}$	0.25+	Distribución Lognormal	${\textstyle \theta _{pcEc.3}+2\sigma }$	${\textstyle \theta _{pcEc.3}-2\sigma }$

* Basado en el informe estadístico de Lignos y Krawinkler [16] sobre pruebas de la fuerza de fluencia en patines y almas de acero grado A572.

⁺La desviación estándar del ajuste lognormal de los datos experimentales de las ecs. (5) y (6), es utilizada como desviación estándar en la distribución lognormal de las rotaciones θ_pyθ_pc. enel método LHS.

Se consideran dos tipos de correlaciones: intra e inter-elemento. La correlación intra-elemento viene dada por la relación entre los tres parámetros simulados para una misma rotula plástica; estas correlaciones derivan de las ecuaciones (5) y (6) [16,17]. La correlación intra-elemento se define en la Tabla 2. La correlación inter-elemento se atribuye a la calidad de mano de obra y del material entre las diferentes secciones de los elementos. Idota et al. [32] y Kazantzi et al. [10] propusieron un valor de 0.65 para la fuerza de fluencia en vigas y columnas del mismo lote de producción. Sobre esta base se propone aquí una correlación entre elementos de 0.65 para secciones del mismo tipo y una correlación nula para secciones diferentes.

Tabla 2 . Correlación intra-elemento para las variables aleatorias de vigas y columnas.

	${\textstyle {\bf {f}}_{y}}$	${\textstyle {\boldsymbol {\theta }}_{p}}$	${\textstyle {\boldsymbol {\theta }}_{pc}}$
${\textstyle {\bf {f}}_{y}}$	1	0	0
${\textstyle {\boldsymbol {\theta }}_{p}}$	0	1	0.69
${\textstyle {\boldsymbol {\theta }}_{pc}}$	0	0.69	1

Para representar mejor la aleatoriedad del problema para cada elemento estructural (columna o viga), se genera una muestra aleatoria de los tres parámetros utilizados (f_y, θ_p y θ_pc). Con éstas, se calculan la resistencia y ductilidad en las rótulas de cada elemento. Se supone que las rótulas son iguales en ambos extremos de los elementos. Por lo tanto, el modelo de 3 pisos con 27 elementos (15 columnas y 12 vigas) tiene 81 variables aleatorias; el modelo del edificio de 7 pisos con 63 elementos (35 columnas y 28 vigas) consta de 189 variables aleatorias y el modelo de 13 pisos con 117 elementos (65 columnas y 52 vigas) tiene 351 variables aleatorias. Con el fin de evaluar el comportamiento sísmico de estos tres edificios considerando un enfoque probabilista, se realizan 200 ADNL para cada modelo estructural. Este número de ADNL obedece a un análisis de sensibilidad basado en obtener mediante análisis estático no lineal, las curvas de capacidad de 1000 modelos probabilistas de cada uno de los 3 modelos estructurales; de manera que se obtuvo el valor medio y desviación estándar considerando 1000 curvas y 200 curvas de forma aleatoria, observando que con 200 curvas los valores medios y desviaciones estándar en todos los 3 casos eran de valores similares al de las 1000 curvas. Esto se atribuye a que el método LHS usado, a diferencia del método Monte Carlo sin LHS, hace un muestreo estratificado sin reemplazo, es decir evita duplicar combinaciones de casos, por lo que con menos muestras se puede obtener una respuesta adecuada.

5. Análisis dinámico incremental probabilista

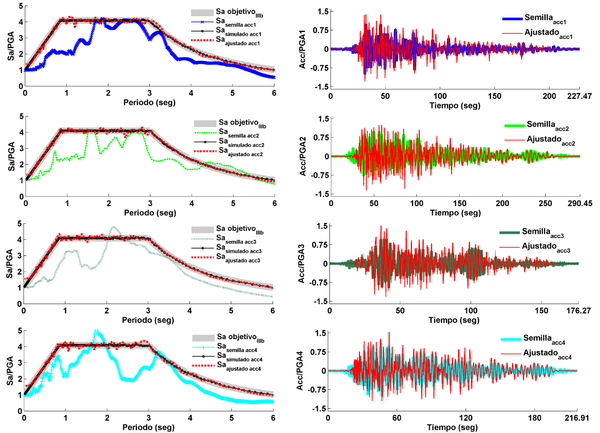
Para el análisis dinámico incremental, IDA, probabilista, se necesita un conjunto de acelerogramas que representen adecuadamente las características de las acciones sísmicas esperadas o de diseño en la zona de estudio considerando las incertidumbres, que son de gran importancia para la evaluación de la respuesta sísmica [33–35]. El primer paso para obtener este conjunto de acelerogramas ha consistido en generar un conjunto de espectros de respuesta aleatorios por medio de simulaciones de LHS de forma que cumplan las tres condiciones siguientes: i) el valor medio coincide con un espectro objetivo; ii) la desviación estándar en cada período debe ser un valor predefinido; y iii) las ordenadas espectrales están correlacionados de tal manera que son realistas. En un segundo paso se ha usa la técnica de ajuste espectral [36] para hacer coincidir el espectro de respuesta de un acelerograma real con cada uno de los espectros simulados. Se ha obtenido así un conjunto de acelerogramas que cumple las siguientes condiciones: i) el espectro medio se ajusta bien al espectro objetivo, ii) el conjunto de espectros obtenidos tiene una desviación estándar predefinida; y iii) los acelerogramas son representativos de las acciones sísmicas esperadas en la zona, ya que están representadas por acelerogramas semilla seleccionado. En este estudio se ha tomado como espectro objetivo el espectro de diseño para la zona IIIb de la NTC-DF [24] de la Ciudad de México. La desviación estándar se ha establecido en el 5% para períodos de 0 a 2 s, ya que es la banda donde se encuentran los períodos de los edificios estudiados, y en el 10% para períodos de más de 2 s. En cuanto a los acelerogramas semilla utilizados, se han seleccionado con el método propuesto por Vargas et al. [7] aplicado a una base de datos de 2554 acelerogramas (tres componentes) registrados en el área de la Ciudad de México. Esta base de datos de acelerogramas fue analizada anteriormente por Díaz et al. [37] . De esta manera, se seleccionaron cuatro acelerogramas de larga duración, ya que 4 es el número mínimo de acelerogramas que la NTC-DF 2004 propone se usen en el análisis dinámico con espectros de respuesta compatibles con el espectro objetivo. La Tabla 3 muestra las características de los acelerogramas seleccionados y los terremotos correspondientes. La Figura 4 muestra el espectro de respuesta objetivo, los acelerogramas semilla seleccionados y sus espectros de respuesta. Para cada acelerograma semilla, se utiliza la técnica del ajuste espectral para obtener 5 nuevos acelerogramas que cumplan las tres condiciones probabilistas descritas anteriormente. De esta manera, se han obtenido 20 acelerogramas, que se han considerado adecuados y suficientes para abordar el enfoque probabilista. Obsérvese cómo la aleatoriedad tanto de las aceleraciones espectrales para los diferentes periodos como, en particular, para los PGA de los sismos generados, se va a conservar automáticamente, cuando estas acciones sean incrementadas con el IDA mediante incrementos de los valores medianos del PGA, y en consecuencia conservando las distribuciones de probabilidad con diferentes valores medianos, pero con las mismas dispersiones predefinidas. Los espectros de respuesta de los 20 acelerogramas compatibles se muestran en la Figura 5 y cada acelerograma es seleccionado de forma aleatoria en cada análisis IDA probabilista. Para el caso determinista se usaron los 4 acelerogramas ajustados mostrados en la Figura 4, de manera que con sus 4 respuestas se genera una curva con sus valores medianos, que representara para este estudio el caso determinista. Si bien se reconoce que en la Ciudad de México se tienen una amenaza sísmica máximas de PGA de 0.165g [24], en este estudio, dado que se quiere analizar el comportamiento sísmico hasta el colapso de los edificios de acero, los acelerogramas son escalados hasta magnitudes muy superiores (del orden de 1 g).

Tabla 3 . Principales características de los 4 sismos seleccionados por su compatibilidad con el espectro de la zona IIIb.

Acc	Estación	Fecha	Duración (seg)	Epicentro			Magnitud (Mw)	Comp.	PGA (cm/s2)	Distancia Epicentral (km)	Azimut Eta-Epi
				Latitud	Longitud	Profundidad (Km)
1	TH35	20/03/2012	227.47	16.25 N	98.52 W	16	7.4	S00E	49.6	340.58	171.34
2	AE02	30/09/1999	290.45	15.95 N	97.03 W	16	7.5	N90W	21.3	442.48	150.64
3	PCSE	11/01/1997	176.27	17.91 N	103.04 W	16	6.5	S65W	14.6	442.84	248.35
4	DM12	14/09/1995	216.91	16.31 N	98.88 W	22	7.3	N00E	19.3	347.79	176.20

Figura 4. Espectro objetivo y espectros de respuesta de los acelerogramas semilla y ajustados (izquierda); y acelerogramas semilla y ajustados (derecha).

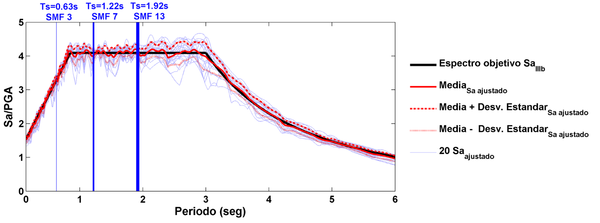
Figura 5. Espectros de respuesta de los 20 acelerogramas ajustados, su media y desviación estándar y periodo fundamental de los edificios

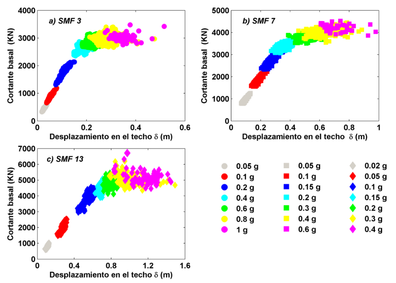
De esta forma se han obtenido relaciones probabilistas PGA-desplazamiento en techo y PGA-cortante en la base. La Figura 6 muestra estas relaciones para diferentes PGA crecientes. Se observa que con el aumento del PGA, cada nube de puntos pierde su organización, aumentando su dispersión de forma significativa. Es decir, cuando el PGA aumenta, la incertidumbre en la respuesta estructural inducida por la incertidumbre en las propiedades mecánicas de los materiales también aumenta.

Figura 6. Relación PGA con desplazamiento en el techo y cortante basal de los edificios

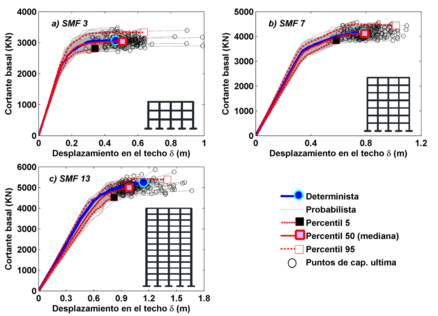
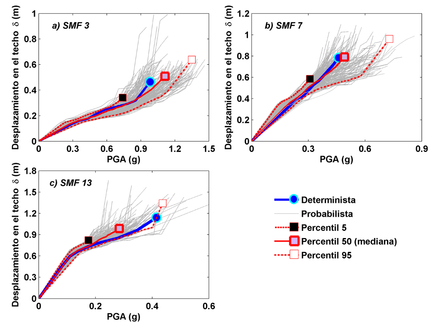
Así se han obtenido curvas de capacidad dinámicas determinista y probabilistas; del conjunto de curvas probabilistas se muestran 3 curvas correspondientes a los percentiles 5, 50 (mediana) y 95. En la Figura 7 se muestran las curvas de capacidad dinámicas obtenidas. Se observa cómo la curva mediana tiene una buena coherencia con el caso determinista para los modelos SMF 3 y SMF 7, pero la concordancia es menor en el caso SMF 13. Los coeficientes de variación (COV) de los Du probabilistas son relativamente bajos (COV_SMF3=0.209, COV_SMF7=0.181 y COV_SMF13=0.179), lo que indica que el Du medio de los análisis representa bien el desplazamiento de colapso. La Figura 8 muestra la relación PGA-desplazamiento en el techo determinista, probabilista y sus respectivas curvas percentiles. Los rangos de PGA disminuyen con el incremento de la altura de los edificios, es decir, para la mediana probabilista el SMF 3 tienen su colapso alrededor de un PGA de 1 g, el SMF 7 alrededor de 0.6 g y el SMF 13 alrededor del 0.4 g. Por lo tanto, para la zona de estudio, los edificios altos tendrían mayores desplazamientos en el techo que los edificios bajos para un mismo PGA. Esto resulta coherente, pues en la Ciudad de México son las estructuras de periodos altos las que están en mayor riesgo sísmico, especialmente por la amplificación de las ondas sísmicas con bajas frecuencias como efecto del suelo blando de esta área.

Figura 7. Curvas de capacidad dinámica deterministas, probabilistas y percentiles de los edificios

Figura 8. Relación PGA-Desplazamiento en azotea deterministas, probabilistas y percentiles de los edificios

Para el análisis del daño esperado se ha elegido el índice de Park y Ang [38] adaptado para estructuras metálicas [39]. El índice de daño global, IDG_{Park yAng}, de las estructuras se obtiene mediante la siguiente ecuación:

${IDG}_{Park\,y\,Ang}=\sum _{i}^{n}{\lambda }_{i}{IDE}_{i\,Park\,y\,Ang\,\,}$

(12)

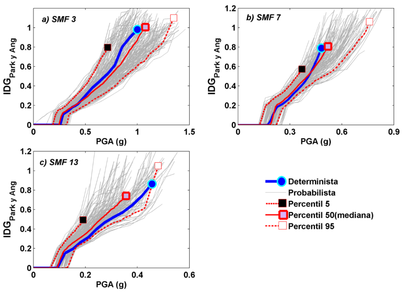
donde IDE_{i Park yAng} es el índice de daño de cada elemento estructural y λ_i es el cociente entre la energía de histéresis disipada por cada elemento y la energía total de histéresis disipada por la estructura. En la Figura 9 se muestra el índice de Park y Ang en función del PGA para los edificios estudiados.

Figura 9. Relación PGA-IDG Park y Ang deterministas, probabilistas y percentiles de los edificios

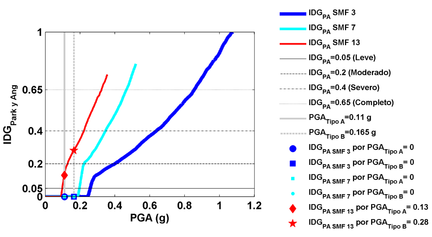
Finalmente, para tener una idea del daño esperado en términos de los 4 estados de daño normalmente usados (1 Leve, 2 Moderado, 3 Grave y 4 completo), se han considerado los umbrales de estos estados tal como se propone en Pujades et al. [11] también en base al índice de daño de Park y Ang. Los valores del IDG_{Park y Ang} respectivamente para estos umbrales son 0.05, 0.2, 0.4 y 0.65 [38,40,41] . Así, teniendo en cuenta que las aceleraciones de diseño en la zona IIIb de acuerdo con la NTC-DF son respectivamente de 0.11g y 0.165 g para estructuras normales (TIPO A=Casa-Habitación, oficinas, etc.) y para estructuras de mayor importancia (TIPO B=Hospitales, escuelas, etc.) [24] puede estimarse el estado de daño esperado para los 3 edificios y para estas aceleraciones de diseño. Los resultados se muestran en la Figura 10. Los edificios fueron diseñados como TIPO A, obsérvese cómo para los edificios SMF 3 (Ts=0.63 seg.) y SMF 7 (Ts=1.22 seg.) no se espera daño, pero para los edificios tipo SMF 13 (Ts=1.92 seg.) podrían darse daños leves. Si se supusiera que los edificios son especiales (TIPO B), el daño esperado para los edificios tipo SMF 3 y SFM 7 también sería nulo, pero los de tipo SMF 13 (edificios relativamente altos) podrían sufrir daño moderado. No conviene perder de vista que las especiales características de México DF con suelos blandos que amplifican las bajas frecuencias, afectan más a los edificios relativamente altos debido a efectos de resonancia.

6. Discusión y conclusiones

En este trabajo se ha presentado y aplicado una metodología para la evaluación sísmica mediante análisis estructural dinámico. El método se ha aplicado de forma determinista y probabilista. El enfoque probabilista permite cuantificar las incertidumbres en la respuesta y en el desempeño de los edificios inducidas por las incertidumbres en sus propiedades mecánicas (resistencia y ductilidad) y en las acciones sísmicas. Las aproximaciones determinista y probabilista se han aplicado a tres tipos de edificios de acero (bajos -3 niveles, de altura intermedia-7 niveles y altos-13 niveles) situados en suelos blandos de la ciudad de México (DF-IIIb). Las acciones sísmicas se han considerado también mediante un enfoque probabilista avanzado, usando acelerogramas seleccionados de acuerdo con la amenaza sísmica de la Ciudad de México y con características de larga duración propia de los registros de esta en la zona. Se ha usado una técnica de ajuste espectral para obtener un conjunto de 20 acelerogramas compatibles con el espectro de diseño de la zona de estudio; vale la pena mencionar que la técnica usada permite el control de error. Las principales conclusiones derivadas de la comparación entre los resultados obtenidos a partir del enfoque determinista clásico y del probabilista son las siguientes: i) El enfoque determinista proporciona resultados adecuados, ya que el análisis determinista usando valores medianos de resistencia-ductilidad de los materiales lleva a resultados comparables con los valores medianos del enfoque probabilistas; la similitud de los resultados con todo es menor para edificios altos. ii) El desplazamiento de daño completo (Du) determinista representa adecuadamente el desplazamiento de colapso de la curva mediana probabilista de los edificios analizados. iii) Los resultados obtenidos muestran que las incertidumbres esperadas en la respuesta son significativas y que su dispersión aumenta al aumentar la intensidad sísmica; debido a que con mayor intensidad sísmica se tienen una mayor incursión en el campo no lineal. Estudios más detallados [42] confirman que la acción sísmica es responsable de la mayor dispersión en la respuesta, siguiendo en importancia la variable fy. La contribución de las dos rotaciones, aunque también significativa, es menor. iv) Los edificios altos han mostrado tener un mayor nivel de daño sísmico para la zona de estudio, lo cual resulta razonable por las amplificaciones que sufren los sismos de largas duraciones en suelos blandos, afectando principalmente a edificios con largos periodos propios de vibración entre 1.5 y 3 segundos. v) Con base en la curva IDG_{Park y Ang} mediana, el comportamiento de los edificios bajos y medianos cumple adecuadamente las condiciones de diseño para el sitio de estudio, sin embargo, los edificios altos podrían tener daños leves o moderados. vi) Finalmente, es importante hacer énfasis en que la evaluación de la vulnerabilidad y del daño sísmico físico, debe considerar el comportamiento no lineal de la estructura, la aleatoriedad de las propiedades mecánicas de los materiales y la incertidumbre asociada a la acción sísmica.

Figura 10. Estimación del daño sísmico esperado en los edificios para la zona de estudio (DF-IIIb).

Agradecimientos

Esta investigación ha sido parcialmente financiada por el Ministerio de Economía y Competitividad (MINECO) del Gobierno de España y por el Fondo Europeo de Desarrollo Regional (FEDER) de la Unión Europea a través de los proyectos de investigación de referencia: CGL2011-23621 y CGL2015-65913-P (MINECO / FEDER, UE). El primer autor dispone de una beca de doctorado de la Universidad Juárez Autónoma de Tabasco (UJAT) y del Programa de Mejoramiento del Profesorado, México (PROMEP). Hidalgo-Leiva DA Leiva también es titular de una beca de doctorado de la Oficina de Asuntos Internacionales y Cooperación Externa (OAICE) de la Universidad de Costa Rica (UCR) y del Consejo Nacional para Investigaciones Científicas y Tecnológicas (CONICIT) del Gobierno de Costa Rica.

Referencias

[1] Vamvatsikos D., Cornell C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn., 31(3):491–514, 2002.

[2] Wen Y.K., Ellingwood B.R., Veneziano D., Bracci J. Uncertainty modeling in earthquake engineering. MAE Center Project FD-2 Report, 2003.

[3] McGuire R.K. Seismic hazard and risk analysis. Institute Earthquake Engineering Research (IEER), 2004.

[4] Vargas Y.F., Pujades L.G., Barbat A.H., Hurtado J.E. Evaluación probabilista de la capacidad, fragilidad y daño sísmico de edificios de hormigón armado. Rev. Int. Mét. Num. Cálc. Diseño Ing., 29(2):63–78, 2013.

[5] Barbat A.H., Vargas Y.F., Pujades L.G., Hurtado J.E. Evaluación probabilista del riesgo sísmico de estructuras con base en la degradación de rigidez. Rev. Int. Mét. Num. Cálc. Diseño Ing., 31(1):39-47, 2016.

[6] Fragiadakis M., Vamvatsikos D. Approximate seismic performance uncertainty estimation using static pushover methods. The 14th World Conference on Earthquake Engineering, Beijing, China, 2008.

[7] Vargas Y.F., Pujades L.G., Barbat A.H., Hurtado J.E. Capacity, fragility and damage in reinforced concrete buildings: A probabilistic approach. Bull. Earthq. Eng., 11(6):2007–2032, 2013.

[8] Vargas Y.F., Barbat A.H., Pujades L.G., Hurtado J.E. Probabilistic seismic risk evaluation of reinforced concrete buildings. ICE Proceedings Structures and Buildings, 167(6):327–336, 2013.

[9] Celarec D., Dolšek M. The impact of modelling uncertainties on the seismic performance assessment of reinforced concrete frame buildings. Eng. Struct., 52:340–354, 2013.

[10] Kazantzi A.K., Vamvatsikos D., Lignos D.G. Seismic performance of a steel moment-resisting frame subject to strength and ductility uncertainty. Eng. Struct., 78:69–77, 2014.

[11] Pujades L.G., Vargas Y.F., Barbat A.H., González-Drigo J.R. Parametric model for capacity curves. Bull. Earthq. Eng., 13(5):1347–1376, 2015.

[12] Vamvatsikos D., Fragiadakis M. Incremental dynamic analysis for estimating seismic performance sensitivity and uncertainty. Earthq. Eng. Struct. Dyn., 39:141–163, 2010.

[13] Ibarra L., Krawinkler H. Variance of collapse capacity of SDOF systems under earthquake excitations. Earthq. Eng. Struct. Dyn., 40:1299–1314, 2011.

[14] Ibarra L.F., Medina R.A., Krawinkler H. Hysteretic models that incorporate strength and stiffness deterioration. Earthq. Eng. Struct. Dyn., 34(12):1489–1511, 2005.

[15] Lignos D.G., Krawinkler H. A Database in support of modeling of component deterioration for collapse prediction of steel frame structures. Struct. Eng. Res. Front., 1–12, 2007.

[16] Lignos D.G., Krawinkler H. Sidesway collapse of deteriorating structural systems under seismic excitations. Stanford Univ. Stanford, CA, 2009.

[17] Lignos D.G., Krawinkler H. Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading. J. Struct. Eng., 137(11):1291–1302, 2011.

[18] Lignos D.G., Krawinkler H. Development and utilization of structural component databases for performance-based earthquake engineering. J. Struct. Eng., 139:1382–1394, 2013.

[19] Lantada N., Irizarry J., Barbat A.H., Goula X., Roca A., Susagna T., Pujades L.G. Seismic hazard and risk scenarios for Barcelona, Spain, using the Risk-UE vulnerability index method. Bull. Earthq. Eng., 8(2):201–229, 2010.

[20] Barbat A.H., Carreño M.L., Cardona O.D., Marulanda M.C. Evaluación holística del riesgo sísmico en zonas urbanas. Rev. Int. Mét. Num. Cálc. Diseño Ing., 27(1):3–27, 2011.

[21] Pujades L.G., Barbat A.H., Gonzalez-Drigo S., Avila R., Lagomarsino J. Seismic performance of a block of buildings representative of the typical construction in the Eixample district in Barcelona (Spain). Bull. Earthq. Eng., 10(1):331–349, 2012.

[22] Gonzalez-Drigo S., Avila-Haro J., Pujades L.G., Barbat A.H. Non-linear static procedures applied to high-rise residential URM buildings. Bull. Earthq. Eng., 15(1):149-174, 2017.

[23] ANSI/AISC 358. Prequalified connections for special and intermediate steel moment frames for seismic applications. American Institute of Steel Construction, 2010.

[24] NTC-DF, Norma Técnica Complementaria del Distrito Federal, México, 2004.

[25] ANSI/AISC 341-10. Seismic Provisions for Structural Steel Buildings. American Institute of Steel Construction, 2010.

[26] Carr A.J. Ruaumoko 2D y 3D Inelastic Dynamic Analysis Program, 2002.

[27] PEER/ATC 72-1, Modeling and acceptance criteria for seismic design and analysis of tall building. Applied Technology Council and Pacific Earthquake Engineering Research Center, 2010.

[28] Krawinkler H. Shear design of steel frame joints. Eng. Journal, 15(3):82-91, 1978.

[29] FEMA 355C, State of the art report on system performance of steel moment frames subject to earthquake ground shaking. SAC Joint Venture Partnership for the Federal Emergency Management Agency, Washington, D.C. 2000.

[30] SAC, Analytical and field investigations of buildings affected by the Northridge earthquake. Report No. SAC-95-04, prepared by SAC Joint Venture, a partnership of SEAOC, ATC and CUREE, 1996.

[31] Bermudez C. Vulnerabilidad sísmica de edificios de acero. Tesis Doctoral, Universidad Politécnica de Cataluña, 2010.

[32] Idota H., Guan L., Yamazaki K. Statistical correlation of steel members for system reliability analysis. In: Proc. 9th Int. Conf. Struct. Saf. Reliab., Osaka, Japan, 2009.

[33] Crowley H., Bommer J.J., Pinho R., Bird J. The impact of epistemic uncertainty on an earthquake loss model. Earthq. Eng. Struct. Dyn., 34:1653–1685, 2005.

[34] Kwon O.S., Elnashai A. The effect of material and ground motion uncertainty on the seismic vulnerability curves of RC structure. Eng. Struct., 28:289–303, 2006.

[35] Kazantzi A.K., Righiniotis T.D., Chryssanthopoulos M.K. Fragility and hazard analysis of a welded steel moment resisting frame. J. Earthq. Eng., 12:596–615, 2008.

[36] Hancock J., Watson-Lamprey N., Abrahamson J., Bommer J., Markatis A., McCoy E., Mendis R. An improved method of matching response spectra of recorded earthquake ground motion using wavelets. J. Earthq. Eng., 10:67–89, 2006.

[37] Diaz S.A., Pujades L.G., Barbat A.H., Félix J.L. Efecto de la direccionalidad en la amenaza sísmica de la Ciudad de México. XX Congr. Nac. Ing. Sísmica. México, Acapulco, Guerrero. ISSN: 2448-5721, 2015.

[38] Park Y., Ang A., Wen Y. Seismic damage analysis of reinforced concrete buildings. J. Struct. Eng. ASCE, 111:740–757, 1985.

[39] Elghazouli A.Y. Evaluation of Fatigue and Park and Ang damage indexes in steel structures. 15th World Conf. Earthq. Eng. Lisbon Port., 2012.

[40] Park Y., Ang A.-S., Wen Y. Damage-limiting aseismic design of buildings. Earthq Spectra., 3 (1):1–26, 1987.

[41] Cosenza E., Manfredi G. Damage indices and damage measures. Prog. Struct. Eng. Mater., 2(1):50–59, 2000.

[42] Diaz S.A., Pujades L.G., Barbat A.H., Hidalgo-Leiva D.A., Vargas-Alzate Y.F. Capacity, damage and fragility models for steel buildings. A probabilistic approach. Bull. Earthq. Eng., Submitted and under review, 2017.