Design of a movil manipulator with optimum mechanical energy using differential evolution

Resumen

En este trabajo se establece el problema de diseño cinemático y dinámico de los eslabones de un manipulador móvil como un problema de optimización numérica, con el objetivo de minimizar la energía mecánica del sistema en las posiciones críticas de un espacio de trabajo pre-establecido. Al cumplir con el objetivo propuesto se disminuye consecuentemente el consumo de energía que necesita el sistema de control durante su operación dentro del espacio de trabajo pre-establecido. Para dar solución al problema de optimización, se incorpora un mecanismo de explotación exhaustiva en el algoritmo tradicional de evolución diferencial, permitiendo mejorar la búsqueda dentro de una vecindad del espacio de diseño. Resultados en simulación muestran el desempeño del algoritmo. A su vez se muestra un menor consumo de energía del diseño resultante comparado con otros 3 diseños.

Abstract

In this work, the design of kinematic and dynamic parameters of links of a mobile manipulator is stated as a numerical optimization problem (NOP). The NOP aims to minimize the mechanical energy of the system in critical positions given by the vertices of a workspace and consequently reduce the energy consumption of the control system during its operation in the workspace. An exhaustive exploitation mechanism is included in the traditional differential evolution algorithm to improve the search into a neighborhood in the design space. Simulation results show the performance of the algorithm. The resulting design shows less energy consumption than other three designs.

Palabras clave

Diseño óptimo ; Manipulador móvil ; Optimización numérica ; Evolución diferencial ; Diseño mecatrónico

Keywords

Optimum design ; Mobile manipulator ; Numeric optimization ; Diferential evolution ; Mechatronic design

1. Introducción

El incremento en la demanda de sistemas mecatrónicos con un alto desempeño ha sido uno de los factores importantes para el estudio de metodologías de diseño mecatrónico [1] , [2] , [3]  and [4] . La filosofía general del concepto de diseño mecatrónico es crear un ambiente de diseño integrado que promueva el diseño simultáneo de las 4 principales áreas que involucra la mecatrónica (ingeniería mecánica, ingeniería electrónica, ingeniería de control e ingeniería informática). Sin embargo, debido a la complejidad que resulta integrar todas las áreas, en los últimos años se ha integrado la estructura mecánica y el sistema de control con el propósito de lograr un desempeño óptimo del sistema. Por lo tanto, el desempeño de un sistema electromecánico no solo depende de su controlador, sino también del diseño de la estructura mecánica. En [5] , se propuso la metodología «Diseño para el control»para un mecanismo de 4 barras. La idea principal es obtener un modelo dinámico simple para facilitar el diseño del controlador. Se propone un esquema de redistribución de masa con el propósito de obtener un sistema dinámico simple y posteriormente se sintoniza un controlador proporcional-derivativo (PD).

Debido a que se requiere satisfacer 2 o varios objetivos de diseño, en la filosofía de diseño mecatrónico se han establecido metodologías en donde se plantea dicha sinergia como un problema de optimización no lineal. En ocasiones dichos objetivos se contraponen, es decir, para maximizar la eficiencia en un objetivo se tendrá que minimizar la eficiencia en otro y viceversa. En [6] se desarrolla un método de diseño concurrente para la geometría de los eslabones, la localización de los actuadores y las ganancias de un control PD de un robot de 2 grados de libertad (g  . d  . l  .). El modelo dinámico del sistema se linealiza para poder optimizar la estructura mecánica y se utiliza un método de proyección del gradiente para resolver el problema de optimización. Un enfoque de diseño iterativo se formula en [7] , en donde se modifica experimentalmente la estructura mecánica y posteriormente el sistema de control, con el propósito de mejorar el desempeño de un robot planar de 2 g  . d  . l  . Se utiliza un algoritmo de búsqueda simple para sintonizar las ganancias del controlador y un algoritmo de mínimos cuadrados recursivo para la optimización de la estructura mecánica. En [8] se propone el diseño simultáneo de un robot manipulador y su sistema de control con una metodología basada en técnicas de optimización numérica. Se utiliza el algoritmo (μ  + λ )-ES para resolver el problema de optimización. También se han realizado trabajos con la filosofía de diseño mecatrónico con robots subactuados [2] , en donde se formula un problema de optimización que considera minimizar el tiempo de posicionamiento de un robot subactuado tomando en consideración encontrar la posición de un sistema de contrapeso así como los intervalos de conmutación de la señal de control bang-bang. Con el propósito de hacer sistemas más robustos, en [4] se propone y se estudia un enfoque en donde se combina el diseño robusto y el control robusto. Debido a la naturaleza del problema, se formula como uno minimax y se utiliza programación cuadrática sucesiva para resolverlo. En [1] se incluyen términos de robustez en el marco de diseño mecatrónico. Se diseña simultáneamente un robot paralelo planar y su sistema de control con el propósito de minimizar los efectos que produce la carga que soporta el efector final en el seguimiento de una trayectoria y en la medida de manipulabilidad. Se utiliza el algoritmo de evolución diferencial para resolver el problema de optimización.

Es importante notar que, para que exista una sinergia en la filosofía de diseño mecatrónico, se requiere de la formulación de un problema de optimización, ya que su solución analítica resulta extremadamente compleja debido a su dinámica de naturaleza no lineal. Para resolver el problema de optimización bajo la filosofía de diseño mecatrónico se ha recurrido al uso de algoritmos meta-heurísticos por la naturaleza del problema. Sin embargo, no se ha dado la suficiente importancia a la selección adecuada del algoritmo en el marco de diseño mecatrónico. En [9] se propone un algoritmo de evolución diferencial con manejo de restricciones para resolver el diseño simultáneo de los parámetros de la estructura mecánica de un robot paralelo y el diseño del sistema de control proporcional-integral-derivativo para realizar una tarea en el espacio cartesiano. Además se integra al algoritmo un mecanismo para reducir el tiempo computacional en el problema de optimización dinámica no lineal. En [10] se presenta un enfoque basado en el algoritmo de evolución diferencial para mejorar las características de reconfiguración paramétrica en el diseño óptimo de una transmisión de variación continua y en un robot paralelo. Este enfoque incluye un mecanismo de diversidad de la solución con una memoria externa que almacena soluciones subóptimas durante el proceso, además de incluir un mecanismo de manejo de restricciones para dirigir la búsqueda hacia una región factible del espacio de búsqueda. En [11] se propone una técnica de optimización híbrida evolutiva-gradiente con el propósito de encontrar mejores soluciones en el espacio de búsqueda en el enfoque de diseño sinérgico de un robot paralelo planar y de su sistema de control. Se muestra que la incorporación de mecanismos de búsqueda local mejora la solución obtenida en el marco de diseño mecatrónico.

Con el propósito de obtener un sistema mecatrónico con un desempeño superior en su estructura mecánica que a su vez beneficia el sistema de control, en este trabajo se formula como un problema de optimización, un enfoque de diseño de la estructura mecánica de un robot paralelo de 5 eslabones montado sobre una plataforma móvil (manipulador móvil) y se propone un mecanismo en el algoritmo de evolución diferencial para explotar las soluciones encontradas en el espacio de búsqueda, con el propósito de obtener mejores soluciones. Este enfoque de diseño tiene como propósito minimizar la energía requerida en el sistema de control dentro de un espacio de trabajo diestro pre-establecido. Además considera el modelo cinemático del manipulador, la energía mecánica del manipulador en posiciones críticas de interés en el espacio de trabajo (posiciones del sistema en donde se ejerce mayor energía mecánica), así como restricciones inherentes en el diseño. Una cuestión importante en la propuesta es que, al minimizar la energía mecánica en las posiciones críticas del espacio de trabajo pre-definido, se reduce la energía mecánica en las posiciones dentro de espacio de trabajo pre-definido y a su vez se reduce la energía proporcionada por el sistema de control. Resultados en simulación numérica muestran que el diseño óptimo resultante consume menos energía cuando el manipulador móvil realiza una tarea en el espacio de trabajo pre-establecido, comparado con otros diseños. Una de las ventajas que presenta el enfoque propuesto en este trabajo es que al modificar la estructura mecánica se puede disminuir la energía en el sistema de control, además de que no requiere de un controlador específico, ni de una trayectoria predefinida como en el caso de [12] , en donde se obtienen los parámetros dinámicos del sistema a partir de la minimización de los términos del sistema de control y se debe establecer una trayectoria particular y considerando un controlador par calculado, asumiendo que la dinámica del control cancela exactamente las no linealidades del sistema.

El artículo se organiza de la siguiente manera: en la sección 2 se formula el problema de optimización en donde se describen las variables de diseño, la función objetivo y las restricciones. Se propone en la sección 3 el mecanismo de explotación exhaustiva (MEE) en el algoritmo de evolución diferencial (ED) para resolver el problema de optimización. Los resultados obtenidos con el algoritmo propuesto se describen en la sección 4 así como su desempeño en el sistema de control para realizar una tarea, mostrando que se obtiene un diseño superior comparado con otros 3 diseños. Finalmente en la sección 5 se muestran las conclusiones pertinentes.

2. Formulación del problema de diseño óptimo

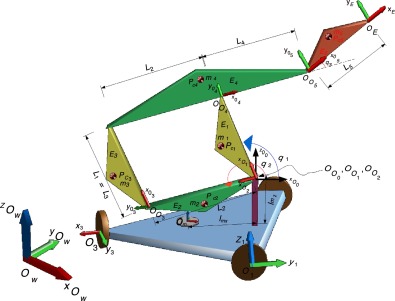
El objetivo del presente trabajo se enfoca en obtener, con base en un problema de optimización, el diseño de los parámetros cinemáticos y dinámicos óptimos de un robot manipulador montado sobre una plataforma móvil mostrado en la figura 1 , con el fin de reducir su energía mecánica en un espacio de trabajo pre-establecido, y a su vez disminuir la energía consumida por el sistema de control cuando realice tareas dentro del espacio de trabajo pre-establecido. Además, se debe cumplir que el espacio de trabajo del robot esté definido por los vértices ${\textstyle ({\overline {x}}_{d_{i,j,k}},{\overline {z}}_{d_{i,j,k}})\forall i,j=1,2}$ . Se considera que el efector final (descrito por el punto ${\textstyle ({\overline {x}}_{i,j,k},{\overline {z}}_{i,j,k})}$ en el plano X  − Z   ) alcance por lo menos 3 diferentes orientaciones (descrito por ${\textstyle {\overline {\phi }}_{i,j,k}}$ con respecto al eje Y del sistema coordenado O₀ , ∀ k  = 1, 2, 3) para cada vértice, y con esto se asegura un espacio de trabajo diestro.

Fig. 1. Representación esquemática del manipulador móvil.

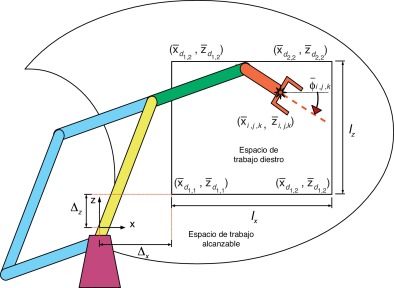
El espacio de trabajo pre-establecido está comprendido por el área formada por l_x  = 0, 40 m y l_z  = 0, 30 m , con un distancia de separación de Δ_x  = 0, 25 m y Δ_z  = 0, 10 m con respecto al origen O₀ , como se muestra en la figura 2 .

Fig. 2. Espacio de trabajo.

En las siguientes secciones se detallarán las variables de diseño, la función objetivo y las restricciones que involucra el problema de optimización.

2.1. Variables de diseño

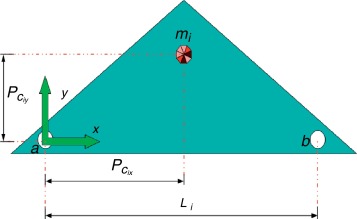
El desempeño cinemático y dinámico del manipulador móvil para realizar una o varias tareas se afecta por la forma de los eslabones, es decir por sus parámetros cinemáticos (longitud de los eslabones) y dinámicos (masa, inercia, centro de masa). Los parámetros cinemáticos y dinámicos de los eslabones del robot se parametrizan en 4 variables que se muestran en la figura 3 , donde L_i es la longitud del eslabón comprendido por la distancia entre el centro de los círculos a -b , m_i es la masa del eslabón y ${\textstyle P_{c_{ix}}}$ , ${\textstyle P_{c_{iy}}}$ es la distancia del centro de masa, comprendida entre el origen del sistema coordenado de referencia x  − y   y el centro de masa del eslabón. Por tal motivo, se considera al vector ${\textstyle p_{a}=[L_{i},p_{c_{ix}},p_{c_{iy}}]\in R^{12}}$ ∀i  = 1, 2, 4, 5 como uno de los vectores que forman el vector de variables de diseño del problema de optimización. Es importante mencionar que la i  − th masa m_i del eslabón no se involucra como variable de diseño debido a que la energía mecánica del manipulador es directamente proporcional al valor de la masa, por lo que el valor de la masa siempre convergerá al mínimo valor que se establezca, cuando se minimice la energía mecánica del manipulador móvil [ver (14) y (15) ].

Fig. 3. Esquema del i-ésimo eslabón.

En este trabajo se considera lo siguiente: i   ) El momento de inercia de los eslabones es dado por ${\textstyle I_{i}=m_{i}(P_{c_{ix}}^{2}+P_{c_{iy}}^{2})^{2}}$ . ii ) El primero y segundo eslabón tienen los mismos parámetros cinemáticos y dinámicos. iii ) La forma del eslabón no se considera con una geometría específica como en [9] , sin embargo en un proceso posterior se encuentra la forma que cumple con los parámetros de diseño obtenidos en este trabajo.

Por otra parte, se involucran las configuraciones articulares del robot para alcanzar los vértices del espacio de trabajo diestro pre-establecido, como otro vector de variables de diseño. Este se representa como: ${\textstyle p_{b}=[q_{1_{i,j,k}},q_{2_{i,j,k}},q_{3_{i,j,k}}]\in R^{36}}$ , ∀ i , j  = 1, 2, k  = 1, 2, 3.

Es así que el vector de variables de diseño p que involucra tanto el diseño de la estructura mecánica como la configuración articular del robot se representa en (1)

$p=[p_{a},p_{b}]^{T}\in R^{48}$

( 1)

2.2. Función objetivo

Uno de los factores importantes a considerar en un robot autónomo como es el caso del manipulador móvil, es el consumo de energía debido al uso de baterías. Con el propósito de reducir el consumo de energía en el sistema de control del manipulador móvil, en este trabajo se propone como función objetivo la energía mecánica del sistema, en posiciones críticas de interés en el espacio de trabajo. Las posiciones críticas del sistema son aquellas en donde el sistema presenta mayor carga, es decir, mayor energía mecánica. Debido a que en los extremos (vértices) de un espacio de trabajo pre-establecido se presentan las mayores cargas, se proponen dichos vértices como las posiciones críticas de interés.

Se parte del hecho siguiente: Considerando q  ∈ Rⁿ como el vector de coordenadas generalizadas, u  ∈ Rⁿ el vector de par de control y τ_m el vector de par de carga dinámica del manipulador y realizando un análisis dinámico de fuerzas y pares (formulación de Newton-Euler) se obtiene (2) -(4)[13] . Se observa que la dinámica del manipulador ${\textstyle \tau _{m}=M\quad {\ddot {q}}+C\quad {\dot {q}}+G}$ depende del lagrangiano ${\textstyle L=K_{l}(q,{\dot {q}})-V_{l}(q)\in R}$ del sistema, donde ${\textstyle K_{l}(q,{\dot {q}})={\frac {1}{2}}{\dot {q}}^{T}M{\dot {q}}}$ es la energía cinética, ${\textstyle V_{l}(q)=\sum _{i=1}^{n}V_{i}}$ es la energía potencial, M  ∈ R^{n ×n} es la matriz de inercia, C  ${\textstyle {\dot {q}}\in R^{n}}$ es el vector de fuerzas centrífuga y de Coriolis y G  ∈ Rⁿ es el vector de gravedad

$u=\tau _{m}$

( 2)

$u={\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}}}-{\frac {\partial L}{\partial q}}$

( 3)

$u=M\quad {\ddot {q}}+C\quad {\dot {q}}+G$

( 4)

Se observa en (2) -(4) que el par de carga dinámico del manipulador τ_m está en función de las matrices M , C y del vector G y para que el par u del sistema de control estabilice el manipulador en alguna posición se tiene que cumplir con u  − τ_m  = 0 de (2) , es decir, que el par de carga y el par aplicado por el controlador sean iguales. Se puede verificar en [13] que el vector ${\textstyle G={\frac {\partial V_{l}}{\partial q}}}$ se obtiene a partir de la energía potencial y los elementos de C  ${\textstyle (dados\quad por\quad C_{kj}=\sum _{i=1}^{n}{\frac {1}{2}}\left({\frac {\partial M_{kj}}{\partial q_{j}}}+{\frac {\partial M_{ki}}{\partial q_{j}}}-{\frac {\partial M_{ij}}{\partial q_{k}}}\right){\dot {q}}_{i})}$ , se calcula a partir de la matriz de inercia M   de la energía cinética ${\textstyle K_{l}(q,{\dot {q}})}$ . Por lo tanto, la energía cinética ${\textstyle K_{l}(q,{\dot {q}})}$ y la energía potencial V_l (q ) del manipulador afectan la dinámica del manipulador (el par de carga del manipulador τ_m ) el cual es directamente proporcional al par de control u (ver (2) ) requerido para estabilizar el sistema (para realizar la tarea). Es así que al minimizar la energía mecánica del manipulador se minimiza el par proporcionado por la señal de control y esta a su vez minimiza el consumo de energía eléctrica en la señal de control, debido a que se puede representar (2) en términos de potencia como se expresa en (5) -(7) , donde P_u y P_m es la potencia consumida por el sistema de control y la potencia de carga del manipulador, respectivamente. Los términos V e I son el voltaje y la corriente aplicada al motor por el sistema de control. Es así que se relaciona la energía mecánica del sistema con el consumo de energía eléctrica y por tal motivo en este trabajo se propone como función objetivo J   a la energía mecánica (energía cinética y potencial) del manipulador móvil, considerando constante el vector de velocidad generalizadas (${\textstyle {\dot {q}}=cte}$ )

$P_{u}-P_{m}=0$

( 5)

$u{\dot {\phi }}-\tau _{m}{\dot {\phi }}=0$

( 6)

$VI-\tau _{m}{\dot {\phi }}=0$

( 7)

Cabe aclarar que la selección del vector de velocidades generalizadas ${\textstyle {\dot {q}}}$ no afecta en la obtención de los parámetros de diseño óptimos bajo la minimización de la función objetivo J   . Esto se debe a que ${\textstyle {\dot {q}}}$ no está relacionada explícitamente con dichos parámetros y por lo siguiente: el vector de velocidades generalizadas ${\textstyle {\dot {q}}}$ únicamente influye en el cálculo de la energía cinética ${\textstyle K_{l}(q,{\dot {q}})={\frac {1}{2}}{\dot {q}}^{T}M{\dot {q}}}$ . Se observa que el vector de velocidad ${\textstyle {\dot {q}}}$ y la matriz de inercia M son 2 términos que influyen en la minimización de la energía cinética. Por definición la matriz de inercia M   es definida positiva. Considere por simplicidad el caso de un manipulador con un grado de libertad. La energía cinética se expresa como ${\textstyle K_{l}(q,{\dot {q}})={\frac {1}{2}}{\dot {q}}^{2}M}$ . Por lo tanto, al minimizar la energía cinética se pueden presentar varias situaciones: i   ) La velocidad ${\textstyle {\dot {q}}}$ converge a cero y el valor de M converge a cualquier constante mayor a cero. ii ) El valor de M   converge a cero y la velocidad ${\textstyle {\dot {q}}}$ a cualquier valor diferente de cero. iii   ) Ambos términos convergen a cero. Es así que se considera una velocidad constante en ${\textstyle {\dot {q}}}$ debido a que no es función explícita de los parámetros de diseño, logrando que se minimice únicamente la matriz M que es función implícita de los parámetros de diseño. Por lo tanto, el valor escogido de la velocidad no afecta a la obtención de las variables de diseño óptimas bajo la minimización de la energía mecánica.

Para obtener la energía mecánica del manipulador móvil se establece que ${\textstyle O_{w}}$ es el origen del sistema coordenado inercial, ${\textstyle O_{m^{'}}}$ es el origen del sistema coordenado del manipulador móvil, O_E es el origen del sistema coordenado del efector final, ${\textstyle O_{O_{i}}}$ ∀i  = 0, . . . , 5 es el origen del sistema coordenado del i-ésimo eslabón, O_j  ∈ R³ ∀j  = 1, 2, 3 es el origen del sistema coordenado de la j-ésima   rueda, ${\textstyle ^{O_{i}}P_{c_{i}}=[P_{c_{x}},P_{c_{y}},0]^{T}\in R^{3}}$ es el vector de posición del centro de masa del i-ésimo eslabón con respecto a O_i , ${\textstyle V_{O_{m^{'}}}\in R^{3}}$ es el vector de velocidad lineal en ${\textstyle O_{m^{'}}}$ . Se considera lo siguiente i ) que no existe deslizamiento en las ruedas, ii   ) el sistema de coordenada ${\textstyle O_{m^{'}}}$ se encuentra en el centro de gravedad del móvil y iii   ) el sistema de coordenada ${\textstyle O_{m^{'}}\in R^{3}}$ se encuentra colineal al sistema de coordenada O_m con una distancia ${\textstyle ^{m^{'}}P_{m}=\left[s_{1},s_{2},0\right]^{T}}$ entre ellos con respecto al sistema de coordenada ${\textstyle O_{m^{'}}}$ . Así, las velocidades lineales absolutas del centro de masa de cada cuerpo (móvil y eslabones) están dadas por las ecs. (8) -(13) , donde ${\textstyle ^{m}V_{c_{i}}\in R^{3},}$${\textstyle w_{i}\in R^{3}}$ es el vector de velocidad lineal y angular absoluta del centro de masa del i-ésimo cuerpo, expresado en las coordenadas del móvil, respectivamente.

$^{m}V_{c_{0}}=V_{O_{m}}+w_{0}\quad \times ^{m}P_{m^{'}}$

( 8)

$^{m}V_{c_{1}}=^{m}V_{c_{0}}+w_{0}\quad \times \quad ^{O_{m}}P_{O_{0}}+_{O_{m}}^{O_{w}}R^{T}\quad w_{1}\quad \times \quad _{1}^{O_{m}}R^{O_{1}}P_{c_{1}}$

( 9)

$^{m}V_{c_{2}}=^{m}V_{c_{0}}+w_{0}\quad \times \quad ^{O_{m}}P_{O_{0}}+_{O_{m}}^{O_{w}}R^{T}\quad w_{2}\quad \times \quad _{2}^{O_{m}}R^{O_{2}}P_{c_{2}}$

( 10)

${\begin{array}{cc}^{m}V_{c_{3}}&=^{m}V_{c_{0}}+w_{0}\quad \times \quad ^{O_{m}}P_{O_{0}}+_{O_{m}}^{O_{w}}R^{T}\quad w_{2}\quad \times \quad _{2}^{O_{m}}R^{O_{2}}P_{O_{3}}\\&+_{O_{m}}^{O_{w}}R^{T}{\mbox{   }}w_{3}\quad \times \quad _{3}^{O_{m}}R\quad ^{O_{3}}P_{c_{3}}\end{array}}$

( 11)

${\begin{array}{cc}^{m}V_{c_{4}}&=^{m}V_{c_{0}}+w_{0}\quad \times \quad ^{O_{m}}P_{O_{0}}+_{O_{m}}^{O_{w}}R^{T}\quad w_{1}\quad \times \quad _{1}^{O_{m}}R^{O_{1}}P_{O_{4}}\\&+_{O_{m}}^{O_{w}}R^{T}\quad w_{4}\quad \times \quad _{4}^{O_{m}}R\quad ^{O_{4}}P_{c_{4}}\end{array}}$

( 12)

${\begin{array}{cc}^{m}V_{c_{5}}&=^{m}V_{c_{0}}+w_{0}\quad \times \quad ^{O_{m}}P_{O_{0}}+_{O_{m}}^{O_{w}}R^{T}\quad w_{1}\quad \times \quad _{1}^{O_{m}}R^{O_{1}}P_{O_{4}}\\&+_{O_{m}}^{O_{w}}R^{T}\quad w_{4}\quad \times \quad _{4}^{O_{m}}R\quad ^{O_{4}}P_{O_{5}}+_{O_{m}}^{O_{w}}R^{T}\quad w_{5}\quad \times \quad _{5}^{O_{m}}R\quad ^{O_{5}}P_{c_{5}}\end{array}}$

( 13)

donde ${\textstyle V_{O_{m}}=\left[{\begin{array}{ccc}{\dot {x}}_{m}&{\dot {y}}_{m}&0\end{array}}\right]^{T},}$${\textstyle w_{0}=\left[{\begin{array}{ccc}0&0&{\dot {\phi }}_{m}\end{array}}\right]^{T},}$${\textstyle ^{O_{m}}P_{O_{0}}=\left[l_{m_{x}},0,l_{m_{z}}\right]^{T},}$${\textstyle ^{O_{2}}P_{O_{3}}=[l_{2},0,0]^{T},}$${\textstyle ^{O_{1}}P_{O_{4}}=[l_{1},0,0]^{T},}$${\textstyle ^{O_{4}}P_{O_{5}}=[l_{4},0,0]^{T},}$${\textstyle ^{O_{5}}P_{O_{E}}=[l_{5},0,0]^{T},}$${\textstyle ^{O_{i}}P_{c_{i}}=[p_{c_{ix}},0,p_{c_{iz}}]^{T}}$ ∀ i  = 1, . . . , 5, ${\textstyle _{i}^{O_{m}}R=}$${\textstyle _{O_{0}}^{O_{m}}R}$${\textstyle _{i}^{O_{0}}R,}$${\textstyle w_{1}=w_{0}+_{1}^{O_{w}}R}$${\textstyle {\dot {q}}_{1}{\overset {\mbox{ˆ}}{Z}},}$${\textstyle w_{2}=w_{0}+_{2}^{O_{w}}R}$${\textstyle {\dot {q}}_{2}{\overset {\mbox{ˆ}}{Z}},}$${\textstyle w_{3}=w_{0}+_{1}^{O_{w}}R}$${\textstyle {\dot {q}}_{1}{\overset {\mbox{ˆ}}{Z}},}$${\textstyle w_{4}=w_{0}+_{4}^{O_{w}}R}$${\textstyle {\dot {q}}_{2}{\overset {\mbox{ˆ}}{Z}},}$${\textstyle w_{5}=w_{4}+_{5}^{O_{w}}R}$${\textstyle {\dot {q}}_{3}{\overset {\mbox{ˆ}}{Z}},}$${\textstyle {\overset {\mbox{ˆ}}{Z}}=\left[{\begin{array}{ccc}0&0&1\end{array}}\right]^{T},}$${\textstyle _{O_{0}}^{O_{m}}R}$${\textstyle =R_{x}({\frac {\pi }{2}}),}$${\textstyle _{O_{m}}^{O_{w}}R}$ = R_z (ϕ_m ), ${\textstyle _{1}^{0}R=_{3}^{0}R=R_{z}(q_{1}),}$${\textstyle _{2}^{0}R=R_{z}(q_{2}),}$${\textstyle _{4}^{0}R=R_{z}(q_{2}+\pi ),}$${\textstyle _{5}^{0}R=R_{z}(q_{2}+q_{3}+\pi ).}$R_{x /y /z} (θ ) ∈ R^3×3 es la matriz de rotación en el eje x / y / z de θ radianes y ^XP_Y  ∈ R³ es el vector de posición del origen del sistema de coordenada Y con respecto al sistema de coordenada X  .

Por lo tanto la energía cinética K_l y la potencial V_l del manipulador móvil está dada en (14) y en (15) , donde ${\textstyle ^{i}w_{i}=_{i}^{O_{w}}R^{T}}$${\textstyle w_{i}}$ ∀ i  = 0, . . . , 5 es la velocidad angular del móvil y del i-ésimo eslabón escrito en su mismo sistema de coordenada y h_i ∀ i  = 0, . . . , 5 es la altura del centro de masa del i-ésimo eslabón en el eje Z del sistema de coordenada O_m , definiéndose ${\textstyle {\overset {\mbox{ˆ}}{Z}}=[0,0,1]^{T}}$ . En (14) se desprecia la energía cinética proporcionada por las llantas del móvil debido a que no tiene relación con las variables de diseño. Para más detalle sobre el cálculo de la energía mecánica del manipulador móvil, consultar [14]

$K_{l}=\sum _{i=0}^{5}{\frac {1}{2}}m_{i}V_{c_{i}}^{T}V_{c_{i}}+\sum _{i=0}^{5}{\frac {1}{2}}\quad ^{i}w_{i}^{T}\quad ^{c_{i}}I_{i}\quad ^{i}w_{i}+{\frac {1}{2}}{\dot {\theta }}^{T}\quad {\overline {J}}\quad {\dot {\theta }}$

( 14)

$V_{l}=\sum _{i=0}^{5}m_{i}gh_{i}$

( 15)

donde:

$h_{0}=0$

( 16)

$h_{i}={\overset {\mbox{ˆ}}{Z}}\left(^{O_{i}}P_{O_{i+1}}\right)-{\overset {\mbox{ˆ}}{Z}}\left(_{i}^{O_{m}}R^{O_{i}}P_{c_{i}}\right)\quad \forall \quad i=1,2$

( 17)

$h_{3}={\overset {\mbox{ˆ}}{Z}}\left(^{O_{2}}P_{O_{3}}+^{O_{3}}P_{O_{4}}\right)-{\overset {\mbox{ˆ}}{Z}}\left(_{2}^{O_{m}}R^{O_{2}}P_{O_{3}}+_{3}^{O_{m}}R^{O_{3}}P_{c_{3}}\right)$

( 18)

$h_{4}={\overset {\mbox{ˆ}}{Z}}\left(^{O_{1}}P_{O_{4}}+^{O_{4}}P_{O_{5}}\right)-{\overset {\mbox{ˆ}}{Z}}\left(_{1}^{O_{m}}R^{O_{1}}P_{O_{4}}+_{4}^{O_{m}}R^{O_{4}}P_{c_{4}}\right)$

( 19)

${\begin{array}{cc}h_{5}&={\overset {\mbox{ˆ}}{Z}}\left(^{O_{1}}P_{O_{4}}+^{O_{4}}P_{O_{5}}+^{O_{5}}P_{O_{E}}\right)\\&-{\overset {\mbox{ˆ}}{Z}}\left(_{1}^{O_{m}}R^{O_{1}}P_{O_{4}}+_{4}^{O_{m}}R^{O_{4}}P_{O_{5}}+_{5}^{O_{m}}R^{O_{5}}P_{c_{5}}\right)\end{array}}$

( 20)

Se considera que el diseño resultante contemple un espacio de trabajo diestro pre-establecido por el usuario (ver fig. 2 ). Es así que las posiciones críticas del manipulador se proponen como la posición cartesiana de los 4 vértices del espacio de trabajo pre-establecido considerando 3 orientaciones diferentes en cada vértice, por lo que se tendrán 12 posiciones-orientaciones críticas agrupadas en ${\textstyle P_{crit}=[{\overline {x}}_{i,j,k},{\overline {z}}_{i,j,k},{\overline {\phi }}_{i,j,k}]^{T}\in R^{12}}$ ∀ i , j  = 1, 2, k  = 1, 2, 3. Por lo tanto se propone la energía mecánica del manipulador móvil (energía cinética y potencial) en las posiciones críticas como la función objetivo a minimizar, la cual se expresa en (21) , donde ${\textstyle {\overline {w}}=}$$\lbrace {\breve {P}}=\left[{\breve {P}}_{1},{\breve {P}}_{2},{\breve {P}}_{3}\right]^{T}\in R^{3}\quad \vert \quad {\breve {P}}\in P_{crit}\rbrace$ . Para el cálculo de la función objetivo se escogen las siguientes velocidades en el móvil ${\textstyle {\dot {x}}=2,77\quad m/s}$ , ${\textstyle {\dot {y}}=2.77m/s}$ , ${\textstyle {\dot {\phi }}={\frac {10}{12}}\pi rad/s}$ y en el manipulador ${\textstyle {\dot {q}}_{1}={\frac {\pi }{2}}rad/s}$ , ${\textstyle {\dot {q}}_{2}={\frac {\pi }{2}}rad/s}$ , ${\textstyle {\dot {q}}_{3}={\frac {\pi }{2}}rad/s}$ . Cabe mencionar que por definición la energía cinética (14) y potencial (15) presentan valores positivos [15]

$J(p)=\int _{\overline {w}}(K_{l}(p)+V_{l}(p))d{\overline {w}}$

( 21)

2.3. Restricciones

El espacio de trabajo diestro de un robot se define como el conjunto de todas las posiciones en el espacio cartesiano que pueden ser alcanzadas por su efector final con diferentes orientaciones [13] . Así, para asegurar el espacio de trabajo diestro en el diseño del robot manipulador, se asume lo siguiente:

• El espacio de trabajo diestro es un área delimitada por 4 vértices ${\textstyle ({\overline {x}}_{d_{i,j,k}},{\overline {z}}_{d_{i,j,k}})\forall i,j=1,2}$ .
• Si el efector final alcanza los 4 vértices del espacio de trabajo diestro deseado con 3 orientaciones distintas ${\textstyle {\overline {\phi }}_{d_{i,j,k}}\forall k=1,2,3}$ , entonces se puede alcanzar cualquier posición interna del espacio de trabajo con al menos 3 orientaciones. Por lo tanto se promueve un espacio de trabajo diestro.

Partiendo de las premisas descritas anteriormente y con el propósito de establecer únicamente un objetivo de diseño en el problema de optimización (optimización mono-objetivo), se propone considerar el espacio de trabajo diestro como una restricción de desigualdad en el problema. Dicha restricción se establece como la suma del error al cuadrado de la posición en el espacio cartesiano (error entre el vértice del espacio de trabajo deseado y la posición del efector final) y el error al cuadrado de la posición articular (error entre la orientación deseada y la orientación real del efector final). Así la función de restricción se puede describir como en (22) , donde ${\textstyle {\overline {w}}=}$$\lbrace {\breve {P}}={\left[{\breve {P}}_{1},{\breve {P}}_{2},{\breve {P}}_{3}\right]}^{T}\in R^{3}\quad \vert \quad {\breve {P}}\in P_{crit}\rbrace$ tal que ${\textstyle P_{crit}=}$${\left[{\overline {x}}_{i,j,k},{\overline {z}}_{i,j,k},{\overline {\phi }}_{i,j,k}\right]}^{T}\in R^{12}$ ∀ i , j  = 1, 2, k  = 1, 2, 3. Las posiciones de los vértices del espacio de trabajo diestro pre-establecido (ver fig. 2 ) son escogidas como ${\textstyle ({\overline {x}}_{d_{1,1,k}},{\overline {z}}_{d_{1,1,k}})=}$$(0,25m,0,10m),$${\textstyle ({\overline {x}}_{d_{1,2,k}},{\overline {z}}_{d_{1,2,k}})=}$$(0,65m,0,10m),$${\textstyle ({\overline {x}}_{d_{2,1,k}},{\overline {z}}_{d_{2,1,k}})=}$$(0,25m,0,40m)$ y ${\textstyle ({\overline {x}}_{d_{2,2,k}},{\overline {z}}_{d_{2,2,k}})=}$$(0,65m,0,40m)$ . El subíndice k   indica las 3 diferentes orientaciones de la posición para cada vértice. Las orientaciones son definidas como ${\textstyle {\overline {\phi }}_{d_{i,j,1}}=}$$-{\frac {\pi }{2}}rad,$${\textstyle {\overline {\phi }}_{d_{i,j,2}}=}$$0rad$ y ${\textstyle {\overline {\phi }}_{d_{i,j,3}}=}$${\frac {\pi }{2}}rad$ ∀ i , j  = 1, 2

${\begin{array}{l}\displaystyle g_{1}:\int _{\overline {w}}\left({\overline {x}}_{d_{i},j,k}-{\overline {x}}_{i,j,k}\right)^{2}d{\overline {w}}+\int _{\overline {w}}\left({\overline {z}}_{d_{i},j,k}-\right.\\\left.\displaystyle -{\overline {z}}_{i,j,k}\right)^{2}d{\overline {w}}\end{array}}$

( 22)

$+{\frac {1.8}{\pi }}\int _{\overline {w}}\left({\overline {\phi }}_{d_{i,j,k}}-{\overline {\phi }}_{i,j,k}\right)^{2}d{\overline {w}}\leq 1\times 10^{-4}$

En la ecuación (22) los primeros 2 términos expresan el error de la posición en el espacio cartesiano, ambos con la misma ponderación, mientras que el tercer término expresa el error angular en radianes. Por lo tanto se propuso la siguiente equivalencia en el tercer término (error de posición angular): un grado (${\textstyle 1^{\circ }={\frac {\pi }{180}}rad}$ ) es proporcional a un milímetro (0,001 m   ). Lo que resulta que el factor de peso del último término sea ${\textstyle {\frac {1,8}{\pi }}}$ . Este factor se obtuvo empíricamente y es necesario para ponderar adecuadamente los términos que involucra la restricción g₁ y así encontrar soluciones que cumplan con la restricción de manera equitativa.

Por otra parte, en (22) se debe calcular la cinemática directa del robot, descrita por las ecuaciones (23) -(25) , para definir la posición ${\textstyle ({\overline {x}}_{i,j,k},{\overline {z}}_{i,j,k})}$ y la orientación ${\textstyle {\overline {\phi }}_{i,j,k}}$ del efector final en el espacio cartesiano.

${\begin{array}{l}\displaystyle {\overline {x}}_{i,j,k}=L_{1}cosq_{1_{i},j,k}-L_{4}cosq_{2_{i},j,k}-\\\displaystyle -L_{5}cos\left(q_{2_{i},j,k}+q_{3_{i},j,k}\right)\end{array}}$

( 23)

${\begin{array}{l}\displaystyle {\overline {z}}_{i,j,k}=L_{1}\quad sen\quad q_{1_{i},j,k}-L_{4}\quad sen\quad q_{2_{i},j,k}-\\\displaystyle -L_{5}sen\left(q_{2_{i},j,k}+q_{3_{i},j,k}\right)\end{array}}$

( 24)

${\overline {\phi }}_{i,j,k}=q_{2_{i,j,k}}+q_{3_{i,j,k}}-\pi$

( 25)

Otra restricción que se incluyó en el diseño del manipulador es la de considerar que la estructura paralela del robot formada por los eslabones 1, 2, 3 y 4 no colisionen entre ellos cuando realicen movimientos en el espacio de trabajo pre-establecido. Así, las restricciones de movimiento angular son descritas por (26) -(27) , donde ${\textstyle Tol_{Max1}={\frac {\pi }{36}}rad}$ y ${\textstyle Tol_{Max2}={\frac {5\pi }{36}}rad}$ son los valores de los ángulos mínimos de seguridad que deben separar a los eslabones para prevenir una colisión. Por tanto se tiene un total de 24 restricciones de desigualdad que se deben satisfacer para cumplir con esta consideración

$g_{2-13}:Tol_{Max2}-q_{2_{i,j,k}}+q_{1_{i,j,k}}\leq 0$

( 26)

$g_{14-25}:q_{2_{i,j,k}}-q_{1_{i,j,k}}-\pi +Tol_{Max2}\leq 0$

( 27)

De forma complementaria, otras 39 restricciones son incluidas como líimites de las variables del vector de diseño p : el ángulo máximo y mínimo en las articulaciones y la longitud permitida de los eslabones. En (28) -(34) se muestran estas restricciones, donde las cotas máximas y mínimas se pueden observar en la tabla 1

Tabla 1. Cotas mínimas y máximas de las variables de diseño.

Variable de diseño	Min	Max
q1[rad]	0	π−5π36
q2[rad]	5π36	32π−5π36
q3[rad]	−π+π36	π−π36
L1[m]	0, 1	0, 5
L2[m]	0, 03	0, 3
L4[m]	0, 1	0, 5
L5[m]	0, 02	0, 2

$g_{26-37}:0<q_{1_{i,j,k}}<\pi -Tol_{Max2}$

( 28)

$g_{38-49}:Tol_{Max2}\leq q_{2_{i,j,k}}\leq {\frac {3}{2}}\pi -Tol_{Max2}$

( 29)

$g_{50-61}:-\pi +Tol_{Max1}\leq q_{3_{i,j,k}}\leq \pi -Tol_{Max1}$

( 30)

$g_{62}:L_{1_{Min}}\leq L_{1}\leq L_{1_{Max}}$

( 31)

$g_{63}:L_{2_{Min}}\leq L_{2}\leq L_{2_{Max}}$

( 32)

$g_{64}:L_{4_{Min}}\leq L_{4}\leq L_{4_{Max}}$

( 33)

$g_{65}:L_{5_{Min}}\leq L_{5}\leq L_{5_{Max}}$

( 34)

2.4. Problema de optimización

El problema de optimización para el manipulador móvil consiste en encontrar el vector de parámetros de diseño óptimo p^*(1) de tal manera que se minimice la energía mecánica del sistema (21) considerando que el manipulador presente un espacio de trabajo diestro pre-establecido (22) y que dentro de este no exista colisión entre los eslabones (26) -(27) , además de considerar los límites en las variables de diseño (28) -(34) . Entonces el problema de optimización se establece formalmente como en (35) -(36)

${\underset {p\in R^{48}}{Min}}\quad J$

( 35)

Sujeto a:

$g(p)\leq 0\in R^{65}$

( 36)

3. Técnica de optimización

Una buena selección de la técnica de optimización es un factor muy importante que permite alcanzar los objetivos deseados. Para realizar dicha selección es necesario identificar las características del problema como: la existencia de restricciones, la naturaleza de las variables de diseño y de las ecuaciones involucradas, la separabilidad y número de funciones, estructura física del problema, entre otras.

En el presente trabajo se implementa una técnica meta-heurística llamada evolución diferencial (ED) para dar solución al problema descrito en la sección previa, debido a que presenta algunas ventajas como son:

• i) Métodos basados en población, por lo que se pueden generar varias soluciones posibles.
• ii) No requieren información adicional durante la búsqueda de soluciones, por ejemplo, el gradiente, matriz hessiana, condiciones iniciales de búsqueda, etc.
• iii) No es necesario que las funciones objetivo y las restricciones sean continuas, ni diferenciables.
• iv) Pueden ser usadas o adaptadas a un gran conjunto de problemas, debido a que no se necesita una formulación matemática específica (transformación del problema) para obtener un conjunto de soluciones.

3.1. Evolución diferencial

El algoritmo de evolución diferencial ha demostrado ser una poderosa herramienta computacional desde que Storn y Price propusieron este algoritmo a mediados de la década de los noventa [16] . Este éxito se debe a la fácil implementación computacional, a la gran adaptabilidad ante diferentes tipos de problemas de optimización y a un razonable tiempo de cómputo, entre otros. Sin embargo, un inconveniente de este algoritmo es que no garantiza la convergencia a un resultado óptimo global. Debido a esto, en varios trabajos de investigación se detalla la implementación de mecanismos para hacer más eficiente la exploración y explotación de los individuos, para así mejorar la búsqueda en el espacio factible y alcanzar una convergencia aproximada al óptimo global [17] , [18]  and [19] . Uno de los enfoques más utilizados es el de manipular o controlar los parámetros del algoritmo de ED. Estos enfoques pueden ser descritos como una solución complementaria debido a que se modifican los parámetros de ED. Esto significa que los parámetros del factor de cruza (CR) y del factor de escala (F) son modificados mientras que la población se mantiene constante durante la ejecución del algoritmo. Así mismo, es importante destacar que el algoritmo de ED debe ser ejecutado varias veces con diferentes valores de los parámetros con el fin de analizar su desempeño [20] . Por otra parte, una propuesta distinta consiste en integrar un mecanismo de búsqueda exhaustiva. En este caso, se ejecuta en una primera etapa una versión estándar del algoritmo ED para dirigir la búsqueda hacia una zona de posibles soluciones. Cuando las posibles soluciones son detectadas, el mecanismo de búsqueda exhaustiva es activado para realizar búsquedas locales dentro de la zona de posibles soluciones [21] .

Una exploración eficiente en el espacio de búsqueda y una explotación efectiva en la región de búsqueda son propiedades deseables de un algoritmo de optimización. Durante la exploración se buscan posibles soluciones factibles entre las diferentes regiones del espacio de búsqueda, mientras que una explotación exhaustiva acelera la búsqueda y la convergencia hacia una solución óptima, dentro de una región determinada del espacio de posibles soluciones. Diversos investigadores han explicado la relación entre la exploración y la explotación [19]  and [10] . Existen muchas variantes del algoritmo ED [17] que permiten la exploración y explotación en el espacio de búsqueda. La principal diferencia entre ellas radica en la selección de los factores de mutación y de cruza. El uso de las variantes del algoritmo de ED depende en gran medida del tipo de problema, como se muestra en [21]  and [22] .

En este artículo se propone una modificación al algoritmo de evolución diferencial con el propósito de promover la explotación de los individuos en una región de interés. Esta modificación consiste en incluir un mecanismo que puede considerarse como un método de búsqueda local y lo llamaremos mecanismo de explotación exhaustiva. Cabe mencionar que la exploración del espacio de búsqueda se realiza de la misma manera que en el algoritmo DE/Rand/1/Bin, por lo que se le nombra como «evolución diferencial con mecanismo de explotación exhaustiva»(EDMEE).

3.1.1. Algoritmo de evolución diferencial con mecanismo de explotación exhaustiva

El algoritmo de evolución diferencial con mecanismo de explotación exhaustiva (EDMEE) consta de un arreglo tridimensional, donde cada generación G  = 0, 1, . . . G_Max está conformada por una población de NP   individuos ${\textstyle {\overset {\rightarrow }{x}}_{G}=[{\overset {\rightarrow }{x}}_{G,1},{\overset {\rightarrow }{x}}_{G,2},...,{\overset {\rightarrow }{x}}_{G,i},...,{\overset {\rightarrow }{x}}_{G,NP}]^{T}}$ llamados población de padres, cada vector padre (individuo) ${\textstyle {\overset {\rightarrow }{x}}_{G,i}\quad \forall i=1,2,...,NP}$ agrupa D   variables de diseño ${\textstyle {\overset {\rightarrow }{x}}_{G,i}=[x_{G,i,1},x_{G,i,2},...,x_{G,i,j}...,x_{G,i,D}]^{T}}$ , siendo cada uno de estos individuos una solución al problema. La población inicial de padres ${\textstyle {\overset {\rightarrow }{x}}_{G=0}}$ se genera aleatoriamente como se muestra en la ecuación (37) , donde rand_j es una distribución aleatoria uniforme en el intervalo [0, 1], ${\textstyle x_{j}^{min}}$ ,${\textstyle x_{j}^{max}}$ ∀j  = 1, 2, …, D es el límite inferior y superior de las variables de diseño

$x_{G=0,i,j}=x_{j}^{min}+rand_{j}(0,1)(x_{j}^{max}-x_{j}^{min})$

( 37)

En cada generación G  = 1, 2, . . . , NP   se crea una nueva población de individuos a partir de un vector de mutación ${\textstyle {\overset {\rightarrow }{v}}_{i}}$ y del factor de cruza CR   . Esta nueva población se nombra población de hijos y está descrita por ${\textstyle {\overset {\rightarrow }{u}}_{G,i}=[u_{G,i,1},u_{G,i,2},...,u_{G,i,j}...,u_{G,i,D}]^{T}}$ ∀ i  = 1, 2, …, NP . Posteriormente, se realiza un proceso de selección elitista entre el i-ésimo   vector hijo ${\textstyle {\overset {\rightarrow }{u}}_{G,i}}$ y el i-ésimo   vector padre ${\textstyle {\overset {\rightarrow }{x}}_{G,i}}$ para determinar el individuo que pasa a la siguiente generación ${\textstyle {\overset {\rightarrow }{x}}_{G+1,i}}$ ; esto se realiza con base en un mecanismo de selección con manejo de restricciones (MSR). Si el vector hijo es seleccionado para pasar a la siguiente generación, el mecanismo de explotación exhaustiva (MEE) analiza y selecciona la información de este vector, en busca de una mejor solución en dicha región. De esta forma se podrán encontrar mejores soluciones en cada generación.

El pseudocódigo del algoritmo EDMEE se muestra en la figura 4 . Los procesos que se realizan en el algoritmo de evolución diferencial con el mecanismo de explotación exhaustiva se detallan a continuación.

Fig. 4. Pseudocódigo del algoritmo EDMEE, donde J es la función objetivo y g la suma de restricciones.

3.1.2. Mutación

El vector de mutación ${\textstyle {\overset {\rightarrow }{v}}_{G,i}}$ se genera a partir de la selección aleatoria de 3 vectores padres (individuos) ${\textstyle {\overset {\rightarrow }{x}}_{G,r_{1}},{\overset {\rightarrow }{x}}_{G,r_{2}},{\overset {\rightarrow }{x}}_{G,r_{3}}}$ , y se obtiene como la suma del vector de diferencia generado por ${\textstyle ({\overset {\rightarrow }{x}}_{G,r_{2}}-{\overset {\rightarrow }{x}}_{G,r_{3}})}$ y el vector base ${\textstyle {\overset {\rightarrow }{x}}_{G,r_{1}}}$ , expresado en (38) - (39) , donde r₁  ≠ r₂  ≠ r₃  ≠ i y F  ∈ [0, 1] es el factor de escala que controla la influencia del vector de diferencia en el vector ${\textstyle {\overset {\rightarrow }{x}}_{G,r_{1}}}$ . En (39) se realiza un acotamiento de ${\textstyle {\overline {v}}_{G,i,j}}$ cuando este sobrepasa los límites inferior y superior de la variable de diseño

${\begin{array}{l}\displaystyle {\overline {v}}_{G,i,j}=x_{G,r_{1},j}+F(x_{G,r_{2},j}-x_{G,r_{3},j})\forall i=1,...\\\displaystyle NP\forall j=1,...,D\end{array}}$

( 38)

$v_{G,i,j}=\left\{{\begin{array}{c}2x_{j}^{min}-{\overline {v}}_{G,i,j}\quad {\mbox{si}}\quad {\overline {v}}_{G,i,j}<x_{j}^{min}\\2x_{j}^{max}-{\overline {v}}_{G,i,j}\quad {\mbox{si}}\quad {\overline {v}}_{G,i,j}>x_{j}^{max}\\{\overline {v}}_{G,i,j}{\mbox{de}}\quad {\mbox{otra}}\quad {\mbox{manera}}\end{array}}\right\}\forall j=1,...,D$

( 39)

3.1.3. Cruza uniforme

El factor de cruza CR es el parámetro que determina el elemento j   del vector de mutación ${\textstyle {\overset {\rightarrow }{v}}_{G,i,j}}$ o el elemento j   del vector padre ${\textstyle {\overset {\rightarrow }{x}}_{G,i,j}}$ que formará parte del nuevo vector hijo ${\textstyle {\overset {\rightarrow }{u}}_{G,i}}$ , con la información combinada de los 2 vectores. Entonces, la influencia del vector de mutación y del vector padre sobre el nuevo vector hijo depende del factor CR . El proceso de cruza se describe en (40)

$u_{G,i,j}=\left\{{\begin{array}{c}v_{G,i,j}\quad {\mbox{si}}\quad (rand(0,1)\leq CR\quad {\mbox{o}}\quad j=j_{rand})\\x_{G,i,j}\quad {\mbox{de}}\quad {\mbox{otra}}\quad {\mbox{manera}}\end{array}}\right\}$

( 40)

3.1.4. Proceso de selección con restricciones

En el proceso de selección se decide el vector (individuo) que formará parte de la población de padres ${\textstyle {\overset {\rightarrow }{x}}_{G+1,i}}$ de la siguiente generación. Esta selección se realiza entre el i-ésimo   vector hijo ${\textstyle {\overset {\rightarrow }{u}}_{G,i}}$ y el i-ésimo   vector padre ${\textstyle {\overset {\rightarrow }{x}}_{G,i}}$ , donde el mejor individuo es el que pasa a la siguiente generación. Teniendo en consideración que el algoritmo tradicional de ED [17] no cuenta con un manejo de restricciones para la solución de problemas de optimización, en [23] se incorpora un mecanismo de selección con manejo de restricciones (MSR) en el algoritmo de ED. El MSR decide el vector que pasa a la siguiente generación. Esta decisión se fundamenta sobre los siguientes criterios:

• Entre 2 soluciones factibles, el que presenta mayor aptitud pasa a la siguiente generación.
• Si una solución es factible y la otra es no factible, la solución factible pasa a la siguiente generación.
• Si ambas soluciones son no factibles, la solución con la suma más baja de restricciones violadas pasa a la siguiente generación.

3.1.5. Mecanismo de explotación exhaustiva

El mecanismo de explotación exhaustiva (MEE) consiste en realizar una búsqueda más profunda en la misma dirección del vector hijo ${\textstyle {\overset {\rightarrow }{u}}_{G,i}}$ cuando este ha sido elegido para pertenecer a la población padre ${\textstyle {\overset {\rightarrow }{x}}_{G+1,i}}$ de la siguiente generación durante el proceso de selección. Este mecanismo realiza una búsqueda alrededor de la vecindad del vector hijo promoviendo así una explotación local. La capacidad de exploración del algoritmo EDMEE no sacrifica las cualidades del algoritmo tradicional DE/rand/1/bin, porque se activa solo cuando el vector hijo es seleccionado sobre el vector padre. Cuando el MEE es activado, un nuevo individuo ${\textstyle {\overset {\rightarrow }{\overset {\mbox{ˆ}}{u}}}_{i}}$ se genera a partir de la misma mutación y cruza, llamado vector hijo gemelo. La diferencia entre el vector hijo y el vector hijo gemelo es el factor de escala que se propone de la siguiente manera: ${\textstyle F_{2}=F(1-{\frac {w}{N_{w}+1}})}$ .

Entonces, si el vector hijo gemelo ${\textstyle {\overset {\rightarrow }{\overset {\mbox{ˆ}}{u}}}_{i}}$ mejora al vector hijo ${\textstyle {\overset {\rightarrow }{u}}_{G,i}}$ , este se convierte en parte de la población padre de la siguiente generación. Este mecanismo se puede repetir ${\textstyle N_{w}}$ veces (número máximo de búsqueda) o cuando el nuevo individuo ${\textstyle {\overset {\rightarrow }{\overset {\mbox{ˆ}}{u}}}_{i}}$ no es mejor al individuo anterior. Es importante hacer notar que el algoritmo de ED con explotación exhaustiva que se propone requiere un parámetro adicional que modifica el factor de escala y a su vez al vector de mutación. El pseudocódigo del mecanismo de explotación exhaustiva se muestra en la figura 5 .

Fig. 5. Pseudocódigo del mecanismo de explotación exhaustiva.

Una vez que la población de la nueva generación de padres ${\textstyle {\overset {\rightarrow }{x}}_{G+1,i}}$ ∀i  = 1, . . . , NP se crea, se repite el proceso de mutación, cruza, selección y explotación exhaustiva, hasta que el criterio de paro se satisface. Para este caso en particular se seleccionó el número máximo de generaciones G_Max  = 60.000, para tal efecto.

4. Resultados

La plataforma sobre la que se desarrolla el presente trabajo consta de una PC con procesador core i 7 − 4770K a 3,5 GHz y 32 GB de RAM, en Windows. El algoritmo de optimización EDMEE se programa en Matlab Versión 7.9, se realizaron un conjunto de 30 corridas con una población de individuos NP  = 200, factor de cruza CR  = 0, 5, factor de escala F   ∈ (0,5-0,9) y factor de búsqueda ${\textstyle N_{w}=6}$ , el criterio de paro queda establecido por la generación máxima G_Max  = 60.000. Con el propósito de comparar los resultados obtenidos del algoritmo EDMEE se incluye una versión del algoritmo de ED con MSR pero sin considerar el mecanismo de explotación exhaustiva (MEE), nombrándolo EDMSR. De igual forma se ejecutan 30 corridas con la versión de EDMSR en Matlab con la misma PC, con factor de escala F   =(0,4-0,9), siendo los demás parámetros los mismos que EDMEE.

En la tabla 2 se muestran los resultados estadísticos del desempeño de los algoritmo de EDMEE y de EDMSR, donde mean (J ) es el promedio de las 30 mejores funciones objetivos encontradas en cada corrida, J^* es el mejor individuo encontrado en las 30 corridas, σ (J ) es la desviación estándar de las 30 mejores funciones objetivos encontradas en cada corrida y mean (Tiempo ) es el tiempo promedio de convergencia de las 30 corridas. Se puede observar que el algoritmo EDMEE encuentra la mejor solución (ver columna J^* de la tabla 2 ), es decir, el sistema presenta menor energía mecánica (J^*  = 41, 1643 Nm ) en las posiciones críticas de interés en comparación con lo obtenido con el algoritmo EDMSR (J^*  = 41, 1721 Nm ). Además se observa en la columna de mean (J ) que en promedio se obtienen mejores resultados con el algoritmo EDMEE que con el algoritmo EDMSR y se muestra en la columna σ (J ) que existe más dispersión en la solución obtenida con el algoritmo EDMEE, debido al mecanismo MEE. Por lo tanto, el mecanismo MEE en el algoritmo EDMEE explota de una mejor manera la región de interés dando como resultado mejores soluciones, las cuales no es posible alcanzar con el algoritmo EDMSR. Sin embargo, si el área de interés no es la adecuada la convergencia podría no ser la mejor (convergencia prematura hacia óptimos locales). Es así que para obtener los mejores resultados con el algoritmo EDMEE se recomienda que se realicen varias corridas del algoritmo.

Tabla 2. Resultados estadísticos del algoritmo EDMEE y del algoritmo EDMSR para 30 corridas.

J* [Nm ]		mean (J )		σ (J ) [Nm ]		mean (Tiempo ) [min ]
EDMEE	EDMSR	EDMEE	EDMSR	EDMEE	EDMSR	EDMEE	EDMSR
41, 1643	41, 1721	41, 3861	41, 3864	3, 6887	3, 4660	57, 38	57, 13

Las 2 desventajas que presenta el algoritmo EDMEE son: i ) Requiere mayor tiempo computacional debido al número de veces que se necesita evaluar la función objetivo dentro del MEE. Sin embargo, utilizando computadoras de alto rendimiento esto podría no ser un inconveniente, o en el diseño en ingeniería, en donde el objetivo primordial es maximizar la eficiencia en el diseño «sin importar»el tiempo computacional. ii ) Se requiere realizar varias corridas del algoritmo para obtener los mejores resultados. iii   ) Se requiere sintonizar un parámetro adicional ${\textstyle N_{w}}$ .

Los parámetros de diseño p_a del mejor individuo (J^* ) de las 30 corridas para los algoritmos EDMEE y EDMSR se nombran como ^*EDMEEp_a y ^*EDMSRp_a , respectivamente, los cuales se muestran en la tabla 3 . En la tabla 4 se muestran los resultados de los parámetros de diseño ^*EDMEEp_b , ^*EDMSRp_b . Se puede observar en la tabla 4 que los ángulos de los eslabones cumplen con las restricciones impuestas en el problema de optimización y se puede observar que el manipulador presenta un espacio de trabajo diestro pre-establecido, es decir, las posiciones x_d y z_d son alcanzadas con diferentes orientaciones ϕ_d , sin violar las restricciones impuestas, por lo tanto podemos asegurar que se satisface el requerimiento del espacio de trabajo diestro.

Tabla 3. Parámetros p_a del mejor individuo encontrado (J^* ) con los algoritmos EDMEE y EDMSR.

Eslabón 1 y 3				Eslabón 2
Algoritmo	Longitud [m]	pcx[m]	pcy[m]	Algoritmo	Longitud [m]	pcx[m]	pcy[m]
EDMEE	0, 3689	0, 0999	0, 0999	EDMEE	0, 0740	0, 0999	−0, 0999
EDMSR	0, 3503	0, 0999	0, 1	EDMSR	0, 0904	0, 0999	−0, 0999
Eslabón 4				Eslabón 5
Algoritmo	Longitud [m]	pcx[m]	pcy[m]	Algoritmo	Longitud [m]	pcx[m]	pcy[m]
EDMEE	0, 4578	−0, 0999	0, 0998	EDMEE	0, 0761	−0, 0689	0, 0318
EDMSR	0, 4604	−0, 0999	0, 0999	EDMSR	0, 0496	−0, 0440	0, 0223

Tabla 4. Parámetros p_b del mejor individuo encontrado J^* con los algoritmos EDMEE y EDMSR.

		${\textstyle (x_{d_{1,1}},z_{d_{1,1}})}$			${\textstyle (x_{d_{1,2}},z_{d_{1,2}})}$			${\textstyle (x_{d_{2,1}},z_{d_{2,1}})}$			${\textstyle (x_{d_{2,2}},z_{d_{2,2}})}$
EDMEE	ϕd[rad]	-1,5707	0	1,5707	-1,5707	0	1,5707	-1,5707	0	1,5707	-1,5707	0	1,5707
	q1[rad]	2,0917	2,3206	1,7228	2,0805	2,3601	2,1652	0,9630	1,0789	0,7907	0,8812	1,2434	1,0198
	q2[rad]	2,8211	2,7592	2,3045	3,4844	3,4519	3,1821	2,8618	2,6294	2,5959	3,5738	3,2539	3,1640
	q3[rad]	-1,2664	0,3827	2,4255	-1,9304	-0,3094	1,5465	-1,3078	0,5119	2,1344	-2,0200	-0,1123	1,5649
		(xd1,1,zd1,1)			(xd1,2,zd1,2)			(xd2,1,zd2,1)			(xd2,2,zd2,2)
EDMSR	ϕd[rad]	-1,5707	0	1,5707	-1,5707	0	1,5707	-1,5707	0	1,5707	-1,5707	0	1,5707
	q1[rad]	2,1320	2,2862	1,9036	2,1248	2,3158	2,1950	0,9322	1,0182	0,8219	0,8592	1,1382	0,9857
	q2[rad]	2,8172	2,7752	2,4877	3,4759	3,4550	3,2861	2,8522	2,6977	2,6780	3,5549	3,3217	3,2692
	q3[rad]	-1,2633	0,3657	2,2416	-1,9219	-0,3143	1,4420	-1,2990	0,4436	2,0507	-2,0013	-0,1813	1,4602

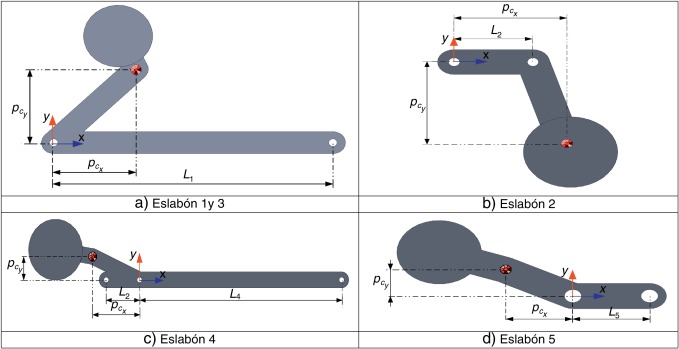
En la figura 6 se muestran las formas de los eslabones obtenidas a partir de los parámetros ^EDMEEp_a , donde la separación entre los ejes de unión es la longitud del eslabón L_i y el centro de masa está representado por las coordenadas ${\textstyle p_{c_{x_{i}}}}$ , ${\textstyle p_{c_{y_{i}}}}$ . La forma del eslabón se obtuvo de un proceso posterior de haber encontrado los parámetros ^EDMEEp_a .

Fig. 6. Representación en CAD con el diseño EDMEEpa obtenido a través del algoritmo EDMEE.

Los resultados obtenidos con el establecimiento formal del problema de optimización consideran el comportamiento cinemático del manipulador y garantizan que la energía mecánica del manipulador es mínima en las posiciones críticas del espacio de trabajo (posiciones del sistema en donde se ejerce mayor energía mecánica).

Con el propósito de validar el comportamiento dinámico del diseño mecánico obtenido con el algoritmo EDMEE (^*EDMEEp_a ), se compara con los siguientes 3 diseños:

• a) Diseño EDMSR. Se consideran los parámetros de diseño ^*EDMSRp_a obtenidos del algoritmo EDMSR.
• b) Diseño NOEDMEE. Se consideran las longitudes de los eslabones L_i obtenidos de ^*EDMEEp_a . Además, se establece lo siguiente: ${\textstyle p_{c_{ix}}={\frac {L_{i}}{2}}m,\quad }$ y${\textstyle \quad p_{c_{y}}=0m}$ .
• c) Diseño NOEDMSR. Se consideran las longitudes de los eslabones L_i obtenidos de ^*EDMSRp_a . Además se establece lo siguiente: ${\textstyle p_{c_{ix}}={\frac {L_{i}}{2}}m,\quad }$ y${\textstyle \quad p_{c_{y}}=0m}$ .

Debido a que se están considerando las posiciones críticas en el espacio de trabajo para la obtención de los parámetros de diseños óptimos, se verifica que la energía mecánica del manipulador en cualquier posición dentro del espacio de trabajo pre-establecido presenta de igual forma una disminución en el par de control aplicado en comparación con los otros 3 diseños.

La comparación consiste en verificar el par entregado (energía) por el sistema de control del robot al realizar una tarea específica. Para realizar dicha comparación, se requiere del modelo dinámico del manipulador móvil (ver [14] ) y se propone el sistema de control PID para el manipulador y el control PD para el móvil en el problema de regulación, es decir, se desea que el manipulador móvil se estabilice en: X_d  = 0, 15 m , Y_d  = 0, 1 m   , ${\textstyle \Phi _{d}={\frac {7}{36}}\pi rad}$ , ${\textstyle q_{1_{d}}={\frac {1}{6}}\pi rad}$ , ${\textstyle q_{2_{d}}=\pi rad}$ , ${\textstyle q_{3_{d}}=0rad}$ . Las ganancias del controlador para cada diseño se proponen de acuerdo a la tabla 5 . Los valores de las ganancias del controlador se escogen de tal manera que el comportamiento del sistema sea semejante en todos los diseños y así la evaluación de la magnitud del par de control se realice considerando una trayectoria similar.

Tabla 5. Parámetros del controlador PID para el diseño EDMEE y EDMSR.

ui	Ganancias ${\textstyle [k_{p_{i}},k_{d_{i}},k_{i_{i}}]}$
u1	[1,3, 2,6, 0]	[1,3, 2,6, 0]	[1,3, 2,6, 0]	[1,3, 2,6, 0]
u2	[1,3, 2,6, 0]	[1,3, 2,6, 0]	[1,3, 2,75, 0]	[1,3, 2,75, 0]
u3	[4, 1,6, 0]	[4, 1,6, 0]	[4, 1,6, 0]	[4, 1,6, 0]
u4	[9,1, 2,05, 5,3]	[9, 2, 5]	[8,2, 2, 3]	[8,2, 1,7, 3]
u5	[5, 1, 6]	[5, 1, 6,3]	[8, 1,4, 6]	[6, 1,4, 4,8]
u6	[0,5, 0,1, 1]	[0,8, 0,19, 1,1]	[1, 0,057, 0,5]	[0,8, 0,057, 1]
	EDMEE	EDMSR	NOEDMEE	NOEDMSR

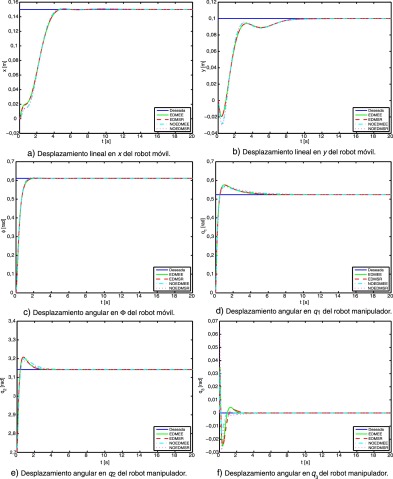
En la figura 7 se muestra el desempeño en el comportamiento del manipulador móvil con el controlador considerando los 3 diseños. Se puede observar que el manipulador móvil presenta un comportamiento similar y que en todos los casos el sistema de control hace que la posición del robot manipulador llegue a la posición deseada.

Fig. 7. Comportamiento dinámico del manipulador móvil considerando todos los diseños.

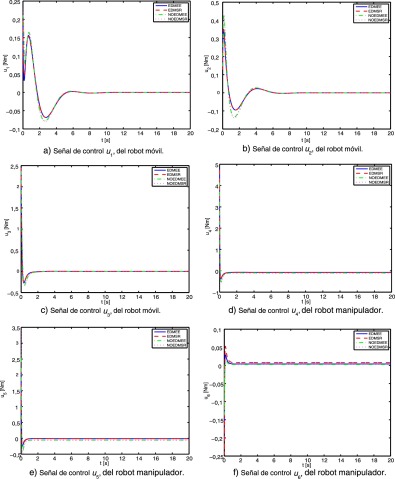
En la figura 8 se muestran de forma individual los elementos del vector de la señal de control u  ∈ R⁶ . Se observa a simple vista que los diseños NOEDMEE y NOEDMSR requieren de mayor par de control para realizar la tarea en comparación con los diseños EDMEE y EDMSR. Se puede observar en la tabla 6 los resultados numéricos de la magnitud de cada elemento del vector de la señal de control u así como en la última columna se muestra la suma de dichas magnitudes, en donde se indica que el diseño EDMEE provee de menos par al manipulador móvil. Es claro que al disminuir el par suministrado por el sistema de control se disminuye la potencia entregada por el mismo y, a su vez, se puede relacionar con el consumo de energía eléctrica que se requiere para estabilizar el sistema. Por lo tanto, el diseño EDMEE requiere de menos energía en el sistema de control para realizar una tarea dentro del espacio de trabajo debido a que minimizó la energía mecánica del manipulador en las posiciones críticas del espacio de trabajo.

Fig. 8. Señal de control para realizar la tarea considerando todos los diseños.

Tabla 6. Consumo de energía del sistema de control del manipulador móvil considerando el comportamiento dinámico del manipulador móvil para realizar la tarea.

Diseño	||u1 || [Nm]	||u2 || [Nm]	||u3 || [Nm]	||u4 || [Nm]	||u5 || [Nm]	||u6 || [Nm]	${\textstyle \sum \left\|u_{i}\right\|}$ [Nm]
a) Diseño EDMEE	2, 2378	2, 9677	7, 0933	9, 6059	4, 7793	0, 4279	27, 1121
b) Diseño EDMSR	2, 2252	2, 9608	7, 0476	9, 9359	4, 2758	0, 7763	27, 2218
c) Diseño NOEDMEE	2, 5369	3, 7943	8, 1505	11, 0552	7, 2971	0, 2731	33, 1073
d) Diseño NOEDMSR	2, 5736	3, 9145	8, 4133	11, 7998	8, 3236	0, 5477	35, 5727

Es así que se muestra que el diseño EDMEE presenta un espacio de trabajo diestro y que las tareas que se generan dentro del espacio de trabajo se realizan con menos consumo de energía en comparación con los 3 diseños propuestos, por lo que se verifica lo que se establece en el problema de diseño.

5. Conclusiones

En este trabajo se desarrolla una metodología de diseño de los eslabones de un manipulador móvil como un problema de optimización mono-objetivo con el propósito de minimizar la energía consumida en el sistema de control dentro de un espacio de trabajo diestro pre-establecido por el diseñador. La formulación del problema se aborda con el uso de la energía mecánica del robot en posiciones críticas de un espacio de trabajo pre-establecido.

Para dar solución al problema de optimización se incluye un mecanismo de explotación exhaustiva (MEE) en el algoritmo Evolución Diferencial. El mecanismo propuesto presenta un mejor comportamiento en la búsqueda de soluciones, ya que permite explotar los individuos en una región. Sin embargo, se tiene la desventaja en aumentar el tiempo computacional, se requiere de diversas corridas y se debe sintonizar un parámetro adicional en el algoritmo. Para efectos de diseño en ingeniería, en donde se desea maximizar su desempeño, la inclusión del MEE en el algoritmo de evolución diferencial resulta muy útil.

Los resultados en simulación del diseño EDMEE muestran que se cumple el objetivo propuesto comparándolo con otros 3 diseños, es decir, se minimiza la energía consumida por el sistema de control.

La metodología de diseño propuesta no solo sirve para las posiciones críticas del espacio de trabajo sino para todo el espacio de trabajo que se cubre. Además funciona para cualquier sistema de control que se implemente.

Agradecimientos

Este trabajo fue apoyado en parte por la Secretaría de Investigación y Posgrado del Instituto Politécnico Nacional (SIP-IPN) bajo el proyecto SIP  − 20140926 y en parte por el Consejo Nacional de Ciencia y Tecnología (CONACYT) bajo el proyecto 182298.

References

1. [1] M. Villarreal-Cervantes, C. Cruz-Villar, J. Alvarez-Gallegos, E. Portilla-Flores; Robust structure-control design approach for mechatronic systems; IEEE/ASME Trans. Mechatronics, 18 (5) (2013), pp. 1592–1601
2. [2] C.A. Cruz-Villar, J. Alvarez-Gallegos, M.G. Villarreal-Cervantes; Concurrent redesign of an underactuated robot manipulator; Mechatronics, 19 (2) (2009), pp. 178–183
3. [3] Q. Li, W. Zhang, L. Chen; Design for control-a concurrent engineering approach for mechatronic systems design; IEEE/ASME Trans. Mechatronics, 6 (2) (2001), pp. 161–169
4. [4] S.F. Alyaqout, P.Y. Papalambros, A.G. Ulsoy; Combined robust design and robust control of an electric dc motor; IEEE/ASME Trans. Mechatronics, 16 (3) (2011), pp. 574–582
5. [5] W. Zhang, Q. Li, L.S. Guo; Integrated design of mechanical structure and control algorithm for a programmable four-bar linkage; IEEE/ASME Trans. Mechatronics, 4 (4) (1999), pp. 354–362
6. [6] J.-H. Park, H. Asada; Concurrent design optimization of mechanical structure and control for high speed robots; J. Dyn. Sys., Meas., Control, 116 (1994), pp. 344–356
7. [7] A.C. Pil, H.H. Asada; Integrated structure/control design of mechatronic systems using a recursive experimental optimization method; IEEE/ASME Trans. Mechatronics, 1 (3) (1996), pp. 191–203
8. [8] T. Ravichandran, D. Wang, G. Heppler; Simultaneous plant-controller design optimization of a two-link planar manipulator; Mechatronics, 16 (3-4) (2006), pp. 233–242
9. [9] M.G. Villarreal-Cervantes, C.A. Cruz-Villar, J. Alvarez-Gallegos, E.A. Portilla-Flores; Differential evolution techniques for the structure-control design of a five-bar parallel robot; Eng. Optimiz., 42 (6) (2010), pp. 535–565
10. [10] E.A. Portilla-Flores, E. Mezura-Montes, J. Alvarez-Gallegos, C.A. Coello-Coello, C.A. Cruz-Villar, M.G. Villarreal-Cervantes; Parametric reconfiguration improvement in non-iterative concurrent mechatronic design using an evolutionary-based approach; Eng. Appl. Artif. Intel., 24 (5) (2011), pp. 757–771
11. [11] M.G. Villarreal-Cervantes, C.A. Cruz-Villar, J. Alvarez-Gallegos; Synergetic structure-control design via a hybrid gradient-evolutionary algorithm; Optim. Eng. (2014), pp. 1–29
12. [12] S. Ogasawara, K. Hiramoto, H. Doki; Global optimal design of dynamic parameters of robot manipulators; IEEE Intl. Conf. Contr. (2007), pp. 307–312
13. [13] M. Spong, S. Hutchinson; Robot Modeling and Control; Wiley (2005)
14. [14] M.G. Villarreal-Cervantes, C.A. Cruz-Villar, S.A. Saldívar-Bárcenas, L.E. García-Sosa; Dynamic coupling between a parallel manipulator and an omnidirectional mobile platform; XV Latinamerican Control Conference (2012), pp. 1–6
15. [15] R. Kelly, V. Santibáñez Davila, J.A. Loría Perez; Control of Robot Manipulators in Joint Space (Advanced Textbooks in Control and Signal Processing); Springer (2005)
16. [16] R. Storn, K. Price; A simple and efficient heuristic for global optimization over continuous spaces; J. Global Optim., 11 (4) (1997), pp. 341–359
17. [17] K. Price, R.M. Storn, J.A. Lampinen; Differential Evolution: A Practical Approach to Global Optimization; Natural Computing Series, Springer-Verlag New York, Inc (2005)
18. [18] J. Dongli, Z. Guoxing, K. Muhammad; An effective memetic differential evolution algorithm based on chaotic local search; Inform. Sciences, 181 (2011), pp. 3175–3187
19. [19] W. Chunquiu, W. Jung, Y. Geng, G. Huajie, Z. Xing; Wind farm micro-siting by gaussian particle swarm optimization with local search strategy; Renew Energ., 48 (2012), pp. 276–286
20. [20] M.G. Epitropakis, D.K. Tasoulis, N.G. Pavlidis, V.P. Plagianakos, M.N. Vrahatis; Enhancing differential evolution utilizing proximitybased mutation operators; IEEE Trans. Evol. Comput., 15 (1) (2011), pp. 99–119
21. [21] M.G. Villarreal-Cervantes, C.A. Cruz-Villar, J. Alvarez-Gallegos, E.A. Portilla-Flores; Kinematic dexterity maximization of an omnidirectional wheeled mobile robot: A comparison of metaheuristic and sqp algorithms; Int. J. Adv. Robot. Syst., 9 (161) (2012), pp. 1–12
22. [22] E. Mezura-Montes, J. Velázquez-Reyes, C.A. Coello-Coello; A comparative study of differential evolution variants for global optimization; Genetic And Evolutionary Computation Conference (2006), pp. 485–492
23. [23] E. Mezura-Montes, C. Coello Coello, E. Tun-Morales; Simple feasibility rules and differential evolution for constrained optimization; Springer, Berlin Heidelberg (2004), pp. 707–716