Data imprecision under λ-geometry model: Range searching problem

Abstract

Because of constraints in exact modeling, measuring and computing, it is inevitable that algorithms that solve real world problems have to avoid errors. Hence, proposing models to handle error, and designing algorithms that work well in practice, are challenging fields. In this paper, we introduce a model called the ${\textstyle \lambda }$ -geometry model   to handle a dynamic form of imprecision, which allows the precision to change monotonically in the input data of geometric algorithms. ${\textstyle \lambda }$ -geometry is a generalization of region-based models and provides the output of problems as functions, with respect to the level of precision. This type of output helps to design exact algorithms and is also useful in decision making processes. Furthermore, we study the problem of orthogonal range searching in one and two dimensional space under the model of ${\textstyle \lambda }$ -geometry, and propose efficient algorithms to solve it.

Keywords

Imprecise data ; Modeling ; Dynamic imprecision ; Computational geometry ; Range searching problem

1. Introduction

It is inevitable that algorithms that solve real world problems have to avoid errors. First, there is error in gathering data because of the limitations of measuring tools and observing methods, like sensor inaccuracies. Also, problem modeling, data processing and, finally, implementing a designed algorithm, are not free of error because of the properties of the real world, which is a non-Euclidean space, and the limitation of computations like finite precision and rounding errors. Accordingly, significant studies have focused on modeling and handling imprecision, and different approaches, such as probability theory  [1] , fuzzy set theory  [2] and rough set theory  [3] , have been presented to deal with uncertainty and imprecision. Beside these approaches, computational geometry has been used also for modeling and handling uncertainty and imprecision  [4] , [5]  and [6] . Computational geometry has applications in designing algorithms for real problems, such as geographic information systems  [7] , planning and robotics  [8] , facility locations  [9] , mechanical design  [10] and pattern processing  [11]  and [12] .

Geometric approaches to handling imprecision focus on the definition of an imprecise point, and model a point by a geometric region; hence, these approaches are called region-based   models. In this area, ${\textstyle \epsilon }$ -geometry   as one of the earliest approach models each imprecise point by a disk whose radius is ${\textstyle \epsilon }$   [13] . In fact, ${\textstyle \epsilon }$ -geometry considers the maximum error, ${\textstyle \epsilon }$ , for an imprecise point in all directions. However, interval geometry and tolerance-based approaches  [14]  and [15] take into account only the error in coordinates, resulting in an axis-aligned rectangular region. Other regions, such as segment, square and convex polygons, have also been considered to represent an imprecise point. A thorough study of region-based models is presented in  [4] . Several problems have been studied under the region-based models. For example, finding the largest/smallest area axis aligned bounding box  [16] , the largest/smallest area/perimeter convex hull  [17] , and the Voronoi diagram and Delaunay triangulation  [5]  and [18] . Also, dependency as a new concept in uncertainty and error handling was introduced in  [6] , and efficient algorithms have been presented for finding the closest and the furthest pairs, as well as solving range searching problems  [19] . The problems of finding the diameter and the minimum enclosing circle for a set of imprecise points modeled by a set of finite candidates have been studied in  [20] . In this type of modeling, each imprecise point has finite weighted elements as candidates, such that the weights govern the probability that the data point is at that particular location.

Although region-based models are easy and efficient approaches to handle imprecision, they are not yet strong enough to deal with circumstances occurring in real world problems. They assume that the probability of the presence of an imprecise point anywhere in its region is the same; in fact they assume a uniform distribution for all instances of an imprecise point, which is not true in most real applications. Moreover, usually, imprecision in the real world can be decreased by spending more. For example, a Geographical Positioning System (GPS) is a popular measuring approach for determining the location of a point on the earth using satellites. But, there is still considerable error in the GPS, due to satellite signal errors, receiver noise, orbital error, multipath error and atmospheric conditions  [21] . A natural technique for increasing the precision of the GPS is to increase the number of satellites, which is called differential GPS. It gathers local information to obtain a more precise measurement. This idea can also be applied to observing and measuring devices, such as light data and ranging  [22] and laser scanning systems  [23] . Generally, by repeating an experiment, we can achieve more precision. Also, it is possible to decrease computational errors by providing more space for floating points and arithmetic calculations.

The issues mentioned above have motivated us to propose a dynamic model, called the ${\textstyle \lambda }$ -geometry model,   for handling imprecision. We have introduced a parameter, ${\textstyle \lambda }$ , representing the level of imprecision. It changes continuously in the interval [0, 1] according to circumstances, such as changes in the precision of measurements or computations. This model is a generalization of static region-based models and allows regions to shrink (or grow), according to increase (or decrease) in the level of precision. So, the outputs of problems under the ${\textstyle \lambda }$ -geometry model are functions based on parameter ${\textstyle \lambda }$ . For values of ${\textstyle \lambda }$ near to 0, the solutions are very similar to exact data solutions, and for values of ${\textstyle \lambda }$ near to 1, algorithms are able to guarantee the correctness of the output, with respect to the worst case of imprecision in the input data. So, for small values of ${\textstyle \lambda }$ , only closer instances to the exact value of an imprecise point affects the output, and by increasing ${\textstyle \lambda }$ , the range of such efficient instances extends as well. Consequently, the ${\textstyle \lambda }$ -geometry model provides different levels of distribution for instances of an imprecise point. We have recently studied the problem of finding the largest axis-aligned bounding box of a set of n imprecise points under this model  [24] . We proposed an ${\textstyle O(n(logn+k))}$ time algorithm to solve this problem, where k   is the maximum complexity of a region representing an imprecise point. To make the paper self-contained, we explain the model of ${\textstyle \lambda }$ -geometry and investigate some of its properties in the next section. In the third section, we study the problem of orthogonal range searching in one dimensional space under the ${\textstyle \lambda }$ -geometry model, and propose efficient algorithms to varieties of the problem. In the fourth section, we extend the algorithm to an application-based version of the problem in the plane, and, finally, we conclude our work in the last section.

2. The model of ${\textstyle \lambda }$ -geometry2. The model of λ {\textstyle \lambda } -geometry

As mentioned above, the region-based models are simple approaches for representing imprecision. When an imprecise point is modeled by a convex object, like a rectangle, it assumed that the point can present anywhere within the object. So, by changing the levels of precision, like increasing the precision of measuring tools, the size of the object changes, too. This means that the object shrinks by increasing the level of precision, however, it is possible that the amount of shrinking is not the same in all directions. Taking into account these concepts, we introduce the model of ${\textstyle \lambda }$ -geometry.

2.1. ${\textstyle \lambda }$ -geometry model2.1. λ {\textstyle \lambda } -geometry model

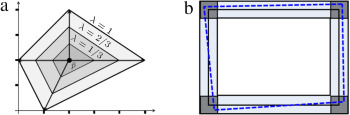
An imprecise d   -dimensional point ${\textstyle p(\lambda )}$ in the ${\textstyle \lambda }$ -geometry model is defined as ${\textstyle p(\lambda )=({\overline {p}},\lambda M)}$ , where ${\textstyle {\overline {p}}}$ is the exact value of the imprecise point p   , ${\textstyle M=[v_{1},v_{1},\ldots ,v_{k}]_{d\times k}}$ is the imprecision matrix   in which each vector ${\textstyle v_{i}}$ , for ${\textstyle i=1,2,\ldots ,k}$ , defines the maximum imprecision in its direction, and parameter ${\textstyle \lambda }$ shows the imprecision level   for each ${\textstyle v_{i}}$ . The parameter, ${\textstyle \lambda }$ , continuously changes in the interval [0, 1]. So, for any ${\textstyle \lambda \in }$ [0, 1], a region is considered for handling an imprecise point. This region, which includes all possible instances of a point, p   , is the convex hull of points defined by the sum of the vectors, ${\textstyle \lambda v_{i}}$ and ${\textstyle {\overline {p}}}$ . Figure 1 a illustrates an imprecise point, p   , in the plane for different ${\textstyle \lambda }$ s, where ${\textstyle {\overline {p}}=[{\begin{array}{c}2\\2\end{array}}]}$ and ${\textstyle M=[{\begin{array}{c}3\\0\end{array}}{\begin{array}{c}0-\\2\end{array}}{\begin{array}{c}2\\0\end{array}}{\begin{array}{c}-1\\-2\end{array}}]}$ .

Figure 1. (a) Imprecise point p   for different imprecision levels, ${\textstyle \lambda =0}$ , 1/3, 2/3 and 1. (b) Example of a rectangle in the model of ${\textstyle \lambda }$ -geometry for ${\textstyle \lambda =0,1}$ ; each vertex of the rectangle is an imprecise point with a square region. Note that in this model, it is possible that the angles of a rectangle are not exactly equal to ${\textstyle \pi /2}$ , e.g. an instance of the rectangle for ${\textstyle \lambda =1}$ is shown by a blue dashed rectangle.

For ${\textstyle \lambda =0}$ , the imprecise point, ${\textstyle p(\lambda )}$ , is just the exact point, ${\textstyle {\overline {p}}}$ , while, for ${\textstyle \lambda =1}$ , it is the convex hull of the points induced by the vectors of M . Such a convex hull can be defined as follows:

${\begin{array}{l}\displaystyle p(\lambda =1)=\lbrace \sum _{i=1}^{k}\alpha _{i}({\overline {p}}+u_{i})\vert ,\alpha _{i}\geq 0fori=1,2,\ldots ,k\\\displaystyle and\sum _{i=1}^{k}\alpha _{i}=1\rbrace {\mbox{,}}\end{array}}$

where ${\textstyle u_{i}}$ , for ${\textstyle i=1,2,\ldots ,k}$ are the endpoints of the imprecision vectors of p . Note that, since we define p by the concept of a convex hull, it is possible for a vector to be ineffective. But, without loss of generality, we assume that all vectors are effective.

Now, we focus on the algebraic definition of an instance of an imprecise point, p   (${\textstyle \lambda }$ , ${\textstyle \gamma }$ ):

$p(\lambda ,\gamma )={\overline {p}}+\lambda M{\mbox{;}}\quad \gamma =[\gamma _{1},\gamma _{1},\ldots ,\gamma _{k}]^{T}$

In this definition, ${\textstyle \gamma }$ is an arbitrary vector that defines an instance, p   (${\textstyle \lambda ,\gamma }$ ), to be anywhere in the convex hull mentioned earlier. So, an imprecise point, ${\textstyle p(\lambda )}$ , is a region defined by:

${\begin{array}{l}\displaystyle p(\lambda )=\lbrace p(\lambda ,\gamma )\vert \forall \gamma =[\gamma _{1},\gamma _{1},\ldots ,\gamma _{k}];0\leq \gamma _{i}\leq 1,fori=1,2\\\displaystyle \ldots ,k;and\sum _{i=1}^{k}\gamma _{i}\leq 1\rbrace {\mbox{.}}\end{array}}$

By using the imprecision matrix, region ${\textstyle p(\lambda )}$ , for an imprecise point, p,   is a polygonal shape. So, a disk shaped region which is a popular and practical, representing a region in an imprecise context, is not supported. However, by using more imprecise vectors, we can approximate a disk shaped region, but this causes an increase in the complexity of the region. To efficiently model a disk shaped region in the ${\textstyle \lambda }$ -geometry model, we define an imprecise point, p,   with a disk shaped region, by ${\textstyle p(\lambda )=({\overline {p}},\lambda r)}$ , where ${\textstyle {\overline {p}}}$ is the center of the disk and r   is its radius, which corresponds to ${\textstyle \lambda =1}$ .

In many models of imprecision, a line is defined by two imprecise points, which is the union of all lines that pass through the corresponding regions of the points. Similarly, the line constructed by two imprecise points, ${\textstyle p(\lambda )}$ and ${\textstyle q(\lambda )}$ , is defined as follows:

${\begin{array}{l}\displaystyle L_{p,q}(\lambda )=\lbrace l(p^{'}\\\displaystyle q^{'})\vert p^{'}andq^{'}are~instances~ofp(\lambda )andq(\lambda )\rbrace {\mbox{,}}\end{array}}$

where ${\textstyle l(p^{'},q^{'})}$ is the line passing through ${\textstyle p^{'}}$ and ${\textstyle q^{'}}$ . This definition can be generalized for defining imprecise segments and polygons as well. Figure 1 b shows a rectangle under the model of ${\textstyle \lambda }$ -geometry.

2.2. Properties of the ${\textstyle \lambda }$ -geometry model2.2. Properties of the λ {\textstyle \lambda } -geometry model

The ${\textstyle \lambda }$ -geometry model is a generalization of region-based models with the advantage that it can handle dynamic imprecision. As aforementioned, in the region-based models, there is no difference between instances of an imprecise point in terms of imprecision probability, and all instances are the same, which is against most real applications. In fact, these models assume a uniform distribution for all instances of an imprecise point. For example, when an imprecise point is modeled by a disk in the region-based models, its center and boundary points have the same probability for the presence of the point, while it is not true in general. Such dissimilarity is handled by defining the distribution function in probability theory, or by the membership function in fuzzy theory, and has been applied to imprecise data  [25]  and [26] . In the ${\textstyle \lambda }$ -geometry model, parameter ${\textstyle \lambda \in [0,1]}$ plays this role by continuously shrinking the region of an imprecise point. Note that, since we are able to define an arbitrary size for the vectors in the imprecision matrix, M   , upper bound 1 for ${\textstyle \lambda }$ is not important and can be replaced by any positive value.

The output of problems under the ${\textstyle \lambda }$ -geometry model is one or more functions based on ${\textstyle \lambda }$ , while it changes continuously in [0, 1]. Such functions can be useful in the decision making process. For instance, the model of ${\textstyle \lambda }$ -geometry helps to handle the zero problem in machines and in designing robust and stable geometric algorithms  [27] . This problem asks if the value of an equation is exactly 0 or not. For example, when we need to determine whether point ${\textstyle p=(x_{0},y_{0})}$ lies on line ${\textstyle l:ax+by+c=0}$ or not, we need to solve the equation “${\textstyle ax_{0}+by_{0}+c=0}$ ”. Because of finite precision in the machine, it is possible for a fatal error to occur in solving this equation. Using the ${\textstyle \epsilon }$ -geometry model  [13] , we solve the problem “Is ${\textstyle \vert ax_{0}+by_{0}+c\vert <\epsilon }$ ?”. Determining an appropriate value for ${\textstyle \epsilon }$ is difficult and it depends on the machine precision. To smooth this problem, we suggest solving the problem under the ${\textstyle \lambda }$ -geometry model, which is “Is ${\textstyle \vert ax_{0}+by_{0}+c\vert <\lambda \epsilon }$ ?” where ${\textstyle \lambda }$ continuously changes in [0, 1]. The solution of this problem is functional and three cases may happen:

• For all values of ${\textstyle \lambda }$ in [0, 1], the solution is true .
• For all values of ${\textstyle \lambda }$ in [0, 1], the solution is false .
• There is a value, ${\textstyle \lambda _{0}}$ , where, for all values of ${\textstyle \lambda }$ in ${\textstyle [0,\lambda _{0}]}$ or ${\textstyle [0,\lambda _{0}]}$ , the solution is false and for other values it is true .

Final decision in two first cases is straightforward and in the last case decision can be dealt with regarding the magnitude of ${\textstyle \lambda _{0}}$ .

The dynamic view in the model of ${\textstyle \lambda }$ -geometry can be seen as a trade-off between costs and benefits associated with the imprecision level, ${\textstyle \lambda }$ . Thus, the model of ${\textstyle \lambda }$ -geometry is a useful tool for decision making in order to find an optimal level of precision. Indeed, the model of ${\textstyle \lambda }$ -geometry finds application in formulating the trade-offs that usually exist between cost and benefit in decision-making problems. For example, in facility location problems  [28] where the objective function is to find the best place to locate some facilities, the geographical location of potential candidates, as an input of the problem, is estimated. It is not clear whether making this estimation more precise is economical, and if so, to what extent. The model of ${\textstyle \lambda }$ -geometry helps decision-makers to find the trade-offs which exist between the costs and the benefits associated with this estimation. The same discussion can be made for problems, such as the location-inventory problem  [29] , lot-sizing with a supplier selection problem  [30] and incorporating the geographical proximity of suppliers.

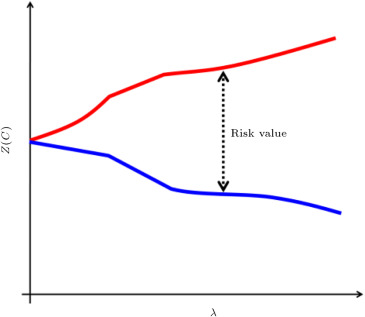
As an example, assume the problem of the p -center, which is one of the challenging facility location problems for locating emergency facilities, like police offices, and fire and emergency rescue stations  [31] . In this problem, we are given n demand points and the goal is finding p facility locations, called p'centers   , such that the maximum distance of the demand points from their closest center is minimized. Formally, if ${\textstyle D=\lbrace p_{1},p_{2},\ldots ,p_{n}\rbrace }$ is a set of n   demand points, and ${\textstyle C=\lbrace c1,c2,\ldots ,cp\rbrace }$ is a set of p   centers, the goal is minimizing ${\textstyle Z(C)=max_{1\leq i\leq n}\lbrace min_{1\leq j\leq p}d(p_{i},c_{j})\rbrace }$ , where ${\textstyle d(.,.)}$ is the distance metric regarding the application, e.g. Euclidean distance, and Z (C ) is the fitness of the solution, C . From the geometric standpoint, this problem is covering n given points by p circles, such that the radius of the largest circle is minimized. Now, assume the problem of the p -center in an imprecise context, where the information about the position of the demand set is not exact or can be changed dynamically. By considering each imprecise point as a demand region, we can discuss the worst and best cases of the fitness of a solution. In fact, the distance between a center and a demand region can be defined as the maximum distance or the minimum distance between them. So, any solution C has two worst and best fitness values. By increasing precision and, consequently, shrinking the demand regions, the difference between the worst and best values of solution C is minimized as well. This difference can be interpreted as concept of risk in an emergency operation. So, any improvement in estimating the demand regions results in reaching a better amount of risk value. Figure 2 illustrates a hypostatical diagram of the worst and best fitness functions, based on parameter ${\textstyle \lambda }$ . When ${\textstyle \lambda =0}$ , the demand region of an imprecise point is exactly one single point, which is the exact position of the imprecise point, and increasing ${\textstyle \lambda }$ causes the demand region to grow. So, there is a trade-off between ${\textstyle Z(C)}$ and the size of the demand points. In other scenarios of this problem, it is asked which precision level of ${\textstyle \lambda }$ results in finding a given risk value or a given fitness value.

Figure 2. A hypostatical diagram of the worst and best fitness functions in p -center problem.

Finally, there is a similarity between the ${\textstyle \lambda }$ -geometry model and mobile and kinetic data  [32]  and [33] . The physical parameter time in mobile and kinetic problems is similar to parameter ${\textstyle \lambda }$ in the model of ${\textstyle \lambda }$ -geometry. The main difference between these concepts is that in the ${\textstyle \lambda }$ -geometry model, we have exactly one instance for a fixed value of ${\textstyle \lambda }$ , which can be selected anywhere in the imprecise region, ${\textstyle p(\lambda )}$ , while, in mobile and kinetic data, we know the exact position of p at any time.

3. One dimensional range searching

Let ${\textstyle P=\lbrace p_{1},p_{2},\ldots ,p_{n}\rbrace }$ be a set of n   points on the real line, and ${\textstyle R=[l:r]}$ be an interval as a query range. The range searching problem is reporting all points over P that lie inside R   . This problem can be solved using a balanced binary search tree in ${\textstyle O(logn+k)}$ query time, where k   is the number of reported points. To this end, we need ${\textstyle O(n)}$ space and ${\textstyle O(nlogn)}$ time to build the tree in a preprocessing step  [34] . Considering imprecise points and ranges, there are three variations of the problem under the ${\textstyle \lambda }$ -geometry model: precise points and imprecise ranges, imprecise points and precise ranges, and imprecise points and imprecise ranges. Also, since instances of each imprecise point or range can be selected anywhere in its region, we focus on the maximum and minimum number of reported points as the worst and best cases of output in the form of two functions, with respect to parameter ${\textstyle \lambda }$ .

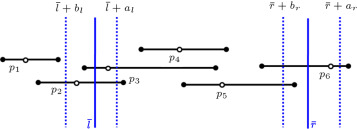
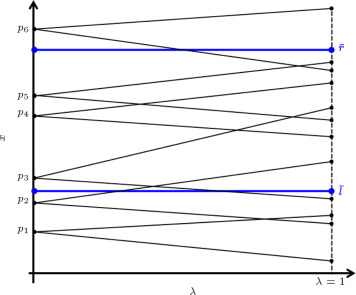
We denote the i   -th imprecise point by ${\textstyle p_{i}(\lambda )=({\overline {p}}_{i},\lambda M_{i})}$ , where ${\textstyle M_{i}=[a_{i}b_{i}]}$ , such that ${\textstyle a_{i}\leq 0}$ and ${\textstyle b_{i}\leq 0}$ . Thus, the leftmost and rightmost instances of ${\textstyle p_{i}(\lambda )}$ are ${\textstyle l_{i}(\lambda )=\lambda b_{i}+{\overline {p}}_{i}}$ and ${\textstyle r_{i}(\lambda )=\lambda a_{i}+{\overline {p}}_{i}}$ for the imprecision level, ${\textstyle \lambda }$ . Similarly, we denote the imprecise range, ${\textstyle R(\lambda )=[l(\lambda ):r(\lambda )]}$ , where ${\textstyle l(\lambda )=({\overline {l}},\lambda [a_{l}b_{l}])}$ and ${\textstyle r(\lambda )=({\overline {r}},\lambda [a_{r}b_{r}])}$ . Figure 3 shows an example of the general version of the problem in one dimension (for simplicity, we depict imprecise points at different heights). Hollow points show the exact positions and bold ones show the leftmost and rightmost instances of points for ${\textstyle \lambda =1}$ . In this figure, when ${\textstyle \lambda }$ increases from 0 to 1, several types of event may occur. Point ${\textstyle p_{2}}$ lies outside the range for ${\textstyle \lambda =0}$ , and by increasing ${\textstyle \lambda }$ , it is possible that its right instances lie inside the range. Also, its left instances lie outside for all ${\textstyle \lambda }$ s. Similar cases occur for points ${\textstyle p_{3}}$ , ${\textstyle p_{5}}$ and ${\textstyle p_{6}}$ , however, point ${\textstyle p_{4}}$ lies inside and ${\textstyle p_{1}}$ lies outside the range for all ${\textstyle \lambda }$ s.

Figure 3. An example of the range searching problem in one dimensional space. All points have same height and only for convenience, they are depicted at different heights.

Therefore, we are interested not only in reporting all such points, but also in computing the corresponding event points for reporting the minimum and maximum output functions, based on ${\textstyle \lambda }$ . A critical   value for ${\textstyle \lambda }$ is a value at which an instance of an imprecise point enters the range or exits from it. Based on such critical values of ${\textstyle \lambda }$ , we can report the minimum and maximum possible query points while ${\textstyle \lambda }$ changes. In what follows, we propose algorithms for the three mentioned cases of the problem.

3.1. Precise points and imprecise range

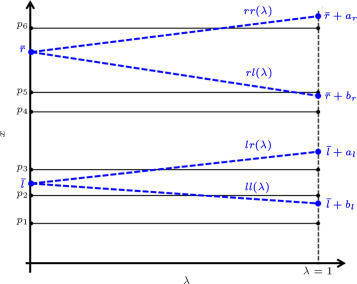
In this case, the positions of points in P   remain fixed when ${\textstyle \lambda }$ changes, and only the range ${\textstyle R(\lambda )}$ is imprecise. So, we can map the problem onto the functional space, with respect to the value of ${\textstyle \lambda }$ in [0, 1]. To this end, we define ${\textstyle p_{i}(\lambda )={\overline {p}}_{i}}$ for ${\textstyle i=1,2,\ldots ,n}$ . Also, we define four linear range functions: ${\textstyle ll(\lambda )=\lambda b_{l}+{\overline {l}}}$ , ${\textstyle lr(\lambda )=\lambda a_{l}+{\overline {l}}}$ , ${\textstyle rl(\lambda )=\lambda b_{r}+{\overline {r}}}$ and ${\textstyle rr(\lambda )=\lambda a_{r}+{\overline {r}}}$ . To rule out degeneracy, we require ${\textstyle lr(1)<rl(1)}$ . Figure 4 shows these functions and the points for the example illustrated in Figure 3 .

Figure 4. Functional space of the example illustrated in Figure 3 for precise points and imprecise range.

To solve the problem, first, as a preprocessing step, we build a binary search tree over set P   in ${\textstyle O(nlogn)}$ time and ${\textstyle O(n)}$ space. Then, in the query phase, we find all range query points for two ranges, ${\textstyle R_{1}=[{\overline {l}}:{\overline {r}}]}$ and ${\textstyle R_{2}=[{\overline {l}}+b_{l}:{\overline {r}}+a_{l}]}$ , on set P   , and store the reported points in ${\textstyle A_{1}}$ and ${\textstyle A_{2}}$ , respectively. Let ${\textstyle k_{1}}$ be the size of ${\textstyle A_{1}}$ and ${\textstyle k_{2}}$ be the size of ${\textstyle A_{2}}$ . To construct the minimum number of range point functions, we compute all ${\textstyle \lambda }$ s corresponding to the intersection of points ${\textstyle A_{1}}$ with ${\textstyle lr(\lambda )}$ and ${\textstyle rl(\lambda )}$ . Note that we need constant time to find the intersection for each point. Similarly, we compute the corresponding intersection ${\textstyle \lambda }$ s for points ${\textstyle A_{2}}$ with ${\textstyle ll(\lambda )}$ and ${\textstyle rr(\lambda )}$ to construct the maximum number of range point functions. Since ${\textstyle A_{1}}$ and ${\textstyle A_{2}}$ are sorted, critical ${\textstyle \lambda }$ s can be extracted in an orderly manner. Therefore, the minimum and maximum output functions can be constructed in ${\textstyle O(logn+k_{1}+k_{2})}$ time.

3.2. Imprecise points and precise range

In this case, we have range ${\textstyle R=[{\overline {l}}:{\overline {r}}]}$ and imprecise point set ${\textstyle P(\lambda )=\lbrace p_{1}(\lambda ),p_{2}(\lambda ),\ldots ,p_{n}(\lambda )\rbrace }$ . We build two binary search trees over set ${\textstyle P(0)}$ and ${\textstyle P(1)}$ in the preprocessing step, in ${\textstyle O(nlogn)}$ time and ${\textstyle O(n)}$ space. ${\textstyle P(0)}$ contains all n   exact points and ${\textstyle P(1)}$ contains all ${\textstyle 2n}$ leftmost and rightmost instances corresponding with ${\textstyle \lambda =1}$ . In the query phase, we find the query results for ${\textstyle R=[{\overline {l}}:{\overline {r}}]}$ over ${\textstyle P(0)}$ and ${\textstyle P(1)}$ . Figure 5 shows the functional space of the example illustrated in Figure 3 for the precise range. Using the results and finding the corresponding intersection ${\textstyle \lambda }$ s, we can report all k   critical ${\textstyle \lambda }$ s in ${\textstyle O(logn+k)}$ time, but to construct the minimum and maximum output functions, we need to sort the critical ${\textstyle \lambda }$ s. Therefore, we use ${\textstyle O(nlogn)}$ time and ${\textstyle O(n)}$ space in the preprocessing step, and the output functions can be constructed in ${\textstyle O(logn+klogk)}$ query time.

Figure 5. Functional space of the example illustrated in Figure 3 for imprecise points and precise range.

Considering the real applications of range searching problems, usually, k is much smaller than n   , however, we can improve the query time to ${\textstyle O(logn+k)}$ by using more space and time in the preprocessing step. To this end, we compute all intersection points in the arrangement of ${\textstyle 2n}$ segments in the functional space. This takes ${\textstyle O(mlogm)}$ time using a sweep line algorithm, where m is the number of intersections  [33] . Finally, in the preprocessing step, we compute all corresponding ${\textstyle \lambda }$ s between any two sequential intersections and store them in order in a list. In the query phase for a given range, ${\textstyle R=[{\overline {l}}:{\overline {r}}]}$ , first, by using a binary search, we find the position of the horizontal lines, ${\textstyle x={\overline {l}}}$ and ${\textstyle x={\overline {r}}}$ , in the sorted list. Then, we find ${\textstyle O(k)}$ sorted ${\textstyle \lambda }$ s in linear time. Therefore, the query time is improved to ${\textstyle O(logn+k)}$ by using ${\textstyle O(mn)}$ preprocessing space and ${\textstyle O(mlogm)}$ preprocessing time.

3.3. Imprecise points and imprecise range

This case is solved by a similar approach to the one described above. We perform two range searching queries with ranges${\textstyle R_{1}=[{\overline {l}}:{\overline {r}}]}$ over set ${\textstyle P(0)}$ and ${\textstyle R_{2}=[{\overline {l}}+b_{l}:{\overline {r}}+a_{l}]}$ over set ${\textstyle P(1)}$ . Similar to the case of imprecise points and precise range, we can report the query points in ${\textstyle O(logn+k)}$ time, and construct the minimum and maximum output functions in ${\textstyle O(logn+klogk)}$ time using ${\textstyle O(nlogn)}$ time and ${\textstyle O(n)}$ space in the preprocessing step. Unfortunately, the idea explained for improving the time for constructing output functions does not work in this case, because the query lines are not horizontal.

4. Two dimensional orthogonal range searching

In this section, we study the problem of imprecise range searching in the plane. In this case, two aspects of each object are stored in a database. For example, assume we store the salary and working hours of an employee per month in a database. So, in a two-dimensional range searching problem, we are interested to find all employees whose number of working hours lies between ${\textstyle h_{1}}$ and ${\textstyle h_{2}}$ hours, and earn between ${\textstyle s_{1}}$ and ${\textstyle s_{2}}$ dollars a month. This problem can be modeled geometrically as follows: let ${\textstyle P=\lbrace p_{1},p_{2},\ldots ,p_{n}\rbrace }$ be a set of n   points in the plane and ${\textstyle R=[l:r]\times [b:t]}$ be a query range. The goal is to find all points which lie in the range. In the presence of imprecision, both database information and range can be imprecise. For example, in the employees’ data, when we record the salary and number of working hours for one or more years, and the query is only for one month, we can use the average and variance of them in the model of ${\textstyle \lambda }$ -geometry for defining the exact point and imprecision matrix, respectively. Indeed, the salary and number of working hours are stored for several months in the database separately, while the query does not indicate a particular month. With regard to the concepts reviewed in the previous section, we only explain how to solve the last case of the problem, in which both range and points are imprecise. The other two, precise points and imprecise range, and imprecise points and precise range, can be solved by using similar approaches.

An imprecise orthogonal range in the plane similar to one dimensional space, is defined by ${\textstyle R(\lambda )=[l(\lambda ):r(\lambda )]\times [b(\lambda ):t(\lambda )]}$ , where ${\textstyle l(\lambda )}$ , ${\textstyle r(\lambda )}$ , ${\textstyle b(\lambda )}$ , ${\textstyle t(\lambda )}$ denote the left, right, bottom and top bounds of the range, respectively. Since imprecision of a point can be appeared both horizontally and vertically (e.g. in the example of the employee database, the x -axis shows the salary and the y -axis shows the number of working hours), the imprecise region of each point can be modeled by an axis-aligned rectangle, which shows the maximum tolerance of the point in x and y axes. Figure 6 a shows an imprecise point with an axis-aligned rectangular region. Similarly, an imprecise range is an imprecise orthogonal axis-aligned region. However, an extension of this problem is to allow the regions and/or the ranges to be arbitrary convex polygons. Figure 6 b shows an example of the range searching problem for a hypostatical range in minimum and maximum cases. As described before, these cases can be defined by linear functions, with respect to ${\textstyle \lambda }$ .

Figure 6. (a) Axis-aligned rectangular imprecise point and its candidate points. (b) Example of range searching problem for 10 imprecise points and an imprecise orthogonal range.

Regarding the imprecision of points and range, we can partition P into three subsets:

• ${\textstyle P_{in}}$ : Set of points in P   which lie in the range for all ${\textstyle \lambda }$ s.
• ${\textstyle P_{out}}$ : Set of points in P   which lie out of the range for all ${\textstyle \lambda }$ s.
• ${\textstyle P_{imp}}$ : Set of points in P   which have instances in both inside and outside the range. In fact ${\textstyle P_{imp}=P/\lbrace P_{in}\cup P_{out}\rbrace }$ . However, we can define a variant version of them, as explained in the previous section.

For the example illustrated in Figure 6 b, ${\textstyle P_{in}=\lbrace p_{2},p_{6}\rbrace }$ , ${\textstyle P_{out}=\lbrace p_{4},p_{9}\rbrace }$ and the other points belong to ${\textstyle P_{imp}}$ . Therefore, for a given imprecise range, ${\textstyle R(\lambda )}$ , the goal is to report subsets ${\textstyle P_{in}}$ and ${\textstyle P_{imp}}$ , and also to construct minimum and maximum output functions. To this end, we define corner points of a rectangular region, ${\textstyle p(\lambda )}$ in ${\textstyle \lambda =1}$ , as four candidate points of p (see Figure 6 a). As aforementioned, these candidate points can be defined by linear functions, with respect to ${\textstyle \lambda }$ . Let ${\textstyle R_{min}}$ and ${\textstyle R_{max}}$ be the minimum and maximum possible ranges of R   (${\textstyle \lambda }$ ) in ${\textstyle \lambda =1}$ . Since both the range and points are axis-aligned rectangles, if imprecise point p   belongs to ${\textstyle P_{imp}}$ , then two cases may arise:

• Some candidate points of p   lie outside ${\textstyle R_{max}}$ and some lie inside ${\textstyle R_{max}}$ .
• Some candidate points of p   lie outside ${\textstyle R_{min}}$ and some lie inside ${\textstyle R_{min}}$ .

By using this observation, we can define set ${\textstyle P_{in}}$ as such imprecise points, all four candidate points of which lie inside ${\textstyle R_{min}}$ . Similarly, ${\textstyle P_{out}}$ contains imprecise points, all four candidate points of which lie outside ${\textstyle R_{max}}$ . Therefore, we perform the following procedure to partition P   into subsets, ${\textstyle P_{in}}$ , ${\textstyle P_{imp}}$ and ${\textstyle P_{out}=P\setminus \lbrace P_{in}\cup P_{imp}\rbrace }$ :

Procedure of orthogonal range searching in the plane

Step   1: Solve the range searching problem for range ${\textstyle R_{min}}$ over all ${\textstyle 4n}$ candidate points. Let ${\textstyle A_{min}}$ be the reported points.

Step   2: Solve the range searching problem for range ${\textstyle R_{max}}$ over all ${\textstyle 4n}$ candidate points. Let ${\textstyle A_{max}}$ be the reported points.

Step   3: Let ${\textstyle P_{in}}$ be all imprecise points, all of whose candidate points lie in ${\textstyle A_{min}}$ .

Step   4: Let ${\textstyle P_{imp}}$ be all imprecise points some of whose candidate points lie in ${\textstyle A_{max}}$ .

Step   5: ${\textstyle P_{imp}=P_{imp}\setminus P_{in}}$ .

After finding ${\textstyle P_{in}}$ and ${\textstyle P_{imp}}$ , we can determine the type of points which lie in the range. More precisely, for a point p   in ${\textstyle P_{imp}}$ , we can find its critical ${\textstyle \lambda }$ s by computing the intersection of ${\textstyle p(\lambda )}$ with the boundary of ${\textstyle R(\lambda )}$ , while ${\textstyle \lambda }$ changes. This can be done in O(1) because the complexity of each imprecise region is constant. In the illustrated range searching problem in Figure 5 b, ${\textstyle p_{5}}$ , ${\textstyle p_{7}}$ and ${\textstyle p_{8}}$ are points, all of whose instances lie inside the maximum possible range, while other points of ${\textstyle P_{imp}}$ always have some instances outside the range, in the worst case.

Let ${\textstyle k_{1}}$ and ${\textstyle k_{2}}$ be the size of ${\textstyle P_{in}}$ and ${\textstyle P_{imp}}$ . The explained procedure runs in ${\textstyle O(logn+k_{1}+k_{2})}$ query time by using a fractional cascading data structure  [35] . This data structure needs ${\textstyle O(nlogn)}$ preprocessing time and space. Because of the trade-off between query time and preprocessing storage, the query can be answered in ${\textstyle O(log2n+k_{1}+k_{2})}$ time using only ${\textstyle O(n)}$ space and ${\textstyle O(nlogn)}$ time in the preprocessing step using a range tree structure  [34] . These complexities are only for reporting query points, and for constructing minimum and maximum output functions, we need to sort all critical ${\textstyle \lambda }$ s, as described in the previous section. Thus, it takes ${\textstyle O(logn+(k_{1}+k_{2})log(k_{1}+k_{2}))}$ time.

5. Conclusion

We introduce a dynamic model; the ${\textstyle \lambda }$ -geometry model based on the level of imprecision to handle error in the input data of geometric problems. The model of ${\textstyle \lambda }$ -geometry, which is a generalization of region based models, provides the output of problems as functions based on the level of precision, which helps the decision maker in the trade-off between cost and benefit. Also, these functions are useful for designing robust and stable geometric algorithms under imprecise data. Since there are many instances of an imprecise point which can be chosen, the definitions of problems under imprecision are not unique. From an application standpoint, usually the worst and best cases of output can be studied in such problems. In this paper, we studied the range searching problem in one and two dimensional space under the ${\textstyle \lambda }$ -geometry model and proposed efficient algorithms to solve different versions of the problems. Studying the range searching problem in a general case, where imprecise points have an arbitrary polygonal region, remains open, as well as studying the problem in higher dimensions.

Acknowledgment

We thank the unknown reviewer whose comments improved the paper considerably.

References

1. [1] P. Walley; Towards a unified theory of imprecise probability; International Journal of Approximate Reasoning, 24 (23) (2000), pp. 125–148
2. [2] L.A. Zadeh; Fuzzy sets; Information and Control, 8 (3) (1965), pp. 338–353
3. [3] Z. Pawlak; Rough sets; International Journal of Computer and Information Sciences, 11 (1982), pp. 341–356
4. [4] Löffler, M. “Data imprecision in computational geometry”, Ph.D. Thesis, University Utrecht (2009).
5. [5] Khanban, A.A. “Basic algorithms of computational geometry with imprecise input”, Ph.D. Thesis, Department of Computing Imperial College, University of London (2005).
6. [6] L. Joskowicz, Y. Ostrovsky-Berman, Y. Myers; Efficient representation and computation of geometric uncertainty: the linear parametric model; Precision Engineering, 34 (1) (2010), pp. 2–6
7. [7] J. Nievergelt, P. Widmayer; Spatial data structures: concepts and design choices; ,in: M. van Kreveld, J. Nievergelt, T. Roos, P. Widmayer (Eds.), Algorithmic Foundations of Geographic Information Systems, Lecture Notes in Computer Science, 1340, , Springer-Verlag (1997)
8. [8] S.M. LaValle; Planning Algorithms, University of Illinois, Cambridge University press (2006)
9. [9] M. Davoodi, A. Mohades; Solving the constrained coverage problem; Applied Soft Computing, 11 (1) (2011), pp. 963–969
10. [10] Y. Ostrovsky-Berman, L. Joskowicz; Tolerance envelopes of planar mechanical parts with parametric tolerances; Computer-Aided Design, 37 (5) (2005), pp. 531–544
11. [11] M.J. Fadili, M. Melkemi, A. El Moataz; Non-convex onion-peeling using a shape hull algorithm; Pattern Recognition Letters, 25 (2004), pp. 1577–1585
12. [12] A. Gheibi, M. Davoodi, A. Javad, F. Panahi, M.M. Aghdam, M. Asgaripour, A. Mohades; Polygonal shape reconstruction; IET Computer Vision, 5 (2) (2011), pp. 97–106
13. [13] Guibas, L., Salesin, D. and Stolfi, J. “Epsilon geometry: building robust algorithms for imprecise computations”, Proceeding of the 5th ACM Annual Symposium on Computational Geometry , pp. 208–217 (1989).
14. [14] M. Segal; Using tolerances to guarantee valid polyhedral modeling results; Computer Graphics, 24 (1990), pp. 105–114
15. [15] Segal, M. and Sequin, C.H. “Consistent calculations of solid modeling”, Proceeding of the ACM Annual Symposium on Computational Geometry , 24, pp. 29–38 (1985).
16. [16] Löffler, M. and van Kreveld, M. “Largest bounding box, smallest diameter, and related problems on imprecise points”, Proc. WADS , pp. 446–457 (2007).
17. [17] M. Löffler, M. van Kreveld; Largest and smallest convex hulls for imprecise points; Algorithmica, 56 (2010), pp. 235–269
18. [18] M. Löffler, J. Snoeyink; Delaunay triangulation of imprecise points in linear time after preprocessing; Computational Geometry: Theory and Applications, 43 (2010), pp. 234–242
19. [19] Myers, Y. and Joskowicz, L. “Point distance and orthogonal range problems with dependent geometric uncertainties”, Proc. 14th ACM Symp. on Solid and Physical Modeling , NY, USA (2010).
20. [20] Jorgensen, A., Löffler, M. and Phillips, M.J. “Geometric computation on indecisive points”, 12th Algorithms and Data Structure Symposium (WADS) , pp. 536–547 (2011).
21. [21] Introduction to the Global Positioning System for GIS and TRAVERSE, http://www.cmtinc.com/gpsbook/ , 2012-06-20.
22. [22] Tasdizen, T. and Whitaker, R. “Feature preserving variational smoothing of terrain data”, Proc. 2nd Workshop on Variational Geometric and Level Set Methods in Computer Vision (2003).
23. [23] E.J. Huising, L.M.G. Pereira; Errors and accuracy estimates of laser data acquired by various laser scanning systems for topographic applications; ISPRS Journal of Photogrammetry and Remote Sensing, 53 (5) (1998), pp. 245–261
24. [24] Davoodi, M., Khanteimouri, P., Sheikhi, F. and Mohades, A. “Data imprecision under ${\textstyle \lambda }$ -geometry: finding the largest axis-aligned bounding box”, EuroCG 2011 , pp. 135–138 (2011).
25. [25] M. Löffler, J. Phillips; Shape fitting on point sets with probability distributions; Proc. 17th European Symposium on Algorithms, LNCS, 5757 (2009), pp. 313–324
26. [26] M.R. Jooyandeh, A. Mohades, M. Mirzakhah; Uncertain Voronoi diagram; Information Processing Letters, 109 (13) (2009), pp. 709–712
27. [27] C.K. Yap; Robust geometric computation; ,in: J.E. Goodman, J. O’Rourke (Eds.), Handbook of Discrete Computational GeometryCRC Press (2004)
28. [28] Z. Drezner; Facility location: a survey of applications and methods; Springer Series in Operations ResearchSpringer Verlag, New York, NY (1995)
29. [29] Z.J.M. Shen, C.R. Coullard, M.S. Daskin; A joint location inventory model; Transportation Science, 37 (1) (2003), pp. 40–55
30. [30] J. Rezaei, M. Davoodi; Multi-objective models for lot-sizing with supplier selection; International Journal of Production Economics, 130 (1) (2011), pp. 77–86
31. [31] M. Davoodi, A. Mohades, J. Rezaei; Solving the constrained ${\textstyle p}$ -center problem using heuristic algorithms  ; Applied Soft Computing, 11 (4) (2011), pp. 3321–3328
32. [32] Abam, M.A. “New data structures and algorithms for mobile data”, Ph.D. Thesis, Eindhoven (2007).
33. [33] B. Speckmann; Kinetic data structures; M.-Y. Kao (Ed.), Encyclopedia of Algorithms, Springer Verlag (2008), pp. 417–419
34. [34] M. de Berg, O. Cheong, M. van Kreveld, M. Overmans; Computational Geometry: Algorithms and Applications; (3rd. Rev. Ed.)Springer-Verlag, Berlin (2008)
35. [35] Lueker, G.S. “A data structure for orthogonal range queries”, Proc. 19th Annual IEEE Symposium Foundation Computer Science , pp. 28–34 (1978).