Abstract
With the major application of MMCs, it is thus necessary to develop an appropriate technology for their efficient machining. Milling is the most common and versatile technology among different machining processes, characterized by an extensive range of metal cutting capacity that places it in a central role in the manufacturing industries. In the present study an attempt has been made to find out the most optimal level of process parameters for CNC milling of Al–4.5%Cu–TiC metal matrix composites using grey-fuzzy algorithm. Taguchis L25 orthogonal array design is used for performing CNC milling operation on the composite plates. The Grey fuzzy optimization of CNC milling parameters consist of three different output characteristics; such as, cutting force Fc, surface roughness Ra and surface roughness Rz. It was found that a cutting speed of 600 rpm, feed of 40 mm/min and a depth of cut of 0.30 mm is the optimal combination of CNC milling parameters that has produced a high value of grey fuzzy reasoning grade of 0.8191 which is close to the reference value. ANOVA analysis is carried out and it is found that among three different process parameters, the cutting speed played a major role on the determination of GFRG.
Keywords
MMCs ; Grey fuzzy logic ; Surface roughness ; Cutting force ; In situ technique
Abbreviations
RSM , response surface methodology ; RSA , response surface analysis ; GRG , grey relational grade ; GFRG , grey fuzzy relational grade ; TiC , titanium carbide ; MMC , metal matrix composite ; Ra , centre line average roughness ; Rz , average maximum height of the profile ; Fc , cutting force in the direction of tool travel ; CNC , computer numerical control ; ANOVA , analysis of variance ; ANN , artificial neural network ; GA , genetic algorithm ; GRC , grey relation coefficient
1. Introduction
Nowadays metal matrix composites are being used in many applications in different engineering fields, which are very significant in the recent progress in material science and hence it is acting as a substitute for several engineering materials. Particularly aircraft, automotive, and locomotive industries are replacing steel and cast iron in different mechanical components with lighter high strength alloys and composites like aluminium (Al) matrix composites. As an outcome of this trend, the machining of metal matrix composites becomes very vital in the final stage of manufacturing, which needs further research.
The first generation of aluminium based composite materials having ceramic reinforcements are found to reveal good quality strength to weight ratio and better corrosion resistance. Currently, the research consideration is directed toward the hybrid composites having more than one reinforcing phase [1] . An ample spread application of these second generation MMCs are not possible without solution to the problems related to cutting [2] and [3] .
Manna and Bhattacharyya [4] have investigated the effect of cutting speed, feed and depth of cut on wear of the cutting tool and built-up edge formation during the turning operation of Al–SiC particulate composite, using a rhombic uncoated tool of carbide material. However, less amount of built up edge formation was found at a lower depth of cut and at higher cutting speed. Ciftci et al. [5] have examined the effect of SiC particulate size on the wear of the tool and surface finish with cubic boron nitride (CBN) tool insert at constant depth of cut, feed and at varying cutting speeds. It was suggested that for 30 µm and 45 µm size of SiC in aluminium metal matrix, optimum cutting speed was achieved at 150 m/min. For better size of SiC reinforcements (110 µm), CBN tool was not found appropriate for turning operation. Chambers [6] have found that the performance of PCD insert was significantly superior than carbides insert while turning Al—5Mg reinforced with a combination of 5 vol.% saffil and 15 vol.% SiCp. Looney et al. [7] have performed a series of turning operations on the Al–25%SiC metal matrix composite using CBN, carbide, and silicon nitride inserts. From these inserts, cubic boron nitride insert has formed the best cutting, and silicon nitride inserts was the worst among all. El-Gallab and Sklad [8] have determined the quality of the surface of Al–20%SiC composite in high speed turning under different cutting parameters. It was found in their investigation that the polycrystalline diamond tools (PCD) exhibited appropriate cutting tool life as when being compared with coated carbide tools and alumina.
Ding et al. [9] has investigated the machining behaviour of Al–SiC MMC using the PCBN and the PCD tools. Surface cracking was observed at the flank face surfaces of the cutting tools; intergranular fractures were observed on the rake faces. The PCD inserts performance was better than the PCBN inserts. Yanming and Zehua [10] reported the mechanism of cutting tool wear during the machining of Al–SiC composite. The cutting tool flank surface was being affected by abrasive wear and it was found that the carbide tool was appropriate for the fine size of SiC reinforced composite. It was also seen that the size of the reinforcement and the volume fraction played a great role in the cutting tool life.
Muthukrishnan et al. [11] reported that better quality of surface finish in turning of A356/SiC MMCs could be achieved by means of medium grade PCD 1500 inserts with less power utilization at the elevated cutting speed. BUE formation was seen on the tip of cutting tools at lower cutting speed. Pramanik et al. [12] have explained the effect of factors, such as tool particle connections, difference in strain, thermal softening, and work hardening, on the variation of cutting forces for metal matrix composites and its alloy. Tamer et al. [13] investigated the influence of machining parameters such as cutting speed, feed and depth of cut on the cutting tool wear and surface roughness of AlSi7 Mg2 reinforced with 5, 10 and 15 wt.% of SiCp. Mahamani [14] has optimized the cutting parameters in machining of in situ Al–5Cu–TiB2 composite using uncoated tungsten carbide inserts. Anandakrishnan and Mahamani [15] have studied the machinability of in situ Al–6061–TiB2 MMCs. The flank wear rate, cutting force, and surface roughness were found to be higher with a higher value of depth of cut.
Rai et al. [16] have studied the cutting force development and chip formation while doing shaping operation of Al–TiC composites and compared them with Al–TiAl3 composite and Al—Si alloys. There was improvement in the quality of the surface machined with the increased quantity of TiC reinforcing particles in the composite. The cutting force developed while machining Al–TiC metal matrix composite was lower than the cutting force developed while machining Al–TiAl3 composite and Al—Si alloy. Kumar et al. [17] have studied the feasibility, dry turning characteristics of Al–4.5%Cu/TiC composites using uncoated ceramic inserts. The influence of the input process parameters on the surface roughness and cutting force was observed. BUE formation was found lower at higher cutting speeds and was found higher at lower cutting speeds. Razavykia et al. [18] evaluated machining process parameters and the modifier element effects on the cutting force and the surface roughness in the dry turning of the Al–Mg2 Si in-situ MMC. The addition of the Bi element as modifier reagent results in the lower cutting force and the lower surface roughness. Kumar and Chauhan [19] also investigates the effect of the cutting speed, feed, approach angle on the surface roughness of Al7075 ceramic composite (10% SiC) and Al7075 hybrid composite (7%SiC and 3% graphite). It was found that in the turning operation of both the composite surface roughness of the hybrid, composite was less than the ceramic composite. Karabulut [20] has fabricated AA7039/Al2 O3 MMC by using powder metallurgy technique and found that material structure was the most effective factor in affecting the cutting force, and surface roughness. The milling test was being performed based on the Taguchi design of experiment. Shoba et al. [21] also investigated the effect of the cutting speed, feed, and depth of cut on cutting force. A comparison study was performed for the reinforced and unreinforced composites, and the result shows that cutting force decreases with the increase in the weight percentage of the reinforcements.
The multi-output optimization problems could be solved by using different methods such as grey relational analysis (GRA), genetic algorithm (GA), artificial neural network (ANN), response surface methodology (RSM) and fuzzy logic [22] .
The investigation based on fuzzy-logic finds applications in unclear and undecided environment. In the recent research trends, fuzzy-logic-based multi-criteria decision making techniques have become very popular in doing optimization of different manufacturing processes. Grey system initiated by Deng [23] is a powerful tool to deal with the poor, incomplete and vague data [24] and [25] . In recent years, researchers have effectively used grey relational technique for solving the intricate interrelationships between the multiple objectives in a variety of fields of manufacturing [26] , [27] , [28] , [29] and [30] . A grey relational grade (GRG) is calculated by doing average of the grey relational coefficient of each response to convert the optimization of the complex performance characteristics into optimization of a single GRG [27] . Lin and Lin [30] researchers have done optimization of EDM process of SKD11 alloy steel with many process responses using grey-fuzzy-logic method. The theory of fuzzy logic proposed by Zadeh can successfully deal with the uncertain and vague information [31] . Therefore, the application of the fuzzy logic theory to the grey relational analysis may further develop its performance in solving multi-response problems for process parameter optimization. In the past, researchers have fruitfully employed grey fuzzy logic [24] , [25] , [26] , [27] , [28] and [29] for optimizing the multiple objectives of the complex manufacturing problems. They found that grey based fuzzy technique can make significant improvement in the performance characteristics of the process.
Rupajati et al. [32] has optimized several performances like recast layer thickness and surface roughness using fuzzy-logic method with Taguchis L18 mixed- orthogonal array. It was found that the application of this optimization technique has significantly improved multiple output responses. Kumar et al. [33] investigated the cutting force development while performing the turning operation on unidirectional glass fibre reinforced plastics composite. Taguchis L18 orthogonal array was being used for conducting the experimentations.
Soepangkat and Pramujati applied integrated approach comprising of GRA and fuzzy-logic for optimizing wire EDM of AISI D2 steel for minimizing surface roughness and layer thickness [34] . Related optimization techniques have been effectively utilized in a variety of manufacturing processes, which are mostly carried out under complex and uncertain environment [24] , [35] , [36] , [37] and [38] .
Even though a very few research works have been carried out to study the influence of CNC milling parameters on different quality and productivity aspects, it is very necessary to establish optimal parametric combination with the intention of obtaining improved machined surface. Thus, the present work is focused on optimization of CNC milling machining parameters of Al–4.5%Cu–TiC metal matrix composite using grey-fuzzy analysis. The experimental work is done on the basis of Taguchis L25 orthogonal array. The essential input milling parameters selected are cutting speed, feed and depth of cut, and the outputs considered are surface roughness and cutting force. For minimizing the values of all the performance characteristics, an optimal combination of input process parameters are required.
2. Experimental description
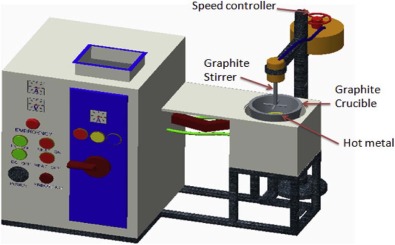
The material used for the experimentation is Al–4.5%Cu–TiC metal matrix composite prepared through the stir casting process. It was prepared at 1250 °C by an in situ technique in an induction furnace. Titanium (99.8% purity), activated charcoal powder (average size 150 µm) and commercial pure aluminium (99.9% purity) and pure copper (99.8% pure) were used as the charge materials in the furnace. In an induction furnace (shown in Fig. 1 ), at first pure aluminium (Al) ingot was melted in a graphite crucible at a temperature of 685 °C, afterwards pure copper (Cu) was added to the molten aluminium at 800 °C and by the help of a graphite stirrer the mixture was endlessly stirred. Pure titanium (Ti) was then added to the liquid material at 1000 °C, and the mixture was endlessly stirred. At 1100 °C activated charcoal powder was added to the Al
Cu
Ti liquid melt and it was held for 5 minutes to permit the occurrence of the reaction thus forming TiC inter-metallic particles in the melt, and the mixture was endlessly stirred. Potassium fluoride and sodium fluoride were used as a flux cover so as to remove the oxide film development from the molten metal surface and for acting as a protective barrier to gas absorption and to make possible impulsive incorporation of the particles into the melt [39] and [40] . Subsequently the hot liquid melt was cast into rectangular metallic mould of size 30 mm × 30 mm × 80 mm for carrying out the CNC milling process.
|
|
|
Fig. 1. Schematic diagram of a stir casting process. |
An end mill cutter of length 75 mm, diameter 8 mm, 4 number of flutes, 25 mm flute length, was used for performing machining operation of Al–4.5%Cu–5TiC metal matrix composite in CNC milling machine in dry condition, shown in Fig. 2 .
|
|
|
Fig. 2. Solid carbide end mill cutter. |
The five level variations of cutting speed, feed, depth of cut chosen for this experimentation is shown in Table 1 . The experiments are designed as per Taguchis L25 orthogonal array of experiments.
| Parameter | Notation | Unit | Level of factors | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||
| Cutting Speed | N | rpm | 400 | 450 | 500 | 550 | 600 |
| Feed | f | mm/min | 20 | 25 | 30 | 35 | 40 |
| Depth of Cut | d | mm | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 |
The experimental set up for the present study is shown in Fig. 3 . The experiments were carried out on a CNC end milling machine manufactured by MTAB Engineers Pvt. Ltd. The cutting force in the direction of the cutting tool travel (Fc) was measured with a dynamometer. Surface roughness parameters were measured by using a 3D profilometer at 20× magnification and at 4.7 mm cut-off distance. All the subsequent measurements were repeated 5 times.
|
|
|
Fig. 3. Experimental set up. |
3. Methodology
3.1. Design of experiment using response surface methodology (RSM)
Response Surface Analysis focuses a renowned new approach to the optimization of the input process parameter models based on physical experiments, simulation experiments and experimental findings. These approximated models need to be assessed statistically for their competence, and then they can be used for an optimization of the initial model. The response surface analysis problems have a handy relation between responses and independent variables, and this relation can be explained by the second-order polynomial model shown below.
|
|
( 1) |
where is estimated response; is the constant; and , and represent the coefficients of linear, quadratic, and cross-product terms, respectively. X is the coded variables. is random error term. The general approach in RSM is to use regression methods based on least square methods.
3.2. Grey relational analysis (GRA)
As the Taguchi method is planned to optimize single response characteristic, the grey relational analysis optimizes multiple outcomes. Therefore, the grey relational analysis method is complicated [41] and [42] . In GRA, the optimization process is done in the following three steps.
In the first step, the measurement values of centre line average roughness (Ra), average maximum height of the profile (Rz), and cutting force (Fc ) are to normalize in the range of zero to one. This is called grey relational normalization. Such normalization is required since the range and the unit in one response may vary from the others. If the response is of ‘higher-the-better’ characteristics, the equation for doing normalizing is as follows:
|
|
( 2) |
If ‘lower-the-better’ condition is to be followed, in that case the following equation is to be utilized for normalizing the related data:
|
|
( 3) |
where and are normalized data and observed data respectively for the ith experiment by using kth response. After doing normalization of the responses, the next step is to calculate the grey relational coefficient (GRC). It can be calculated by using the Eq. (4) .
|
|
( 4) |
where is absolute value of the difference between and and . and are global maximum and global minimum values in different data series, respectively. The distinguishing coefficient (ζ ) lies between 0 and 1, which is to expand or to compress the range of GRC, generally, ζ = 0.5 is taken.
In third step, the grey relational grade is computed by finding the average of the grey relational coefficient corresponding to each performance characteristics. This degree is being estimated with the following equation:
|
|
( 5) |
where the grey relational grade and n is the number of process response. The optimal value of the GRG can be predicted by using Eq. (6) .
|
|
( 6) |
where is total mean of the GRG value, q is number of input process parameters, and is mean GRG value at the optimal level for the ith parameter. ANOVA method is also used to find out the statistical importance of each factor and the percentage contribution of each input parameter on the responses.
3.3. Fuzzy rule based modeling
In grey relational analysis, the use of lower-the-better, higher-the-better and nominal-the-better performance characteristics shows that there is some uncertainty in the obtained results. This vagueness can be efficiently checked by using fuzzy logic [23] .
In the first step, the fuzzifier uses membership function to fuzzify inputs (ξ1 = grey relation coefficient for Ra, ξ2 = grey relation coefficient for Rz and ξ3 = grey relation coefficient for Fc). The membership function is used defining how the values of the input (ξ1, ξ2 and ξ3) and output (η0 = Grey Fuzzy Relational Grade (GRFG)) are mapped to a value between 0 and 1. In the next step twenty five fuzzy rules for the three inputs and one output are developed using the Eq. (4) derived from the results obtained from experiments for inference.
|
|
( 7) |
where Ai , Bi , Ci and Di are the fuzzy subsets defined by the corresponding membership functions, i.e., , , and . The inference engine then performs fuzzy reasoning on fuzzy rules by taking max–min inference (Eq. (8) ) for generating a fuzzy value .
|
|
( 8) |
where is minimum operation, and is maximum operation respectively.
Finally the defuzzifier converts the fuzzy value into crisp output using the centroid defuzzification method (Eq. (9) ); i.e. grey fuzzy reasoning grade (η0 ) is calculated from the fuzzy multi-response output using the following equation:
|
|
( 9) |
GFRG corresponds to optimal setting of the input process parameter for multi-response characteristics.
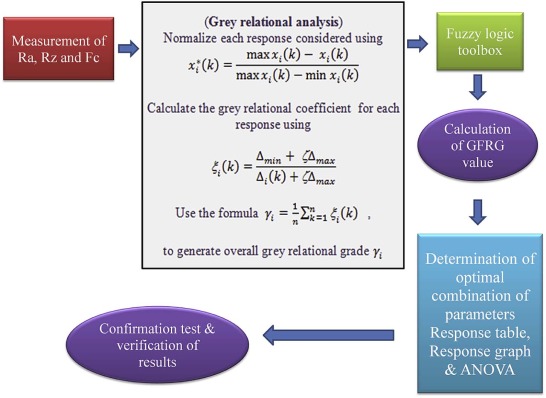
3.4. Steps for the grey-fuzzy-logic method
The procedure adopted for determining the optimum machining parameters for the multi-response optimization is shown in Fig. 4 . The methodology consists of a six step approach shown below:
- Step 1 : Selecting the machining parameters and their levels. Perform the experiments by using full factorial design.
- Step 2 : Normalization of all the responses (Data pre-processing) obtained by using Eq. (2) . Calculation of the grey relational coefficient ξi (k ) for each response by using Eq. (4) . Eq. (5) was used to generate the overall grey relational grade γi .
- Step 3 : Fuzzification of the grey relational coefficient obtained from each responses and fuzzification of the overall grey relational grade by using the membership function. Also, establishing the fuzzy rules in linguistic form relating grey relational coefficient and overall grey relational grade.
- Step 4 : By using max–min interface operation (Eq. (8) ) calculation of the fuzzy multi-response output and then employing centroid defuzzification (Eq. (9) ) to calculate a grey-fuzzy reasoning grade η0 .
- Step 5 : Selecting the optimum combination of parameters through the response table and response graph. Finding out the contribution of each factor and their interactions on the multi response output by using analysis of variance (ANOVA).
- Step 6: Carrying out confirmation tests for verifying the results obtained (using Eq. (6) ).
|
|
|
Fig. 4. Proposed grey-fuzzy-logic method. |
4. Results and discussion
4.1. Calculating the grey relational coefficients
The pre-processed data of experimental results, the grey relational coefficients and the overall grey relational grade for each of the combination of parameters is given in Table 2 . For all the responses, ‘lower-the-better’ criterion is preferred. On the other hand, in order to obtain an improved quality in the performances and to decrease the vagueness in the data, grey-fuzzy logic method is additionally used for computing the GFRG.
| Normalized value of the experimental results | Grey relational coefficient | Grey relational grade | GFRG | |||||
|---|---|---|---|---|---|---|---|---|
| Ra (µm) | Rz (µm) | Fc (N) | Ra (µm) | Rz (µm) | Fc (N) | |||
| 1 | 0.3220 | 0.3607 | 0 | 0.4244 | 0.5462 | 0.3333 | 0.435 | 0.502 |
| 2 | 0.3024 | 0.6621 | 0.5607 | 0.4175 | 0.3333 | 0.5323 | 0.428 | 0.372 |
| 3 | 0.3805 | 0.5845 | 0.1339 | 0.4466 | 0.5192 | 0.3660 | 0.444 | 0.445 |
| 4 | 0.4488 | 0 | 0 | 0.4756 | 0.5219 | 0.3333 | 0.444 | 0.559 |
| 5 | 0.3024 | 0.5369 | 0.5116 | 0.4175 | 0.5013 | 0.5059 | 0.475 | 0.294 |
| 6 | 0.3268 | 0.5419 | 0.5674 | 0.4262 | 0.4845 | 0.5361 | 0.482 | 0.339 |
| 7 | 0.5122 | 0.5025 | 0.4512 | 0.5062 | 0.3333 | 0.4767 | 0.439 | 0.406 |
| 8 | 0.5610 | 0.4680 | 0.2558 | 0.5325 | 0.5076 | 0.4019 | 0.481 | 0.837 |
| 9 | 0.3951 | 0 | 0.8977 | 0.4525 | 0.6516 | 0.8302 | 0.645 | 0.500 |
| 10 | 0.4976 | 0.5149 | 0.6698 | 0.4988 | 0.5127 | 0.6023 | 0.538 | 0.815 |
| 11 | 1 | 0.7327 | 0.8372 | 1 | 0.4903 | 0.7544 | 0.748 | 0.501 |
| 12 | 0.5641 | 0.5248 | 0.4605 | 0.5342 | 0.5549 | 0.4810 | 0.523 | 0.847 |
| 13 | 0.3526 | 0.4802 | 1 | 0.4358 | 0.6779 | 1 | 0.705 | 0.500 |
| 14 | 0.5128 | 0.5990 | 1 | 0.5065 | 0.4975 | 1 | 0.668 | 0.499 |
| 15 | 0.4167 | 0.7624 | 0.9760 | 0.4616 | 1 | 0.9542 | 0.805 | 0.954 |
| 16 | 0.6538 | 0.4950 | 0.2036 | 0.5909 | 0.3333 | 0.3857 | 0.437 | 0.537 |
| 17 | 0.6474 | 1 | 0.7485 | 0.5864 | 0.3491 | 0.6653 | 0.534 | 0.687 |
| 18 | 0.4167 | 0 | 1 | 0.4616 | 0.3649 | 1 | 0.609 | 0.571 |
| 19 | 0 | 0.0679 | 0.0759 | 0.3333 | 1 | 0.3511 | 0.561 | 0.597 |
| 20 | 0.9661 | 0.1296 | 0 | 0.9365 | 0.7594 | 0.3333 | 0.676 | 0.850 |
| 21 | 1 | 1 | 0.8200 | 1 | 0.5586 | 0.6354 | 0.731 | 0.852 |
| 22 | 1 | 0.3967 | 0.4700 | 1 | 0.5586 | 0.3718 | 0.643 | 0.857 |
| 23 | 0.7045 | 0 | 0.6800 | 1 | 1 | 0.495 | 0.832 | 0.500 |
| 24 | 0 | 0 | 1 | 0.7333 | 0.5461 | 1 | 0.76 | 0.937 |
| 25 | 0.4 | 0.6621 | 0.3727 | 1 | 0.3333 | 1 | 0.778 | 0.710 |
4.2. Grey-fuzzy reasoning analysis
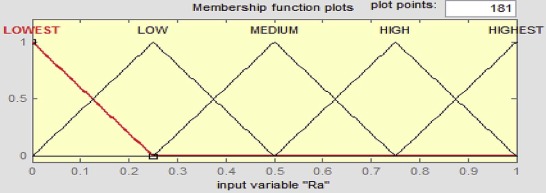
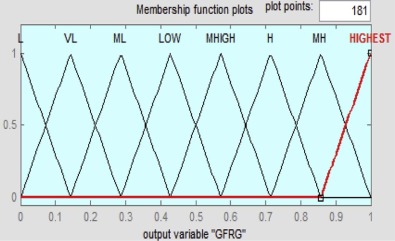
In this present paper, three inputs and one output (GFRG) fuzzy-logic system is used. The inference engine (Mamdani fuzzy inference system) performs fuzzy reasoning with fuzzy rules for generating a fuzzy value. These fuzzy rules are shown in the form of ‘if–then’ control rule. Grey relational coefficients for Ra , Rz and Fc are inputs to the fuzzy logic system. The linguistic membership function for instance Lowest, Low, Medium, High and Highest are used to represent the grey relational coefficients (GRC) of input variables Ra , Rz and Fc . Likewise the output grey relational grade is being represented by the membership functions such as Lowest (L), Very Low (VL), Medium Low (ML), Low, Medium High (MHIGH), Higher (H), Medium Higher (MH), Highest. The triangular shaped membership function, which is used in this work, is shown in Fig. 5 and Fig. 6 . A total of 25 numbers of fuzzy rules are used for this purpose. The rule-based fuzzy-logic reasoning is shown in Fig. 7 . Maximum–minimum compositional operation by tracking the fuzzy reasoning yields a fuzzy output. At last, the defuzzifier converts the fuzzy predicted values into a GRFG by using MATLAB (R2010b) fuzzy logic toolbox. This GFRG values are tabulated in Table 2 .
|
|
|
Fig. 5. Membership functions for the cutting force and surface roughness. |
|
|
|
Fig. 6. Membership function for multi-response output. |
|
|
|
Fig. 7. Fuzzy logic rules viewer. |
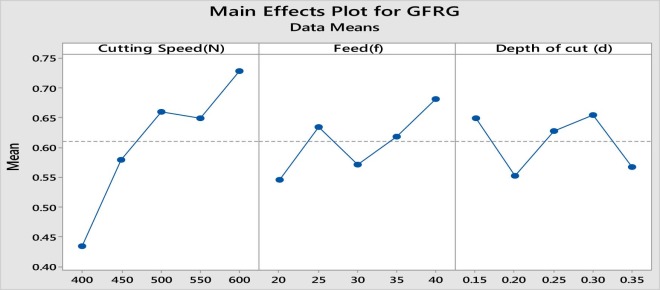
The higher values of GFRG exhibits the best multiple performance characteristics. Analysis of the mean is performed for GFRG. Based on Δ (Delta) statistics, which is the difference among the highest and the lowest average of GFRG for each of the factor, the rank of the parameters, which affects the multiple performance response, is listed in Table 3 . These values are plotted in Fig. 8 like the response graph for the machining parameters. The greater the inclination of the response graph, the larger the effect of the process parameters on the multiple performance response.
| Machining Parameters | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 | Δ(Max-Min) | Rank |
|---|---|---|---|---|---|---|---|
| Cutting speed (N) | 0.4344 | 0.5794 | 0.6602 | 0.6484 | 0.7276 | 0.2932 | 1 |
| Freed rate (f) | 0.5462 | 0.6338 | 0.5706 | 0.6184 | 0.6810 | 0.1348 | 2 |
| Depth of cut (d) | 0.6488 | 0.5524 | 0.6278 | 0.6628 | 0.5666 | 0.1104 | 3 |
The bold values in the table indicate the level numbers which have the highest GFRG value for cutting speed, feed and depth of cut respectively. We can see that the GFRG value is higher at level 5 for cutting speed, GFRG value is higher at level 5 for feed, and GFRG value is higher at level 4 for depth of cut.
According to Table 1 in the manuscript, the value of cutting speed at level 5 is 600 rpm, the value of feed at level 5 is 40 mm/min, and the value of depth of cut at level 4 is 0.30 mm, which are the optimal combination of the said input parameters.
|
|
|
Fig. 8. Response graph for every level of machining parameters. |
A fuzzy set in a universe of discourse X is being characterized by a membership function , which maps every element x in X to a real number in the interval of [0, 1]. The function value is termed as the grade of membership of x in . The nearer value of to unity, the higher the grade of membership of x in .
A triangular fuzzy membership function is being represented as . The membership function of the triangular fuzzy number is given as:
|
|
where are the real numbers. For a triangular fuzzy number .
Fig. 5 is drawn to show the fuzzification of the three inputs e.g. Ra (taking their grey relational coefficient value). The triangular membership function graph is shown to define how the values of the input and output (Y = GFRG) are mapped to a value between 0 and 1. The linguistic membership function such as LOWEST, LOW, MEDIUM, HIGH and HIGHEST are used to represent the grey relational coefficient (GRC) of input variables. Similarly, the output grey relational grade is represented by the membership functions such as LOWEST(L), VERY LOW(VL), MEDIUM LOW(ML), LOW, MEDIUM HIGH (MHIGH), HIGHER (H), MEDIUM HIGHER(MH), HIGHEST. The triangular shaped membership function used in this work is shown in Fig. 6 .
Based on Table 3 and Fig. 8 , the optimum setting of the machining process parameters is found to the experimental run no. 25 i.e. with cutting speed at level five (600 m/min) (N5), feed rate at level five (40 mm/min) (f5) and depth of cut at level four (0.30 mm) (d4). This is indicated in bold font in Table 3 . The use of these conditions will at the same time minimize the Ra , Rz and Fc throughout machining within the range of factors studied.
The response equation of the GFRG is shown in Eq. (10) . The main influencing factor for multi-performance is the maximum of this value (i.e. rank 1), which is cutting speed (N). Also the same information can be obtained from Fig. 8 .
|
|
( 10) |
ANOVA is performed for analyzing the role of each factor on the multiple performance characteristics. The analysis is done at a confidence level of 95%. Fishers F-test is employed to find out the change in which the process parameters have a significant effect on multiple performance characteristics. Larger F-value shows that the change of process parameters has a stronger influence on the performance characteristic. The results of the ANOVA are shown in Table 4 . As in the ANOVA table of GFRG, the P value of the cutting speed is less than 0.05. This indicates that the cutting speed played a main role to determine the GFRG.
| Source of variance | DOF | SS | MS | F | P |
|---|---|---|---|---|---|
| Regression | 3 | 0.249030 | 0.083010 | 2.48 | 0.089 |
| Cutting Speed, N | 1 | 0.214775 | 0.214775 | 6.41 | 0.019 |
| Feed rate, f | 1 | 0.032309 | 0.032309 | 0.96 | 0.337 |
| Depth of cut, d | 1 | 0.001947 | 0.001947 | 0.06 | 0.812 |
| Error, e | 21 | 0.703552 | 0.033502 | ||
| Total | 24 | 0.952582 |
The obtained results are verified by doing the confirmatory experiment. Table 5 shows the confirmation test results of surface integrity aspects relating to initial and optimal machining conditions. It is obvious that machining with the optimum parametric combination would minimize Ra from 2.04 to 1.88 µm, Rz from 2.57 to 1.91 µm and decrease Fc from 600 to 499 µm. The estimated or predicted GFRG ( ) at the optimal level of the machining parameters can be calculated by using Eq. (11) .
|
|
( 11) |
| Levels | Initial machining parameters level | Optimum machining parameters level | |
|---|---|---|---|
| N = 400 , f = 20, d = 0.15 | N = 600 , f = 40, d = 0.30 | ||
| Predicted | Experimental | ||
| Ra () | 2.04 | 1.88 | |
| Rz () | 2.57 | 1.91 | |
| Fc () | 600 | 499 | |
| GFRG | 0.502 | 0.7853 | 0.7100 |
| Improvement in the GFRG | 0.2833 | 0.2100 | |
where is total mean of the GFRG for all the experimental runs, q is number of input parameters, and is mean GFRG value at the optimum level for the ith parameter. Also Table 5 indicates that the machining with optimum setting would result in an improvement of GFRG of 0.2833 and 0.2100 for predicted and experimental values respectively. Hence, the present study clearly implies that grey-fuzzy-logic method can be effectively utilized for multi-characteristics optimization of process parameters.
Microscopic images of the surface before and after CNC milling machining are shown in Fig. 9 (a, b).
|
|
|
Fig. 9. Microscopic images of the surface (a) before CNC machining and (b) after CNC machining. |
After pouring the hot liquid material from the graphite crucible to the rectangular shaped metallic mould, the specimens were machined in shaper before performing machining operation in the CNC milling machine. The specimens were machined in the shaper for making the surfaces of the specimens free from any casting burrs and casting defects in the surface. Fig. 9 (a) shows the microscopic image of the upper surface of the specimen before performing CNC milling operation, which shows cut marks of the shaper single point cutting tool and results in more roughness in the surface, whereas Fig. 9 (b) shows the image of the surface after performing CNC milling operation with end mill cutter, which shows less surface roughness as compared to shaping operation.
5. Conclusion
In this present paper, machining of in situ Al–4.5%Cu/TiC metal matrix composite is carried out with input parameters considered as cutting speed, feed and depth of cut, and the response parameters as surface roughness, and cutting force in CNC milling machine. Taguchis L25 orthogonal array design is used for performing CNC milling operation on the composite plates.
- It was found that a cutting speed of 600 rpm, feed of 40 mm/min and a depth of cut of 0.30 mm is the optimal combination of input parameters.
- ANOVA statistics exposed that cutting speed is the most influencing factor in effecting the response parameters.
- Therefore, it is concluded that the optimization procedure proposed in this present paper significantly improved the production of CNC milling of Al–4.5%Cu/TiC metal matrix composite.
Acknowledgements
The authors like to thank HOD of Mechanical and Production Engineering Department, NIT Agartala and all supporting staffs of the Production Engineering Department, NIT Agartala, for their priceless help and guidance while performing the experimental work.
References
- [1] S. Gururaja, M. Ramulu, W. Pedersen; Machining of MMCs: a review; Mach. Sci. Technol, 17 (1) (2013), pp. 41–73
- [2] G. Chryssolouris; Laser Machining: Theory and Practice; Springer Verlag, Berlin; Heidelberg, GmbH & Co. (2013) K978-3540974987
- [3] H.Y. Zheng, Z.Z. Han, Z.D. Chen, W.L. Chen, S. Yeo; Quality and cost comparisons between laser and water jet cutting; J. Mater. Process. Technol, 62 (4) (1996), pp. 294–298
- [4] A. Manna, B. Bhattacharyya; Influence of machining parameters on the machinability of particulate reinforced Al/SiC–MMC; Int J. Adv. Manuf. Technol, 25 (2005), p. 850
- [5] I. Ciftci, M. Turker, U. Seker; Evaluation of tool wear when machining SiCp-reinforced Al – 2014 alloy matrix composites; Mater. Des, 25 (2004), p. 251
- [6] A.R. Chambers; The machinability of light alloy MMCs; Compos. Part A Appl. Sci. Manuf, 27A (1996), pp. 143–147
- [7] L.A. Looney, J.M. Monaghan, P.O. Reilly, D.M.R. Taplin; The turning of an A1/SiC metal–matrix composite; J. Mater. Process. Technol, 33 (1992), p. 453
- [8] M. El-Gallab, M Sklad; Machining of Al:SiC particulate metal–matrix composites Part I: tool performance; J. Mater. Process. Technol, 83 (1998), p. 151
- [9] X. Ding, W.Y.H. Liew, X.D. Liu; Evaluation of machining performance of MMC with PCBN and PCD tools; Wear, 259 (2005), p. 1225
- [10] Q. Yanming, Z. Zehua; Tool wear and its mechanism for cutting SiC particle-reinforced aluminium matrix composites; J. Mater. Process. Technol, 100 (2000), p. 194
- [11] N. Muthukrishnan, M. Murugan, K. Prahlada Rao; Machinability issues in turning of Al–SiC (10p) metal matrix composites; Int. J. Adv. Manuf. Technol, 39 (2008), p. 211
- [12] A. Pramanik, L.C. Zhang, J.A. Arsecularatne; Machining of metal matrix composites: effect of ceramic particles on residual stress, surface roughness and chip formation; Int J. Mach. Tool Manuf, 48 (2008), pp. 1613–1625
- [13] O. Tamer, K. Erol, C. Orhan; Investigation of mechanical and machinability properties; J. Mater. Process. Technol, 198 (2008), p. 220
- [14] A. Mahamani; Machinability study of Al–5Cu–TiB2 in situ metal matrix composites fabricated by flux-assisted synthesis; J. Miner. Mater. Charact. Eng, 10 (13) (2011), pp. 1243–1254
- [15] V. Anandakrishnan, A. Mahamani; Investigations of flank wear, cutting force, and surface roughness in the machining of Al-6061–TiB2 in situ metal matrix composites produced by flux-assisted synthesis; Int. J. Adv. Manuf. Technol, 55 (2011), p. 65
- [16] R.N. Rai, G.L. Datta, M. Chakraborty, A.B. Chattopadhyay; A study on the machinability behaviour of Al–TiC composite prepared by in situ technique; Mater. Sci. Eng. A, 428 (2006), p. 34
- [17] A. Kumar, M.M. Mahapatra, P.K. Jha; Effect of machining parameters on cutting force and surface roughness of in situ Al–4.5%Cu/TiC metal matrix composites; Measurement, 48 (2014), pp. 325–332
- [18] A. Razavykia, S. Farahany, N. Mohd Yusof; Evaluation of cutting force and surface roughness in the dry turning of Al–Mg2 Si in-situ metal matrix composite inoculated with bismuth using DOE approach ; Measurement, 76 (2015), pp. 170–182
- [19] R. Kumar, S. Chauhan; Study on surface roughness measurement for turning of Al7075/10/SiCp and Al 7075 hybrid composites by using response surface methodology (RSM) and artificial neural networking (ANN); Measurement, 65 (2015), pp. 166–180
- [20] S. Karabulut; Optimization of surface roughness and cutting force during AA7039/Al2 O3 metal matrix composites milling using neural networks and Taguchi method ; Measurement, 66 (2015), pp. 139–149
- [21] C. Shoba, N. Ramanaiah, D. Nageswara Rao; Effect of reinforcement on the cutting forces while machining metal matrix composites – an experimental approach; Eng. Sci. Technol, 18 (2015), pp. 658–663
- [22] K. Krishnaiah, P. Shahabudeen; Applied Design of Experiments and Taguchi Methods; (first ed.)PHI Learning Pvt Ltd, New Delhi, India (2012)
- [23] J. Deng; Introduction to grey system; J. Grey. Syst, 1 (1) (1989), pp. 1–24
- [24] S. Pattnaik, D.B. Karunakar, P.K. Jha; Multi-characteristic optimization of wax patterns in the investment casting process using grey-fuzzy logic; Int. J. Adv. Manuf. Tech, 67 (5–8) (2013), pp. 1577–1587
- [25] N.M. Liu, J.T. Horng, K.T. Chiang; The method of greyfuzzy logic for optimizing multi-response problems during the manufacturing process: a case study of the light guide plate printing process; Int. J. Adv. Manuf. Tech, 41 (2009), pp. 200–210
- [26] C. Ahilan, S. Kumanan, N. Shivakamaran; Multi objective optimization of CNC turning process using grey based fuzzy logic; Int. J. Mach. Mach. Mater, 5 (2009), pp. 434–451
- [27] Y.F. Hsiao, Y.S. Tarng, W.J. Huang; Optimization of plasma arc welding parameters by using the Taguchi method with the grey relational analysis; Mater. Manuf. Processes, 23 (2008), pp. 51–58
- [28] A. Krishnamoorthy, S. Rajendra Boopathy, K. Palanikumar, J. Paulo Davim; Application of grey fuzzy logic for the optimization of the drilling parameters for CFRP composites with multiple performance characteristics; Measurement, 45 (2012), pp. 1286–1296
- [29] K.T. Chiang, F.P. Chang; Application of grey-fuzzy logic on the optimal process design of an injection-molded part with a thin shell features; Int. Commun. Heat. Mass. Transfer, 33 (2006), pp. 94–101
- [30] J.L. Lin, C.L. Lin; The use of grey-fuzzy for the optimization of the manufacturing process; J. Mater. Process. Technol, 160 (2005), pp. 9–14
- [31] L. Zadeh; Fuzzy sets; Inf. Control, 8 (1965), pp. 338–353
- [32] P. Rupajati, B.O.P. Soepangkat, B. Pramujati, H.C.K. Agustin; Optimization of recast layer thickness and surface roughness in the wire EDM process of AISI H13 tool steel using Taguchi and fuzzy logic; Appl. Mech. Mater, 493 (2014), pp. 529–534
- [33] S. Kumar, M. Gupta, P.S. Satsangi; Multiple-response optimization of cutting forces in turning of UD-GFRP composite using distance-based pareto genetic algorithm approach; Eng. Sci. Technol, 18 (2015), pp. 680–695
- [34] B.O.P. Soepangkat, B. Pramujati; Optimization of surface roughness and recast thickness in the wire-EDM process of AISI D2 tool steel using Taguchi-greyfuzzy; Appl. Mech. Mater, 393 (2013), pp. 21–28
- [35] T. Rajmohan, K. Palanikumar, S. Prakash; Grey-fuzzy algorithm to optimise machining parameters in drilling of hybrid metal matrix composites; Compos. Part B Eng, 50 (2013), pp. 297–308
- [36] R.K. Pandey, S.S. Panda; Optimization of bone drilling parameters using greybased fuzzy algorithm; Measurement, 47 (2014), pp. 386–392
- [37] A. Krishnamoorthy, S.R. Boopathy, K. Palanikumar, J.P. Davim; Application of grey fuzzy logic for the optimization of drilling parameters for CFRP composites with multiple performance characteristics; J. Int. Meas. Confeder, 45 (5) (2012), pp. 1286–1296
- [38] Y.S. Yang, W. Huang; A grey-fuzzy Taguchi approach for optimizing multiobjective properties of zirconium-containing diamond-like carbon coatings; Exp. Syst. Appl, 39 (1) (2012), pp. 743–750
- [39] A. Karantzalis, E.S. Wyatt, A.R. Kennedy; The mechanical properties of Al-TiC metal matrix composite fabricated by a flux-casting technique; Mater. Sci. Eng. A, 237 (1997), p. 200
- [40] I. Kaasta, M. Boyd; Designing a neural network for forecasting financial and economic time series; Neurocomputing, 10 (1996), pp. 215–236
- [41] P.N. Singh, K. Raghukandan, B.C. Pai; Optimization by grey relational analysis of EDM parameters on machining Al–10% SiCP composites; J. Mater. Process. Technol, 155-156 (2004), pp. 1658–1661
- [42] M. Kurt, S. Hartomacioglu, B. Mutlu, U. Koklu; Minimization of the surface roughness and form error on the milling of free-form surfaces using a grey relational analysis; Mater. Technol, 46 (2012), pp. 205–213
Document information
Published on 10/04/17
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?