Optimización basada en confiabilidad de célula de carga multiaxial utilizando algoritmos genéticos
Resumo
A construção de uma célula de carga multiaxial requer ferramentas robustas a fim de analisar o comportamento da mesma quando submetida a carregamentos estáticos e dinâmicos. Neste trabalho, é dada uma ênfase ao problema da otimização de um modelo de célula de carga multiaxial (6 componentes de força) do tipo Lywood, utilizando‐se do conceito de otimização baseada em confiabilidade. É tratado o problema da análise de confiabilidade estrutural, incluindo o efeito da variabilidade geométrica de suas propriedades físicas. A célula de carga foi analisada pelo método de elementos finitos e a restrição da confiabilidade é aplicada para o limite de falha do material. Por meio de mudanças em sua geometria objetivou‐se a maximização da primeira frequência natural e, ao mesmo tempo, a redução de massa e consequente aumento da deformação medida sem que a restrição de confiabilidade das tensões seja violada. São mostradas comparações entre o procedimento determinístico de otimização e o proposto, onde constatou‐se que a otimização determinística apresentou pontos com elevada probabilidade de falha, sendo justificada a aplicação da otimização baseada em confiabilidade para este tipo de problema. Também foram aplicados diferentes valores do fator de segurança ao modelo de otimização, onde foi possível analisar, a posteriori , a confiabilidade do resultado da otimização.
Abstract
The manufacturing process of a multi‐axial load cell requires robust tools to analyze the structural behavior when it is subjected to static and dynamic loads. In this work, it is given focus to the problem of optimizing a multi‐axial load cell model (6 load components) of Lywood type considering concepts of reliability‐based design optimization. The reliability structural analysis problem is handled including the variability effect of geometric and physical properties. The load cell is analyzed by finite element method and the reliability constraint is applied to the strength limit. The objective is the maximization of the first natural frequency and simultaneously reducing the mass and corresponding strains without violating reliability limit set as a limit. Comparisons between the deterministic optimization procedure and the proposed method are presented and it is found that the deterministic optimization points may have a high probability of failure so justifying in this type of problem the reliability‐based optimization. Different values of the safety factor were also tested with the optimization model, and it was possible to analyze, a posteriori, the reliability of the optimization results.
Resumen
La construcción de una célula de carga multiaxial requiere herramientas robustas para analizar el comportamiento de los mismos cuando se somete a cargas estáticas y dinámicas. En este trabajo se da un énfasis al problema de la optimización de un modelo de célula de carga multiaxial (6 componentes de fuerza) de tipo Lywood utilizando el concepto de optimización basado en la confiabilidad. Se abordó el problema de análisis de fiabilidad estructural incluyendo el efecto de la variabilidad geométrica de sus propiedades físicas. La célula de carga se analizó por el método de elementos finitos y la restricción de fiabilidad se aplica al límite de falla del material. A través de cambios en la geometría destinadas a aumentar al máximo la primera frecuencia natural, mientras que se viola la reducción de la masa y el consiguiente aumento de la deformación medido sin la fiabilidad de la restricción de tensiones sea violada. Las comparaciones se muestran entre el procedimiento de optimización determinista y propusieron, donde se encontró que los puntos de optimización deterministas con alta probabilidad de fallo. Fueron también aplicados diferentes valores del factor de seguridad para el modelo de optimización, donde fue posible analizar, retrospectivamente, la confiabilidad del resultado de la optimización.
Palavras‐chave
Otimização estrutural ; Análise de confiabilidade ; Célula de carga multiaxial
Keywords
Structural optimization ; Reliability analysis ; Multiaxial load cell
Palabras clave
Optimización estructural ; Análisis de confiabilidad ; Célula de carga multiaxial
1. Introdução
O desejo de obter projetos ótimos, com baixos custos e alta eficiência, sempre foi um grande objetivo da engenharia. Entretanto, se não forem consideradas incertezas de parâmetros ou mesmo variáveis, os pontos ótimos encontrados pelos métodos de otimização determinística podem pecar por apresentar probabilidade de falha não admissível.
Uma forma de considerar incertezas dentro dos modelos de otimização é a utilização da confiabilidade estrutural [1] , [2] , [3] and [4] . Este procedimento é chamado de otimização baseada em confiabilidade, do inglês, reliability based design optimization (RBDO). Esta metodologia pode ser resumida como a tentativa de encontrar projetos ótimos que atendam a determinado nível de confiabilidade requerido levando em conta diversas fontes de incertezas. Não deve ser confundido com a otimização robusta (robust design [RD]), na qual o projeto ótimo é encontrado mantendo a sensibilidade desta solução o menos sensível possível aos parâmetros incertos considerados. Neste caso, não há informação a respeito da confiabilidade final atingida pelo projeto. De acordo com [5] , o termo confiabilidade estrutural é comummente utilizado para designar a medida de segurança de determinado sistema estrutural frente a um determinado desempenho esperado. Segundo [5] and [6] , as incertezas em projetos podem ser divididas basicamente em 2 grandes grupos: aleatórias e epistêmicas. São exemplos destas incertezas, mas não limitadas a apenas estas, as incertezas físicas, estatísticas, incertezas devido a fatores humanos, incertezas fenomenológicas provenientes da existência de eventos não previsíveis e incertezas de modelagem provenientes das simplificações e hipóteses adotadas.
Os tamanhos, as formas e as aplicações das células de carga são as mais diversas. Para cada aplicação, é imprescindível determinar a geometria adequada para a aplicação. Para casos onde as células de carga estarão sujeitas a carregamentos dinâmicos, como, por exemplo, em túneis de vento, pode ser importante maximizar as frequências dos modos de vibração, de maneira a que o sinal que servirá para medir a força aplicada não seja distorcido, ou que ocorra ressonância. Um balanço da razão entre a rigidez e a massa deve ser feito para que ocorra a maximização das frequências naturais sem que a devida sensibilidade da célula de carga aos esforços para que foi projetada seja perdida, justificando assim o uso de métodos de otimização para o projeto destas células de carga. Uma vez que também se objetive a minimização da massa e a consequente maximização da deformação mensurável, juntamente com a maximização das frequências naturais, tem‐se um problema de otimização multiobjetivo.
Neste trabalho pretende‐se determinar parâmetros ótimos para uma estrutura, onde o índice de confiabilidade é considerado como um requisito do projeto. Para a análise de confiabilidade utiliza‐se o método de confiabilidade de primeira ordem (first order reliability method [FORM]) e como procedimento de otimização se utilizam algoritmos genéticos (AG).
2. Método de confiabilidade de primeira ordem
Segundo [7] , a confiabilidade pode ser aplicada a diversas áreas da engenharia. Ela está relacionada com o complemento da probabilidade de falha, ou seja, a chance de ocorrência de determinado evento. Uma expressão matemática para a falha de um sistema (violação de determinada restrição) pode ser, em geral, colocado da seguinte forma:
|
|
( 1) |
onde g representa a função de estado limite que define a restrição a ser cumprida, e Xi as n variáveis que afetam a restrição em questão [8] . Muitas destas variáveis podem possuir componente aleatória. O termo significa que o sistema está no domínio da falha e significa que o sistema está no domínio da segurança. A probabilidade de falha pode ser calculada usando a função de densidade de probabilidade conjunta :
|
|
( 2) |
onde D é a região para , Φ (− β ) representa a função de distribuição acumulada padrão do índice de confiabilidade que é mostrado a seguir, como se está apresentando a probabilidade de falha, o sinal negativo se faz necessário. Considerando, por exemplo, σi como uma tensão mecânica encontrada em um componente i , assumindo uma situação de falha quando a mesma exceda um determinado valor limite de material (σlim ). A mesma equação para a função de estado limite pode ser colocada como:
|
|
( 3) |
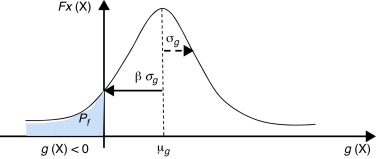
A integração da equação (2) é considerada difícil, pois se está trabalhando com diversas variáveis aleatórias n . Além disso, a função geralmente não é conhecida a priori , principalmente quando não há dados estatísticos suficientes. Dessa forma, de uma maneira muito simplificada, para obter um índice de confiabilidade β costuma‐se usar o primeiro e o segundo momentos (média e variância) da distribuição da função de estado limite . Quando a função é linear e as variáveis aleatórias são independentes e normalmente distribuídas, o índice de confiabilidade β pode ser aproximado como ( fig. 1 ):
|
|
( 4) |
onde μg e σg representam a média e o desvio padrão da função .
|
|
|
Figura 1. Definição geométrica de confiabilidade. |
Quando a margem de segurança é não linear, os valores aproximados de μg e σg são obtidos pela linearização da função por meio da expansão da função em série de Taylor truncada até os termos lineares. O ponto em torno do qual é feito o desenvolvimento da série de Taylor afeta os valores de μg e σg . Um método para obter o índice de confiabilidade β que seja independente da formulação empregada para definir a função de estado limite, conhecido como advanced first order second moment (AFOSM), foi proposto por [9] . No caso de variáveis aleatórias independentes, as variáveis aleatórias Xi são transformadas em variáveis normais padronizadas Ui fazendo‐se:
|
|
( 5) |
onde são, respectivamente, a função de distribuição acumulada de Xi e a inversa da função de distribuição acumulada padrão. Dessa forma, a função de estado limite no espaço real X e′ transformada para o espaço normal padrão U :
|
|
( 6) |
A linearização da função de estado limite é feita em um ponto U* que tenha a menor distância entre a superfície de falha e a origem do espaço U . O ponto U* é chamado de ponto de projeto e β é calculado como a distância entre a origem e este ponto.
|
|
( 7) |
2.1. Algoritmo de Rackwitz – Fiessler
Para resolver o problema da equação (7) utiliza‐se o algoritmo proposto por Rackwitz e Fiessler (1978), que pode ser descrito da seguinte forma:
- Passo 1: definir a função que representa função de estado limite .
- Passo 2: assumir valores iniciais para o ponto de projeto no espaço real X * = (X1 , …, Xn )T e calcular o correspondente valor da função g (X ) (por exemplo, assume‐se o ponto de projeto como sendo as médias das variáveis de projeto).
- Passo 3: avaliar a média e o desvio padrão equivalente para as variáveis.
|
|
( 8) |
- Passo 4: transformar variáveis do espaço real X para o espaço normal padrão U . Os valores das variáveis no ponto de projeto e no espaço normal padrão serão:
|
|
( 9) |
- Passo 5: calcular as sensibilidades no ponto de projeto X *.
- Passo 6: calcular as derivadas parciais no espaço normal padrão, usando a regra da cadeia
|
|
( 10) |
- Passo 7: calcular um novo valor para o ponto de projeto para a iteração k + 1 com base na iteração atual (k ) no espaço normal padrão através da seguinte expressão:
|
|
( 11) |
- Passo 8: calcular a distância deste novo ponto até à origem e estimar novo índice de confiabilidade.
|
|
( 12) |
- Passo 9: verificar a convergência de β para um determinado valor de tolerância pré‐determinado.
- Passo 10: calcular os valores do ponto de projeto no espaço original fazendo:
|
|
( 13) |
- Passo 11: calcular o valor de g (X ) para o novo ponto de projeto e verificar o critério de convergência para tolerância e tolerância.
- Passo 12: se ambos os critérios de convergência forem satisfeitos, parar o algoritmo, caso contrário, repetir os passos 3‐11.
Neste algoritmo todas as variáveis do espaço original são assumidas como não correlacionadas. Caso exista correlação entre as mesmas calcula‐se, por meio da decomposição de Cholesky, a matriz de covariância que transforma as variáveis correlacionadas em não correlacionadas [10] and [11] .
3. Reliability based design optimization
Na RBDO tem‐se como objetivo otimizar uma determinada função objetivo (FO), satisfazendo as restrições probabilísticas de confiabilidade especificada, a qual é colocada como critério inicial do problema. Análises de probabilidade de falha são realizadas ao longo do processo de otimização, a fim de verificar a adequação do critério estabelecido e guiar a otimização em direção ao nível de confiabilidade requerida.
A formulação mais simples e usual de implementação da RBDO é aquela implementada em laço duplo, onde a otimização é dividida em 2 níveis: (a) no primeiro nível é feita a otimização da FO obtendo‐se as variáveis de projeto e (b) no segundo nível é realizado o processo de análise da confiabilidade do projeto ótimo obtido no nível anterior. Mais detalhes podem ser encontrados em [6] . Com base em [12] , um modelo de otimização determinística para minimização pode ser definido genericamente da seguinte forma:
|
|
( 14) |
onde, as vp é o vetor de variáveis de projeto, p é o vetor de parâmetros fixos do problema de otimização, é a i‐ ésima restrição de igualdade do modelo de um total ne restrições de igualdade e nr − ne restrições de desigualdade, é o vetor que contém os limites inferiores das variáveis de projeto e o vetor que contém os limites superiores das variáveis de projeto do modelo.
Entretanto, uma otimização determinística não considera as incertezas nas próprias variáveis e nem nos parâmetros de projeto. No método RBDO, às restrições determinísticas são adicionadas restrições de probabilidade. Sabe‐se que o índice de confiabilidade pode ser definido em função da probabilidade de falha (e vice‐versa) como:
|
|
( 15) |
onde Φ é a função acumulada de probabilidades padrão. Para este trabalho, a restrição com relação à confiabilidade é expressa como:
|
|
( 16) |
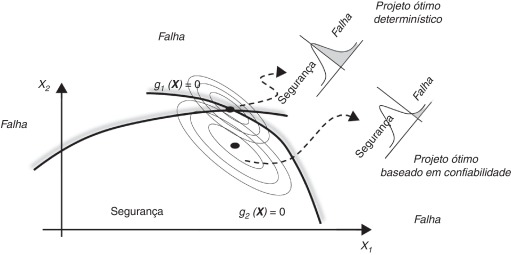
onde é a razão expressa adimensionalmente entre o índice de confiabilidade calculado β e o índice de confiabilidade alvo βt . Isso quer dizer que, se o índice de confiabilidade β calculado durante a otimização for maior que o índice de confiabilidade alvo βt estipulado, então e o critério probabilístico estará satisfeito. Caso contrário, haverá uma penalização aplicada à FO. A figura 2 faz uma definição geométrica da diferença entre a otimização determinística e aquela baseada em confiabilidade. A implementação da otimização baseada em confiabilidade pode ser feita basicamente por 2 aproximações, pelo método reliability index approach (RIA) ou pela aproximação performance measure approach (PMA).
|
|
|
Figura 2. Definição geométrica de otimização determinística e baseada em confiabilidade. |
3.1. Aproximação por índice de confiabilidade (reliability index approach )
Nesta aproximação a restrição de confiabilidade é tratada como uma restrição extra e formulada no espaço das variáveis não correlacionadas Gaussianas padrão, e dada pelo índice de confiabilidade β . Portanto, o seguinte pode ser escrito:
|
|
( 17) |
sendo u o vetor de variáveis aleatórias não correlacionadas Gaussianas padrão e gk e hk as restrições de igualdade e desigualdade determinísticas juntamente com p igualdades ou q desigualdades probabilísticas.
3.2. Aproximação por medida de desempenho (performance measure approach )
Esta formulação é feita como o inverso da análise de confiabilidade em RIA, de forma que pode ser colocado como:
|
|
( 18) |
sendo u o vetor de variáveis não correlacionadas padrão e gk e hk as p restrições probabilísticas de desigualdade e q de igualdade. As vantagens e desvantagens de se utilizar uma ou outra aproximação podem ser obtidas em [13] .
4. Algoritmos genéticos
Os AG representam, atualmente, uma poderosa ferramenta para a busca de soluções de problemas com grande complexidade e não linearidade, posta à prova e validada em diversos trabalhos nos mais variados ramos da engenharia. Este método é utilizado na procura por mínimos/máximos de funções onde a busca é baseada na teoria da evolução de Darwin, que pressupõe que indivíduos, que evoluam gerando benefícios para sua espécie em consonância com o ambiente, tenham mais chances de sobrevivência e de passarem estas características para seus descendentes [14] . O funcionamento do método de AG começa com a geração de uma população aleatória de cromossomos, onde essas estruturas são avaliadas e associadas a uma probabilidade de reprodução de tal forma que maiores probabilidades são associadas a cromossomos que apresentam uma melhor (maior ou menor, dependendo se for maximização ou minimização) função de aptidão no problema de otimização. A aptidão da solução é tipicamente definida com relação à população corrente. Esta função de aptidão é uma modificação da FO a fim de atender necessidades do processo de seleção dos indivíduos [15] . Os AG simulam simplificadamente o processo evolutivo numericamente. Eles representam os parâmetros de um dado problema codificando‐os num vetor. Como na genética, genes são constituídos por cromossomos. Similarmente, nos AG na sua forma simplificada, os vetores de que contém as variáveis de projeto são codificados em «bits». Um vetor de «bits» pode ser descodificado no respectivo valor do parâmetro do problema e a avaliação total do vetor de «bits» para um indivíduo pode ser ponderada, seguindo‐se alguma função de aptidão representativa da solução representada pelo indivíduo para aquele conjunto de «bits».
Um AG simples constitui‐se de 3 operadores básicos, sendo eles, reprodução, cruzamento ou recombinação e mutação. Análises sobre estes operadores são apresentados em trabalhos como [16] . O algoritmo começa com uma população de indivíduos cada um deles representando uma possível solução para o problema. Os indivíduos, como na natureza, se utilizam destes 3 operadores básicos e evoluem em gerações onde a teoria de Darwin para esta evolução prevalece e, como consequência, uma população de indivíduos mais adaptados surge como uma evolução natural do processo. Ao nível da reprodução, a avaliação da função de aptidão indica quais indivíduos irão ter mais chances de transferir material genético a proles futuras. Nas operações genéticas, os genes de pares de indivíduos são trocados e, como na natureza, esta troca pode se dar de diversas formas, sendo então comummente chamadas de crossover ou recombinação.
Algumas das vantagens dos AG frente a técnicas convencionais podem ser resumidas como segue:
- Os AG operam de forma codificada na tarefa de procura dos parâmetros e não diretamente sobre os parâmetros.
- Os AG trabalham com uma população de soluções, que representam uma variedade de possíveis soluções do problema e não com apenas uma solução por vez.
- Diferentemente na maioria dos algoritmos de otimização, os quais requerem avaliações das derivadas da FO, AG somente requerem o uso do valor da função aptidão.
- Somente regras probabilísticas e a regra da seleção natural são utilizadas com AG, o que possibilita a saída do algoritmo de soluções ótimas locais com mais chances de obter ótimos globais.
A representação binária tem uma importância histórica devido ao primeiro uso por [17] . Quando se trabalha com o AG na forma binária, cada um dos parâmetros reais bi a serem otimizados são traduzidos num código binário seguindo a seguinte equação:
|
|
( 19) |
onde binn indica a tradução binária para um vetor binário s de n «bits», n significando o número de «bits», significando os mínimos e os máximos valores permitidos para cada variável. Para transformar o código binário para valores reais, a seguinte equação é utilizada como indicado em sequência:
|
|
( 20) |
onde significa a tradução dos valores codificados em binário para os respectivos valores reais. Deve ser notado que está implícito que o mapeamento tem uma resolução de . Isto restringe a procura no espaço dos parâmetros reais a valores discretos, os quais podem induzir ótimos locais. Isto pode ser contornado utilizando‐se um AG com codificação real. Esta aproximação assume valores reais para cada variável. As principais mudanças são encontradas no operador de crossover (recombinação). Há diversas formas de tratar a recombinação em AG com codificação real, tais como: a recombinação plana, a recombinação simples, a recombinação aritmética, etc. Neste trabalho, a recombinação BLX‐α (blended crossover ) é utilizada devido ao fato dela operar, inicialmente, com uma fase exploratória abrangente do campo de parâmetros, seguida de uma fase de pesquisa mais detalhada para melhoria da resolução dos parâmetros.
A figura 3 resume os principais passos seguidos pelo AG com codificação real para maximizar funções. O AG utilizado está apresentando em [11] and [18] , a implementação do algoritmo foi realizada no software Matlab® , onde aplica‐se a codificação real.
|
|
|
Figura 3. Pseudocódigo para o algoritmo genético com codificação real (adaptado de: Gomes e Silva [19] ). |
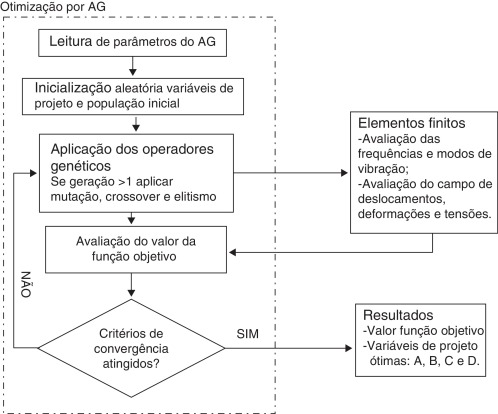
Na figura 4 tem‐se um fluxograma da interação entre o algoritmo otimizador (AG) e o método de elementos finitos, utilizado por meio do software comercial Ansys® .
|
|
|
Figura 4. Fluxograma da lógica de otimização (interação entre AG e elementos finitos). |
5. Otimização da célula de carga
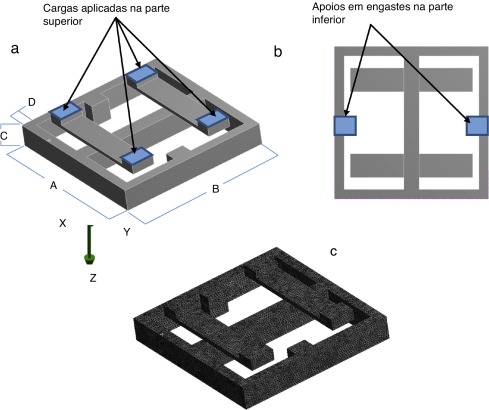
Para célula de carga analisada, têm‐se 4 variáveis de projeto geométricas para a maximização da primeira frequência natural e minimização da massa ao mesmo tempo. São elas as dimensões A, B, C e D, apresentadas na figura 5 a). Os outros parâmetros da célula, como espessura das peças e posição de barras, são parametricamente gerados de forma a evitar o surgimento de amostras com geometrias não factíveis; a região de engaste está mostrada na figura 5 b), que ocorre na parte inferior da célula de carga, e a malha de elementos finitos gerada com a geometria base na figura 5 c).
|
|
|
Figura 5. a) Célula de carga para 6 componentes de esforços, b) condição de contorno, c) malha de elementos finitos. |
O valor dos carregamentos para o projeto desta célula e aplicados em cada uma das faces é: Fx = 0,25 kN, Fy = 0,5 kN, Fz = 0,75 kN, Mx = 0,075 kN.m, My = 0,0125 kN.m e Mz = 0,0175 kN.m, originado do projeto da célula. Estes valores seguem uma necessidade específica para este tipo de célula numa aplicação em túnel de vento. O engaste da peça é realizado na região inferior. Na prática, em função de processos de manufatura desta célula de carga, os parâmetros geométricos podem apresentar incertezas.
Duas otimizações foram realizadas para o modelo estrutural: uma primeira, considerando as incertezas geométricas (chamada, de agora em diante, RBDO), e uma segunda, considerando os valores médios dos parâmetros como determinísticos (a que se chamou de otimização determinística).
Para o modelo RBDO, tanto as variáveis de projetos e algumas propriedades físicas do material foram consideradas como variáveis aleatórias. Na tabela 1 estão apresentados os limites inferiores e superiores das variáveis de projeto, bem como o tipo de distribuição e o coeficiente de variação que existem para cada uma das variáveis de projeto.
| Parâmetros | Limite inf. (m) | Limite sup. (m) | Distribuição | Coef. de variação σ /μ |
|---|---|---|---|---|
| A | 0,150 | 0,250 | Normal | 0,02 |
| B | 0,130 | 0,200 | Normal | 0,02 |
| C | 0,020 | 0,045 | Normal | 0,02 |
| D | 0,003 | 0,010 | Normal | 0,02 |
Para o problema estrutural, também se considerou o limite de escoamento do material (σe ) e o módulo de elasticidade (E) como variáveis aleatórias. Na tabela 2 são apresentadas as características estatísticas para o campo estocástico correspondente a estes parâmetros. Perceba‐se que as variáveis de projeto da otimização também são variáveis aleatórias neste problema.
| Variável | Distribuição | Unidade | Média μ | Coeficiente de variação σ /μ |
|---|---|---|---|---|
| E | Log‐normal | MPa | 171 | 0,10 |
| σe | Log‐normal | MPa | 280 | 0,02 |
O limite de confiabilidade admissível para as tensões em qualquer ponto da célula de carga no projeto foi assumido βL ≥ 3 (no caso da RBDO) e, para a otimização determinística, a restrição foi imposta no valor médio de limite de escoamento do material. A FO visa considerar a maximização da 1.ª frequência natural f e, ao mesmo tempo, a minimização da massa total da célula de carga M . Desta forma, é necessário obter uma normalização dos parâmetros, uma vez que são de grandezas diferentes. Uma simples representação pode ser dada por:
|
|
( 21) |
onde f é a primeira frequência natural da célula de carga. Devido à diferença de grandezas entre os 2 principais termos da FO a serem otimizados, foi realizada a normalização dos valores. Para se determinarem os termos (f0 e M0 ) que serão para normalização dos parâmetros obtidos, os valores da 1.ª frequência e massa foram obtidos com o intervalo médio das variáveis, ou seja (limite inferior + limite superior/2) correspondentes respectivamente a 33.308 Hz e 264 gramas. O cálculo de massa da célula de carga para este trabalho é , onde n é o número de elementos, ρ é a densidade do material utilizado e Vi é o volume do i ‐ésimo elemento.
Também foi inserida uma ponderação com relação à importância de cada um dos fatores, dada por ∝ = 0,6, para priorização da maximização da frequência natural em relação à massa. A FO resultante é definida como:
|
|
( 22) |
Neste caso, para as variáveis de projeto, o próprio algoritmo garante que não ocorra violação para os limites superiores e inferiores. Entretanto, para o limite do índice de confiabilidade, a técnica de penalidade foi aplicada. O valor da penalidade é aumentado de acordo com o aumento na violação da restrição do índice de confiabilidade calculado a cada iteração da otimização. Especificamente, a penalidade é dada por:
|
|
( 23) |
onde H é a função passo, a qual é 0 seg ≤ 0 ou próprio valor de g se g > 0, onde , onde βe é o índice de confiabilidade encontrado e C é um valor constante (neste trabalho foi assumido C = 10). A FO a ser otimizada é mostrada como FO na equação 24, que foi reformulada a fim de satisfazer a exigência do método de otimização. O algoritmo de otimização deve encerrar para o número máximo de gerações estabelecido para o AG ou a redução do coeficiente de variação da FO menor que uma tolerância. Neste trabalho, os parâmetros tomados para o AG foram de 50 gerações, 50 indivíduos, fator de cruzamento igual a 0,8, fração de mutação de 0,5 e elitismo igual a 2. Mais informações sobre a aplicação destes parâmetros podem ser encontradas em [15]
|
|
( 24) |
Desta forma, o modelo matemático de otimização, pode ser reescrito como:
|
|
( 25) |
onde pL e pU são, respectivamente, os limites inferiores e superiores das variáveis de projeto . Alterar o termo ∝ para valorizar os termos de interesse do projeto (mínima massa ou máxima frequência). Isto irá gerar soluções pareto‐ótimas não apresentadas neste trabalho, entre as quais, uma solução não dominada deverá ser escolhida pelo projetista para a construção da célula de carga. A forma da equação em termos de somas ou de divisões adimensionais e normalizadas, p.e. , também é uma escolha do projetista e, a menos do custo computacional gasto na otimização, não deve substancialmente afetar a qualidade das soluções.
É importante mencionar que, devido a critérios de projeto, parâmetros relacionados à malha do modelo de elementos finitos foram considerados previamente por meio de testes de convergência do projeto calculado com seus limites superiores e inferiores, como, por exemplo, a razão de aspecto assim como o tamanho máximo dos elementos.
6. Resultados e discussões
6.1. Otimização determinística e otimização baseada em confiabilidade
Após as otimizações terem sido executadas, pôde‐se verificar os resultados indicados na tabela 3 , onde constam as comparações entre os valores encontrados com RBDO e com a otimização determinística.
| Parâmetros | RBDO (m) | Otimização determinística (m) |
|---|---|---|
| A | 0,1617 | 0,1533 |
| B | 0,1501 | 0,1359 |
| C | 0,0316 | 0,0271 |
| D | 0,0100 | 0,0100 |
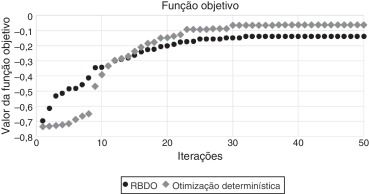
Para a solução obtida com RBDO, o valor da primeira frequência foi de 19.610 Hz e massa de 324,38 gramas, enquanto para a otimização determinística a frequência ficou em 21.721 Hz (11% maior) e a massa igual a 299,65 gramas (8% mais leve). O valor da FO obtido com a RBDO foi de ‐0,1382, enquanto para a otimização determinística foi de ‐0,0627.
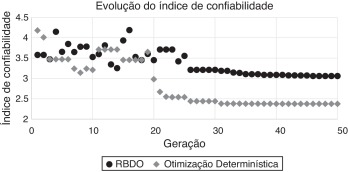
Entretanto, ao avaliar o valor final da otimização determinística, constata‐se que a confiabilidade da solução ótima apresenta um índice igual a 2,38, o que pode ser considerado baixo ao se inserir incertezas no modelo. Para a RBDO, o índice de confiabilidade limite foi respeitado, obtendo dessa forma, um valor de 3,06. O gráfico que apresenta a convergência dos valores da FO para a RBDO e para a otimização com dados determinísticos está na figura 6 .
|
|
|
Figura 6. Convergência do valor da função objetivo. |
Um gráfico que mostra o comportamento do índice de confiabilidade para a RBDO e para a otimização determinística foi gerado (fig. 7 ). Para a otimização determinística, o cálculo do índice de confiabilidade foi calculado após a otimização ter sido finalizada para comparar com os valores obtidos com RBDO. Alguns dos pontos da comparação ficaram sem valores definidos de confiabilidade por apresentarem, ao longo das iterações, uma configuração geométrica onde a confiabilidade não é definida (probabilidade de falha maior que 50%).
|
|
|
Figura 7. Análise do índice de confiabilidade para cada iteração do AG e da otimização determinística. |
6.2. Relação do índice de confiabilidade e coeficiente de segurança
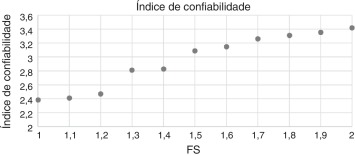
Foram realizadas análises do índice de confiabilidade em confronto com a utilização de coeficientes de segurança impostos de forma empírica. Para isso, foram realizadas otimização determinísticas para diferentes valores do limite de escoamento , onde FS é o fator de segurança (FS), que varia de um até 2 com o passo 0,1. O valor do índice de confiabilidade é calculado a posteriori , para se verificar o efeito da aplicação do FS aplicado a todo o material do projeto. Um gráfico que mostra os valores do índice de confiabilidade para cada FS está apresentado na figura 8 .
|
|
|
Figura 8. Análise do índice de confiabilidade para cada iteração do AG. |
Pela análise do gráfico, constatou‐se que é necessário utilizar um FS = 1,5 para se obter um valor do índice de confiabilidade maior ou igual a 3, que foi o valor de referência utilizado no RBDO. Entretanto, para este caso, o valor da FO é de ‐0,1519, ou seja, 9,88% maior (em módulo) do que o valor obtido com a RBDO. Pode‐se verificar que a simples utilização do FS pode gerar configurações aparentemente ótimas com índice de confiabilidade que atende ao critério probabilístico, quando o índice de confiabilidade é calculado a posteriori . Entretanto, o valor da FO no modelo de RBDO, além de atender ao critério de confiabilidade, resultou em função de custo inferior com projeto mais leve em termos de massa.
7. Conclusões
Neste trabalho foi apresentada uma metodologia de otimização baseada em confiabilidade para otimização de uma estrutura tridimensional de uma célula de carga submetida a esforços multiaxiais.
O índice de confiabilidade relativo às tensões mecânicas em qualquer ponto da estrutura foi considerado como uma restrição do modelo de otimização, onde o método de otimização utilizado foi o AG, devido às suas características de robustez que o tornam capaz de escapar de mínimos locais.
As análises baseadas em confiabilidade incluíram a aleatoriedade geométrica das variáveis de projeto, bem como variabilidade das propriedades do material do modelo estrutural.
Obviamente, técnicas diferentes de análise de confiabilidade podem ser utilizadas na metodologia apresentada, como, por exemplo, o método de Monte Carlo. Entretanto, por se tratar de um modelo estrutural de elementos finitos que exige um certo esforço computacional, a otimização pode se tornar inviável uma que o número de chamadas à função estado limite é consideravelmente maior que utilizando FORM.
Um gráfico da evolução do valor da FO ao longo das iterações do método de AG foi apresentado, onde foi possível verificar a estabilização do valor para RBDO e a otimização determinística, onde fica evidente a influência e importância de se considerar restrições de confiabilidade.
Constatou‐se que o fato de se utilizar empiricamente valores para o FS pode fazer com que se obtenham projetos confiáveis; entretanto, o valor da FO pode ser consideravelmente maior, como foi no caso apresentado.
Conclui‐se, portanto, a importância de que estudos de otimização levem em conta incertezas, uma vez que foi possível constatar neste trabalho que a solução obtida com a otimização determinística tornou‐se menos segura quanto à falha, quando comparada com a solução obtida com RBDO na presença de incertezas geométricas de construção, assim como incertezas das propriedades dos materiais.
Bibliografia
- [1] H. Agarwal; Reliability based design optimization: Formulation and methodologies; Aerospace and Mechanical Engineering, University of Notre Dame (2004)
- [2] M. Papadrakakis, Y. Tsompanakis, N.D. Lagaros, M. Fragiadakis; Reliability based optimization of steel frames under seismic loading conditions using evolutionary computation; JTAM., 42 (3) (2004), pp. 585–608
- [3] K.K. Choi, B.D. Youn; Hybrid analysis method fot reliability‐base design optimization; DETC2001/DAC‐21044 ‐ ASME 2001 Design Engineering Technical Conferences and Computers and Information in Engineering Conference (2001)
- [4] G. Cheng, L. Xu, L. Jiang; A sequential approximate programming strategy for reliability‐based structural optimization; Elsevier Ltd (2006) http://dx.doi.org/10.1016/j.compstruc.2006.03.006
- [5] A.M. Awruch, H.M. Gomes; Análise da confiabilidade de estruturas de concreto armado com uma metodologia para inclusão de efeitos estocásticos de propriedades dos materiais; Rev. int. métodos numér. cálc. diseño, 30 (2) (2013), pp. 85–96 http://dx.doi.org/10.1016/j.rimni.2013.01.002
- [6] R.E. Melchers; Structural Reliability Analysis and Prediction; (second edition)C. John Wiley & Sons Ltd (1999) Ed. 456. ISBN: 978‐0‐471‐98771‐0
- [7] A.H.-S. Ang, W.H. Tang; «Probability Concepts in Engineering: Emphasis on Applications to Civil and Environmental Engineering»; Wiley (2006) Ed. 420. ISBN: 047172064X
- [8] I.G. Torné, R.B. Prieto, S.L. Choy, A.d.C. Serpa; Determinación de la confiabilidad en interruptores de potencia: caso de estudio, Ingeniare; Rev. chil. ing, 21 (2) (2013), pp. 271–278 http://dx.doi.org/10.4067/S0718‐33052013000200010
- [9] A.M. Hasofer, D. Lind; An exact and invariant first‐order reliability format; J. Eng. Mech., 100 (1974), pp. 111–121
- [10] A. Haldar, S. Mahadevan; «Probability, Reliability and Statistical Methods in Engineering Design»; J.W. Sons (1999) ISBN: 9780471331193
- [11] H.M. Gomes, «Reliability analysis of reinforced concrete structures. Ph.D. Thesis. In Portuguese (Técnicas de Avaliação da Confiabilidade em Estruturas de Concreto Armado)». Programa de Pós‐Graduação em Engenharia Civil da Escola de Engenharia da Universidade Federal do Rio Grande do Sul.UFRGS: Porto Alegre, Brazil, 2001.
- [12] A.D. Belegundu and T.R. Chandrupatla, «Optimization Concepts and Applications in Engineering». 2 ed, ed. P.‐H. Inc., Ed. 2: Cambridge University Press. 480. 1999. ISBN: 1107674174.
- [13] J. Tu, K.K. Choi; A New Study on Reliability‐Based Design Optimization; J. Mech. Design., 121 (1999), pp. 557–564 DOI: 10.1115/1.2829499
- [14] J.H. Holland, «Adaptation in natural and artificial systems», ed. A.A. University of Michigan Press, MI. Ed.: University of Michigan Press. 1975. ISBN: 9780262581110.
- [15] D.E. Goldberg, «Genetic Algorithms in search, optimization and machine learning». Ed., Reading Addison‐Wesley Publishing. 1989. ISBN: 0201157675.
- [16] R.H. Torres, M.I. Mesa, O.L. Santiago, L.D.T. Câmara, A.J.d.S. Neto, L.M.Z.d. Cárdenas; Comparación de diferentes algoritmos metaheurísticos en la estimación de parámetros del modelo relacional general de cromatografía líquida en coluna. In Spanish; Rev. chil. ing., 22 (1) (2014), pp. 14–25 http://dx.doi.org/10.4067/S0718‐33052014000100003
- [17] F. Maggioni, M. Kaut, L. Bertazzi; Stochastic optimization models for a single‐sink transportation problem; Comput. Manag. Sci., 6 (2) (2009), pp. 251–267 http://dx.doi.org/10.1007/s10287‐008‐0086‐z
- [18] L.L. Corso, «Reliability based design optimization using global search algorithm for structural problems. Ph.D. Thesis. In Portuguese (Otimização baseada em confiabilidade utilizando algoritmos de busca global.)». Programa de Pós‐Graduação em Engenharia Mecânica da Escola de Engenharia da Universidade Federal do Rio Grande do Sul.UFRGS: Porto Alegre, Brazil., 2010.
- [19] H.M. Gomes, N.R.S. Silva; Some comparisons for damage detection on structures using genetic algorithms and modal sensitivity method; Appl Math Model, 32 (11) (2008), pp. 2216–2232 http://dx.doi.org/10.1016/j.apm.2007.07.002
Document information
Published on 01/12/16
Accepted on 06/07/15
Submitted on 23/03/15
Volume 32, Issue 4, 2016
DOI: 10.1016/j.rimni.2015.07.002
Licence: Other
Share this document
claim authorship
Are you one of the authors of this document?