Resumo
O presente trabalho aborda o problema de identificação de danos estruturais em placas a partir da matriz de flexibilidade. O dano é continuamente descrito por um parâmetro de coesão definido no domínio da estrutura. O problema de identificação de danos é, então, definido como um problema de otimização, onde o objetivo é minimizar, com relação ao campo de coesão, um funcional definido a partir da diferença entre a matriz de flexibilidade obtida experimentalmente e a correspondente matriz prevista por um modelo de elementos finitos da estrutura. O método de otimização enxame de partículas foi considerado para a resolução do problema de otimização. A avaliação numérica do método de identificação de danos proposto foi realizada considerando-se uma placa de Kirchhoff retangular, engastada em uma das extremidades. O cenário de dano constituiu-se de um dano duplo e com as formas modais corrompidas com diferentes níveis de ruído aditivo. Os resultados numéricos mostram a potencialidade do método em identificar a presença de danos a partir de uma quantidade reduzida de dados experimentais corrompidos com ruído.
Abstract
The present work addresses the structural damage identification problem in plates by using the flexibility matrix. The damage is continuously described by a cohesion parameter defined in the elastic structure domain. The damage identification problem is, then, defined as an optimization one, whose aim is to minimize, with respect to the cohesion field, a functional based on the difference between the experimental flexibility matrix and the corresponding one predicted by a finite element model of the structure. The particle swarm optimization method was considered to solve the optimization problem. The numerical tests of the proposed damage identification method are carried out taking into account a rectangular Kirchhoff plate with one clamped edge. The considered damage scenario is composed by two damaged regions and the mode shapes are corrupted with different additive noise levels. The numerical results show the potentiality of the proposed method in identifying damages from a reduced number of noise corrupted experimental data.
Palavras-chave
Modelo Contínuo de Dano ; Matriz de Flexibilidade ; Otimização por Enxame de Partículas ; Estrutura do tipo Placa
Keywords
Continuum damage identification ; Flexibility matrix ; Particle swarm optimization ; Plate like structures
1. Introdução
Danos estruturais podem comprometer o desempenho e a integridade de uma estrutura, colocando, portanto, vidas humanas em risco. A identificação de danos num estágio inicial e o monitoramento contínuo de uma estrutura têm despertado o interesse de vários pesquisadores, pois possibilitam a redução de custos de manutenção e reparo, além de aumentar sua vida útil, a segurança e o conforto humano.
Muitos métodos de identificação de danos, mesmo se tratando de ensaios não destrutivos de inspeção – que, por definição, são aqueles que não interferem na condição de operação da estrutura – ou são baseados em observações visuais ou são métodos experimentais localizados, como, por exemplo, a inspeção através de líquido penetrante, ultras som, campo magnético, etc. Esses métodos, porém, apresentam certas desvantagens quando aplicados a estruturas complexas, como a necessidade do conhecimento a priori da localização do dano e a acessibilidade da porção da estrutura sendo inspecionada.
Os crescentes avanços na tecnologia da computação, do processamento de sinais e dos sensores contribuíram para o desenvolvimento de métodos de identificação de danos baseados no comportamento vibratório da estrutura [25] . Isso se deve, principalmente, ao fato de essas técnicas serem diretamente aplicáveis em estruturas lineares com geometria complexa e de, em sua maioria, serem baseadas na análise modal [1] , [6] and [7] . Recentemente, o desenvolvimento de técnicas baseadas em dados no domínio do tempo têm permitido, também, a formulação do problema de identificação de danos em estruturas não-lineares, altamente amortecidas ou com elevada densidade modal, situações nas quais a formulação baseada na análise modal pode ser extremamente difícil [3] and [14] .
Embora distintas abordagens de identificação de danos sejam encontradas na literatura, pode-se observar uma atenção especial àquelas que envolvem seu comportamento dinâmico. Estes compreendem perspectivas determinísticas [16] ou estatísticas [14] and [18] . Alguns consideram diferentes tipos de dados, tais como parâmetros modais [13] and [30] , séries temporais [3] , respostas em frequência [25] e diversas formulações matemáticas e algoritmos numéricos para a solução do problema inverso correspondente [17] and [24] .
Abordagens de identificação de dano estrutural que consideram a abordagem modal tradicional são, em geral, construídas sobre a atualização do método de elementos finitos (FEM) [6] . A ideia básica das abordagens vibratórias é que as propriedades modais da estrutura (frequências, formas modais e amortecimento modal) são funções de suas propriedades físicas (massa, rigidez e amortecimento) e, portanto, alterações nas propriedades físicas devido à presença de danos resultam em alterações em suas propriedades modais. O problema inverso de identificação de danos pode ser definido a partir das frequências naturais não amortecidas [9] , destas e suas formas modais [15] , curvatura das formas modais [19] and [21] , energia de deformação modal [1] and [4] , ou, alternativamente, a matriz de flexibilidade da estrutura [20] and [27] . Uma das vantagens de se utilizar a matriz de flexibilidade é a relação inversa entre esta e o quadrado das frequências naturais não-amortecidas da estrutura, o que permite que uma boa estimativa da matriz de flexibilidade possa ser obtida experimentalmente a partir dos modos de vibração de mais baixa frequência.
Neste projeto, os parâmetros modais são utilizados para a obtenção da matriz de flexibilidade da estrutura, definida como a inversa da matriz de rigidez que, por sua vez, é parametrizada por um atributo estrutural, denominado parâmetro de coesão, que descreve de forma contínua a integridade estrutural. O problema de identificação de danos é, então, definido como um problema de otimização, onde o objetivo é minimizar um funcional definido a partir da diferença entre a matriz de flexibilidade prevista por um modelo de elementos finitos (MEF) e a correspondente matriz experimental, obtida a partir de um ensaio realizado na estrutura supostamente danificada [5] . Identificação de danos compreende uma vasta categoria de problemas inversos que, em geral, são malpostos e malcondicionados [12] . Métodos convencionais de otimização, tais como os métodos determinísticos baseados em gradiente, têm sua convergência dependente de um bom ponto de partida, de modo a não recaírem em um mínimo local. Esse aspecto pode ser contornado utilizando-se métodos de regularização [29] ou aplicando-se um dos diversos métodos estocásticos de otimização disponíveis. Métodos tais como o evolução diferencial, o método de Luus-Jaakola e a otimização por enxame de partículas, adotado neste trabalho, têm sido reportados na literatura [10] , [22] and [28] .
Um método de identificação de danos via matriz de flexibilidade estrutural, onde o campo de danos é modelado utilizando o FEM por meio de um parâmetro de coesão β , é apresentado em [27] . O parâmetro de coesão β ∈ [0, 1] pode ser interpretado como um estado de coesão local do material. Resultados das simulações numéricas de casos de dano em uma viga engastada são apresentados, considerando um número reduzido de sensores e diferentes níveis de ruído. Dando continuidade ao trabalho desenvolvido por [27] , apresenta-se em [5] uma avaliação do comportamento das frequências naturais e da matriz de flexibilidade para uma viga de Euler-Bernoulli simplesmente apoiada e para uma viga engastada na presença de danos. Essa análise permite também o conhecimento das regiões onde há maior sensibilidade ao dano, ajudando a traçar estratégias para melhorar a identificação de danos em regiões que sofrem poucas alterações na presença de falhas estruturais. Diversos métodos de localização de danos e de otimização são avaliados na tentativa de identificar os danos simulados na presença de dados ruidosos e quando apenas um subconjunto dos graus de liberdade (GDL) da estrutura estão disponíveis. Por fim, o modelo é expandido, permitindo identificar danos em uma placa de Kirchhoff.
No presente trabalho, resultados numéricos da identificação de danos em uma placa retangular de Kirchhoff para diferentes cenários de dano e níveis de ruído nos dados experimentais sintéticos são apresentados. A principal contribuição deste trabalho consiste em se aplicar a matriz de flexibilidade na identificação de danos na presença de ruído, em um modelo de dano contínuo, testado com sucesso em uma estrutura bidimensional.
2. Modelo contínuo de dano – placa
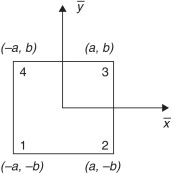
Considerando-se um elemento retangular padrão de uma placa de Kirchhoff, com 4 nós, conforme ilustrado na fig. 1 , o campo de deslocamentos , no interior do elemento, é dado por
|
|
|
Figura 1. Elemento finito retangular com origem no centro da figura. |
|
|
( 1) |
onde e são as coordenadas espaciais locais, com origem no centro do elemento; , e são, respectivamente, o deslocamento transversal, a rotação em e a rotação em no nó local 1; , e são, respectivamente, o deslocamento transversal, a rotação em e a rotação em no nó local 2; , e são, respectivamente, o deslocamento transversal, a rotação em e a rotação em no nó local 3; e , e são, respectivamente, o deslocamento transversal, a rotação em e a rotação em no nó local 4; , , …, são as funções de forma (ou interpolação) convencionais de um elemento finito de placa de Kirchhoff.
Considerando-se a aproximação para o campo de deslocamentos, dada pela Eq. (1) , a matriz de rigidez de um elemento supostamente danificado pode ser escrita como
|
|
( 2) |
onde,
|
|
( 3) |
e
|
|
( 4) |
onde βe é um parâmetro que descreve o dano no interior do elemento, é o operador diferencial, h0 representa a espessura nominal da placa, E e ν são, respectivamente, o módulo de elasticidade e o coeficiente de Poisson, a matriz Be é composta pelas funções de interpolação apropriadas ao modelo de Kirchhoff. Neste trabalho, em nome da clareza e simplicidade do texto, porém, sem perda de generalidade do ponto de vista teórico, serão considerados como danos estruturais exclusivamente alterações na espessura da placa em questão.
O parâmetro β está relacionado com a ligação entre os pontos materiais do corpo, podendo ser interpretado como uma medida do estado de coesão local do material. Por esse motivo, β será denominado parâmetro de coesão. Se β = 1, considera-se que todas as ligações entre os pontos materiais foram preservadas, ou seja, a estrutura encontra-se livre de danos. Se β = 0, significa que todas as ligações entre os pontos materiais foram desfeitas e, assim, uma ruptura local é considerada. Considerando-se a Eq. (2) , pode-se observar que o parâmetro de coesão contabiliza qualquer alteração, devido à presença de dano, no módulo de elasticidade ou momento de inércia da seção transversal da estrutura. Na literatura especializada, é largamente aceita a hipótese de que a matriz de massa da estrutura danificada é a mesma da estrutura original, ou seja, as alterações acarretadas na mesma pelo dano estrutural são desprezíveis.
Considerando-se funções de interpolação lineares, no interior de um elemento finito, o campo de coesão é aproximado por
|
|
( 5) |
onde , , e são, respectivamente, os valores nodais de coesão nos nós locais 1, 2, 3 e 4; e , , e são as funções de interpolação do campo de coesão. Deve-se notar que a discretização espacial do campo de coesão βe não depende da discretização do campo de deslocamentos, de forma que diferentes malhas poderiam ser adotadas.
Por questões de simplicidade na interpretação dos cenários de dano analisados, será considerado que o módulo de elasticidade se mantém uniforme ao longo da placa, mesmo na presença de danos. Sendo assim, será considerado que o dano altera apenas as propriedades geométricas da placa e, portanto, o campo de coesão pode ser escrito como
|
|
( 6) |
onde h (x , y ), uma função contínua, indica a espessura da placa na posição (x , y ) e h0 representa a espessura nominal da mesma.
3. Matriz de flexibilidade estrutural
A matriz de flexibilidade G de uma estrutura com n GDL é a matriz n × n definida como a inversa de sua matriz de rigidez K . Portanto, em um problema estático, a matriz de flexibilidade relaciona a força f aplicada na estrutura com o deslocamento u resultante,
|
|
( 7) |
Sendo assim, de acordo com a Eq. (7) , a i-ésima coluna de G representa o deslocamento da estrutura quando uma força unitária é aplicada ao seu i-ésimo GDL. Ademais, a matriz de flexibilidade é simétrica, ou seja,
|
|
( 8) |
significando que o padrão de deslocamento observado em todos os GDL, devido a um carregamento no GDL i , é o mesmo que os deslocamentos observados somente no GDL i , quando a carga unitária é aplicada sucessivamente em cada GDL.
Embora a matriz de flexibilidade relacione um carregamento estático com o deslocamento resultante, esta pode ser obtida a partir dos parâmetros modais da estrutura como se segue.
As frequências naturais e as formas modais não-amortecidas de uma estrutura com n GDL podem ser obtidas a partir do problema de autovalor-autovetor
|
|
( 9) |
onde M e K são, respectivamente, as matrizes de massa e rigidez, de dimensão n × n , Φ é a matriz modal da estrutura, de dimensão n × n , cuja i-ésima coluna corresponde à forma modal ϕi (i-ésimo autovetor) e Λ é uma matriz diagonal, n × n , cujo i-ésimo componente (autovalor) é dado pelo valor quadrático da correspondente frequência natural não amortecida do sistema, ou seja, .
Considerando as formas modais da estrutura normalizadas em relação à matriz de massa, tem-se
|
|
( 10) |
|
|
( 11) |
onde I é a matriz identidade e T representa a transposição de uma matriz.
Partindo da Eq. (11) e do fato de a matriz de flexibilidade de uma estrutura ser definida como a inversa da matriz de rigidez, tem-se
|
|
( 12) |
Na prática, sempre haverão limitações experimentais, de sorte que o número de dados efetivamente medidos será sempre menor do que o ideal. Desse modo, tem-se a seguinte aproximação para a matriz de flexibilidade experimental Gexp da estrutura,
|
|
( 13) |
onde nexp < n é o número de modos obtidos do ensaio experimental, ωi ,exp e ϕi ,exp são, respectivamente, a i -ésima frequência natural não-amortecida e forma modal obtidas de um ensaio modal realizado na estrutura supostamente danificada. Observe-se que enquanto as matrizes em questão têm dimensão n × n e o somatório presente na Eq. (12) envolve n termos, a matriz de flexibilidade experimental – na grande maioria das situações – terá um dimensão menor e o somatório da Eq. (13) possuirá nexp termos.
Da Eq. (13) observa-se que, devido à relação inversa com o quadrado da frequência natural, uma boa estimativa para a matriz de flexibilidade pode ser obtida experimentalmente a partir de modos de mais baixa frequência da estrutura que, na prática, são os modos que podem ser mais facilmente obtidos.
Deve-se notar que a dimensão da matriz Gexp depende apenas do número m de GDL medidos no ensaio de vibrações, que é equivalente ao número de componentes dos modos experimentais ϕi ,exp . Sendo assim, a matriz de flexibilidade possui dimensão m × m . Portanto, para se definir um problema de identificação de danos estruturais baseado na matriz de flexibilidade, torna-se necessária a determinação de uma matriz de flexibilidade analítica reduzida – relacionada apenas aos m GDL medidos no ensaio de vibrações – que contenha informações a respeito das propriedades de rigidez da estrutura como um todo. Para tal, a matriz de rigidez original deve ser particionada na forma
|
|
( 14) |
onde os índices m e o referem-se, respectivamente, aos GDL medidos e omitidos . Pode-se mostrar [2] que a matriz de flexibilidade analítica é igual à inversa da matriz de rigidez reduzida, obtida pela redução estática de Guyan [8] , ou seja,
|
|
( 15) |
4. Problema inverso
Definindo-se o vetor de parâmetros de coesão
|
|
( 16) |
onde βi é o valor do parâmetro de coesão no i-ésimo nó da discretização espacial desse campo e np é o número total de nós da malha; o problema inverso de identificação de danos pode, então, ser definido como um problema de otimização com restrição, onde o objetivo é minimizar, com respeito ao vetor de parâmetros de coesão β , o funcional
|
|
( 17) |
onde Gexp é a matriz de flexibilidade obtida de um ensaio na estrutura supostamente danificada e é a correspondente matriz prevista pelo modelo.
4.1. Algoritmo de otimização enxame de partículas
Para resolver o problema de identificação de danos proposto utilizou-se o método de otimização enxame de partículas (particle swarm optimization – PSO), desenvolvido por Kennedy e Eberhart [11] , o qual é inspirado em um modelo de interação social. Nesse método, cada indivíduo ou partícula na posição p representa uma solução candidata, a qual se move no espaço de busca com velocidade v , dinamicamente ajustada de acordo com sua própria experiência de movimento e pela experiência de movimento do grupo.
Em cada geração t , as partículas são manipuladas de acordo com as seguintes relações:
|
|
( 18) |
|
|
( 19) |
onde é denominado termo de inércia, c1 e c2 são coeficientes de aceleração; r1 e r2 são valores aleatórios no intervalo [0, 1]; bi é a melhor posição ocupada pela partícula i , e bg é a melhor posição encontrada por todo o grupo.
Altos valores de favorecem a habilidade do enxame em explorar amplas regiões do espaço de busca (exploration ), enquanto que pequenos valores concentram a busca ao redor de uma área promissora (exploitation ), que tem como finalidade refinar a solução candidata. Além disso, baixos valores de c1 e c2 promovem uma trajetória suave das partículas, enquanto que altos valores promovem maior aceleração e movimentos abruptos. Entretanto, valores pequenos para esses parâmetros de otimização podem render uma convergência lenta, enquanto valores altos podem render uma convergência prematura.
Para promover um balanço entre exploration e exploitation , o termo de inércia pode ser ajustado [26] , como
|
|
( 20) |
onde e são os valores iniciais e finais do termo de inércia, respectivamente, Nmax é o número máximo de gerações avaliadas, ou um número suficiente para assegurar que, ao longo das iterações, o termo possa decrescer linearmente.
Uma estratégia para melhorar o desempenho do PSO através da variação adaptativa dos coeficientes de aceleração é apresentada em [23] . Essa estratégia baseia-se no fato de que, com um alto valor para o componente cognitivo, c1 , e um pequeno valor para o componente social, c2 , no início do processo iterativo, as partículas podem mover-se em torno do espaço de busca, em vez de caminhar para a melhor posição do grupo, que nessa etapa do processo ainda é uma posição pouco precisa. Com o decorrer das iterações, o valor de c1 diminui e o valor de c2 aumenta, favorecendo a confiança na experiência adquirida pelo grupo. Matematicamente, essa variação é dada por:
|
|
( 21) |
|
|
( 22) |
onde c1,max , c1,min , c2,max , e c2,min são constantes.
No presente trabalho, foram consideradas 100 partículas; o parâmetro de inércia foi ajustado conforme a Eq. (20) ; e os parâmetros c1 e c2 foram ajustados, respectivamente, de acordo com as Eqs. (21) e (22) , com c1,min = c2,min = 0, 5, c1,max = c2,max = 1, 5.
Os seguintes critérios de parada foram considerados: ; z ≤ 10−3 , onde ou o valor do funcional não se altera durante 50 iterações consecutivas.
Apezar das considerações para melhorar o desempenho do método PSO, este apresentou um custo computacional muito elevado para minimizar o funcional para o caso da placa, sendo necessário buscar-se uma forma de contornar esse obstáculo. Uma estratégia encontrada partiu do fato de que busca-se identificar danos em estágio inicial, quando o mesmo atinge poucas regiões da estrutura e, assim, o valor da maior parte dos parâmetros será β = 1. Dessa forma, na estratégia adotada, quando as soluções (partículas) iniciais são geradas aleatoriamente, todas aquelas que representam um dano com profundidade maior que 25% da espessura da estrutura são substituídas pelo valor β = 1. Além disso a estremidade livre da placa é considerada intacta para 80% das partículas, ou seja, a maioria dos parâmetros de coesão dessa região possuem valor unitário. Deve-se notar que tal estratégia não impede que um dano nos elementos finais da placa sejam identificados. Com isso, o tempo médio para obtenção dos resultados apresentados no presente trabalho ficou em torno de 2 h e 40 min, considerando-se um computador com processador Intel Core 2 duo de 4 gigabytes de memória e usando-se o software Matlab.
5. Resultados numéricos
Esta seção apresenta uma avaliação numérica da potencialidade da abordagem de identificação de danos aqui proposta. Nos resultados que se seguem, foi considerada uma placa retangular de alumínio, com dimensão 0,4 m × 0,6 m × 0,005 m, engastada em um dos lados de menor dimensão (0,4 m). As propriedades materiais da placa são: massa específica p = 2.700 kg/m3 , módulo de elasticidade nominal E0 = 72,582 GPa e coeficiente de Poisson ν = 0,33. A placa foi discretizada considerando-se 7 × 9 elementos retangulares. Foram adotados elementos com 4 nós, onde cada ponto nodal possui 3 GDL — um transversal, um de rotação em x e um de rotação em y — e um parâmetro de coesão. A estrutura possui um total de 80 pontos nodais e, assim, 80 parâmetros de coesão e 216 GDL, pelo fato de 8 pontos nodais encontrarem-se no engaste.
Foram considerados como medidos em um ensaio modal 36 GDL transversais igualmente espaçados e os modos de vibração na faixa de frequências entre 0-460 Hz. A tabela 1 mostra a frequência dos 10 primeiros modos medidos.
| Modo de vibração | Frequência (Hz) |
|---|---|
| 1 | 12,09 |
| 2 | 39,89 |
| 3 | 75,10 |
| 4 | 135,45 |
| 5 | 186,10 |
| 6 | 218,03 |
| 7 | 278,23 |
| 8 | 293,27 |
| 9 | 423,38 |
| 10 | 457,53 |
Com o objetivo de simular de forma mais realística os dados experimentais, um ruído aditivo, com média nula e distribuição uniforme, foi adicionado às formas modais de vibração, segundo a equação
|
|
( 23) |
onde corresponde a i-ésima forma experimental sintética sem ruído, p é o nível de ruído aditivo acrescentado, r é um vetor com números aleatórios uniformemente distribuídos no intervalo [− 1, 1] e nexp é o número de modos considerados no ensaio modal sintético.
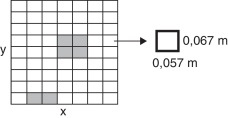
A imposição do defeito é realizada através de uma redução na espessura relativa h (x , y )/h0 na região defeituosa, onde h (x , y ) é a espessura da placa na posição (x ,y ). Nos nós defeituosos tem-se h (x , y )/h0 ≠ 1 e nos nós onde não há defeitos h (x , y )/h0 = 1, onde x e y representam as coordenadas dos respectivos nós. Quando um dano é prescrito por um único valor de h (x , y )/h0 ≠ 1, fora da borda da placa, este possui a forma de uma pirâmide, devido às funções de interpolação utilizadas, além disso a região danificada engloba 4 elementos. Para um dano situado na borda da placa a região danificada engloba apenas 2 elementos. O MEF, com os valores prescritos referentes ao dano, é utilizado para gerar os modos de vibração da extrutura danificada, que, após a adição de ruído, representam os dados experimentais sintéticos.
A tabela 2 apresenta os cenários de dano considerados neste trabalho. No primeiro caso não foi considerado ruído nas medições, enquanto que nos demais casos os modos de vibração foram contaminados com ruído de 1-3%, respectivamente. Para uma melhor compreensão, a fig. 2 ilustra a malha de elementos finitos, com as dimensões destes, e as regiões onde os danos foram impostos. A placa encontra-se engastada em y = 0.
| Caso | Posição (x;y)(m) | h (x , y )/h0 | Nível de ruído (%) |
|---|---|---|---|
| 1 | (0,11; 0); (0,23; 0,33) | 0,93; 0,93 | 0 |
| 2 | (0,11; 0); (0,23; 0,33) | 0,8; 0,8 | 1 |
| 3 | (0,11; 0); (0,23; 0,33) | 0,8; 0,8 | 3 |
|
|
|
Figura 2. Discretização espacial da placa e regiões danificadas. |
É importante destacar que em nenhuma das simulações realizadas adotou-se como medidos os GDL de rotação, devido às dificuldades experimentais associadas à sua medição.
Como em um problema real, não há informações sobre a correta localização e severidade do dano, faz-se necessário estabelecer estratégias que permitam concluir sobre a qualidade do processo de identificação. Uma forma simples de se avaliar a qualidade do resultado obtido é comparar as frequências naturais da estrutura, antes e depois do processo de identificação de danos (ajuste do modelo), a partir do indicador de erro dado por
|
|
( 24) |
onde ωi (β ) e ωi ,exp representam as frequências naturais do modelo e as frequências naturais experimentais, respectivamente. Com a informação gerada pelo ωIE pode-se decidir se um determinado resultado obtido foi validado ou não. Essa metodologia foi adotada no presente trabalho.
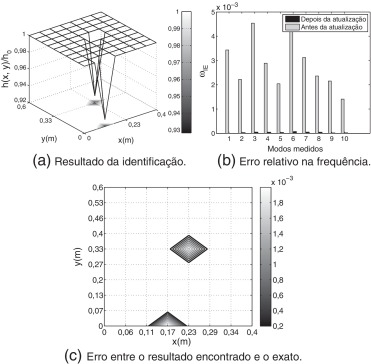
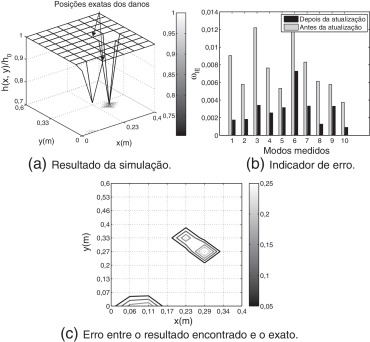
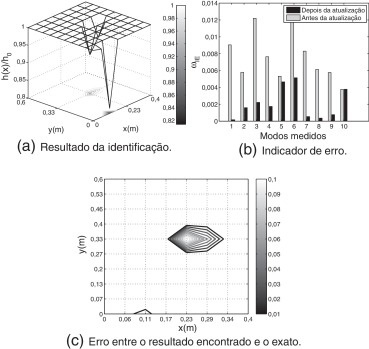
A fig. 3 apresenta o resultado da identificação de danos para o Caso 1. Como pode-se observar da fig. 3 a, na ausência de ruído, a abordagem proposta foi capaz de identificar com acurácia o campo de dano da estrutura. Na Fig. 3 b, corroborando com o resultado da identificação, observa-se claramente que, após a identificação, o erro relativo das frequências naturais dos 10 modos de vibração medidos é praticamente nulo. Além disso, é possível verificar, por meio da fig. 3 c, que a diferença entre o resultado encontrado e o resultado exato é muito pequena.
|
|
|
Figura 3. Identificação de danos para o Caso 1. |
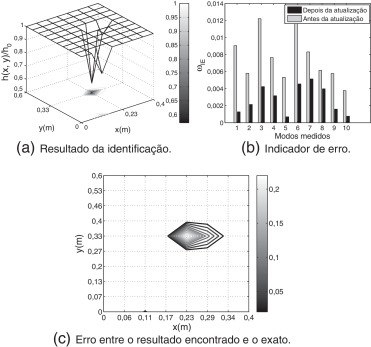
Apesar de o resultado encontrado pela abordagem de identificação de danos proposta ser bastante acurado, é importante analisar a capacidade do método em identificar danos frente às incertezas provenientes da medição dos sinais em um experimento real. Devido à dificuldade adicional proveniente dos dados estarem com um certo grau de ruído, os casos considerados a partir de agora possuirão severidade um pouco mais elevada, ver tabela 2 . Na fig. 4 apresentam-se os resultados obtidos para o Caso 2, onde 1% de ruído é adicionado aos modos medidos. Nesse caso, devido à presença de ruído, observa-se uma maior dificuldade na identificação de danos. Da fig. 4 a observa-se que o dano na região extrema da placa foi identificado com acuraria; o mesmo não ocorrendo com o dano na região central. Na região central, o dano identificado apresentou, em relação ao dano existente, uma menor intensidade e uma maior região, conforme evidenciado pela fig. 4 c. Da fig. 4 b observa-se uma redução significativa nos indicadores de erro, o que, por sua vez, valida o resultado da identificação apresentado na fig. 4 a.
|
|
|
Figura 4. Identificação de danos para o Caso 2. |
No Caso 3 considera-se que os dados experimentais são corrompidos com ruído de maior intensidade (3%). Os resultados dessa simulação são apresentados na fig. 5 . De acordo com a diferença entre o campo de dano estimado e o campo de dano exato, fig. 5 c, percebe-se claramente a dificuldade encontrada na identificação de danos frente a dados corrompidos com ruído. As alterações na matriz de flexibilidade experimental sintética, devido à presença de ruído nas formas modais, resultaram em erros nas estimativas tanto da intensidade quanto da localização dos danos presentes na estrutura.
|
|
|
Figura 5. - Identificação de danos para o Caso 3. |
Com o intuito de minimizar o efeito do ruído no resultado de identificação de danos, a simulação anterior (Caso 3) foi refeita, considerando-se, agora, no processo de identificação, uma matriz de flexibilidade experimental média, obtida como o resultado de uma média aritmética envolvendo matrizes de flexibilidade obtidas de ensaios experimentais independentes. No caso, foram considerados 7 ensaios modais. Os resultados dessa simulação são apresentados na fig. 6 . Conforme pode ser observado, tanto a localização quanto a intensidade do dano foram determinados com bastante acurácia. Já para o dano na região central da viga, é possível verificar que a sua posição foi identificada corretamente e, além deste, foi indicado um dano adjacente de baixa intensidade, figs. 6 a e 6c. Ademais, comparando-se as figs. 6 b e 5b, percebe-se claramente a superioridade do resultado de identificação de danos obtido a partir da utilização da matriz de flexibilidade média. Ou seja, em um problema de identificação de danos, os efeitos da presença de ruído nas medições pode ser minimizado com a utilização de uma matriz de flexibilidade média, envolvendo matrizes de flexibilidade obtidas de ensaios modais independentes.
|
|
|
Figura 6. - Identificação de danos para o Caso 3 (matriz de flexibilidade experimental média). |
6. Conclusões
O presente trabalho aborda o problema inverso de identificação de danos estruturais em placas a partir da matriz de flexibilidade. Diferentemente da maioria dos trabalhos presente na literatura, o campo de dano é, aqui, continuamente descrito por um parâmetro de coesão. O FEM foi considerado para discretizar espacialmente o campo de coesão e o problema de identificação de danos foi, então, definido como um problema de minimização. O método de otimização PSO foi considerado para a resolução do problema em questão. Os resultados de identificação de danos mostraram que, para o caso de uma placa engastada em uma extremidade, a matriz de flexibilidade é mais sensível à presença de danos na região do engaste. A abordagem proposta foi capaz de identificar com acurácia a presença de dano nesta região, mesmo para um elevado nível de ruído nas formas modais (3%), considerando-se, nesse caso, a matriz de flexibilidade experimental média. Ademais, tanto a localização quanto a intensidade do dano na região central da placa foram estimados de forma bastante satisfatória. Portanto, apesar da presença de ruído nos dados experimentais sintéticos, do número limitado de informação modal considerado no cômputo da matriz de flexibilidade e da não consideração de informação a priori a respeito da localização das regiões danificadas, a abordagem de identificação de danos proposta apresentou resultados acurados nos casos estudados.
Agradecimentos
Os autores agradecem ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) e à Fundação de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ) pelo apoio financeiro ao presente projeto de pesquisa.
References
- [1] A. Alvandi, C. Cremona; Assessment of vibration-based damage identification techniques.; Journal of Sound and Vibration, 229 (2) (2006), pp. 179–202
- [2] K.F. Alvin, L.D. Peterson, K.D. Park; Method for determining minimum-order mass and stiffness matrices from modal test data.; AIAA Journal, 1 (1995), pp. 128–135
- [3] P. Cacciola, N. Maugeri, G. Muscolino; Structural identification through the measure of deterministic and stochastic time-domain dynamic response; Computers and Structures, 89 (2001), pp. 1812–1819
- [4] P.J. Cornwell, S.W. Doebling, C.R. Farrar; Application of the strain energy damage detection method to plate-like structures; Journal of Sound and Vibration, 224 (2) (1999), pp. 359–374
- [5] R. A. P. Corrêa. “Identificação de Danos em Estruturas Bi-dimensionais via Matriz de Flexibilidade Baseada em um Modelo de Dano Contínuo”. Tese de doutorado, Universidade do Estado do Rio de Janeiro, Nova Friburgo, RJ, 2013.
- [6] S.W. Doebling, C.R. Farrar, M.B. Prime; A summary review of vibration-based damage identification; The Shock and Vibration Digest, 30 (2) (1998), pp. 91–105
- [7] W. Fan, P. Qiao; Vibration-based damage identification methods: a review and comparative study; Structural Health Monitoring, 10 (2011), pp. 83–111
- [8] R.J. Guyan; Reduction of stiffness and mass matrices; American Institute of Aeronautics and Astronautics Journal, 3 (1965), p. 380
- [9] W. Hasan; Crack detection from the variation of the eigenfrequencies of a beam on elastic foundation; Engineering Fracture Mechanics, 52 (3) (1995), pp. 409–421
- [10] F. Kang, J-j. Li, Q. Xu; Damage detection based on improved particle swarm optimization using vibration data; Applied Soft Computing, 12 (2012), pp. 2329–2335
- [11] J. Kennedy, R.C. Eberhart; Particle swarm optimization; Proceedings of the International Conference on Neural Networks, Piscataway, NJ, V 4 (1995), pp. 1942–1948
- [12] A. Kirsch; An Introduction to the Mathematical Theory of Inverse Problems; Springer, New York (1996)
- [13] L.M. Khoo, P.R. Mantena, P. Jadhav; Structural Damage Assesment Using Vibration Modal Analysis; Structural Health Monitoring, 3 (2004), pp. 177–194
- [14] F.P. Kopsaftopoulos, S.D. Fassois; Vibration based health monitoring for a lightweight truss structure: Experimental assessment of several statistical time series methods; Mech. Syst. Signal Process., 24 (2010), pp. 1977–1997
- [15] J. Maeck, G. De Roeck; Damage assesment using vibration analysis on the Z24-bridge; Mechanical Systems and Signal Processing, 17 (1) (2003), pp. 133–142
- [16] J.E. Mottershead, M. Link, M.I. Friswell; The sensitivity method in finite element model updating: A tutorial; Mechanical Systems and Signal Processing, 25 (2011), pp. 2275–2296
- [17] C. Na, S-P. Kim, H-G. Kwak; Structural damage evaluation using genetic algorithm; Journal of Sound and Vibration, 330 (2011), pp. 2772–2783
- [18] J.M. Nichols, E.Z. moore, K.D. Murphy; Bayesian identification of a cracked plate using a population-based Markov Chain Monte Carlo method; Computers and Structures, 89 (2011), pp. 1323–1332
- [19] A.K. Pandey, M. Biswas, M.M. Samman; Damage detection from changes in curvature mode shapes; Journal of Sound and Vibration, 145 (1) (1991), pp. 321–332
- [20] A. Park, G. Reich, K.F. Alvin; Structural damage detection using localized flexibilities; Journal of Intelligent Material Systems and Structures, 9 (1998), pp. 911–919
- [21] E. Parloo, P. Guillaume, M.V. Overmeire; Damage assesment using mode shape sensitivities; MEchanical Systems and Signal Processing., 17 (3) (2003), pp. 499–518
- [22] A.R.M. Rao, K. Lakshmi, D. Venkatachalam; Damage diagnostic technique for structural health monitoring using POD and self adaptive differential evolution algorithm; Computers and Structures, 106 (2012), pp. 228–244
- [23] A. Ratnaweera, S. Halgamuge, H. Watson; Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients; IEEE Transactions on Evolutionary Computation, 8 (3) (2004), pp. 240–255
- [24] W.X. ren, H.B. Chen; Finite element model updating in structural dynamics by using the response surface method; Engineering Structures, 32 (2010), pp. 2455–2465
- [25] J.V.A. Santos, N.M.M. Maia, C.M.M. Soares Structural damage identification: A Survey. In: B.H.V. Topping, M. Papadrakakis, editors. Trends in computational structures technology. Stirlingshire, Scotland: Saxe-Coburg Publications, 2008.
- [26] Y. Shi, R.C. Eberhart; A modified particle swarm optimizer; Proceedings IEEE World Congr. Comput. Intell., 6 (1998), pp. 9–73
- [27] L.T. Stutz, D.A. Castello, F.A. Rochinha; A flexibility-based continuum damage identification approach; Journal of Sound and Vibration, 279 (2005), pp. 641–667
- [28] R.A. Tenenbaum, L.T. Stutz, K.M. Fernandes; Damage identification in Bars with a Wave Propagation Approach: Performance Comparison of Five Hybrid Optimization Methods; Shock and Vibration, 20 (2013), pp. 863–878
- [29] B. Titurus, M.I. Friswell; Regularization in model updating; International Journal for Numerical Methods in Engineering, 75 (2008), pp. 440–478
- [30] A. Tomaszewska; Influence of statistical errors on damage detection based on structural flexibility and mode shape curvature; COmputers and Structures, 88 (2010), pp. 154–164
Document information
Published on 01/03/16
Accepted on 24/11/14
Submitted on 01/08/14
Volume 32, Issue 1, 2016
DOI: 10.1016/j.rimni.2014.11.004
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?