Research on safety assessment method for bridge structure based on variable weight synthesis method

Summary

Variable weight synthesis method is a safety assessment method which is using the varied weight principle, based on analytic hierarchy process and combining the theory of grey relevancy, it reduce influence that secondary cause is not obvious in assessment process, and make the result more correct and dependable. In the paper, variable weight principle and the assessment method were expounded in detail.

Keywords

Variable weight synthesis method ; Bridge structure ; Safety assessment

Variable weight principle and variable weights method

Variable weight principle

In the literature (Bai, 2007  and Liu et al., 2004 ), variable weight synthesis method is the definition of:

• Assume that a m-dimensional vector, ${\textstyle W^{0}=(W_{1}^{0},W_{2}^{0},\ldots ,W_{m}^{0})}$ , if present ${\textstyle W_{j}^{0}\in (0,1)}$ makes ${\textstyle \sum _{j=1}^{m}W_{J}^{0}=1}$ correct for arbitrary variables j  ∈ {1, 2, …, m };
• Given a m –d vector of parts keep weight W (X )Δ[W₁ (X )2W₁ (X ), …, W_m (X )], for given mapping: W  : [0, 1]^m  → (0, 1], it makes that:
• ${\textstyle \sum _{j=1}^{m}W_{j}(X)=1}$
• Assume that α_j , β_j  ∈ [0, 1], and α_j  ≤ β_j , for arbitrary variables j  ∈ {1, 2, …, m }, present W_j in regard to x_j in the internal [0, α_j ] and [β_j , 1] respectively decrease and increase progressively.
• Assume that the vector S (X )Δ[S₁ (X ), S₂ (X ), …, S_m (X )] is a m –d vector of parts variable weight, for the given mapping S  : [0, 1]^m  → (0, + ∞)^m , for arbitrary variables j  ∈ {1, 2, …, m }, assume α_j , β_j  ∈ [0, 1], and α_j  ≤ β_j present that:
• For arbitrary variables j  ∈ {1, 2, …, m   } for fixed weights vector ${\textstyle W^{0}=(W_{1}^{0},W_{2}^{0},\ldots ,W_{m}^{0})}$ , ${\textstyle W_{j}(X)=((W_{j}^{0}S_{j}(X))/(\sum _{k=1}^{m}W_{k}^{(0)}S_{k}(X)))}$ in the internal [0, α_j ] and [β_j , 1] respectively decrease and increase progressively.
• If 0 ≤ x_i  ≤ x_k  ≤ α_i  ∧ α_k , S_i (x ) ≥ S_k (x ), and β_i  ∨ β_k  ≤ x_i  ≤ x_k  ≤ 1, then

${\frac {w^{0}\cdot S(x)}{\sum _{j=1}^{m}w_{j}^{0}S_{j}(x)}}\triangleq \left\{{\frac {w_{1}^{0}\cdot S_{1}(x)}{\sum _{j=1}^{m}w_{j}^{0}S_{j}(x)}},{\frac {w_{2}^{0}\cdot S_{2}(x)}{\sum _{j=1}^{m}w_{j}^{0}S_{j}(x)}},\cdots ,{\frac {w_{m}^{0}\cdot S_{m}(x)}{\sum _{j=1}^{m}w_{j}^{0}S_{j}(x)}}\right\}$

( 1)

be called m –d vector of parts variable weight。

Amendment of variable weights method

In the variable weights method, when synthesis assessment the assessed value of hundred-mark system, it will result data with denominator larger, and produce larger round-off error. For convenience of calculations and considering the required precision, to transform hundred-mark system into percentage of system, and then, by adjusting coefficients in the formulas, getting the synthesis assessed value of hundred-mark system. in addition, for some sequences of inspection data, it is impossible to collect all the data, but it is needed to compare the curve of sequences of inspection data, so in this paper, considering base on the grey theory related principle to offset the malconformation and incomprehensive of data (Lan and Shi, 2001 ). The paper makes the improvement.

$V=\sum _{j=1}^{m}100w_{j}(x_{1},\ldots ,x_{m},w_{1}^{(0)},\ldots ,w_{m}^{(0)})x_{j}$

( 2)

In formula: V   is the assessed value; ${\textstyle w_{j}^{(0)}}$ is initial weight value of the j   th indicators, and ${\textstyle \sum _{j=1}^{n}w_{j}^{(0)}=1}$ ; ${\textstyle w_{j}}$ is weight value after variable weight; x_j is the percentage of assessment value of the j th indicators, and

${\begin{array}{l}\displaystyle w_{j}(x_{1},\ldots ,x_{n},w_{1}^{(0)},\ldots \\\displaystyle w_{n}^{(0)})={\frac {w_{j}^{(0)}((\partial B(x_{1},\ldots ,x_{n}))/\partial x_{j})}{\sum _{k=1}^{n}w_{k}^{(0)}((\partial B(x_{1},\ldots ,x_{n}))/\partial x_{k})}}\end{array}}$

( 3)

In formula, B (x₁ , …, x_n ) is balanced function, according to experience of engineering practice, the balanced function is:

$B(x_{1},\ldots ,x_{n})=\sum _{j=1}^{n}x_{j}^{\alpha }{\mbox{ }}(0<\alpha \leq 1)$

( 4)

simultaneous Eqs. (3)  and (4) , it can get:

$w_{j}(x_{1},\ldots ,x_{n},w_{1}^{(0)},\ldots ,w_{n}^{(0)})={\frac {w_{j}^{(0)}x_{j}^{\alpha -1}}{\sum _{k=1}^{n}w_{k}^{(0)}x_{k}^{\alpha -1}}}$

( 5)

so

$V=\sum _{j=1}^{m}{\frac {100w_{j}^{(0)}x_{j}^{\alpha }}{\sum _{k=1}^{n}w_{k}^{(0)}x_{k}^{\alpha -1}}}$

( 6)

α : balance coefficient, according to experience of engineering practice, α  = 0.2, it can meet most of engineering situation.

The inspection data of bridge can be divided into three categories: the first kind is non-numeric data with describing the state of bridge components only or dividing grade simply; the second is a single numerical; and the third is a data series. It is needed that applies dimensionless method to the third kind data, compare and analyse the two curves of data series. Introduce grey correlativity analysis and calculate non-uniform variation coefficient to get the assessment result, the formula as follows:

$V=\sum _{j=1}^{m}{\frac {100w_{j}^{(0)}x_{j}^{\alpha }}{\sum _{k=1}^{n}w_{k}^{(0)}x_{k}^{\alpha -1}}}r(x_{0},x_{i})$

( 7)

And r (x₀ , x_i ) calculate according to the formula as below (5)  and (8) :

${\begin{array}{l}\displaystyle r(X_{0}\\\displaystyle X_{i})={\frac {1}{n-1}}\sum _{k=1}^{n-1}\left[1+\left|{\frac {a^{(1)}(x_{0}(k+1))}{x_{0}(k+1)}}-\right.\right.\\\left.\left.\displaystyle -{\frac {a^{(1)}(x_{i}(k+1))}{x_{i}(k+1)}}\right|\right]^{-1}\end{array}}$

( 8)

Advantage of variable weight synthesis method

Compared with constant weight synthesis method, variable weight synthesis method can make the influence of components with damage badly more prominent. In structure, maybe individual component damage can be lead to the bridge operational be limited, even impact to the safety of the bridge (Gao and Wang, 2000 , Lan and Shi, 2001 , Wu and Xiang, 1995 , Xiang and Wu, 2005  and Zhang and Feng, 2001 ). Comparison with the result of constant weight synthesis method and variable weight synthesis method is given.

Using the data in Table 2.1  and Table 2.2 , assessment of the health of bridge with variable weight synthesis method and constant weight synthesis method is shown.

• Constant weight synthesis method:

${\begin{array}{l}\displaystyle BCI_{2}=80\times 0.31+80\times 0.13+75\times 0.14+80\times 0.37+5\times 0.04=\\\displaystyle =75.51>6\end{array}}$

The conclusion is “qualified”;

• Variable weight synthesis method (α  = 0.2):

${\begin{array}{l}\displaystyle \sum _{k=1}^{m}w_{k}^{(0)}x^{\alpha -1}=\sum _{k=1}^{9}w_{k}^{(0)}x_{k}^{-0.8}=\\\displaystyle =0.31\times 0.80^{-0.8}+0.13\times 0.80^{-0.8}+0.14\times 0.75^{-0.8}+\\\displaystyle +0.37\times 0.80^{-0.8}+0.04\times 0.05^{-0.8}=1.5840\end{array}}$

score V₂ :

${\begin{array}{l}\displaystyle V_{2}={\frac {100w_{j}^{(0)}x_{j}^{\alpha }}{\sum _{k=1}^{n}w_{j}^{(0)}x_{k}^{\alpha -1}}}={\frac {100}{1.5840}}(0.2965+0.1243+0.1322+\\\displaystyle +0.3539+0.0220)=58.64\end{array}}$

The conclusion is “disqualified”.

Table 2.1. Assess table of a bridge.

Indicator	Weight	Technical status	Explain
Pier and abutment	0.31	80	Better
Girder	0.13	80	Better
Pylon	0.14	75	Normal
Stay cable	0.37	80	Better
Subsidiary facilities	0.04	5	Failure badly

Table 2.2. Consultable table of equal coefficient.

Equal coefficient	α  = 0	α  = 0.2	α  = 0.5	α  = 0.8	α  = 1.0
Score of girder	49.52	58.64	68.59	74.19	75.51

Explain: The value of α reflects tolerance of local damage, with the increase of α , tolerance increase.

By the above examples, it can be got that when the subsidiary facilities damage badly, the result of constant weight synthesis method is “qualified” while variable weight synthesis method is “disqualified”. It is show that variable weight synthesis method can well reflect the local defect and considering the malconformation into assessment. It is more tallies with the actual situation.

Application example of method

The inspection data of line shape control about abridge is in Table 3.1 .

Table 3.1. Level evaluation of reference point.

Coordinate (m )	Designed elevation (X0 )	Measured elevation (Xi )	Error (m )	Assessed value (Di )
0	86.550	86.538	0.012	90
20	86.844	86.830	0.014	90
40	87.079	87.056	0.023	80
60	87.247	87.235	0.012	90
80	87.432	87.419	0.013	90
100	87.534	87.520	0.014	90
120	87.541	87.517	0.024	80
140	87.531	87.508	0.023	80
160	87.371	87.357	0.014	90
180	87.168	87.153	0.015	90
200	86.993	86.977	0.016	90
220	86.774	86.752	0.022	80
240	86.537	86.526	0.011	90

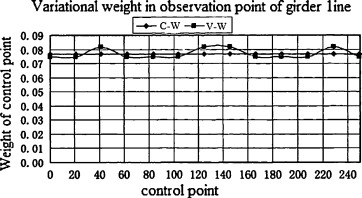
According to formula (5) , calculate variation of weight shown in Fig. 3.1 .

Figure 3.1. Variational weight in observation point of girder line.

According to formula (7)  and (8) calculate as:

$V=\sum _{j=1}^{m}{\frac {100w_{j}^{(0)}x_{j}^{\alpha }}{\sum _{k=1}^{n}w_{k}^{(0)}x_{k}^{\alpha -1}}}r(x_{0},x_{i})=84.14$

x_k  = D_i /100, D_i : assessed value. ${\textstyle w^{(0)}=1/n}$ (n  = 13) initial weight value, see Table 3.1 .

${\begin{array}{l}\displaystyle r(X_{0}\\\displaystyle X_{i})={\frac {1}{n-1}}\sum _{k=1}^{n-1}\left[1+\left|{\frac {a^{(1)}(x_{0}(k+1))}{x_{0}(k+1)}}-\right.\right.\\\left.\left.\displaystyle -{\frac {a^{(1)}(x_{i}(k+1))}{x_{i}(k+1)}}\right|\right]^{-1}=0.968\end{array}}$

• X₀  = [X₀ (1), X₀ (2), …, X₀ (13)] designed elevation;
• X_i  = [X_i (1), X_i (2), …, X_i (13)] measured elevation.

Assessment score of girder alignment is 84.14, contrast Table 3.2 , the bridge can be classified grade 1.

Table 3.2. The reference standard of bridge technique condition evaluation.

Score	Grade	Explain
80 < V  ≤ 100	Grade 1	Well, only daily maintenance
60 < V  ≤ 80	Grade 2	Normal, daily maintenance and minor repair
40 < V  ≤ 60	Grade 3	Weak, repair and load test
20 < V  ≤ 40	Grade 4	Bad, Stop running and strengthen
0 < V  ≤ 20	Grade 5	Danger, considering dismantle and rebuild

Note : The evaluation standard is made according to “Evaluation procedure for bearing capacity of highway bridge”.

Conclusion and prospect

In the safety process of assessment, the method, by using the variable weight principle to assess actual state of the assessment indexes, extrude the influence of the parts of damaged badly, especially the effect of secondary cause. And on this basis, apply method of grey relational to calculate the correlation degree of sequence data, it make up malconformation and incomplete collection of the test data.

The article explains the variable weight synthesis method, and applies the method into the process of bridge assessment. Though it has the rationality of the method, but it still exist some problem. First, although the assessment applies new method, but most of the index still reference codes and specifications and previous research results, it needs to do a more in-depth discussion. Second, the initial weight value used in the paper, it is still the average weight which has certain blindness, it needs to do a more in-depth discussion, too.

Conflict of interest

The author declares that there is no conflict of interest.

References

1. Bai, 2007 Y. Bai; The application of variable weight synthesis method in estimate of real estate investment environment; J. Adult Educ. Coll. Hebei Univ., 9 (3) (2007)
2. Gao and Wang, 2000 H. Gao, J. Wang; A review of research and application of detective and evaluation technology for bridges; World Inf. Earthq. Eng., 16 (2) (2000)
3. Lan and Shi, 2001 H. Lan, J. Shi; Degree of grey incidence and variable weight synthesizing applied in bridge assessment; J. Tongji Univ., 29 (l) (2001)
4. Liu et al., 2004 S. Liu, Y. Dang, Z. Fang; The Grey System Theory and Application; Science publishing house, Beijing (2004)
5. Wu and Xiang, 1995 H. Wu, Y. Xiang; Assessment the tension and the linetype state cable 2 stayed bridge based on variable weight synthesis; China Rail. Sci., 4 (1995), p. 16
6. Xiang and Wu, 2005 Y. Xiang, H. Wu; Research on condition assessment system of long-span prestressed concrete cable-stayed bridge; J. China Foreign Highw., 25 (5) (2005)
7. Zhang and Feng, 2001 Y. Zhang, Z. Feng; To evaluate the bridge safety by AHP; J. Xi’an Highway Univ., 21 (3) (2001)