Abstract

The objective of this study was to develop an adaptive thermal comfort equation for naturally ventilated buildings in hot–humid climates. The study employed statistical meta-analysis of the American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE) RP-884 database, which covered several climatic zones. The data were carefully sorted into three climate groups including hot–humid, hot–dry, and moderate and were analyzed separately. The results revealed that the adaptive equations for hot-humid and hot-dry climates were analogous with approximate regression coefficients of 0.6, which were nearly twice those of ASHRAE and European standards 55 and EN15251, respectively. The equation using the daily mean outdoor air temperature had the highest coefficient of determination for hot–humid climate, compared with other mean temperatures that considered acclimatization of previous days. Acceptable comfort ranges showed asymmetry and leaned toward operative temperatures below thermal neutrality for all climates. In the hot–humid climate, a lower comfort limit was not observed for naturally ventilated buildings, and the adaptive equation was influenced by indoor air speed rather than indoor relative humidity. The new equation developed in this study can be applied to tropical climates and hot–humid summer seasons of temperate climates.

Keywords

Thermal comfort ; Adaptive model ; Hot–humid climate ; Naturally ventilated building ; ASHRAE RP-884 database

1. Introduction

Defined by the American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE) as that condition of mind that expresses satisfaction with the thermal environment (ASHRAE, 2010 ), thermal comfort is one of the most essential aspects of user satisfaction and energy consumption in buildings (Nicol et al., 2012 ). This subjective term is far-reaching; indoor thermal environment standards are also important factors considered in building designs. In view of the current energy challenges, such standards must balance reductions in cooling/heating energy requirements of a building with improvements in occupant comfort.

Current standards are essentially based on either heat balance or adaptive models. The most notable example of the former is the predicted mean vote (PMV) model developed by Fanger (1972) , which is applied in International Organization for Standardization (ISO) 7730 (BSI, 2006 ) and ASHRAE Standard 55 (ASHRAE, 2010 ). The latter model is also used in ASHRAE Standard 55 (ASHRAE, 2010 ) as the code for naturally conditioned spaces and in European Standard (EN) 15251 (BSI, 2008 ) for buildings without mechanical cooling systems. In principle, the heat balance model analyzes thermal physiology in detail by assuming controlled steady-state conditions and high accuracy for all analyzed variables such as activity level, thermal resistance of clothing, air temperature, mean radiant temperature, relative air velocity, and water vapor pressure in ambient air (Fanger, 1972 ). In contrast, the adaptive model investigates the dynamic relationship between occupants and their general environments based on the principle that people tend to react to changes that produce discomfort by seeking methods of restoring their comfort levels (Humphreys and Nicol, 1998 ). Such adaptation encompasses physiological, psychological, and behavioral adjustments simultaneously (Brager and de Dear, 1998 ; Humphreys and Nicol, 1998  ;  Humphreys et al ., 2007 ). Therefore, the adaptive model provides greater flexibility in matching optimal indoor temperatures with outdoor climate, particularly in naturally ventilated buildings (de Dear and Brager, 2002 ; Deuble and de Dear, 2012 ; Humphreys, 1981  ;  Nicol and Humphreys, 2010 ). Adaptive standards are thus considered more appropriate for supporting comfort in low-energy buildings (de Dear and Brager, 2002 ; Humphreys et al ., 2007  ; Kwok and Rajkovich, 2010 ; Nicol and Humphreys, 2002  ;  Nicol et al ., 2012 ).

In hot–humid regions, many large developed and rapidly developing cities face increasing energy use for air-conditioning in buildings. Natural ventilation is a traditional, well-accepted passive cooling technique used in such regions. Previous studies have shown that the PMV model covers narrow ranges of moderate climatic conditions and is not applicable to warm environments in buildings (Humphreys and Nicol, 2002 ). Because climatic context is a primary consideration in the adaptive model, it is imperative to evaluate the comfort requirements of people worldwide, particularly in tropical regions that lack comprehensive standards (Nicol, 2004  ;  Toe and Kubota, 2011 ).

General standards may not be appropriate for all climates, however. In a Brazilian study, Cândido et al ., 2010  ;  Cândido et al ., 2011 demonstrated that although thermal acceptability was determined to be within the ASHRAE adaptive standard (ASHRAE, 2010 ), occupants required more air velocity. They proposed minimum air velocity at three ranges of operative temperature including 0.4 m/s at 24–27 °C, 0.41–0.8 m/s at 27–29 °C, and >0.81 m/s at 29–31 °C (Cândido et al., 2011 ). In addition, they determined that neutral operative temperatures were nearly the same as mean daily outdoor air temperatures at Brazils northeast coast (Cândido et al., 2011 ). This relationship had a higher gradient than those specified in the existing adaptive standards (ASHRAE, 2010  ;  BSI, 2008 ).

On the contrary, Nguyen et al. (2012) determined that the adaptive algorithm of EN15251 (BSI, 2008 ) was appropriate to their adaptive comfort equation derived from southeast Asian studies in naturally ventilated buildings. They indicated that air velocity and humidity were negligible factors in comfort temperature (Nguyen et al., 2012 ). However, their database and analysis also contained data of mild cold–dry seasons (Nguyen et al., 2012 ). These conflicting results warrant further investigation through collective analysis of larger regions that share a clearly defined similar climate.

One of the main methods applied to form the adaptive model is meta-analysis of a larger database that includes several thermal comfort field surveys. Several such resources include the Humphreys 1975–81 database (Humphreys, 1981 ); the ASHRAE RP-884 database (de Dear, 1998  ;  de Dear et al ., 1997 ), which was used to develop the ASHRAE adaptive standard (ASHRAE, 2010 ); and the European Smart Controls and Thermal Comfort (SCATs) Project database (McCartney and Nicol, 2002 ), which was used to develop the EN15251 adaptive standard (BSI, 2008 ). Among these well-established resources, the comprehensive ASHRAE RP-884 database, which consistently covers several climatic zones including hot–humid, has been analyzed by numerous researchers including Arens et al ., 2009  ;  Arens et al ., 2010 , de Dear et al. (1997) , de Dear and Brager (1998) , Farghal and Wagner (2010) , Humphreys et al ., 2007  ;  Humphreys et al ., 2010 , Humphreys and Nicol, 2000a ; Humphreys and Nicol, 2000b ; Humphreys and Nicol, 2002  ;  Humphreys and Nicol, 2004 , Nicol (2004) , Schweiker and Shukuya (2012) , and Toftum (2004) . However, with the exceptions of Nicol (2004) and Farghal and Wagner (2010) , none of these studies explored climatic classification; that is, data from different climates were not analyzed separately. To examine the relationship between comfort and humidity, Nicol (2004) classified the data from ASHRAE RP-884 into three datasets according to mean outdoor relative humidity. His study suggested that occupants may require comfort temperatures approximately 1 °C lower than that specified by the overall data when the outdoor relative humidity is greater than 75%.

In addition, Farghal and Wagner (2010) used the ASHRAE RP-884 database to classify naturally ventilated buildings into seven climatic zones among which significant differences were noted in thermal neutralities. Their analysis utilized only a mean neutral temperature for each building and did not include raw database values. Moreover, they conducted field surveys in Cairo and proposed a steeper adaptive comfort equation for hot–dry climate than those of existing adaptive standards (ASHRAE, 2010  ;  BSI, 2008 ). They did not suggest equations for other climatic zones.

Based on these previous studies, we hypothesized that reanalysis of the ASHRAE RP-884 database according to climate would clarify any differences in thermal adaptation among climates. We determined that it is relevant to identify climates in defining the adaptive model because this approach considers typical environment and adaptive actions that are useful in particular sets of circumstances (Brager and de Dear, 1998  ;  Humphreys and Nicol, 1998 ). Climate significantly affects such factors. In particular, the typical conditions of warm environments generally differ from those of moderate environments; in response to heat, the former require adaptive actions such as sweating and increased air movement. Accordingly, the adaptive model should also differ under warm conditions. Considering this factor, the adaptive model can more effectively explain discrepancies between predicted and actual thermal responses among climates.

The primary objectives of the present study are to examine the thermal adaptation of occupants and to develop an adaptive thermal comfort equation to be used as a standard for naturally ventilated buildings in the hot–humid climate. This study employs statistical meta-analysis of the ASHRAE RP-884 database. With reference to the two major adaptive standards (ASHRAE, 2010  ;  BSI, 2008 ), the main criteria for discussion include formulation of an adaptive comfort equation, temporal characterization of outdoor air temperature in the equation, acceptable comfort limits, and allowance for increased comfort temperature by considering the effects of indoor air speed and humidity. Although the study focuses on hot–humid climate, the results of hot–dry and moderate climates are also discussed for comparison. However, the effects of indoor air speed and humidity are considered for only hot climates.

2. Meta-analysis method

2.1. Data classification by climate

The first step in the data preparation was to classify each data file supplied in the ASHRAE RP-884 database (The University of Sydney, 2010 ) into one of three climate groups including hot–humid, hot–dry, and moderate according to survey location and season. The widely employed Köppen–Geiger climate classification map updated by Peel et al. (2007) was used to define the three groups. In this classification system, five climates including tropical (A), arid (B), temperate (C), cold (D), and polar (E) are categorized into 30 climate types on the basis of quantitative criteria for temperature and precipitation (Peel et al., 2007 ).

In the present analysis, all locations with A climate types were regarded as hot–humid climate. However, it should be noted that the database did not contain data during the driest month in the tropical savannah climate, which is considered to be a transition between hot–humid and hot–dry climates. Moreover, the Cfa type summer season (temperate; hot summer with no dry season) was also classified as hot–humid.

Conversely, all locations with B climate types were considered to be hot–dry climate, except for the winter season with seasonal mean outdoor air temperatures below 18 °C. (Seasonal mean outdoor air temperature was determined on the basis of meteorological data in the Supplementary Material Section in Peel et al., 2007 .) Similarly, the summer seasons of Csa (temperate; dry and hot summer) and Cwa (temperate; dry winter and hot summer) climate types were included in this group. All other files in the database were in locations with C climate types; these and the winter exceptions were classified as moderate climate in this study.

Table 1 shows that of the 10,065 observations for naturally ventilated buildings in the database, 1682 represent hot–humid climate while 4339 represent hot–dry climate. The remaining 4044 observations apply to moderate climate. Both residential buildings and offices were surveyed in each climate. Previous research conducted by de Dear and Brager (2002) to establish the ASHRAE adaptive standard (ASHRAE, 2010 ) excluded the data files of Kwok (1998) , which are available in the database downloader and would had been classified as hot–humid. Similarly, these files were not used in the present study. The Kwok survey involved mainly young high school students and was not representative of adult occupants (Kwok, 1998 ). Despite the unequal sample sizes among climates, the number of hot–humid observations was considered as sufficient to facilitate a reliable statistical analysis.

Table 1. Classification of the American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE) RP-884 database for naturally ventilated buildings according to climate.
Climate Survey location and season where applicable Number of observations
Original database Refined database
Hot–humid Bangkok; Jakarta; Brisbane summer; Singapore 1682 1673
Hot–dry Karachi summer and winter; Multan summer; Peshawar summer; Quetta summer; Saidu Sharif summer; Athens summer 4339 2776
Moderate Melbourne summer; Peshawar winter; Quetta winter; Saidu Sharif winter; Oxford summer; San Francisco summer and winter; Liverpool summer and winter 4044 3213
All 10065 7662

2.2. Data consistency and refinement

The second step involved checking the consistency of each variable to be analyzed and refining the data where necessary. Variables analyzed in the regression models were determined on the basis of three groups in the database including a thermal questionnaire containing subjective votes and personal variables; calculated indices including averaged physical variables and thermal indices; and outdoor meteorological observations (de Dear, 1998  ;  de Dear et al ., 1997 ).

There was no strong justification to suspect error in or by checking other variables against the subjective votes. Detection of vote error would have involved the difficult process of thoroughly tracing each original field survey. Moreover, the adaptive principle underlying our analysis implies the ability to adapt according to the situation; hence, thermal responses of the subjects could be varied and subjective in each environment. Nonetheless, one observation with a subjective vote outside its scale, which may have been a data entry error, was omitted.

Data standardization for personal variables and all calculated indices has been conducted by de Dear (1998) and de Dear et al. (1997) . Such variables included clothing and chair insulation, operative temperature, and standard effective temperature (SET* ). A further check for random error in individual physical measurements resulted in the removal of 27 observations from the database; these were mainly outliers.

A main focus of this study was to determine the statistical relationship between indoor comfort temperature, Tcomf , and outdoor temperature, Tout . The expected linear equation (Eq. (1) ) has outdoor temperature as its independent variable.

( 1)

The original outdoor meteorological data in the database were obtained from various resources and therefore contained a mixture of daily observations and long-term averages (de Dear, 1998  ;  de Dear et al ., 1997 ). We attempted to standardize the outdoor temperature for all observations by using the daily (24-h) mean outdoor air temperature for each exact survey date and station in the survey location. These data were obtained from Global Surface Summary of Day Data Version 7, which has undergone quality control measures by the National Oceanic and Atmospheric Administration (NOAA) National Climatic Data Center (NCDC, 2012 ). Weather data for Saidu Sharif in addition to several survey dates in Multan, Peshawar, Quetta, and Melbourne were not available. Moreover, adaptive equations developed by using the original and newly attached outdoor data differed in some cases due to inconsistency in the original outdoor temperature data. The standardization further allowed us to calculate and examine the various characterizations of outdoor temperature (Section 3.2 ) from the same data source. For this purpose, outdoor air temperature data of seven sequential days prior to respective survey days and entire survey months were also obtained from NCDC (2012) .

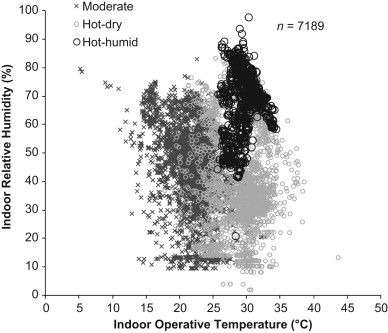
The final refined database for analysis consisted of 7662 observations (Table 1 ). Each observation contained both indoor operative temperature and standardized daily mean outdoor air temperature data; other variables may have been missing. The scatter diagram of indoor conditions is illustrated in Fig. 1 , which clearly shows that the indoor conditions in the hot–humid climate were concentrated at indoor operative temperatures higher than 25 °C and indoor relative humidity greater than 45% (Fig. 1 ). A summary of their descriptive statistics is also given in Table 2 . Most of the statistical characteristics from the original database were maintained in the refined database for hot–humid and hot–dry climates despite the reduction in observation number.


Scatter diagram of indoor operative temperatures and indoor relative humidity in ...


Fig. 1.

Scatter diagram of indoor operative temperatures and indoor relative humidity in the refined database.

Table 2. Descriptive statistics of the refined database.
Variable Hot–humid climate Hot–dry climate Moderate climate
Min. Max. Mean SD Min. Max. Mean SD Min. Max. Mean SD
Indoor air temperature (°C) 24.7 34.2 29.3 1.74 17.4 42.5 29.4 3.06 6.2 31.5 21.9 2.94
Indoor relative humidity (%) 20.9 97.8 67.6 10.55 2.0 85.7 40.5 17.61 9.6 83.1 45.2 13.86
Indoor air speed (m/s) 0.05 2.25 0.27 0.19 0.00 3.72 0.31 0.34 0.00 1.47 0.12 0.17
Indoor mean radiant temperature (°C) 23.2 34.5 29.4 1.88 17.8 44.7 29.3 3.03 3.7 34.1 21.9 3.06
Indoor operative temperature (°C) 25.6 34.4 29.4 1.80 17.7 43.6 29.4 3.02 5.1 32.7 21.9 2.98
Indoor ET* (°C) 25.4 36.1 30.6 2.38 17.6 37.8 28.9 3.06 5.2 30.9 21.8 2.85
Indoor SET* (°C) 22.8 36.1 29.5 2.64 11.8 38.3 28.6 2.97 10.7 34.5 24.1 2.79
Metabolic rate (met) 0.8 2.6 1.2 0.16 0.6 3.8 1.2 0.42 0.6 3.8 1.2 0.36
Clothing and chair insulation (clo) 0.2 1.1 0.6 0.17 0.2 2.0 0.6 0.31 0.2 2.4 0.9 0.35
Daily mean outdoor air temperature (°C) 19.4 30.5 26.7 2.32 19.1 34.5 26.2 3.71 2.0 27.7 13.5 4.10

Min.: minimum; Max.: maximum; SD: standard deviation.

2.3. Data analysis

The refined database was then analyzed mainly by employing two types of regression models including linear regression and probit regression. Both models used the least-squares method.

The linear regression model related indoor comfort temperatures and outdoor temperatures to provide an adaptive equation that could predict indoor comfort from outdoor conditions (Eq. (1) ). This type of model is commonly used in adaptive comfort analysis for naturally ventilated buildings. However, representations of indoor comfort temperature, generally denoted as Tcomf in Eq. (1) , varied among previous studies partly due to its subjectivity, thus yielding no single superior method. For example, de Dear and Brager, 1998  ;  de Dear and Brager, 2002 , in developing the existing standards, used a binning method and calculated neutral temperature by solving each buildings regression model for a mean sensation of zero. They also used the binning method and fitted probit models to obtain a preferred temperature for each building. Both temperatures were the same in case of naturally ventilated buildings (de Dear and Brager, 2002 ). However, Nicol and Humphreys (2010) used the Griffiths method to estimate a neutral temperature for every comfort vote that was not zero.

Table 3 outlines the available subjective votes in the refined database, which include thermal sensation, thermal preference, and thermal acceptability votes. No thermal acceptability vote was given for hot–humid climate. The indoor temperature at thermal neutrality, which is the observed indoor temperature with a thermal sensation vote equaling zero on the ASHRAE scale, was applied as the indoor comfort temperature in this analysis. This measure was conducted so that the regression line would predict the neutral temperature without further data treatment that may have modified thermal adaptation and regression. The Griffiths method (Nicol et al., 2012 ) was not used because a correct Griffiths coefficient could not be determined with certainty in the present study or in previous research (Humphreys et al ., 2007  ;  Nguyen et al ., 2012 ). However, this coefficient would have significantly affected the adaptive equation.

Table 3. Statistical summary of subjective votes in the refined database.
Climate Thermal sensation vote, tsva Thermal preference vote, tpvb Thermal acceptability vote, tavc
All tsv “Neutral” All tpv “No change” All tav “Acceptable”
n Mean n (%) n Mean n (%) n Mean n (%)
Hot–humid 1671 +0.9 332 (20) 992 1.3 207 (21) 0 – –
Hot–dry 2767 +0.6 1205 (44) 2776 1.6 1223 (44) 1600 1.8 1224 (77)
Moderate 3193 +0.1 1300 (41) 2837 2.0 1617 (57) 374 1.6 213 (57)

a. tsv scale: −3 “cold”; −2 “cool”; −1 “slightly cool”; 0 “neutral”; +1 “slightly warm”; +2 “warm”; +3 “hot”.

b. tpv scale: 1 “want cooler”; 2 “no change”; 3 “want warmer”.

c. tav scale: 1 “unacceptable”; 2 “acceptable”.

Acceptable comfort limits were analyzed with the probit regression model by considering thermal sensation and thermal preference votes. Probit regression analysis is a widely employed statistical method used for data forming a sigmoid response curve such as thermal comfort assessments with unequal increments between scale points (Ballantyne et al., 1977 ). This method was used in recent studies (Nicol and Humphreys, 2007 ) for a purpose similar to that of the present study, which was to predict probability of comfort or discomfort as a function of temperature deviation from the comfort temperature. As previously stated, the definition of comfort temperature differed among existing studies; therefore, the term was used as a general notation in this paper, particularly when referring to such research. It should be clarified that in the present study, neutral temperature refers to temperatures with neutral thermal sensation votes of zero, and comfortable temperature refers to temperatures with thermal sensation votes of ±1 in the three central categories of the ASHRAE scale. Comfortable temperatures were used to define comfort limits (Section 3.3 ).

Analyses of both regression models were conducted at the individual observation level with raw data used as a single unit. It was assumed that climate was the major factor influencing occupants' thermal adaptation, which considered location and season as applied to the above data classification (Section 2.1 ). Thus, no further data grouping was determined for statistical analysis. It should be noted that points of grouped bins were plotted in some figures in Section 3 only to clarify the illustration. All transverse and longitudinal surveys in the database were treated similarly.

3. Results and discussion

3.1. Adaptive thermal comfort equation

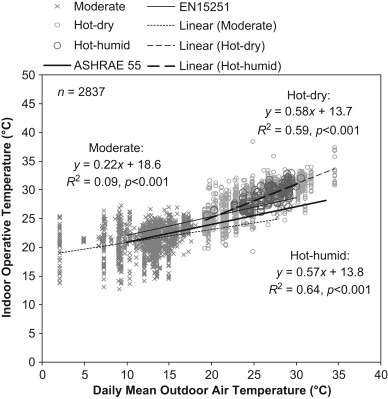
A scatter diagram of observed indoor operative temperatures at thermal neutrality and the corresponding daily mean outdoor air temperatures is presented in Fig. 2 . The existing major adaptive standards (ASHRAE, 2010  ;  BSI, 2008 ) utilize operative temperature. It is clear that data for each climate have a distinguishable range of daily mean outdoor air temperatures. For hot–humid and hot–dry climates, their daily mean outdoor air temperatures are higher than approximately 20 °C (Fig. 2 ) and extend to approximately 30 °C and 35 °C, respectively. In contrast, most of the data for moderate climate appear below the daily mean outdoor air temperature of 20 °C (Fig. 2 ).


Scatter diagram of indoor operative temperatures at thermal neutrality and daily ...


Fig. 2.

Scatter diagram of indoor operative temperatures at thermal neutrality and daily mean outdoor air temperatures. Discontinuous lines denote linear regression models used in this study and represent adaptive equations for predicting neutral temperatures.

The adaptive thermal comfort equations used for predicting neutral temperatures in respective climates are illustrated by discontinuous linear regression lines in Fig. 2 . The comfort temperature lines for naturally ventilated buildings prescribed in ASHRAE Standard 55 (ASHRAE, 2010 ) and EN15251 (BSI, 2008 ) are also compared in the figure. The adaptive comfort equations underlying ASHRAE and EN15251 standards are

( 2)
( 3)

respectively, where Tcomfop is indoor comfort operative temperature (°C), Toutmm is monthly mean outdoor air temperature (°C), and Toutrm is running mean outdoor air temperature (°C) ( de Dear and Brager, 2002  ;  Nicol and Humphreys, 2010 ). Both equations share nearly the same regression coefficients (gradient). It is considered that both standards suggest a change in indoor comfort temperature per unit change of the outdoor temperature at a similar rate. The EN15251 equation consistently predicts a higher comfort temperature than that of the ASHRAE equation by 1 °C (Fig. 2 ).

The regression lines for hot–humid, hot–dry, and moderate climates are defined by the following equations, respectively:

( 4)

( 5)

( 6)

where Tneutop is indoor neutral operative temperature (°C) and Toutdm is daily mean outdoor air temperature (°C) (Fig. 2 ). All are significant at the 0.1% level. As indicated, these regression lines differ among themselves and from those of the standards in terms of their gradients and the outdoor temperature ranges (Fig. 2 ). Compared with the ASHRAE adaptive equation, the regression lines for hot–humid and hot–dry climates are nearly twice as steep with regression coefficients close to 0.6. The regression line for moderate climate, which covers lower outdoor air temperatures, shows a slightly lower regression coefficient than that of ASHRAE (Fig. 2 ). Within the observed daily mean outdoor air temperature ranges, these equations predict neutral operative temperatures of 24.9–31.2 °C, 24.8–33.7 °C, and 19.0–24.7 °C for hot–humid, hot–dry, and moderate climates, respectively. The analysis of variance (ANOVA) reveals a significant mean difference of F(2, 2834)=2525.12, p <0.001. This result supports our hypothesis such that climate is a major influence on the thermal adaptation of occupants in naturally ventilated buildings.

This result also implies that people living in hot climates, particularly regions with daily mean outdoor air temperatures higher than 20 °C, adapt to a wider and higher range of indoor operative temperatures relative to the same magnitude of outdoor air temperature increases than those living in colder climates. These statistical findings reveal that the ability of adapting to obtain thermal neutrality in naturally ventilated buildings differs among climatic zones, likely due to different adaptation needs and opportunities. In particular, the adaptive equations for hot–humid and hot–dry climates differ markedly from current major adaptive standards (ASHRAE, 2010  ;  BSI, 2008 ), which implies that the standards predict neutral operative temperature that do not match the occupants' thermal neutrality in warm conditions. The predicted neutral operative temperatures appear to be analogous in hot–humid and hot–dry climates. Nevertheless, the contributory thermal adaptation processes of occupants in both climates may differ. This aspect is investigated further in Section 3.4 by considering the varied effects of indoor air speed and humidity.

3.2. Characterization of outdoor air temperature

Three methods of characterizing the outdoor air temperature in the adaptive equations, noted in Section 3.1 , include monthly mean outdoor air temperature (ASHRAE, 2010 ), running mean outdoor air temperature (BSI, 2008 ), and daily mean outdoor air temperature (present analysis). Researchers' interest of these characterizations is related to the role of past thermal experiences on occupants' responses. The sensitivity of these temporal averaging techniques and the recently introduced prevailing mean outdoor air temperature (ASHRAE, 2012 ) to the above adaptive equations is analyzed in Table 4 . Equations for the daily mean are obtained from Fig. 2 and Eqs. (4) , (5)  ;  (6) .

Table 4. Adaptive equation for different characterizations of the outdoor air temperature.
Outdoor air temperature Hot–humid climate Hot–dry climate Moderate climate
Adaptive equation R2 Sig.a Adaptive equation R2 Sig.a Adaptive equation R2 Sig.a
Daily mean, Toutdm (n =2837) Tneutop =0.57Toutdm +13.8 0.64 *** Tneutop =0.58Toutdm +13.7 0.59 *** Tneutop =0.22Toutdm +18.6 0.09 ***
Monthly mean, Toutmm (n =2837) Tneutop =0.53Toutmm +14.5 0.51 *** Tneutop =0.56Toutmm +14.3 0.60 *** Tneutop =0.18Toutmm +19.3 0.08 ***
Running mean, Toutrm (n =2102) Tneutop =0.55Toutrm +14.2 0.54 *** Tneutop =0.63Toutrm +12.4 0.59 *** Tneutop =0.33Toutrm +17.4 0.09 ***
Prevailing mean, Toutpm (n =2102) Tneutop =0.54Toutpm +14.6 0.53 *** Tneutop =0.60Toutpm +13.0 0.58 *** Tneutop =0.35Toutpm +17.1 0.09 ***

Sig.: significant level.

a. *** 0.1% significant level; ** 1% significant level; * 5% significant level.

As described in Section 2.2 , the daily mean is the 24-h average of the observed outdoor air temperatures for each day with a minimum of four observations per day (NCDC, 2012 ). The monthly mean follows the definition given by ASHRAE (2010) , which is the average of the mean daily minimum and mean daily maximum outdoor air temperatures for the survey month. The running and prevailing means are calculated by using the above-mentioned daily mean outdoor air temperatures of seven sequential days prior to the survey date. The prevailing mean is a simple arithmetic mean of the temperatures (ASHRAE, 2012 ). The running mean is defined as an exponentially weighted average of previous days' daily mean air temperatures in a series (Nicol and Humphreys, 2010 ). This value puts greater weight on the temperature for days closer to the present by assuming that more recent experiences are more influential in a persons thermal history. In this study, the running mean is calculated by using the formula given in EN15251 (BSI, 2008 ) at 0.8 exponential weight:

( 7)

where Toutdm-1–7 is the daily mean outdoor air temperature for the first previous day through the last seven days.

Table 4 reveals all equations predict similar neutral operative temperatures for hot–humid climate. The adaptive equation based on the daily mean outdoor air temperature shows the highest coefficient of determination (R2 ) and predicts at least 10% more variability in the neutral operative temperature compared with other characterizations. For hot–dry and moderate climates, the adaptive equations based on all outdoor air temperature characterizations show similar coefficients of determination (Table 4 ). These results imply that consideration of acclimatization to outdoor air temperatures of previous days is not necessarily superior to predicting thermal responses of occupants in all climates. This finding is in agreement with two statements reported in previous studies. The first is that the process of acclimatization is slow and less influential than other adaptive processes; however, expectations based on past thermal experiences occur on time scales of weeks to months that translate into seasonal processes (Brager and de Dear, 1998 ). The second is that adaptive comfort equations and the strength of the equations are not very sensitive to the exponential weight of the running mean outdoor temperature, which was determined by Nicol and Humphreys (2010) through statistical analysis of the SCATs database. These statements imply that adaptation related to thermal history is covered more effectively in the climate classification that considers season than in that considering the previous weeks outdoor temperatures. The dependence on previous days' acclimatization in the hot–humid climate is even likely less due to the small changes in its daily outdoor weather conditions over the entire year.

These results imply that the choice of an appropriate outdoor air temperature length and averaging technique for predicting thermal neutrality in naturally ventilated buildings for most climates can be based on practical factors such as data availability and application. The daily mean and monthly mean may be used in standards that guide building design and post-occupancy evaluation because a time lapse is required to gather the days or months data. The running mean and prevailing mean would be useful for real-time monitoring of buildings such as those involving adaptive controls. Nonetheless, the daily mean outdoor air temperature has been used throughout this study because the study objective is to develop an equation that can be used as a standard for hot–humid climate.

3.3. Acceptable comfort limits

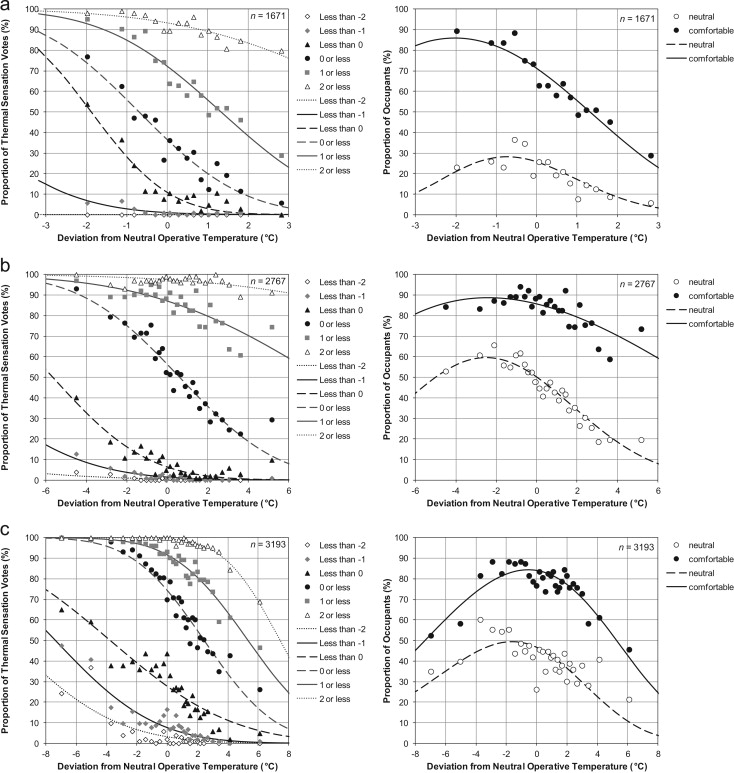
An acceptable range of temperature deviation from the predicted neutral operative temperature (Eqs. (4) , (5)  ;  (6) ) for each climate is analyzed in Fig. 3  ;  Fig. 4 by using probit models in consideration of the thermal sensation votes and thermal preference votes, respectively. For thermal sensation votes, probit analysis is first used to predict the proportion of thermal sensation votes for each category less than a particular value (left side of Fig. 3 ). The proportion of occupants voting “neutral” (0) is then taken as the difference between the proportions of votes of 0 or less and less than 0. The proportion of occupants voting “comfortable” (±1) is the difference between the proportions of votes of 1 or less and less than -1 (right side of Fig. 3 ).


Proportion of thermal sensation votes (left) and proportion of occupants voting ...


Fig. 3.

Proportion of thermal sensation votes (left) and proportion of occupants voting “neutral” (0) and “comfortable” (±1) (right) as a function of deviation from the predicted neutral operative temperature. (a) Hot–humid climate; (b) hot–dry climate; (c) moderate climate. Lines indicate probability predicted by probit regression models. Points represent observed values for equal bins of the temperature deviation (102–105 data per bin). In the left figure, dashed lines and black points represent “neutral” votes (0); continuous lines and grey points represent “comfortable” votes (±1).


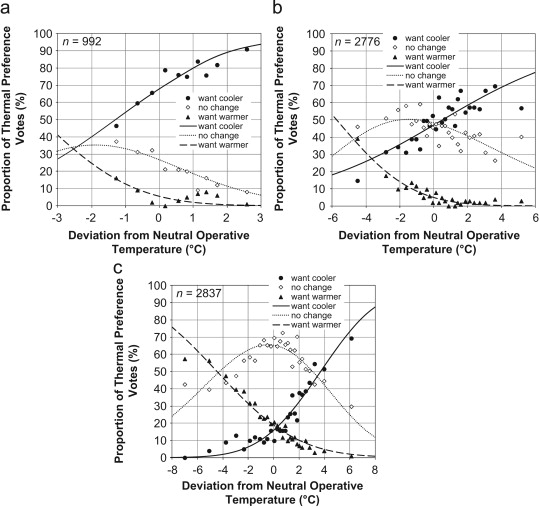
Proportion of thermal preference votes as a function of deviation from the ...


Fig. 4.

Proportion of thermal preference votes as a function of deviation from the predicted neutral operative temperature. (a) Hot–humid climate; (b) hot–dry climate; (c) moderate climate. Lines indicate probability predicted by probit regression models. Points represent observed values for equal bins of the temperature deviation (99–103 data per bin).

Fig. 3 a shows that the proportion of occupants voting “neutral” does not exceed 30% and peaks at approximately 1 °C lower than the neutral operative temperature for hot–humid climate. The probit line for “comfortable” thermal sensation, which includes “slightly cool,” “neutral,” and “slightly warm,” or -1, 0, +1, respectively, is one-tailed and has no symmetry within the observed temperature range (Fig. 3 a). The proportion of occupants who voted “comfortable” increases from 30% at 2.5 °C higher than the predicted neutral temperature to 86% at 2 °C below the predicted neutral temperature (Fig. 3 a). Eighty percent “comfortable” votes are predicted at 0.7 °C less than the neutral temperature for hot–humid climate.

In comparison, at least 80% of the occupants voting “comfortable” appear within temperature deviations of approximately 2 °C above and 6 °C below the predicted neutral temperature for hot–dry climate (Fig. 3 b) and approximately 1.5 °C above and 2.5 °C below that for moderate climate (Fig. 3 c). The results show that the acceptable comfort ranges are asymmetric and lean toward operative temperatures below thermal neutrality for all climates. Ninety percent "comfortable" votes are not predicted by the probit models in all climates (Fig. 3 ). The comfortable temperature range is largest for hot–dry climate, at 8 °C for 80% of “comfortable” votes, likely because adapting to a wider temperature range is easier when humidity is low.

Analysis of the thermal preference votes in Fig. 4 provides similar results. In the figure, preferred temperature is observed at the intersection of the two probit lines that represent “want cooler” and “want warmer” votes. Preferred temperatures for hot–humid and hot–dry climates appear at 2.5 °C and 3.5 °C below the neutral operative temperatures, respectively (Fig. 4 a and b). The highest proportion of occupants voting “no change” also occur at temperatures below thermal neutrality for both climates (Fig. 4 a and b). The result clearly agrees with the concept such that although occupants adapt to higher neutral temperatures in hot climates, as discussed previously, they prefer cooler conditions (Humphreys and Nicol, 2004 ). Fig. 4 c indicates that the preferred temperature nearly matches the neutral temperature for moderate climate, which is similar to the findings reported by de Dear and Brager (2002) . Nevertheless, the probit line fitted to the “no change” votes shows a slightly skewed curve similar to that of the “comfortable” sensation votes, albeit at a lower proportion (Figs. 4 c and 3 c).

We have inferred from the analysis that the upper and lower comfort limits must be considered separately for each climate. These limits could be determined on the basis of thermal sensation votes; thermal preference votes show similar patterns. Currently, both the ASHRAE and EN15251 adaptive standards provide symmetrical limits of ±2–4 °C away from the comfort temperature for various categories of occupant acceptability or buildings (ASHRAE, 2010  ;  BSI, 2008 ). The comfort limits for each climate could be determined from Fig. 3 a–c for the respective percentages of “comfortable” votes. In particular, a lower comfort limit is not observed for naturally ventilated buildings in hot–humid climate. The upper comfort limit for this climate is recommended to not exceed 0.7 °C below the predicted neutral operative temperature so that at least 80% of the occupants would be in comfort. The 80% “comfortable” votes follow the acceptability level for typical applications in the ASHRAE adaptive standard (ASHRAE, 2010 ). Further studies to confirm whether 80% acceptability is appropriate for the adaptive model in various climates are encouraged.

3.4. Effects of indoor air speed and humidity

As discussed in Section 3.1 , the adaptive thermal comfort equations for hot–humid and hot–dry climates are steeper than that for moderate climate. Previous studies of naturally ventilated buildings in hot–humid climate indicate that comfort temperatures voted by respondents increase with higher indoor air speeds (Cândido et al ., 2011  ; Khedari et al ., 2000  ; Mallick, 1996  ;  Wijewardane and Jayasinghe, 2008 ). As previously mentioned, Nicol (2004) has suggested that outdoor relative humidity influences indoor comfort temperatures. In this section, we analyze the indoor air speed and indoor humidity levels as two possible factors affecting the thermal adaptation in hot–humid and hot–dry climates.

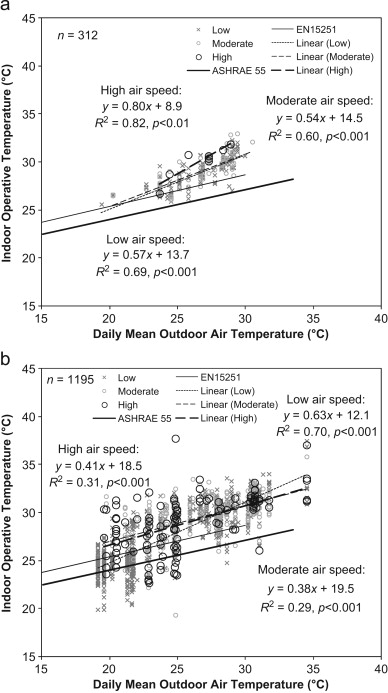
The effects of indoor air speed on the adaptive equations are analyzed in Fig. 5 . In the figure, the data are categorized into three groups of indoor air speeds including low (<0.3 m/s), moderate (0.3 to <0.65 m/s), and high (≥0.65 m/s). As mandated in the ASHRAE addendum (ASHRAE, 2012 ) and in EN15251 (BSI, 2008 ), increased air speed may be applied to elevate the upper comfort temperature limit when indoor operative temperatures exceed 25 °C. This temperature marks the lower end of the regression lines for the hot climates in Fig. 2 . The air speed allowance is obviously targeted to hot climates, although no distinction between hot–humid and hot–dry climates is mentioned in the standards.


Scatter diagram of indoor operative temperatures at thermal neutrality and daily ...


Fig. 5.

Scatter diagram of indoor operative temperatures at thermal neutrality and daily mean outdoor air temperatures at various indoor air speeds. (a) Hot–humid climate; (b) hot–dry climate.

Fig. 5 a shows similar linear regression lines for low and moderate air speeds that maintain regression coefficients at 0.5–0.6 for hot–humid climate. These regression lines predict that moderate air speed has little to no effect on neutral temperatures compared with low air speed. Still air conditions (0 m/s) do not generally occur in naturally ventilated buildings in hot–humid climate (Table 2 ). The regression line for high air speed is steeper and higher than that for low air speed by up to approximately 2 °C at 29 °C daily mean outdoor air temperature (Fig. 5 a). The analysis of variance also reveals a significant mean difference of F(2, 309)=4.52, p <0.05. These results imply that air movement is likely a possible factor for increasing the gradient of the adaptive equation for hot–humid climate. Occupants in the hot–humid climate likely adapt to neutral temperatures by making use of air movement at all times to aid evaporative heat loss in indoor high-humidity conditions.

For hot–dry climate the analysis of variance shows a significant mean difference among the air speed groups. Nevertheless, the regression lines predict no constant increase in indoor neutral operative temperature at moderate and high air speeds when compared with low air speed (Fig. 5 b). This result emphasizes that the thermal adaptation processes of occupants in dry air conditions differ in humid air conditions at high temperatures. Increased air speed allowance is not applicable to hot–dry climate.

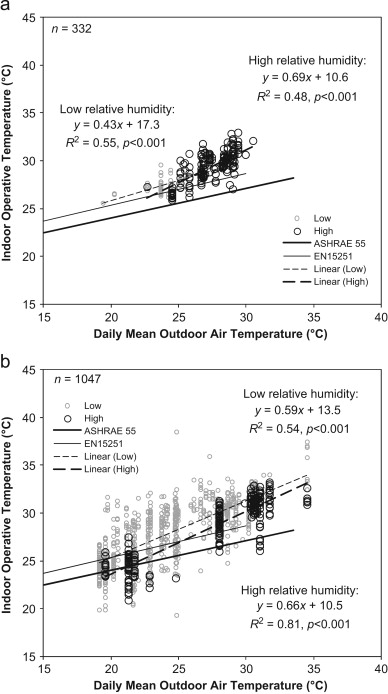
Fig. 6 further illustrates the effects of indoor relative humidity on the adaptive equations for the two hot climates. Low relative humidity represents values below 60%; high relative humidity represents the remaining values. Fig. 6 b shows that for hot–dry climate, the regression line for low relative humidity predicts higher neutral operative temperatures than for high relative humidity by 0.6–1.7 °C. The analysis of variance shows a significant mean difference at F(1, 1045)=9.29, p <0.01. The indoor relative humidity values show these effects likely because they are evaluated at respective temperatures and indirectly account for the effect of water vapor pressure on evaporation. A similar effect is not apparent in the regression lines for hot–humid climate ( Fig. 6 a), although a significant mean difference is obvious. Indoor relative humidity is high (≥60%) more than 75% of the time in hot–humid climate. This result indicates that humidity influences the predicted neutral temperature in hot–dry climate but not in hot–humid climate.


Scatter diagram of indoor operative temperatures at thermal neutrality and daily ...


Fig. 6.

Scatter diagram of indoor operative temperatures at thermal neutrality and daily mean outdoor air temperatures at various percentages of indoor relative humidity. (a) Hot–humid climate; (b) hot–dry climate.

It is concluded that a thermal comfort standard for naturally ventilated buildings in hot–humid climate should consider occupants' thermal adaptation to various indoor air speeds. Within the limitation of the study analysis, the adaptive equation developed in Section 3.1 , Eq. (4) , is proposed because of its closeness to the regression lines for low and moderate air speeds, which are dominant values in the database. It is considered that a minimum indoor air speed of 0.65 m/s is required to increase the neutral operative temperature predicted by this adaptive equation. Further research to develop an increased air speed allowance for hot–humid climate will be useful.

4. Implications for an adaptive thermal comfort standard in hot–humid climate and concluding remarks

The statistical meta-analysis of the ASHRAE RP-884 database by climate highlights several key differences in the thermal adaptation of occupants in naturally ventilated buildings among climates and the existing standards (ASHRAE, 2010  ;  BSI, 2008 ). These differences are summarized in the following points:

  • The adaptive equations for hot–humid and hot–dry climates are analogous with regression coefficients of approximately 0.6, which are nearly twice those of existing standards. The adaptive equation for moderate climate has a slightly lower regression coefficient than those of the existing standards. Moreover, people in hot climates adapt to higher neutral operative temperatures.
  • The adaptive equation based on the daily mean outdoor air temperature has the highest coefficient of determination for hot–humid climate. For hot–dry and moderate climates, the adaptive equations based on all outdoor air temperature characterizations show similar coefficients of determination. Acclimatization of previous days is less important in predicting occupants' thermal responses in hot–humid climate.
  • The proportion of occupants voting “comfortable” increases from 30% at 2.5 °C above the predicted neutral temperature to 86% at 2 °C below the predicted neutral temperature for hot–humid climate. A lower comfort limit is not observed in hot–humid climate. Acceptable comfort ranges also show asymmetry and lean towards operative temperatures below thermal neutrality for hot–dry and moderate climates.
  • Air movement is a possible factor for increasing the gradient of the adaptive equation for hot–humid climate. In contrast, indoor relative humidity influences the adaptive equation for hot–dry climate.

For a final conclusion, the study anticipates that regions of hot–humid climate will require their own adaptive thermal comfort standards. A basic set of adaptive thermal comfort criteria for naturally ventilated buildings in hot–humid climate is thus proposed in Table 5 based on the present study findings. Major international standards can be modified to incorporate new criteria for better applicability. Further studies are recommended, particularly to determine suitable percentages of occupants in comfort, to develop an increased air speed allowance, and to verify the applicability of these criteria to the driest month in the tropical savannah climate.

Table 5. Proposed adaptive thermal comfort equation and related criteria for naturally ventilated buildings in hot–humid climate.
No. Aspect Criterion Note
(i) Climate type All A climate types; and Summer season of Cfa climate type. Climate type refers to the Köppen–Geiger climate classification system.
(ii) Neutral operative temperature, Tneutop (°C) Tneutop =0.57Toutdm +13.8 Toutdm is daily mean outdoor air temperature (°C), i.e., the 24-h arithmetic mean for the day in question.
(iii) Daily mean outdoor air temperature, Toutdm (°C) Range from 19.4 to 30.5. Recommended applicable range for criterion no. (ii).
(iv) Lower comfort operative temperature limit, Tlower (°C) No required limit. –
(v) Upper comfort operative temperature limit, Tupper (°C) Tupper =Tneutop −0.7 for 80% comfortable thermal sensation votes. Graphical representation can be referred in Fig. 3 a (continuous line in the right figure) for a different percentage of comfortable thermal sensation votes.
(vi) Indoor air speed, v (m/s) <0.65 at and below neutral operative temperature; ≥0.65 above neutral operative temperature. Recommended to provide non-still air and occupants' control to adjust the indoor air speeds according to their preferences.
(vii) Indoor humidity, RH (%) No required limit. –

Acknowledgements

This study was funded by the Nichias Corporation and the Asahi Glass Foundation . Our sincerest gratitude is given to Richard J. de Dear, Gail S. Brager, Donna Cooper, and all of the field study contributors to the ASHRAE RP-884 database. We greatly appreciate the advice offered by Associate Prof. Dr. Hom B. Rijal of Tokyo City University and Dr. Nakaya of Gifu National College of Technology. The scholarship from The Hitachi Scholarship Foundation is gratefully acknowledged.

References

  1. Arens et al., 2010 E. Arens, M.A. Humphreys, R. de Dear, H. Zhang; Are ‘class A’ temperature requirements realistic or desirable?; Building and Environment, 45 (1) (2010), pp. 4–10
  2. Arens et al., 2009 E. Arens, S. Turner, H. Zhang, G. Paliaga; Moving air for comfort; ASHRAE Journal, 51 (5) (2009), pp. 18–28
  3. ASHRAE, 2010 ASHRAE, 2010. ANSI/ASHRAE Standard 55-2010: Thermal Environmental Conditions for Human Occupancy. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc., Atlanta.
  4. ASHRAE, 2012 ASHRAE, 2012. ANSI/ASHRAE Addendum c to ANSI/ASHRAE Standard 55-2010: Thermal Environmental Conditions for Human Occupancy. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc., Atlanta.
  5. Ballantyne et al., 1977 E.R. Ballantyne, R.K. Hill, J.W. Spencer; Probit analysis of thermal sensation assessments; International Journal of Biometeorology, 21 (1) (1977), pp. 29–43
  6. Brager and de Dear, 1998 G.S. Brager, R.J. de Dear; Thermal adaptation in the built environment: a literature review; Energy and Buildings, 27 (1) (1998), pp. 83–96
  7. BSI, 2006 BSI, 2006. BS EN ISO 7730:2005, Ergonomics of the Thermal Environment – Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria. British Standards Institute, London.
  8. BSI, 2008 BSI, 2008. BS EN 15251:2007, Indoor Environmental Input Parameters for Design and Assessment of Energy Performance of Buildings Addressing Indoor Air Quality, Thermal Environment, Lighting and Acoustics. British Standards Institute, London.
  9. Cândido et al., 2011 C. Cândido, R. de Dear, R. Lamberts; Combined thermal acceptability and air movement assessments in a hot humid climate; Building and Environment, 46 (2) (2011), pp. 379–385
  10. Cândido et al., 2010 Cândido, C., Lamberts, R., de Dear, R., Bittencourt, L., 2010. Towards a Brazilian standard for naturally ventilated buildings: guidelines for thermal and air movement acceptability. In: Proceedings of Conference, Adapting to Change: New Thinking on Comfort. 9–11 April, Windsor, UK. Network for Comfort and Energy Use in Buildings, London. 〈http://nceub.org.uk〉 .
  11. de Dear, 1998 R.J. de Dear; A global database of thermal comfort field experiments; ASHRAE Transactions, 104 (1b) (1998), pp. 1141–1152
  12. de Dear and Brager, 1998 R.J. de Dear, G.S. Brager; Developing an adaptive model of thermal comfort and preference; ASHRAE Transactions, 104 (1a) (1998), pp. 145–167
  13. de Dear and Brager, 2002 R.J. de Dear, G.S. Brager; Thermal comfort in naturally ventilated buildings: revisions to ASHRAE Standard 55; Energy and Buildings, 34 (6) (2002), pp. 549–561
  14. de Dear et al., 1997 de Dear, R.J., Brager, G., Cooper, D., 1997. Developing an Adaptive Model of Thermal Comfort and Preference. Final Report on ASHRAE RP-884. Macquarie University, Sydney.
  15. Deuble and de Dear, 2012 M.P. Deuble, R.J. de Dear; Mixed-mode buildings: a double standard in occupants' comfort expectations; Building and Environment, 54 (2012), pp. 53–60
  16. Fanger, 1972 P.O. Fanger; Thermal Comfort: Analysis and Applications in Environmental Engineering; McGraw-Hill Book Company, New York (1972)
  17. Farghal and Wagner, 2010 Farghal, A., Wagner, A., 2010. Studying the adaptive comfort model a case study in a hot dry climate, Cairo, Egypt. In: Proceedings of Conference, Adapting to Change: New Thinking on Comfort. 9–11 April, Windsor, UK. Network for Comfort and Energy Use in Buildings, London. 〈http://nceub.org.uk〉 .
  18. Humphreys, 1981 M.A. Humphreys; The dependence of comfortable temperatures upon indoor and outdoor climates; K. Cena, J.A. Clark. (Eds.), Bioengineering, Thermal Physiology and Comfort, Elsevier, Amsterdam (1981), pp. 229–250
  19. Humphreys and Nicol, 1998 M.A. Humphreys, J.F. Nicol; Understanding the adaptive approach to thermal comfort; ASHRAE Transactions, 104 (1b) (1998), pp. 991–1004
  20. Humphreys and Nicol, 2000a M.A. Humphreys, J.F. Nicol; Outdoor temperature and indoor thermal comfort: raising the precision of the relationship for the 1998 ASHRAE database of field studies; ASHRAE Transactions, 106 (2) (2000), pp. 485–492
  21. Humphreys and Nicol, 2000b M.A. Humphreys, J.F. Nicol; Effects of measurement and formulation error on thermal comfort indices in the ASHRAE database of field studies; ASHRAE Transactions, 106 (2) (2000), pp. 493–502
  22. Humphreys and Nicol, 2002 M.A. Humphreys, J.F. Nicol; The validity of ISO-PMV for predicting comfort votes in every-day thermal environments; Energy and Buildings, 34 (6) (2002), pp. 667–684
  23. Humphreys and Nicol, 2004 M.A. Humphreys, J.F. Nicol; Do people like to feel “neutral”? Response to the ASHRAE scale of subjective warmth in relation to thermal preference, indoor and outdoor temperature; ASHRAE Transactions, 110 (2) (2004), pp. 569–577
  24. Humphreys et al., 2007 M.A. Humphreys, J.F. Nicol, I.A. Raja; Field studies of indoor thermal comfort and the progress of the adaptive approach; Advances in Building Energy Research, 1 (2007), pp. 55–88
  25. Humphreys et al., 2010 Humphreys, M.A., Rijal, H.B., Nicol, J.F., 2010. Examining and developing the adaptive relation between climate and thermal comfort indoors. In: Proceedings of Conference, Adapting to Change: New Thinking on Comfort. 9–11 April, Windsor, UK. Network for Comfort and Energy Use in Buildings, London. 〈http://nceub.org.uk〉 .
  26. Khedari et al., 2000 J. Khedari, N. Yamtraipat, N. Pratintong, J. Hirunlabh; Thailand ventilation comfort chart; Energy and Buildings, 32 (3) (2000), pp. 245–249
  27. Kwok, 1998 A.G. Kwok; Thermal comfort in tropical classrooms; ASHRAE Transactions, 104 (1) (1998), pp. 1031–1047
  28. Kwok and Rajkovich, 2010 A.G. Kwok, N.B. Rajkovich; Addressing climate change in comfort standards; Building and Environment, 45 (1) (2010), pp. 18–22
  29. Mallick, 1996 F.H. Mallick; Thermal comfort and building design in the tropical climates; Energy and Buildings, 23 (3) (1996), pp. 161–167
  30. McCartney and Nicol, 2002 K.J. McCartney, J.F. Nicol; Developing an adaptive control algorithm for Europe; Energy and Buildings, 34 (6) (2002), pp. 623–635
  31. NCDC, 2012 NCDC, 2012. Climate Data Online. Global Surface Summary of Day Data Version 7. 〈http://gis.ncdc.noaa.gov/map/viewer/#app=cdo&cfg=cdo&theme=daily&layer=111&node=gis〉 and 〈http://www7.ncdc.noaa.gov/CDO/GSOD_DESC.txt〉 (accessed 20.04.2012).
  32. Nguyen et al., 2012 A.T. Nguyen, M.K. Singh, S. Reiter; An adaptive thermal comfort model for hot humid South-East Asia; Building and Environment, 56 (2012), pp. 291–300
  33. Nicol, 2004 F. Nicol; Adaptive thermal comfort standards in the hot-humid tropics; Energy and Buildings, 36 (7) (2004), pp. 628–637
  34. Nicol and Humphreys, 2002 J.F. Nicol, M.A. Humphreys; Adaptive thermal comfort and sustainable thermal standards for buildings; Energy and Buildings, 34 (6) (2002), pp. 563–572
  35. Nicol and Humphreys, 2007 F. Nicol, M. Humphreys; Maximum temperatures in European office buildings to avoid heat discomfort; Solar Energy, 81 (3) (2007), pp. 295–304
  36. Nicol and Humphreys, 2010 F. Nicol, M. Humphreys; Derivation of the adaptive equations for thermal comfort in free-running buildings in European standard EN15251; Building and Environment, 45 (1) (2010), pp. 11–17
  37. Nicol et al., 2012 F. Nicol, M. Humphreys, S. Roaf; Adaptive Thermal Comfort: Principles and Practice; Routledge, London (2012)
  38. Peel et al., 2007 M.C. Peel, B.L. Finlayson, T.A. McMahon; Updated world map of the Köppen-Geiger climate classification; Hydrology and Earth System Sciences, 11 (5) (2007), pp. 1633–1644
  39. Schweiker and Shukuya, 2012 M. Schweiker, M. Shukuya; Adaptive comfort from the viewpoint of human body exergy consumption; Building and Environment, 51 (2012), pp. 351–360
  40. The University of Sydney, 2010 The University of Sydney, 2010. ASHRAE RP-884 Adaptive Model Project – Data Downloader. 〈http://sydney.edu.au/architecture/staff/homepage/richard_de_dear/ashrae_rp-884.shtml〉 (accessed 3.02.2010).
  41. Toe and Kubota, 2011 Toe, D.H.C., Kubota, T., 2011. A review of thermal comfort criteria for naturally ventilated buildings in hot–humid climate with reference to the adaptive model. In: Conference Proceedings of the 27th International Conference on Passive and Low Energy Architecture. 13–15 July, Louvain-la-Neuve, Belgium, vol. 1, pp. 457–462.
  42. Toftum, 2004 J. Toftum; Air movement – good or bad?; Indoor Air, 14 (Suppl 7) (2004), pp. 40–45
  43. Wijewardane and Jayasinghe, 2008 S. Wijewardane, M.T.R. Jayasinghe; Thermal comfort temperature range for factory workers in warm humid tropical climates; Renewable Energy, 33 (9) (2008), pp. 2057–2063
Back to Top
GET EPUB

Document information

Published on 12/05/17
Submitted on 12/05/17

Licence: Other

Document Score

0

Views 146
Recommendations 0

Share this document

Keywords

• • • •

claim authorship

Are you one of the authors of this document?

I am an author