Estimating the specific chemical exergy of municipal solid waste

Abstract

A new model for predicting the specific chemical exergy of municipal solid waste (MSW) is presented; the model is based on the content of carbon, hydrogen, oxygen, nitrogen, sulfur, and chlorine on a dry ash-free basis (daf). The proposed model was obtained from estimations of the higher heating value (HHV) and standard entropy of MSW using statistical analysis. The ultimate analysis of 56 different parts of MSW was used for the derivation of the HHV expression. In addition, 30 extra parts were used for validation. One hundred and seventeen relevant organic substances that represented the main constituents in MSW were used for derivation of the standard entropy of solid waste. The substances were divided into different waste fractions, and the standard entropies of each waste fraction and for the complete mixture were calculated. The specific chemical exergy of inorganic matter in the waste was also investigated by considering the inorganic compounds in the ash. However, as a result of the extremely low value calculated, the exergy of inorganic matter was ignored. The results obtained from the HHV model show a good correlation with the measured values and are comparable with other recent and previous models. The correlation of the standard entropy of the complete waste mixture is less accurate than the correlations of each individual waste fraction. However, the correlations give similar results for the specific chemical exergy, indicating that HHV has a greater impact when estimating the specific exergy of solid waste than entropy.

Introduction

The quantities of solid wastes increase as the population continues to grow throughout the world, whereas the available space for disposal decreases. If this waste is not properly treated and handled, it will pollute the air, land, ground water, and soil as well as has a negative impact on the hygienic conditions of the people [1]. A waste-to-energy (WTE) plant is one of the most robust and effective posttreatment options to decrease the volume of produced waste, reduce greenhouse gas emissions, and utilize the energy content in nonrecyclable waste for the production of electricity and heat, thereby reducing the dependence on fossil fuel.

For the efficient design of energy conversion processes, the chemical exergy and energy content of the fuel are basic properties to be considered to estimate the maximum available energy entering the system for performance analysis and optimization of the entire process. This can be done by detecting and evaluating quantitatively the thermodynamic imperfection (exergy loss) of the process under consideration, its main sources of loss and possible ways of improving such process can be indicated [2]. Estimating the chemical exergy of fuel is an important step when performing exergy analysis [3] in waste-to-energy plants. Exergy analysis is a method that uses the conservation of mass and energy together with the second law of thermodynamics. This analysis method is useful to achieve a more efficient energy-resource use because it enables the locations, types, and magnitudes of losses to be identified and to determine meaningful efficiencies [4].

However, because many solid fuels have unknown structures and chemical compositions, their exergy values cannot be calculated directly because of the lack of standard absolute entropy values [5]. Many models for the prediction and estimation of the chemical exergy of carbon-based fuels with complex bond interactions and unknown thermodynamics properties have been proposed based on the characteristics of the known homogeneous organic substances in the fuel. The first attempt was performed by Rant [6], involving the formulation of a semiempirical model to evaluate the availability (exergy) content of a structurally complicated material species. In that model, the chemical exergy of a fuel is evaluated from the computation of pure organic substances of known absolute entropies. Rant evaluated the ratios of the estimated chemical exergies and the higher heating values for seven gases and 12 liquid organic substances. Szargut and Styrylska [7] improved Rant′s correlation by considering the chemical composition of the fuels. They obtained correlation formulas to express the dependence between the ratio of the standard chemical exergy to the lower heating value using mass ratios of hydrogen, oxygen, nitrogen and sulfur to carbon that describe the chemical composition of the fuel. Due to lack of thermodynamic data, sulfur was not considered in their model for solid fuels, and their correlations were theoretically limited to Szargut′s reference environmental (R.E) model.

Using a model for estimating the thermodynamic properties of coal, char, tar, and ash, Eisermann et al. [8] approximated the standard entropy of coal by comparing the behavior of the standard entropies of a number of aliphatic and aromatic hydrocarbons as a function of several elemental ratios: H/(C + N), O/(C + N), N/(C + N) and S/(C + N). Shieh and Fan [9] estimated the specific chemical exergy of a structurally complicated material by adopting the concepts of the dead (or reference) state and the properties of the constituents in the material based on the first and second laws of thermodynamics. It was assumed that the entropy of a fuel is equal to the entropies of its constituent elements. This assumption is not accurate in many cases. Ikumi et al. [10] developed a method for estimating the entropies of coals based on the mole ratios of hydrogen, oxygen, nitrogen, and sulfur elements to the carbon element. Bilgen and Kaygusuz [11] used the entropy correlation proposed by Eisermann et al. [8] to improve the Shieh and Fan [9] model for the calculation of the chemical exergy of coals, and Stepanov [5] applied the entropy model developed by Ikumi et al. [10] to modify Shieh and Fan [9] to calculate the exergies of coke-oven gases of different metallurgical mills. These models are limited to coal fuels only because their constituent organic compounds have been derived from the standard entropies of the relevant organic substances of coals.

Song et al. [3] developed a model based on Shieh and Fan [9] to estimate the specific entropy of the organic matter in biomass used for the exergy calculations. Although their model showed a high accuracy and was simpler than the Szagut and Styrylskas correlation, it has a limited application, as it is only applicable to biomass. Song et al. [12] also proposed a model for estimating the entropy of solid fuels and then extended the Shieh and Fan [9] model using the major organic constituents of solid fuel for the prediction of the specific chemical exergy of solid fuels. However, they combined the higher heating value derived on a dry basis (db) with values of the standard entropy obtained based on a dry ash-free basis (daf) for the estimation of the chemical exergy. Furthermore, their model cannot be used for estimating the chemical exergy of substances containing elements other than C, H, O, N, and S and for combustible materials, such as certain categories of leather, plastic, and rubber, that are part of municipal solid waste. To the authors knowledge, no model has been found in the literature that is derived for predicting the chemical exergy of MSW.

The objective of this work is to propose a model for calculating the specific chemical exergy of MSW containing the C, H, O, N, S, and Cl from its elemental compositions on a dry ash-free basis.

Derivation of the Estimated Model

Municipal Solid Waste consists of a complex, heterogeneous mixture of organic and inorganic substances. The organic elements in MSW are mainly C, H, O, N, S, and Cl, which can be obtained from ultimate analysis, whereas the inorganics are commonly Si, Ca, K, P, Al, Mg, Fe, S, Na, Zn, Cu, Mn, and Cr, from which their oxides can be obtained from ash analysis data. Previous reports have shown that the influence of inorganic matters on the exergy value can be neglected in solid fuel as a result of their relatively small value [3, 12].

The standard chemical exergy of a substance that is not present in the environment can be evaluated by considering a reaction of the substance with other substances for which the chemical exergies are known [13]. The exact calculation of the chemical exergy of a material with complicated structures is difficult [14]; as a result, the standard chemical exergy of the substance in the environment is not readily available.

Standard chemical exergy of a substance

The chemical exergy of a substance is equal to the maximum amount of work that can be obtained from the substance by taking it to chemical equilibrium with the reference environment [15]. The standard exergy of a substance can be evaluated by considering an idealized reaction of the substance with other substances (generally reference substances) of known chemical exergies [16]. The known chemical exergies can be obtain from the table of standard chemical exergy based on Szarguts R.E model (Model II), as shown in Table 1. With consideration of the reversible reaction for chemical formation of a compound, Szargut et al. [2] expressed the standard chemical exergy of elements or compounds as

$b_{ch}^{o}\quad =\quad \Delta G_{f}^{o}+{\sum }_{i}n_{i}b_{chi}^{o}\quad \left({\mbox{kJ}}/{\mbox{mol}}\right)$

(1)

Table 1. Standard chemical exergy and standard entropies of various compounds

Substance	e0 (kJ/mol)	s0 (kJ/mol K)
l, liquid phase. Source: [3, 17, 18].
CO2	19.87	0.214
H2Ol	0.95	0.070
O2	3.97	0.205
N2	0.72	0.192
SO2	310.93	0.248
SiO2	1.636	0.041
HCl	85.5	0.187
CaO	129.881	0.038
K2O	412.544	0.102
P2O5	377.155	0.117
Al2O5	4.479	0.051
MgO	62.417	0.027
Fe2O3	17.656	0.087
SO3	242.003	0.257
Na2O	296.32	0.075
MnO	122.390	0.060
ZnO	37.080	0.042
Cr	538.610	0.024
Pb	226.940	0.065
As	477.040	0.035
Cd	290.920	0.052
Cl	163.940	0.166

where ${\textstyle \Delta G_{f}^{o}}$, n_i, and ${\textstyle b_{chi}^{o}}$ represent the standard Gibbs energy of formation, the mole fraction of component i in the mixture, and the standard chemical exergy of the constituent element i, respectively.

Calculation of the specific chemical exergy of municipal solid waste

For simplicity, suppose 1 kg of MSW (daf), expressed as C_mH_nN_pO_qC_rS_t, undergoes complete combustion at a standard state for the steady condition to produce carbon dioxide, water, nitrogen, hydrogen chloride, and sulfur dioxide as follows:

${\begin{array}{cl}&C_{m}H_{n}N_{p}O_{q}{\mbox{Cl}}_{r}S_{t}+\left(m,+,t,-,{\frac {q}{2}},+,{\frac {n-r}{4}}\right)O_{2}\\&\rightarrow \quad \quad {\mbox{mCO}}_{2}+\left({\frac {n-r}{2}}\right)H_{2}O+{\frac {P}{2}}N_{2}+r{\mbox{HCl}}+{\mbox{tS}}O_{2}\end{array}}$

(2)

All substances are assumed to enter and exit at the reference temperature, T₀ = 298.15 K, and reference pressure, P₀ = 101.325 kPa. The subscripts m, n, p, q, r, and t are the numbers of atoms of C, H, N, O, Cl, and S, respectively, in kmol/kg MSW or the molal compositions per kg of MSW expressed as:

$m={\frac {0.01C}{12.011}}\quad {\mbox{kmol/kg}}\quad {\mbox{or}}\quad {\frac {10C}{12.011}}\quad {\mbox{mol/kg}}$

(3)

$n={\frac {0.01H}{1.008}}\quad {\mbox{kmol/kg}}\quad {\mbox{or}}\quad {\frac {10H}{1.008}}\quad {\mbox{mol/kg}}$

(4)

$p={\frac {0.01N}{14.007}}\quad {\mbox{kmol/kg}}\quad {\mbox{or}}\quad {\frac {10N}{14.007}}\quad {\mbox{mol/kg}}$

(5)

$q={\frac {0.01O}{15.999}}\quad {\mbox{kmol/kg}}\quad {\mbox{or}}\quad {\frac {10O}{15.999}}\quad {\mbox{mol/kg}}$

(6)

$r={\frac {0.01{\mbox{Cl}}}{35.45}}\quad {\mbox{kmol/kg}}\quad {\mbox{or}}\quad {\frac {10{\mbox{Cl}}}{35.45}}\quad {\mbox{mol/kg}}$

(7)

$t={\frac {0.01S}{32.066}}\quad {\mbox{kmol/kg}}\quad {\mbox{or}}\quad {\frac {10S}{32.066}}\quad {\mbox{mol/kg}}$

(8)

where the elements in Equations (3)-(8) are expressed in wt% (daf). For the steady state, under the standard condition, the energy balance of the reaction in Equation (2) is given by

${\begin{array}{rl}W\quad =\quad &Q+h_{MSW}^{0}+\left(m,+,t,-,{\frac {q}{2}},+,{\frac {n-r}{4}}\right)h_{O_{2}}^{0}-mh_{{CO}_{2}}^{0}\\&-\left({\frac {n-r}{2}}\right)h_{H_{2}O}^{0}-{\frac {p}{2}}h_{N_{2}}^{0}-{rh}_{HCl}^{0}-th_{{SO}_{2}}^{0}\end{array}}$

(9)

The entropy balance is expressed as

${\begin{array}{rl}0\quad =\quad &{\frac {Q}{T_{o}}}+s_{MSW}^{0}+\left(m,+,t,-,{\frac {q}{2}},+,{\frac {n-r}{4}}\right)s_{O_{2}}^{0}-ms_{{CO}_{2}}^{0}\\&-\left({\frac {n-r}{2}}\right)s_{H_{2}O}^{0}-{\frac {p}{2}}s_{N_{2}}^{0}-rs_{HCl}^{0}-ts_{{SO}_{2}}^{0}+S_{gen}\end{array}}$

(10)

where W and Q are the work and heat transfer, respectively. S_gen is the entropy generated by the irreversibility in the reaction, and s⁰ and h⁰ represent the standard entropy and enthalpy, respectively.

Eliminating the heat transfer Q between Equation (9) and (10) gives the following:

${\begin{array}{rl}W\quad =\quad &h_{MSW}^{0},+,\left(m,+,t,-,{\frac {q}{2}},+,{\frac {n-r}{4}}\right),h_{O_{2}}^{0},-,h,s_{{CO}_{2}}^{0}\\&-\left({\frac {n-r}{2}}\right)h_{H_{2}O}^{0}-{\frac {p}{2}}h_{N_{2}}^{0}-rh_{HCl}^{0}-th_{{SO}_{2}}^{0}\\&-T_{o}s_{MSW}^{0}+\left(m,+,t,-,{\frac {q}{2}},+,{\frac {n-r}{4}}\right)s_{O_{2}}^{0}\\&-hs_{{CO}_{2}}^{0}-\left({\frac {n-r}{2}}\right)s_{H_{2}O}^{0}-{\frac {p}{2}}s_{N_{2}}^{0}-rs_{HCl}^{0}-ts_{{SO}_{2}}^{0}-T_{o}S_{gen}\end{array}}$

(11)

The maximum work, W_max, will occur when there is no irreversibility in the system. Hence, Equation (11) can be expressed as

${\begin{array}{rl}W_{max}\quad =\quad &h_{MSW}^{0}+\left(m,+,t,-,{\frac {q}{2}},+,{\frac {n-r}{4}}\right)h_{O_{2}}^{0}-mh_{{CO}_{2}}^{0}\\&-\left({\frac {n-r}{2}}\right)h_{H_{2}O}^{0}-{\frac {p}{2}}h_{N_{2}}^{0}-rh_{HCl}^{0}-th_{{SO}_{2}}^{0}\\&-T_{o}s_{MSW}^{0}+\left(m,+,t,-,{\frac {q}{2}},+,{\frac {n-r}{4}}\right)s_{O_{2}}^{0}-ms_{{CO}_{2}}^{0}\\&-\left({\frac {n-r}{2}}\right)s_{H_{2}O}^{0}-{\frac {p}{2}}s_{N_{2}}^{0}-rs_{HCl}^{0}-ts_{{SO}_{2}}^{0}\end{array}}$

(12)

or

${\begin{array}{rl}W_{max}\quad =\quad &-\Delta H_{r}^{o}-T_{o}s_{MSW}^{0}+\left(m,+,t,-,{\frac {q}{2}},+,{\frac {n-r}{4}}\right)s_{O_{2}}^{0}\\&-ms_{{CO}_{2}}^{0}-\left({\frac {n-r}{2}}\right)s_{H_{2}O}^{0}-{\frac {p}{2}}s_{N_{2}}^{0}-rs_{HCl}^{0}-ts_{{SO}_{2}}^{0}\end{array}}$

(13)

where ${\textstyle \Delta H_{r}^{o}}$ represents the heat of reaction of the combustion process, which is equal to the negative higher heating value [9], that is

$\Delta H_{r}^{o}\quad =\quad -{\mbox{HHV}}$

(14)

then

${\begin{array}{rl}W_{max}\quad =\quad &{\mbox{HHV}}-T_{o}s_{msw}+\left(m,+,t,-,{\frac {q}{2}},+,{\frac {n-r}{4}}\right)s_{O_{2}}^{0}-ms_{{CO}_{2}}^{0}\\&-\left({\frac {n-r}{2}}\right)s_{H_{2}O}^{0}-{\frac {p}{2}}s_{N_{2}}^{0}-rs_{HCl}^{0}-ts_{{SO}_{2}}^{0}\end{array}}$

(15)

Assume that the reaction in Equation (2) at 298.15 K and 101.325 kPa is an adiabatic process with no irreversibility. The exergy balance equation, in absence of changes in the kinetic and potential energy for reacting systems, is given by

${\begin{array}{rl}0\quad =\quad &-W_{max}+e_{MSW}+\left(m,+,t,-,{\frac {q}{2}},+,{\frac {n-r}{4}}\right)e_{O_{2}}^{0}-me_{{CO}_{2}}^{0}\\&-\left({\frac {n-r}{2}}\right)e_{H_{2}O}^{0}-{\frac {p}{2}}e_{N_{2}}^{0}-re_{HCl}^{0}-te_{{SO}_{2}}^{0}\end{array}}$

(16)

where e represents the specific chemical exergy. Substituting Equation (15) into Equation (16), the specific chemical exergy of MSW (daf), e_MSW, is presented as

${\begin{array}{rl}e_{MSW}\quad =\quad &{\mbox{HHV}}-T_{o}s_{MSW}^{0}+\left(m,+,t,-,{\frac {q}{2}},+,{\frac {n-r}{4}}\right)s_{O_{2}}^{0}-ms_{{CO}_{2}}^{0}\\&-\left({\frac {n-r}{2}}\right)s_{H_{2}O}^{0}-{\frac {p}{2}}s_{N_{2}}^{0}-rs_{HCl}^{0}-ts_{{SO}_{2}}^{0}+me_{{CO}_{2}}^{0}\\&+\left({\frac {n-r}{2}}\right)e_{H_{2}O}^{0}+{\frac {p}{2}}e_{N_{2}}^{0}+re_{HCl}^{0}\\&+e_{{SO}_{2}}^{0}-\left(m,+,t,-,{\frac {q}{2}},+,{\frac {n-r}{4}}\right)e_{O_{2}}^{0}\end{array}}$

(17)

or

${\begin{array}{rl}e_{MSW}\quad =\quad &m\left(e_{{CO}_{2}}^{0},+,T_{o},s_{{CO}_{2}}^{0}\right)-\left(e_{O_{2}}^{0},+,T_{o},s_{O_{2}}^{0}\right)\\&+{\frac {n}{2}}\left(e_{H_{2}O}^{0},+,T_{o},s_{H_{2}O}^{0}\right)-{\frac {1}{2}}\left(e_{O_{2}}^{0},+,T_{o},s_{O_{2}}^{0}\right)\\&+{\frac {q}{2}}\left(e_{O_{2}}^{0},+,T_{o},s_{O_{2}}^{0}\right)+{\frac {p}{2}}\left(e_{N_{2}}^{0},+,T_{o},s_{N_{2}}^{0}\right)\\&+t\left(e_{{SO}_{2}}^{0},+,T_{o},s_{{SO}_{2}}^{0}\right)-\left(e_{O_{2}}^{0},+,T_{o},s_{O_{2}}^{0}\right)\\&-{\frac {r}{2}}\left(e_{H_{2}O}^{0},+,T_{o},s_{H_{2}O}^{0}\right)-{\frac {1}{2}}\left(e_{O_{2}}^{0},+,T_{o},s_{O_{2}}^{0}\right)\\&-2\left(e_{HCl}^{0},+,T_{o},s_{HCl}^{0}\right)+{\mbox{HHV}}_{MSW}-T_{o}s_{MSW}^{0}\quad \left({\mbox{kJ}}/{\mbox{kg}}\right)\end{array}}$

(18)

where e⁰ is the standard exergy in kJ/mol and s⁰ is the standard entropy in kJ/mol K, as tabulated in Table 1. ${\textstyle s_{MSW}^{0}}$ is the standard entropy of municipal solid waste, in kJ/K kg (daf), and HHV_MSW is the higher heating value (HHV) of MSW, in kJ/kg (daf). The specific chemical exergy of MSW can be calculated once the standard chemical exergies of CO_2, H₂O(l), N₂, O₂, SO₂, and HCl; the higher heating value; and the absolute entropies are known.

Estimating the higher heating value of municipal solid waste

In the absence of a measured value, the HHV of fuel can be estimated from their elemental composition [19, 20]. In this study, the HHV estimate was performed by considering 56 data points and 30 data points of MSW samples for the derivation and validation of the correlation, respectively; in addition, the chemical composition and HHV of each sample was collected from the published literature and presented in Tables A1 and A2 (Appendix 1). These data cover six categories of combustible MSW fractions, namely, food, wood, paper, textiles, plastics, and rubber waste [21, 22]. For the selection of a suitable model, 9 assumed algebraic expressions from previous work based on the correlation of the HHV and ultimate analysis of solid fuel (daf) were used, as shown in Table 2. Using regression analysis based on the generalized method of least squares [19] on the 56 data points, the constant terms of these algebraic expressions were evaluated. The correlation that has the least error and highest coefficient of determination, as described in 'Selection of the best correlation', was selected. The newly estimated correlation was compared with the experimental values of HHV and the results of previous models collected from the open literature, for further validation.

Table 2. Assumed correlations used for the selection of the proposed model for HHV (daf)

S. No.	Assumed expression	Criteria for selection	Reference
where C, H, O, N, S, and Cl represents carbon, hydrogen, oxygen, nitrogen, sulfur, and chlorine, respectively, in % by mass on a dry ash free basis. a0, a, b, c, d, e, and f are constants of correlation.
1.	HHV = aC + bH + cO + dN + eS + fCl	Assuming fuel HHV to be a linear function of it constituents.	Current model
2.	HHV = aC + bH + cO + dN + eS	Based on Gumzs criteria	[19]
3.	HHV = a0 + bH + cO + dN + eS + fCl	Based on Changs criteria	[23]
4.	HHV = aC + b (H − O/8) + eS	Based on Dulongs criteria	[19]
5.	HHV = aC + bH + cO + eS	Based on modified version of Dulongs criteria	[19]
6.	HHV = a0 + aC + bH + cO2	Based on Seylers criteria	[19]
7.	HHV = a (C − (3/8) O) + b (3/8) O) + c (H − (1/6) O) + eS	Based on Steuers criteria	[19]
8.	HHV = a (C − 0.75 (O/2)) + b (H − 0.125 (O/2)) + eS	Based Sumegis criteria	[19]
9.	HHV = aC + bH + c ((N + O − 1)/8) + eS	Dulong-Berthelots criteria	[19]

Estimating the standard entropy of municipal solid waste

Municipal solid waste (MSW) contains mainly organic polymers in plastics, wood, paper, textile, rubber, and food waste. The entropies of these polymers in the organic waste are estimated or evaluated by the entropies of their organic monomers structures as there is no significant difference between the entropies of the solid organic monomers and their polymers [24]. The difference ranges from 0.1 to 12.5% (Table 3).

Table 3. Standard entropies of some solid organic polymers and monomers at 298.15 K

S. No.	Substance	S0 (J/mol K)
Source: [24].
1.	C6H11NO	173.21
	(C6H11NO)n	173.0
2	C4H4O4	157.2
	(C4H4O4)n	151.4
3	C15H10N2O2	332.5
	(C15H10N2O2)n	294
4	C13H24O2	401.9
	(C13H24O2)n	351.6

The standard entropy of MSW was derived from organic substances with known standard entropies. In this work, 117 samples of organic compounds relevant to MSW were collected from the published literature [3, 8, 10, 12, 17, 24] and tabulated in Table A3 (Appendix 1). The data points where selected based on the molecular structures of the organic substances that are associated or linked with the formation of larger molecular structure network of municipal solid waste. The organic compounds were grouped into the six categories of waste fractions, as previously used for the higher heating value, namely: food, plastic, textile, rubber, wood, and paper. This was accomplished by considering the molecular structures of the organic substances that can be found in each of the molecular structures of the waste fractions. For wood, it contains three major chemical components: cellulose, hemicelluloses, and lignin [25]. Each of the chemical structure of the wood constituents [26, 27] was studied and organic compounds (monomers) that can be made or found from these structures are selected. In the food, the main structural elements identified are proteins, carbohydrate and lipids [28]. The molecular structures of these food components [29, 30] were also investigated and organic monomers that are linked with the structure are selected. The same method was carried on chemical structures of plastic [31], textile [32, 33], and rubber [34] materials with identifications of biologically important molecules which form the building structure of their polymers. Based on the absolute entropies and elemental compositions of the selected organic substances, a first-order polynomial correlation was derived statistically for the standard entropy of the waste fractions and the mixture.

Selection of the best correlation

Three statistical parameters were used as evaluating parameters for both HHV and the standard entropy of MSW, which are computed as follows:

${\mbox{Average absolute error (AAE)}}\quad =\quad {\frac {1}{n}}\sum _{i=1}^{n}\left|{\frac {Z_{est}-Z_{exp}}{Z_{exp}}}\right|\times 100\%$

(19)

${\mbox{Average bias error (ABE)}}\quad =\quad {\frac {1}{n}}\sum _{i=1}^{n}{\frac {Z_{est}-Z_{exp}}{Z_{exp}}}\times 100\%$

(20)

${\mbox{Coefficient of determination}}\quad \left(R^{2}\right)\quad =$$\quad 1-\sum _{i=1}^{n}{\frac {{\left(Z_{est},-,Z_{exp}\right)}^{2}}{{\left(Z_{exp},-,\quad ,{\overline {Z}}_{exp}\right)}^{2}}}$

(21)

where Z_est and Z_exp denote the estimated and experimental values, respectively. ${\textstyle {\overline {Z}}_{exp}}$ is the experimental average value. AAE is the average error of a correlation. A smaller error of correlation will occur when AAE is low, which indicates higher accuracy. ABE denotes the average bias error of correlation. A positive value of ABE indicates an overall overestimation, whereas a negative value implies an overall underestimation. The smaller the absolute value of ABE, the smaller the bias of correlation. R² is used as a comprehensive parameter to measure the accuracy of the model. A higher R² value means a better estimation and fitting [20]. These three parameters are the important statistical criteria and are primarily employed to assess correlations [3, 12, 19].

Specific chemical exergy of inorganic matter in municipal solid waste

Inorganic substances of waste materials are contained in the ash and obtained from complete combustion of solid fuel; ash is mainly contained in various metallic oxides and has a high thermal stability [35, 36]. The specific chemical exergy of inorganic matter in kJ/kg MSW was calculated from the major ash compositions data in Table 4 from a stoker-type incinerator [37] as follows [3, 12, 36]:

$e_{ioc}\quad =\quad 0.01A\left(\sum ,n_{i},x_{i},e_{ioc}^{0},+\right.$$\left.,R,T_{o},\sum ,n_{i},x_{i},{\mbox{ln}},x_{i}\right)\quad \left({\mbox{kJ/kg}}\right)$

(22)

Table 4. Chemical composition of MSW ashes

Component	Bottom ash, BA (wt%)	Fly ash, FA (wt%)
Source: [37].
SiO2	37.8	2.47
CaO	20.79	44.5
K2O	0.85	3.01
P2O5	3.63	0.26
Al2O3	13.4	0.55
MgO	2.91	0.57
Fe2O3	7.46	0.32
SO3	1.01	1.61
Na2O	5.38	4.39
ZnO	0.52	2.25
CuO	0.51	0.096
MnO	0.17	0.04
Cr	0.63	0.008
Pb	0.22	0.51
As	0.021	0.062
Cd	0.0003	0.003
Cl	3.51	35.15

where n_i represents number of moles of the component in inorganic matter, in mol/kg. ${\textstyle e_{ioc}^{0}}$ and x_i are the standard chemical exergy and mole fraction of components i in inorganic matter, respectively. R is the universal gas constant, 0.0083145 kJ/mol K, and A is the ash content of MSW in wt%.

Results and Discussion

Correlation based on the higher heating value

For the higher heating value of MSW, the correlation derived that showed the minimum error with a higher accuracy among the nine assumed correlations used in Table 2 was expressed as

${\begin{array}{rl}{\mbox{HHV}}\quad =\quad &0.364C+0.863H-0.075O\\&+0.028N-1.633S+0.062{\mbox{Cl}}\quad ({\mbox{MJ}}/{\mbox{kg}})\end{array}}$

(23)

${\begin{array}{rl}35.8\%&\leq C\leq 86.1\%,4.1\%\leq H\leq 13.9\%,0.0\%\\&\quad \leq O\leq 54.9\%,0.0\%\leq N\leq 20.3\%,0.0\%\\&\quad \leq S\leq 2.7\%,0.0\%\leq Cl\leq 56.4\%,\quad \\&\quad 13.0\quad MJ/kg\leq HHV\leq 43.2\quad MJ/kg.\end{array}}$

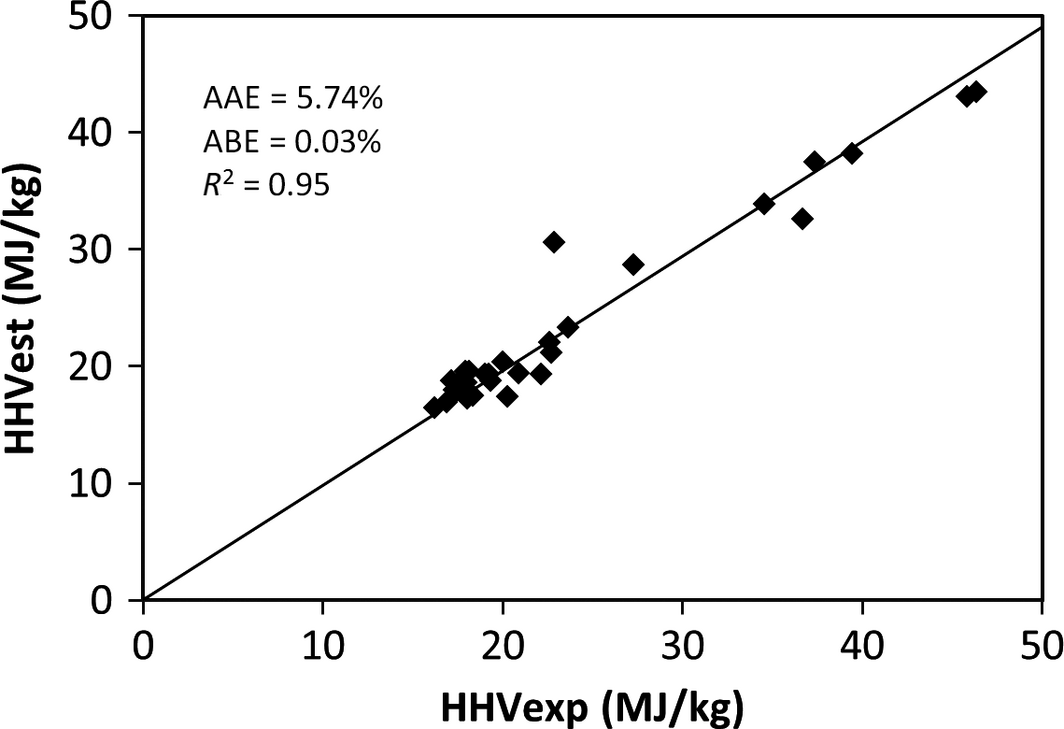
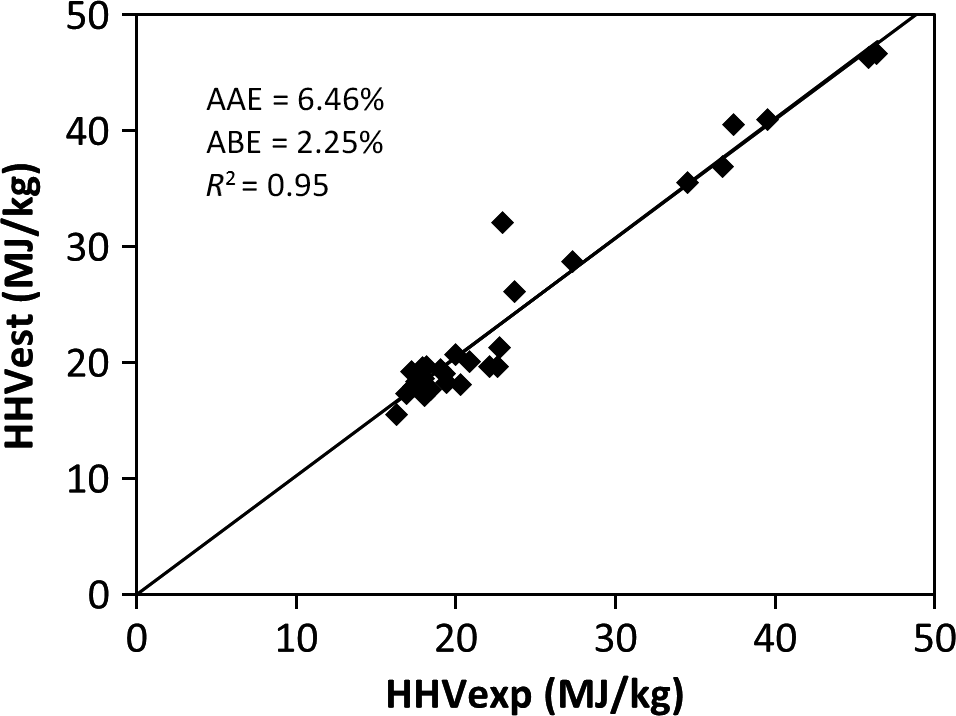
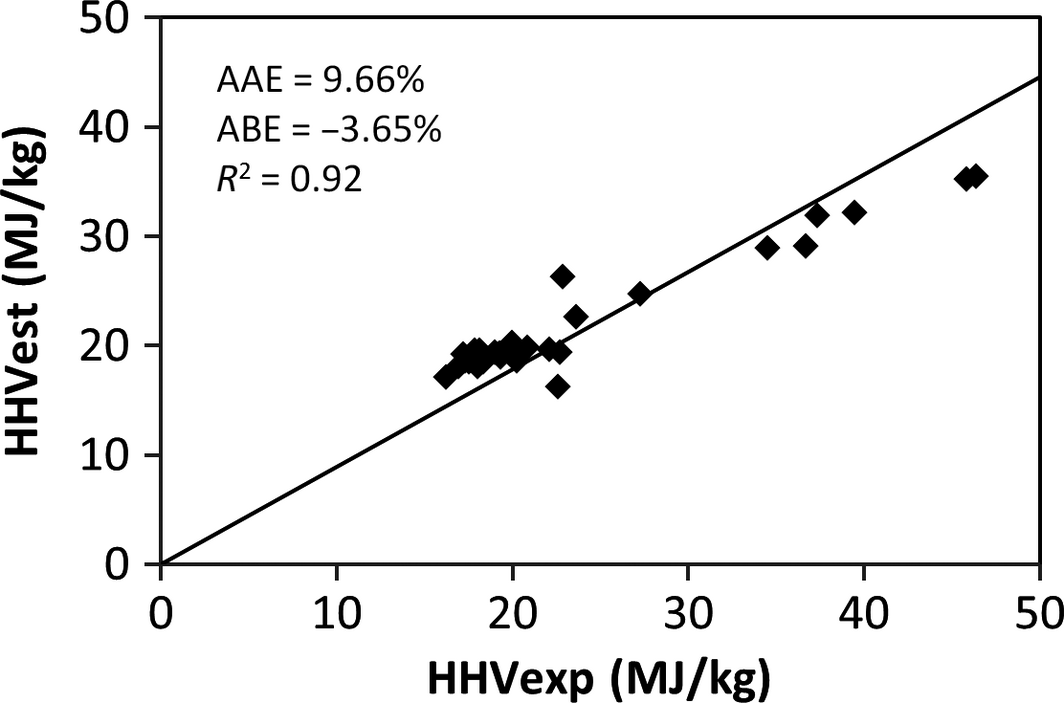
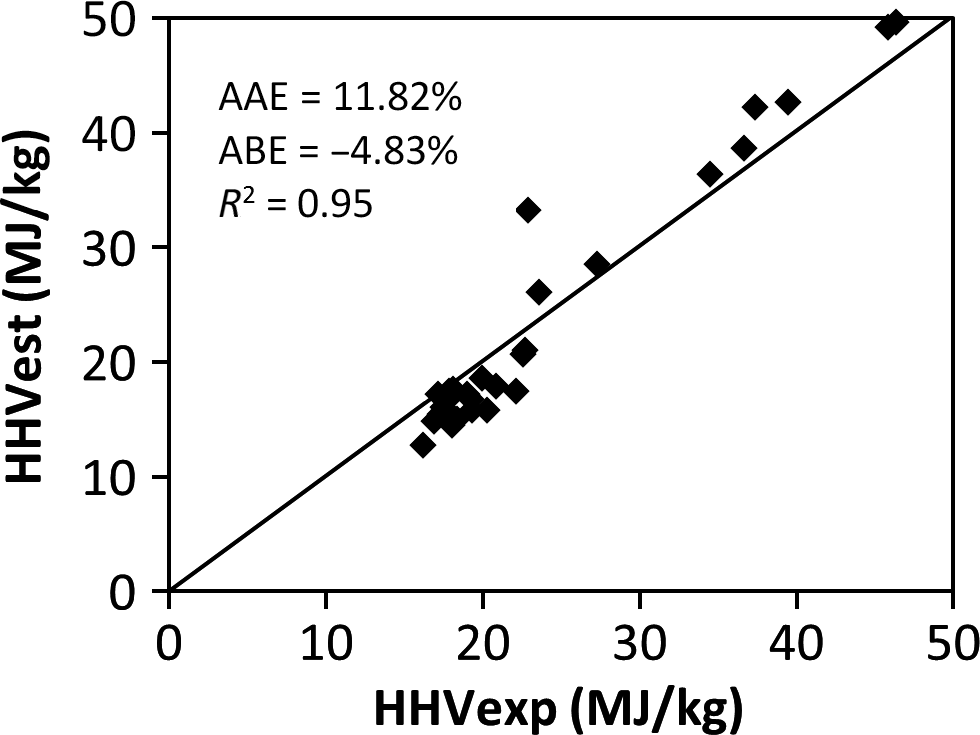
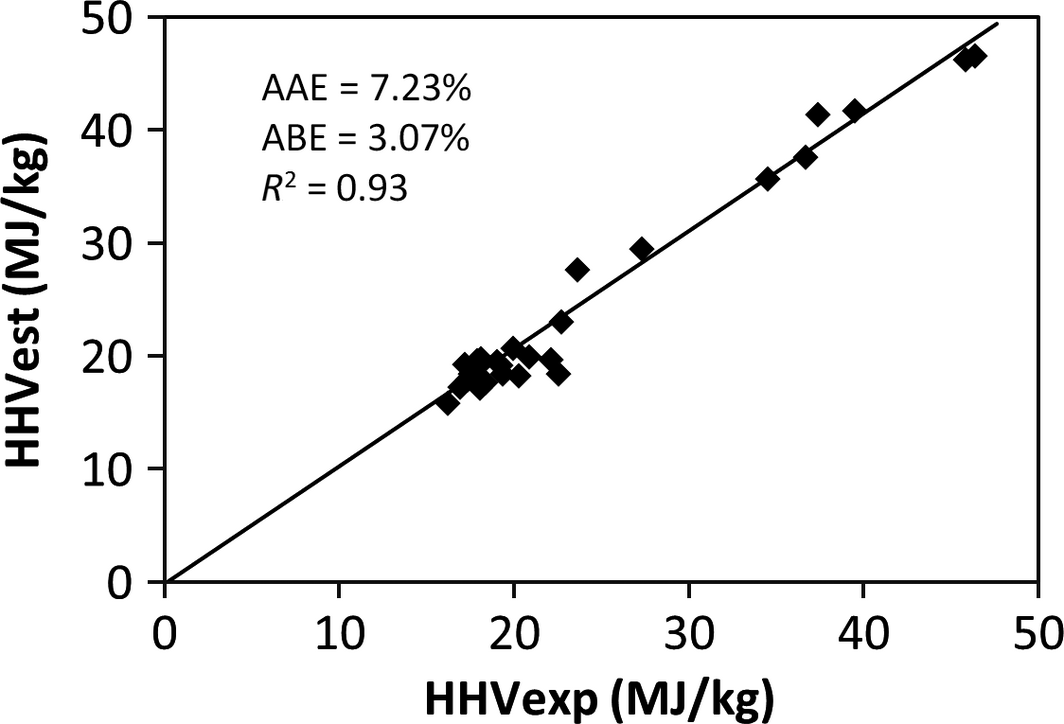
The results of the validation of the derived model and the comparison with published correlations using the experimental values of 30 samples of MSW in the different categories of food, wood, plastic, textile, rubber, and paper waste are shown in Table 5 and represented in Figures 1-5. Figures 1, 2, and 4 show the best correlation with experimental data (highest coefficient of determination), representing the model developed in this work, model by Channiwala and Parikh [19] and Dulongs correlation. However, the proposed model shows significantly better estimations when considering the errors (AAE and ABE) compared to the other models. This is not surprising, as these models have been derived from mixed solid fuel and coal. Figure 3 shows a correlation proposed by Sheng and Azevedo [20]. Although the correlation has a good coefficient of determination (R² = 0.92), it has a higher error and underestimated the HHV. In addition, the correlation is limited to biomass. The correlation proposed by Chang (Table 5 and Fig. 5) has a considerable accuracy, with a coefficient of determination of R² = 0.93. Although this correlation was derived from MSW, it overestimated the correlation and has a higher error value when compared with the present model.

Table 5. Derived correlation compared with previous models

S No.	Name	Correlation (MJ/kg)	Application	AAE (%)	ABE (%)	R2	Reference
(*) shows the correlations obtained in % by mass on a dry basis, whereas the others are on dry ash-free basis.
1.	Proposed Model	HHV = 0.364C + 0.863H − 0.075O + 0.028N − 1.633S + 0.062Cl	MSW	5.738	0.032	0.95	Current model
2.	Channiwala and Parikh	HHV* = 0.3491C* + 1.1783H* + 0.1005S*− 0.1034O* − 0.0151N* − 0.0211A*	Mixed waste	6.456	2.254	0.95	[19]
3.	Sheng and Azevedo	HHV* = −1.3675 + 0.3137C* + 0.7009H* + 0.0318 (100 − C* − H* − A*)	Biomass	9.657	−3.650	0.92	[20]
4.	Dulong	HHV = 0.3383C + 1.443 (H − (O/8))  + 0.0942S	Coal	11.822	−4.832	0.95	[19]
5.	Chang	HHV = 35.8368 + 0.7523H − 0.2674S − 0.4654O − 0.3814Cl − 0.2802N	MSW	7.234	3.067	0.93	[19]

Figure 1. Comparison between the experimental and the estimated HHV by the developed correlation.

Figure 2. Comparison between the experimental and the estimated HHV by the Channiwala and Parikh [19] correlation.

Figure 3. Comparison between the experimental and the estimated HHV by the Sheng and Azevedo [20] correlation.

Figure 4. Comparison between the experimental and the estimated HHV by Dulongs correlation.

Figure 5. Comparison between the experimental and the estimated HHV by Changs correlation.

Standard entropy of municipal solid fuel

For the prediction of the standard entropy of the organic substance in MSW, a correlation in the form of the first-order polynomial was used. The five correlations derived for estimating the standard entropy of waste fractions and the mixture of waste were expressed as follows:

For Plastic waste

${\begin{array}{rl}s_{pl}^{0}\quad =\quad &0.0087C+0.0753H+0.0134O\\&+0.0077N+0.0084{\mbox{Cl}}\quad ({\mbox{kJ}}/K\quad {\mbox{kg}})\end{array}}$

(24)

${\begin{array}{rl}10.3\%&\leq C\leq 94.7\%,0.0\%\leq H\leq 14.3\%,0.0\%\leq O\leq 54.2\%,\\&\quad 0.0\%\leq N\leq 66.7\%.\end{array}}$

With ABE, AAE, and R² of 0.722, 7.314, and 0.7674, respectively.

For Textile/Rubber waste

${\begin{array}{rl}s_{tr}^{0}\quad =\quad &0.0097C+0.0635H+0.0128O+0.0136N\\&+0.0165S\quad ({\mbox{kJ}}/K\quad {\mbox{kg}})\end{array}}$

(25)

${\begin{array}{rl}15.8\%\leq &C\leq 95.1\%,3.0\%\leq H\leq 9.7\%,0.0\%\leq O\leq 55.2\%,\\&0.0\%\leq N\leq 66.7\%,0.0\%\leq S\leq 42.1\%\end{array}}$

With ABE, AAE, and R² of 0.714, 6.476, and 0.5457, respectively.

For Wood/Paper waste

$s_{wp}^{0}\quad =\quad 0.0162C+0.0116H+0.0081O+0.00691{\mbox{Cl}}\quad \left({\mbox{kJ}}/K\quad {\mbox{kg}}\right)$

(26)

${\begin{array}{rl}26.7\%&\leq C\leq 77.8\%,0.4\%\leq H\leq 7.7\%,5.1\%\leq O\leq 71.1\%,\\0.0\%&\leq {\mbox{Cl}}\leq 66.3\%\end{array}}$

With ABE, AAE, and R² of 0.329, 5.215, and 0.728, respectively.

For Food waste

(27)

${\begin{array}{rl}19.2\%\leq C&\leq 92.3\%,1.4\%\leq H\leq 14.1\%,0.0\%\leq O\\&\leq 59.7\%,0.0\%\leq N\leq 51.9\%,0.0\%\leq S\leq 34.0\%\end{array}}$

With ABE, AAE, and R² of 0.414, 5.886, and 0.6922, respectively.

For Mixed waste

${\begin{array}{rl}s_{msw}^{0}\quad =\quad &0.0101C+0.0630H+0.0106O+0.0108N\\&+0.0155S+0.0084{\mbox{Cl}}\quad ({\mbox{kJ}}/K\quad {\mbox{kg}})\end{array}}$

(28)

${\begin{array}{rl}10.3\%\leq &C\leq 95.1\%,0.00\%\leq H\leq 14.3\%,0.0\%\leq O\leq 71.1\%,0.0\%\\&\leq N\leq 66.7\%,0.0\%\leq S\leq 42.1\%,0.0\%\leq {\mbox{Cl}}\leq 89.7\%,\end{array}}$

with ABE, AAE, and R² of 1.118, 8.293, and 0.5414, respectively.

Comparing the five equations obtained, the results show that the standard entropy correlations for each waste fraction in MSW are more accurate than the standard entropy correlation for the waste mixture. This is as a result of complicated mixture, heterogeneous molecule structure and variation in municipal solid waste chemical compositions and properties. Nevertheless, because the standard entropy of plastic, textile/Rubber, wood/paper, food, and waste mixture gave similar average values for the specific exergy of the MSW estimation of 24,359, 24,364, 24,426, 24,393, and 24,387 (kJ/kg), respectively, the correlation of the standard entropy of the waste mixture can be used for the derivation of exergy.

Specific chemical exergy of municipal solid fuel (daf) and specific chemical exergy of ash

By substituting Equation (3)–(8), (23), and (24)–(28) into Equation (18), along with the standard chemical exergy data from Table 1, the specific chemical exergy of solid waste on a dry ash-free basis can be expressed as follows:

For Plastic waste:

${\begin{array}{rl}e_{P}\quad =\quad &376.879C+787.351H-58.654O+46.398N\\&-1533.261S+100.981{\mbox{Cl}}\quad ({\mbox{kJ}}/{\mbox{kg}})\end{array}}$

(29)

For Textile/Rubber waste:

${\begin{array}{rl}e_{TR}\quad =\quad &376.580C+790.869H-58.475O+44.639N\\&-1538.180S+98.566{\mbox{Cl}}\quad ({\mbox{kJ}}/{\mbox{kg}})\end{array}}$

(30)

For Wood/Paper waste

${\begin{array}{rl}e_{WP}\quad =\quad &374.642C+806.343H-57.074O+48.693N\\&-1533.261S+101.425{\mbox{Cl}}\quad ({\mbox{kJ}}/{\mbox{kg}})\end{array}}$

(31)

For Food waste

${\begin{array}{rl}{\mbox{Food}}\quad e_{F}\quad =\quad &377.535C+785.711H-58.446O+45.682N\\&-1536.242S+103.486{\mbox{Cl}}\quad ({\mbox{kJ}}/{\mbox{kg}})\end{array}}$

(32)

For mixed waste

${\begin{array}{rl}e_{msw}\quad =\quad &376.461C+791.018H-57.819O+45.473N\\&-1536.242S+100.981{\mbox{Cl}}\quad ({\mbox{kJ}}/{\mbox{kg}})\end{array}}$

(33)

The minimum, maximum, and average specific exergy values of municipal solid waste calculated were 17,602, 43,396, and 24,387 in (kJ/kg), respectively. Although Equation (33) slightly underestimated the specific chemical exergy calculated by Equations (29) and (30), that is, an ABE of −0.139 and −0.113, respectively, and slightly overestimated the exergy estimated by Equations (31) and (32), that is, an ABE of 0.179 and 0.009, respectively, when compared, the coefficient of determination shows that Equations (29)-(32) are similar to Equation (33) (i.e., a value of 1 was achieved in all cases). This result indicates that Equation (33) can be used to estimate the specific exergy of municipal solid waste, that is, the HHV has more impact on the exergy.

The overall average ratio of the specific exergy of MSW developed with the higher heating value was obtained as 1.036, showing that the value of exergy is slightly higher than the HHV. The ratio of exergies to heating values obtained in this work is similarly when compared with Szargut and Styrylska [7] model with ratio of 1.047. As their methods were commonly used for evaluating the chemical exergy of solid fuels. This result indicates that the present model is reliable and accurate. However, the slight variation in the ratios is due to different types of fuel used.

The specific exergies of inorganic matter in MSW calculated from Equation (22) using the chemical ash composition data in Table 4 are 0.86 and 1.79 kJ/kg for bottom ash and fly ash, respectively. These values are very small when compared with the average specific chemical exergy values, 24,387 kJ/kg of MSW (daf) estimated, demonstrating that the specific chemical exergy of inorganic matter can be neglected.

Conclusions

Following the evaluations of the previous equations for estimating the specific chemical exergy of solid fuels, the present proposed models in this study were found to be more accurate when using municipal solid waste as a fuel. All other methods have either ignored the inclusion of chlorine from the elemental compositions of waste or have used other solid fuels with a limited amount of MSW. In this work, a simple method for estimating the specific exergy of municipal solid waste on (daf) from their ultimate analysis based on HHV, standard entropy, and exergy equation of reaction was proposed.

The higher heating values of the estimated MSW showed a good correlation and a higher accuracy compared with previous models. It is calculated as

${\begin{array}{rl}{\mbox{HHV}}=\quad &0.364C+0.863H-0.075O+0.028N\\&-1.633S+0.062{\mbox{Cl}}\quad ({\mbox{MJ}}/{\mbox{kg}})\end{array}}$

The standard entropy of the estimated waste mixture has a rather low accuracy when compared with the waste fractions. However, the standard entropy can be used for the estimation of the specific chemical exergy of a solid, as it showed a similar result with the standard entropy of waste fractions; the standard entropy is expressed as

${\begin{array}{rl}s_{msw}^{0}\quad =\quad &0.0101C+0.0630H+0.0106O+0.0108N\\&+0.0155S+0.0084{\mbox{Cl}}\quad ({\mbox{kJ}}/K\quad {\mbox{kg}}).\end{array}}$

This result indicates that a higher heating value has more impact on the derivation of the specific chemical exergy of solid waste than entropy. In other words, the specific exergy of MSW mainly depends on the values of HHV.

Due to very low calculated values of specific chemical exergy of inorganic matter in MSW, the specific chemical exergy developed in this work is equal to the specific chemical exergy of the organic matter in MSW and is presented as

${\begin{array}{rl}E_{msw}\quad =\quad &376.461C+791.018H-57.819O\\&+45.473N-1536.242S+100.981{\mbox{Cl}}\quad ({\mbox{kJ}}/{\mbox{kg}}).\end{array}}$

The results obtained demonstrate that the specific chemical exergy is always slightly higher than the highest heating value, indicating the validity and accuracy of the model.

The present correlation can be accepted for estimating the specific chemical exergy of MSW using the elemental compositions of the fuel within the range specified based on a dry ash-free basis. The model is applicable for the efficient modeling of a combustion system in a waste-to-energy plant.

Acknowledgments

The authors acknowledge the Nigerian Government and Michael Okpara University of Agriculture Umudike, Abia State, Nigeria, for supporting this work through TETfund Academic Staff Training and Development.

Conflict of Interest

None declared.

Nomenclature

AAE

average absolute error

A

ash content in the waste (%)

ABE

average bias error

E

chemical exergy (kJ)

e

specific chemical exergy (kJ/kg) or (kJ/mol)

FC

fixed carbon (%)

G

Gibbs energy (kJ/kg) or (kJ/mol)

H

enthalpy (kJ/kg)

HHV

higher heating value (kJ/kg)

MSW

municipal solid waste

P

pressure (kpa)

R²

coefficient of determination

S

entropy (kJ/K)

S_gen

entropy generated

s

specific entropy (kJ/kg K) or (kJ/mol K)

T

Temperature (K)

V

volatile matter (%)

Subscripts

ba

bottom ash

daf

dry ash-free basis

est

estimate

exp

experiment

fa

fly ash

f

formation

fo

food

ioc

inorganic compound

max

maximum

msw

municipal solid waste or mixed solid waste

o

standard state

pl

plastic

R

reaction

tr

textile/rubber

wp

wood/paper

Superscripts

0

reference state

Greek Symbols

∆

change

∑

summation

Appendix

Table A1. Chemical characteristics of MSW (daf) used for derivation

MSW groups, Subgroup and variety	Proximate analysis (wt %)			Ultimate analysis (wt %)						HHV (MJ/kg)	Reference
	A	V	FC	C	H	O	N	S	Cl
All the proximate, ultimate analysis data and HHV on dry basis are converted to dry ash-free basis. Also all HHV are converted to MJ/kg.
Food waste
1. Flour	–	–	–	42.78	6.19	48.39	2.48	0.15	–	18.157	[21]
2. Rice	0.40	84.42	15.18	45.97	6.35	45.74	1.67	0.25	–	18.213	[22]
3. Peanut shell	–	–	–	53.6	6.70	38.3	1.20	0.20	–	20.598	[21]
4. Pea	–	–	–	42.13	5.88	48.62	3.14	0.22	–	16.533	[21]
5. Scallion	–	–	–	48.12	6.27	41.74	3.09	0.78	–	18.042	[21]
6. Potato	3.15	79.52	17.33	44.41	5.33	47.82	1.81	0.64	–	17.656	[22]
7. Spinach	15.97	65.26	18.77	47.58	6.48	43.93	1.57	0.43	–	20.326	[22]
8. Celery	14.58	65.36	20.06	38.46	6.16	54.52	0.21	0.65	–	15.886	[22]
9. Pakchoi	18.44	63.97	17.59	43.37	5.93	48.64	1.25	0.81	–	23.173	[22]
10. Tangerine peel	2.91	76.49	20.6	48.74	5.92	43.83	1.43	0.08	–	19.024	[22]
11. Banana peel	10.85	64.38	24.77	35.8	4.79	54.93	4.37	0.10	–	18.385	[22]
12. Orange peel	2.44	76.27	21.29	43.93	5.64	48.93	1.34	0.07	0.08	18.550	[21]
13. Rib	–	–	–	52.92	8.83	25.63	2.29	0.32	–	17.277	[21]
14. Fish bone	39.82	56.25	3.93	63.87	8.01	19.08	8.39	0.64	–	26.245	[21]
15. Food waste	6.1	82.11	18.00	51.54	7.14	37.06	3.13	0.21	0.92	21.619	[38]
Wood waste
16. Poplar wood	7.54	73.85	18.61	51.36	5.86	41.00	1.52	0.22	–	20.009	[22]
17. Poplar leaf	15.69	68.74	15.57	49.54	5.24	43.30	1.32	0.59	–	19.986	[22]
18. Chinar leaf	9.23	69.74	21.03	52.95	4.88	40.51	1.01	0.65	–	21.064	[22]
19. Gingko leaf	11.62	73.19	15.19	41.35	5.54	50.88	1.36	0.87	–	17.289	[22]
20. Pine wood	0.95	83.5	15.54	50.51	5.95	43.39	0.11	0.03	–	19.834	[21]
21. Sawdust	0.42	81	18.58	49.42	7.26	42.92	0.39	0.01	–	21.267	[21]
22. Wood	1.00	81.62	18.38	50.10	6.16	43.47	0.17	0.02	0.07	19.697	[38]
23. Wood chips	1.95	82.66	15.4	49.54	6.21	44.06	0.12	0.04	0.03	19.544	[21]
24. Bamboo	0.69	81.03	18.27	50.46	6.32	42.73	0.22	0.1	0.16	19.716	[21]
25. Leaves	8.92	73.7	17.38	47.25	5.57	46.26	0.19	0.73	–	18.882	[21]
26. Pine needles	–	–	–	52.57	6.3	40.44	0.54	0.16	–	20.843	[21]
27. King grass	7.44	74.12	18.43	46.91	5.89	46.3	0.7	0.21	–	19.428	[21]
Paper waste
28. Blank printing paper	10.69	79.33	9.98	45.12	5.31	48.91	0.38	0.28	–	15.127	[22]
29. Tissue paper	0.52	90.47	9.01	45.18	6.13	48.32	0.25	0.11	–	17.340	[22]
30. Newspaper	8.07	79.54	12.39	48.01	5.71	45.86	0.33	0.09	–	18.666	[22]
31. Magazine	29.49	62.44	8.07	41.04	8.99	49.15	0.42	0.4	–	16.771	[21]
32. Writing paper	–	–	–	43.66	5.84	50.16	0.16	0.18	–	13.69	[21]
33. Cardboard	5.27	81.75	12.97	46.09	5.36	48.02	0.32	0.21	–	18.239	[21]
34. Carton	7.22	83.95	8.82	48.97	6.14	44.52	0.21	0.16	–	18.430	[21]
35. Printing paper	9.70	82.83	17.17	47.51	5.98	46.25	0.14	0.03	0.09	18.051	[38]
36. Packaging paper	12.2	85.88	14.12	46.92	5.92	46.74	0.22	0.09	0.10	17.654	[38]
Textile
37. Absorbent cotton gauze	0.14	94.85	5.01	46.74	5.69	47.23	0.27	0.08	–	14.664	[22]
38. Cotton cloth	3.09	78.71	18.21	56.49	5.87	33.3	3.52	0.18	0.65	14.664	[21]
39. Wool	1.24	84.76	14.00	60.07	4.24	31.48	2.65	1.55	–	21.183	[21]
40. Acrylic fiber	0.14	75.25	24.61	66.78	5.2	7.31	20.26	0.45	–	29.812	[21]
41. Chemical fiber	–	–	–	48.09	7.16	34.06	9.43	1.26	–	21.959	[21]
42. Polyester taffeta	0.44	90.63	8.93	60.1	4.5	35.11	0.28	0.01	–	22.178	[21]
43. Terylene	0.49	88.6	10.91	62.16	4.14	33.12	0.29	0.28	–	20.963	[22]
44. Textiles	1.40	82.86	17.14	52.54	6.19	39.26	1.76	0.20	1.42	21.197	[38]
Plastics waste
45. PS	0.04	99.57	0.39	86.06	6.27	1.93	5.73	–	–	38.946	[22]
46. LDPE	–	99.98	0.02	85.98	11.20	2.61	0.21	–	–	46.480	[22]
47. HDPE	0.18	99.57	0.25	85.35	12.70	1.90	0.05	0.14	–	46.444	[22]
48. PVC	–	94.93	5.07	38.34	4.47	–	0.23	0.61	56.35	20.830	[22]
49. PET	0.09	90.44	9.47	63.01	4.27	32.69	0.04	–	–	23.111	[22]
50. PE	0.15	99.85	–	85.45	14.32	–	0.16	0.07	–	46.388	[21]
51. PP	0.02	99.97	0.01	85.41	12.51	1.85	0.23	–	–	46.248	[21]
52. Packaging plastic	3.90	95.21	4.79	75.75	9.78	12.00	0.35	0.03	2.08	26.951	[38]
53. Other plastic	1.30	99.09	0.91	84.90	9.63	0.97	3.35	0.03	1.11	41.135	[38]
Rubber waste
54. Rubber	8.36	84.77	6.86	77.72	10.12	7.42	0	2.66	2.08	25.474	[21]
55. Tire	25.70	68.05	6.25	79.19	8.45	11.38	0.69	0.28	–	35.654	[21]
Other combustibles
56. Other combustibles	20.40	90.83	9.17	70.48	8.79	17.53	1.63	0.83	0.74	32.161	[38]

Table A2. Chemical characteristics of MSW (daf) used for validation

MSW groups, Subgroup and variety	Proximate analysis (wt %)			Ultimate analysis (wt %)						HHV (MJ/kg)	Reference
	A	V	FC	C	H	O	N	S	Cl
All the proximate, ultimate analysis data and HHV on dry basis are converted to dry ash-free basis. Also all HHV are converted to MJ/kg.
Food waste
1. Rice	0.42	87.74	11.84	44.2	5.73	48.75	1.20	0.1	0.02	18.048	[21]
2. Potato	–	–	–	42.09	6.5	49.06	2.12	0.23	–	16.912	[21]
3. Orange peel	2.91	76.49	20.6	48.74	5.92	43.72	1.43	0.19	–	19.024	[21]
4. Rib	38.22	61.56	0.23	51.61	6.38	31.91	9.48	0.69	–	22.716	[21]
Wood waste
5. Wood	0.82	81.64	17.54	48.35	6.62	44.7	0.04	0.29	–	20.868	[21]
6. Wood chips	3.45	81.5	15.05	49.03	5.69	44.98	0.22	0.07	–	19.255	[21]
7. Wooden chopsticks	2.18	83.45	14.37	48.79	5.16	45.7	0.3	0.04	–	19.355	[39]
8. Bamboo	1.79	81.36	16.84	51.42	6.01	41.92	0.36	0.29	–	19.974	[40]
9. Leaves	9.43	74.32	16.25	47.18	5.61	46.35	0.18	0.68	–	20.278	[21]
10. King grass	–	–	–	48.37	6.30	44.58	0.49	0.25	–	22.127	[21]
Paper waste
11. Newspaper	5.43	85.04	9.53	45.24	7.17	47.1	0.25	0.23	–	17.204	[21]
12. Printing paper	12.3	87.65	0.04	44.93	4.55	50.43	0.09	–	–	16.233	[21]
13. Cardboard	–	–	–	46.71	5.31	47.35	0.32	0.32	–	18.367	[21]
14. Toilet paper	0.52	90.47	9.01	45.18	6.13	48.32	0.25	0.11	–	17.337	[21]
15. Paper food cartons	6.93	–	–	48.07	6.55	45.04	0.16	0.17	–	18.137	[41]
16. Magazine stock	29.26	–	–	46.55	6.56	46.44	0.16	0.30	–	17.967	[41]
17. Plastic-coated paper	2.77	–	–	44.53	6.35	46.80	0.19	0.08	–	17.556	[41]
Textile
18. Cotton cloth	1.52	84.53	13.95	46.51	5.8	46.98	0.43	0.28	–	17.699	[22]
19. Cotton	1.45	86.7	11.85	46.19	6.12	47.07	0.54	0.08	–	17.500	[21]
20. Wool	–	–	–	58.53	6.48	18.23	15.12	1.65	–	23.632	[22]
21. Shoe heel and sole	30.09	–	–	76.13	10.14	11.10	0.72	1.92	–	36.676	[41]
22. leather	10.1	–	–	66.74	8.90	12.79	11.12	0.44	–	22.892	[41]
23. Upholstery	2.80	–	–	48.46	6.28	44.86	0.31	0.10	–	17.891	[41]
Plastics waste
24. PE	0.15	99.85	–	85.45	14.32	–	0.16	0.07	–	46.388	[42]
25. PP	0.16	99.84	–	84.3	14.44	1.05	0.18	0.03	–	45.842	[21]
26. PVC	0.04	95.16	4.8	38.75	5.21	–	0.22	–	55.82	22.575	[21]
27. Polyurethane	4.38	87.29	8.32	66.17	6.55	18.46	6.26	0.02	2.53	27.300	[41]
28. Plastic film	6.72	–	–	72.05	10.42	16.96	0.49	0.08	–	34.519	[41]
Rubber waste
29. Rubber	15.38	65.26	19.36	89.18	8.54	–	1.23	1.05	–	39.473	[21]
30. Tire	19.27	63.11	17.61	88.56	8.52	0.88	0.75	1.29	–	37.364	[21]

Table A3. Standard entropies at 298.15K of organic compounds relevant to MSW

Name	Formula	S0 (kJ/kg K)
Source: [3, 8, 10, 12, 17, 24].
Food
1. Allantoin	C4H6N4O3	1.233
2. Alloxan	C4H2N2O4	1.314
3. Arginine	C6H14N4O2	1.439
4. Asparagine	C4H8N2O3	1.322
5. Aspartic acid	C4H7NO4	1.279
6. Citric acid	C6H8O7	1.312
7. Creatine	C4H9N3O2	1.445
8. Cystine	C6H12N2O4S2	1.347
9. d-Glutamic acid	C5H9NO4	1.230
10. l-Lactic acid	C3H6O3	1.579
11. l-Phenylalanine	C9H11NO2	1.293
12. l-Proline	C5H9NO2	1.425
13. Maleic acid	C4H4O4	1.373
14. Malic acid	C4H6O5	1.199
15. Methionine	C5H11NO2S	1.552
16. Phenanthrene	C14H14	1.207
17. Trytophan	C11H12N2O2	1.229
18. Tyrosine	C9H11NO3	1.181
19. Uric acid	C5H4N4O3	1.030
20. Valine	C5H11NO2	1.527
21. Xanthine	C5H4N4O2	1.059
22. Stearic acid	C18H36O2	1.531
23. Taurine	C2H7NO3S	1.231
24. Urea	CH4N2O	1.742
25. Hexadecanoic acid	C16H32O2	1.764
26. Adenine	C5H5N5	1.118
27. Creatinine	C4H7ON3	1.483
28. l-Serine	C3H7O3N	1.419
29. l-Glutamine	C5H10O3N2	1.335
30. dl-Alanyl glycine	C5H10O3N2	1.460
31. Glycylglycine	C4H8N2O3	1.438
32. Alanine	C3H7NO2	1.450
33. Cysteine	C3H7NO2S	1.402
34. Dimethyl sulfone	C2H6O2S	1.509
35. d-Lactic acid	C3H6O3	1.593
36. Fumaric acid	C4H4O4	1.447
37. Guanine	C5H5N5O	1.061
38. Gycine	C2H5NO2	1.379
39. Isoleucine	C6H13NO2	1.586
40. Leucine	C6H13NO2	1.586
41. l-Glutamic acid	C5H9NO4	1.279
42. 1-Hexadecanol	C16H34O	1.864
43. Hypoxanthine	C5H4ON4	1.070
44. Glycolide	C4H4O4	1.354
Plastic
45. 1,3,5-Trioxane	C3H6O3	1.476
46. Benzophenone	C13H10O	1.346
47. Biphenyl	C12H10	1.358
1.002	48. Hexachloroethane	C2Cl6
49. Diphenyl carbonate	C13H10O3	1.300
50. Diphenyl ether	C12H10O	1.372
51. Diphenylcarbinol	C13H12O	1.330
52. Polypropylene, isotatic	(C3H6)n	1.662
53. Polypropylene, syndiotic	(C3H6)n	1.798
54. Pyromellitic dianhydride	C10H2O6	1.087
55. Naphthalene	C10H8	1.306
56. Succinic acidic	C4H6O4	1.417
57. Cyanuric acid	C3H3N3O3	1.947
58. Acetamide	C2H5NO	1.840
59. Durene	C10H14	1.166
60. Hexamethlenetetramine	C6H12N4	1.116
61. Triphenylene	C18H12	1.273
62. Hydroquinone	C6H602	1.182
63. Melamine	C3H6N6	1.251
64. Phthalic acid	C8H6O4	1.215
65. Phathalic anhydide	C8H4O3	1.405
66. Triethylenediamine	C6H12N2	1.947
67. 4,4′-diphenylmethane diisocyanate	C15H10N2O2	1.329
68. Polyisocyanurate	(C15H10N2O2)n	1.175
69. Tridecanolactone	C13H24O2	1.893
70. Polytridecanolactone	(C13H24O2)n	1.656
71. Polyvinylidene chloride	(C2H2Cl2)n	0.894
72. Polyvinyl chloride	(C2H3Cl)n	1.042
73. poly(1-butene), isotactic	(C4H8)n	1.836
74. Polystyrene	(C8H8)n	1.294
Textile
75. 3-Nitrobenzoic acid	C7H5NO4	1.227
76. 1,2-Diphenylethene	C14H12	1.39
77. Adipic acid	C6H10O4	1.504
78. 2-Methlnaphthalene	C11H10	1.547
79. Acenaphthene	C12H10	1.225
80. Anthracene	C14H10	1.164
81. 1,4-Benzoquinone	C6H4O2	1.506
82. Diphenylamine	C12H11N	1.666
83. Pyrene	C16H10	1.112
84. Thiourea	CH4N2S	1.523
85. Ammonium thiocyanate	CH4N2S	1.842
86. 3-Nitroaniline	C6H6N2O2	1.276
87. Resorcinol	C6H6O2	1.341
88. Triphenylmethane	C19H16	1.277
89. Triphenylmethanol	C19H16O	1.265
90. Isoquinoline	C9H7N	1.324
91. Acridine	C13H9N	1.161
92. 2-Nitrobenzoic acid	C7H5O4N	1.247
93. 1,3-Phenylenediamine	C6H8N2	1.429
94. Dicyanodiamide	C2H4N4	1.538
95. ε-Caprolactam	C6H11NO	1.531
96. Poly-ε-Caprolactam	(C6H11NO)n	1.529
97. Polyglycolide	(C4H4O4)n	1.304
Wood
98. l-Sorbose	C6H12O6	1.226
99. o-Cresol	C7H8O	1.530
100. Oxalic acid	C2H2O4	1.220
101. p-Cresol	C7H8O	1.547
102. Sucrose	C12H22O11	1.052
103. d-Mannitol	C6H14O6	1.309
104. Pentachlorophenol	C6HCl5O	0.946
105. Galactose	C6H12O6	1.14
106. Phenol	C6H6O	1.53
107. 2-Hydroxybenzoic acid	C7H6O3	1.29
108. Glucose	C6H12O6	1.161
109. Xylose	C5H10O5	0.956
110. 3-Hydroxybenzoic acid	C7H6O3	1.281
111. 4-Hydroxybenzoic acid	C7H6O3	1.272
112. Benzoic acid	C7H6O2	1.372
113. Catechol	C6H6O2	1.364
114. Lactose	C12H22O11	1.128
115. o-Hydroxybenzoic acid	C7H6O3	1.29
116. o-Hydroxybenzoic acid	C7H6O3	1.281
117. o-Hydroxybenzoic acid	C7H6O3	1.272

References

1. Georgieva, K., and K. Varma. 1999. Municipal solid waste incineration. World Bank Technical Guidance Report. Washington D.C.
2. Szargut, J., D. R. Morris, and F. R. Steward. 1988. Exergy analysis of thermal, chemical, and metallurgical processes. Hemisphere, New York, NY.
3. Song, G., L. Shen, and J. Xiao. 2011. Estimating specific chemical exergy of biomass from basic analysis data. Ind. Eng. Chem. Res.50:9758–9766.
4. Dincer, I., and M. A. Rosen. 2007. Exergy, energy, environment and sustainable development. Wiley, New York, NY.
5. Stepanov, V. S.1995. Chemical energies and exergies of fuels. Energy20:235–242.
6. Rant, Z.1961. Towards the estimation of specific exergy of fuels (in German). Allg. Wärmetech10:172–176.
7. Szargut, J., and T. Styrylska. 1964. Approximate evaluation of the exergy of fuels (in German). Brennst. Wärme Kraft16:589–596.
8. Eisermann, W., P. Johnson, and W. L. Conger. 1980. Estimating thermodynamic properties of coal, char, tar and ash. Fuel Process. Technol.3:39–53.
9. Shieh, J. H., and L. T. Fan. 1982. Estimation of energy (enthalpy) and exergy (availability) contents in structurally complicated materials. Energy Sources6:1–46.
10. Ikumi, S., C. D. Luo, and C. Y. Wen. 1982. Method of estimating entropies of coals and coal liquids. Can. J. Chem. Eng.60:551–555.
11. Bilgen, S., and K. Kaygusuz. 2008. The calculation of the chemical exergies of coal-based fuels by using the higher heating values. Appl. Energy85:776–785.
12. Song, G., J. Xiao, H. Zhao, and L. Shen. 2012. A unified correlation for estimating specific chemical exergy of solid and liquid fuels. Energy40:164–173.
13. Bejan, A., G. Tsatsaronis, and M. Moran. 1996. Thermal design and optimization. John Wiley, New York, NY.
14. Bilgen, S.2014. The estimation of chemical availability (Exergy) values for various types of coals in geographical regions of Turkey. Energy Sources36:830–842.
15. Rivero, R., and M. Garfias. 2006. Standard chemical exergy of elements updated. Energy31:3310–3326.
16. Kaygusuz, K.2009. Chemical exergies of some coals in Turkey. Energy Sources31:299–307.
17. Standard thermodynamic properties of chemical substances. 2000. CRC Press. Available at http://www.update.uu.se/~jolkkonen/pdf/CRC_TD.pdf (accessed 3 July 2015).
18. Kotas, T. J.1995. The exergy method of thermal plant analysis. Krieger Publishing Company, Malabar, FL.
19. Channiwala, S. A., and P. P. Parikh. 2002. A unified correlation for estimating HHV of solid, liquid and gaseous fuels. Fuel81:1051–1063.
20. Sheng, C., and J. L. T. Azevedo. 2005. Estimating the higher heating value of biomass fuels from basic analysis data. Biomass Bioenergy28:499–507.
21. Zhou, H., A. Meng, Y. Long, Q. Li, and Y. Zhang. 2014. Classification and comparison of municipal solid waste based on thermochemical characteristics. J. Air Waste Manag. Assoc.64:597–616.
22. Zhou, H., Y. Long, A. Meng, Q. Li, and Y. Zhang. 2015. Classification of municipal solid waste components for thermal conversion in waste-to-energy research. Fuel145:151–157.
23. Kathiravale, S., M. N. M. Yunus, K. Sopian, A. H. Samsuddin, and R. A. Rahman. 2003. Modeling the heating value of municipal solid waste. Fuel82:1119–1125.
24. Domalski, E. S., and E. D. Hearing. 1996. Heat capacities and entropies of organic compounds in the condensed phase. Volume III. J. Phys. Chem. Ref. Data25:1–525.
25. Pandey, K. K.1999. A study of chemical structure of soft and hardwood and wood polymers by FTIR spectroscopy. J. Appl. Polym. Sci.17:1969–1975.
26. Dietrich, F., and W. Gerd. 1983. Wood: chemistry, ultrastructure, reactions. De Gruyter, Berlin, pp. 66–181.
27. Bledzki, A. K., V. E. Sperber, and O. Faruk. 2002. Natural wood and fiber reinforcement in polymers. Smithers Rapra, Shropshire, United Kingdom. pp. 4–18.
28. Fundo, J. F., M. A. C. Quintas, and C. L. M. Silva. 2015. Molecular dynamics and structure in physical properties and stability of food systems. Food Eng. Rev.7:384–392.
29. Wrolstad, R. E.2011. Food carbohydrate chemistry. Wiley-Blackwell, West Sussex, United Kingdom.
30. Coultate, T. P.2002. Food: the chemistry of its components. Royal Society of Chemistry, Cambridge, United Kingdom, pp. 7–408.
31. Brydson, J. A.1999. Plastics materials, 7th ed. Butterworth-Heinemann, Oxford, United Kingdom. pp. 205–813.
32. Fan, Q.2005. Chemical testing of textile, 1st ed. Woodhead Publishing, Cambridge, England.
33. Gordon, S., and Y. L. Hsieh. 2007. Cotton: science and technology. Woodhead Publishing, Cambridge, England.
34. Simpson, R. B.2002. Rubber basics. Smithers Rapra, United Kingdom.
35. Wang, S.2008. Application of solid ash based catalysts in heterogeneous catalysis. Environ. Sci. Technol.42:7055–7063.
36. Song, G., L. Shen, J. Xiao, and L. Chen. 2013. Estimation of specific enthalpy and exergy of biomass and coal ash. Energy Sources35:809–816.
37. Park, K., J. Hyun, S. Maken, S. Jang, and J. W. Park. 2005. Vitrification of municipal solid waste incinerator fly ash using Browns gas. Energy Fuels19:258–262.
38. Hla, S. S., and D. Roberts. 2015. Characterisation of chemical composition and energy content of green waste and municipal solid waste from Greater Brisbane, Australia. Waste Manag.41:12–19.
39. Xiao, G., M. Ni, Y. Chi, B. Jin, R. Xiao, Z. Zhong, et al. 2009. Gasification characteristics of MSW and an ANN prediction model. Waste Manage. (Oxford)29:240–244.
40. Xiao, G., M. J. Ni, H. Huang, Y. Chi, R. Xiao, Z. P. Zhong, et al. 2007. Fluidized-bed pyrolysis of waste bamboo. J. Zhejiang Univ. Sci. A8:1495–1499.
41. Meraz, L., A. Domínguez, I. Kornhauser, and F. Rojas. 2003. A thermochemical concept-based equation to estimate waste combustion enthalpy from elemental composition. Fuel82:1499–1507.
42. Zheng, J., Y. Jin, Y. Chi, J. Wen, X. Jiang, and M. Ni2009. Pyrolysis characteristics of organic components of municipal solid waste at high heating rates. Waste Manage. (Oxford)29:1089–1094.