Fragility curves based on the numerical analysis of masonry walls against subsidence, using the Abaqus / CAE software and relying on the pulldown technique

Resumen

El hundimiento paulatino de la superficie provocado por la subsidencia es un fenómeno geológico que afecta a varios países alrededor del mundo y ha sido el causante de cuantiosos daños materiales en elementos con baja resistencia a la tensión. Las estructuras de mampostería se han vistomuy afectadas por estos asentamientos diferenciales, debido a subaja resistenciaante esta solicitación.

Con el objetivo de poder evaluar de manera precisa el estado de daño presente en estas estructuras, durante la investigación se analiza el comportamiento de muros de mampostería de diferentes dimensiones, bajo la acción de asentamientos diferenciales. Los modelos numéricos fueron desarrollados a través de una micro-modelación detallada en el software Abaqus/CAE. Los tabiques y el mortero se consideraron con un comportamiento elastoplástico Mohr-Coulomb y Drucker-Prager, unidos por elementos de interface representados en todas las juntas verticales y horizontales. Se realizó un estudio de mallas para definir la densidad de mallado óptima y su utilizó un elemento finito de primer orden. Los modelos numéricos fueron calibrados con resultados experimentales, para luego estudiar la influencia de las dimensiones del muro en su resistencia, obtener los valores de distorsión angular para los cuales la estructura comienza a tener deformaciones irreversibles, construir las curvas carga vs distorsión angular y elaborar las curvas de fragilidad del material, a través de las cuales se puede evaluar el estado de daño de un muro de mampostería, sometido a un determinado valor de distorsión angular.

Palabras clave: Curvas de fragilidad, distorsión angular, pushover, pulldown, subsidencia

Abstract

The gradual sinking of the surface caused by the subsidence is a geological phenomenon that affects several countries around the world and has been the cause of substantial material damage in elements with low stress strength. Masonry structures have been greatly affected by these differential settlements, due to their low resistance to this solicitation. In order to be able to accurately assess the state of damage present in these structures, during the investigation the behavior of masonry walls of different dimensions is analyzed, under the action of differential settlements. The numerical models were developed through a detailed micro-modeling in the Abaqus / CAE software. The partitions and mortar were considered with Mohr-Coulomb and Drucker-Pragerelastoplastic behavior, joined by interface elements represented in all vertical and horizontal joints. A mesh study was conducted to define the optimum mesh density and its use of a finite first order element. The numerical models were calibrated with experimental results, to then study the influence of the dimensions of the wall in their resistance, obtain the values of angular distortion for which the structure begins to have irreversible deformations, construct the load curves vs. angular distortion and elaborate the fragility curves of the material, through which the damage status of a masonry wall can be assessed, subject to a certain angular distortion value.

Keywords: Fragility curves, angular distortion, pushover, pulldown, subsidence

1. Introducción

El hundimiento paulatino de la superficie provocado por la subsidencia, afecta a varios países de Europa, Asia y América Latina. Este se considera un fenómeno geológico que tiene lugar debido a la extracción de sólidos (minerales) o fluidos (gas, petróleo, vapor y agua) del subsuelo y que se manifiesta en hundimientos paulatinos o súbitos de la superficie y en la generación de agrietamientos en la masa del relleno granular [1].

El primer agrietamiento por subsidencia fue documentado, en la localidad del Picacho, enel Centro-Sur de Arizona, en una zona con un alto potencial de consolidación, rodeada de montañas y con una elevada sobreexplotación de acuíferos.

Actualmente se conoce que para que se presente la subsidencia y el agrietamiento del terreno, debe existir un basamento incompresible con importantes irregularidades, abatimiento en el nivel freático y que al menos un estrato del material de relleno posea una plasticidad de media a baja [2].

1.1 Tipos de subsidencia

La subsidencia se manifiesta a través de diferentes mecanismos de deformación de la superficie y el interior de la corteza terrestre, que se pueden clasificar en dos tipos: endógenos y exógenos.

La subsidencia endógena hace referencia a los hundimientos del terreno que son el resultado de la acción de procesos geológicos del interior de la superficie terrestre (pliegues, fallas, vulcanismo y sismicidad) y la exógena se refiere a los procesos de deformación superficial relacionados con la compactación natural o antrópica de los suelos [3]. Este fenómeno también se puede clasificar en dependencia de las causas que lo desencadenan, como las actividades de extracción de mineral en galerías subterráneas, el descenso del nivel freático, la disolución natural del terreno y el lavado de materiales por efecto del agua, los procesos tectónicos y de sedimentación, la consolidación de suelos blandos u orgánicos y la extracción de fluidos (agua, petróleo o gas) acumulados en reservorios subterráneos.

1.2 Comportamiento de la mampostería frente a la subsidencia

Los daños por hundimientos diferenciales en las estructuras de mampostería dependen en gran medida de la configuración de los mismos. Esta configuración se divide en tres componentes: asentamientos uniformes en todo el elemento, más un giro que provoca inclinación o desplome y los asentamientos diferenciales en los apoyos. El Reglamento de Construcción del Distrito Federal [4] establece los límites admisibles para cada tipo de hundimiento, los que dependen de la capacidad de cada estructura para disipar las fuerzas internas. Más importante que la magnitud del asentamiento diferencial lo que se relaciona con los efectos en la estructura, es la distorsión angular, es decir, la relación de desplazamiento entre dos puntos, sobre la longitud entre ellos [2]. La velocidad con la que ocurren los hundimientos, también influye significativamente en los efectos que se presentan en la estructura.

El Reglamento de Construcción del Distrito Federal [4] establece los valores más pequeños de distorsión angular en los muros de mampostería, debido a la baja resistencia a tensión de este material.

1.3.Modelos constitutivos para el análisis de la mampostería

1.3.1. Criterios de rotura biaxial

La modelación numérica de la mampostería requiere un análisis detallado del modelo del material, teniendo en cuenta su gran influencia en el tipo de fallo que presenta el elemento estructural en estudio y considerando las características anisótropas de la fábrica. Varios investigadores han propuesto diferentes simplificaciones en el análisis, cuyo objetivo principal es obtener un modelo que refleje con determinada precisión, las características y el comportamiento real de la mampostería.

El criterio de rotura propuesto por Page en 1980, 1981 y 1983 [5], se derivó de una extensa campaña experimental a escala reducida de paneles de ladrillo con mortero de cemento y cal, sometidos a compresión biaxial, tensión - compresión y tensión – tensión, donde seccionó la superficie de falla esfuerzo cortante último vs esfuerzo normal en tres etapas, la falla en tensión, la falla por cortante puro y la falla combinada entre el cortante y la tensión en el tabique. Además fue el primero en utilizar elementos de interfaz para modelar el comportamiento no lineal de las juntas de mortero, considerando el tabique como un elemento homogéneo elástico e isótropo.

Lourenco realiza un análisis donde considera un comportamiento no lineal de la interface ladrillo-mortero, que tiene en cuenta la falla a tensión, falla a cortante y falla a compresión [6]. A las piezas de mampostería les asigna propiedades que permanecen elásticas y que incluyen únicamente la falla a tensión en la mitad de la pieza. Oliveira en el año 2003 realiza una extensión del modelo de Lourenco, para poder modelar el comportamiento de estructuras de mampostería en cargas cíclicas y Van Zijl en 2004 propone un modelo para representar el ángulo de dilatación, lo que complementa el modelo de Lourenco [5].

Mann y Muller desarrollaron una teoría para predecir la resistencia a cortante de la mampostería bajo distintas condiciones de carga y teniendo en cuenta la influencia del ladrillo, el mortero, el coeficiente de fricción y la cohesión en la interface. Su teoría predice bajo que combinación de esfuerzos normales y cortantes puede ocurrir la rotura, asumiendo que las juntas verticales no transmiten esfuerzos de corte y que los esfuerzos tangenciales que actúan en las juntas horizontales producen momentos en las uniones ladrillo-mortero [7].

Su teoría fue probada sobre un modelo construido con juntas de goma, para reproducir de una manera más clara las deformaciones. Finalmente, definieron tres criterios de rotura: uno en las juntas horizontales que se presentaba de manera escalonada entre juntas verticales y horizontales, que dependería del coeficiente de fricción y la cohesión en la unión, otro producido por tensión excesiva sobre las piezas, que se manifiesta con la fractura de los ladrillos y por último la rotura a compresión de la mampostería, que se produce cuando este esfuerzo es superior a la resistencia a compresión del material.

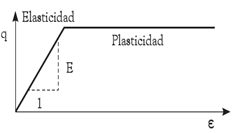
El criterio Morh-Coulomb fue uno de los primeros utilizados por la mecánica de suelos para describir el comportamiento elasto-plástico de materiales frágiles como rocas, mampostería, concreto y suelos. El modelo considera un conjunto de funciones que establecen el límite entre el comportamiento elástico y plástico del material (Figura 1) y define el espacio de esfuerzos principales, como una superficie de fluencia fija que representa un comportamiento del material perfectamente elástico para valores de esfuerzos menores al límite de fluencia [8]. Su formulación involucra dos elementos generales: la elasticidad perfecta y la plasticidad asociada al desarrollo de deformaciones plásticas o irreversibles.

Figura 1. Formulación básica del modelo elastoplástico perfecto Morh-Coulomb [8]

El modelo constitutivo se considera una aproximación de primer orden al comportamiento elastoplástico isotrópico no lineal del suelo, a partir de la ley de Hooke y el criterio de falla Mohr-Coulomb

${\textstyle \sigma ={D}^{e}{\epsilon }^{e}}$

(1)

donde ${\textstyle \sigma }$ son las tensiones normales, ${\textstyle {D}^{e}}$ la matriz de rigidez elástica del material y ${\textstyle {\epsilon }^{e}}$ las deformaciones elásticas.

Para las deformaciones irreversibles incorpora una función de potencial plástico, que evita una sobreestimación del fenómeno de dilatancia. De esta forma, la formulación del modelo exige cinco parámetros básicos de entrada: el módulo de Young, la relación de Poisson, la resistencia por cohesión del suelo, el ángulo de fricción interna y el ángulo de dilatancia.

1.3.2 Fenómeno del reblandecimiento en la mampostería

Un análisis adecuado de la mampostería debe tener en cuenta el fenómeno del reblandecimiento del material.Este fenómeno consiste en una disminución gradual de las propiedades mecánicas bajo un incremento sostenido de la carga aplicada, bien sea para un elemento o para una estructura [6]. Es una característica observada en materiales heterogéneos, en los cuales el fallo se presentaa través de un proceso de degradación, que se manifiesta en microfisuras internas, que comienzan a aumentar su tamaño bajo la acción de las cargas aplicadas, hasta convertirse en grandes fisuras que provocan el colapso.

En el caso de la mampostería, la influencia del fenómeno reblandecimiento es de suma importancia para comprender su comportamiento como material compuesto, debido a que el mortero contiene microfisuras, incluso antes de comenzar a aplicarse las cargas, que son producto del acortamiento durante el curado, mientras que los ladrillos de arcilla, contienen discontinuidades propias de su proceso de horneado. Las tensiones y fisuras iniciales, así como las variaciones de la rigidez y resistencia interna, causan un crecimiento progresivo de la fisuración cuando el material es sujeto a deformación progresiva.

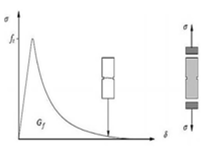
En un ensayo de deformación controlada el crecimiento de las macrofisuras produce reblandecimiento. En el fallo a cortante también se observa manifestado el fenómeno de reblandecimiento, a través de la degradación de la cohesión en el modelo de fricción de Coulomb. El proceso de ablandamiento para la falla a tensión puede representarse con la energía de fractura en tensión $G_{f}$ (Figura 2).

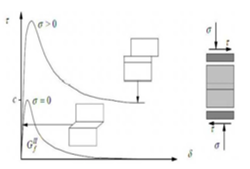
(a) Prueba a tensión uniaxial	(b) Prueba a corte con distintos niveles de carga axial
Figura 2. Comportamiento típico de materiales cuasi-frágiles y definición de la energía de fractura $G_{f}$ [6]

1.4 Análisis numérico de la mampostería

Para el análisis de la mampostería, se han utilizado una amplia diversidad de métodos numéricos. Un ejemplo es el análisis límite para conocer la carga máxima de la estructura. Los investigadores Orduña y Lourenco realizaron modelos, considerando bloques rígidos para determinar la carga máxima que puede resistir un muro sin refuerzo, cargado lateralmente sin juntas de mortero [5]. Casolo en el año 2004 [5], propone un modelo que representa al material como un elemento rígido unido por resortes, con el objetivo de evaluar el comportamiento dinámico global de la estructura en el rango elástico. Giamundo en el año 2014 [5], utiliza el método de los elementos distintos para estudiar el comportamiento de elementos de mampostería sin refuerzo. Pero, sin duda, el método de los elementos finitos es el método numérico de mayor aceptación y utilización por la comunidad científica en los últimos años para analizar el comportamiento de las obras de fábrica.

1.4.1 Análisis numérico de la mampostería

El método de elementos finitos permite solucionar problemas de ingeniería que requieren el empleo de geometrías complejas y cargas no distribuidas. Este procedimiento aproxima el comportamiento de una estructura con infinitos grados de libertad, por el de otra con aproximadamente las mismas propiedades físicas y geométricas, pero con un número finito de grados de libertad [9].

El análisis de la mampostería mediante el método de elementos finitos presenta dos enfoques conocidos como macromodelación y micromodelación simplificada o detallada.

Micromodelación detallada: los ladrillos y el mortero están representados por elementos continuos, mientras que el comportamiento de la interfaz ladrillo-mortero, está representado por elementos discontinuos.

Micromodelación simplificada: los materiales están representados por un elemento continuo y el comportamiento de las juntas de mortero está representada por discontinuidades.

Macromodelación: los ladrillos, el mortero y las interfaces, están representados globalmente por el mismoelemento [10].

1.4.1.1 Análisis Pushover y Pulldown

Pushover

El análisis pushover es aquel en el que el modelo de la estructura, se somete a una carga horizontal monotónica, previamente definida, la cual se va incrementando hasta que se alcance la deformación máxima considerada o que la estructura falle [11]. El propósito del análisis pushover, es evaluar el desempeño estructural, estimando la resistencia y capacidades de deformación usando un análisis estático no lineal y comparando estas capacidades con las demandas en los niveles de desempeño correspondiente.

El análisis pushover se representa por medio de la curva de capacidad de carga última de la estructura y resulta un método sencillo y muy preciso que permite realizar una evaluación directa de la respuesta de una estructura, sometidas a desplazamientos horizontales, generados por sismos de magnitud considerable.

Pulldown

El efecto de pulldown en una estructura, es considerado cuando alguno de los apoyos sufre un desplazamiento vertical. Este tipo de análisis resulta ser similar al que ocurre cuando se realiza un análisis pushover, la diferencia radica en la dirección en que la se evalúan los desplazamientos.

En el análisis pushover se evalúan desplazamientos horizontales, mientras que en el análisis pulldown estos se consideran en sentido vertical, los que pueden generarse por diferentes causas, siendo la más común los asentamientos en el terreno. Una característica importante, en este tipo de asentamiento vertical, es la velocidad de los desplazamientos, que depende del tipo de deslizamiento del suelo que afecte a la estructura.

1.5 Definición del modelo constitutivo propuesto

El análisis numérico de la mampostería se realizó utilizando la micromodelación detallada, que fue descrita por Lourenco en 1996 [6], como la representación tanto del tabique como del mortero, con interfaces definidas por elementos de interfaz. Se utilizó el software Abaqus/Cae versión 6.14.

El comportamiento de los tabiques se consideró elastoplástico, definido por el modelo constitutivo Mohr-Coulomb y sus cinco parámetros básicos de entrada: el módulo de Young, la relación de Poisson, la resistencia por cohesión, el ángulo de fricción interna y el ángulo de dilatancia, cuyos valores se encuentran descritos en la Tabla 6 de la sección 2.2.2 del presente artículo. El material fue representado como un elemento deformable, homogéneo e isótropo, con las mismas propiedades en todos los sentidos.

El criterio de Mohr-Coulomb ha sido utilizado por muchos investigadores para describir el comportamiento de la mampostería sometida a diferentes solicitaciones. El modelo, como ya se había descrito en la sección 1.3.1 del presente artículo, involucra dos elementos generales: la elasticidad perfecta y la plasticidad asociada al desarrollo de deformaciones plásticas o irreversibles.

El mortero fue analizado como un elemento deformable, homogéneo e isótropo y las propiedades del material se representaron utilizando el modelo de daño plástico Drucker-Prager, el cual ha sido utilizado en varias investigaciones para simular el comportamiento elastoplástico del concreto (Maharaj en 2003, Broche en 2005 y Bonilla en 2008).

El criterio Drucker-Prager reproduce la falla en el concreto por la no disipación de la energía en tensión, lo que genera un modelo numérico con cierta suavidad, que no presenta muchos problemas en el cálculo, aunque en su versión clásica no reproduce al cien por ciento el comportamiento real del concreto [12]. El software Abaqus/CAE considera una modificación del criterio original, recomendando un valor igual a 0.8 para el rango de esfuerzos que genera deformación plástica [12].

Otro parámetro que utiliza el modelo es la tensión de fluencia plástica para diferentes valores de resistencia a compresión del concreto, la cual se define por la ec.(2). Los valores de tensión de fluencia plástica, obtenidos a través de la ec.(2), fueron graficados por el investigador Kmiecik en el año 2011

${\textstyle {\xi }_{c}^{pl}={\xi }_{c}^{in}-e\displaystyle {\frac {{d}_{c}}{(1-{d}_{c})}}\cdot \displaystyle {\frac {{\sigma }_{c}}{{E}_{0}}}}$

(2)

donde ${\textstyle {d}_{c}}$ es la tensión de fluencia plástica, ${\textstyle {\xi }_{c}^{pl}}$ la deformación plástica, ${\textstyle {\xi }_{c}^{in}}$ la deformación inelástica, ${\textstyle {E}_{0}}$ el módulo de elasticidad y ${\textstyle {\sigma }_{c}}$ la tensión de compresión.

El criterio establece valores de deformación plástica absoluta para el análisis de concretos con plasticidad variable, donde se tiene en cuenta la influencia de la temperatura. En la presente investigación se consideran valores constantes de plasticidad, lo que se traduce en una deformación plástica absoluta igual a cero. El modelo también utiliza como parámetros básicos de entrada el ángulo de fricción interna y el ángulo de dilatancia del concreto. El ángulo de fricción ($\phi$) y el ángulo de dilatancia ($\Psi$) se consideran igual a cero para concretos que no presentan daños y toman su valor máximo ($\phi =36^{\rm {o}}$ y ${\textstyle \Psi =15^{\rm {o}}}$) cuando este se encuentra defectuoso [9].

Además de los cinco parámetros básicos definidos por el criterio de Drucker-Prager, también se consideró el módulo de elasticidad, el coeficiente de Poisson y la densidad del concreto.

En la interfaz ladrillo-mortero se considera un comportamiento no lineal, con cierta rigidez normal y tangencial, que permite la falla a tensión y la falla a cortante de las juntas verticales y horizontales.

Las interacciones responden al modelo de Lourenco de 1996, modificado por Oliveira en el año 2003 [13], quien propone dos ecuaciones para determinar los valores de rigidez normal y tangencial de las juntas, a partir de un valor de carga aplicada (ecs. (3) y (4))

${K}_{n}$= ${\textstyle \displaystyle {\frac {1}{h\ast (\displaystyle {\frac {1}{{E}_{m}}}-{\frac {1}{{E}_{p}}})}}}$

(3)

donde ${\textstyle {K}_{n}}$ es la rigidez normal de la junta, $h$ la altura del bloque, $E_{m}$ el módulo de elasticidad del muro y $E_{p}$ el módulo de elasticidad de la pieza

${K}_{s}=\displaystyle {\frac {{K}_{n}}{2\left(1+v\right)}}\,$

(4)

donde ${\textstyle {K}_{s}}$ es la rigidez tangencial de la junta y $v$ el coeficiente de Poisson.

Al finalizar su campaña experimental, Oliveira obtiene los valores de rigidez normal y tangencial en las juntas de mortero, sometidas a un determinado valor de carga (Tabla 1).

Tabla 1. Rigideces calculadas para las juntas de mortero [13]

Walls	${\textstyle {K}_{n}}$ (N/mm3)	${\textstyle {K}_{s}}$ (N/mm3)
SW.30	5.87	2.45
SW.100	8.08	3.37
SW.200	11.4	4.73
SW.250	13	5.43

El software Abaqus/Cae considera los valores de rigidez normal y tangencial de las juntas en el modelo de interacción Cohesive Behavior, mientras que los mecanismos de falla en la interfaz se representan por el modelo Damage.

Modo de falla a tensión

Se asume un comportamiento elástico en la interfaz, hasta alcanzar el esfuerzo máximo de tensión y luego se considera el ablandamiento del material, definido con la energía de fractura en tensión ${\textstyle {G}_{f}}$. Estos parámetros han sido caracterizados por varios investigadores durante sus campañas experimentales. Durante la presente investigación, se utilizaron los valores propuestos por Alfonso Hernández Bueno en el año 2014 [14], debido a que no se contaban con las pruebas experimentales para obtener estos parámetros.

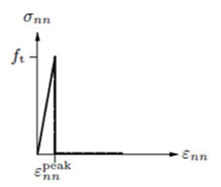
La energía de fractura en tensión corresponde a una expresión utilizada por Hernández Bueno [14], a partir del esfuerzo máximo en tensión (Figura 3 )

${G}_{f}=\displaystyle {\frac {1}{2}}{f}_{t}{\epsilon }_{nn}^{pico}h$

(5)

donde ${\textstyle {G}_{f}}$ es la energía de fractura en tensión, ${\textstyle {f}_{t}}$ el esfuerzo máximo en tensión, ${\textstyle {\epsilon }_{nn}^{pico}}$ la deformación pico ${\textstyle {\epsilon }_{nn}^{pico}=\displaystyle {\frac {{f}_{t}}{E}}}$, $E$ el módulo de elasticidad y h el ancho de fisura.

Figura 3. Tensión deformación para un comportamiento frágil [14]

Modo de falla a cortante

Para representar el mecanismo de fallo a cortante se consideró el criterio de Mohr-Coulomb, que tiene en cuenta una reducción de la cohesión y la fricción debido al efecto del reblandecimiento. Los valores de cohesión y la energía de fractura al corte, también fueron tomados de la investigación desarrollada por Alfonso Hernández Bueno en el año 2014 [14].

Los valores de cohesión y fricción que consideran el reblandecimiento del material, fueron obtenidos por Hernández Bueno utilizando las ecs.(6) y (7)

$c\left(\sigma ,K\right)={c}_{0}\ast {e}^{\displaystyle {\frac {{c}_{0}}{G{\acute {}}{\acute {}}f\,}}}$

(6)

donde ${\textstyle c\left(\sigma ,K\right)}$ es la cohesión reducida por el reblandecimiento, ${\textstyle {c}_{0}}$ la cohesión inicial de la interface y G´´f la energía de fractura al corte

${\textstyle \varnothing \left(\sigma ,K\right)={\varnothing }_{0}+{(\varnothing }_{R}-}$${\varnothing }_{0})\displaystyle {\frac {{c}_{0}-c}{{c}_{0}}}$

(7)

donde ${\textstyle \varnothing \left(\sigma ,K\right)}$ es la fricción reducida por el reblandecimiento, ${\textstyle {\varnothing }_{0}}$ la fricción inicial de la interface, ${\textstyle {\varnothing }_{R}}$ la fricción residual, c la cohesión reducida por el reblandecimiento y ${\textstyle {c}_{0}}$ la cohesión inicial de la interface.

Los parámetros de cohesión y de fricción se encuentran por regresión lineal de los datos experimentales de cortante, mientras que la energía de fractura se determina por la integración de la respuesta de tensión-ancho de grieta [14].

2. Metodología

Metodología numérica

Como primer paso en la metodología numérica, se propone la obtención de un modelo geométrico en el software Abaqus/CAE, enfocado en la micro-modelación detallada, donde los ladrillos y el mortero serán representados como elementos independientes, ensamblados hasta alcanzar las dimensiones deseadas del muro. El efecto de las interacciones será tomado en cuenta en ambos sentidos, en todas las uniones del elemento. Las dimensiones del modelo corresponderán a las campañas experimentales I y III desarrolladas por Daniel Charry Ablanque en 2009 [15] y que se encuentran descritas en la sección 2.1 del presente artículo.

Los modelos geométricos serán analizados bajo la acción de dos pasos de carga, comenzando por una carga vertical que será aplicada en forma de presión en toda la sección transversal del muro y luego comenzará la acción de una carga horizontal, que irá aumentando paulatinamente, hasta alcanzar la falla del elemento.

Los resultados numéricos serán comparados con los experimentales obtenidos por Daniel Charry Ablanque en su tesis de doctorado [15], con el objetivo de obtener un modelo calibrado, cuyo comportamiento describa de manera detallada el comportamiento de un muro de mampostería ante estas solicitaciones. El error relativo entre los modelos, se obtuvo a través de la ec.(8) descrita en la sección 2.1 del presente artículo, teniendo en cuenta las curvas carga vs desplazamiento, correspondientes a ambos análisis.

A partir del modelo calibrado, se construyen muros de 1m x 1m, que serán analizados bajo la acción de asentamientos diferenciales, los que serán simulados utilizando la técnica del pulldown. Para ello se considera un comportamiento elastoplástico de las piezas y el mortero, unidos por elementos de interfaz que permiten la falla a tensión y cortante de la junta. Los muros se empotraron en la mitad de su base y se colocaron cargas en el extremo libre de 250 y 300 kN/m². Al concluir el análisis se observan las zonas más esforzadas del elemento, se describen los mecanismos de falla presentes en el muro, se obtienen los valores de distorsión angular y se construyen las curvas de carga vs distorsión angular.

Luego se construyen muros de dimensiones variables (1m x 1m, 1.5m x 1.5m y 2m x 2m) sometidos a una carga de 350 kN/m², aplicada igualmente en el extremo libre del modelo y donde se observó la influencia de las dimensiones en la resistencia del elemento, se obtuvieron las zonas de mayor concentración de esfuerzos, los valores de distorsión angular, los principales mecanismos de falla y las curvas de carga vs distorsión angular.

Posteriormente, se utilizaron estos valores para elaborar las curvas de fragilidad de los elementos, a través de una distribución de probabilidad de logaritmo normal, presentada en la sección 4 del presente artículo. Dichas curvas representan la probabilidad de ocurrencia de daño leve, moderado y severo, en muros de mampostería sometidos a diferentes valores de distorsión angular.

2.1 Calibración del modelo numérico

Para la calibración de los modelos numéricos, se utilizaron los resultados de las campañas experimentales I, y III desarrolladas por Daniel Charry Ablanque [15] en su tesis de doctorado. Durante la campaña experimental I el autor analizó 10 muros de 1.20m x 1.0m, mientras que en la III consideró 15 muros a escala reducida de 0.3m x 0.25m, sometidos a diferentes estados de carga. Las propiedades de los materiales las obtuvo en ensayos independientes que realizó sobre las piezas y el mortero.

Para la aplicación de las cargas, utilizó un actuador servo - hidráulico (MTS) integrado a un marco, que generaba las cargas verticales y un gato hidráulico acoplado a un contrafuerte para las horizontales. En cada una de las campañas, aplicó las cargas de manera uniforme, comenzando con la vertical a una velocidad de 1 kN/s y una vez concluida, comenzaba la horizontal a una velocidad de 0.205 kN/s. El autor consideró varias combinaciones de carga, hasta provocar el fallo de los muros.

Durante la calibración del modelo numérico, se utilizaron las características geométricas de las campañas experimentales I y III, desarrolladas por Charry Ablanque [15]. Los materiales fueron considerados deformables, homogéneos e isótropos y se utilizó la técnica de micromodelación detallada. Se utilizaron los modelos constitutivos Mohr-Coulomb para los tabiques y Drucker - Prager para el mortero. Las juntas fueron representadas considerando la falla a tensión y cortante de la unión, con modelos definidos en Abaqus/CAE para comportamiento normal (Normal Behavior) y tangencial (Tangencial Behavior) de la interfaz. Estos criterios exigen como parámetros de entrada, únicamente el coeficiente de fricción de la unión.

El coeficiente de fricción de las juntasse consideró igual a 1 para la campaña experimental I y 0.82 para la campaña experimental III, lo que corresponde a los resultados obtenidos en el ensayo biaxial de corte desarrollado por Charry Ablanque en el año 2009 [15].

Durante la calibración, solo se consideró una combinación de carga y esta fue aplicada en dos pasos, siguiendo la descripción del ensayo realizado por Charry Ablanque [15] en su tesis de doctorado.

La diferencia porcentual o error relativo entre los modelos se determinó utilizando la ec.(8) y se consideró aceptable hasta un error del 15%

${\textstyle {Dif}_{\%}={\frac {{U}_{e\,i}-{U}_{m\,i}}{{U}_{m\,i}}}\,}$

(8)

donde ${\textstyle Ue(i)}$ es el desplazamiento correspondiente a la carga (i) en el ensayo experimental y ${\textstyle {U}_{m}(i)}$ el desplazamiento correspondiente a la misma carga en la modelación matemática.

Para determinar la diferencia porcentual, se utilizó el desplazamiento lateral correspondiente a la máxima carga horizontal aplicada, tomado en el nodo del extremo opuesto a la zona de aplicación de la carga.

2.1.1 Calibración campaña experimental I

Charry Ablanque [15] durante su primera campaña experimental, analizó 10 muros de 1.20m x 1.0m, sometidos a 10 estados de carga diferentes. Las probetas estaban compuestas por 16 hiladas de ladrillo macizo de 290 x 140 x 50mm, con juntas de mortero de 10 mm y una resistencia a la compresión de 11.6 MPa.

El comportamiento de los tabiques fue considerado elastoplástico, tomando en cuenta los cinco parámetros básicos del criterio Mohr-Coulomb y la densidad del material, cuyos valores corresponden a los ensayos experimentales realizados por Charry Ablanque en su tesis de doctorado [15] (Tabla 2).

Tabla 2. Propiedades de los tabiques campaña experimental I [15]

Módulo de elasticidad (MPa)	Coeficiente de Poisson	Cohesión (MPa)	Ángulo de fricción (°)	Ángulo de dilatancia (°)	Densidad (kN/m3)
3760.03	0.15	0.32	45	15	13

El mortero fue analizado considerando el modelo de daño plástico Drucker–Prager, teniendo en cuenta las especificaciones planteadas en la sección 1.5 del presente artículo (Tabla 3).

Tabla 3. Propiedades del mortero campaña experimental I [15]

Deformación plástica	Tensión de fluencia plástica (MPa)	Ángulo de fricción (°)	Ángulo de dilatancia (°)	Deformación plástica absoluta
0.8	5	0	0	0

El módulo de elasticidad del mortero se consideró de 3760.03 MPa, el coeficiente de Poisson de 0.2 y la densidad de 20 kN/m³. El modelo se representó empotrado en su base, con giro superior libre y carga máxima de 150 kN (vertical) y de 80 kN (horizontal), solicitaciones con las que se observó una mayor concentración de esfuerzos en el extremo superior del muro, donde fue aplicada la carga horizontal, los que se fueron distribuyendo de manera escalonada, con una inclinación de aproximadamente 45° hasta la base del elemento.

Se puede concluir que los esfuerzos comienzan a manifestarse en las juntas horizontales y que al aumentar las solicitaciones, estos se van distribuyendo escalonadamente hacia las unidades, viéndose menos afectadas las juntas verticales (Figura 4).

Figura 4. (a) Campaña experimental I 150V80H [15]. (b) Modelo numérico 150V80H (elaboración propia)

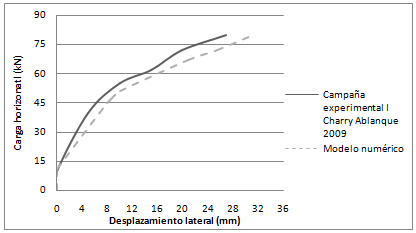
La diferencia porcentual calculada entre el modelo numérico y el experimental, para una carga horizontal de 80 kN, fue de 13.57%, considerando desplazamientos laterales de 31.24 mm en el modelo numérico y de 27 mm en el experimental (Figura 5).

Figura 5. Comparación entre la carga horizontal y el desplazamiento lateral, correspondientes a la campaña experimental I de Charry Ablanque (2009) y el modelo numérico (elaboración propia)

El análisis fue realizado utilizando un elemento finito de primer orden C3D8, con una densidad de malla de 2.5 cm. Los resultados del modelo se consideran aceptables y por tanto el modelo calibrado.

2.1.2 Calibración campaña experimental III

Charry Ablanque [15] durante su tercera campaña experimental analizó 15 muros a escala reducida 1:4 de 0.3m $\times$ 0.25m, sometidos a 15 estados de carga diferentes. Las probetas estaban compuestas por ladrillos macizos de $72.5\times 35\times 1.25$mm, con juntas de mortero de 2.5mm y una resistencia a la compresión de 0.46 MPa. El comportamiento de los tabiques fue considerado elastoplástico, tomando en cuenta los cinco parámetros básicos del criterio Mohr-Coulomb, cuyos valores corresponden a los ensayos experimentales realizados por Charry Ablanque en su tesis de doctorado (Tabla 4). La densidad del material fue tomada igual 13 kN/m³.

Tabla 4. Propiedades de los tabiques campaña experimental III [15]

Módulo de elasticidad (MPa)	Coeficiente de Poisson	Cohesión (MPa)	Ángulo de fricción (°)	Ángulo de dilatancia (°)
5246.40	0.15	0.46	33.42	3.42

El mortero fue analizado considerando el modelo de daño plástico Drucker–Prager, teniendo en cuenta las especificaciones planteadas en la sección 1.5 del presente artículo (Tabla 5).

Tabla 5. Propiedades del mortero campaña experimental III [15]

Deformación plástica	Tensión de fluencia plástica (MPa)	Ángulo de fricción (°)	Ángulo de dilatancia (°)	Deformación plástica absoluta
0.8	0.23	0	0	0

El módulo de elasticidad del mortero se consideró de 5246.40 MPa, el coeficiente de Poisson de 0.2 y la densidad de 20 kN/m³.

Para la calibración, se consideraron 9 kN de carga vertical máxima y 5 kN horizontal, con giro superior libre y base empotrada. Al comenzar la aplicación de carga se observa la mayor concentración de esfuerzos en las juntas horizontales, los que se van extendiendo hacia las unidades de manera escalonada, desde el extremo superior del muro hasta la base del elemento, viéndose menos afectadas las juntas verticales.

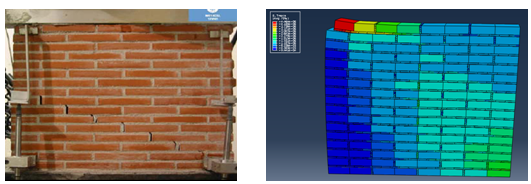
En el modelo numérico, se puede observar el deslizamiento en las juntas horizontales y el fallo a tensión de los ladrillos (Figura 6).

Figura 6. (a) Campaña experimental III9V5H [15]. (b) Modelo numérico 9V5H (elaboración propia)

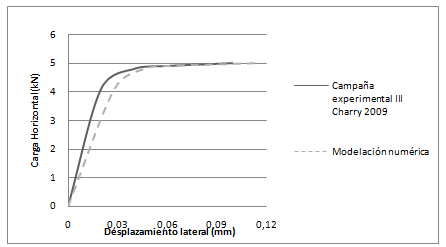
La diferencia porcentual entre el modelo numérico y el experimental para una carga horizontal de 5 kN, fue de 12.39%, considerando desplazamientos laterales máximos de 0.114mm en el modelo numérico y de 0.1mm en el experimental (Figura 7).

Figura 7. Comparación entre la carga horizontal y el desplazamiento lateral, correspondientes a la campaña experimental III de Charry Ablanque (2009) y el modelo numérico (elaboración propia)

El análisis fue realizado utilizando un elemento finito de primer orden C3D8, con una densidad de malla de 2.5cm. Los resultados del modelo se consideran aceptables y por tanto el modelo calibrado.

2.2 Diseño de experimento

Una vez calibrado el modelo numérico, se establecen las variables dependientes e independientes que se estudiarán en la primera ysegunda etapa de investigación.

En la primera etapa se considerará un muro aislado, no confinado y no reforzado de 1m x 1m, que se someterá a diferentes valores de carga, la cual se irá incrementando hasta alcanzar la falla del elemento. Esta carga se aplicará en la mitad de la base del muro, simulando un asentamiento diferencial.

En la segunda etapa se analizarán tres muros aislados, no confinados y no reforzados de dimensiones variables (1m $\times$ 1m, 1.5m $\times$ 1.5m y 2m $\times$ 2m) sometidos al mismo valor de carga, con el objetivo de analizar la influencia de las dimensiones del muro, en la resistencia a los hundimientos diferenciales de la mampostería.

Variables independientes

Primera etapa: valores de la carga.

Segunda etapa: dimensiones del muro.

Variable dependiente

Primera etapa: distorsión angular.

Segunda etapa: distorsión angular.

2.2.1 Geometría

Los muros se considerarán compuestos por piezas macizas de tabique rojo recocido de 29 $\times$ 14 $\times$ 7cm, con juntas de mortero de 1.0cm. Sus dimensiones fueron especificadas en la sección 2.2 del presente artículo.

2.2.2 Modelación de los materiales

Los modelos constitutivos empleados para caracterizar el comportamiento de los elementos de la mampostería y su interface, fueron descritos en la sección 1.5 del presente artículo. Es importante mencionar que estos deben basarse en las características físico - mecánicas de las partículas que lo componen y, por tal razón, deben ser capaces de reproducir los giros, deslizamientos y deformaciones que en ellas ocurren. Sin embargo, en el estado del conocimiento actual, no existe un modelo que cumpla con todas estas exigencias, aunque muchos de ellos permiten obtener aproximaciones muy cercanas a la realidad [16].

Tabiques

El comportamiento de los tabiques se reprodujo a través del modelo constitutivo Mohr-Coulomb, cuyos parámetros básicos son el ángulo de fricción, la cohesión, el ángulo de dilatancia, el módulo de elasticidad y el coeficiente de Poisson. Además, en el modelo, se tuvo en cuenta el valor de la densidad de las piezas.

Se consideró un ángulo de fricción de 35°, una cohesión de 0.4 MPa y un ángulo de dilatancia de 0°. Estos valores fueron obtenidos de las recomendaciones de E. Dumova-Jovanoskay S. Churilov para tabiques de arcilla [17].

El módulo de elasticidad, el coeficiente de Poisson y la densidad de los tabiques se obtuvieron de las Normas Técnicas Complementarias del Distrito Federal (Tabla 6) [18].

Tabla 6. Propiedades de los tabiques (elaboración propia)

Densidad (kN/m3)	Módulo de Elasticidad (kN/m2)	Coeficiente de Poisson
13	4170000	0.15

Mortero

La simulación del comportamiento del mortero se realizó a través del modelo de daño plástico Drucker-Prager. Este modelo constitutivo exige cinco parámetros de entrada básicos, el ángulo de fricción interna, el ángulo de dilatancia, el rango de esfuerzos que origina deformación plástica, la tensión de fluencia y la deformación plástica absoluta, además del módulo de elasticidad, el coeficiente de Poisson y la densidad del material.

El ángulo de fricción y el ángulo de dilatancia fueron tomados de las especificaciones del modelo constitutivo presentadas en la sección 1.5 del presente artículo. Para este análisis, se considera un mortero sin daños estructurales, por lo que el ángulo de fricción y el ángulo de dilatancia son considerados igual a 0.

El rango de esfuerzos que origina deformación plástica (kp) varía entre cero y uno. Para kp=0, no se producen daños en el material y para kp=1 se establece el daño plástico en su totalidad [9]. El software Abaqus/CAE considera una modificación del criterio original, estableciendo el rango de esfuerzos que genera deformación plástica igual a 0.8, valor que se considera en el análisis estructural.

La tensión de fluencia plástica depende de la resistencia a compresión del mortero, para una resistencia de 8 MPa, la tensión es de 4 MPa [12], mientras que la deformación plástica absoluta se considera nula para valores constantes de plasticidad que no tienen en cuenta la influencia de la temperatura. El módulo de elasticidad, el coeficiente de Poissony la densidad del mortero, se obtuvieron de las Normas Técnicas Complementarias del Distrito Federal (Tabla 7) [18].

Tabla 7. Propiedades del mortero (elaboración propia)

Densidad (kN/m3)	Módulo de Elasticidad (kN/m2)	Coeficiente de Poisson
20	4170000	0.2

2.2.3 Interacciones

El análisis de la interface ladrillo-mortero se realizó teniendo en cuenta el fallo a tensión y cortante de las juntas verticales y horizontales. Los criterios utilizados fueron descritos en la sección 1.5 del presente artículo. Las interacciones pieza-mortero se definen con un contacto de superficie a superficie (surface to surface), considerando los parámetros elásticos (rigidez normal y tangencial) e inelásticos (energías de fractura en tensión y cortante) de las juntas.

Parámetros elásticos

Las interacciones responden al modelo de Lourenco de 1996 [6], modificado por Oliveira en el año 2003 [13], quien utiliza métodos analíticos para determinar los parámetros de rigidez de las juntas mortero-ladrillo (ecs.(3) y (4)), determinando que estos dependen fundamentalmente de la carga vertical de pre-compresión [13]. En este caso, se consideró la rigidez normal igual a 420.3 N/mm³ y la rigidez tangencial igual a 195.49 N/mm³, valores recomendados por Oliveira para cargas mayores de 250 kN (Tabla 1).

El software Abaqus/Cae considera los valores de rigidez normal y tangencial de las juntas, en el modelo de interacción Cohesive Behavior.

Parámetros inelásticos

Los parámetros inelásticos de las juntas se obtuvieron de la investigación realizada Hernández Bueno en el año 2014 [14]. Los criterios utilizados para describir los mecanismos de falla en tensión y cortante, así como el reblandecimiento de la mampostería, fueron descritos en la sección 1.5 del presente artículo. En el software se utilizó el modelo de interacción Damage, que considera el esfuerzo máximo y la energía de fractura en tensión, así como la cohesión reducida por el reblandecimiento y la energía de fractura al corte (Tabla 8).

Tabla 8. Parámetros inelásticos de las juntas [14]

Tensión		Cortante
Esfuerzo máximo ft (MPa)	Energía de fractura Gf (MPa)	Cohesión reducida por el reblandecimiento c (MPa)	Energía de fractura G´´f (MPa)
0.55	0.13	0.4	0.045

2.2.4 Mallado

Tipo de elemento finito

El nivel de precisión en el análisis estructural con el método de los elementos finitos, depende del tipo y densidad de mallado que se le aplique al modelo. El software Abaqus/CAE utiliza elementos finitos tetraédricos, de cuña y hexaédricos de primero y segundo orden para el análisis. El análisis matemático con elementos finitos de interpolación cuadrática (segundo orden), es más preciso, pero requiere equipos de alta velocidad y capacidad de procesamiento. Sin embargo, el elemento finito de primer orden del tipo C3D8, requiere menos tiempo de cálculo y ha sido utilizado satisfactoriamente por varios investigadores, por tanto se utilizará en el mallado de los muros mampostería.

Densidad de malla

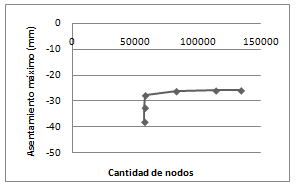
Además del tipo de elemento finito, es fundamental definir la densidad de malla óptima para la cual los resultados convergen en el menor tiempo posible. Durante el estudio de mallas, se analizaron seis densidades de malla diferentes y se obtuvieron asentamientos máximos para cada mallado. Luego se calculó la diferencia porcentual o error relativo entre las mallas (ec.(8)) tomando como referencia la malla más fina analizada y se midieron los tiempos de cálculo en cada una de las corridas (Figura 8).

Figura 8. Estudio de malla (elaboración propia)

A partir de 2.5cm de mallado, los asentamientos comienzan a converger a un mismo valor y solo se diferencian los modelos en el tiempo de análisis, por lo que se establece 2.5cm como densidad de malla óptima.

2.2.4 Cargas y Condiciones de frontera

En el análisis numérico, se consideró un paso de carga y dos iniciales, donde el software define las interacciones, las condiciones de frontera y el peso propio del elemento. Las cargas aplicadas variaron en las etapas de análisis, en la primera se consideraron valores de 250 y 300 kN/m² y en la segunda se aumentó hasta 350 kN/m². En todos los casos el muro se representó empotrado en la mitad de su base, con un extremo libre.

3. Resultados

Una vez planteada la metodología y calibrado el modelo numérico, se inicia el análisis de los muros de mampostería sometidos a asentamientos diferenciales. Este proceso estuvo dividido en dos etapas, cuyas características, cargas y condiciones de frontera se encuentran descritas en la sección 2.2 del presente artículo.

Primera etapa

En la primera etapa, se modelaron dos muros de 1m x 1m con diferentes solicitaciones y se observaron las zonas de mayor concentración de esfuerzos, se obtuvieron los desplazamientos verticales en los nodos donde se aplicó la carga y se determinaron los valores de distorsión angular.

La falla del elemento se produce inicialmente por tensión en las piezasy con el aumento de las cargas se extiende hacia las juntas ladrillo-mortero. Los esfuerzos comienzan en la base del muro y se van extendiendo escalonadamente con una inclinación de aproximadamente 45° hacia los laterales, por las unidades y el resto de las juntas, lo que se traduce en agrietamientos a 45°, que se inician en el apoyo que se ha desplazado diferencialmente y se extienden hacia el lateral, provocando fractura en las piezas y pérdida de juntas (Figura 9).

Figura 9. Modo de falla del muro de 1m x 1m. (a) Carga de 250 kN/m2. (b) 300 kN/m2 (elaboración propia)

Para un valor de carga de aproximadamente 240 kN/m² y una distorsión angular de 0.04, el material comienza a plastificarse y se inician las deformaciones irreversibles hasta la falla del elemento (Figuras 10 y 11).

Este valor de distorsión angular coincide con el máximo propuesto por Meli en el año 2014 para muros de mampostería sometidos a asentamientos diferenciales [19].

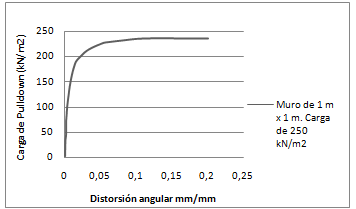
Figura 10. Curva Carga vs Distorsión Angular, muro de 1m x 1m, carga de 250 kN/m2 (elaboración propia)

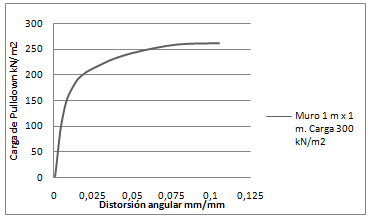
Figura 11. Curva Carga vs Distorsión Angular, muro de 1m x 1m, carga de 300 kN/m2 (elaboración propia)

Segunda etapa

En la segunda etapa, se modelaron tres muros con dimensiones variables (1m $\times$ 1m, 1.5m $\times$ 1.5m y 2m $\times$ 2m) considerando un mismo valor de carga, aplicado a la mitad de su base. Se observaron las zonas de mayor concentración de esfuerzos, la influencia de las dimensiones en la resistencia última del elemento, se obtuvieron los desplazamientos en los nodos donde se aplicó la carga y se determinaron los valores de distorsión angular.

El muro de 1m $\times$ 1m comienza a plastificarse para menores valores de carga, lo que demuestra que al aumentar las dimensiones del elemento, aumenta su rigidez y con ella la resistencia a los asentamientos diferenciales.

El mecanismo de falla se iniciacon la falla a tensión en los ladrillos y a medida que aumenta la carga, se producen deslizamientos en las juntas y se presentan zonas con esfuerzos excesivos, aunque en el muro de 2m x 2m se aprecia únicamente la rotura por tensión en las piezas, debido a que el elemento presenta una mayor resistencia. En todos los casos los esfuerzos se inician en la base del muro y se van extendiendo de manera escalonada con una inclinación de aproximadamente 45° hacia los laterales. Esto supone que los agrietamientos comienzan en el apoyo que se ha desplazado diferencialmente y se van distribuyendo hacia los bordes del muro, a medida que aumentan los valores de asentamientos (Figura 12).

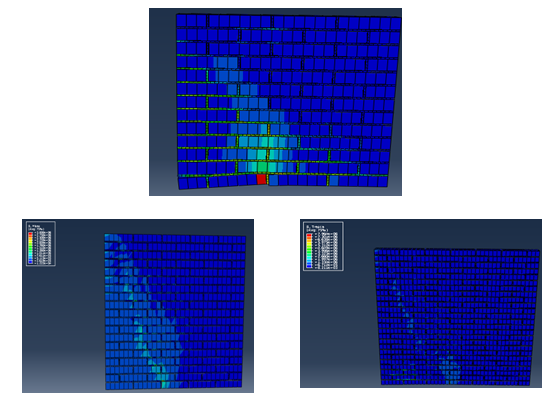
Figura 12. Modos de falla para un valor de carga de 350 kN/m2. (a) Muro de 1m $\times$ 1m. (b) Muro de 1.5m $\times$ 1.5m. (c) Muro de 2m $\times$ 2m (elaboración propia)

El muro de 1m $\times$ 1m comienza a plastificarse para cargas de aproximadamente 240 kN/m², con valores de distorsión angular de 0.04. En el muro de 1.5m $\times$ 1.5m las deformaciones irreversibles se presentan para cargas de 300 kN/m², con valores de distorsiones cercanos a los 0.05, mientras que en el de 2m $\times$ 2m la carga de rotura es superior a los 350 kN/m², por lo que se fue aumentando hasta alcanzar la falla en el elemento, la que se produce igualmente para valores de distorsiones cercanos a los 0.05.

Al comparar las curvas carga vs distorsión angular, se observa que el muro de 1m $\times$ 1m, presenta mayores valores de distorsión que el de 1.5m $\times$ 1.5m y el de 2m $\times$ 2m, para cargas similares, lo que demuestra que al aumentar las dimensiones del elemento (manteniendo la relación ancho/largo igual a 1), crece su resistencia ante asentamientos diferenciales, necesitando esfuerzos mayores para llegar a su falla (Figura 13).

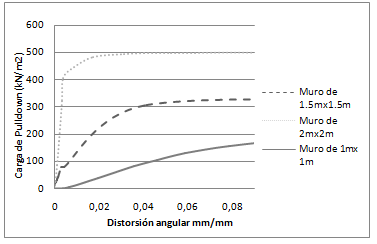
Figura 13. Curva Carga vs Distorsión Angular, muro de 1m $\times$ 1m, 1.5m $\times$ 1.5m y 2m $\times$ 2m (elaboración propia)

Muros de 1m$\times$ 1mMuros de 1m × {\displaystyle \times } 1m

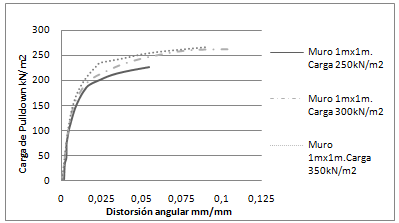
Al comparar las curvas de carga vs distorsión angular en los muros de 1m $\times$ 1m, se observa una mayor ductilidad para condiciones de carga menores, al presentar distorsiones angulares superiores a 0.03, con esfuerzos más pequeños y aun sin alcanzar la falla del elemento (Figura 14).

Figura 14. Curva Carga vs Distorsión Angular, muro de 1m x 1m sometido a diferentes valores de carga (elaboración propia)

4. Curvas de fragilidad

Las curvas de fragilidad describen la posibilidad de que una estructura exceda un determinado estado de daño, en función de un parámetro que define la intensidad en el movimiento [20]. Estas representan un método muy eficiente para evaluar el nivel de daño de una estructura de mampostería, pues permiten establecer una medida de vulnerabilidad en términos probabilísticos del comportamiento de un determinado sistema. Se elaboran en base a una distribución de probabilidad de logaritmo normal, cuya función de densidad corresponde con la ec.(9)

${\textstyle F\left(X\right)=\displaystyle {\frac {1}{\sigma \surd 2\pi }}exp\left(-\displaystyle {\frac {(X-{\mbox{ϻ}})^{2}}{2\cdot \sigma ^{2}}}\right)}$ (9)

donde $F(X)$ es la probabilidad de que el elemento sea dañado a un estado de daño $X$ y ϻ y $\sigma$ son la media y la desviación estándar del logaritmo natural de la variable $X$.

El valor de dispersión σ representa el grado de incertidumbre en el cual un estado de daño es posible que se inicie en un elemento [21]. Cuando los parámetros de fragilidad se determinan sobre una base de datos limitada, se deben considerar dos componentes de dispersión $\sigma _{r}$ y $\sigma _{u}$ (ec.(10))

${\textstyle \sigma ={\sqrt {{\sigma }_{r}+{\sigma }_{u}}}}$

(10)

donde $\sigma _{r}$ representa la variabilidad aleatoria que se observa en los datos de prueba disponibles y $\sigma _{u}$ la incertidumbre de que las pruebas representen las condiciones actuales de instalación y carga que pueda experimentar la estructura, o bien que los datos disponibles sean una muestra adecuada que representa la variabilidad aleatoria de las variables [20].

ATC 58 recomienda utilizar un valor de $\sigma _{u}$ igual a 0.25 cuando los datos de prueba disponibles corresponden a cinco o menos especímenes [21].

En la presente investigación, se consideraron tres muros con diferentes dimensiones y condiciones de carga y la variable $X$ a la que se hace referencia, corresponde al máximo valor de distorsión angular y a los asociados a un 50% y un 65% del valor de carga máxima, que representan niveles de daño severo, leve y moderado en el elemento.

Estos niveles de daño fueron definidos por las especificaciones del ATC 58, que además considera la estructura sin daño y en el momento del colapso [21]. Los límites en el estado de daño se determinan en cada caso a partir de los modelos numéricos de los muros.

4.1 Muros de 1m $\times$ 1m4.1 Muros de 1m × {\displaystyle \times } 1m

Los resultados obtenidos a través de la modelación de los muros de 1m x 1m, fueron utilizados para construir las primeras curvas de fragilidad, que relacionan la probabilidad de ocurrencia de un nivel de daño, para un determinado valor de distorsión angular.

Los niveles de daño se consideraron leve (50% de la carga aplicada), moderado (65% de la carga aplicada) y severo (100% de la carga aplicada), para los cuales se obtuvieron los valores de distorsión angular correspondientes a cada valor de carga (Tabla 9 y Figura 15).

Tabla 9. Distorsión angular asociada a cada nivel de daño en los muros de 1m x 1m (elaboración propia)

Muros de 1m $\times$ 1m	Distorsión angular en %
	0,5 Tensión máxima	0,65 Tensión máxima	Tensión máxima
1m $\times$ 1m $P=250$ kN/m2	1.0	1.8	6.0
1m $\times$ 1m $P=300$ kN/m2	1.2	2.0	5.0
1m $\times$ 1m $P=350$ kN/m2	1.3	1.89	6.0

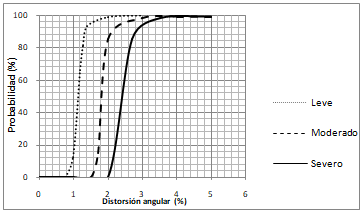
Figura 15. Curvas de fragilidad correspondientes al muro de 1m x 1m (elaboración propia)

En correspondencia con los resultados obtenidos en la presente investigación, las curvas de fragilidad representan una probabilidad del 100% de que se presente un nivel de daño severo en el elemento, para una distorsión angular de aproximadamente 0.04.

Si tomamos como referencia un valor de distorsión angular menor al máximo admisible establecido por el Reglamento de Construcción del Distrito Federal [4] para muros de mampostería, por ejemplo 0.02, la probabilidad de ocurrencia de un daño severo es de 0%, de aproximadamente un 90% para el nivel de daño moderado, de 9% para un nivel de daño leve y de 1% de que no se presente daño.

4.2 Muros de 1m $\times$ 1m, 1.5m $\times$ 1.5m y 2m $\times$ 2m4.2 Muros de 1m × {\displaystyle \times } 1m, 1.5m × {\displaystyle \times } 1.5m y 2m × {\displaystyle \times } 2m

El comportamiento de los muros de mampostería de 1m $\times$ 1m, 1.5m $\times$ 1.5m y 2m $\times$ 2m, fue estudiado durante la segunda etapa de investigación, considerando un valor de carga de 350 kN/m². Los valores de distorsión angular correspondientes al 50% de la carga aplicada, al 65% de la carga aplicada y al 100% de la carga aplicada, fueron utilizados para elaborar las curvas de fragilidad del material y se observó que al aumentar las dimensiones del elemento, aumenta su resistencia a los asentamientos diferenciales (Tabla 10 y Figura 16).

Tabla 10. Distorsión angular asociada a cada nivel de daño muros de 1m x 1m, 1.5m x 1.5m y 2m x 2m (elaboración propia)

Etapa 2	Distorsión angular en %
	0,5 Tensión máxima	0,65 Tensión máxima	Tensión máxima
1m $\times$ 1m $P=350$ kN/m2	1.9	1.98	6.0
1.5m $\times$ 1.5m $P=350$ kN/m2	1.4	1.89	5.2
2m $\times$ 2m $P=350$ kN/m2	0.7	1.0	4.0

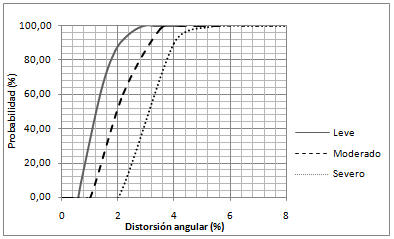
Figura 16. Curvas de fragilidad correspondientes alos muros de 1m $\times$ 1m, 1.5m $\times$ 1.5m y 2m $\times$ 2m (elaboración propia)

Las curvas de fragilidad, correspondientes a los muros de 1m x 1m, muestran una probabilidad de ocurrencia de un daño severo del 100% para un valor de distorsión angular de 0.04, lo que corresponde con el límite de la etapa elástica que se muestra en las curvas de capacidad de carga como el punto donde se inician las deformaciones irreversibles. Sin embargo, en el muro de 1.5m $\times$ 1.5m y en el 2m $\times$ 2m, se observa una mayor resistencia a los asentamientos diferenciales y, por tanto, la falla se produce para un valor ligeramente superior a los 0.04, lo que se manifiesta en una reducción al 91% de la probabilidad de ocurrencia de daño severo en los elementos, para este valor de distorsión.

Si tomamos como referencia un valor de distorsión angular menor al máximo admisible establecido por el Reglamento de Construcción del Distrito Federal [4] para muros de mampostería, por ejemplo 0.02, la probabilidad de ocurrencia de un daño severo es de 0%, de aproximadamente un 52% para el nivel de daño moderado, de 36% para un nivel de daño leve y de 12% de que no se presente daño.

5. Conclusiones

Al finalizar la investigación se presentan las curvas de fragilidad como una alternativa eficaz para estimar la probabilidad de ocurrencia de daño leve, moderado y severo, en muros de mampostería sometidos a asentamientos diferenciales. Además, se pudo concluir que la modelación computacional, empleando el software Abaqus/CAE basado en el método de elementos finitos, constituye una herramienta muy precisa para el análisis de muros de mampostería frente a la subsidencia, y que los modelos constitutivos utilizados para simular la rotura a tensión y cortante de las juntas, describen satisfactoriamente los mecanismos de falla de los elementos, observándose que los esfuerzos comienzan en el apoyo que se ha desplazado diferencialmente y se van extendiendo hacia los laterales, con una inclinación de aproximadamente 45°. También se pudo observar que al iniciar la aplicación de la carga, la mayor concentración de esfuerzos se presenta en las unidades y que al aumentar las solicitaciones, estos se van distribuyendo a la interfaz ladrillo-mortero, hasta producirse la falla en tensión diagonal de los elementos. Este comportamiento es similar al obtenido en varios ensayos experimentales a escala real, de muros de mampostería sometidos a asentamientos diferenciales.

También se pudo observar que para una distorsión angular de aproximadamente 0.04, comienzan a producirse deformaciones irreversibles en la estructura, estableciendo un límite admisible para la evaluación del estado de daño de un muro de mampostería sometido a hundimientos diferenciales. Este valor tiene correspondencia con el presentado por Meli en el año 2014 [19] para establecer los límites de agrietamiento en estructuras de fábrica.

También se puede concluir, que al aumentar las dimensiones de los muros crece su resistencia a los hundimientos diferenciales, presentando menores distorsiones angulares para estados de carga similares, aunque la falla se produce igualmente para un valor de distorsión de aproximadamente 0.04. Este ligero aumento en la rigidez se ve reflejado en las curvas de fragilidad, al disminuir la probabilidad de ocurrencia de daño severo a un 91%, mientras que en el caso de los muros de 1m x 1m, esta probabilidad se mantuvo en el 100%.

Finalmente, se presentan las curvas de fragilidad como una herramienta capaz de predecir la probabilidad de ocurrencia de daño leve, moderado y severo, en un muro de mampostería bajo la acción de asentamientos diferenciales.

Referencias

[1] Jesús P.M., Jorge A.F. Análisis multicapa de la subsidencia en el valle Querétaro, México. Revista Mexicana de Ciencias Geológicas, 24(3):389-402, 2007.

[2] Hernández-Castillo L.A., Ortiz-Lozano J.A., Hernández-Martin M., Pacheco-Martínez J., Zermeño-DeLeón M. E., Soto-Bernal J.J., Soto-Zamora M.A. Fragility curves for thin-walled cold-formed steel wall frames affected by ground settlements due to land subsidence. 22nd International Specialty Conference on Recent Research and Developments in Cold-Formed Steel Design and Construction, Vol. 87, 857–871, 2014.

[3] Roberto T. et al. Subsidencia del terreno. Ground Subsidence, 2009.

[4] Reglamento de Construcciones del Distrito Federal 24082018. 1–125, 2018.

[5] Pereda, J. F. L., Escalante, J. J. P.G. (n.d.). Modelación no lineal de muros de mampostería empleando elementos de contacto. Sociedad Mexicana de Ingeniería Estructural, 55:1–12, 2012.

[6] Lourenco P. B. Computational strategy for masonry structures. Tesis de Doctorado, Delft University Press, 1996.

[7] Mann W., Muller H. Failure of shear-stressed masonry – An enlarged theory, tests and aplications to shear walls. Proc. 2nd Canadian Masonry Symposium, 1982.

[8] Leal A.N., Tauta Camacho J.F., Blanco E.F.R. Determinación de parámetros para los modelos elastoplásticos Mohr-Coulomb y Hardening Soil en suelos arcillosos. Revista Ingenierías Universidad de Medellín, 8(15):75-91, 2009.

[9] Oller S. Mecánica de la fractura. Un enfoque global. CIMNE, Barcelona, 286 pp., 2001.

[10] Oller S., Oñate E., Lubliner J. A homogeneous constitutive model for masonry. International Journal for Numerical Methods in Engineering, 46(10):1651–1671, 1999.

[11] Ramos R.F.J. Simulación numérica y experimental de estructuras de acero rolado en frío por hundimientos diferenciales asociados al fenómeno de la subsidencia. Universidad Autónomade Aguascalientes, 2013.

[12] Kmiecik P., Kamiński M. Modelling of reinforced concrete structures and composite structures with concrete strength degradation taken into consideration. Archives of Civil and Mechanical Engineering, 11(3):623–636, 2011.

[13] Oliveira D.V. Experimental and numerical analysis of blocky masonry structures under cyclic loading. Structural Technology Laboratory of Universidad Politécnica de Cataluña, PhD Thesis, 2003.

[14] Hernández A. Simulación del comportamiento de paredes de obra de fábrica deladrillo bajo estados de carga biaxial mediante micromodelización. E.T.S. Ingenieros de Caminos, Canales y Puertos de Barcelona, 2014.

[15] Charry J.A., Roca P. Estudio experimental del comportamiento deparedes de obra de fábrica de ladrillo ante la acción de cargas laterales. Universidad Politécnica deCataluña. Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos de Barcelona, Thesis, 2010.

[16] Chen, W.-F. Limit Analysis and Soil Plasticity. Vol.1, Elsevier Scientific. In., United States of America, January 1975.

[17] Dumova-Jovanoska E., Churilov S., Mazzolani F.M. Calibration of a numerical model for masonry with application to experimental results. Proceedings of the International Conference on Protection of Historical Buildings (PROHITECH 09), Vol. 21-24:1139–1145, 2009.

[18] Gobierno del Distrito Federal. Normas Técnicas Complementarias para Diseño y Construcción de Estructuras de Mampostería NTCDF. 1–50, 2004

[19] Meli, R. Diseño estructural (2da ed.). Ed. Limusa S.A., 200 pp., México, D.F., 2014.

[20] Grummel, A. C. Development of Fragility Curves for Cold-Formed Steel Light-Framed Structural Systems: a Two-Pronged Approach. 1-110, 2010.

[21] ATC-58. Guidelines for seismic performance assessment of buildings. Prepared for U.S. Department of Homeland Security (DHS), Applied Technology Council, 2009.