A shock-capturing method based on shape functions for high order discontinuous Galerkin

Resumen

En este artículo se presenta un método de alto orden de Galerkin discontinuo para problemas de flujo compresible, en los cuales es muy frecuente la aparición de choques. La estabilización se introduce mediante una nueva base de funciones. Esta base tiene la flexibilidad de variar localmente (en cada elemento) entre un espacio de funciones polinómicas continuas o un espacio de funciones polinómicas a trozos. Así, el método propuesto proporciona un puente entre los métodos estándar de alto orden de Galerkin discontinuo y los clásicos métodos de volúmenes finitos, manteniendo la localidad y compacidad del esquema. La variación de las funciones de la base se define automáticamente en función de la regularidad de la solución y la estabilización se introduce mediante el operador salto, estándar en los métodos Galerkin discontinuo. A diferencia de los clásicos métodos de limitadores de pendiente, la estrategia que se presenta es muy local y robusta, y es aplicable a cualquier orden de aproximación. Además, el método propuesto no requiere refinamiento adaptativo de la malla ni restricción del esquema de integración temporal. Se consideran varias aplicaciones de las ecuaciones de Euler que demuestran la validez y efectividad del método, especialmente para altos órdenes de aproximación.

Abstract

This article presents a high-order Discontinuous Galerkin method for compressible flow problems, in which is very frequent the formation of shocks. The stabilization is introduced by a new basis functions. This base has the flexibility to vary locally (within each element) between continuous polynomial functions space and a space of piecewise polynomial functions. Thus, the proposed method provides a bridge between the standard methods of high-order Discontinuous Galerkin and classical Finite Volume methods, maintaining the locality and compactness of the scheme. The variation of basis functions is automatically set according to the regularity of the solution and the stabilization is introduced by the jump operator, standard in Discontinuous Galerkin methods. Unlike the classical methods of slope limiting, the strategy here presented is very local, robust, and applies to any order of approximation. Moreover, the proposed method does not require adaptive mesh refinement techniques and it can be used with any temporal integration scheme. Several applications of the Euler equations are shown, demonstrating the validity and effectiveness of the method, especially for high orders of approximation.

Palabras clave

Galerkin discontinuo de alto orden ; Ecuaciones de Euler ; Captura de choques ; Funciones de forma ; Sensor

Keywords

High-order discontinous Galerkin ; Euler equations ; Shock-capturing ; Shape functions ; Sensor

1. Introducción

El desarrollo de métodos numéricos cada vez más precisos para la resolución de problemas de dinámica de fluidos es una imperante necesidad. Dos de los campos de la dinámica de fluidos computacional que requieren esquemas de máxima precisión son la turbulencia y la aeroacústica. Las ecuaciones involucradas son las de Navier-Stokes y las de Euler. En la última década, el desarrollo de métodos numéricos de alta precisión ha ido ligado, en general, al aumento del orden de los esquemas numéricos en mallas no estructuradas. Sin embargo, los esquemas de alto orden para el cálculo de flujo compresible son computacionalmente inestables debido a la aparición de oscilaciones espurias físicamente inaceptables [1]  and [2] .

Los métodos de Galerkin discontinuo [3] , [4] , [5] , [6]  and [7] se presentan como una buena alternativa para la solución de problemas de propagación de ondas y, en general, de leyes de conservación hiperbólicas. Estos métodos proporcionan un puente entre la aproximación mediante funciones de forma de elementos finitos continuos y la tecnología de los métodos de volúmenes finitos [8]  and [9] . Para problemas puramente hiperbólicos los métodos Galerkin discontinuo proporcionan un esquema muy compacto para cualquier orden de aproximación y cualquier tipo de malla no estructurada e incluso con nodos colgantes. Lamentablemente, en presencia de choques y cuando se utilizan altos órdenes de aproximación (p  ≥ 1) el mecanismo estabilizador introducido por los métodos Galerkin discontinuo mediante el operador salto no es suficiente. En estos casos es necesario utilizar otras técnicas más robustas de estabilización que, en general, van acompañadas del refinamiento adaptativo de la malla.

Entre las técnicas posibles de resolución de choques destacan las técnicas de limitación [5] , [10] , [11] , [12]  and [13] y las técnicas de difusión artificial [14] , [15]  and [16] . Los limitadores de pendiente se introducen inicialmente para los métodos de volúmenes finitos [2] y posteriormente se extienden a métodos de Galerkin discontinuo [4]  and [17] . Estos esquemas buscan la monotonicidad de la solución en los valores promedios y, por lo tanto, reducen la aproximación a orden constante o, en el mejor de los casos, lineal, no solo en la región donde se localiza el choque, sino también en su entorno. Además, para poder garantizar estabilidad no lineal en una seminorma arbitraria solo pueden emplearse en combinación con una clase particular de esquemas de integración temporal Runge-Kutta explícitos que hasta el momento, según el conocimiento de los autores, como mucho son de cuarto orden [18] , [19]  and [20] . En resumen, las técnicas de limitadores de pendiente añaden difusión artificial de orden h (siendo h tamaño de la malla) proporcionando una solución estable, pero a costa de perder el alto orden de precisión. Esto hace necesario el uso de técnicas de refinamiento adaptativo, que además deben tener en cuenta el carácter direccional del choque.

Otras técnicas de reconstrucción más sofisticadas que han centrado la atención de varios autores son los métodos de reconstrucción no oscilatorios de alto orden ENO y WENO [19] , [21]  and [22] . Estos métodos preservan la estabilidad no lineal del esquema así como el alto orden de aproximación proporcionando soluciones libres de oscilaciones. No obstante, añaden grados de libertad adicionales y pierden la compacidad del esquema, debido al uso de stencils amplios. Además el uso de estos métodos queda esencialmente restringido a mallas uniformes y estructuradas, raramente empleadas en el tratamiendo de choques y problemas complejos.

La segunda alternativa consiste en la introducción de difusión artificial para obtener soluciones estables. Esta técnica ya fue introducida en los años cincuenta por Von Neumann y Richtmyer [14] . En su extensión a los métodos Galerkin discontinuo es habitual definir la constante en cada elemento, de esta forma se obtiene una solución precisa que mantiene el grado de la aproximación. En general, la solución es de orden superior al de los limitadores de pendiente. Recientemente se han presentado nuevos enfoques donde el orden obtenido es h /p o h^k con k  ≤ p , siendo p el grado de aproximación [15]  and [16] . Sin embargo, estos métodos presentan serias dificultades en su extensión al caso multidimensional. Por un lado, ajustar la magnitud de la difusión no es sencillo, así como tampoco el efecto de propagación multidireccional del choque. Por otro lado, añadir difusión constante en todo elemento puede derivar en una pérdida de resolución significativa cuando se utilizan mallas groseras en presencia de capas límite o estructuras no dimensionales, como los choques o discontinuidades. Además, la introducción de difusión artificial implica la resolución de una ecuación diferencial parcial de segundo orden, lo cual conlleva un error asociado a la ecuación original, así como un incremento del coste computacional [23]  and [24] .

En este trabajo se explota la flexibilidad que ofrecen los métodos de Galerkin discontinuo, variando el espacio de aproximación en cada elemento, así como también para distintos instantes de la simulación. Un espacio de funciones continuas debe emplearse para aproximar soluciones suaves, y un espacio de funciones discontinuas a trozos es apropiado para soluciones con discontinuidades o gradientes pronunciados. Basándose en esta idea, se introduce una nueva base de funciones polinómicas que dependen linealmente de un parámetro. Este parámetro permite definir funciones de la base localmente según la regularidad de la solución. Así, para un valor del parámetro la base permite una representación continua de alto orden de la solución. Variando el valor del parámetro se introduce una representación local, mediante una expansión polinómica a trozos en el interior de cada elemento. El objetivo reside en aprovechar la potente tecnología que proporcionan los métodos de volúmenes finitos en el contexto de leyes hiperbólicas de conservación, y en general, para problemas de convección dominante. Una de las principales ventajas del método propuesto respecto a los métodos de difusión artificial dependientes de uno o más parámetros es que en este caso el parámetro que define la base de funciones no es arbitrario y está controlado por un indicador de regularidad.

El método propuesto utiliza el principio estabilizador de los métodos de Galerkin discontinuo en la interfaz de los elementos mediante el operador salto y lo extiende al interior de ellos, tomando como idea un argumento similar a las técnicas de volúmenes finitos. A diferencia de estos últimos, el método propuesto tiene la propiedad de calibrar la magnitud de las discontinuidades introducidas y, por lo tanto, de controlar la difusión en el interior del elemento. Adicionalmente, la nueva base de funciones se define únicamente en el dominio espacial, y por lo tanto no interfiere en el esquema de integración temporal empleado, permitiendo el uso de esquemas explícitos o implícitos de cualquier orden.

El artículo se divide según sigue: en la sección 2 se resume brevemente el método de Galerkin discontinuo estándar para funciones de forma hiperbólicas, en particular para las ecuaciones de Euler. En la sección 3 se define la nueva base de funciones de forma y el criterio de regularidad impuesto. También se detalla el sensor de discontinuidades utilizado. La sección 4 recoge varios tests numéricos que demuestran la aplicabilidad del método para diversas situaciones frente a otros métodos clásicos, así como su eficiencia para altos órdenes de aproximación. Finalmente en la sección 5 se resumen las conclusiones obtenidas.

2. El método de Galerkin discontinuo para las ecuaciones de Euler

En esta sección se resume brevemente el método de Galerkin discontinuo para las ecuaciones de Euler. Sin pérdida de generalidad se asume el caso bidimensional ${\textstyle (x_{1},x_{2})\in {\mathbb {R} }^{2}}$ .

Las ecuaciones de Euler de la dinámica de gases computacional [1] expresan la conservación de la masa, el momento y la energía para un fluido ideal compresible y no viscoso. En ausencia de fuerzas externas, las ecuaciones de Euler se expresan de forma conservativa como el siguiente sistema

${\frac {\partial }{\partial t}}\left({\begin{array}{c}\rho \\\rho u\\\rho v\\\rho E\\\end{array}}\right)+{\frac {\partial }{\partial x_{1}}}\left({\begin{array}{c}\rho u\\\rho u^{2}+p\\\rho uv\\u(\rho E+p)\end{array}}\right)+{\frac {\partial }{\partial x_{2}}}\left({\begin{array}{c}\rho v\\\rho uv\\\rho v^{2}+p\\v(\rho E+p)\end{array}}\right)={\boldsymbol {0}}$

( 1)

definido en un dominio acotado ${\textstyle \Omega \subset {\mathbb {R} }^{2}}$ con condiciones de contorno en ∂Ω. En esta expresión ρ representa la densidad del fluido, u   y ${\textstyle v}$ son las componentes del vector velocidad ${\textstyle {\boldsymbol {v}}}$ , p es la presión y E es la energía total. Para completar el sistema se define una ecuación de estado, que relaciona la energía interna con la presión y la densidad. Para un gas perfecto politrópico la ecuación de estado es

$p=(\gamma -1)(E-{\frac {\rho \vert \vert {\boldsymbol {v}}\vert \vert ^{2}}{2}})$

donde γ es el exponente adiabático, con valor γ  = 1,4 para el aire.

De forma compacta el sistema (1) se expresa como

${\frac {\partial {\boldsymbol {\mbox{U}}}}{\partial t}}+$${\frac {\partial {\boldsymbol {\mbox{F}}}_{k}({\boldsymbol {\mbox{U}}})}{\partial x_{k}}}=$${\boldsymbol {0}}\quad para\quad k=1{\mbox{,}}2$

( 2)

donde se utiliza el criterio de Einstein para la notación, con

${\boldsymbol {\mbox{U}}}=\left({\begin{array}{c}\rho \\\rho u\\\rho v\\\rho E\\\end{array}}\right)\quad {\boldsymbol {\mbox{F}}}_{\boldsymbol {1}}=$$\left({\begin{array}{c}\rho u\\\rho u^{2}+p\\\rho uv\\u(\rho E+p)\end{array}}\right)\quad y\quad {\boldsymbol {\mbox{F}}}_{\boldsymbol {2}}=$$\left({\begin{array}{c}\rho v\\\rho uv\\\rho v^{2}+p\\v(\rho E+p)\end{array}}\right)$

En el desarrollo posterior se emplea el número de Mach, definido como ${\textstyle M={\frac {\parallel {\boldsymbol {v}}\parallel }{c}}}$ donde ${\textstyle c={\sqrt {\gamma p/\rho }}}$ es la velocidad del sonido.

El método de Galerkin discontinuo para un sistema hiperbólico de leyes de conservación se describe como sigue. Se divide el dominio computacional Ω en una partición de elementos no superpuestos entre sí:

${\overline {\Omega }}={\bigcup }_{e=1}^{n_{el}}{\overline {\Omega }}_{e}\quad tal\quad que\quad {\Omega }_{i}\bigcap {\Omega }_{j}=$$\varnothing \quad para\quad i\not =j$

( 3)

donde n_el es el número total de elementos de la partición.

Sea ${\textstyle {\boldsymbol {\mbox{W}}}\in [P^{p}({\Omega }_{e})]^{n_{sd}+2}}$ una función de test, donde n_sd respresenta la dimensión del espacio vectorial de trabajo (en este artículo se trabaja con n_sd  = 2). Además, ${\textstyle P^{p}({\Omega }_{e})}$ es el conjunto de polinomios de grado menor o igual a p en Ω_e . Multiplicando (2) por la función de test, integrando sobre el elemento Ω_e y usando el teorema de la divergencia se obtiene la forma débil

${\int }_{{\Omega }_{e}}{\boldsymbol {\mbox{W}}}\cdot {\frac {\partial {\boldsymbol {\mbox{U}}}_{e}}{\partial t}}\quad d\Omega -$${\int }_{{\Omega }_{e}}{\frac {\partial {\boldsymbol {\mbox{W}}}}{\partial x_{k}}}\cdot {\boldsymbol {\mbox{F}}}_{k}({\boldsymbol {\mbox{U}}}_{e})\quad d\Omega +$${\int }_{\partial {\Omega }_{e}}{\boldsymbol {\mbox{W}}}\cdot {\boldsymbol {\mbox{F}}}_{{\boldsymbol {\mbox{n}}}_{e}}({\boldsymbol {\mbox{U}}}_{e})\quad d\Gamma =$$0\quad \forall {\boldsymbol {\mbox{W}}}\in [P^{p}({\Omega }_{e})]^{n_{sd}+2}$

( 4)

donde U_e es la restricción de U en el elemento Ω_e y ${\textstyle {\boldsymbol {\mbox{F}}}_{{\boldsymbol {\mbox{n}}}_{e}}({\boldsymbol {\mbox{U}}}_{e})}$ es la función de flujo normal. Como consecuencia de la discontinuidad, la función de flujo normal ${\textstyle {\boldsymbol {\mbox{F}}}_{{\boldsymbol {\mbox{n}}}_{e}}}$ tiene 2 valores en la interfaz de los elementos. Por ello se introduce un flujo numérico ${\textstyle {\overset {\mbox{ˆ}}{\boldsymbol {\mbox{F}}}}_{{\boldsymbol {\mbox{n}}}_{e}}({\boldsymbol {\mbox{U}}}_{e},{\boldsymbol {\mbox{U}}}_{e}^{out})}$ que depende de los estados de la variable U a ambos lados de cada interfaz entre elementos, y del vector unitario normal a esta, n_e :

${\boldsymbol {\mbox{U}}}_{e}^{out}={\underset {\varepsilon \rightarrow 0^{+}}{l{\acute {\imath }}m}}{\boldsymbol {\mbox{U}}}({\boldsymbol {x}}+$$\varepsilon {\boldsymbol {\mbox{n}}}_{e})\quad para\quad {\boldsymbol {x}}\in {\Omega }_{e}$

Para el flujo numérico ${\textstyle {\boldsymbol {\overset {\mbox{ˆ}}{\mbox{F}}}}_{{\boldsymbol {\mbox{n}}}_{e}}}$ es posible emplear cualquiera de los Riemann solvers estándar de los métodos de volúmenes finitos [9] . En los ejemplos numéricos que se presentan en este artículo se ha elegido el flujo de Roe [25] . Así, la forma débil del método Galerkin discontinuo para cada elemento Ω_e se escribe como

${\int }_{{\Omega }_{e}}{\boldsymbol {\mbox{W}}}\cdot {\frac {\partial {\boldsymbol {\mbox{U}}}_{e}}{\partial t}}\quad d\Omega -$${\int }_{{\Omega }_{e}}{\frac {\partial {\boldsymbol {\mbox{W}}}}{\partial x_{k}}}\cdot {\boldsymbol {\mbox{F}}}_{k}({\boldsymbol {\mbox{U}}}_{e})\quad d\Omega +$${\int }_{\partial {\Omega }_{e}}{\boldsymbol {\mbox{W}}}\cdot {\overset {\mbox{ˆ}}{\boldsymbol {\mbox{F}}}}_{{\boldsymbol {\mbox{n}}}_{e}}({\boldsymbol {\mbox{U}}}_{e},{\boldsymbol {\mbox{U}}}_{e}^{out})\quad d\Gamma =$$0\quad \forall {\boldsymbol {\mbox{W}}}\in [P^{p}({\Omega }_{e})]^{n_{sd}+2}$

( 5)

Discretizando la forma débil en cada elemento se obtiene el sistema de ecuaciones diferenciales ordinarias

${\boldsymbol {\mbox{M}}}{\frac {d{\boldsymbol {U}}}{dt}}+{\boldsymbol {\mbox{R}}}({\boldsymbol {U}})=$${\boldsymbol {0}}$

( 6)

donde en este caso U representa el vector de coeficientes de la aproximación, M es la matriz de masa, que resulta diagonal por bloques, y R (U ) es el vector residuo. El sistema (6) puede resolverse con diversos esquemas de integración temporal. En el presente trabajo se utiliza un método estándar Runge-Kutta explícito [1] . La condición de estabilidad viene determinada por una acotación del número de Courant:

$C=\vert {\lambda }_{m{\acute {a}}x}\vert {\frac {\Delta t}{h}}\leq {\frac {1}{2p+1}}$

donde h es el tamaño elemental y p   es el grado de la aproximación. El valor escalar ${\textstyle {\lambda }_{m{\acute {a}}x}}$ es el valor propio máximo en valor absoluto de la matriz de Jacobi del flujo, ${\textstyle {\frac {\partial {\boldsymbol {\mbox{F}}}}{\partial {\boldsymbol {\mbox{U}}}}}}$ , es decir, ${\textstyle {\lambda }_{m{\acute {a}}x}=}$${m{\acute {a}}x}_{j}\vert {\lambda }_{j}\vert$ para j  = 1, …, n_sd  + 2.

Observación 2.1.

En el caso de un sistema hiperbólico de ecuaciones, como las ecuaciones de Euler, los valores propios λ_j no son más que las velocidades de propagación de las cantidades características. Para más detalles, consultar [1]  and [26] .

3. Base de funciones

El método propuesto se caracteriza por la introducción de la nueva base de funciones polinómicas ${\textstyle {\overline {N}}_{i}}$ . Como es habitual en los métodos de Galerkin discontinuo, se aproxima la solución U elemento a elemento con una base de funciones de grado p:

${\boldsymbol {\mbox{U}}}_{e}=\sum _{i=1}^{n_{en}(p)}{\overline {N}}_{i}({\boldsymbol {x}};\alpha ){\boldsymbol {U}}_{i}\quad para\quad e=$$1\ldots n_{el}$

( 7)

donde n_en (p ) es el número de nodos en cada elemento (es decir, el número de grados de libertad por elemento).

La base de funciones ${\textstyle {\overline {N}}({\boldsymbol {x}};\alpha )}$ tiene un papel crucial en la precisión de la aproximación. Las funciones ${\textstyle {\overline {N}}_{i}}$ se definen en cada elemento como una combinación convexa de las funciones de forma continuas estándar de los métodos Galerkin discontinuo N_i , y unas funciones de forma constantes a trozos en el elemento, ϕ_i . Es decir,

${\overline {N}}_{i}({\boldsymbol {x}};\alpha ):=\alpha N_{i}({\boldsymbol {x}})+$$(1-\alpha ){\phi }_{i}({\boldsymbol {x}})\quad para\quad i=$$1,\ldots ,n_{en}(p)$

( 8)

donde α es un parámetro que toma valores entre 0 y 1 en función de la suavidad de la aproximación.

Una de las ventajas de los métodos de Galerkin discontinuo reside en su inherente mecanismo estabilizador mediante la función salto ${\textstyle {\mbox{〚 }}{\boldsymbol {\mbox{U}}}\cdot {\boldsymbol {\mbox{n}}}_{e}{\mbox{〛}}=}$${\boldsymbol {\mbox{U}}}_{e}\cdot {\boldsymbol {\mbox{n}}}_{e}+$${\boldsymbol {\mbox{U}}}_{e}^{out}\cdot {\boldsymbol {\mbox{n}}}_{out}$ para aproximaciones constantes y lineales, véase por ejemplo [6] , [12]  and [17] . La base de funciones propuesta (8) explota esta propiedad y la extiende al interior de los elementos, permitiendo así discontinuidades no solo en la interfaz, sino también en el interior del elemento. Asimismo, según la definición (8) para α  = 0 se obtiene la base de funciones discontinuas a trozos (${\textstyle {\overline {N}}_{i}={\phi }_{i}}$ ) y para α  = 1 se obtiene la base de funciones continuas (${\textstyle {\overline {N}}_{i}=N_{i}}$ ), recuperando en este caso la forma estándar del método de Galerkin discontinuo.

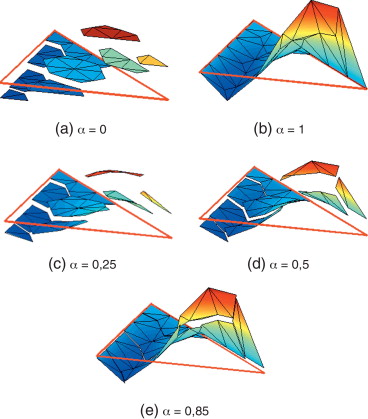
La figura 1 muestra una función ${\textstyle {\overline {N}}_{i}({\boldsymbol {x}};\alpha )}$ de grado p  = 3 para distintos valores de α   . Los casos particulares ${\textstyle {\overline {N}}_{i}({\boldsymbol {x}};\alpha )=}$${\phi }_{i}$ y ${\textstyle {\overline {N}}_{i}({\boldsymbol {x}};\alpha )=}$$N_{i}$ corresponden a las figura 1 (a) y (b) respectivamente.

Figura 1. Función de forma asociada a uno de los nodos arista de la base de funciones de grado p  = 3 para distintos valores de α .

La nueva base de funciones debe ser capaz de representar cualquier perfil de la solución, ya sea suave o con tendencia a formar frentes o discontinuidades. Por lo tanto, es de gran importancia elegir de manera adecuada, tanto el parámetro α como la base de funciones discontinuas ϕ . En los siguientes apartados se detallan ambas elecciones.

3.1. Definición de la base de funciones discontinuas

La definición de la base de funciones discontinuas ϕ_i tiene una estrecha relación con los métodos de volúmenes finitos [9] , [27]  and [28] . En estos métodos se discretiza el dominio computacional en un conjunto de volúmenes de control (o celdas) no superpuestos entre sí y se impone la conservación de las ecuaciones en cada una de ellas. Siguiendo esta idea, se define la base ϕ de la siguiente manera.

Se considera la partición arbitraria del elemento Ω_e en un conjunto de n_en (p ) volúmenes de control que no se solapan entre sí,

${\overline {\Omega }}_{e}={\bigcup }_{k}^{n_{en}(p)}{\overline {\Omega }}_{e}^{k}\quad tal\quad que\quad {\Omega }_{e}^{l}\bigcap {\Omega }_{e}^{m}=$$\varnothing \quad para\quad l\not =m$

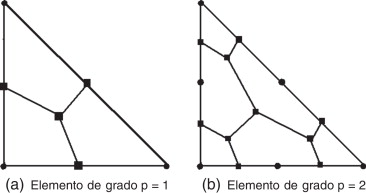
donde cada celda ${\textstyle {\Omega }_{e}^{k}}$ contiene un nodo del elemento. La figura 2 muestra la partición para elementos de primer y segundo orden, donde se puede ver que las interfases quedan de forma arbitraria en una malla no estructurada.

Figura 2. Partición en volúmenes de control de un elemento de primer y segundo orden. Los nodos del elemento están representados con puntos y los vértices de las celdas de control con cuadrados.

Observación 3.1.

La partición del elemento Ω_e en volúmenes de control no es única. Por simplicidad, en este trabajo se ha construido a partir de una subtriangulación del elemento que se obtiene uniendo los nodos. Se considera entonces el centroide de cada subtriángulo y los puntos medios de sus aristas. Uniendo el conjunto de puntos que forman de manera que cada polígono contenga uno y solo uno de los nodos elementales se obtiene una partición del elemento en n_en (p ) celdas.

Dada esta partición, cada función ϕ_i se define como una función real ${\textstyle {\phi }_{i}({\boldsymbol {x}}):{\Omega }_{e}\longrightarrow \mathbb {R} }$ constante a trozos en cada volumen de control ${\textstyle {\Omega }_{e}^{k}}$ . Es decir, ∀x  ∈ Ω_e

${\phi }_{i}({\boldsymbol {x}})={\begin{array}{ll}{\phi }_{i}^{k}=cst&si\quad {\boldsymbol {x}}\in {\Omega }_{e}^{k}\\0&si\quad {\boldsymbol {x}}\not \in {\Omega }_{e}^{k}\\&\end{array}}\quad \forall {\boldsymbol {x}}\quad para\quad k=$$1,\ldots ,n_{en}(p)$

( 9)

Por construcción, las funciones de forma continuas N_i verifican la condición de reproducibilidad constante, o sea:

$\sum _{i=1}^{n_{en}(p)}N_{i}({\boldsymbol {x}})=1$

( 10)

Para que la nueva base de funciones ${\textstyle {\overline {N}}_{i}}$ verifique también esta propiedad debe cumplirse

$\sum _{i=1}^{n_{en}(p)}{\overline {N}}_{i}({\boldsymbol {x}};\alpha )=$$\alpha +(1-\alpha )\sum _{i=1}^{n_{en}(p)}{\phi }_{i}({\boldsymbol {x}})=$$1$

( 11)

o equivalentemente, ${\textstyle {\sum }_{i=1}^{n_{en}(p)}{\phi }_{i}^{k}=}$$1$ .

Existen varias opciones para definir ${\textstyle {\phi }_{i}^{k}}$ de manera que se satisfaga (11) . La primera y más obvia opción es considerar ${\textstyle {\phi }_{i}^{k}={\frac {1}{n_{en}(p)}}\quad \forall \quad k=}$$1,\ldots ,n_{en}(p)$ . Esta opción lleva a una distribución constante y continua en cada elemento, sin ninguna aportación relevante a las funciones ${\textstyle {\overline {N}}_{i}({\boldsymbol {x}};\alpha )}$ .

Una segunda opción consiste en definir ${\textstyle {\phi }_{i}^{k}={\delta }_{ik}}$ . Esta opción proporciona una aproximación simple y eficaz, pero se descarta debido a que no tiene en cuenta el tamaño de la celda ${\textstyle {\Omega }_{e}^{k}}$ correspodiente.

Así pues, con el fin de establecer una relación entre el tamaño de las celdas y el valor de la función de forma asociada, se define ${\textstyle {\phi }_{i}^{k}}$ como

${\phi }_{i}^{k}={\frac {1}{meas({\Omega }_{e}^{k})}}{\int }_{{\Omega }_{e}^{k}}N_{i}({\boldsymbol {x}})\quad d\Omega$

( 12)

donde ${\textstyle {\Omega }_{e}^{k}}$ es el subelemento que contiene el nodo x_i . De este modo, se prioriza la contribución de ϕ_i al elemento para cada celda, de manera que esta sea equivalente a la contribución de la función de forma N_i del nodo ${\textstyle {\boldsymbol {x}}_{i}\in {\Omega }_{e}^{k}}$ .

Observación 3.2.

La condición de reproducibilidad constante (11) es independiente del valor del parámetro α . Es decir,

${\frac {\partial }{\partial \alpha }}{\int }_{{\Omega }_{e}^{k}}{\overline {N}}_{i}({\boldsymbol {x}};\alpha )\quad d{\boldsymbol {x}}=$$0\quad \forall k=1,\ldots ,n_{en}(p)$

3.2. Parámetro α

Una de las principales ventajas de los métodos Galerkin discontinuo es su flexibilidad respecto al espacio de aproximación. Esencialmente, cualquier espacio lineal puede usarse como espacio de aproximación local, y este puede variar elemento a elemento, así como para cada instante de tiempo. La introducción del parámetro α permite explotar esta propiedad adaptando la base localmente en función de la regularidad de la solución.

Por su definición, ver (8) , las funciones de forma ${\textstyle {\overline {N}}_{i}({\boldsymbol {x}};\alpha )}$ dependen linealmente de α , que actúa como función de peso entre las bases N_i y ϕ_i . El espacio de aproximación queda definido localmente según el valor de α . Tal y como se ha mencionado en la sección anterior, para α  = 1 se tiene la base de funciones estándar, continua en el elemento, mientras que para α  = 0 se introducen saltos en el interior de los elementos (en particular, en la interfaz de los subelementos ${\textstyle {\Omega }_{e}^{k}}$ ), obteniendo una base constante a trozos en Ω_e . La magnitud de los saltos interiores está controlada por α según la expresión (1− α ) 〚 ϕ_i (x_j )n_j  〛 para los puntos ${\textstyle {\boldsymbol {\mbox{x}}}_{j}\in \partial {\Omega }_{e}^{k}}$ , siendo n_j el vector normal unitario a x_j . El control, vía el parámetro α , de la potencia del salto también permite un control sobre la estabilización introducida por los Riemann solvers.

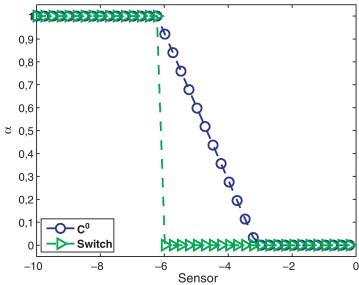
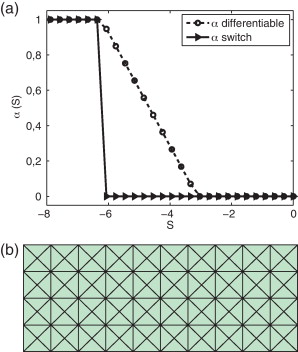
La elección de α permite una cierta flexibilidad. En primer lugar se podría recurrir a una función switch (α  = 0 o 1) entre una discretización con volúmenes finitos constante a trozos o una discretización clásica de Galerkin discontinuo. Esta opción, además de ser muy restrictiva, no resulta apropiada para problemas estacionarios, ya que el uso de funciones no diferenciables dificulta alcanzar el estado estacionario. Este hecho ya ha sido señalado por otros autores haciendo referencia a técnicas de limitación o estabilización basadas en operadores discontinuos [29]  and [30] . Otras opciones razonables consisten en modelar el parámetro α   como una función ${\textstyle C^{k}}$ con k  ≥ 0. La introducción de funciones continuas permite una variación suave elemento a elemento de α , así como un rango más amplio de valores. Por simplicidad, en este artículo se ha considerado α   como una función ${\textstyle C^{0}}$ , pero otras alternativas pueden ser también válidas. La figura 3 muestra el perfil de una posible función α y una función tipo switch.

Figura 3. Función-tipo α continua y switch.

Con el fin de adaptar la base de funciones a la regularidad de la solución, α debe estar necesariamente controlada por un detector de choques que permita discernir gradientes pronunciados frente a perfiles suaves. En este trabajo se utiliza el sensor propuesto recientemente por Persson y Peraire [15]  and [31] , S_e (s ), definido a nivel elemental Ω_e . Este sensor depende únicamente de la cantidad física s , obtenida a partir de la variable de estado U . Esta cantidad se conoce como variable de detección . Para el caso particular de las ecuaciones de Euler, otras referencias indican que el número de Mach es una variable de detección más precisa que otras cantidadas físicas como la entropía o la densidad, propuestas en otros trabajos [13]  and [15] .

En la figura 3 se distinguen 3 regiones en el perfil de la función α (s ): una primera región tal que si S (s ) < s₁ entonces α  = 1, una segunda región donde α toma valores entre 0 y 1, y una tercera región S (s ) > s₀ para la cual α  = 0. La aproximación de la solución en el interior del elemento es continua para valores del sensor de la primera región (i.e., α  = 1). En este sentido s₁ representa un umbral para discernir entre funciones suaves o funciones con gradientes pronunciados o discontinuidades.

Observación 3.3.

La experiencia con diferentes cáculos indica que la función α se comporta de manera robusta respecto a estos 2 valores, es decir, pequeñas variaciones de s₀ y s₁ no afectan al comportamiento global de la aproximación.

Seguidamente se define el sensor de discontinuidades S (s ), así como los valores s₁ y s₀ .

3.2.1. El sensor de discontinuidades

El sensor de discontinuidades se define a nivel elemental por un operador no lineal ${\textstyle S_{e}(s):{\Omega }_{e}\longrightarrow \mathbb {R} }$ , donde la variable de detección s  = s (U ) es una componente o función del vector de estado U . El sensor proporciona una medida escalar de la regularidad de la aproximación.

A continuación se resume brevemente el sensor para el caso unidimensional, detallado en trabajos previos de los autores [15]  and [16] . Posteriormente se extiende al caso bidimensional.

Sea la base de polinomios ortonormal de Legendre, P_i para i  = 1, …, n_en (p ). Las aproximaciones de grado p y p  − 1 de la variable de detección s en esta base se expresan como

$s(x)=\sum _{i=1}^{n_{en}(p)}s_{i}P_{i}(x)\quad {\overset {\mbox{ˆ}}{s}}(x)=$$\sum _{i=1}^{n_{en}(p-1)}s_{i}P_{i}(x)$

( 13)

donde, debido a las propiedades jerárquicas de la base, ${\textstyle {\overset {\mbox{ˆ}}{s}}(x)}$ se ha obtenido truncando la serie polinómica s (x ).

El sensor de discontinuidades para el elemento unidimensional I_e queda definido como

$S_{e}(s)={log}_{10}({\frac {\parallel s-{\overset {\mbox{ˆ}}{s}}{\parallel }_{2}^{2}}{\parallel s{\parallel }_{2}^{2}}})$

donde ∥ • ∥ ₂ es la norma L₂ de la variable. El cálculo del sensor con estas normas se simplifica gracias a la ortonormalidad de la base de polinomios de Legendre. En efecto, sea ${\textstyle {\boldsymbol {\mbox{s}}}^{T}=(s_{1},\ldots ,s_{n_{en}(p)})}$ el vector de valores nodales de la aproximación s (x ), se tiene

$\parallel s{\parallel }_{2}^{2}={\int }_{I_{e}}s^{2}\quad dx=$${\int }_{I_{e}}(\sum _{i}^{n_{en}(p)}s_{i}P_{i}(x))^{2}\quad dx=$${\boldsymbol {\mbox{s}}}^{T}{\boldsymbol {\mbox{M}}}{\boldsymbol {\mbox{s}}}$

donde M es la matriz de masa diagonal obtenida con los polinomios ortonormales de Legendre:

${\boldsymbol {\mbox{M}}}_{ij}={\int }_{I_{e}}P_{i}(x)P_{j}(x)\quad dx=$${\delta }_{ij}$

Con esta definición y teniendo en cuenta la jerarquía de la base, el sensor de discontinuidades resulta

$S_{e}(s)={log}_{10}({\frac {\left(0,\ldots ,0,s_{n_{en}(p)})^{T}\quad {\boldsymbol {\mbox{M}}}\quad (0,\ldots ,0,s_{n_{en}(p)}\right)}{{\boldsymbol {\mbox{s}}}^{T}{\boldsymbol {\mbox{M}}}{\boldsymbol {\mbox{s}}}}})$

( 14)

El sensor de discontinuidades en 2D se construye de manera análoga pero utilizando la base de polinomios ortonormales de Koornwinder [32] para cada elemento. La expresión ${\textstyle \parallel s-{\overset {\mbox{ˆ}}{s}}{\parallel }_{2}^{2}}$ en (14) representa una medida de las frecuencias altas de la aproximación y vive en el espacio de polinomios ${\textstyle ([P^{p}]\backslash [P^{p-1}])^{2}}$ . En el caso bidimensional la matriz de masa se construye utilizando la base de polinomios de Koornwinder. La norma asociada a las frecuencias altas de la aproximación se obtiene de nuevo mediante una proyección de la solución s (x ) en el espacio de polinomios ${\textstyle ([P^{p}]\backslash [P^{p-1}])^{2}}$ . Así pues, las proyecciones en norma L₂ del sensor (14) para el caso multidimensional se expresan como

$E=\parallel s{\parallel }_{2}^{2}={\boldsymbol {\mbox{s}}}^{T}{\boldsymbol {\mbox{M}}}{\boldsymbol {\mbox{s}}},\quad E_{H}=$$\parallel s-{\overset {\mbox{ˆ}}{s}}{\parallel }_{2}^{2}=$${\boldsymbol {\mbox{s}}}^{T}{\boldsymbol {\mbox{M}}}_{H}{\boldsymbol {\mbox{s}}}\quad$

donde M_H no es más que la matriz de masa calculada con los monomios de Koornwinder de grado únicamente p . Para ello se considera V la matriz de Vandermonde en la base de Koornwinder, con las columnas ordenadas por bloques de polinomios de menor a mayor grado. Sea n_L el número de modos hasta grado p  − 1 y n_H los restantes (n_L  + n_H  = n_en (p )), la matriz M_H es la proyección ${\textstyle {\boldsymbol {\mbox{M}}}_{H}={\boldsymbol {\mbox{F}}}_{H}^{T}{\boldsymbol {\mbox{M}}}{\boldsymbol {\mbox{F}}}_{H}}$ , donde F_H es la matriz filtro siguiente

${\boldsymbol {\mbox{F}}}_{H}={\boldsymbol {\mbox{V}}}{\boldsymbol {\mbox{P}}}_{H}{\boldsymbol {\mbox{V}}}^{-1}\quad con\quad {\boldsymbol {\mbox{P}}}_{H}=$$diag({\underset {n_{L}}{\underbrace {0\ldots 0} }},{\underset {n_{H}}{\underbrace {1\ldots 1} }})$

Con estas definiciones el sensor (14) para cualquier dimensión es el logaritmo del cociente entre la energía asociada a las altas frecuencias y la energía total

$S_{e}(s)={log}_{10}(E_{H}/E)$

( 15)

El sensor, (14) y (15) , considera la solución de alto orden como si estuviera comprendida por una secuencia de modos de Fourier. Para una función continua los coeficientes de la serie de Fourier tienden a 0 rápidamente, a una velocidad aproximada de 1/p² . Teniendo en cuenta que la definición del sensor involucra cantidades al cuadrado y logaritmos, se espera que para funciones suaves ${\textstyle C^{k}}$ , con k  ≥ 0, el sensor se comporte como un valor de orden ≲−4 log ₁₀ (p ). Sin embargo, en una discontinuidad todos los modos de Fourier tienen un valor significativo en la aproximación y el sensor S_e toma valores mayores al orden esperado. Esta idea guarda una estrecha relación con los indicadores del error para métodos espectrales [33] .

Observación 3.4.

El siguiente teorema relativo a la expansión en series de Fourier justifica la hipótesis relativa al comportamiento de S_e .

Teorema 3.1.

Sea la función f (x   ). Si se considera que la aproximación en términos de serie de Fourier periódica ${\textstyle SF(f)={\sum }_{n=-\infty }^{\infty }g_{n}e^{inx}}$ . Si ${\textstyle f(x)\in C^{k-1}}$ y ∂^kf /∂x^k es continua, entonces |g_n | ∼ n^−k para n ⟶ ∞.

En base a este comportamiento la función α (S ) queda unívocamente determinada por los valores s₁  = C (− 4 log ₁₀ (p )) y s₀  = −4 log ₁₀ (p ), siendo C una constante estrictamente positiva. Por experiencia numérica de los autores, se ha comprobado que el valor C  = 2 proporciona resultados óptimos.

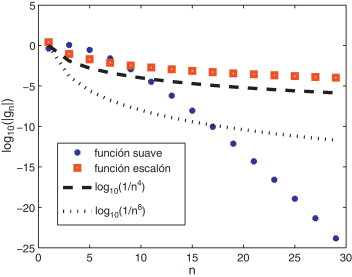
La figura 4 muestra la tasa de decaimiento para los coeficientes de la expansión de Fourier de una función continua y una función escalón, comparadas con los límites s₁ y s₀ determinados. Se puede comprobar que en efecto, la suavidad de la función dicta la velocidad de decaimiento de los coeficientes de su serie de Fourier; veáse por ejemplo [34] .

Figura 4. Tasa de decaimiento de los coeficientes de Fourier para curvas de diferente regularidad para el caso bidimensional. La curva log 10 (1/n8 ) corresponde al umbral s1 establecido.

Observación 3.5.

El sensor de discontinuidades S_e (s ) es poco fiable para aproximaciones de bajo orden (p  ≤ 2). La hipótesis de caracterizar el comportamiento de una expansión polinómica con la serie discreta de Fourier y, por lo tanto, la validez del teorema, se verifica para grado p suficientemente alto. En consecuencia se tiene que el sensor de discontinuidades es más preciso para aproximaciones de alto orden. Los tests numéricos ratifican esta propiedad.

4. Ejemplos numéricos

En esta sección se presentan diversos ejemplos numéricos de flujo compresible estacionario, en regímenes transónicos y supersónicos. Para todos los tests se han utlizado mallas triangulares y un esquema de integración temporal de tipo Runge-Kutta explícito. Para problemas estacionarios, el criterio de parada se impone mediante el residuo R (U ), ver (6) . Esta cantidad se evalúa a nivel local nodo a nodo, debido a que la solución en estado estacionario no tiene un comportamiento uniforme en todo el dominio. Los resultados obtenidos muestran el buen comportamiento de la metodología propuesta en problemas de aplicación práctica. Se demuestra el carácter local del método, así como la eficacia para altos órdenes de aproximación.

4.1. Tubo de choque o problema de Riemann

El primer ejemplo es el problema clásico del tubo de choque [35] , ampliamente usado para validar código y metodologías en dinámica de fluidos computacional. El dominio espacial es el rectángulo de dimensiones [0, 1] × [0, 0,4]. La condición inicial utilizada es la siguiente

$(\rho ,{\boldsymbol {v}},p)={\begin{array}{ll}&({\rho }_{l},{\boldsymbol {v}}_{l},p_{l})=(1,{\boldsymbol {0}},1)\quad para\quad x<1/2\\&({\rho }_{r},{\boldsymbol {v}}_{r},p_{r})=(0.1,{\boldsymbol {0}},0.125)\quad para\quad x>1/2\\&\end{array}}$

La solución en el estado estacionario se caracteriza por una onda de choque, una discontinuidad de contacto y un abanico de expansión.

El objetivo de este ejemplo es mostrar la importancia de requerir continuidad a esta función, proporcionando un rango más amplio de valores de α . Para ello se consideran 2 funciones α (S   ): una función ${\textstyle C^{0}}$ y una función tipo switch con umbral s₁ ; veáse la figura 5 (a). Todos los cálculos se han efectuado en una malla de 20 elementos longitudinales, representada en la figura 5 (b) y con aproximaciones de grado p  = 6.

Figura 5. Tubo de choque: (a) funciones α (S ) y (b) malla computacional.

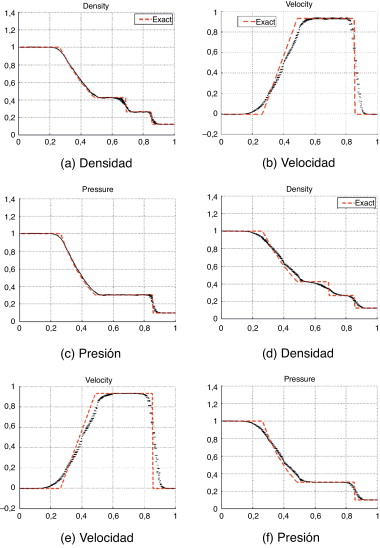
Los resultados obtenidos con ambas aproximaciones se muestran en la figura 6 . Para poder hacer una mejor comparación con la solución unidimensional se ha representado un corte a lo largo de la sección horizontal para las variables densidad, velocidad y presión. Las soluciones obtenidas con la función α (S ) continua proporcionan perfiles más angulosos que se ajustan mejor a la solución exacta. En cambio, la función switch introduce más difusión, llegando incluso a inhibir el perfil escalón característico de la solución (veáse por ejemplo la variable densidad en la figura 6 d). Además, con α -switch se obtienen perfiles que no son localmente suaves. Aunque los resultados obtenidos son satisfactorios, el método propuesto permite utilizar refinamiento adaptativo para obtenter una mejor resolución en las discontinuidades de contacto, por ejemplo, en la variable velocidad.

Figura 6. Tubo de choque: perfiles para las variables densidad, velocidad y presión calculadas con aproximaciones de grado p  = 6. Arriba: con una función α (S ) continua. Abajo: con una función α (S ) discontinua tipo switch.

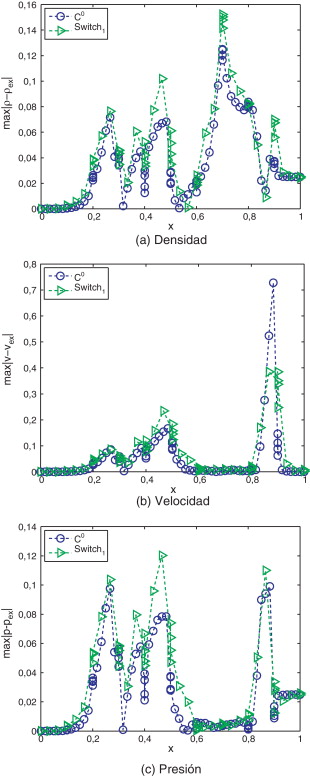
A continuación, para confirmar el buen comportamiento del método, se ha representado en la figura 7 el error absoluto entre la aproximación y la solución aproximada para las variables densidad, velocidad y presión. El análisis del error confirma los resultados observados en los perfiles de las variables: los errores obtenidos con α (S ) continua son ligeramente menores que los errores correspondientes a la solución con α -switch. Sin embargo, destaca en la variable velocidad el pico alrededor del punto x  = 0,9, debido al suavizado en la discontinuidad de contacto. Para obtener mayor precisión se deben aplicar técnicas de refinamiento local, ya que una reducción de la cantidad de difusión (i.e., valores de α más cercanos a 1) produciría la aparición de oscilaciones en las variables densidad y presión.

Figura 7. Tubo de choque: error absoluto para las funciones α (S ) testeadas.

4.2. Flujo supersónico alrededor de un bache circular

El siguiente ejemplo es un test clásico en simulaciones de flujo compresible estacionario, tanto en régimen transónico como supersónico. Veánse, por ejemplo, los trabajos [36] , [37]  and [38] . El problema consiste en un canal de dimensiones rectangulares con un bache circular de altura 4% en la pared inferior. El bache está centrado en la mitad de la pared inferior y tiene amplitud igual a 1. El número de Mach de entrada es M  = 1,4. En las paredes superior e inferior se han utilizado condicones de contorno de pared sólida no penetrante.

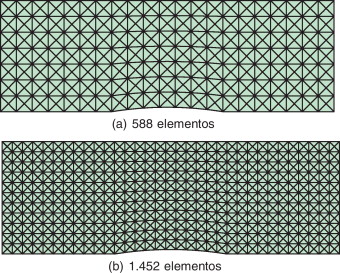
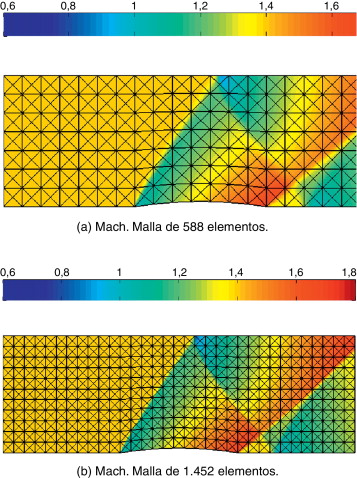
El objetivo de este test es mostrar, por una parte, el buen comportamiento del método para mallas estructuradas y alto orden de aproximación, y, por otra parte, comprobar la robustez del método, mostrando como a medida que se refina la malla, la amplitud del choque también disminuye. Se ha resuelto el problema en 2 mallas uniformes, la primera una malla grosera de 588 elementos (fig. 8 a) y en segundo lugar se ha utilizado una malla refinada de 1.452 elementos (fig. 8 b). En ambos casos se ha utiliizado una aproximación de alto orden de grado p  = 5.

Figura 8. Flujo supersónico alrededor de un bache circular: mallas de cálculo.

En las figura 9 (a) y (b) se muestra el número de Mach obtenido con ambas aproximaciones. Cualitativamente ambas aproximaciones son comparables: el choque se captura con precisión sin propagarse en los elementos vecinos. Es remarcable, especialmente para la malla grosera, la precisión del método incluso con elementos grandes: en efecto, el choque queda contenido en un elemento sin necesidad de adaptar la malla, mostrando la capacidad del método de obtener choques de espesor del orden h /p mucho menor que el tamaño del elemento. Con el fin de hacer una comparación más precisa entre ambas aproximaciones se considera una sección a lo largo del dominio correspondiente a y  = 0,4. En la figura 10 se muestran los resultados obtenidos. Por una parte, se aprecia como en ambos casos el método permite capturar choques con alta precisión evitando oscilaciones espurias, típicamente presentes en los métodos de alto orden (p  ≥ 1). Por otra parte, se puede comprobar que con la malla refinada se reduce el espesor del choque y se obtienen gradientes más fuertes.

Figura 9. Flujo supersónico alrededor de un bache circular: número de Mach.

Figura 10. Flujo supersónico alrededor de un bache circular: número de Mach.

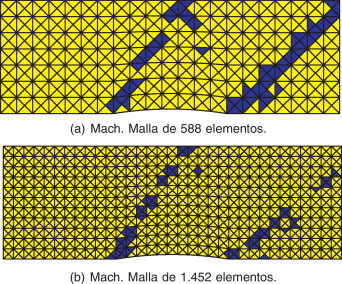
Finalmente, en las figura 11 (a) y (b) se muestra el mapa de elementos donde se ha detectado el choque. En efecto, puesto que el sensor de discontinuidades actúa elemento a elemento, el espesor de la zona detectada para la malla fina es mucho menor que en el caso de las malla grosera.

Figura 11. Flujo supersónico alrededor de un bache circular: valor del parámetro α de la base de funciones. Azul (0 ≤ α  ≤ 1), amarillo (α  = 1).

4.3. Supersonic NACA 0012

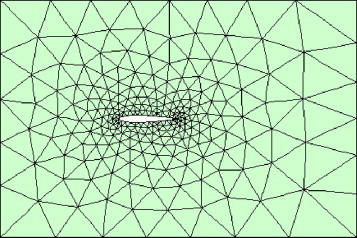
El último ejemplo corresponde al flujo aldedor de un perfil NACA0012. El flujo de la corriente libre viene dado por un número de Mach igual a 1,2 y un ángulo de incidencia β  = 0°. La malla utilizada es de 450 elementos triangulares, y 14 sobre la cuerda del perfil (en cada cara). Se ha utilizado una aproximación de grado p  = 4, en contraposición a los trabajos realizados hasta el momento por otros autores [39] , [40]  and [41] , donde se utilizan métodos de volúmenes finitos (p  = 0) o aproximaciones lineales con mallas no estructuradas y refinadas para resolver el problema. Persson y Peraire [15] resuelven también este problema con alto orden y Galerkin discontinuo utilizando un método clásico de difusión artificial, pero la especificación del término de difusión supone un problema añadido que no es fácil de de solventar (fig. 12 ).

Figura 12. Flujo supersónico alrededor de un perfil NACA0012: malla de cálculo.

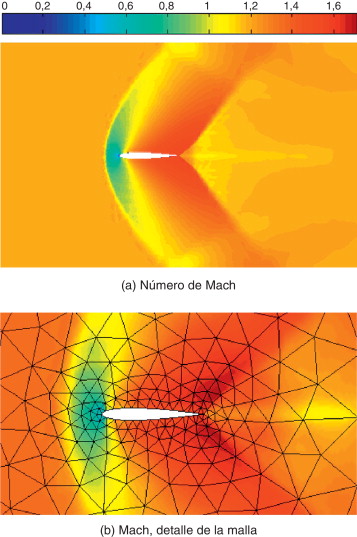
Pese a que la malla es muy grosera (compárese con la malla utilizada en otros trabajos [42] de más de 10.000 elementos), el choque queda resuelto con precisión en el interior de un solo elemento, tal y como se puede apreciar en la figura 13 (b), que muestra el detalle del número de Mach sobre la malla de fondo. Nótese que se ha utilizado una malla muy grosera (excepto en la punta del perfil aerodinámico) sin refinamiento adaptativo alrededor del choque. De nuevo en este ejemplo, la transición brusca entre la región supersónica y subsónica queda resuelta dentro de un único elemento. Cabe destacar que, en contraposición al trabajo [15] donde la solución pierde la simetría en la cola del ala, pese a utilizar el mismo sensor de discontinuidades, los resultados obtenidos con el presente método mantienen la simetría.

Figura 13. Flujo supersónico alrededor de un perfil NACA0012: número de Mach y detalle de la malla. M∞  = 1,25.

En la figura 14 se representa el mapa de valores de α . El sensor permanece inactivo en prácticamente todo el dominio, en contraste con otros métodos donde se aplica estabilización no solo en la zona del choque, sino también en los elementos adyancentes al perfil [15]  and [40] .

Figura 14. Flujo supersónico alrededor de un perfil NACA0012: elementos detectados tal que α  < 1. M∞  = 1,25.

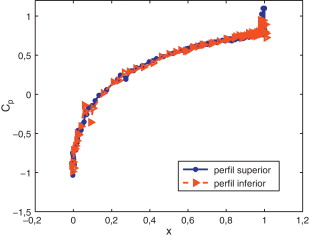
Finalmente se muestra el coeficiente de presión, que constituye una medida común para validar la precisión del método. El perfil a ambos lados del contorno de la NACA es simétrico, y no se observan apenas oscilaciones. Los resultados además son comparables con los obtenidos en la literatura [43] (fig. 15 ).

Figura 15. Flujo supersónico alrededor de un perfil NACA0012: distribución de la presión en la superficie superior e inferior del perfil del ala. M∞  = 1,25.

5. Conclusiones

En este trabajo se presenta una nueva formulación para los métodos de Galerkin discontinuo que permite tratar soluciones discontinuas, no solo en la interfaz de los elementos, sino también dentro del propio elemento. El método combina la habilidad de los métodos Galerkin discontinuo de alto orden para obtener soluciones precisas utilizando mallas groseras con la tecnología estabilizadora de los métodos de volúmenes finitos. La estabilización es inherente en el método y se evita el uso de parámetros no arbitrarios. Pese a que el método permite el uso de elementos grandes y no requiere refinamiento para obtener soluciones precisas, el uso de técnicas adaptativas es compatible con el método. Con el fin de mejorar la precisión de los resultados obtenidos los autores creen que debería hacerse un estudio más preciso entre la opción de refinamiento h o p localmente.

References

1. [1] J. Donea, A. Huerta; Finite element methods for flow problems; John Wiley & Sons, Chichester (2003)
2. [2] R.J. LeVeque; Numerical methods for conservation laws. Lectures in Mathematic ETH Zürich; (second ed.)Birkhäuser Verlag, Basel (1992)
3. [3] F. Bassi, S. Rebay; A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier-Stokes equations; J. Comput. Phys., 131 (2) (1997), pp. 267–279
4. [4] B. Cockburn, C.-W. Shu; TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. II. General framework; Math. Comp., 52 (186) (1989), pp. 411–435
5. [5] R. Biswas, K.D. Devine, J.E. Flaherty; Parallel, adaptive finite element methods for conservation laws; Appl. Numer. Math., 14 (1-3) (1994), pp. 255–283
6. [6] B. Cockburn, C.-W. Shu; Runge-Kutta discontinuous Galerkin methods for convection-dominated problems; J. Sci. Comput., 16 (3) (2001), pp. 173–261
7. [7] L. Krivodonova, J. Xin, J.-F. Remacle, N. Chevaugeon, J.E. Flaherty; Shock detection and limiting with discontinuous Galerkin methods for hyperbolic conservation laws; Appl. Numer. Math., 48 (3-4) (2004), pp. 323–338 Workshop on Innovative Time Integrators for PDEs
8. [8] T. J. Barth, Aspects of unstructured grids and finite-volume solvers for the Euler and Navier-Stokes equations (part 4). AGARD, Special Course on Unstructured Grid Methods for Advection Dominated Flows(SEE N92-27671 18-34), Provided by the SAO/NASA Astrophysics Data System, 1992.
9. [9] R.J. LeVeque; Finite volume methods for hyperbolic problems. Cambridge Texts in Applied Mathematics; Cambridge University Press, Cambridge (2002)
10. [10] B. Cockburn, S.Y. Lin, C.-W. Shu; TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. III. One-dimensional systems; J. Comput. Phys., 84 (1) (1989), pp. 90–113
11. [11] C.E. Baumann, J.T. Oden; An adaptive-order discontinuous Galerkin method for the solution of the Euler equations of gas dynamics; Int. J. Numer. Methods Eng., 47 (1-3) (2000), pp. 61–73
12. [12] A. Burbeau, P. Sagaut, C.-H. Bruneau; A problem-independent limiter for high-order Runge-Kutta discontinuous Galerkin methods; J. Comput. Phys., 169 (1) (2001), pp. 111–150
13. [13] L. Krivodonova; Limiters for high-order discontinuous Galerkin methods; J. Comput. Phys., 226 (1) (2007), pp. 879–896
14. [14] J. Von Neumann, R.D. Richtmyer; A method for the numerical calculation of hydrodynamic shocks; J. Appl. Phys., 21 (1950), pp. 232–237
15. [15] P. Persson, J. Peraire; Sub-cell shock capturing for discontinuous Galerkin methods; Proc. of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada (2006) AIAA-2006-0112
16. [16] E. Casoni, J. Peraire, A. Huerta; One-Dimensional Shock-Capturing for High-Order Discontinuous Galerkin Methods; 14 of ECCOMAS Multidisciplinary Jubilee Symposium. Computational Methods in Applied Sciences, Springer, Netherlands (2009)
17. [17] G. Chavent, B. Cockburn; The local projection P⁰P¹ -discontinuous-Galerkin finite element method for scalar conservation laws  ; RAIRO Model. Math. Anal. Numer., 23 (4) (1989), pp. 565–592
18. [18] C.-W. Shu; Total-variation-diminishing time discretizations; SIAM J. Sci. Statist. Comput., 9 (6) (1988), pp. 1073–1084
19. [19] C.-W. Shu, S. Osher; Efficient implementation of essentially nonoscillatory shock-capturing schemes; J. Comput. Phys., 77 (2) (1988), pp. 439–471
20. [20] S. Gottlieb, C.-W. Shu, E. Tadmor; Strong stability-preserving high-order time discretization methods; SIAM Rev., 43 (1) (2001), pp. 89–112 (electronic)
21. [21] D. Balsara, C.-W. Shu; Monotonicity preserving weighted essentially non-oscilllatory schemes with increasing high order of accuracy; J. Comput. Phys., 160 (2000), pp. 405–452
22. [22] J. Qiu, C.-W. Shu; Runge-Kutta discontinuous Galerkin method using WENO limiters; SIAM J. Sci. Comput., 26 (3) (2005), pp. 907–929 (electronic)
23. [23] D.N. Arnold, F. Brezzi, B. Cockburn, L.D. Marini; Unified analysis of discontinuous Galerkin methods for elliptic problems; SIAM J. Numer. Anal., 39 (5) (2001/02), pp. 1749–1779 (electronic)
24. [24] P. Castillo, B. Cockburn, I. Perugia, D. Schötzau; An a priori error analysis of the local discontinuous Galerkin method for elliptic problems; SIAM J. Numer. Anal., 38 (5) (2000), pp. 1676–1706 (electronic)
25. [25] P.L. Roe; Approximate Riemann solvers, parameter vectors, and difference schemes; J. Comput. Phys., 135 (2) (1997), pp. 250–258
26. [26] C. Hirsch; Numerical Computation of Internal and External Flows, Volume 2, Computational Methods for Inviscid and Viscous Flows; John Wiley & Sons, Brussels, Belgium (1990)
27. [27] B.V. Leer; Towards the ultimate conservative difference scheme v. a second order sequel to godunovs method; J. Comput. Phys., 135 (1997), pp. 229–248
28. [28] L. Cueto-Felgueroso, I. Colominas; High-order finite volume methods and multiresolution reproducing kernels; Arch. Comput. Methods Eng., 15 (2) (2008), pp. 185–228
29. [29] J. Barth, D. Jespersen; The design and application of upwind schemes on unstructured meshes; Proc. of the 27th AIAA Aerospace Sciences Meeting, Reno, NV (1989) AIAA-89-0366
30. [30] V. Venkatakrishnan; Convergence to steady state solutions of the euler equations on unstructured grids with limiters; J. Comput. Phys., 118 (1) (1995), pp. 120–130
31. [31] N. Nguyen, P.-O. Persson, J. Peraire; Rans solutions using high order discontinuous galerkin methods; Proc. of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada (2007) AIAA-2007-0914
32. [32] T. Koornwinder; Askey-wison polynomials for root systems of type bc; Contempo. Math., 138 (1992), pp. 189–204
33. [33] C. Mavriplis; Adaptive mesh strategies for the spectral element method; Comput. Methods Appl. Mech. Engrg., 116 (1994), pp. 77–86
34. [34] D. Gottlieb, J.S. Hesthaven; Spectral methods for hyperbolic problems; J. Comput. Appl. Math., 128 (1-2) (2001), pp. 83–131 Numerical analysis 2000, VII, Partial differential equations
35. [35] G. Sod; A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws; J. Comput. Phys., 27 (4) (1978), pp. 1–31
36. [36] F. Moukalled, M. Darwish; A high-resolution pressure-based algorithm for fluid flow at all speeds; J. Comput. Phys., 168 (1) (2001), pp. 101–133
37. [37] H. Luo, J.D. Baum, R. Löhner; A hermite weno-based limiter for discontinuous galerkin method on unstructured grids; J. Comput. Phys., 225 (1) (2007), pp. 686–713
38. [38] V. Dolejsí, M. Feistauer; A semi-implicit discontinuous Galerkin finite element method for the numerical solution of inviscid compressible flow; J. Comput. Phys., 198 (2) (2004), pp. 727–746
39. [39] L. Cueto-Felgueroso, Partículas, volúmenes finitos y mallas no estructuradas: simulación numérica de problemas de dinámica de fluidos. PhD thesis, Universidad da Coruña, España, 2006.
40. [40] X. Nogueira, et al.; Detección de ondas de choque mediante el métodos de mínimos cuadrados móviles para discretizaciones de alto orden en mallas no estructuradas; Proceedings of Congreso de Métodos Numéricos en Ingeniería 2009, Barcelona, España (2009)
41. [41] M. Aksas, A.H. Benmachiche; Multidimensional upwind schemes for the euler equations on unstructured grids; IJE, 3 (2) (2009), pp. 185–200
42. [42] O. Arias, O. Falcinelli, N. Fico, S. Elaskar; Finite volume simulation of a flow over a NACA 0012 using Jamseon, MacCormack, Shu and TVD esquemes; Mecánica Computacional, XXVI (2007), pp. 3097–3116
43. [43] H. Viviand; Numerical solutions of two-dimensional reference tests cases; AGARD AR-211 (1985)