Coloración en gráficas de mapas en la Tierra y mapas en la Luna

1 Introducción

La coloración de mapas de la tierra es uno de los problemas de optimización más estudiados en la Teoría de Grafos. El problema de la coloración de un mapa consiste en asignar un color a cada vértice (país) de tal manera que dos vértices conectados por una arista obtengan colores diferentes, minimizando el número total de colores utilizados.

Ahora, la siguiente afirmación no es verdadera:

"Es posible asignar uno de cuatro colores a cada país en cualquier mapa, de manera que ningún par de países que compartan una frontera tengan el mismo color." [1]

Sin embargo, este no es el enunciado del famoso Teorema de los Cuatro Colores, que fue demostrado hace más de 30 años utilizando numerosas comprobaciones por computadora.

La figura 1 muestra un pequeño ejemplo de un mapa que necesita cinco colores si cada par de países adyacentes debe recibir colores diferentes. La característica importante es que un país (5) es desconectado y está compuesto por dos regiones.

Figure 1: Un mapa plano que necesita cinco colores. Mapa tomado de [1].

Los mapas que incluyen países desconectados son posibles; un ejemplo es el mapa de América del Norte. Esto plantea la siguiente pregunta: ¿Es posible colorear el mapa actual del mundo con cuatro colores de manera que todas las partes de cada país reciban el mismo color y que dos países diferentes con un arco fronterizo en común no reciban el mismo color? Para dar una respuesta afirmativa a dicha pregunta nos apoyaremos en el siguiente teorema.

Teorema de los Cuatro Colores: Este teorema establece que cualquier mapa dibujado en el plano puede colorearse con solo cuatro colores, de tal manera que cada par de regiones conectadas que comparten un borde reciban colores diferentes.

Escrito en términos de grafos:

Teorema 1: [2]Cualquier grafo planar simple ${\textstyle G}$ es ${\textstyle 4}$-coloreable.

Donde:

Definición 1: Un grafo es una pareja ordenada ${\textstyle G=(V,E)}$, donde ${\textstyle V}$ es un conjunto no vacío de objetos llamados vértices (nodos) y ${\textstyle E}$ es un conjunto de aristas (líneas) entre los pares de vértices de ${\textstyle G}$. Antes de continuar estableceremos la siguiente notación.

• Sea ${\textstyle V}$ el conjunto de vértices. Es habitual utilizar letras minúsculas para representar dichos vértices, es decir ${\textstyle V=\{a,b,c,\dots \}}$. También se usan letras enumeradas con subíndices, esto es ${\textstyle V=\{v_{1},v_{2},v_{3},\dots \}}$.

• El conjunto de aristas ${\textstyle E\subseteq V\times V}$, describe una relación entre los vértices de ${\textstyle G}$. Comúnmente se describe a ${\textstyle E}$ etiquetando cada arista, es decir, ${\textstyle E=\{e_{1},e_{2},e_{3},\dots \}}$, donde la arista ${\textstyle e_{i}:=(u_{i},v_{i})}$ o ${\textstyle (v_{i},u_{i})}$ denota la conexión entre los vértices ${\textstyle u_{i}}$ y ${\textstyle v_{i}}$. También usaremos la siguiente manera más simplificada ${\textstyle E=\{u_{1}v_{1},u_{2}v_{2},\dots \}}$.

Definición 2: Una coloración (o coloración propia) de vértices en grafos es una asignación de colores a los vértices de un grafo ${\textstyle G}$. De tal manera que cualquiera vértices adyacentes tienen distintos colores. Es decir, se busca una función

$\varphi :V\longrightarrow Colores=\left\{1,2,\dots ,k\right\}$

de tal forma que si ${\textstyle uv\in E{\hbox{ entonces }}\varphi (u)\neq \varphi (v).}$

• Una coloración usando exactamente ${\textstyle s}$ colores se llama s-coloración.
• Un grafo es k-coloreable si existe una ${\textstyle s}$-coloración de G para algún entero ${\textstyle s\leq k}$.

Este resultado fue propuesto por primera vez en 1852 por Francis Guthrie. Una demostración fue publicada en 1879 por Kempe, pero 11 años después, Heawood encontró un error en la prueba. Finalmente, en 1976, el teorema fue demostrado por Appel y Haken, aunque de una manera inusual. Brevemente, la demostración de Appel y Haken consiste en mostrar que cada mapa plano contiene solo una de una lista de al menos 1,800 configuraciones, y que cada configuración admite una reducción, permitiendo una demostración por inducción. Aunque los números involucrados son inusualmente grandes, la parte más inusual de la prueba es que se utilizaron aproximadamente 1,200 horas de tiempo de computadora para generar la lista de 1,800 configuraciones y verificar que las coloraciones de estas admitían la reducción necesaria [1].

El mapa de la figura 1 también podría representar límites políticos en los que el área 5 represente, por ejemplo, un imperio. Cuando Heawood encontró tanto un error en el argumento de Kempe como descubrió que no podía corregirlo, inventó generalizaciones sobre la coloración de mapas que, hasta cierto punto, pudo resolver. Su investigación dio origen al campo de la Teoría de Grafos Topológicos tal como se estudia hoy en día. Primero investigó el problema de la coloración de imperios: si los mapas están formados por países unidos en imperios, ¿cuántos colores se necesitan para colorear tales mapas, siempre que todos los países en un imperio reciban el mismo color y que los imperios con una frontera común reciban colores diferentes?

Ringel sugirió una variación del problema de la coloración de imperios. Supongamos que la Luna fuera colonizada y quisiéramos colorear un mapa de la tierra y la luna con el mínimo número de colores de tal forma que:

1. Las regiones adyacentes en la tierra o en la luna reciban colores diferentes, y
2. Un país en la tierra y su colonia lunar reciban el mismo color.

A este problema se le conoce como el Problema de la Tierra-Luna. Este problema ha estado abierto durante más de 20 años.

Por último se añade un teorema y un corolario que usaremos más adelante:

Teorema 2: Sea G un grafo de orden n y tamaño m, cuyo conjunto de vértices es ${\textstyle V=\{v_{1},v_{2},\dots ,v_{n}\}}$. Entonces se satisface que;

$\sum _{i=1}^{n}deg(v_{i})=2m.$

Corolario 1: Si ${\textstyle G}$ es un grafo planar de orden ${\textstyle n\geq 3}$ y tamaño ${\textstyle m}$, entonces se cumple la siguiente desigualdad:

$m\leq 3n-6.$

2 Complejidad computacional de problemas que involucran coloración en grafos.

Comenzaremos con algunas definiciones antes de pasar a los resultados principales. Tanto en las matemáticas como en la teoría de la informática se han estudiado diferentes aspectos de los problemas de decisión. Algunos de estos estudios se enfocan en determinar si existen algoritmos eficientes para resolverlos y en qué medida algunos problemas de decisión son más difíciles de resolver que otros. Al analizar estos problemas, encontramos que algunos presentan mayor complejidad que otros. Un problema de decisión importante dentro de la teoría de grafos, que será el principal objeto de estudio en esta sección, es el llamado 3-coloración de grafos planares. Este problema consiste en:

Determinar si dado cualquier grafo planar no dirigido $G$, es posible colorear los vértices de $G$ con tres colores, digamos (Azul, Rojo y Verde) de tal manera que ningún par de vértices adyacentes tenga el mismo color.

El problema de determinar si es posible colorear un grafo planar con 3 colores se convierte en un problema de decisión con el siguiente formato:

Problema: 3-coloración de grafos planares G.

Entrada: Un grafo planar no dirigido. ¿Es 3-coloreable?

Salida: Sí o No. ${\textstyle {\begin{array}{l}\\\end{array}}}$ Sí, nos dice que el grafo es 3-coloreable; No, nos dice que no lo es.

La segunda pregunta que nos hacemos en este caso es:

¿Qué tan difícil es este problema desdel punto de vista computacional?

Para la elaboración de esta sección se consultaron los libros [3] [4] [5] y los artículos [6] [7].

Definición 3: Un problema de decisión es aquel que admite únicamente dos posibles respuestas: “Sí” o “No”, para cualquier entrada.

Para resolver problemas de decisión y otros tipos de problemas matemáticos, a menudo recurrimos a algoritmos. Estos son fundamentales para la solución de problemas tanto en computación como en matemáticas. Su definición es la siguiente:

Definición 4: Un algoritmo es un conjunto finito de instrucciones matemáticas bien definidas, que, cuando se ejecutan correctamente, produce un resultado específico a partir de una entrada dada.

Los algoritmos suelen ser vistos como una secuencia de instrucciones matemáticas para resolver problemas.

Un problema de decisión que puede ser resuelto a través de un algoritmo en un tiempo finito se llama decidible.

Entender los algoritmos es fundamental para resolver problemas computacionales. Sin embargo, no solo es importante encontrar una solución, sino también evaluar cuan eficiente es el algoritmo que utilizamos. Aquí es donde entra en juego el concepto de complejidad de un algoritmo, que a continuación definimos.

Definición 5: La complejidad de un algoritmo se refiere al tiempo y la memoria requeridos para ejecutar el algoritmo en función del tamaño de la entrada.

Para cuantificar la complejidad, utilizamos la notación Big-O, denotada como ${\textstyle O(g(n))}$, que describe el crecimiento de una función ${\textstyle f}$ en términos del tamaño de la entrada. La comprensión de la notación Big-O es esencial para evaluar y comparar algoritmos en términos de su eficiencia.

Definición 6: (Big-O) Sean ${\textstyle f}$, ${\textstyle g}$ ${\textstyle :\mathbb {N} \rightarrow \mathbb {R} }$ dos funciones definidas en los números enteros positivos, ${\textstyle \mathbb {N} }$. Decimos que ${\textstyle g}$ es una cota superior asintótica para ${\textstyle f}$ si existe un número real ${\textstyle C\in \mathbb {R} }$ y un entero positivo ${\textstyle n_{0}\in \mathbb {N} }$ tal que:

$|f(n)|\leq C|g(n)|\quad {\mbox{para todo numero entero positivo }}n\geq n_{0}.$

En tal caso, se escribe

$f=O(g){\mbox{ o }}f\in O(g).$

La cota superior asintótica ${\textstyle g(n)}$ se elige típicamente de manera que sea lo más simple y pequeña posible. Decimos que ${\textstyle f(n)}$ tiene un crecimiento lineal, cuadrático, cúbico o polinomial en ${\textstyle n}$ si ${\textstyle f(n)}$ pertenece a ${\textstyle O(n)}$, ${\textstyle O(n^{2})}$, ${\textstyle O(n^{3})}$ o ${\textstyle O(n^{k})}$ para algún ${\textstyle k\in \mathbb {N} }$, respectivamente. Cuando hablamos de la eficiencia de un algoritmo, nos referimos al tiempo que este tarda en ejecutarse en función del tamaño de la entrada. Los algoritmos con tiempo de ejecución polinomial, como la suma o multiplicación de números, se consideran eficientes. Por otro lado, si un algoritmo necesita iterar sobre cada instancia de un conjunto con ${\textstyle 2^{n}}$ elementos, su complejidad es exponencial en $n$. Un problema se considera difícil si no existe un algoritmo eficiente, es decir, de tiempo polinomial, que pueda resolverlo.

Existen clases distintas de problemas; aquellos cuyos algoritmos tienen tiempo de ejecución polinomial, o no.

3 Clases de problemas

A continuación definimos las clases de problemas más usados, para preparar esta sección nos basamos en las notas del curso Design and Analysis of Algoritms del Profesor Erick Demaine [6].

Definición 7:  

• Un algoritmo es polinomial si para algún ${\textstyle k}$, su tiempo de ejecución sobre las entradas de tamaño ${\textstyle n}$ es ${\textstyle O(n^{k})}$. La clase de problemas tractables, denotada por P, comprende los problemas de decisión que se pueden resolver mediante un algoritmo de tiempo polinomial. Estos problemas se consideran eficientes.

• La clase de problemas NP, denominada tiempo polinomial no determinista es la clase de problemas de decisión en los que se permite adivinar y verificar su solución en tiempo polinomial. El hecho de que una solución pueda adivinarse a partir de muchas opciones polinomiales en tiempo constante se le conoce como no-determinista.

Definición 8: Dentro de la clase de problemas NP hay una clase de problemas denominados NP-completos, que en términos generales son considerados difíciles de resolver y si existe un algoritmo que pueda resolver un problema NP-completo en tiempo polinomial, entonces también puede resolver cualquier otro problema NP en tiempo polinomial. En otras palabras, un problema ${\textstyle X}$ es NP-completo si ${\textstyle X\in }$ NP-hard (véase definición abajo).

En la práctica, verificar si una prueba es válida parece ser más sencillo que encontrar la solución a un problema. Sin embargo, en el campo de la informática, persiste una pregunta fundamental sin resolver: ¿Es la clase NP estrictamente más grande que la clase P? Esta pregunta es una de las incógnitas más importantes en la teoría de algoritmos.

Definición 9: Una reducción del problema ${\textstyle A}$ al problema ${\textstyle B}$ en tiempo polinomial, denotada por ${\textstyle A\leq _{p}B}$, es una transformación tal que existe un algoritmo que convierte las entradas del problema ${\textstyle A}$ en entradas equivalentes del problema ${\textstyle B}$ en tiempo polinomial. Equivalente significa que para cualquier entrada, el problema ${\textstyle A}$ y el problema ${\textstyle B}$ producen la misma respuesta (sí o no). Sea ${\textstyle A\leq _{p}B}$:

• Si ${\textstyle A\in NP-hard}$, entonces ${\textstyle B\in NP-hard.}$

• Si ${\textstyle B\in P}$, entonces ${\textstyle A\in P}$.
• Si ${\textstyle B\in NP}$, entonces ${\textstyle A\in NP}$.

Definición 10: Un problema ${\textstyle X}$ es NP-hard o NP-duro si cada problema ${\textstyle Y\in NP}$ se reduce a ${\textstyle X}$. Es decir, un problema es NP-hard si es al menos tan dificil como todos los problemas en NP.

Con lo anterior podemos definir formalmente los problemas NP-completos.

Definición 11: Un problema ${\textstyle X}$ es NP-completo si ${\textstyle X\in NP}$ y ${\textstyle X}$ es ${\textstyle NP}$-hard.

Un ejemplo muy famoso de problemas ${\textstyle NP}$-completos es el problema denominado ${\textstyle 3}$SAT, con el fin de hacer este trabajo auto contenido y definir formalmente un problema ${\textstyle 3}$SAT introduciremos las siguientes definiciones.

Definición 12: Una fórmula booleana es una expresión formada con las variables ${\textstyle u_{1},\ldots ,u_{n}}$ con ${\textstyle u_{i}\in \{0,1\}}$ para ${\textstyle i\in \{1,2,\dots ,n\}}$, junto con los operadores lógicos y (${\textstyle \wedge }$), no (¬) y o (${\textstyle \vee }$). Sea ${\textstyle \varphi }$ una fórmula booleana y ${\textstyle z\in \{0,1\}^{n}}$, entonces ${\textstyle \varphi (z)}$ denota el valor de ${\textstyle \varphi }$ cuando a las variables de ${\textstyle \varphi }$ se les asignan los valores ${\textstyle z}$. Se dice que una fórmula ${\textstyle \varphi }$ satisface (o tiene solución) si existe alguna asignación ${\textstyle z}$ tal que ${\textstyle \varphi (z)}$ sea verdadera. Una fórmula booleana está en forma CNF (Forma Normal Conjuntiva) si es una conjunción (y) de disyunciones (o) de variables o sus negaciones. Es decir, una fórmula CNF tiene la forma

$\bigwedge _{i}\left(\bigvee _{j}v_{ij}\right),$

donde cada ${\textstyle v_{ij}}$ es un literal que puede ser la variable ${\textstyle u_{k}}$ o su negación ${\textstyle \neg u_{k}}$. Los términos ${\textstyle v_{ij}}$ se llaman literales y las expresiones ${\textstyle \left(\bigvee v_{ij}\right)}$ se llaman cláusulas. Un $k$CNF es una fórmula CNF en la cual todas las cláusulas contienen a lo sumo ${\textstyle k}$ literales.

Con esta definición podemos dar paso a una definición formal de un tipo de fórmula booleana denominada $3$SAT, para después demostrar que el problema de decidir si una fórmula booleana que está en 3CNF es o no válida se reduce a un problema de ${\textstyle 3}$-coloración en grafos en tiempo polinomial y viceversa. Así que son equivalentemente difíciles y concluiremos que el problema de ${\textstyle 3}$-coloración en grafos es NP-completo pues ${\textstyle 3}$SAT lo es.

Definición 13: $3$SAT: El problema de decisión ${\textstyle 3}$SAT se puede plantear como sigue. Dada una fórmula booleana de la forma:

$(x_{1}\vee x_{3}\vee x_{6})\wedge ({\overline {x_{2}}}\vee x_{3}\vee x_{7})\wedge \ldots ,$

¿Existe una asignación de variables verdadero (1) y falso (0), tal que toda la fórmula evalúe a verdadero (1)?

Fue probado que el problema $3$SAT resulta ser NP-completo por Cook en 1971 [4]. A continuación, enunciamos el teorema y definimos formalmente el problema:

Teorema 3: (Teorema de Cook-Levin [4]) Sea SAT el lenguaje de todas las fórmulas CNF que tienen solución y ${\textstyle 3}$SAT el lenguaje de todas las fórmulas 3CNF que tienen solución. Entonces:

1. SAT es NP-completo.
2. ${\textstyle 3}$SAT es NP-completo.

En el problema de decisión de 3-coloración, se nos da un grafo ${\textstyle G}$ y nos preguntamos si existe una forma de colorear los vértices de dicho grafo utilizando tres colores, a saber: rojo, verde o amarillo, de tal manera que ningún par de vértices adyacentes comparta el mismo color.

El objetivo de esta sección es demostrar una reducción en tiempo polinomial del problema ${\textstyle 3}$SAT al problema de 3-coloración. Es decir, demostraremos el siguiente teorema:

Teorema 4: 3${\textstyle SAT\leq _{p}3-}$Coloración.

Antes de demostrar este teorema, esbozaremos la estrategia de la prueba. Dada una entrada del problema ${\textstyle 3}$SAT (una fórmula booleana), debemos construir un grafo que será 3-coloreable si y solamente si la fórmula booleana tiene solución. La idea de la siguiente prueba fue tomada de [7].

La demostración se ejecutará en varios pasos.

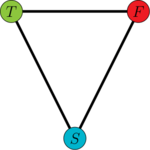
• Paso 1: Comenzamos construyendo un grafo que contiene 3 vértices etiquetados como ${\textstyle T}$, ${\textstyle F}$, y ${\textstyle S}$, conectados formando un triángulo. Coloreamos estos vértices con tres colores diferentes. Sin pérdida de generalidad, podemos colorearlos como se muestra en la figura 2:

Figure 2: Primer paso

En esta construcción, el color verde indica los valores verdaderos, el color rojo indica los valores falsos y el color de ${\textstyle S}$ no representa ningún valor.

• Paso 2: En nuestra fórmula, tenemos variables y negaciones de variables, conocidas como literales. Debemos asignar valores a los literales, por lo que basta asignar valores a su variable correspondiente. Para asegurar esto, hacemos lo siguiente:

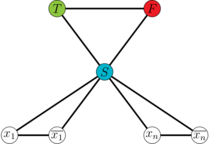
Para cada varibale ${\textstyle x_{i}}$ y su negación ${\textstyle {\overline {x_{i}}}}$, creamos dos vértices en nuestro grafo y conectamos estos vértices al vértice ${\textstyle S}$, como se muestra en la figura 3.

Figure 3: Segundo paso

Esto asegura que los literales ${\textstyle x_{i}}$ y ${\textstyle {\overline {x_{i}}}}$ no reciban el mismo color que el vértice ${\textstyle S}$, ya que están conectadas a ${\textstyle S}$ y, por lo tanto, deben ser coloreadas de rojo o verde. Para garantizar que ${\textstyle x_{i}}$ y ${\textstyle {\overline {x_{i}}}}$ no reciban el mismo color (es decir, que si ${\textstyle x_{i}}$ es verdadero, entonces ${\textstyle {\overline {x_{i}}}}$ sea falso, y viceversa), conectamos el vértice ${\textstyle x_{i}}$ con el vértice ${\textstyle {\overline {x_{i}}}}$, como se muestra en la figura 3.

De esta manera, si coloreamos el grafo de una forma válida, obtendremos valores de verdad para las variables y sus negaciones que son consistentes.

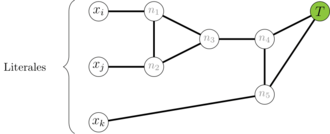
• Paso 3: Finalmente, necesitamos representar cada cláusula de la fórmula booleana a través de un grafo. Para ello, representaremos el operador booleano ${\textstyle OR}$ mediante una construcción que llamaremos “gadget” (véase figura 4). Este gadget es ${\textstyle 3}$-coloreable si y solo si al menos una de las literales en la cláusula es asignada o coloreada con ${\textstyle T}$ (verdadero), como veremos a continuación.

Figure 4: Tercer paso

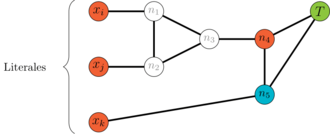
En el gadget de la figura 4, si todas las literales se colorean como Falso (rojo), el vértice ${\textstyle n_{5}}$ debe ser coloreado de azul, ya que está conectado a ${\textstyle T}$ (verde) y a ${\textstyle x_{k}}$ (rojo). A continuación, el vértice ${\textstyle n_{4}}$ debe ser coloreado de rojo, ya que está conectado a ${\textstyle T}$ (verde) y a ${\textstyle n_{5}}$ (azul), como se muestra en la figura 5:

Figure 5: Coloración del tercer paso

Esto implica que ni el vértice ${\textstyle n_{3}}$, ni ${\textstyle n_{1}}$, ni ${\textstyle n_{2}}$ pueden ser coloreados de rojo. Por lo tanto, solo pueden tener los colores verde o azul. Sin embargo, al tratarse de tres vértices y solo dos colores disponibles, necesariamente habrá un par de vértices que compartan el mismo color. Como estos tres vértices están conectados entre sí, se produciría una contradicción, ya que dos vértices conectados tendrían el mismo color. De este modo, si las tres literales son falsas, es imposible colorear el gadget.

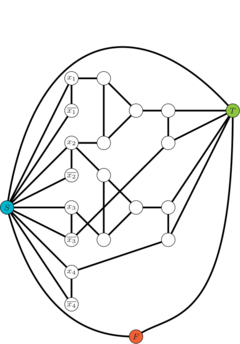
• Paso 4: El paso final consiste en intersectar los gadgets, es decir, se crea un gadget por cada cláusula y se busca empatar esos gadgets. Aunque el resultado es grande, está bien estructurado, como se muestra en la figura 6. De este modo, el grafo resultante es 3-coloreable si y solo si la fórmula booleana se satisface.

En el caso de que la fórmula booleana representada por la figura no se satisfaga, es decir, si ${\textstyle x_{1}}$, ${\textstyle x_{2}}$, y ${\textstyle {\overline {x_{3}}}}$ son coloreadas de rojo, entonces al aplicar el proceso descrito en el paso 3, se llega a la conclusión de que es imposible colorear el grafo.

Figure 6: Reducción completa de la fórmula $3$SAT $(x_{1}\vee x_{2}\vee {\overline {x_{3}}})\wedge (x_{2}\vee x_{3}\vee x_{4})$ a una $3$-coloración

• Paso 5: Para demostrar que esta reducción se realiza en tiempo polinomial, supongamos que la fórmula tiene ${\textstyle n}$ variables y ${\textstyle m}$ cláusulas. Entonces, el número de vértices y aristas se calcula de la siguiente manera:

Vértices:

• 3 vértices para el triángulo formado por los vértices ${\textstyle T}$, ${\textstyle F}$ y ${\textstyle S}$ (figura 2).
• 2 vértices por cada variable: se requieren ${\textstyle 2n}$ vértices extra (figura 3).
• 5 vértices por cada cláusula: se requieren ${\textstyle 5m}$ vértices extra (figura 4).

${\textstyle {\begin{array}{l}\\\end{array}}}$ Aristas:

• 3 aristas para el triángulo formado por los vértices ${\textstyle T}$, ${\textstyle F}$ y ${\textstyle S}$ (figura 2).
• Aristas entre pares ${\textstyle (x_{i},{\overline {x_{i}}})}$ opuestos a las literales: ${\textstyle n}$ aristas (figura 3).
• Aristas de las literales al vértice ${\textstyle S}$: Se tienen ${\textstyle 2n}$ aristas (figura 3).
• 10 aristas por cláusula (gadget): Se tienen ${\textstyle 10m}$ aristas (figura 4).

De este modo, el grafo generado tiene ${\textstyle 2n+5m+3}$ vértices y ${\textstyle 3n+10m+3}$ aristas. La construcción del grafo se realiza en un número de pasos que es polinomial respecto a ${\textstyle n}$ y ${\textstyle m}$, garantizando así que la reducción se lleva a cabo en tiempo polinomial.

Hasta ahora hemos probado que un problema ${\textstyle 3}$SAT se reduce a un problema de ${\textstyle 3}$-coloración en grafos en general. Como ${\textstyle 3}$SAT es un problema NP-completo por la reducción la ${\textstyle 3}$-coloración en grafos también lo es.

Otra forma de demostrar que los problemas de ${\textstyle 3}$-coloración en grafos son NP es modelar este problema como un problema de satisfacción de restricciones, dado que estos últimos son NP. En general, aunque en 2017 se demostró que, en el caso de que P ${\textstyle \neq }$ NP [8], los problemas de satisfacción de restricciones pertenecen a la clase de problemas en los que se satisface la dicotomía; es decir, son P o son NP.

4 Problemas de Satisfacción de Restricciones.

Los Problemas de Satisfacción de Restricciones (CSP, por sus siglas en inglés) constituyen un área fundamental en la teoría de la computación. Estos se definen como conjuntos de objetos que deben satisfacer una serie de restricciones o limitaciones.

A continuación, los definiremos formalmente:

Definición 14: Un Problema de Satisfacción de Restricciones CSP se define como una tripleta ${\textstyle \langle X,D,C\rangle }$, donde:

• ${\textstyle X=\{x_{1},x_{2},x_{3},\ldots \}}$ es un conjunto de variables, que puede o no ser infinito.
• ${\textstyle D=\{d_{1},d_{2},d_{3},\ldots \}}$ es el conjunto de valores que pueden tomar las variables o dominio.
• ${\textstyle C=\{c_{1},c_{2},\ldots ,c_{k}\}}$ es un conjunto finito de restricciones, donde cada restricción ${\textstyle c_{i}}$ = ${\textstyle \langle t_{i},R_{i}\rangle }$ para ${\textstyle i\in \{1,2,\dots ,k\}}$ consiste de una ${\textstyle n_{i}}$-tupla de variables ${\textstyle t_{i}=(x_{i1},x_{i2},\ldots ,x_{in_{i}})}$ y una relación $n_{i}$-aria ${\textstyle R_{i}}$ sobre ${\textstyle D}$.

Definición 15: Una evaluación de las variables es una función

$\varphi :X\rightarrow D.$

Decimos que una evaluación ${\textstyle \varphi }$ satisface una restricción ${\textstyle c_{i}=\langle t_{i},R_{i}\rangle }$ con ${\textstyle t_{i}=(x_{i1},x_{i2},\ldots ,x_{in_{i}})}$ si la tupla de valores ${\textstyle (\varphi (x_{i1}),\varphi (x_{i2}),\ldots ,\varphi (x_{in_{i}}))}$ pertenece a la relación ${\textstyle R_{i}}$. Una solución del CSP es una evaluación que satisface todas las restricciones del problema.

Muchos problemas prácticos pueden modelarse como problemas de satisfacción de restricciones. Un ejemplo clásico de esto es el problema de satisfacibilidad booleana (SAT) visto en la sección anterior. En esencia, este problema implica encontrar asignaciones de valores a variables que hagan que una fórmula lógica proposicional sea verdadera. A continuación mostraremos como un problema SAT se modela como un problema CSP. El siguiente ejemplo se construyó tomando como base el ejemplo del libro [5].

Ejemplo 1: El problema de satisfacibilidad booleana (SAT) consiste en determinar si existen valores de ceros y unos para las variables de una fórmula lógica proposicional como la siguiente, que hagan verdadera la fórmula. Consideremos la siguiente fórmula:

$t(x_{1},x_{2},x_{3},x_{4}):=(x_{1}\lor x_{2}\lor x_{3}\lor x_{4})\land ({\overline {x_{1}}}\lor {\overline {x_{2}}}\lor x_{3})\land$ $({\overline {x_{3}}}\lor {\overline {x_{4}}}\lor x_{1})\land ({\overline {x_{3}}}\lor {\overline {x_{2}}}\lor x_{4})\land ({\overline {x_{1}}}\lor {\overline {x_{3}}}).$

El problema consiste en asignar valores de ${\textstyle 0}$ o ${\textstyle 1}$ para ${\textstyle a_{1},a_{2},a_{3},a_{4}}$ de tal manera que al evaluar la fórmula ${\textstyle t}$, esta resulte verdadera, es decir, ${\textstyle t(a_{1},a_{2},a_{3},a_{4})=1}$. Este tipo de problemas se puede expresar como un CSP, en específico, de la siguiente manera:

• Sea ${\textstyle V=\{x_{1},x_{2},x_{3},x_{4}\}}$.
• Sea ${\textstyle D=\{0,1\}}$.
• Sea ${\textstyle C}$ el conjunto de restricciones definido por:

$C:=\left\{c_{1},c_{2},c_{3},c_{4},c_{5}\right\}$

donde:

• ${\textstyle c_{1}:=((x_{1},x_{2},x_{3},x_{4}),D^{4}\setminus \{(0,0,0,0)\})}$.
• ${\textstyle c_{2}:=((x_{1},x_{2},x_{3}),D^{3}\setminus \{(1,1,0)\})}$.
• ${\textstyle c_{3}:=((x_{3},x_{4},x_{1}),D^{3}\setminus \{(1,1,0)\})}$.
• ${\textstyle c_{4}:=((x_{3},x_{2},x_{4}),D^{3}\setminus \{(1,1,0)\})}$.
• ${\textstyle c_{5}:=((x_{1},x_{3}),D^{2}\setminus \{(1,1)\})}$.

Por lo tanto, la solución del ejemplo anterior consiste en encontrar las asignaciones de valores ${\textstyle \varphi :X\rightarrow D}$ que satisfagan todas las restricciones del problema. En este caso, las soluciones son las siguientes:

${\begin{matrix}\quad &x_{1}&x_{2}&x_{3}&x_{4}\\\end{matrix}}$

${\begin{matrix}\varphi _{1}&\\\varphi _{2}&\\\varphi _{3}&\\\varphi _{4}&\\\varphi _{5}&\\\varphi _{6}&\end{matrix}}{\begin{matrix}0&0&0&1\\0&0&1&0\\0&1&0&0\\0&1&0&1\\1&0&0&0\\1&0&0&1\end{matrix}}$

Los CSP abarcan una amplia gama de problemas, desdel famoso Problema de las Ocho Reinas hasta el desafiante Teorema de los Cuatro Colores en la coloración de mapas. Numerosos juegos y rompecabezas, como por ejemplo el Sudoku, pueden modelarse como problemas de satisfacción de restricciones.

A continuación, formularemos el problema de coloración de mapas como un problema CSP, donde la tarea consiste en determinar si un mapa dado puede ser coloreado con tres colores distintos de manera que ningún par de regiones adyacentes tenga el mismo color.

Definición 16: El Problema de Coloración de un grafo (véase teorema 2). Sea un grafo ${\textstyle G=(V,E)}$ donde ${\textstyle V=\{v_{1},v_{2},\dots ,v_{n}\}}$ es el conjunto de vértices y ${\textstyle E=\{e_{1},e_{2},\dots ,e_{m}\}}$ es el conjunto de aristas. El problema consiste en determinar si es posible colorear los vértices de ${\textstyle G}$ con ${\textstyle k}$ colores de tal manera que vértices adyacentes tengan colores diferentes.

El problema anterior lo formularemos como un CSP, donde:

• ${\textstyle X=\{v_{1},v_{2},\ldots ,v_{n}\}}$ es el conjunto de vértices de ${\textstyle G}$.
• ${\textstyle D=\{d_{1},d_{2},\ldots ,d_{k}\}}$ es el conjunto de colores que pueden asignarse a los vértices.
• ${\textstyle C=\{c_{1},c_{2},\ldots ,c_{m}\}}$ es el conjunto de restricciones, donde cada restricción ${\textstyle c_{i}=}$ ${\textstyle \langle e_{i},\neq _{D}\rangle }$ para ${\textstyle i\in \{1,2,\dots ,m\}}$, con ${\textstyle e_{i}=(u_{i},v_{i})}$ representando las aristas de ${\textstyle G}$ y ${\textstyle \neq _{D}}$ la relación de desigualdad sobre ${\textstyle D}$, definida como:

$\neq _{D}=\{(d_{i},d_{j})\in D^{2}\mid d_{i}\neq d_{j}\}.$

Por lo tanto, una solución al problema de colorear el mapa consiste en encontrar una función

$\varphi :X\longrightarrow D$

que asigne un color a cada vértice en ${\textstyle v_{i}\in X}$ con ${\textstyle i\in \{1,2,\dots ,n\}}$ tal que

${\hbox{para todo }}e_{i}=(u_{i},v_{i})\in E{\hbox{ entonces }}(\varphi (u_{i}),\varphi (v_{i}))\in \neq$

Lo anterior equivale a ver si

${\hbox{para todo }}e_{i}=(u_{i},v_{i})\in E{\hbox{ entonces }}\varphi (u_{i})\neq \varphi (v_{i})$

Finalizaremos esta sección modelando un problema de ${\textstyle 3}$-coloración como un problema ${\textstyle 3}$SAT.

Ejemplo 2: Modelando un problema de $3$-coloración de grafos como un problema $3$SAT.${\textstyle {\begin{array}{l}\\\end{array}}}$ Sea un grafo ${\textstyle G=(V,E)}$. Formularemos este problema como un ${\textstyle 3}$SAT de la siguiente manera:

• Las variables del conjunto ${\textstyle u\in \{u_{1,i},u_{2,i},\dots ,u_{n,i}\}}$ con ${\textstyle i\in \{1,2,3\}}$ representan los colores asignados a los vértices en ${\textstyle G}$. Hay 3 variables por cada vértice en ${\textstyle G}$, una por cada color posible.
• El dominio ${\textstyle D=\{0,1\}}$ indica los valores que puede tomar cada variable ${\textstyle u}$, donde 1 significa que el color es asignado y 0 que no lo es.
• Para cada vértice ${\textstyle v_{j}\in V}$ con ${\textstyle j\in \{1,2,\dots ,n\}}$, asignamos las siguientes restricciones:

• Cada vértice debe ser coloreado con al menos un color, es decir, se debe satisfacer la siguiente fórmula:

$u_{j,1}\vee u_{j,2}\vee u_{j,3}$

para esta restricción se necesita una sola cláusula por cada vértice, es decir ${\textstyle n}$ cláusulas en total para el grafo.

• En nuestro problema de coloración no se pueden asignar dos colores al mismo tiempo al mismo vértice y esto se logra con la siguiente expresión lógica:

$({\overline {u_{j,1}}}\vee {\overline {u_{j,2}}})\wedge ({\overline {u_{j,1}}}\vee {\overline {u_{j,3}}})\wedge ({\overline {u_{j,2}}}\vee {\overline {u_{j,3}}})$

para esta restricción se necesitan ${\textstyle 3\times n}$ cláusulas.

• Cada par de vértices adyacentes son de diferente color. Para todo ${\textstyle e_{j}=(v_{j},v_{k})\in E}$ se tiene la restricción:

$({\overline {u_{j,1}}}\vee {\overline {u_{k,1}}})\wedge ({\overline {u_{j,2}}}\vee {\overline {u_{k,2}}})\wedge ({\overline {u_{j,3}}}\vee {\overline {u_{k,3}}})$

para esta restricción se necesitan ${\textstyle 3\times m}$ cláusulas

Así, el problema de 3-coloración se reduce a encontrar una asignación a las variables ${\textstyle z\in \{0,1\}^{3n}}$ que haga que la fórmula booleana descrita por la intercesión de todas las clausulas anteriores sea verdadera. Con este ejemplo, observamos que para cualquier grafo ${\textstyle G=(V,E)}$ se puede escribir como un problema ${\textstyle 3}$SAT utilizando un total de ${\textstyle n+3n+3m=4n+3m}$ restricciones. De este modo hay una reducción de un problema de coloración en grafos a un problema ${\textstyle 3}$SAT en tiempo polinomial.

Para demostrar que el problema de decidir si un grafo planar se puede colorear con 3 colores es NP-completo, se realiza una reducción en tiempo polinomial desdel problema de colorear cualquier grafo con 3 colores. Es decir, se demuestra el siguiente teorema:

Teorema 5: El problema de decidir si un grafo es ${\textstyle 3}$-coloreable se reduce en tiempo polinomial al problema de decidir si un grafo planar es ${\textstyle 3}$-coloreable.

${\hbox{Grafo 3-coloreable}}\leq _{p}{\hbox{Grafo planar 3-coloreable}}$

La estrategia consiste en comenzar con un grafo no planar que tenga cruces, y reemplazar cada cruce por un gadget planar: un subgrafo de 11 vértices que puede ser coloreado con 3 colores. Este proceso se realiza para cada cruce, transformando así el grafo original en un grafo planar que es 3-coloreable si, y solo si, el grafo original no planar también lo es. El lector interesado en los detalles de la reducción puede consultar [9].

A partir del teorema anterior y de la reducción del problema 3-SAT al problema de 3-coloración, obtenemos que:

${\hbox{3-SAT}}\leq _{p}{\hbox{Grafo planar 3-coloreable.}}$

Y, dado que 3-SAT es NP-completo, concluimos que el problema de 3-coloración en grafos planares también es NP-completo.

5 El Problema de la Tierra-Luna (Earth-Moon Problem).

El problema de la Tierra-Luna es un problema que permanece abierto dentro del ámbito de la coloración de grafos, planteado por Gerhard Ringel en 1959 [1]. Como vimos en la introducción este problema es una extensión del problema de la coloración de mapas planos, cuya solución se obtiene a través del Teorema de los Cuatro Colores (véase teorema 1).

De manera intuitiva, el problema puede enunciarse de la siguiente forma:

¿Cuántos colores se necesitan para colorear los mapas políticos de la tierra y la luna en un futuro hipotético, donde cada país de la tierra tiene una colonia en la luna que debe recibir el mismo color?

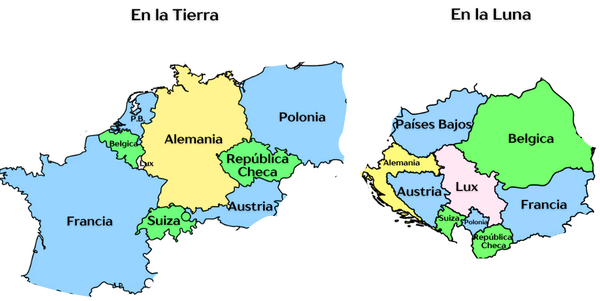
Figure 7: Territorio de países en tierra y luna.

En la figura 7 se muestra un ejemplo de una coloración para la tierra y la luna. Nótese que cada país debe ser coloreado con el mismo color tanto en la tierra como en la luna, aunque la disposición geográfica es diferente en ambos cuerpos celestes.

La pregunta anterior se puede formular de la siguiente manera: ¿Cuál es el número mínimo de colores necesarios para colorear un conjunto de países, de tal forma que no haya dos países que compartan una frontera común y estén coloreados con el mismo color, bajo la condición de que cada país consiste en una región en la tierra y una región en la luna?

En términos de teoría de grafos, esta pregunta se puede reformular como sigue:

¿Cuál es el número cromático máximo de un grafo ${\textstyle G}$ que es la unión de dos grafos planares (sobre el mismo conjunto de vértices)?

Nos gustaría establecer algunas cotas sobre el número de colores necesarios. Comenzaremos con un ejemplo dado por Thom Sulanke en 1974, que refuta la conjetura de Ringel, la cual postulaba que 8 colores serían suficientes para resolver la pregunta.

Antes de continuar, es importante señalar que para la preparación de esta sección se consultaron los artículos [10], [1] y [11]. La mayoría de las demostraciones aquí expuestas se completaron o se hizo una demostración alternativa.

Ejemplo 3: Supongamos que tenemos la coloración del mapa en “la tierra” donde cada letra ${\textstyle \{A,B,C,D,E,F,P,Q,R,S,T\}}$ representa un país diferente.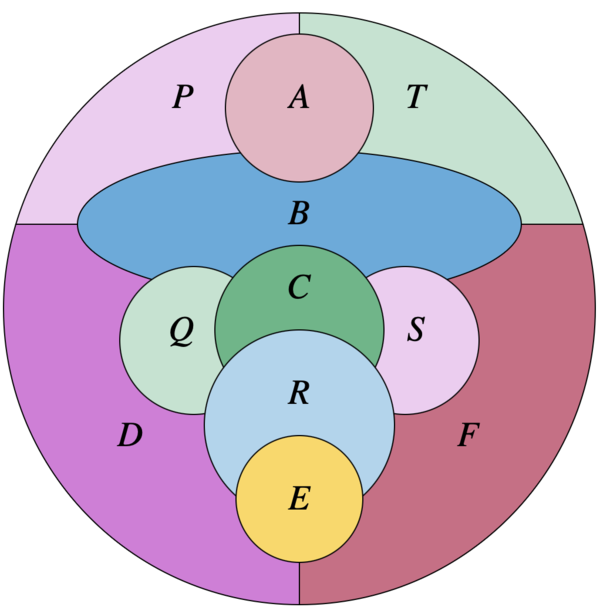

Figure 8: Coloración en “la tierra”.

El grafo correspondiente ${\textstyle G_{1}}$ (figura 9) para este mapa tiene 11 vértices (uno por cada país) y 26 aristas (una por cada colindancia), cumpliendo la desigualdad de Euler para grafos planos, ${\textstyle m=26<3\times 11-6}$, donde ${\textstyle m}$ es el número de aristas y 11 es el número de vértices. Así,

$G_{1}=(V_{1},E_{1})$

queda definido por

$V_{1}=\left\{A,B,C,D,E,F,P,Q,R,S,T\right\}$

$E_{1}=\left\{{\begin{array}{l}AT,AB,AP,BC,BD,BF,BT,BP,BS,BQ,\\CQ,CS,CR,DP,DQ,DR,DE,DF,ER,EF,FT,\\FS,FR,PT,QR,RS\end{array}}\right\}$

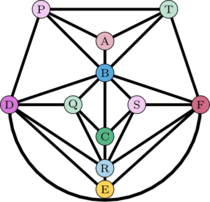
Figure 9: Grafo de mapa en “la tierra”. $G_{1}$

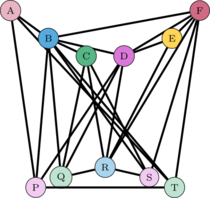
Figure 10: Grafo de mapa en “la tierra”.

El grafo ${\textstyle G_{1}}$ es isomorfo al grafo de la figura 10, que a simple vista no parece ser plano; sin embargo, como se observa en la figura 9, sí posee una representación plana. Más adelante usaremos este grafo para simplicidad visual. A continuación, analizamos el mapa en la luna. Supongamos que los 11 países del mapa terrestre se mantienen en la luna, pero en este caso, cada país está dividido en regiones diferentes a las del mapa terrestre. Esta variación en la división regional altera las colindancias entre las regiones en la luna, en comparación con las del mapa de la tierra.

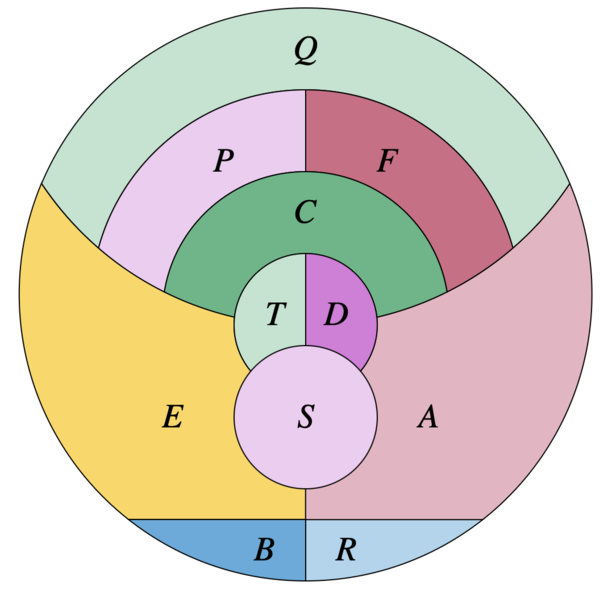
Figure 11: Coloración en “la luna”.

Denotemos por ${\textstyle G_{2}}$ el grafo que representa el mapa lunar (figura 12). En ${\textstyle G_{2}}$ las aristas indican las nuevas colindancias entre las regiones lunares. El grafo ${\textstyle G_{2}}$ correspondiente al mapa lunar tiene 11 vértices (uno por cada región) y 24 aristas. Así, ${\textstyle G_{2}=(V_{2},E_{2})}$ queda definido por

$V_{2}=\left\{A,B,C,D,E,F,P,Q,R,S,T\right\}$

$E_{2}=\left\{{\begin{array}{l}AC,AQ,AF,AD,AS,AE,AR,\\BR,BE,CF,CD,CT,CE,CP,\\DS,DT,ET,ES,EQ,EP,\\FQ,FP,PQ,ST\end{array}}\right\}$

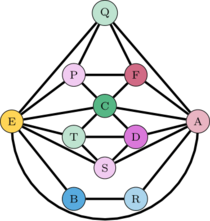
Figure 12: Grafo de mapa en “la luna”. $G_{2}$

Reordenando los vértices alfabéticamente para facilitar el análisis, obtenemos el grafo de la figura 13.

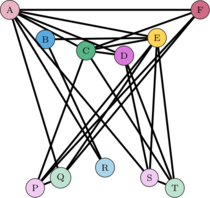
Figure 13: Grafo de mapa en “la luna”.

Para garantizar que las colindancias sean consistentes entre los dos mapas, debemos considerar la unión de los grafos ${\textstyle G_{1}}$ y ${\textstyle G_{2}}$. En dondel conjunto de vértices ${\textstyle \{A,B,C,D,E,F,P,Q,R,S,T\}}$ es el mismo, pero el de aristas será la unión dellos. Al grafo resultante, que representa la combinación de las regiones de ambos mapas, le llamamos ${\textstyle G_{3}=(V_{3},E_{3})}$ donde:

$V_{3}=V_{1}=V_{2}=\left\{A,B,C,D,E,F,P,Q,R,S,T\right\}$

$E_{3}=E_{1}\cup E_{2}=\left\{{\begin{array}{l}AC,AQ,AF,AD,AS,AE,AR,BR,BE,CF,\\CD,CT,CE,CP,DS,DT,ET,ES,EQ,EP,\\FQ,FP,PQ,ST,AT,AB,AP,BD,BF,BT,\\BP,BS,BQ,CQ,CS,CR,DP,DQ,DR,DE,\\ER,EF,FT,FS,FR,PT,QR,RS\end{array}}\right\}$

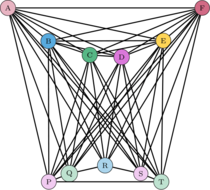
Figure 14: Grafo Tierra-Luna. $G_{3}$

El grafo final ${\textstyle G_{3}}$ combina las coloraciones de las regiones de la Tierra y la Luna, respetando las adyacencias especificadas en ambos mapas. La pregunta clave es: ¿cuál es el número mínimo de colores necesarios para colorear este grafo de manera que no haya dos regiones adyacentes con el mismo color? En este caso, hemos determinado que se requieren al menos 9 colores, y este número es óptimo. Esto se debe a que el subgrafo formado por los vértices ${\textstyle A}$ a ${\textstyle F}$ y las aristas que los conectan es un grafo completo ${\textstyle K_{6}}$, donde cada vértice está conectado con todos los demás. Por lo tanto, se necesitan al menos 6 colores para colorear ${\textstyle K_{6}}$. Por otro lado, el subgrafo formado por los vértices ${\textstyle P}$ a ${\textstyle T}$ es un ciclo ${\textstyle C_{5}}$, que también requiere colores distintos de los usados en ${\textstyle K_{6}}$. Para colorear un ciclo ${\textstyle C_{5}}$, se necesitan al menos 3 colores adicionales. Dado que ${\textstyle G_{3}}$ es la unión de ${\textstyle K_{6}}$ y ${\textstyle C_{5}}$, la cota mínima de colores necesarios es 9. Además, este número es suficiente, como se ha demostrado en el ejemplo, donde se logra una coloración correcta con 9 colores.

Como se puede observar, el Problema de la Tierra-Luna se puede formular como un grafo ${\textstyle G=(V,E)}$ cuyo conjunto de vértices es el mismo, pero cuyo conjunto de aristas se puede dividir para formar dos grafos planares ${\textstyle G_{1}}$ y ${\textstyle G_{2}.}$ A la operación inversa, es decir, construir un grafo de Tierra-Luna la llamaremos unión.

Definición 17: Sean ${\textstyle G_{1}=(V,E_{1})}$ y ${\textstyle G_{2}=(V,E_{2})}$ dos grafos planos definidos sobre el mismo conjunto de vértices ${\textstyle V}$, definimos la unión de estos grafos como el grafo ${\textstyle G=(V,E)}$, donde ${\textstyle E=E_{1}\cup E_{2}}$. Es decir, el grafo unión mantiene el mismo conjunto de vértices y su conjunto de aristas corresponde a la unión de las aristas de ${\textstyle G_{1}}$ y ${\textstyle G_{2}}$. Por el corolario 1, sabemos que un grafo planar con ${\textstyle n\geq 3}$ vértices tiene a lo sumo ${\textstyle m\leq 3n-6}$ aristas. De este modo, el Problema de la Tierra-Luna tendrá como máximo ${\textstyle 3n-6}$ aristas en un grafo plano ${\textstyle G_{1}}$ y ${\textstyle 3n-6}$ aristas en el grafo plano ${\textstyle G_{2}}$.

Por lo tanto, tenemos el siguiente corolario.

Corolario 2: Si ${\textstyle G}$ es un grafo con ${\textstyle n\geq 3}$ vértices que es la unión de dos grafos planares, entonces ${\textstyle G}$ tendrá como máximo ${\textstyle |E|\leq 2(3n-6)=6n-12}$ aristas.

Corolario 3: Si ${\textstyle G}$ es un grafo que es la unión de dos grafos planares, existe al menos un vértice con grado no mayor a 11.

Si ${\textstyle n\leq 2}$ el resultado es trivial, ya que todos los vértices tendrán grado no mayor a 11. Supongamos que ${\textstyle n\geq 3}$.

El resultado se obtendrá por contradicción. Supongamos, que tenemos un grafo ${\textstyle G=(V,E)}$ unión de dos planares de orden ${\textstyle n}$ y tamaño ${\textstyle m}$ en el cual todos sus vértices tienen un grado mayor o igual a 12. ${\textstyle {\begin{array}{l}\\\end{array}}}$ Usando el corolario anterior (2) y el teorema 2, podemos afirmar que:

$\sum _{i=1}^{n}deg(v_{i})=2m\leq 2(6n-12)=12n-24.$

Sin embargo, bajo nuestra hipótesis de que todos los vértices tienen un grado mayor o igual a 12, y aplicando nuevamente el teorema 2, obtenemos:

$12n\leq \sum _{i=1}^{n}deg(v_{i})=2m.$

Combinando las dos desigualdades anteriores obtenemos:

$12n\leq 2m\leq 12n-24.$

Esta última desigualdad es una contradicción. Por lo tanto, llegamos a la conclusión de que debe existir al menos un vértice en ${\textstyle G}$ con un grado a lo más de 11.

Teorema 6: [1] El grafo ${\textstyle G}$ del Problema de la Tierra-Luna es ${\textstyle 12}$-coloreable.

Probaremos este teorema usando inducción matemática sobre el orden de ${\textstyle G}$. Sea n el orden de ${\textstyle G}$.

Base de inducción: Supongamos que ${\textstyle n\leq 12}$. Si ${\textstyle G}$ tiene ${\textstyle n\leq 12}$ vértices, entonces existe una ${\textstyle 12}$-coloración para G, ya que, basta con asignar un color distinto a cada vértice, y por construcción, no habrá dos vértices adyacentes con el mismo color. Por lo tanto, el resultado se cumple para ${\textstyle n\leq 12}$.

Hipótesis de inducción: Supongamos que todo grafo planar de orden ${\textstyle n}$ es ${\textstyle 12}$-coloreable.

Paso de inducción: Por demostrar que cualquier grafo ${\textstyle G=(V,E)}$ de orden ${\textstyle n+1}$ es ${\textstyle 12}$-coloreable. Por el colorario 3 sabemos que en cualquier grafo que es la unión de dos grafos planares existe al menos un vértice ${\textstyle v}$ con ${\textstyle deg(v)\leq {11}}$. Sea ${\textstyle G'=(V',E)}$ el subgrafo de ${\textstyle G}$, donde ${\textstyle V'=V\setminus \{v\}}$ y ${\textstyle E'}$ incluye todas las aristas que no son incidentes con ${\textstyle v}$. En otras palabras, ${\textstyle G'}$ es el grafo resultante de “eliminar” ${\textstyle v}$ y todas las aristas que lo conectan. Entonces, el orden de ${\textstyle G'}$ es ${\textstyle n}$, y por la hipótesis de inducción, obtenemos que ${\textstyle G'}$ es ${\textstyle 12}$-coloreable. De lo anterior se sigue que existe una ${\textstyle s}$-coloración para ${\textstyle G'}$ con ${\textstyle s\leq 12}$. Utilizamos esta ${\textstyle 12}$-coloración para ${\textstyle G}$ con los colores ${\textstyle \{c_{1},c_{2},\dots ,c_{12}\}}$, y solo falta asignar un color a ${\textstyle v}$. Sabemos que ${\textstyle v}$ tiene a lo más ${\textstyle 11}$ aristas incidentes a él. Supongamos sin pérdida de generalidad que estas aristas están conectadas a lo más a ${\textstyle 11}$ vértices diferentes ${\textstyle \{v_{1},v_{2},\dots ,v_{11}\}}$. Asignamos el color no utilizado para ${\textstyle \{v_{1},v_{2},\dots ,v_{11}\}}$ a ${\textstyle v}$. De esta manera, se conservan las características de la ${\textstyle 12}$-coloración en ${\textstyle G}$, y ${\textstyle G}$ de orden ${\textstyle n+1}$ es ${\textstyle 12}$-coloreable.

Hasta aquí, el ejemplo 14 demuestra que se requieren al menos 9 colores para resolver el Problema de la Tierra-Luna. Por otro lado, el teorema 6 establece que es posible utilizar hasta 12 colores. Esto plantea la pregunta: ¿es factible lograr una coloración con menos de 12 colores? Por lo que sabríamos que la respuesta al mínimo número de colores necesarios se encuentra en el conjunto:

$\{9,10,11,12\}$

Dejando abiertas las posibilidades de exploración en torno a la existencia de configuraciones que requieran 10 u 11 colores. Esta incertidumbre resalta la complejidad del problema y nos surge la pregunta de cual es la complejidad computacional del problema de ${\textstyle n}$-coloración de la Tierra-Luna con ${\textstyle 3\leq n\leq 11}$.

Para concluir esta sección, modelaremos el Problema de la Tierra-Luna mostrado en la figura 7 como un Problema de Satisfacción de Restricciones (CSP).

Con el objetivo de analizar su complejidad computacional, en la siguiente sección presentaremos la modelación del Problema de la Tierra-Luna como un CSP, con el propósito de demostrar que es un problema de complejidad NP-hard.

6 Problema de la Tierra-Luna a través de los CSP.

Empezamos esta sección construyendo el siguiente ejemplo. Tenemos una porción de países europeos: Alemania, Austria, Bélgica, Francia, Países Bajos, Luxemburgo, Polonia, República Checa y Suiza (véase figura 7). El problema consiste en colorear los países utilizando el mínimo número de colores de tal manera que no haya dos países colindantes que compartan el mismo color.

Primero, describiremos el mapa como dos grafos, donde cada vértice representará un país y una arista unirá dos países si estos colindan, i.e. Sea ${\textstyle G_{t}=(V,E)}$ el grafo en la tierra donde:

• ${\textstyle V_{=}\{Al,Au,Be,Fr,Pb,Lu,Po,Re,Su\}}$ representa los países de Alemania, Austria, Bélgica, Francia, Pblanda, Luxemburgo, Polonia, República Checa y Suiza respectivamente.
• ${\textstyle E_{t}}$ representa colindancias entre los países en la tierra: ${\textstyle E_{t}=\{AlPo}$, ${\textstyle AlRe}$, ${\textstyle AlAu}$, ${\textstyle AlSu}$, ${\textstyle AlFr}$, ${\textstyle AlLu}$, ${\textstyle AlBe}$, ${\textstyle AlPb}$, ${\textstyle AuRe}$, ${\textstyle AuSu}$, ${\textstyle BePb}$, ${\textstyle BeLu}$, ${\textstyle BeFr}$, ${\textstyle FrLu}$, ${\textstyle FrSu}$, ${\textstyle PoRe\}}$

Además, sea ${\textstyle G_{l}=(V,E)}$ el grafo en la luna donde:

• ${\textstyle V_{=}\{Al,Au,Be,Fr,Pb,Lu,Po,Re,Su\}}$ representa los países de Alemania, Austria, Bélgica, Francia, Países Bajos, Luxemburgo, Polonia, República Checa y Suiza respectivamente.
• ${\textstyle E_{l}}$ representa colindancias entre los países en la luna: ${\textstyle E_{l}=\{AlPb}$, ${\textstyle AlLu}$, ${\textstyle AlAu}$, ${\textstyle AuLu}$, ${\textstyle AuSu}$, ${\textstyle BeFr}$, ${\textstyle BeLu}$, ${\textstyle BePb}$, ${\textstyle FrLu}$, ${\textstyle FrRe}$, ${\textstyle PbLu}$, ${\textstyle LuPo}$, ${\textstyle LuRe}$, ${\textstyle LuSu}$, ${\textstyle PoRe}$, ${\textstyle PoSu\}}$

Por lo tanto, los grafos planares que representa los mapas en la tierra y en la luna están representados en la figura 15. Una vez dada la representación gráfica, formularemos este problema como una instancia de CSP. El Problema Tierra-Luna de arriba se puede plantear como un CSP de la siguiente manera:

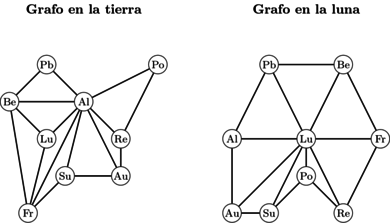
Figure 15: Representación gráfica del Problema de la Tierra-Luna.

• Sea ${\textstyle X=\{Al,Au,Be,Fr,Pb,Lu,Po,Re,Su\}}$ nuestro conjunto de variables, representando cada país.
• Sea ${\textstyle D=\{V,Az,R,Am\}}$ el dominio de los valores de las variables, que representan los colores (por ejemplo, Verde, Azul, Rosa y Amarillo) que se pueden asignar a los vértices.
• Sea ${\textstyle C}$ el conjunto de restricciones sobre las variables. Definimos las restricciones de colindancia de la siguiente manera:

• Tierra: Los países adyacentes deben tener colores diferentes. Las colindancias son:

$C_{t}=\left\{{\begin{array}{l}\langle AlPo,\neq \rangle ,\langle AlRe,\neq \rangle ,\langle AlAu,\neq \rangle ,\\\langle AlSu,\neq \rangle ,\langle AlFr,\neq \rangle ,\langle AlLu,\neq \rangle ,\\\langle AlBe,\neq \rangle ,\langle AlPb,\neq \rangle ,\langle AuRe,\neq \rangle ,\\\langle AuSu,\neq \rangle ,\langle BePb,\neq \rangle ,\langle BeLu,\neq \rangle ,\\\langle BeFr,\neq \rangle ,\langle FrLu,\neq \rangle ,\langle FrSu,\neq \rangle ,\\\langle PoRe,\neq \rangle \end{array}}\right\}$

• Luna: Similarmente, las colindancias para el grafo en la luna son:

$C_{l}=\left\{{\begin{array}{l}\langle AlPb,\neq \rangle ,\langle AlLu,\neq \rangle ,\langle AlAu,\neq \rangle ,\\\langle AuLu,\neq \rangle ,\langle AuSu,\neq \rangle ,\langle BeFr,\neq \rangle ,\\\langle BeLu,\neq \rangle ,\langle BePb,\neq \rangle ,\langle FrLu,\neq \rangle ,\\\langle FrRe,\neq \rangle ,\langle PbLu,\neq \rangle ,\langle LuPo,\neq \rangle ,\\\langle LuRe,\neq \rangle ,\langle LuSu,\neq \rangle ,\langle PoRe,\neq \rangle ,\\\langle PoSu,\neq \rangle \end{array}}\right\}$

En este contexto, la relación binaria ${\textstyle \neq }$ establece que los colores asignados a países adyacentes deben ser distintos tanto en la tierra como en la luna.

Por lo tanto, una solución al problema de colorear el mapa en la tierra consiste en encontrar una función

$\varphi :X\longrightarrow D$

que asigne un color a cada vértice en ${\textstyle v_{i}\in X}$ con ${\textstyle i\in \{1,2,3,\ldots ,9\}}$ tal que

${\hbox{para todo }}(v_{i},v_{j})\in E_{t}{\hbox{ entonces }}(\varphi (v_{i}),\varphi (v_{j}))\in \neq$

Esto último es equivalente a decir que ${\textstyle \varphi (v_{i})\neq \varphi (v_{j})}$.

De manera similar, para el problema de la Luna, buscamos la misma función

$\varphi :X\longrightarrow D$

que asigne un color a cada vértice en ${\textstyle v_{i}'\in X}$ tal que

${\hbox{para todo }}(v_{i}',v_{j}')\in E_{l}{\hbox{ entonces }}(\varphi (v_{i}'),\varphi (v_{j}'))\in \neq$

Ahora, dado que buscamos satisfacer simultáneamente las restricciones tanto en la tierra como en la luna, el CSP que representa la unión de estas condiciones implica que ${\textstyle X}$ es el conjunto de variables definido anteriormente, y ${\textstyle D}$ representa los mismos colores. El conjunto de restricciones es la unión de las restricciones de colindancia para ambos contextos:

• Tierra-Luna: Los países adyacentes deben tener colores diferentes, tanto en la tierra como en la luna. La unión de las colindancias es:

$C_{tl}=\left\{{\begin{array}{l}\langle AlPo,\neq \rangle ,\langle AlRe,\neq \rangle ,\langle AlAu,\neq \rangle ,\\\langle AlSu,\neq \rangle ,\langle AlFr,\neq \rangle ,\langle AlLu,\neq \rangle ,\\\langle AlBe,\neq \rangle ,\langle AlPb,\neq \rangle ,\langle AuRe,\neq \rangle ,\\\langle AuSu,\neq \rangle ,\langle BePb,\neq \rangle ,\langle BeLu,\neq \rangle ,\\\langle BeFr,\neq \rangle ,\langle FrLu,\neq \rangle ,\langle FrSu,\neq \rangle ,\\\langle PoRe,\neq \rangle ,\langle PbLu,\neq \rangle ,\langle LuPo,\neq \rangle ,\\\langle LuRe,\neq \rangle ,\langle LuSu,\neq \rangle ,\langle PoSu,\neq \rangle \end{array}}\right\}$

Por lo tanto, una solución al problema de colorear el mapa en la Tierra-Luna consiste en encontrar una función ${\textstyle \varphi :X\longrightarrow D}$ que asigne un color a cada vértice ${\textstyle v_{i}\in X}$ con ${\textstyle i\in \{1,2,3,\ldots ,9\}}$, de manera que

${\hbox{para todo }}(v_{i},v_{j})\in (E_{t}\cup E_{l}){\hbox{ entonces }}(\varphi (v_{i}),\varphi (v_{j}))\in \neq$

Esto es equivalente a afirmar que ${\textstyle \varphi (v_{i})\neq \varphi (v_{j})}$.

Una posible solución para el Problema de la Tierra-Luna es:

${\begin{aligned}&\varphi (Al)=Am,\quad \varphi (Au)=Az,\quad \varphi (Be)=V,\\&\varphi (Fr)=Az,\quad \varphi (Pb)=Az,\quad \varphi (Lu)=R,\\&\varphi (Po)=Az,\quad \varphi (Re)=V,\quad \varphi (Su)=V.\end{aligned}}$

Estas soluciones se ilustran en la figura 16, que corresponde a cada uno de los mapas.

Finalmente, en la figura 16 se presenta los grafos que modelan la tierra y la luna, asociados a esta solución. Adicionalmente, en la figura 17 se representa el grafo que es la unión de estos dos grafos planares, y sería el que se modeló al final.

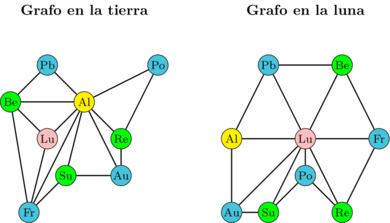
Figure 16: Una solución gráfica del Problema de la Tierra-Luna.

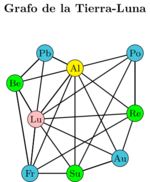
Figure 17: Grafo combinado de la Tierra-Luna.

Hasta el momento, hemos demostrado que el problema de coloración del modelo Tierra-Luna presenta desafíos significativos, con un mínimo de 9 colores necesarios y la posibilidad de utilizar hasta 12. Este análisis nos lleva a considerar la complejidad intrínseca de la coloración de grafos y abre la puerta a la exploración de la complejidad computacional para la ${\textstyle n}$-coloración del Problema de la Tierra-Luna con ${\textstyle 3\leq n\leq 8}$. Debra Boutin, Ellen Gethner y Thom Sulanke en [12] proporcionaron un catálogo de 40 nuevos ejemplos (configuraciones) del Problema de la Tierra-Luna que pueden ser coloreados con 9 colores. Además, presentan una nueva metodología para construir configuraciones adicionales, lo que permite crear una familia infinita de ejemplos de problemas de la Tierra-Luna que son 9-coloreables.

Debido a que el Problema de la Tierra-Luna puede ser modelado como un problema de satisfacción de restricciones (CSP), sabemos que este problema tiene una complejidad en NP-hard. Sin embargo, para ${\textstyle n\geq 12}$, el teorema 6 establece que el problema de decidir si un grafo que representa un problema de la Tierra-Luna es ${\textstyle n}$-coloreable siempre tiene una solución afirmativa. Esto implica que dicho problema puede resolverse en tiempo polinomial. El problema de la 3-coloración en la Tierra es NP-completo, ya que se redujo del problema 3-SAT a la 3-coloración de grafos. Por lo tanto, el Problema de la Tierra-Luna con 3 colores también será NP-completo, dado que en la tierra y la luna lo es.

Para concluir esta sección, construiremos una reducción en tiempo polinomial del problema ${\textstyle 3}$SAT al problema de 3-coloración de la Tierra-Luna. De esta manera, probaremos de forma independiente, y sin hacer uso del hecho de que el problema de 3-coloración en la Tierra es NP-completo, que el problema de 3-coloración de la Tierra-Luna también es NP-completo.

Teorema 7: $3SAT\leq _{p}Problema{\hbox{ de la }}Tierra-Luna$.

Antes de demostrar este teorema, esbozaremos la estrategia de la prueba. Dada una entrada del problema ${\textstyle 3SAT}$ (una fórmula booleana), debemos construir un mapa en la tierra y un mapa en la luna que será 3-coloreable si y solamente si la fórmula booleana tiene solución.

La demostración se ejecutará en varios pasos. Sea una entrada del problema ${\textstyle 3SAT}$ con ${\textstyle n}$ variables y ${\textstyle m}$ cláusulas.

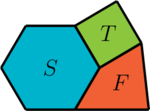
• Paso 1: Empezamos construyendo un mapa de la tierra que incluye tres países adyacentes, etiquetados como ${\textstyle T}$, ${\textstyle F}$, y ${\textstyle S}$. Aquí, ${\textstyle T}$ es un cuadrado, ${\textstyle F}$ es un ${\textstyle (m+2)}$-ágono, y ${\textstyle S}$ es ${\textstyle (n+2)}$-ágono. Asignamos a cada país un color distinto utilizando tres colores diferentes. Sin pérdida de generalidad, los colores se distribuyen como se muestra en la figura 18:

Figure 18: Primer paso.

En esta construcción, el color verde representa los valores verdaderos, el rojo representa los valores falsos y el color de ${\textstyle S}$ no indica ningún valor específico.

• Paso 2: En nuestra fórmula, se incluyen variables y sus negaciones, denominadas literales. Asignamos valores a cada literal de manera que si una literal ${\textstyle x_{i}}$ es verdadera su negación ${\textstyle {\overline {x_{i}}}}$ sea falsa. Para garantizar esta condición, procedemos de la siguiente forma:

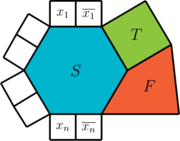
Para cada literal ${\textstyle x_{i}}$ y su negación ${\textstyle {\overline {x_{i}}}}$, agregamos dos países (cuadrados) en nuestro mapa de la tierra. Estos países se conectan entre sí y a uno de los lados disponibles del país ${\textstyle S}$ (disponibles ${\textstyle n}$ lados, uno para cada variable y su negación), como se ilustra en la figura 19.

Esto asegura que las literales ${\textstyle x_{i}}$ y ${\textstyle {\overline {x_{i}}}}$ no reciban el mismo color que el país ${\textstyle S}$, ya que sus países están conectadas a ${\textstyle S}$ y, por lo tanto, deben ser coloreadas de rojo o verde. Para garantizar que ${\textstyle x_{i}}$ y ${\textstyle {\overline {x_{i}}}}$ no reciban el mismo color (es decir, que si ${\textstyle x_{i}}$ es verdadero, entonces ${\textstyle {\overline {x_{i}}}}$ sea falso, y viceversa), conectamos el país ${\textstyle x_{i}}$ con el país ${\textstyle {\overline {x_{i}}}}$, como se muestra en la figura 19.

De esta manera, si coloreamos el mapa de una forma válida, obtendremos valores de verdad para las variables y sus negaciones que son consistentes.

Figure 19: Segundo paso.

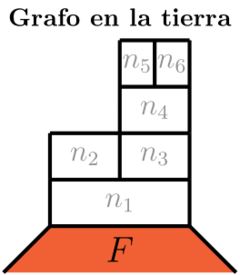
• Paso 3: Finalmente, debemos representar cada cláusula de la fórmula booleana en el mapa. Para esto, utilizaremos una construcción denominada “gadget” para simular el operador booleano ${\textstyle {\hbox{OR}}}$ (véase la figura 20). Este gadget es ${\textstyle 3}$-coloreable si y solo si al menos uno de los países representado por las literales en la cláusula se asigna o colorea con ${\textstyle T}$ (verdadero), como se explicará a continuación.

El gadget que construiremos es análogo al descrito en el paso 3 de la demostración del Teorema 4, con la diferencia de que en esta ocasión se conecta al país que representa el valor Falso. Una parte del gadget se sitúa en la “tierra” y consiste en varios países conectados a uno de los lados del país correspondiente a ${\textstyle F}$. Dado que el polígono que representa a ${\textstyle F}$ tiene ${\textstyle m+2}$ lados, podemos utilizar un lado distinto para cada gadget asociado a cada cláusula de la fórmula booleana.

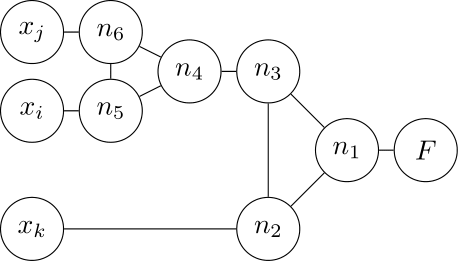
Cada uno de estos gadgets incluye también países en la “luna”, los cuales representan los literales de la cláusula correspondiente. Para ello, cada literal se modela mediante un polígono en la luna: específicamente, utilizamos un ${\textstyle m}$-ágono para cada literal, o un triángulo en caso de que ${\textstyle m<3}$. Esta construcción permite representar adecuadamente la estructura lógica de cada cláusula dentro del grafo, respetando las restricciones de adyacencia y colorabilidad necesarias para la reducción.

Figure 20: Tercer paso (tierra).

Estos países de las literales en la luna no serán colindantes entre sí. En este modelo, para cada cláusula, adicional se agregarán algunos de los países del gadget en uno de los lados de los ${\textstyle m}$-ágonos que representan las literales utilizadas en esa cláusula.

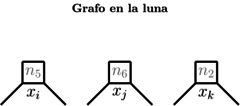
Figure 21: Tercer paso (luna).

En el gadget mostrado en la figura 20 que se representa con los grafos de las figura 20 y la figura 21, si todos los países asociados a literales se colorean como Falsas (rojo), ninguno de los países ${\textstyle n_{1}}$, ${\textstyle n_{5}}$, ${\textstyle n_{6}}$ o ${\textstyle n_{2}}$ puede ser coloreado de rojo, ya que colindan con los países correspondientes a las literales y ${\textstyle F}$. Además, dado que en la tierra el país ${\textstyle n_{5}}$ colinda con ${\textstyle n_{6}}$, si ${\textstyle n_{5}}$ es verde, ${\textstyle n_{6}}$ debe ser azul, y viceversa. Esto implica que el país ${\textstyle n_{4}}$ debe ser coloreado de rojo, ya que colinda con ${\textstyle n_{5}}$ (verde/azul) y con ${\textstyle n_{6}}$ (azul/verde).

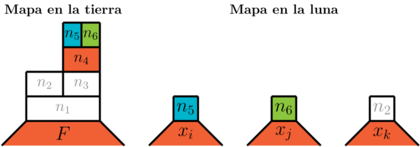
Figure 22: Tercer paso (coloración).

Por lo tanto, el país ${\textstyle n_{3}}$ debe ser coloreado de verde o azul, dado que está conectado a ${\textstyle n_{4}}$ (rojo). Por lo tanto, los países ${\textstyle n_{2}}$, ${\textstyle n_{1}}$ y ${\textstyle n_{3}}$ solo pueden tener los colores verde o azul. Sin embargo, al tratarse de tres países y solo dos colores disponibles, necesariamente habrá un par de vértices que compartan el mismo color. Como estos tres países están conectados entre sí, se produciría una contradicción, ya que dos países conectados tendrían el mismo color. De este modo, si los países de las tres literales son falsas, es imposible colorear el gadget. Adicionalmente, es sencillo ver que si alguno es verde, se puede colorear el gadget.

Paso 4: El paso final consiste en intersectar los gadgets, de manera que no colinden con los países ya existentes, es decir, se crean los mapas por cada clausal y se busca empatar esos gadgets. Aunque el resultado es grande, está bien estructurado, como se muestra en la figura 23. De este modo, el mapa resultante es 3-coloreable si y solo si la fórmula booleana se satisface.

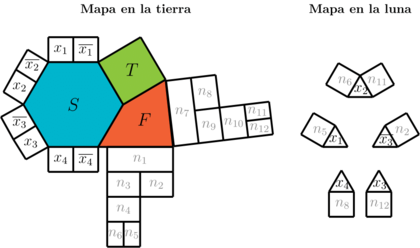
Figure 23: Reducción completa de la fórmula $3SAT$ $(x_{1}\vee x_{2}\vee {\overline {x_{3}}})\wedge (x_{2}\vee x_{3}\vee x_{4})$ a una $3$-coloración.

En el caso de que la fórmula booleana representada por la figura no se satisfaga, es decir, si ${\textstyle x_{1}}$, ${\textstyle x_{2}}$, y ${\textstyle {\overline {x_{3}}}}$ son coloreadas de rojo, entonces al aplicar el proceso descrito en el paso 3, se llega a la conclusión de que es imposible colorear el mapa.

• Paso 6: Para demostrar que esta reducción se realiza en tiempo polinomial, supongamos que la fórmula tiene ${\textstyle n}$ literales y ${\textstyle m}$ cláusulas. Entonces, el número de países se calcula de la siguiente manera:

Países en la tierra:

• 3 países para ${\textstyle T}$, ${\textstyle F}$ y ${\textstyle S}$ (figura 18).
• 2 países por cada variable: se requieren ${\textstyle 2n}$ países extra (figura 19).
• 6 países por cada cláusula: se requieren ${\textstyle 6m}$ países extra (figura 21).

Países en la luna:

• 1 país por cada literal: se requieren a lo más ${\textstyle 2n}$ países extra (figura 21).
• 3 países conectados a las literales por cada clausal: se requieren ${\textstyle 3m}$ países adicionales (figura 21).

De este modo, los mapas generados tienen en total ${\textstyle 4n+9m+3}$ países.

Hasta ahora, hemos demostrado que un problema ${\textstyle 3}$SAT puede reducirse al Problema de la Tierra-Luna de forma general. Dado que ${\textstyle 3}$SAT es un problema NP-completo, la reducción implica que el Problema de la Tierra-Luna también es NP-completo.

7 Conclusión

Este trabajo ha ofrecido una revisión sobre los problemas de coloración en grafos. Que se profundiza más en la tesis de la cual se deriva este artículo.

Se permitió profundizar en la complejidad computacional de los problemas de decisión, destacando la relevancia de la clasificación de problemas en P, NP, NP-completo y NP-hard. Además, la modelación de la 3-coloración coo un Problema de Satisfacción de Restricciones (CSP) proporcionó un marco útil para abordar estos problemas desde distintos enfoques. Adicionalmente, se presentó un importante resultado: ${\textstyle 3{\hbox{SAT}}\leq _{p}}$ Grafo ${\textstyle 3}$-coloreable (esto significa que cualquier instancia del problema de 3-satisfacibilidad booleana puede transformarse en tiempo polinomial en una instancia equivalente de un grafo ${\textstyle 3}$-coloreable), acompañado de dos reducciones significativas.

${\hbox{Grafo 3-coloreable}}\leq _{p}{\hbox{3SAT}}$

${\hbox{Grafo 3-coloreable}}\leq _{p}{\hbox{Grafo planar 3-coloreable}}$

Estas reducciones permiten concluir que la 3-coloración de mapas en la tierra es un problema NP-completo, dado que ${\textstyle 3{\hbox{SAT}}}$ lo es.

Finalmente, se abordó el problema de colorear mapas de la Tierra-Luna, que ilustra la evolución del pensamiento en la teoría de grafos y la necesidad de seguir investigando áreas abiertas para avanzar en nuestra comprensión de la coloración de grafos. Se concluye con la demostración ${\textstyle 3{\hbox{SAT}}\leq _{p}}$ Problema Tierra-Luna, es decir, que se el problema ${\textstyle 3}$SAT se puede reducir en tiempo polinómico a una instancia del Problema Tierra-Luna, de dicha reducción se puede concluir que este problema último es NP-completo. La demostración se hizo en colaboración con mi asesora Edith Vargas y el profesor Mike Behrisch, hasta la fecha dicha demostración no ha sido encontrada en alguna bibliografía. Se continuó investigando y podemos afirmar que el problema de colorear mapas en la Tierra-Luna es un problema NP-completo para ${\textstyle n=4}$, ${\textstyle n=5}$ y ${\textstyle n=6}$ colores. Las pruebas de estas afirmaciones se encontrarán en un futuro artículo.

BIBLIOGRAFÍA

[1] Hutchinson, Joan P. (1993) "Coloring ordinary maps, maps of empires, and maps of the moon", Volume 66. Taylor & Francis. Mathematics Magazine 4 211–226

[2] Kempe, Alfred B. (1879) "On the geographical problem of the four colours", Volume 2. JSTOR. American journal of mathematics 3 193–200

[3] McEliece, Robert J. (1978) "A public-key cryptosystem based on algebraic", Volume 4244. Coding Thv 114–116

[4] Arora, Sanjeev and Barak, Boaz. (2009) "Computational complexity: a modern approach". Cambridge University Press

[5] Lau, Dietlinde. (2006) "Function algebras on finite sets: Basic course on many-valued logic and clone theory". Springer Science & Business Media

[6] Demain, Erick and Ku, Jason and Solomon, Justin. (2020) "Lecture 19: Complexity". MIT OpenCourse

[7] Tsiatas, Alexander. (2008) "Phase transitions in Boolean satisfiability and graph coloring". Department of Computer Science, Cornell University

[8] Zhuk, Dmitriy. (2020) "A proof of the CSP dichotomy conjecture", Volume 67. ACM New York, NY, USA. Journal of the ACM (JACM) 5 1–78

[9] Gorrie, Daniel. (2014) "Scribe Notes: Planar Graphs and Space Complexity" https://people.eecs.berkeley.edu/ gorrie/cs170/notes/planar.pdf

[10] Ringel, Gerhard. (2012) "Map color theorem", Volume 209. Springer Science & Business Media

[11] Gonthier, Georges and others. (2008) "Formal proof–the four-color theorem", Volume 55. Notices of the AMS 11 1382–1393

[12] Boutin, Debra L and Gethner, Ellen and Sulanke, Thom. (2008) "Thickness-two graphs part one: New nine-critical graphs, permuted layer graphs, and Catlin's graphs", Volume 57. Wiley Online Library. Journal of Graph Theory 3 198–214