Resumen
Este trabajo consiste en determinar la carga crítica de pandeo con deformaciones de flexión y torsión de una barra de acero de sección de tipo doble-T. Para su cálculo, se considera el modelo 3D de flexión de barras esbeltas (teoría de la flexión de Navier-Bernouilli) y el modelo de torsión no uniforme o por alabeo restringido (teoría de la torsión de Vlasov).
Abstract
This work is based on calculating the critical buckling load with bending and torsional deformations of a steel wide-flange section type. To solve the problem is considered the 3D bending model of slender beams (theory of Navier-Bernoulli beams) and the model of the torsion is non uniform or by warping restricted (Vlasov torsion theory).
Palabras clave
Pandeo 3D ; Bimomento ; Flexión biaxial
Keywords
3D Buckling ; Bimoment ; Biaxially bending moments
1. Introducción
El uso cada vez más frecuente de estructuras formadas por elementos muy esbeltos y livianos y el empleo de materiales altamente resistentes permiten realizar grandes construcciones que resultaban impensables hasta hace poco. Por ello, el análisis de la inestabilidad de dichas estructuras ha cobrado gran importancia y ha desplazado incluso, en muchos casos, el clásico análisis resistente, centrado únicamente en la aparición de tensiones que superan el límite elástico del material.
Numerosos estudios y trabajos de investigación se han dedicado al análisis del pandeo de tipologías estructurales tales como barras, placas y láminas, desde el punto de vista experimental, analítico o computacional. Este último enfoque ha experimentado un gran avance en los últimos años, gracias a dos factores: el perfeccionamiento progresivo de los métodos numéricos de simulación, sobre todo el gran auge del método de los elementos finitos, y la mejora imparable de las prestaciones de las computadoras actuales.
Son innumerables los estudios y las investigaciones dedicados al análisis de fenómenos de inestabilidad estructural, pero fue Euler (1744) el primero en proporcionar, de forma analítica, resultados del estudio del pandeo de columnas, que posteriormente serían completados por Lagrange (1788). Un siglo más tarde, apareció la teoría general de la bifurcación del equilibrio, desarrollada por Poincaré (1885), y Liapunov (1892) le dio un tratamiento más riguroso, desde el punto de vista matemático. Otra aportación importante al desarrollo de este problema fue la teoría no lineal de bifurcación de Koiter (1945), dedicada sobre todo al pandeo de placas y láminas.
La pérdida de estabilidad y la aparición de puntos de bifurcación son fenómenos habituales en el estudio de la mecánica del medio continuo. En el análisis estructural, existe una gran cantidad de bibliografía dedicada al estudio del pandeo de barras, placas y láminas, tanto desde el punto de vista analítico (Timoshenko y Gere,1961; Chajes, 1974), como numérico (Bathe y Dvorkin, 1975; Seydel, 1979; Riks, 1972, y Bushnell, 1982, entre otros).
Por otro lado, la barra es una tipología estructural que ha tenido un desarrollo extenso. Su formulación ha sido objeto de revisión continuamente, intentando incorporar todos los efectos observados experimentalmente. En este trabajo, se presenta un modelo de barra tridimensional con formulación geométricamente no lineal. El modelo de barra incorpora deformaciones a cortante y a torsión, así como el efecto del alabeo. Desde el punto de vista computacional, la inclusión del alabeo se resuelve con la adición de un séptimo grado de libertad a los seis habituales de la formulación clásica, que representa la amplitud del alabeo en cada sección de la barra. Dicho efecto es de gran importancia para ciertos tipos de secciones, como los perfiles de pared delgada y, sobre todo, las secciones abiertas y en que el alabeo aparece restringido, que dan lugar a torsión no uniforme.
Una de las aplicaciones prácticas de este modelo es la simulación numérica de fenómenos de inestabilidad, sobre todo en aquellos casos en que el alabeo es fundamental, como ocurre en los casos de pandeo lateral o pandeo por torsión.
Los puntos en que la matriz de rigidez de una estructura llega a ser singular se denominan puntos críticos y tienen una gran importancia desde el punto de vista de la estabilidad estructural. El significado físico de estos puntos en un análisis lineal es la aparición de desplazamientos indeterminados en un estado de carga constante. Lógicamente, en un análisis no lineal, ello no sucede, pero la consecuencia es la aparición de grandes desplazamientos y rotaciones y, en la mayoría de los casos, un gran aumento de las tensiones. En muchas ocasiones, pues, la estructura pierde su funcionalidad, bien sea por colapso plástico o por la aparición de desplazamientos no admisibles.
Los problemas asociados al fenómeno del pandeo en elementos estructurales de acero son, en ocasiones, la causa más importante de fallo mecánico [1] ; [3] ; [4] ; [26] ; [27] . Por otro lado, se considera que el método exacto que plantea el estudio detallado de los problemas de inestabilidad estructural de las barras de acero presenta una gran dificultad matemática [12] ; [13] ; [24] ; [29] . Además, no siempre se conocen con precisión las restricciones existentes en los extremos del tramo más crítico de la barra, lo cual hace que los resultados obtenidos sean poco fiables [7] ; [9] .
Sin embargo, la formulación del método matricial de rigidez 3D para el caso de no linealidad geométrica en hipótesis de linealidad material facilita la estimación teórica de la carga crítica de pandeo de forma sistemática con la ayuda del ordenador [10] ; [11] ; [21] ; [23] . Ello permite abordar problemas con casos de carga y condiciones de contorno en desplazamientos que no se incluyen en los casos descritos en la normativa vigente, y cuyo cálculo lógicamente es necesario abordar con rigor y con suficiente precisión desde el punto de vista práctico y de la seguridad estructural [2] ; [5] ; [8] ; [14] .
El trabajo se ha organizado de la manera siguiente: en primer lugar, tras esta introducción, se presenta la metodología utilizada. A continuación, se muestran varios ejemplos de aplicación y, en el último apartado, se presentan las principales conclusiones obtenidas de este trabajo.
2. Metodología
Todo problema de inestabilidad requiere plantear el equilibrio en la configuración deformada de la estructura. Para el caso de interés, es necesario analizar la barra objeto de estudio como elemento estructural espacial o 3D. Por tanto, lo más sencillo es formular las ecuaciones de equilibrio de fuerzas y momentos de forma integral a partir del principio de los trabajos virtuales (PTV), que, en el caso de las barras, tiene la expresión siguiente [6] ; [17] ; [18] ; [19] :
|
|
( 1) |
donde σ es la tensión normal; τξς , της son tensiones tangenciales; ɛ es la deformación longitudinal; γξς , γης son las deformaciones transversales; ti es el vector de fuerzas externas de superficie y ui son las componentes de desplazamiento de los puntos materiales de aplicación de dicho sistema de cargas exteriores.
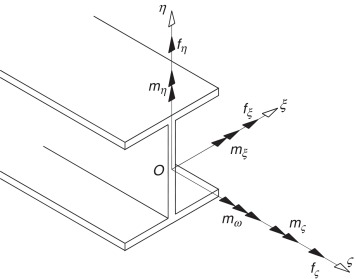
A partir de las magnitudes representadas en la figura 1 y tomando como base la teoría de la flexión de Navier-Bernouilli y la teoría de la torsión de Vlasov, se hace la siguiente definición de esfuerzos internos en la barra:
|
|
( 2) |
donde fς es el esfuerzo axil; fξ , fη son los esfuerzos cortantes; mη , mξ son los momentos flectores; mς es el momento torsor; mω es el esfuerzo bimomento; A es el área de la sección transversal de la barra; ξ , η son las coordenadas del punto material de la sección; el torsor según la teoría de la torsión uniforme o de Saint-Venant; Tω es el torsor restringido, y ω es lo que se conoce como área sectorial principal en la teoría de la torsión no uniforme de Vlasov.
|
|
|
Figura 1. Esfuerzos en la sección. |
En cuanto a las solicitaciones exteriores, en el modelo 1D/unidimensional se definen como cargas por unidad de longitud según cada uno de los ejes de referencia: qξ , qη , qς , siendo estas las más habituales en este tipo de problemas.
La necesidad de plantear el equilibrio en la configuración deformada o actual requiere la definición de deformación de Euler-Lagrange, que lleva a las siguientes relaciones entre deformaciones y desplazamientos:
|
|
( 3) |
También se asume la hipótesis de pequeños desplazamientos, con lo cual resulta:
|
|
( 4) |
donde uξ , uη , uς son las componentes de desplazamiento de un punto material cualquiera de la barra según cada uno de los ejes de coordenadas; uξ 0 , uη 0 , uς son los desplazamientos de los puntos de la directriz de la barra; θς es el ángulo girado por la sección según el eje longitudinal; es la magnitud del alabeo de la sección correspondiente, y, por último, son las cotas de la posición del centro de esfuerzos cortantes con respecto al centro de gravedad de la sección.
Según los modelos de flexión y torsión adoptados, se llegan a plantear las siguientes ecuaciones de compatibilidad-comportamiento:
|
|
( 5) |
donde Iξ , Iη son los momentos principales de inercia, Iω es el módulo de alabeo y KT es la constante de rigidez torsional.
2.1. Aproximación de desplazamientos
En cuanto al campo de desplazamientos, se asume que las barras son suficientemente esbeltas para considerar despreciable el efecto de las deformaciones transversales asociadas a los esfuerzos cortantes, lo cual implica las relaciones siguientes:
|
|
( 6) |
Para los desplazamientos longitudinales, se supone una variación lineal:
|
|
( 7) |
donde es la coordenada longitudinal adimensional en el elemento y son los valores nodales del desplazamiento longitudinal.
Sin embargo, para la aproximación de desplazamientos transversales a la sección, se supone una variación cúbica:
|
|
( 8) |
donde y son los valores de los desplazamientos y de giros escalados en las secciones extremas del elemento.
Y, por último, también se asume una variación cúbica para el giro según el eje longitudinal:
|
|
( 9) |
donde son los valores del giro y del alabeo escalado en los nodos del elemento.
2.2. Ecuaciones aproximadas
Para el cálculo de las ecuaciones de equilibrio mecánico, también se supone que el esfuerzo axil es constante y que los momentos flectores tienen una variación de tipo lineal a lo largo del elemento de barra considerado:
- Flexión en el plano ς − ξ :
|
|
( 10) |
- Flexión en el plano ς − η :
|
|
( 11) |
- Torsión:
|
|
( 12) |
donde son los coeficientes que cuantifican el efecto Wagner en cada uno de los extremos del elemento: nodo inicial (p ) y nodo final (q ).
- Extensión:
|
|
( 13) |
Y donde se ha hecho uso de la definición de las siguientes matrices:
|
|
( 14) |
2.3. Matriz de rigidez
A continuación, se organizan y se escalan el vector de grados de libertad y el vector de fuerzas del elemento, de la manera siguiente:
|
|
( 15) |
Así, el conjunto de ecuaciones de equilibrio de la barra puede expresarse de forma matricial como se indica a continuación:
|
|
( 16) |
La matriz KS es la parte material de la matriz de rigidez y tiene la expresión explícita siguiente:
|
|
( 17) |
donde los coeficientes de la matriz son:
|
|
( 18) |
Por otro lado, la matriz KG es la matriz geométrica, también denominada matriz de tensión inicial , y se define por:
|
|
( 19) |
siendo sus términos:
|
|
( 20) |
2.4. Fuerzas de empotramiento
En caso de tener cargas aplicadas dentro del elemento barra, debe calcularse su efecto equivalente en los nudos. Y la ecuación del comportamiento mecánico del elemento barra se modifica ligeramente [15] ; [25] ; [30] :
|
|
( 21) |
siendo Femp el vector de fuerzas de empotramiento del elemento.
Por tanto, este vector de fuerzas de empotramiento se debe calcular sobre la base de su expresión en el PTV:
|
|
( 22) |
De hecho, si se particulariza para el caso más habitual de carga distribuida uniforme, se obtiene:
|
|
( 23) |
2.5. Ensamblaje de los elementos
Una vez determinado el comportamiento mecánico de cada elemento barra, dado por la ecuación (21), es necesario imponer las condiciones de equilibrio y de compatibilidad de desplazamientos en los nodos. Este proceso es conocido en la formulación del método directo de rigidez como la etapa de ensamblaje de la matriz de rigidez de la estructura y del vector de fuerzas [16] ; [20] ; [22] .
Para llevar a cabo este proceso, un requisito previo es expresar la ecuación (21) en un sistema de referencia global , común para todos los elementos barra que forman la estructura objeto de análisis. Es decir, se requiere un cambio de base 3D del sistema de ejes local al sistema global, para obtener para cada elemento la matriz de rigidez en las coordenadas globales:
|
|
( 24) |
siendo T la correspondiente matriz de transformación de coordenadas de locales a globales. El vector es el vector de fuerzas equivalentes en los nodos, que ya se ha expresado en el sistema global según la fórmula siguiente:
|
|
( 25) |
A continuación, se lleva a cabo la fase de ensamblaje de la matriz de rigidez y del vector de fuerzas, y se llega a una expresión matricial que representa las ecuaciones de equilibrio en todos los nodos de la estructura, esto es:
|
|
( 26) |
donde Fest es el vector de fuerzas aplicadas en los nodos, es el vector de fuerzas equivalentes, Kest es lo que se conoce como matriz de rigidez de la estructura y es el vector de desplazamientos en los nodos de la estructura.
2.6. Pandeo/Inestabilidad
Por último, en este trabajo interesa estimar los valores de las cargas críticas que pueden originar fenómenos de inestabilidad estructural asociados a deformaciones de flexión y/o torsión con respecto al centro de esfuerzos cortantes [14] ; [16] ; [28] ; [31] .
Para llevar a cabo este cálculo, lo más inmediato es, en primer lugar, imponer en el sistema de ecuaciones (26) las condiciones de contorno en desplazamientos, giros y la posibilidad de alabeo de los nodos de la estructura que se pretende analizar.
Por tanto, los valores críticos de carga son aquellos para los cuales la rigidez de la estructura se reduce al valor nulo, esto es:
|
|
( 27) |
siendo λ el factor de carga proporcional, un coeficiente por el cual se multiplica a todas las cargas que solicitan la estructura, y es la matriz de rigidez de la estructura tras la imposición de las condiciones de contorno en los desplazamientos.
3. Resultados y discusión
A continuación, se presentan varios ejemplos de aplicación de la metodología expuesta en el apartado anterior.
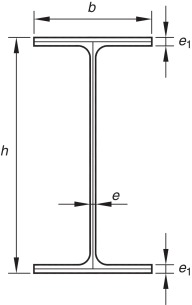
Para todos los cálculos, los datos son: longitud , sección de tipo doble-T , que corresponde al perfil comercial IPE300 (véase la fig. 2 ), y el acero como material .
|
|
|
Figura 2. Perfil laminado de la serie IPE. |
3.1. Pandeo con deformaciones de flexión y/o torsión
El ejemplo consiste en una viga biapoyada, sometida en sus secciones extremas a una carga de compresión centrada de valor P ( fig. 3 ). Los apoyos son ambos de tipo horquilla, es decir, tales que se impide el giro longitudinal, mientras que se permite el libre alabeo de la sección.
|
|
|
Figura 3. Viga biapoyada, sometida a compresión. |
La tabla 1 indica el primer valor crítico de la carga. Para este tipo de perfil, una sección con doble simetría, el valor teórico P1 se corresponde con la conocida fórmula de Euler y equivale al fenómeno de inestabilidad por flexión en el plano débil del perfil. En dicha tabla, también se indican los resultados obtenidos con la formulación de este trabajo (columna de la derecha), donde indica el número de elementos que se han considerado.
| n | P1 (N ) | |
| 2 | 788980,0 | |
|---|---|---|
| 4 | 782814,0 | |
| 8 | 782439,0 | |
| 16 | 782415,0 | |
| 20 | 782414,0 |
La tabla 2 indica el valor crítico de la carga P2 , asociado al fenómeno de inestabilidad por torsión alrededor del centro de esfuerzos cortantes del perfil. El valor teórico se indica en la tabla y coincide con el que se obtiene en este trabajo para al menos dieciséis elementos barra.
| n | P2 (N ) | |
| 2 | 1.96056 · 106 | |
|---|---|---|
| 4 | 1.95369 · 106 | |
| 8 | 1.95322 · 106 | |
| 16 | 1.95319 · 106 | |
| 20 | 1.95319 · 106 |
Por último, por su interés teórico-práctico, se incluye el valor de la carga crítica P6 asociado al fenómeno de inestabilidad por flexión en el plano fuerte del perfil (tabla 3 ). Se comprueba que, puesto que el problema de inestabilidad es no lineal, si se emplea un número suficiente de elementos de tipo barra se obtiene con precisión la solución exacta, según la expresión teórica de Euler.
| n | P6 (N ) | |
| 2 | 1.02045 · 107 | |
|---|---|---|
| 4 | 1.00772 · 107 | |
| 8 | 1.08298 · 107 | |
| 16 | 1.08294 · 107 | |
| 20 | 1.08294 · 107 |
3.2. Pandeo lateral o vuelco
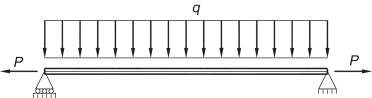
Este segundo ejemplo corresponde al problema de una viga biapoyada solicitada por cargas de flexión en el plano vertical, momentos concentrados en las secciones extremas de la barra (fig. 4 ) o carga distribuida uniforme (fig. 5 ) a lo largo de todo el elemento. De nuevo, se considera que ambos apoyos son de tipo horquilla.
|
|
|
Figura 4. Viga biapoyada. Momentos puntuales en los extremos. |
|
|
|
Figura 5. Viga biapoyada. Carga distribuida uniforme. |
La tabla 4 indica el valor del momento crítico de vuelco tanto teórico como estimado con la metodología de este trabajo para el caso de la figura 4 . Se comprueba que los resultados tienen precisión suficiente, desde el punto de vista práctico, incluso empleando un número bajo de elementos por barra, por ejemplo 4. Y que, si se aumenta el número, se obtiene la solución teórica exacta, concretamente si se emplean 16 elementos barra.
| n | Mcri (N · m ) | |
| 2 | 160470.0 | |
|---|---|---|
| 4 | 159631.0 | |
| 8 | 159574.0 | |
| 16 | 159570.0 |
Pandeo por flexión en el plano débil (plano ς − ξ ) y torsión).
A continuación, se muestran los resultados para el caso de carga distribuida (figura 5 , v. tabla 5 ). En dicha tabla, se incluyen los valores críticos de la carga distribuida que originan el fenómeno de la inestabilidad, con deformaciones de flexión en el plano débil del perfil junto con torsión alrededor del centro de esfuerzos cortantes.
| n | qcri (N /m ) |
|---|---|
| 2 | 109.298,0 |
| 4 | 94.735,8 |
| 8 | 91.330,6 |
| 16 | 90.528,7 |
| 20 | 90.433,8 |
Pandeo por flexión en el plano débil (plano ς − ξ ) y torsión)
3.3. Pandeo combinado / Pandeo 3D
Este caso reproduce el problema anterior con una carga adicional (P) de tracción o de compresión. Se consideran, de nuevo, los casos de momentos puntuales (fig. 6 ) y carga distribuida (fig. 7 ).
|
|
|
Figura 6. Viga biapoyada. Cargas (M, P). |
|
|
|
Figura 7. Viga biapoyada. Cargas (q, P). |
En las Tabla 6 ; Tabla 7 , se muestran los resultados estimados del momento crítico de vuelco para los casos de momentos concentrados en los extremos de la barra y carga adicional de tracción (tabla 6 ) o de compresión (tabla 7 ). Si comparamos estos valores con los obtenidos en el ejemplo anterior (v. tabla 4 ), se comprueba que una carga adicional de compresión ayuda a que el fenómeno de pandeo ocurra antes, es decir, a un nivel de carga menor y que, en cambio, un axil de tracción rigidiza la barra y aumenta el valor del momento flector necesario para que pueda originarse el fenómeno de inestabilidad.
| P = +1.0 · 105N | n | Mcri (N · m ) |
| 2 | 174.635,0 | |
|---|---|---|
| 4 | 173.805,0 | |
| 8 | 173.748,0 | |
| 16 | 173.745,0 | |
| 20 | 173.744,0 |
| P = −1.0 · 105N | n | Mcri (N · m ) |
| 2 | 146.073,0 | |
|---|---|---|
| 4 | 145.221,0 | |
| 8 | 145.163,0 | |
| 16 | 145.159,0 | |
| 20 | 145.159,0 |
Como es lógico, la conclusión es exactamente la misma en el caso de la carga distribuida uniforme. Para ello, se pueden comparar los resultados de las Tabla 8 ; Tabla 9 (tracción y compresión, respectivamente) con el caso sin esfuerzo axil adicional (v. tabla 5 ).
| P = +1.0 · 105N | n | qcri (N /m ) |
| 2 | 118.599,0 | |
|---|---|---|
| 4 | 102.948,0 | |
| 8 | 99.254,5 | |
| 16 | 98.385,9 | |
| 20 | 98.283,2 |
| P = −1.0 · 105N | n | qcri (N /m ) |
| 2 | 99.790,2 | |
|---|---|---|
| 4 | 86.355,1 | |
| 8 | 83.244,5 | |
| 16 | 82.511,3 | |
| 20 | 82.424,6 |
3.4. Inestabilidad de una estructura espacial
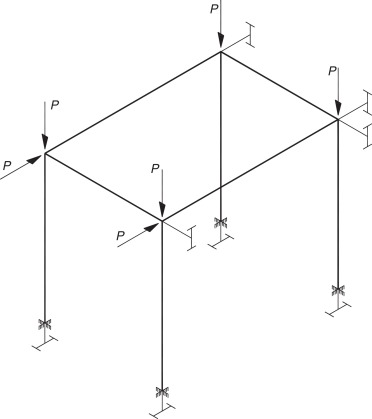
Como último ejemplo, se ha elegido resolver una estructura espacial de barras de tipo pórtico 3D. El sistema de barras que se quiere analizar se ilustra en las Figura 8 ; Figura 9 . Son casos de cargas puntuales y de carga distribuida uniforme, respectivamente. Se supone que todas las barras tienen la misma longitud (L), que las bases de los pilares están perfectamente empotradas y que todos los nudos son rígidos. Todas las barras son de perfil de tipo IPE300 y su disposición espacial es la que se indica (v. Figura 8 ; Figura 9 ).
|
|
|
Figura 8. Pórtico 3D. Cargas puntuales. |
|
|
|
Figura 9. Pórtico 3D. Carga distribuida uniforme. |
Para el caso del pórtico con cargas puntuales (fig. 8 ), los resultados de la carga crítica de pandeo estimada se muestran en la tabla 10 . Se comprueba que, debido a la no linealidad del problema, es necesario emplear un número elevado de elementos por barra de la estructura.
| n | Pcri (N ) |
|---|---|
| 2 | 379.356,0 |
| 4 | 417.295,0 |
| 8 | 511.979,0 |
| 16 | 550.498,0 |
| 20 | 555.725,0 |
En este último ejemplo y caso de carga (v. tabla 11 ), se confirma que, desde el punto de vista práctico del análisis de estructuras reales, los resultados se obtienen con precisión numérica suficiente y del lado de la seguridad utilizando discretizaciones del conjunto de cuatro elementos por barra de la estructura en 3D.
| n | qcri (N /m ) |
|---|---|
| 2 | 30.626,4 |
| 4 | 42.512,4 |
| 8 | 47.688,4 |
| 16 | 49.733,9 |
| 20 | 50.052,0 |
4. Conclusiones
En este trabajo, se resume la metodología de análisis no lineal de estructuras espaciales de barras que permite resolver problemas de inestabilidad con deformaciones de flexión y/o torsión, así como calcular el momento crítico de vuelco para cualquier caso de carga y condiciones de sustentación, y combinaciones de las situaciones anteriores, que es lo que durante el desarrollo del trabajo se ha decidido denominar pandeo combinado o pandeo 3D .
Asimismo, se da la posibilidad de aplicar esta metodología al estudio de las inestabilidades de sistemas espaciales de barras que se deforman según el modelo general de tracción/compresión-flexión-torsión. Dicha estructura 3D será susceptible de pandear por la combinación de deformaciones de flexión según ambos planos y de torsión respecto del centro de esfuerzos cortantes de la sección.
Se observa la importancia de incluir efectos como las deformaciones a cortante y torsión y el alabeo en la formulación de la barra, sobre todo este último, para el análisis del pandeo lateral en perfiles con baja rigidez torsional, como es el caso de los perfiles abiertos de pared delgada. En muchas ocasiones, los momentos o cargas críticas hallados al considerar el fenómeno del alabeo son muy inferiores a los obtenidos en aquellos casos en que no se ha considerado dicho fenómeno. Por ello, es importante utilizar un modelo de barra que tenga en cuenta este efecto para el análisis del pandeo lateral.
Este trabajo posibilita la realización de nuevas curvas de pandeo para una mayor cantidad de perfiles, condiciones de apoyo y tipos de carga. Puede ser de ayuda para el proyectista la realización de estas curvas, que proporcionan el agotamiento por la aparición de inestabilidad y que, por otros medios, analíticos o experimentales, sería imposible o muy costoso obtener. Además de las curvas de pandeo lateral, también se pueden realizar análisis de pandeo por flexión, torsión, flexotorsión, etc. El único efecto que no podría analizarse por este método sería la abolladura de partes del perfil, aunque este estudio también podría realizarse mediante una discretización del perfil por medio de elementos de tipo lámina.
Por tanto, los problemas que este trabajo permiten resolver van más allá de los casos particulares recogidos en la normativa vigente, que solo considera el estudio de elementos estructurales aislados.
Referencias
- [1] M. Cacho-Pérez, A. Lorenzana; Cálculo directo de la carga crítica de pandeo de pórticos. Parte II; Rev. Int. Mét. Num. Cálc. Dise. Ing., 26 (2010), pp. 31–38
- [2] W.F. Chen, T. Atsuta; Theory of beam-columns. Volume 1: in-plane behaviour and design; J. Ross Pub Inc (2007)
- [3] A. Lorenzana, M. Cacho-Pérez; Cálculo directo de la carga crítica de pandeo de pórticos. Parte I; Rev. Int. Mét. Num. Cálc. Dise. Ing., 25 (3) (2009), pp. 247–258
- [4] M.A. Ortega, J.L. Romero, E. Rosa; A historical study of the problem of straight prismatic elements subjected to compression; Informes de la Construcción, 59 (507) (1997), pp. 69–81
- [5] M. Cacho-Pérez, A. Lorenzana; Optimización global de pórticos 2D con barras de sección variable; DYNA, 85 (8) (2010), pp. 667–675
- [6] W.F. Chen, T. Atsuta; Theory of beam-columns. Volume 2: space behaviour and design; J. Ross Pub Inc (2007)
- [7] Z. Lei, T.G. Shu; Lateral buckling of web-tapered I-beams: A new theory; J. Constr. Steel Res., 64 (12) (2008), pp. 1379–1393
- [8] M. Kovac; Lateral-torsional buckling of web-tapered I-beams. 1D and 3D FEM approach; 23rd Czech and Slovak Conference on Steel Structures and Bridges, 40 (2012), pp. 217–222
- [9] S.E. Kim, C.M. Uang, S.H. Choi, K.Y. An; Practical advanced analysis of steel frames considering lateral-torsional buckling; Thin-Walled Structures, 44 (7) (2006), pp. 709–720
- [10] N. Hoveidae, B. Rafezy; Global buckling prevention condition of all-steel buckling restrained braces; J. Theor. App. Mech., 51 (4) (2013), pp. 891–902
- [11] M.A. Serna, A. Lopez, I. Puente, D.J. Yong; Equivalent uniform moment factors for lateral-torsional buckling of steel members; J. Constr. Steel Res., 62 (6) (2006), pp. 566–580
- [12] J.D. Aristizabal-Ochoa; Column stability and minimum lateral bracing: Effects of shear deformations; J. Eng. Mech., 130 (10) (2004), pp. 1223–1232
- [13] A. Andrade, D. Camotim, P.B. Dinis; Lateral-torsional buckling of singly symmetric web-tapered thin-walled I-beams: 1D model vs. shell FEA; Comput. Struct., 85 (17-18) (2007), pp. 1343–1359
- [14] W.F. Chen, E.M. Lui; Stability design of steel frames; CRC Press, Inc (2000)
- [15] W. McGuire, R.H. Gallagher; Matrix Structural Analysis; Wiley, New York (1979)
- [16] H. Kardestuncer; Introducción al análisis estructural con matrices; McGraw-Hill (1975)
- [17] M.A. Martínez, M. Doblaré, L. Gracia; Estudio mediante elementos finitos del fenómeno de pandeo lateral en perfiles conformados en frío; Rev. Int. Mét. Num. Cálc. Dise. Ing., 17 (4) (2001), pp. 427–445
- [18] C. Dou, Y.L. Guo, Y.L. Pi, S.Y. Zhao; Flexural-Torsional Buckling and Ultimate Resistance of Parabolic Steel Arches Subjected to Uniformly Distributed Vertical Load; Journal of Structural Engineering, 140 (10) (2014), p. 04014075
- [19] P. Vargas, E. Oñate, S. Oller; Formulación de elementos finitos para vigas de sección abierta formadas por laminados compuestos incluyendo las deformaciones tangenciales por cortante y torsión; Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 30 (4) (2014), pp. 238–246
- [20] N.S. Trahair; Bending and buckling of tapered steel beam structures; Engineering Structures, 59 (2014), pp. 229–237
- [21] C.K. Iu, M.A. Bradford; Higher-order non-linear analysis of steel structures. Part I: elastic second-order formulation; Advanced Steel Construction, 8 (2) (2012), pp. 168–182
- [22] N.S. Trahair; Inelastic buckling design of monosymmetric I-beams; Engineering Structures, 34 (2012), pp. 564–571
- [23] Y.L. Pi, M.A. Bradford, G.S. Tong; Elastic lateral-torsional buckling of circular arches subjected to a central concentrated load; International Journal of Mechanical Sciences, 52 (6) (2010), pp. 847–862
- [24] N. Challamel, C.M. Wang; Exact lateral-torsional buckling solutions for cantilevered beams subjected to intermediate and end transverse point loads; Thin-Walled Structures, 48 (1) (2010), pp. 71–76
- [25] R.E. Erkmen, M. Mohareb, M.A. Bradford; Complementary Energy Based on Formulation for Torsional Buckling of Columns; Journal of Engineering Mechanics-ASCE, 135 (12) (2009), pp. 1420–1426
- [26] N.S. Trahair; Buckling analysis design of steel frames; Journal of Constructional Steel Research, 65 (7) (2009), pp. 1459–1463
- [27] Y.L. Pi, M.A. Bradford, F. Tin-Loi; IN-PLANE STRENGTH OF STEEL ARCHES; Advanced Steel Construction, 4 (4) (2008), pp. 306–322
- [28] N.S. Trahair; Lateral buckling of monorail beams; Engineering Structures, 30 (11) (2008), pp. 3213–3218
- [29] W.H. Duan, C.M. Wang; Exact solution for buckling of columns including self-weight; Journal of Engineering Mechanics-ASCE, 134 (1) (2008), pp. 116–119
- [30] Y.L. Pi, M.A. Bradford, F. Tin-Loi; Flexural-torsional buckling of shallow arches with open thin-walled section under uniform radial loads; Thin-Walled Structures, 45 (3) (2007), pp. 352–362
- [31] N.S. Trahair; Biaxial bending and torsion of steel equal angle section beams; Journal of Structural Engineering-ASCE, 133 (1) (2007), pp. 78–84
Document information
Published on 01/03/17
Accepted on 03/09/15
Submitted on 05/10/14
Volume 33, Issue 1, 2017
DOI: 10.1016/j.rimni.2015.09.005
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?