Abstract
In this part of the paper we shall use the formulation given in the first part to assess the quality of recovery based error estimators using two recovery methods, i.e. Superconvergent Patch Recovery (SPR) and Recovery by Equilibrium in Patches (REP). The recovery methods have been shown to be asymptotically robust and superconvergent when applied to two dimensional problems. In this study we shall examine the behavior of the recovery methods on several three dimensional mesh patterns for patches located either inside or at boundaries. This is performed by first finding an asymptotic finite element solution, irrespective of boundary conditions at far ends of the domain, and then applying the recovery methods. The test procedure near kinked boundaries is explained in a step by step manner. The results are given in a series of tables and figures for various cases of three dimensional mesh patterns. It has been experienced that the full superconvergent property is generally lost due to presence of boundary layer solution and the definition of the recoveries near boundaries though the results of the robustness test is still within an acceptable range.
Keywords: Recovery, Error Estimate, Superconvergent, Robustness test, three dimensional
1. INTRODUCTION
In the first part of this paper [1], we introduced a method for capturing boundary layer solution near kinked boundaries. As we described, the boundary layer solution is a part of asymptotic finite element solution which is used in the robustness test. In this part of the paper we shall employ the proposed method to carry out tests on some error estimates.
Error estimators are usually classified into two categories, i.e. residual based error estimators and recovery based error estimator. The first thoughts for error evaluation were in the form of the former category and the well known paper by Babuška and Rheinboldt [2] appears to be the pioneering one. About a decade later the latter approach was introduced by Zienkiewicz and Zhu [3]. A projection method was suggested for evaluation of continuous gradient fields. Soon it became clear that the projection method works for certain class of elements. The reason was detected as the lack of adequate convergence of the solution. Few years later, the authors introduced another projection method called Superconvergent Patch Recovery (SPR) and showed its performance through some benchmark problems [4]. It has also been proven that if a projection method exhibits a slightly more convergence than the finite element solution the adaptive procedure leads the solution towards the exact solution [5]. The recovery method uses information on some sampling points at element level. The error estimator using SPR method is sometimes called “ZZ” estimator. Many researchers soon began to use the method and many reports were published concerning the effectiveness of the method most of which admitting its superiority. Some amendments were also introduced for further increase of the convergence [6,7] or improvement of the results near boundaries [8].
Despite the efforts made for improvement of SPR, the original form is still the most effective and economical version. This has been confirmed in studies performed by Bubuška et al reported in a series of papers [9-11]. One of the outcomes of the studies was a routine for testing the error estimates in an asymptotic sense which we explained in the first part of the paper [1]. Some of the error estimators studied by Bubuška and co workers are of residual based type. It has been shown that among all error estimators suggested to the date, for problems with smooth exact solution, the recovery based one using SPR is superior in performance.
The success and popularity of SPR is due to two important features, i.e. simplicity and accuracy. However, in terms of accuracy there is an argument when singularity in solution is of concern. In other studies by Bubuška et al it is shown that another source of error may encounter to a finite element solution called as “pollution error” [12-14]. This sort of error cannot be captured by error estimators that use local information such as those use recovery methods. This is much pronounced when the element sizes are reasonably large especially around the singular points. This is considered as a mathematical deficiency for recovery based error estimators such as “ZZ”. However, from engineering point of view there is an argument for such deficiency which still keeps the recovery based error estimator on top. It has been experienced that when using “ZZ” estimator in problems with singularities, the locations of the singular points are spotted very fast. The reason for such effect lies in the fact that the error estimated near such points is usually large and thus in a real adaptive procedure the subsequent meshes become extensively fine around the singular points. This leads to reduction of the pollution error in other parts of the domain and therefore the accuracy of the recovery results increases. Nevertheless, according to the studies in [12-14] the criterion for termination of the adaptive procedure must carefully be revised.
Based on above discussion, it may be concluded that assumption made in [1], initially used in [9-11], will be valid for wide range of problems when the study is performed in an asymptotic sense. In present study we focus on performance of SPR basically in three dimensional problems. Meanwhile we shall study the behavior of another recovery method called Recovery by Equilibrium in Patches introduced in [15]. The recovery uses a weighted form of equilibrium equations; similar to FEM formulation, on patches of elements and exhibits similar behavior to SPR in two dimensional benchmarks. The method does not need any information at special points. The improved version of the method was introduced in [16] where the results of robustness test were given. Since there is no need for especial information, REP may be applied to nonlinear problems such as those involving plastic deformation [17,18]. A hybrid recovery from combination of SPR and REP can be seen in the literature [19] which may be considered as an improved version of SPR since it still needs information at sampling points and thus does not reflect full advantages of REP.
The layout of this part of the paper is as follows; in the next section we shall explain the test procedure including the generalized formulation given in the first part of the paper. Some sample problems are added to the section in order to give insight to operations needed especially for the new part of the formulation. In Section 3, a brief overview of the error estimators used are given. In Section 4 the results obtained from application of the test to heat and elasticity problem are presented and discussed. Finally, in Section 5 we shall summarize the conclusions made throughout the paper.
In this part of the paper we shall frequently refer to relations and equation numbers in the previous part. In order to distinguish the equation numbers from the current part and the previous one, we use symbol “ ![]() ” in the quotation of the numbers when the equation belongs to the first part, e.g. (30-
” in the quotation of the numbers when the equation belongs to the first part, e.g. (30- ![]() ) refers to equation number 30 of the first part.
) refers to equation number 30 of the first part.
2. THE TEST PROCEDURE
In the first part of the paper [1], preliminary concepts related to the model problem and error definition were discussed. The test procedure for patch locations at interior parts as well as at flat boundaries originally proposed by Babuška and co workers [9-11], was revisited. A generalization for such a patch test was also introduced in the previous part. Here we shall give some details for the procedure of test near kinked boundaries.
As is seen in the first part, the test procedure is consisting of two main parts; first part is evaluation of the asymptotic finite element solution for a given exact solution as monomials of a polynomial and the second part is estimation of the error and calculation of the upper and lower bounds of the effectivity index.
The asymptotic finite element solution is considered as summation of two sets of solutions, one as an asymptotic solution for interior parts of the domain and another as a boundary layer solution which plays the role of a correction to the first set when the patch used is near a flat or a kinked boundary.
The boundary layer solution is in fact a spurious mode which decays towards the interior parts of the domain. The asymptotic boundary layer solution near flat boundaries may be obtained using the method proposed by Babuška et al in [20] through which an eigenvalue problem is defined and solved in order to impose the decay condition in direction of normal to the boundary. However, one may invariably use the extended formulation given in the first part by fixing one of the proportionality factors to unity. For the case of kinked boundaries the solution is performed in a spectral form using an eigenvalue solution for each component. It is shown that the procedure is able to produce a finite element solution for an unbounded domain [1].
Having found the asymptotic finite element solution for a monomial, the test procedure is further continued towards evaluation of the error. In this paper we shall examine the performance of some recovery based error estimators. In such an error estimator new fields of gradients are constructed and the error is evaluated approximately as
|
|
(1) |
Where parameters with star represent the enhanced-recovered solutions and those with subscript denote the corresponding values from asymptotic finite element solution. Therefore the error norms required for definition of effectivity index ( 6- ![]() ) are written as (7-
) are written as (7- ![]() ).
).
Of course the approximate error norm may be compared to the norm of the exact errors obtained from the difference of the exact gradients, pertinent to the monomial used as the exact solution, and the asymptotic finite element solution. Considering all possible error norms from the monomials one can calculate the upper and lower bounds of the effetivity index as (19- ![]() ) to (22-
) to (22- ![]() ) and the robustness index as (8-
) and the robustness index as (8- ![]() ).
).
In summary the test procedure near intersecting boundaries or even a flat boundary may be described as below
- (a) Select a repeatable pattern for the patch.
- (b) Select a proper monomial with one order higher than the order of the shape functions.
- (e) Consider a (or ) macro patch. If the test procedure is to be performed near a corner ,with three intersecting flat boundaries, use a (or ) macro patch.
- (f) Construct the stiffness matrix of each patch in the macro patch and condense out those degrees of freedoms which are not shared with adjacent patches. Assemble the stiffness matrices to construct the macro patch stiffness matrix.
- (h) Select a number of patches along the axes with non periodic conditions (along axes with periodic conditions just one patch is enough).
- (i) Choose a numerical integration scheme and select a series of integration points.
- (l) For each integration point find the roots of the determinant of and the associative null space vectors. Choose the roots that satisfy decay condition.
- (o) Find and (or if Neumann conditions are to be applied).
- (p) Repeat from (j) to complete the integration procedures for two matrices in (o).
- (r) Apply the boundary conditions
- For Neumann boundary conditions; Evaluate defined in (74-
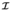 ) and (75-
) and (75- 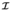 ) and use Equation (84-
) and use Equation (84- 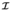 ) or (88-
) or (88- 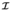 ) to find for the whole domain. If Equation (84-
) to find for the whole domain. If Equation (84- 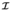 ) is to be used, must be evaluated through Equation (82-
) is to be used, must be evaluated through Equation (82- 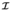 ) in advance. The prescribed nodal forces may also be calculated as the right hand side of Equation (36-
) in advance. The prescribed nodal forces may also be calculated as the right hand side of Equation (36- 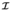 ).
).
- For Neumann boundary conditions; Evaluate defined in (74-
- (s) If necessary repeat from step number (h) by increasing the number patches along the axes to ensure that no significant change happens and reasonable convergence is achieved.
- (u) Perform the recovery procedure using FEM solution from previous step.
- (v) Repeat from (b) to (u) for all possible monomials.
- (x) Find eigenpairs of .
In following sample problem we give some numeric details.
Sample problem 1
Supposing that a repeatable pattern of patches of elements as Figure 1 is prepared, we shall look for an asymptotic finite element solution, , for a scalar type of problem when a monomial as plays the role of exact solution and Dirichlet boundary condition is of concern. The mash pattern has been used once in the first part of this paper for solution of a general unbounded domain. Here we specifically focus on evaluation of near corner of the domain since numeric details of the rest of the procedure are similar to what has been given in reference [20] for flat boundaries.
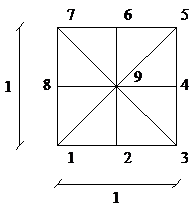
|
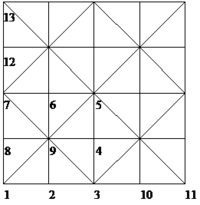
|
| (a) | (b) |
| Figure 1:Node numbering at the basic patch and the edges of the domain for sample problem No.1. | |
As a first step, we find and to be used in Equation (32- ![]() ) for boundary conditions at and . If the nodes are numbered as Figure 1a the nodal values of the periodic finite element solution will be
) for boundary conditions at and . If the nodes are numbered as Figure 1a the nodal values of the periodic finite element solution will be
|
|
and . The independent nodal values are arranged as .
The prescribed values of are calculated through equation (32- ![]() ). For simplicity in the step by step numerical presentation, we shall apply the boundary condition on a small domain of patches.
). For simplicity in the step by step numerical presentation, we shall apply the boundary condition on a small domain of patches.
Application of steps (e) to (i) leads to evaluation of as the one given in the sample problem of first part of the paper. Instead of evaluation of a parametric form of in terms of both and , one can choose a value for as an integration point and write in terms of the other parameter. Note that the patch size in this sample problem is unity which is different from patch sizes used in [1] but this does not affect the computations pertinent to the characteristic equation and the null space. We choose a 30 point Gauss integration rule for (and ). For example an integration point as one may calculate
|
|
from the characteristic equation (see in the sample problem of part I). The null space of are then obtained as
|
We choose vectors associated with , i.e. , and , reflecting decay condition. For each case we define the transformation matrix in order to construct , for instance for two patches along each axis (see Figure 1-b)
|
|
Therefore
|
|
Similar steps are repeated for evaluation of in terms of . We evaluate matrix as (71- ![]() ) the details of which can not be given here because of numerous operations involved
) the details of which can not be given here because of numerous operations involved
|
|
The solution for is obtained through Equation (73- ![]() ) using following prescribed values
) using following prescribed values
|
|
For example, if the nodal values for the corner patch is of concern, one may first define as in (64- ![]() ) like the following one for
) like the following one for
|
|
Thus for three pairs at point , vectors are evaluated as
|
|
Evaluation of for other integration points and use of and as given above in (73- ![]() ) leads to the following values for the boundary layer nodal values
) leads to the following values for the boundary layer nodal values
|
The ninth nodal value in the corner patch may be obtained from an inverse static condensation as . Now summation of the nodal values as gives
|
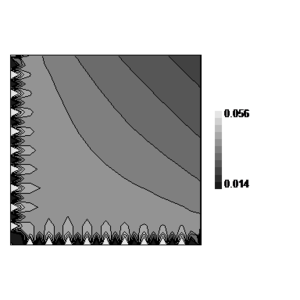
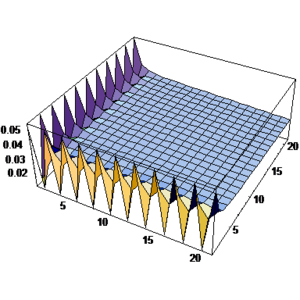
In order to study the boundary layer solution, variation of near corner is illustrated in Figure 2. In this solution 10 patches are used along each axis.
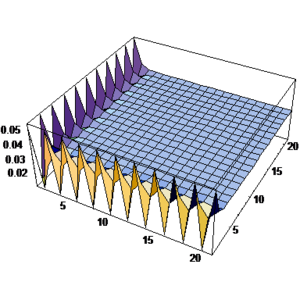
It may be noticed that it is not easy to give a direct finite element solution for comparison since no clear information is available for boundary conditions at the other two edges of the domain. However, one may take either of two conditions given in (28- ![]() ) in an approximate manner, i.e. or . This means that approximately either a homogeneous Dirichlet or Neumann boundary condition might be chosen for far ends of the domain. Depending on the main boundary conditions near the corner, each case may have some drawbacks such as presence of singular points and etc. However, if the domain, nominated for direct finite element solution, is chosen very large then the effects of such imperfections at far ends of the domain become negligible at the patches near the corner. Our experience shows that use of Neumann boundary condition gives good results when the dimensions of the domain are very large. Figure 3 depicts the variation of obtained form such approximate and direct finite element solution. Comparison of the results with those shown in Figure 2, for the proposed method, illustrates the similarities between the two sets (the difference between the contour presentations in the two figures is basically due to the difference between the levels of solutions after the first layers of the elements).
) in an approximate manner, i.e. or . This means that approximately either a homogeneous Dirichlet or Neumann boundary condition might be chosen for far ends of the domain. Depending on the main boundary conditions near the corner, each case may have some drawbacks such as presence of singular points and etc. However, if the domain, nominated for direct finite element solution, is chosen very large then the effects of such imperfections at far ends of the domain become negligible at the patches near the corner. Our experience shows that use of Neumann boundary condition gives good results when the dimensions of the domain are very large. Figure 3 depicts the variation of obtained form such approximate and direct finite element solution. Comparison of the results with those shown in Figure 2, for the proposed method, illustrates the similarities between the two sets (the difference between the contour presentations in the two figures is basically due to the difference between the levels of solutions after the first layers of the elements).
|
|
| (a) | (b) |
| Figure 2:Boundary layer solution obtained from the proposed method for the sample problem No. 1 using patches with pattern of Fig. 1 and Dirichlet boundary condition at and obtained from monomial as the exact solution; (a) Contour line presentation, (b) Three dimensional plot presentation. | |

|
|
| (a) | (b) |
| Figure 3:Standard finite solution for the sample problem No. 1 using patches with pattern of Fig. 1 and Dirichlet boundary condition at and obtained from monomial as the exact solution and Neumann condition at the other two boundaries; (a) Contour line presentation, (b) Three dimensional plot presentation. | |
Sample problem 2
In this example we shall use regular pattern of triangles as Figure 4a. Once again, the problem is to find near corner of the domain. For the asymptotic finite element solution, the boundary condition to be imposed is of a Neumann form extracted from monomial as an exact solution. For convenience in giving numeric details, we use a patch of two elements as the basic repeating unit of the mesh.
According to the node numbering in Figure 4b, the nodal values of periodic finite element solution, evaluated from Equation (23- ![]() ) and conditions (24-
) and conditions (24- ![]() ), are as
), are as
|
|
The tractions are calculated from (33- ![]() ). Then the prescribed nodal forces for three patches (here elements) along and are obtained as (see numbering of the nodes in Figure 4b)
). Then the prescribed nodal forces for three patches (here elements) along and are obtained as (see numbering of the nodes in Figure 4b)
|
|
Note that five nodes are nominated for satisfaction of the boundary conditions (nodes shown in dashed box in Figure 4b) though twelve nodes are involved in the computation since seven nearby nodes are contributing to traction resultants at nominated nodes through the adjacent elements shown in shaded gray area in Figure 4b. Stiffness matrix of the patch is evaluated as
|
We apply the proportionality relations to obtain the following characteristic equation
|
|
Note that in this simple case no null space solution is required since just one independent DOF is remaining. Now for an integration point as one may calculate form above characteristic equation. We construct and for nodes 1 to 12, in Figure 4-b, from the proportionality factors as
|
|
Also is evaluated, for DOFs shown in shaded area of Figure 6-b, as
|
|
Performing numerical integration in (82- ![]() ) for points selected for both and , matrix is evaluated as
) for points selected for both and , matrix is evaluated as
|
|
Now we define for nodes 1, 2, 3, 5, 6 and 8 for example, through the following transformation
|
Boundary layer solution, , is obtained from Equation (84- ![]() )
)
|
|
The asymptotic finite element solution for the patch is determined from where is calculated from (16- ![]() ). For patch shown in Figure 4-b
). For patch shown in Figure 4-b
|
|
We note that the values obtained for may still have slight rigid body motion since the decay condition has not been satisfied effectively and thus the values of are of high error except for the gradients at element level (see also the discussion for the sample problem in [1]). The rest of the procedure for finding upper and lower bounds of effectivity index is straight forward and may be found in literature.
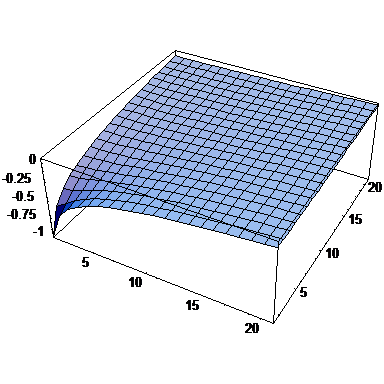
It is worthy to make some insight for distribution of boundary layer solution. Figure 5 shows the solution when twenty patches are used along each axis. For comparison, we have included the results for larger patches constructed from patches with similar pattern. It can be seen that the solution decays fast towards the interior parts. In another point of view, the solution suggests the use of homogenous Neumann boundary condition if an approximate direct FEM solution is to be applied on a finite domain. When Neumann conditions are of concern at main boundaries, as is the case of this example, use of Neumann conditions at the other edges of the domain makes some difficulties for obtaining the solution. However, to solve the problem one may restrain the most remote DOFs. Of course, as discussed in the first example, this may introduce a sort of singularity in the domain. Figure 6 show a standard finite element solution for the problem when Neumann boundary conditions have been used for far edges and the most remote DOF is restrained. The results show reasonable agreement between the two solutions near the corner.

|

|
|
| (a) | (b) | (c) |
| Figure 5: Boundary layer solutions obtained from the proposed method for sample problem No. 2 using Neumann boundary condition at and obtained from monomial as the exact solution; (a) Contour line presentation for solution using 20x20 patches with pattern of Fig 4a, (b) Contour line presentation for solution using 10x10 larger patches constructed from 2x2 patches with similar pattern, (c) Three dimensional plot presentation. | ||

|

|
| (a) | (b) |
| Figure 6. Standard finite solution for sample problem No. 2 using 20x20 patches with pattern of Fig. 4a and Neumann boundary condition at and obtained from monomial as the exact solution and Neumann condition at the other two boundaries - the most remote node is restrained as essential boundary condition; (a) Contour line presentation, (b) Three dimensional plot presentation. | |
3. THE ERROR ESTIMATORS
In this study we shall use some recovery based error estimators proven to be robust in two dimensional problems. Apparently, robustness of a recovery based estimate lies in the quality of the recovered fields used and this means that the recovery should show superconvergent or semi-superconvergent property. A recovery based error estimate is said to be “asymptotically exact” when the recovery procedure used is at least “asymptotically superconvergent”. We shall examine the performance of the recoveries when applied to three dimensional cases.
The use of recovery based error estimates in robustness test is consistent with assumption made, in the first part, for smoothness of the exact solution. Generally the test results may not be used for predicting the performance of the recovery method near singularities. Recent studies by Babuška et al on use of recovery based error estimates in problems with singularities show that pollution error is dominant over the whole domain [12-14] which may not be captured by use of local recovered information in the error estimation. However, as we discussed in the introduction this deficiency is practically overcome in an adaptive procedure when the mesh becomes finer at singularities. Excessive refinement around singular points leads to fast reduction of the pollution error and thus even at points not very far from the singularities the assumptions made for smoothness of the solution will be valid. Therefore if the estimated error shows reasonable asymptotic behavior the results of estimated error becomes more accurate while the mesh becomes finer.
3.1 Recoveries used
Superconvergent Patch Recovery (SPR)
One of the most robust recovery methods was proposed by Zienkiewicz and Zhu in 1992 [4]. Although at the time of its proposal some benchmark problems were used to demonstrate its performance, later comprehensive studies by Babuška and co-workers [9-11] proved its superiority over the other methods in terms of robustness and asymptotic convergence rate in two dimensional problems. It is noteworthy to mention that the studies in [9-11] show that none of the augmented forms of SPR, as some researches suggest [6-8] can compete with the original formulation. In this paper we shall perform a comprehensive study on the performance of SPR when applied to three dimensional problems.
The procedure of SPR may be found in many texts and papers [4,5,21-24]. The procedure starts with assuming a continuous gradient field, in the form of a polynomial, over a patch of elements built on a vertex node
|
|
(2) |
In which contains the monomials, in this paper a complete polynomial in a three dimensional space, and is a matrix of the unknown coefficients. Minimization of a functional, as an error norm built from summation of errors between the enhanced field and the finite element solution at some sampling points, as
|
|
(3) |
with respect to polynomial coefficients results to the following expression for local recovered stress/gradient field
|
|
(4) |
The enhanced recovered gradient field for the whole domain is constructed by calculation of the above local field at patch point and interpolation of the nodal values obtained for the whole domain via shape functions used for the main unknowns .
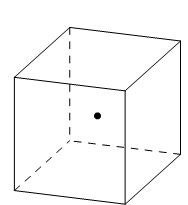
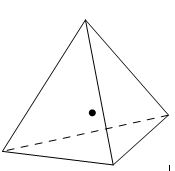
In this paper the sampling points used for three dimensional linear elements are shown in Figure 7. For further details of the procedure the reader may consult to references [4,5,21-24].
|
|
| (a) | (b) |
| Figure 7:Sampling points used for linear elements in SPR procedure; (a) point at in normalized coordinates for cuboids, (b) point at in volume coordinates for tetrahedral elements. | |
Recovery by Equilibrium in Patches (REP)
Another superconvergent recovery method, REP, was first proposed in [15] and then improved in [16]. In the latter research it was shown that although the original form of REP loses its robustness for patches with high aspect ratios, the improved version is as robust as SPR and can be considered as an alternative when the location of sampling points are not defined a priori. The procedure is based on an integral form of equilibrium equation. The idea is to find a local continuous field of gradient so that the equilibrium of patch is preserved, at least, approximately
|
(5) |
In above subscript denotes patch-wise view of notations, represent the matrix of stresses/gradients each of its components is expressed as (2) and is a vector of forces induced by finite element stress/gradient field maintaining the patch in equilibrium state. The procedure resembles to the solution of a system, as small as a patch, using a set of piecewise continuous weight functions and a set of generalized coordinates as the polynomial terms. The formulation can be written for strain or even displacement field.
The original form of REP, proposed in [15], directly employs Equation (5) to construct enhanced field of gradients in a coupled form, while the improved version uses spectral form of (5) to construct the recovered gradient field for each gradient component separately.
Original form
In this version a least square procedure is used for reducing the difference between forces induced by finite element gradients and those induced by the recovered fields. Hence the following functional
|
|
(6) |
is minimized with respect to coefficients in leading to a coupled system of equations. The rest of the procedure is similar to that of SPR mentioned above. The reader may also consult to the references [15,16,24] for further explanation.
Improved form
In reference [16] it has been shown that the formulation given for original REP loses robustness for meshes with high aspect ratio. The sensitivity to aspect ration is effectively rediuced if we write both the finite element and recovered stress vectors, ![]() and
and ![]() , as:
, as:
|
(7) |
and substitute in Equation (5) to obtain
|
|
(8) |
and split the equilibrium equations accordingly. The procedure continues with minimization of a series of functionals as
|
|
(9) |
with respect to coefficients in . The rest of procedure is again similar to SPR as mentioned before.
Enhanced gradients at boundaries
Because in this paper assessment of the recoveries at boundaries of the domain is aimed, it is necessary to specify the way that nodal values of recovered gradients are calculated. The reader may note that there are several ways for gradient calculation at boundaries. An efficient way which was suggested in [23,24] is using the information from patches nearby the boundary node. This means that one can directly use the smooth field obtained in (2) for patches near boundary and substitute the coordinates (or local normalized coordinates) of the boundary node in the polynomial terms. Since a node at the boundary may generally fall in several patches, especially in three dimensional domains, it is preferred to obtain the information from patch of closest internal nodal point. However, this makes some ambiguity when unstructured meshes are used since the distances between a boundary node and the nodes around it may not be so different. Therefore, here, we employ an averaging approach.
4. TEST RESULTS
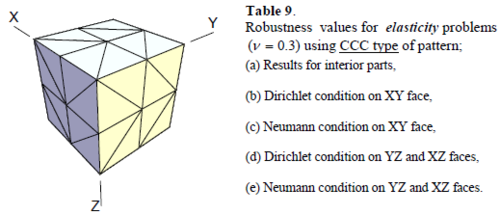
In this section we shall present the results of the tests on some patterns of linear elements for three dimensional heat conduction and elasticity problems. The results for elasticity problems are taken for Poisson’s ratio equal to 0.3.
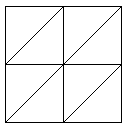
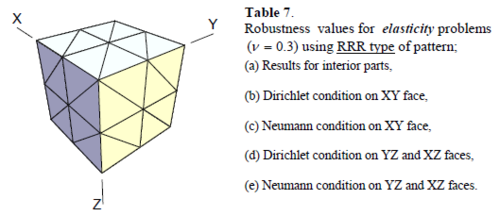
The three dimensional patterns of tetrahedral elements are recognized from the two dimensional patterns appearing on the faces of the cuboid. Four well known patterns of triangles in two dimensional problems as shown in Figure 8 are used for naming the three dimensional patterns (see Figure 9). For example RRR, according to this terminology, represents a 3D pattern having Regular arrangements of elements at three faces. Since there will be two cases which can be named as CCC, i.e. the cuboids with Criss-cross and Chevron faces, we recognize the former as III.
|
|
|
|
| Regular | Union-jack | Chevron | Criss-cross |
| Figure 8:Two dimensional patterns used for naming three dimensional patches to be used in tests. | |||
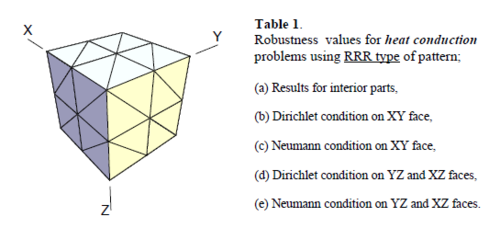
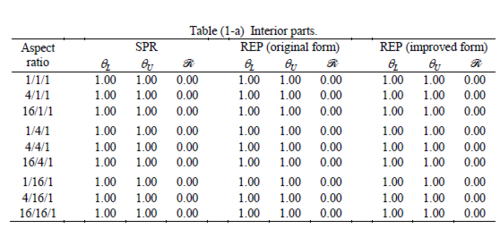
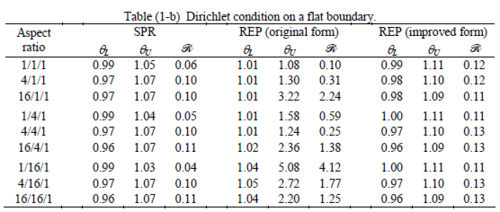
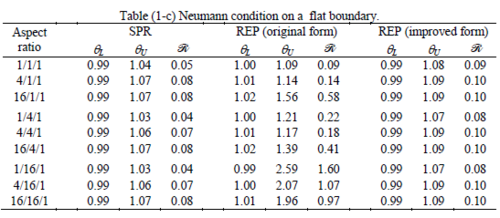
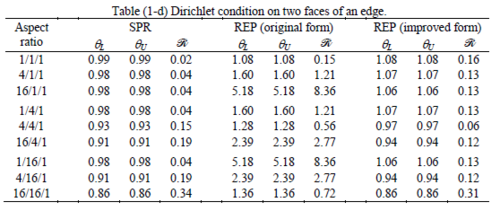
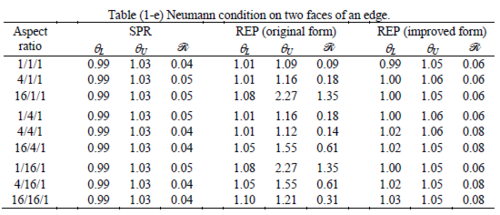
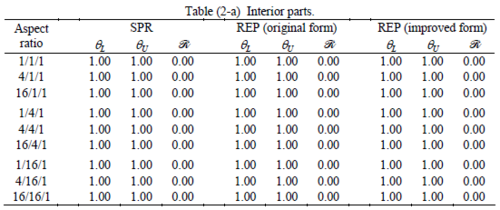
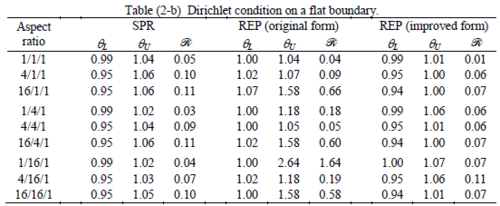
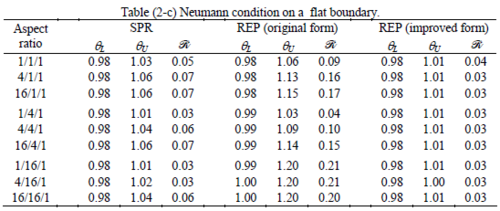
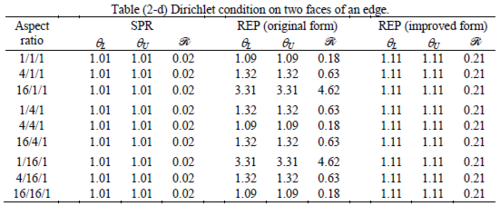
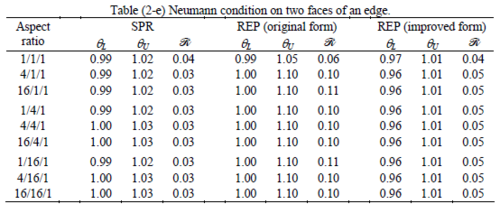
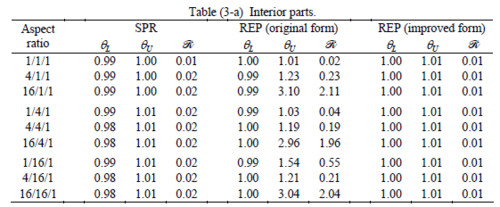
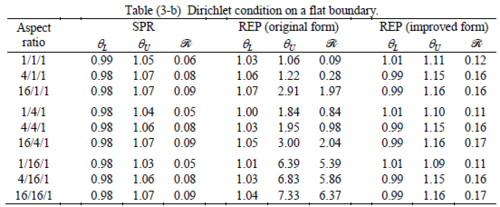
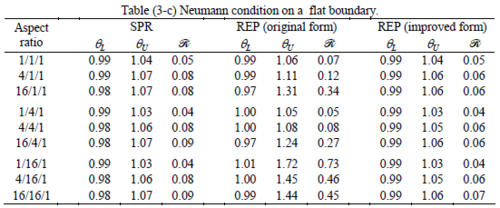
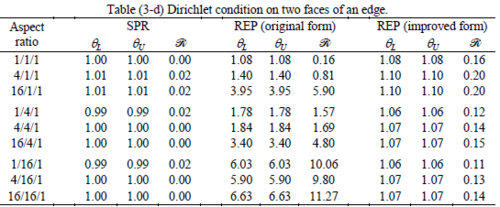
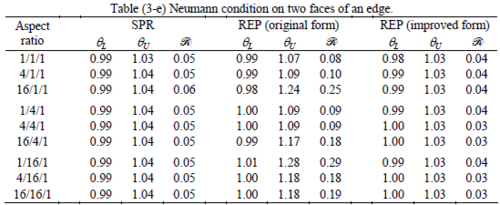
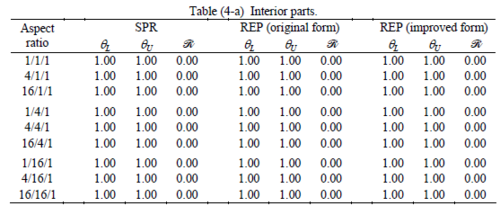
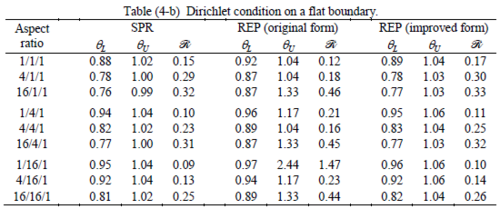
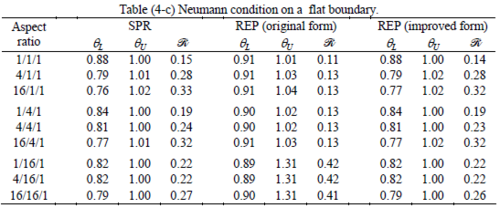
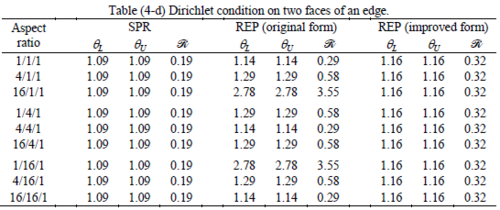
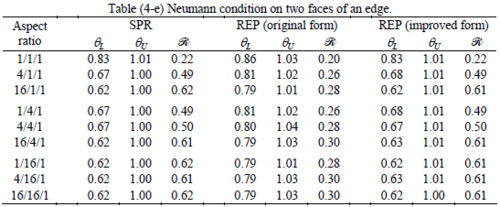
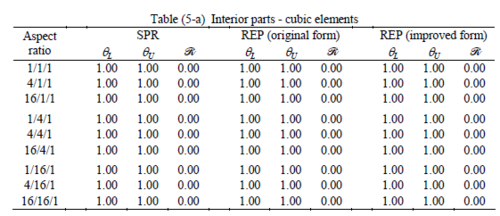
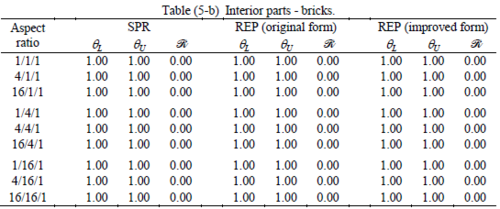
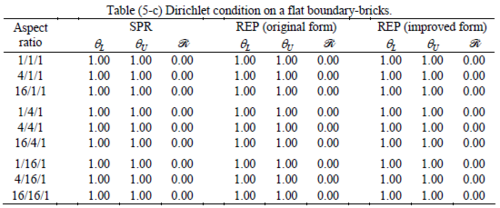
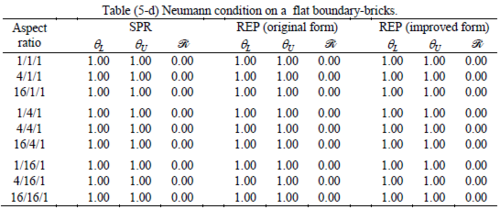
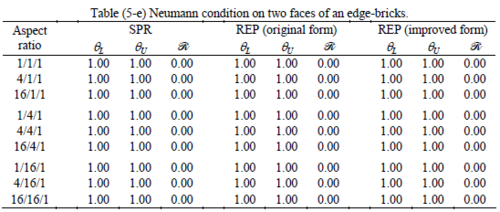
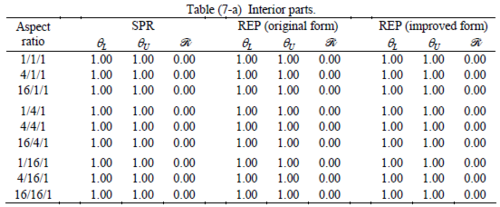
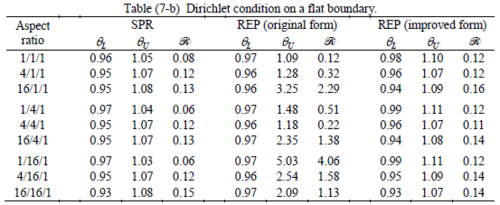
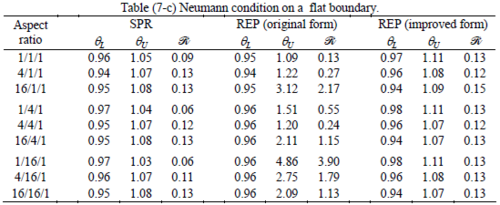
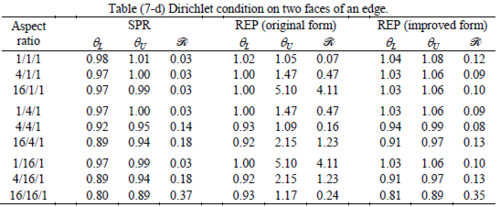
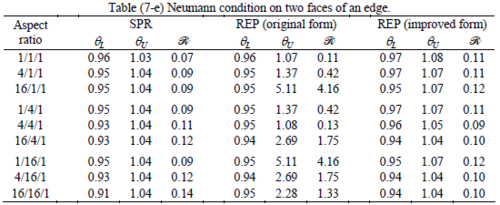
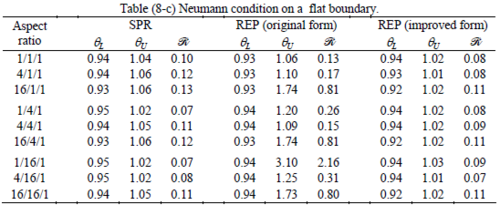
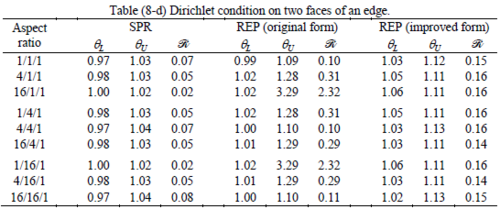
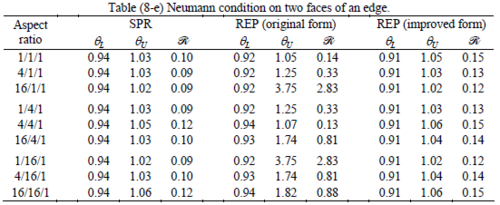
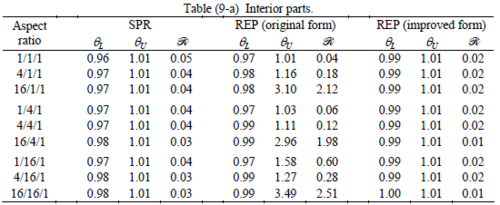
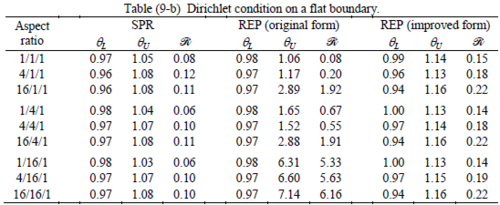
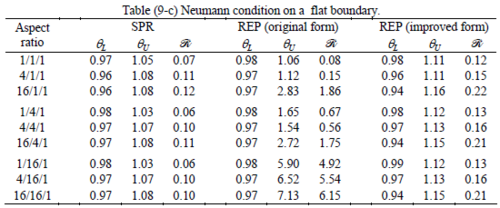
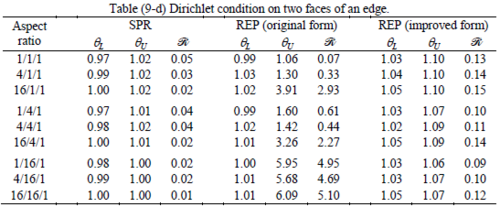
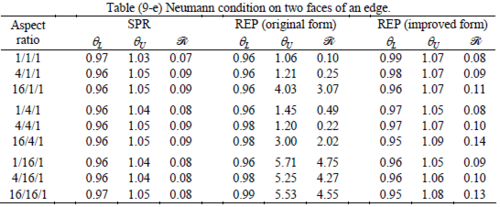
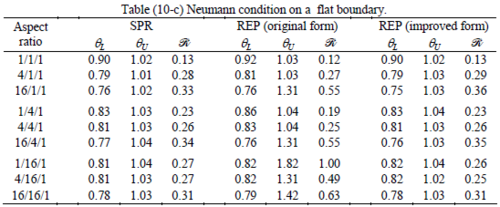
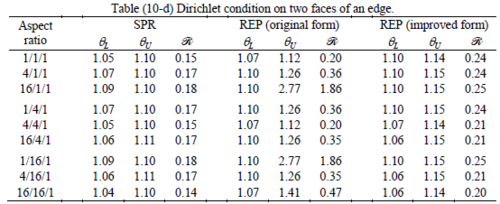
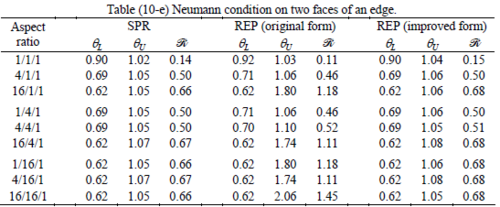
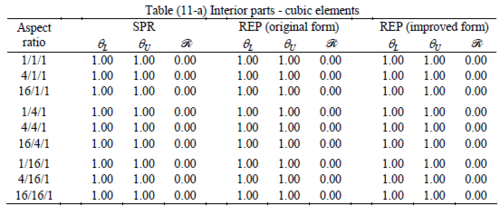
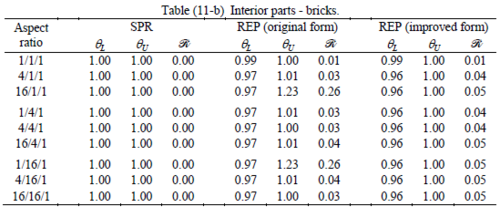
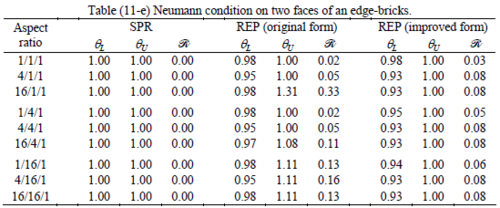
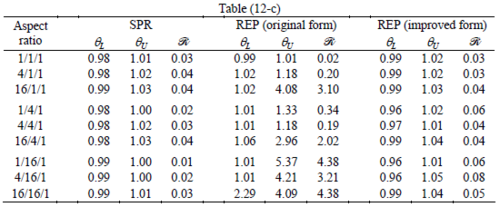
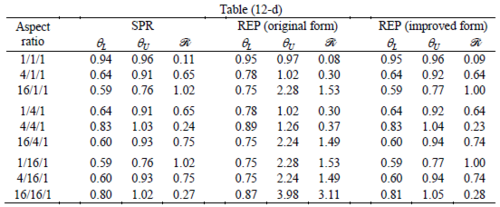
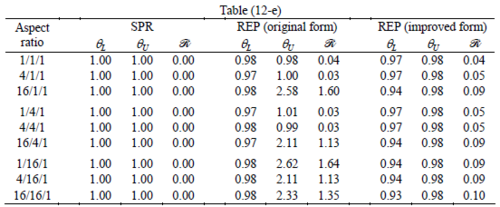
The results of the tests for tetrahedral elements are summarized in Tables 1 to 4 for different aspect ratios. We have also included the results of linear brick elements in Table 5.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
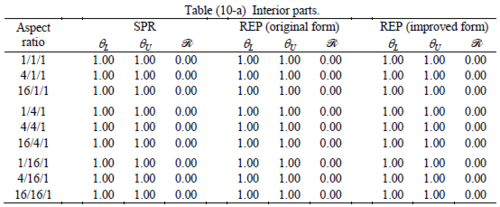
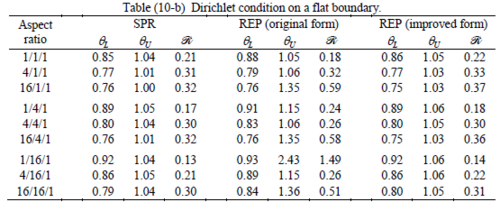
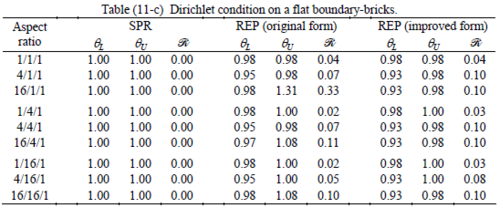
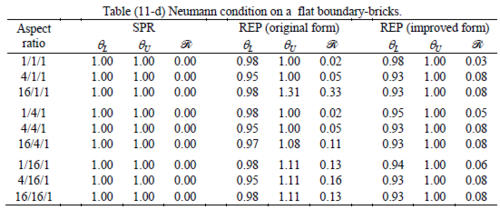
All Tables contain the lower and upper bounds as well as the robustness values for SPR and the two versions of REP. In each table the results of the test at interior parts with periodicity in all directions, at flat boundaries with periodicity in two directions, and at kinked boundaries with periodicity in one direction, are listed. Except for the tests at interior parts, two sets of results pertaining to the type of boundary conditions, i.e. Neumann or Dirichlet type, are given in each case.
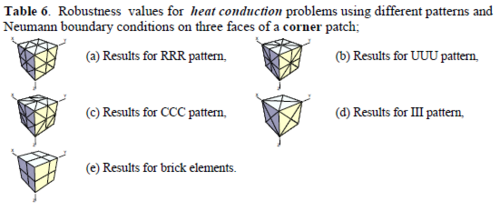
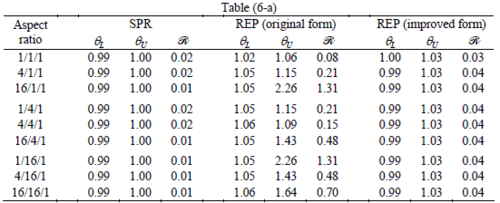
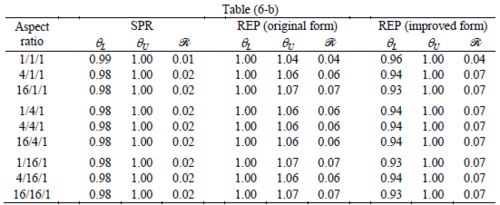
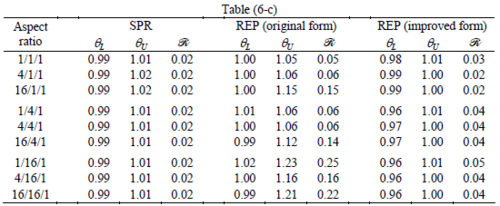
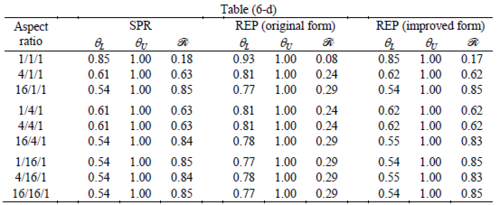
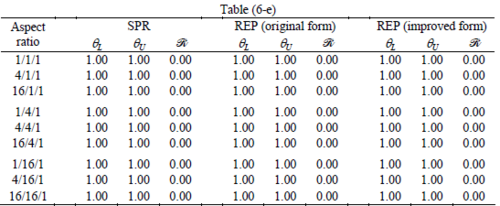
The results for patches at corners, where the periodicity is lost in all directions, with Neumann type of condition are given in Table 6. We have not reported the results of patches at corners with Dirichlet condition since the frequency of happening such situations in practical engineering problems is much smaller than the other cases presented.
|
|
|
|
|
|
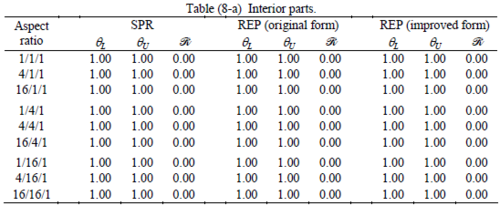
When the patch is located at interior of the domain, the tables clearly show that all recovery methods give superconvergent results, for all patterns except for the CCC. For high aspect ratios of CCC pattern, however, REP in its original form fails to give superconvergent results while the improved version of REP and SPR still give satisfactory results but of course not fully superconvergent. Superconvergence is also seen for brick elements for patches at interior parts.
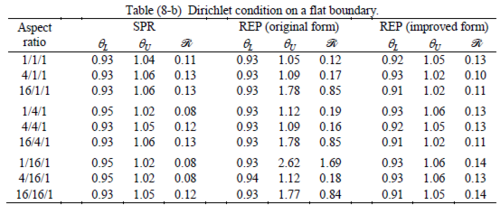
Interesting to note is that when patches are located at boundaries, none of the recovery methods are able to produce full superconvergent results. However, the results for upper and lower values are within satisfactory ranges. Exception may be seen for III pattern, i.e. a cuboid with Criss-cross pattern at all faces, when used near Neumann boundaries for which the lower bound values are less than the other cases.
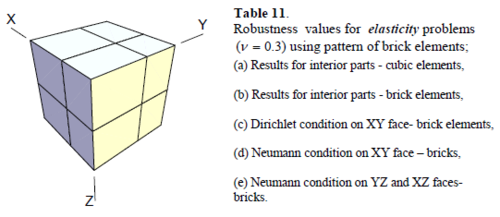
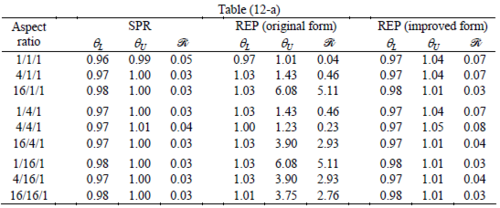
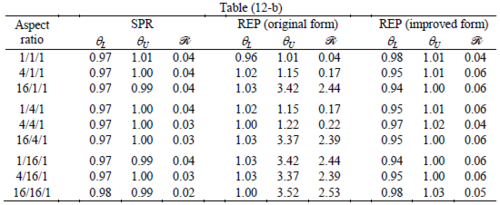
Similar conclusions may be made from the results obtained for elasticity problems. Tables 7 to 12 show the robustness obtained for this class of problems. Although the robustness indices are still in an acceptable range, they are of higher values than those obtained for heat conduction problems. There is also an exception for results of brick elements, Table 11, in which full superconvergent effect is still seen from application of SPR similar to the heat cases. Comparison of all lower bounds for tetrahedral elements shows, again, that those of III pattern are of less value.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The main reason for loss of superconvergent effect lies in the definition of the recoveries near boundaries. This has also been quoted in studies of reference [20] performed for two dimensional problems with flat boundaries. In fact, the minimizations performed in each of the recoveries leads to best answers near center of the patch, due to concentration of information around the patch point. This inherently means that, even for interior parts of the mesh, for some types of elements the polynomial fitted in the recovery does not thoroughly capture the exact field. Nevertheless, in such cases it usually happens that the polynomial passes the exact solution at the patch node or at vicinity of it and since the recovered field is constructed by interpolation of nodal values the final result may show full on semi superconvergent effect.
Another reason for loss of superconvergent effect seems to be the presence of spurious boundary layer modes. This kind of undesirable solution usually vanishes within a distance of few elements length. The affected distance is obviously dependent on the type of elements used. This latter reason seems to be less pronounced than the first one since our experience shows that the amplitude of the spurious modes is small compared to the nodal values of asymptotic finite element solution. However, this observation confirms that producing enhanced gradients from local information at elements on the boundaries may not lead to a full superconvergent effect especially when the whole patch, used in the recovery procedure, falls inside the affected region. In this respect, the behavior is similar to cases with presence of a singularity in the domain [12-14]. But we note that in the present cases the exact solutions are smooth.
From above discussion it may be concluded that two remedies may be thought for loss of superconvergent effect. One is to use information from inner layers, beyond the first layer, and extrapolate the effect to the boundaries while devising some means for preventing lack of fitness in the least square procedure. This may be performed by extrapolating the recovered nodal values obtained for patch nodes at neighborhood of the boundary node. Another remedy, which should be considered simultaneously with the first one, is capturing the boundary layer modes and removing them from the enhanced solution which is not an easy task but still possible by considering that in this paper we have introduced a suitable tool for study of behavior of boundary layers. Both remedies are beyond of the scopes of this paper and we shall refer to these in subsequent contributions.
As a final conclusion from comparison between SPR and improved REP applied to heat and elasticity problems, it may be stated that although full superconvergent property is lost for tetrahedral elements, results from both recoveries exhibit similar robustness. However for brick elements, both methods produce full superconvergent gradients in an asymptotic sense for heat problems, but for elasticity problems, just SPR is able to produce full superconvergent effect.
Complementary results
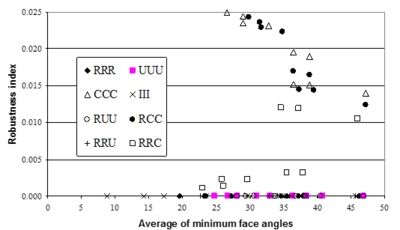
As is seen from tests results for interior parts, full superconvergent effect is lost for some mesh configuration. Here we shall investigate the possibility of losing the effect by producing mesh configuration form combination of patterns at three main faces of a cuboid. The aspect ratios considered are identical to those given in the first columns of Tables 1 to 12. To give more insight to the problem we present the results of robustness indices with respect to average minimum angle between the faces of tetrahedral elements in a patch (here “patch” refers to the smallest unit of the repeating patterns). Minimum angle in a mesh is, in fact, one of the concerns of those who work on mesh generation part of an adaptive procedure.
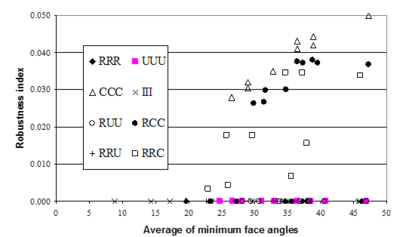
Figures 10 and 11 demonstrate the results obtained from application of SPR to heat and elasticity problems.
|
| Figure 10:Robustness index obtained from application of SPR to heat conduction type of problems versus average minimum angle between faces of the elements in the patch. |
|
| Figure 11:Robustness index obtained from application of SPR to elasticity type of problems versus average minimum angle between faces of the elements in the patch. |
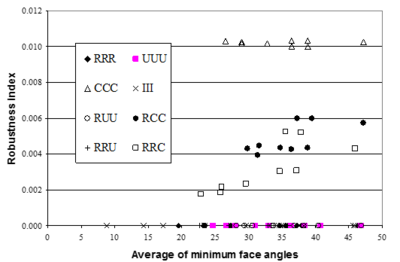
Interesting to note is that the results obtained from all patterns consisting of 2D Chevron pattern, at least at one face, lose superconvergent property. Similar conclusion may be made from application of REP to the problem as shown in Figures 12 and 13.
|
| Figure 12:Robustness index obtained from application of REP (improved) to heat conduction type of problems versus average minimum angle between faces of the elements in the patch. |
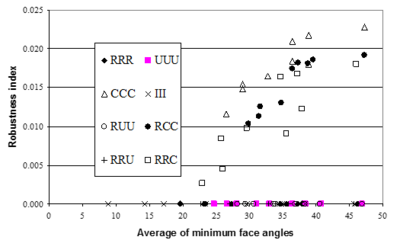
|
| Figure 13:Robustness index obtained from application of REP (improved) to elasticity type of problems versus average minimum angle between faces of the elements in the patch. |
It may be noticed that existence of superconvergence is independent of the average of minimum angles since there are some cases in which the average minimum angle are quite small while the results are still superconvergent. This means that, regarding error estimation part in an adaptive procedure, a mesh generation program should face more limitations with respect to mesh pattern. On the other hand, if the results of recovery methods are taken as approximate gradients, the restrictions regarding minimum angle, i.e. skewness of elements, may be relaxed.
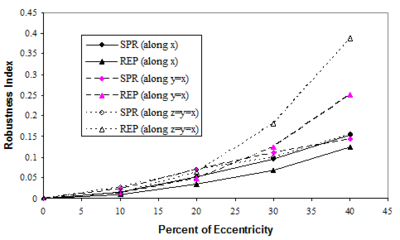
Since we have so far studied structured mesh configurations, a question regarding the structure of the output mesh from a 3D mesh generation program, structured/unstructured mesh, may now be raised. Obviously, it is not possible to consider all possible unstructured mesh configurations and thus the answer needs an engineering judgment for generalization of the present results to unstructured meshes though the need of more studies, in this regard, is felt. Nevertheless, in this study, we examine the performance of the recovery methods in some artificially produced unstructured patterns. For this we select the pattern of RRR and change the location of central node to produce skew elements inside the patch. The results obtained, for some specific locations of the inside node with respect to the center of the patch are shown in Figure 14. In this figure the patch is considered to be at interior parts of a fictitious domain. It can be seen that the robustness values are still in an acceptable range when the mesh becomes very skew though SPR exhibits better robustness for highly distorted meshes.
5. CONCLUSIONS
In this part of the paper we have presented a study on asymptotic behavior of two recovery methods, i.e. SPR and REP, in producing superconvergent gradients for three dimensional heat and elasticity problems. It has been shown that application of both methods leads to similar robustness values either for interior of the domain or near boundaries.
Full superconvergent property is lost for tetrahedral elements when used near boundaries. This effect is much pronounced for results from elasticity problems. However, for brick elements the results exhibit the property in an asymptotic sense. One of the reasons for loss of full superconvergent property seems to be the definitions of the recoveries near boundaries which basically use extrapolated information from polynomials fitted at inner patches. Another reason is the fact that in both methods the information used for recovery procedure is extracted from the region in which boundary layer has not sufficiently decayed. This effect seems to be much pronounced for tetrahedral elements since for brick elements asymptotic superconvergent property is still seen. It may be concluded that some further research is needed to find better definitions for recovery methods near boundaries so that either the information from inner layers of recovered nodal values is utilized or the spurious boundary layer modes are captured and removed during the recovery procedures. The method proposed in this paper provides a suitable tool for such studies.
Some complementary results have been given for tests results for interior parts when various combinations of patters appear at three faces of a cuboid. The conclusion is that all configurations produced by Chevron pattern at least in one face lose the full superconvergent effect. This means that in mesh generation programs should face more restrictions regarding the error estimation part in adaptive solutions. Some more results on artificially produced unstructured meshes have been given to examine the performance the recoveries in an asymptotic manner. It is seen that even for highly distorted mesh configurations the robustness indices remain in an acceptable range for both recovery methods considered.
References
[1] Boroomand, B. and Mossiaby, F., “On Application of robustness test for error estimators to patches near kinked boundaries in three dimensional problems: Part I, Formulation”, CIMNE, June 2004.
[2] Babuška, I. and Rheinboldt, W.C., “A posteriori error estimates for finite element method”, Int. J. Numer. Meth. Engrg., Vol. 12, pp. 1597-1615, 1978.
[3] Zienkiewicz, O.C. and Zhu, Z., “A simple error estimator and adaptivity procedure for practical engineering analysis”, Int. J. Numer. Meth. Engrg., Vol. 24, pp. 337-357, 1987.
[4] Zienkiewicz, O.C. and Zhu, Z., “The superconvergent patch recovery and a posteriori error estimates. Part I: The recovery technique”, Int. J. Numer. Meth. Engrg., Vol. 33, pp. 1331-1364, 1992.
[5] Zienkiewicz, O.C. and Zhu, Z., “The superconvergent patch recovery and a posteriori error estimates. Part II: Error estimates and adaptivity”, Int. J. Numer. Meth. Engrg., Vol. 33, pp. 1365-1382, 1992.
[6] Wiberg, N. E. and Abdulwahab, F., “Patch recovery based on superconvergent derivatives and equilibrium”, Int. J. Numer. Meth. Engrg., Vol. 36, pp. 2703-2724, 1993.
[7] Blacker, T.D. and Belytschko, T., “Superconvergent patch recovery with equilibrium and conjoint interpolation enhancement’ Int. J. Numer. Meth. Engrg., Vol. 37, pp. 517-536, 1994.
[8] Wiberg, N. E., Abdulwahab, F. and Ziukas, S., “Enhanced superconvergent patch recovery incorporation equilibrium and boundary condition”, Int. J. Numer. Meth. Engrg., Vol. 37, pp. 3417-3440, 1994.
[9] Babuška, I., Strouboulis, T. and Upadhyay, C.S., “ A model study of the quality of a posteriori error estimaors for linear elliptic problems. Error estimation interior of patchwise uniform grids of triangles”, Comput. Methods Appl. Mech. Eng., Vol. 114, pp. 307-378, 1994.
[10] Babuška, I., Strouboulis, T., Upadhyay, C.S., Gangaraj, S.K. and Copps, K., “Validation of a posteriori error estimators by numerical approach”, Int. J. Numer. Meth. Engrg., Vol. 37, pp. 1073-1123, 1994.
[11] Babuška, I., Strouboulis, T., Upadhyay, C.S., Gangaraj, S.K. and Copps, K. “An objective criterion for assessing the reliability of a posteriori error estimators in finite element computations”, U.S.A.C.M. Bulletin, No.7 , pp. 4-16, 1994.
[12] Babuška, I., Strouboulis, T., Mathur, A. and Upadhyay, C.S., “Pollution-error in the h-version of the finite element method and the local quality of a posteriori error estimators”, Finite Elem. Anal. Des., Vol. 17, pp. 237-321, 1994.
[13] Babuška, I., Strouboulis, T., Upadhyay, C.S. and Gangaraj, S.K., “A posteriori estimation and adaptive control of the pollution error in the h-version of the finite element method”, Int. J. Numer. Meth. Engrg., Vol. 38, pp. 4207-4235, 1995.
[14] Babuška, I., Strouboulis, T., Gangaraj, S.K. and Upadhyay, C.S., “Pollution error in the h-version of the finite element method and the local quality of the recovered derivatives”, Comput. Methods Appl. Mech. Eng., Vol. 140, pp. 1-39, 1997.
[15] Boroomand, B. and Zienkiewicz, O.C., “Recovery by equilibrium in patches (REP)”, Int. J. Numer. Meth. Engrg., Vol. 40, pp. 137-164, 1997.
[16] Boroomand, B. and Zienkiewicz, O.C., “An improved REP recovery and efectivity robustness test”, Int. J. Numer. Meth. Engrg., Vol. 33, pp. 3247-3277, 1997.
[17] Zienkiewicz, O.C., Boroomand, B. and Zhu, Z., “Recovery procedures in error estimation and adaptivity; Part I: Adaptivity in linear problems”, Comput. Methods Appl. Mech. Eng., Vol. 176, pp. 111-125, 1999.
[18] Boroomand, B. and Zienkiewicz, O.C., “Recovery procedures in error estimation and adaptivity; Part II: Adaptivity in nonlinear problrms of elaso-plasticity behavior”, Comput. Methods Appl. Mech. Eng., Vol. 176, pp. 127-16, 1999.
[19] Lo, S.H. and Lee, C.K., “On using different recovery procedures for the construction of smoothed stress in finite element method”, Int. J. Numer. Meth. Engrg., Vol. 43, pp. 1223-1252, 1998.
[20] Babuška, I., Strouboulis, T. and Upadhyay, C.S., “A model study of the quality of a posteriori error estimators for finite element solutions of linear elliptic problems, with particular reference to the behavior near the boundary”, Int. J. Numer. Meth. Engrg., Vol. 40, pp. 2521-2577, 1997.
[21] Zienkiewicz, O.C. and Zhu, Z., “The superconvergent patch recovery (SPR) and adaptive finite element refinement”, Comput. Methods Appl. Mech. Eng., Vol. 101, pp. 207-224, 1992.
[22] Zienkiewicz, O.C., Zhu, Z. and Wu, J., “Superconvergent recovery technique-some further tests”’ Commun. Num. Meth. Eng., Vol. 9, pp.251-258,1993.
[23] Zienkiewicz, O.C. and Zhu, Z., “Superconvergence and the superconvergent patch recovery”, Finite Elem. Anal. Design., Vol. 19, pp.11-23, 1995.
[24] Zienkiewicz, O. C. and Taylor, R. L., “The finite element method”, 5th edition, Butterworth-Heineman, 2000.
Document information
Published on 01/01/2004
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?