Numerical computation of a large-scale jet fire of high-pressure hydrogen in process plant

Abstract

Due to numerous hazardous chemicals to handle, the process plant industry has a higher risk of fire, explosion, and toxic release than other industries. Reviewing the accidents at process plants in the past, it is clear that fire accidents occur with the highest frequency, leading this study to consider accidental fire scenarios at process plants. For the scenario of an incident, a jet fire involving a massive amount of hydrogen gas to be processed or delivered at the process plant has been selected. The analysis of incident outcome resulting from the hydrogen jet fire has been implemented through the computational fluid dynamics simulation methodology Kameleon FireEx. Based on the outcome of this simulation, the consequences of a jet fire with high temperature and heat radiation are analyzed and evaluated. In addition, the results from Phast ver. 7.11 simulation for the same scenario are presented for comparison and further validation.

Introduction

Hydrogen is the most abundant element on the Earth and can be obtained from water and natural gas. Once hydrogen is used as fuel, it returns back to the form of water, which makes it ecologically crucial in the production of cleaner fuels. The ideal method of producing hydrogen involves the use of renewable energy sources like solar power or wind power, but as these methods result in considerable cost of production, hydrogen is often produced using fossil fuel [1, 2]. In South Korea, the annual production of hydrogen amounts to about 9.3 million Nm3, and a significant portion of this is produced as byproduct gas. Hydrogen is mostly consumed in petrochemical plants, with only about 15% used in other industries. In particular, the rate of hydrogen consumption in the energy industry is about 1%, representing a very minor portion of consumption [2]. Hydrogen consumed in a process plant is usually treated and delivered under high pressure. In these conditions, once hydrogen is leaked from equipment and immediately ignited, it creates a jet fire, which generally seems to result in less damage compared to explosion or toxic release. However, if the facilities and devices installed around the equipment in the process plant are congested, a severe secondary accident may occur due to the jet fire.

Analyses of past accidents have shown that fire accidents represent a primary cause of numerous large-scale accidents [3-5]. Moreover, at a process plant, fire represents one of the frequent accident types [6]. Yet, recent studies on the risk of hydrogen gas have been mostly related to explosions of hydrogen charge facilities [7, 8]. Preliminary studies on hydrogen fires have been performed to evaluate the flame behavior of small-scale jet fires [9, 10].

In contrast to the aforementioned studies, here, numerical analysis was performed of hydrogen jet fire in a complex, large-scale structure within an industrial process plant to realistically predict its substantial effects. Thereafter, through the outcome of computation, the influence of the flame intensity on surrounding process facilities and devices was evaluated and analyzed. Following various references, computational fluid dynamics (CFD) simulations are available for various conditions such as congestion of the facility and devices, turbulence, obstacles, and weather effects; their results are very similar to the actual outcome [11-13].

Numerical Simulation

For the hydrogen jet fire analysis, the Kameleon FireEX (KFX) CFD code developed by ComputIT for fire analysis was used. KFX applies a precise code based on fire and gas diffusion within a complex structure and is now widely used as a safety analysis code in various industrial fields.

The Combustion Model

The governing equations, eqs. (1)-(7) of KFX, determine the mass conservation (eq. (1)), the mass species fractional equation (eq. (2)), momentum conservation along the coordinate direction using Navier–Stokes equations (eq. (3)), and total energy equation for compressible gas flows (eq. (5)).

${\frac {\partial {\overline {\rho }}}{\partial t}}+{\frac {\partial {\overline {\rho }}{\overset {\sim }{u}}_{j}}{\partial x_{j}}}=$${\overline {\rho }}{\overset {\sim }{R}}_{liq}.$

(1)

Here, R_liq is a source due to the liquid phase transition, ρ is the density of gas, the — symbol represents time-averaged quantities, and the ″ and ~ symbols are fluctuation and mean of Favre-averaged quantities.

Species mass fraction equations

${\frac {\partial {\overline {\rho }}{\overset {\sim }{Y}}_{\iota }}{\partial t}}+$${\frac {\partial {\overline {\rho }}{\overset {\sim }{u}}_{j}{\overset {\sim }{Y}}_{\iota }}{\partial x_{j}}}=$$-{\frac {\partial }{\partial x_{j}}}\left({\overline {\rho Y_{\iota }V_{\iota j}}}\right)-$${\frac {\partial }{\partial x_{j}}}\left({\overline {\rho u_{j}^{''}Y_{\iota }^{''}}}\right)+$${\overline {\rho }}{\overset {\sim }{R}}_{\iota }+{\overline {\rho }}{\overset {\sim }{R}}_{liq,\iota }.$

(2)

In this equation, Y_ι is the species mass fraction and V_ιj is the molecular diffusion velocity of species ι in the direction j. In addition, R_ι is a chemical source term and R_liq,ι is a source due to the liquid phase transition which is not considered since hydrogen is all gaseous phase in the study.

Momentum equations

${\frac {\partial {\overline {\rho }}{\overset {\sim }{u}}_{i}}{\partial t}}+$${\frac {\partial {\overline {\rho }}{\overset {\sim }{u}}_{j}{\overset {\sim }{u}}_{i}}{\partial x_{j}}}=$$-{\frac {\partial {\overline {p}}}{\partial x_{i}}}+{\frac {\partial }{\partial x_{j}}}\left({\overline {{\tau }_{ij}}}-\right.$$\left.{\overline {\rho u_{j}^{''}u_{i}^{''}}}\right)+$${\overline {\rho f_{i}}}+{\overline {\rho }}{\overset {\sim }{F}}_{liq,i}.$

(3)

${\overline {{\tau }_{\iota j}}}=\mu \left({\frac {\partial {\overset {\sim }{u}}_{i}}{\partial x_{j}}}+\right.$$\left.{\frac {\partial {\overset {\sim }{u}}_{j}}{\partial x_{i}}}\right)+$$\left(\kappa -{\frac {2}{3}}\mu \right)\left({\frac {\partial {\overset {\sim }{u_{\kappa }}}}{\partial x_{\kappa }}}\right){\delta }_{ij}$

(4)

Here, f_i are mass forces by which the gas is influenced, τ_ij is the tension [N/m²], k is the second viscosity coefficient, and δ_ij is the Kronecker delta.

The Eddy Dissipation Concept (EDC) is used for turbulent combustion. Its basis is physical consideration of the structure of turbulent flow. The mixing on molecular level, which is a necessity for chemical reactions to occur, is located in structures where turbulent kinetic energy is dissipated into heat due to action of viscous forces on the local strain [14].

Enthalpy equations

${\begin{array}{rl}{\frac {\partial }{\partial t}}\left({\overline {\rho }}{\overset {\sim }{e}}_{T}\right)+{\frac {\partial }{\partial x_{j}}}\left({\overline {\rho }}{\overset {\sim }{u}}_{j}{\overset {\sim }{e}}_{T}\right)=&{\frac {\partial }{\partial x_{j}}}\left({\overline {\left({\tau }_{ij}-p\right)u_{j}}}\right)+{\frac {\partial }{\partial x_{j}}}\left({\overline {k_{\iota }{\frac {\partial T}{\partial {\chi }_{j}}}}}-{\overline {\rho }}{\overset {\sim }{u}}_{j}^{''}{\overset {\sim }{e}}_{T}^{''}\right)\\&+{\overline {Q}}_{gs}+{\overline {Q}}_{Rad}+{\overline {\rho }}{\overset {\sim }{S}}_{liq}.\end{array}}$

(5)

$e_{T}=e+{\frac {1}{2}}u_{i}u_{j}.$

(6)

$e=\sum _{\iota }Y_{\iota }e_{\iota }\left(T\right)$

(7)

In this equation, ${\textstyle {\overline {Q}}_{gs}}$ is the heat transport form solid to gas phase, ${\textstyle {\overline {Q}}_{Rad}}$ is the net radiative transfer to the gas phase, ${\textstyle {\overset {\sim }{S}}_{liq}}$ is the net heat transfer for the liquid phase, ${\textstyle k_{\iota }}$ is the conductivity, ${\textstyle e_{T}}$ is the total energy, and e is the total internal energy.

The Turbulence Model

For turbulent flow, KFX uses the extended formula of the conventional k − ε formula for buoyancy and some low-Reynolds numbers. The modeled equation for k and ε is presented in eq. (8), and the rate of dissipation of turbulent kinetic energy ε is given in eq. (9) [11].

${\frac {\partial \left({\overline {\rho }}k\right)}{\partial t}}+$${\frac {\partial \left({\overline {\rho }}{\overset {\sim }{u}}_{i}k\right)}{\partial x_{i}}}=$${\frac {\partial }{\partial x_{i}}}\left({\frac {{\mu }_{eff}}{{\sigma }_{k}}}{\frac {\partial k}{\partial x_{i}}}\right)+$$P-{\overline {\rho }}\epsilon +B.$

(8)

${\begin{array}{rl}{\frac {\partial \left({\overline {\rho }}\epsilon \right)}{\partial t}}+{\frac {\partial \left({\overline {\rho }}{\overset {\sim }{u}}_{i}\epsilon \right)}{\partial x_{i}}}=&{\frac {\partial }{\partial x_{i}}}\left({\frac {{\mu }_{eff}}{{\sigma }_{\epsilon }}}{\frac {\partial \epsilon }{\partial x_{i}}}\right)+C_{1}f_{1}P{\frac {\epsilon }{k}}\\&-C_{2}f_{2}\rho {\frac {{\epsilon }^{2}}{k}}+C_{1}C_{2}{\frac {\epsilon }{k}}B.\end{array}}$

(9)

$P={\overline {\rho }}{\nu }_{t}\left({\frac {\partial {\overset {\sim }{u}}_{i}}{\partial x_{j}}}+\right.$$\left.{\frac {\partial {\overset {\sim }{u}}_{j}}{\partial x_{i}}}\right){\frac {\partial {\overset {\sim }{u}}_{j}}{\partial x_{i}}}.$

(10)

$B={\overline {\rho }}{\overset {\sim }{u_{i}^{''}{\rho }^{''}}}g_{i}.$

(11)

${\mu }_{t}=C_{D}^{\backprime }\quad f_{\mu }\rho {\frac {k^{2}}{\epsilon }}.$

(12)

$f_{u}=exp\left[{\frac {-2.5}{1+R_{t}/50}}\right].$

(13)

$R_{t}={\frac {\rho k^{2}}{\mu \epsilon }}$

(14)

${\mu }_{eff}={\mu }_{\iota }+{\mu }_{t}.$

(15)

In these equations, P is the production of turbulent kinetic energy by the mean motion, B is a buoyancy, ${\textstyle {\mu }_{t}}$ is a turbulence diffusion coefficient, R_t is a turbulent Reynolds number, f₁, f₂ are the functions in the low-Reynolds number model, and ${\textstyle f_{u}}$ is a low-Reynolds number correction factor. The constants in the turbulence model are as follows:

$C_{D}=0.09,\quad {\sigma }_{k}=1.0,\quad {\sigma }_{\epsilon }=$$1.3,\quad C_{1}=1.44,\quad C_{2}=1.92.$

(16)

The accuracy and utility of KFX have been verified through numerous experiments and on-the-job projects, and the simulation has shown relatively satisfactory outcome compared to actual experiments [11-13, 15].

Incident Outcome of a High-Pressure Hydrogen Leak

While it is one of the essential materials for production in a petrochemical process plant, hydrogen is simultaneously produced as a byproduct within the production process. In the case of oil-refinery processing, hydrocracking, heavy oil (H-Oil), and desulfurization units require hydrogen, and the general naphtha reforming unit produces hydrogen as a byproduct gas. The production reaction of hydrogen in a naphtha reforming unit is as shown below:

$C_{n}H_{m}\left({\mbox{Naptha}}\right)+{\mbox{nH}}_{2}O\rightarrow {\mbox{nCO}}+$$\left({\mbox{2n + m}}\right)/{\mbox{2 H}}_{2}$

(17)

${\mbox{CH}}_{4}+H_{2}O\rightarrow {\mbox{CO}}+3H_{2}$

(18)

${\mbox{CO}}+H_{2}O\rightarrow {\mbox{CO}}_{2}+H_{2}$

(19)

For heavy oil upgrading of crude oil, a massive amount of high-temperature and high-pressure hydrogen gas is consumed. Therefore, many chemical factories have installations to produce hydrogen gas from raw materials like naphtha to fulfill their hydrogen requirements autonomously. Since numerous installations and devices within such processing plants are gathered in a limited space, this is regarded as a high-risk process. If the hydrogen gas leaks and causes a fire, it may cause severe defects in surrounding facilities and devices, leading to simultaneous accidents [16-18]. In general, the treatment of hydrogen at a process plant is carried out under a high pressure of over 160 kg_f/cm². In a scenario where hydrogen leaks from a pipe to cause an accident, its speed at the leak point is greater than the speed of sound, as computed by eqs. (20) and (21) [19].

$S_{C}={\frac {P_{a}}{P_{1}}}\leq {\frac {P_{CF}}{P_{1}}}$

(20)

${\frac {P_{CF}}{P_{1}}}={\mbox{Ma}}{\sqrt {\frac {2+\left(\gamma -1\right){\mbox{Ma}}^{2}}{\gamma +1}}}$

(21)

Here, S_c is the sonic or supersonic flow in the pipe, P_a is the ambient pressure, P₁ is the pressure before the hole, P_CF is the choked pressure, γ is the heat capacity ratio, and Ma is the Mach number. In the case study, it is a choked flow due to high pressure, so that an equivalent leak position was used instead of the actual leak position. The distance between them in this study is around 0.6 m. The inlet conditions must also contain some information on the turbulence energy level and the dissipation of turbulence energy. Such information may be obtained from experiments or by resolving the under-expanded jet structure by numerical calculations. A similar problem also exists for the jets entrainment of ambient fluid, which is neglected in the method since the near-field effects of entrainment are smaller than further downstream.

The minimum ignition energy of hydrogen is 0.018 mJ; considering the minimum ignition energy of typical hydrocarbon – methane (0.28 mJ), propane (0.25 mJ), and butane (0.26 mJ) – hydrogens minimum ignition energy is about 13.9–15.6 times lower [20]. This makes it easily ignitable within only a few seconds after a leakage.

The radiation on KFX is solved by an enhanced version of the discrete transfer model [21]. The basic concept of this model is that radiation exchange is calculated by integration of radiation absorption and emittance along a huge number of rays (lines) throughout the calculation domain. From the boundary of a box inside the calculation domain, rays are sent at a discrete number of directions from each control volume surface on the enclosing box.

CFD Modeling Description

The process to be simulated in this study is residue-hydro-desulfurization (RHDS) or Hyvahl, which consumes a large amount of high-pressure hydrogen within an oil refinery.

This process is carried out to reduce the concentration of metal, asphaltenes, nitrogen, and sulfur from vacuum residue (VR) from a crude distillation unit (CDU), vacuum gas oil (VGO), or atmosphere residue (AR) from a lower CDU. Furthermore, it produces hydrotreated (HDT) residue by bringing about a chemical reaction, and it is a high-risk chemical process under the operation conditions of 643–703 K and 160–170 kg_f/cm² [17].

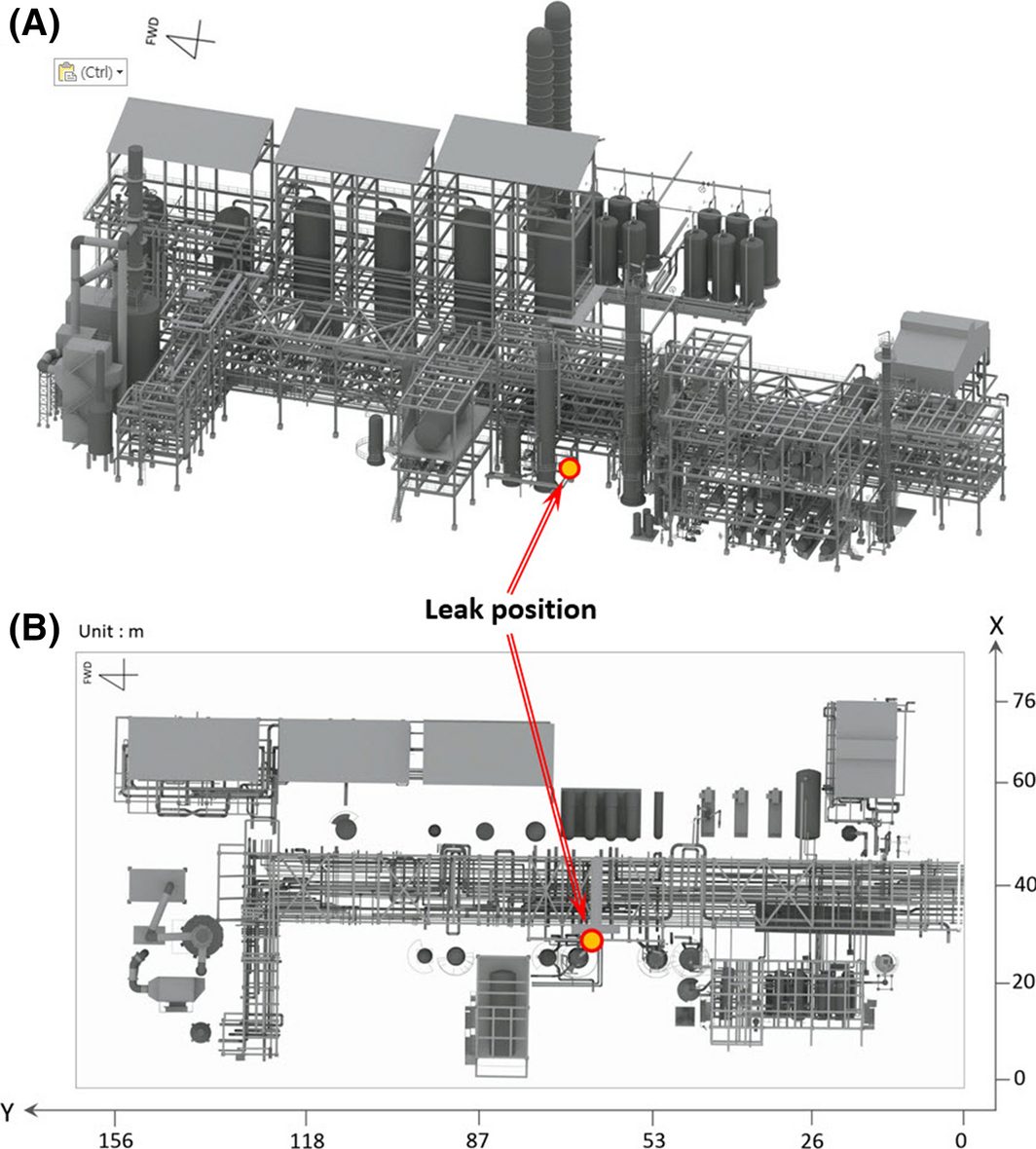
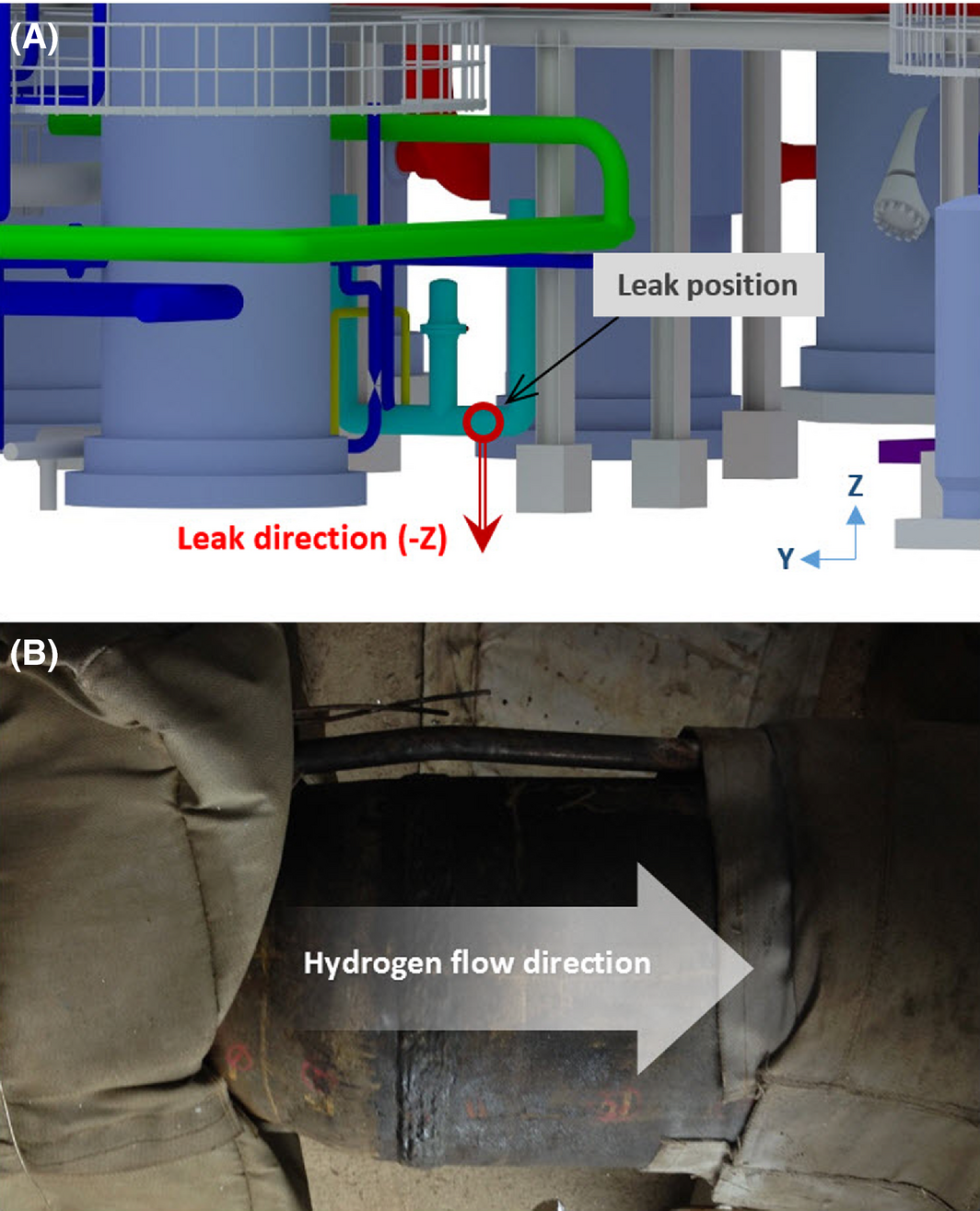
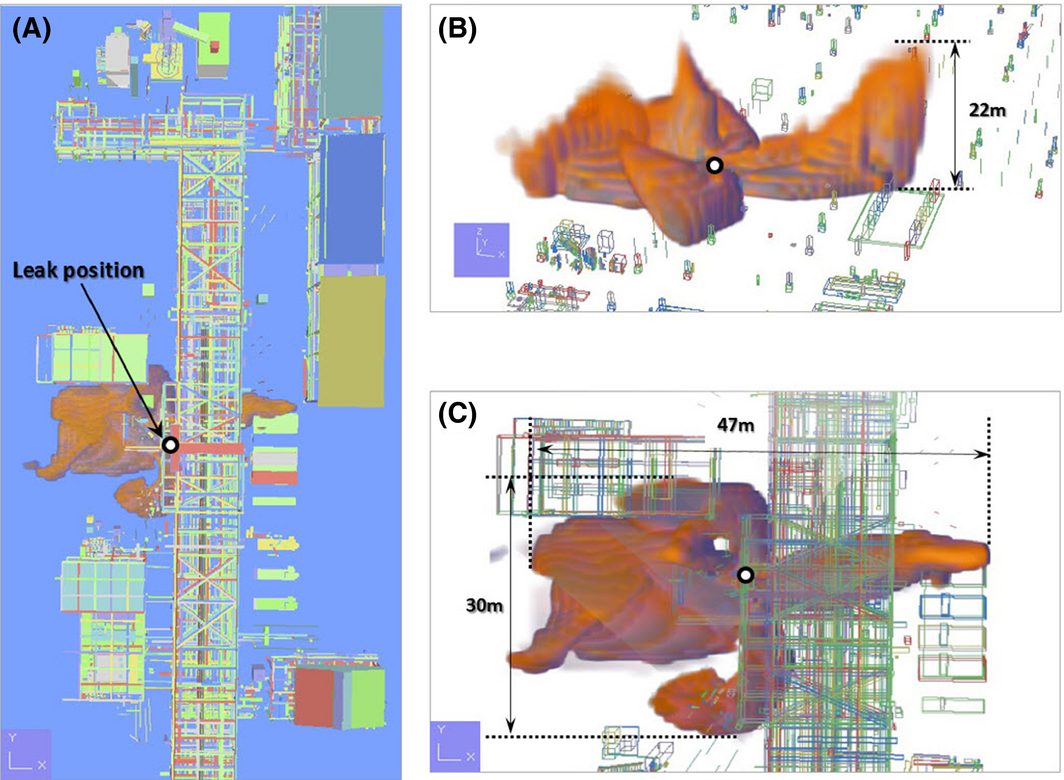
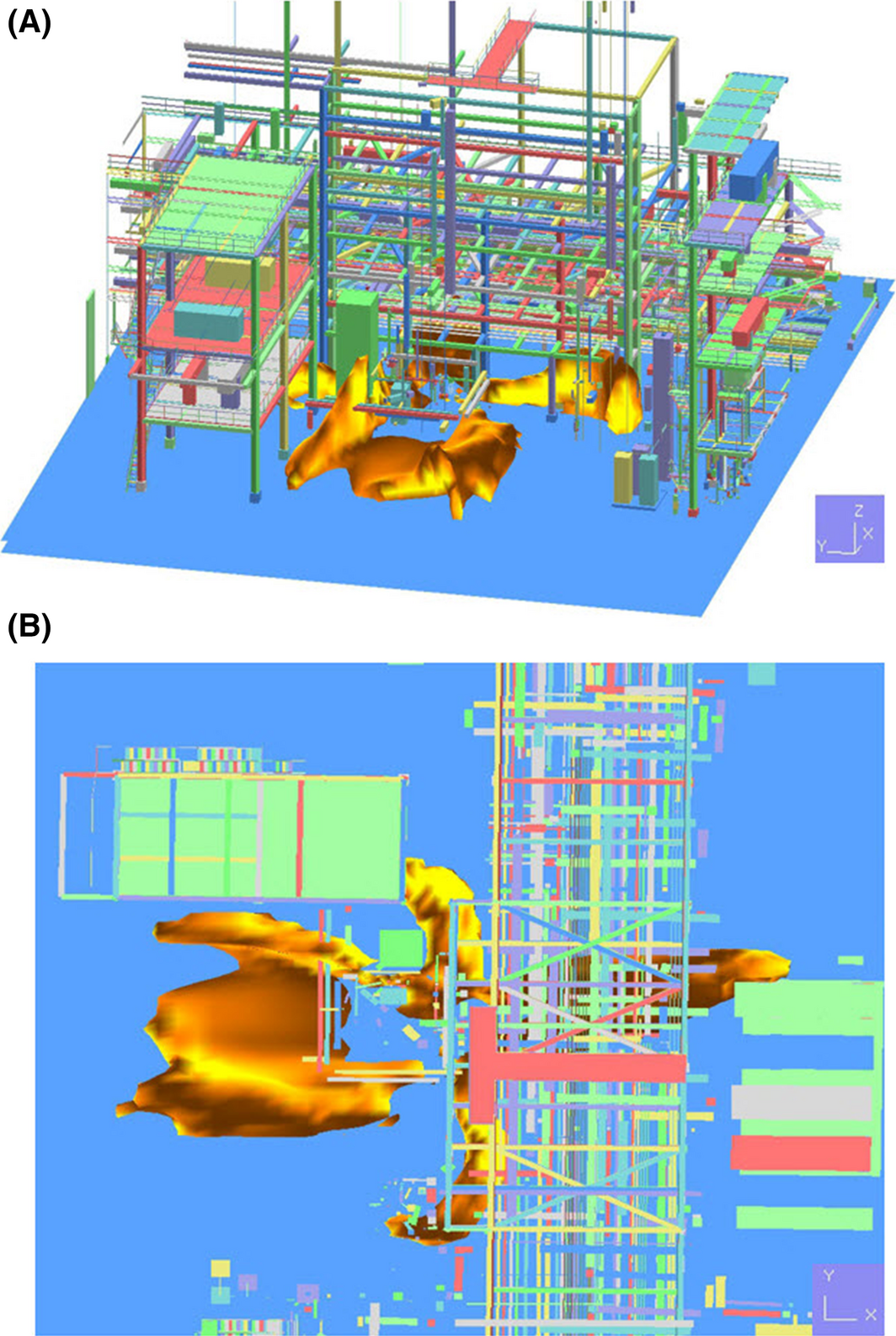
The general RHDS process within an oil refinery is described in Figure 1. For the simulation scenario, the analytical data on jet fire accidents from process plants has been evaluated [4]. As the most frequent accident type, 13 jet fire accidents has been found at a pipework, with the major cause observed as a “leaking coupling or flange” due to a mechanical problem. Therefore, the potential hazard of a hydrogen pipe has been confirmed and selected for the scenario. The leak point is a welded area of the reducer of a pipe used to transfer hydrogen, and the inner pressure and temperature of the pipe are 161.8 barg and 333 K, respectively. The size of the leak hole at the welded area of the reducer is 0.00157 m², and the leakage rate is 15.0 kg/sec. Using the aforementioned leak conditions, the proposed form of the leak point, leakage direction, and wind condition are illustrated in Figures 2 and 3. The leakage direction is in the Z-direction from the lower area of the reducer (Fig. 2). The inputs for scenario simulation are shown in Table 1.

Figure 1. Illustration of the simulated process and leak point: (A) isometric view, (B) for top view.

Figure 2. Specific position of (A) the hydrogen leak point and (B) the features of the reducer.

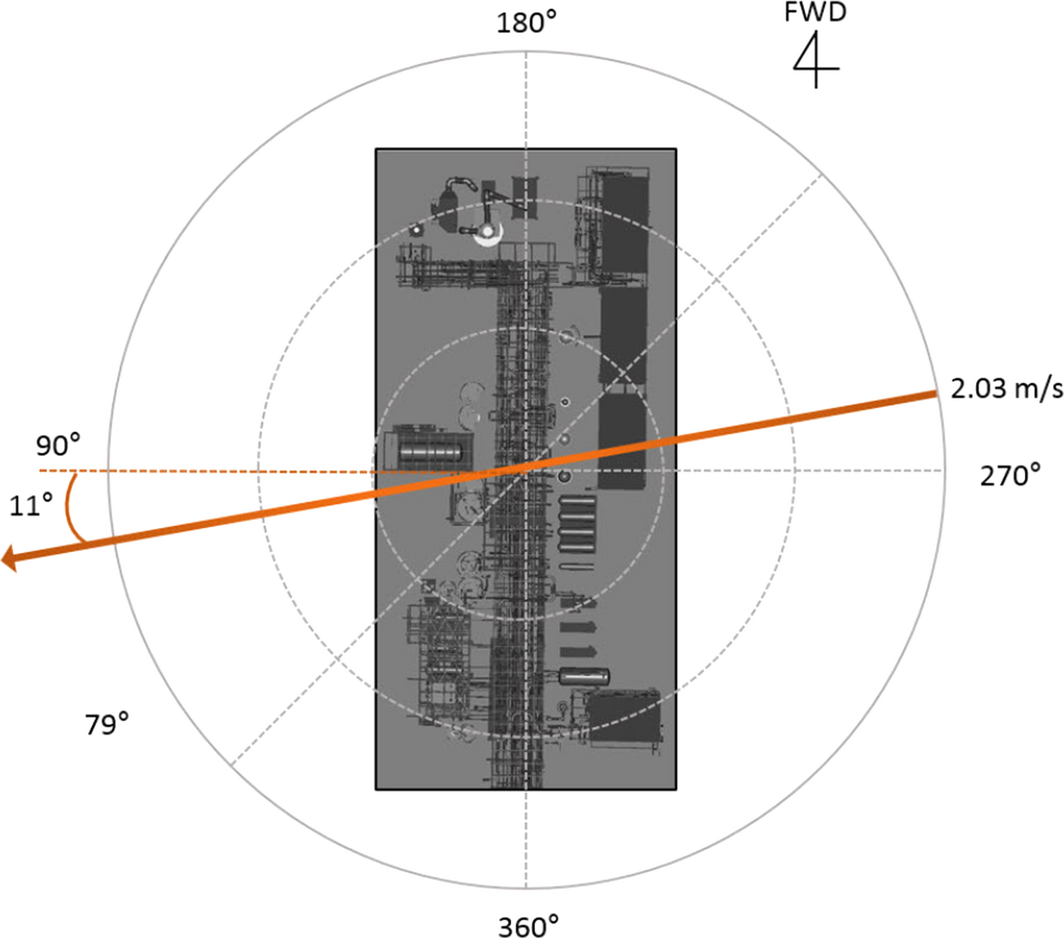
Figure 3. Boundary conditions applied in the simulation.

Table 1. Grid form generated within the simulation domain of residue-hydro-desulfurization

Area (m2)	0.00157
Discharge rate (kg/sec)	15.0
Duration (sec)	60
Wind	Velocity	2.03 m/sec
	Direction	Angle	79°
		U	−0.3835
		V	−1.97
Pasquill category	F
Temperature (K)	294.8

The grid is the most influential factor on the outcome of simulation. Since the effect of damage by a jet fire is generally smaller than accidents caused by explosion or toxic release, the grid density of the domain where flame propagation is expected will be high. KFX creates this grid using a grid generator, and based on vertical and horizontal sizes of domain to be calculated, it decides on the number of grids independently [22].

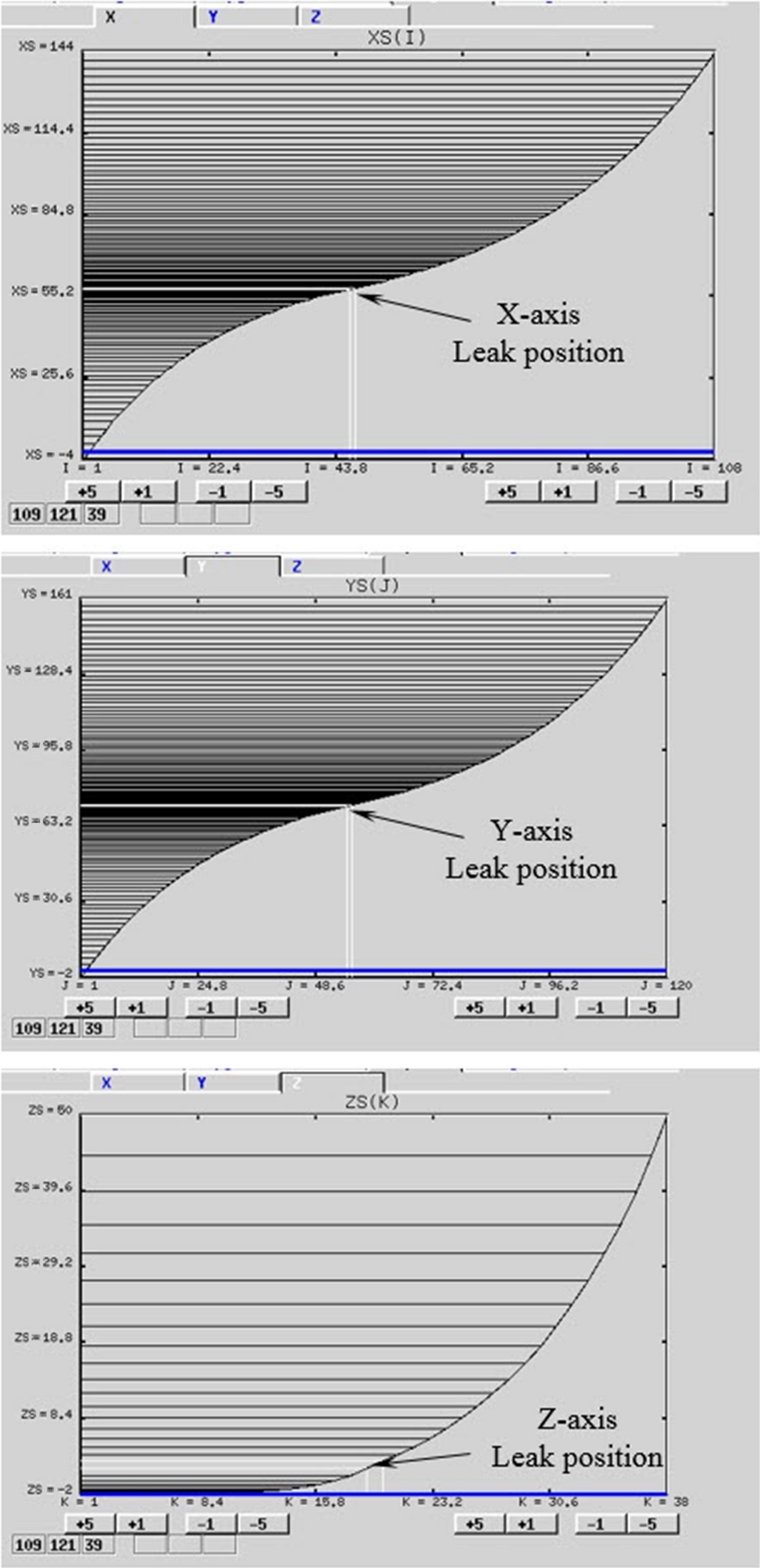
In this study, the grid dimensions applied for the jet fire analysis were 148, 163, and 52 m on the X-axis, Y-axis, and Z-axis, respectively. Following this, to compute the outcome of jet fire within this domain, the grid was created. Figure 4 indicates the grids in the X-axis, Y-axis, and Z-axis created for the simulation, and the dense grid was generated in the fire zone domain around the leak position. Using this step with the KFX grid generator, 514,371 grids were created.

Figure 4. Grid form generated within the simulation domain of residue-hydro-desulfurization.

Grid sensitivity analyses have been carried out to ensure grid independence in this work and other researches using KFX [23].

The boundary condition is also one of the important factors in the simulation [22]. In this study, various values were entered to set the boundary conditions as follows: The wind direction was 79°, the atmospheric stability was assumed to be very stable, (F), the wind speed was 2.03 m/sec at a height of 10 m (Fig. 3), and the atmospheric temperature was 294.8 K.

Figure 5 shows grids on each X, Y, Z-axis created by KFX grid generator. White lines in the figure represents locked grid line at the leak position and black lines unlocked grid lines. Smooth and stretch was performed to the direction of domain boundary. For jet release case, the smallest control volume is generated at the leak point, and gradually increased toward the boundaries.

Figure 5. Grid X, Y, Z-axis created by the Kameleon FireEX grid generator for simulation.

In the simulation process, the equations of continuity, momentum, k - ε, components and energy equations are solved by SIMPLE algorithm.

Simulation Results

The outcomes required to estimate the damage or cause of a fire accident may be categorized as flame, temperature, and radiant heat. As the outcome of the simulation, this study presents the flame propagation step, governing domain, and temperature and radiation heat due to the jet fire.

Jet Flame

As one of the results of the jet fire simulation involving the immediate ignition of leaked high-pressure hydrogen, the flame propagation step is shown in Figure 6. This figure indicates the rapid expansion of flame; there was a rapid volumetric expansion within 3 sec, and from 3 to 9 sec, the propagated flame showed irregular volumetric expansion. Furthermore, after 9 sec, the average volumetric expansion of flame reached the equilibrium. Although there was a slight difference due to wind, after about 9 sec, most of the jet fire maintained similar form of flame and volume. The proposed flame domain of the jet fire is illustrated in Figure 7. Based on the propagation direction of the flame, each flame showed a different form. The maximum height (+Z) of flame among them was 22 m in Figure 7B, of which complex geometries are intentionally removed to clearly show the height only for the purpose of display. The maximum size on the X-axis was 47 m, and the maximum size on the Y-axis was 30 m (Fig. 7C). When a jet fire occurs due to leakage of high-pressure hydrogen, this flame may have an extreme thermal effect on facilities and devices around the leak point, thereby causing secondary accidents. This may lead to escalation into a large-scale accident.

Figure 6. Propagation of the jet fire reflected from the ground in the process plant.

Figure 7. Footprint and three-dimensional features of propagation of the jet fire in the process plant.

Temperature

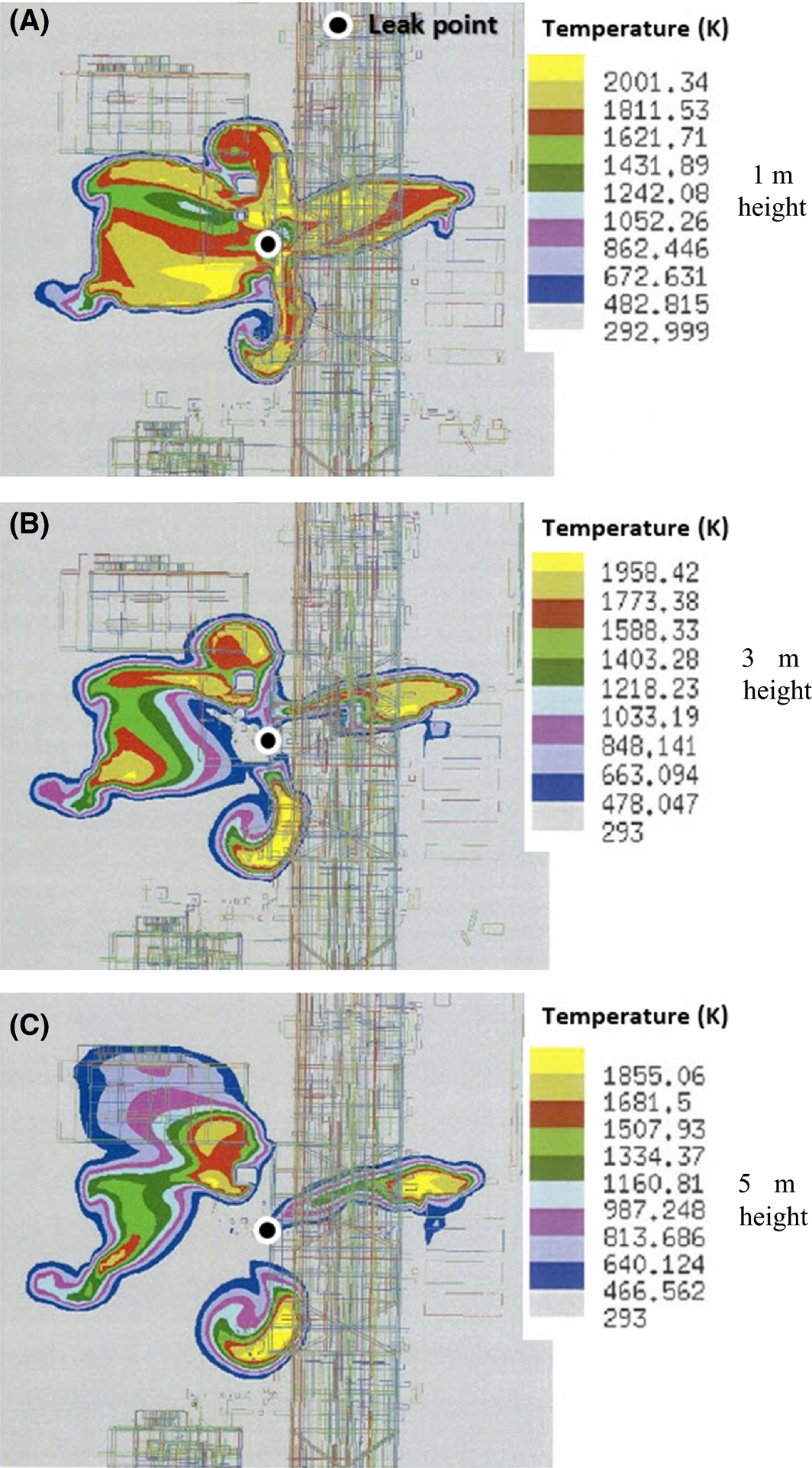
The temperature distribution of the jet fire computed through the simulation was categorized by height and is shown in Figure 8. Here, the height of the region of interest was set from 1 to 5 m in the +Z direction, and this height was again segmented by 1 m. The result in Figure 8 indicates that the region around the leak point had the highest temperature. The maxima of temperature at each height were 2191.16 K at 1 m, 2197.41 K at 2 m, 2143.47 K at 3 m, 2087.21 K at 4 m, and 2028.62 K at 5 m, revealing that all maxima of temperature exceeded 2000 K.

Figure 8. Temperature distribution (top view) at each height of 1, 3, 5 m from the ground around the leak point.

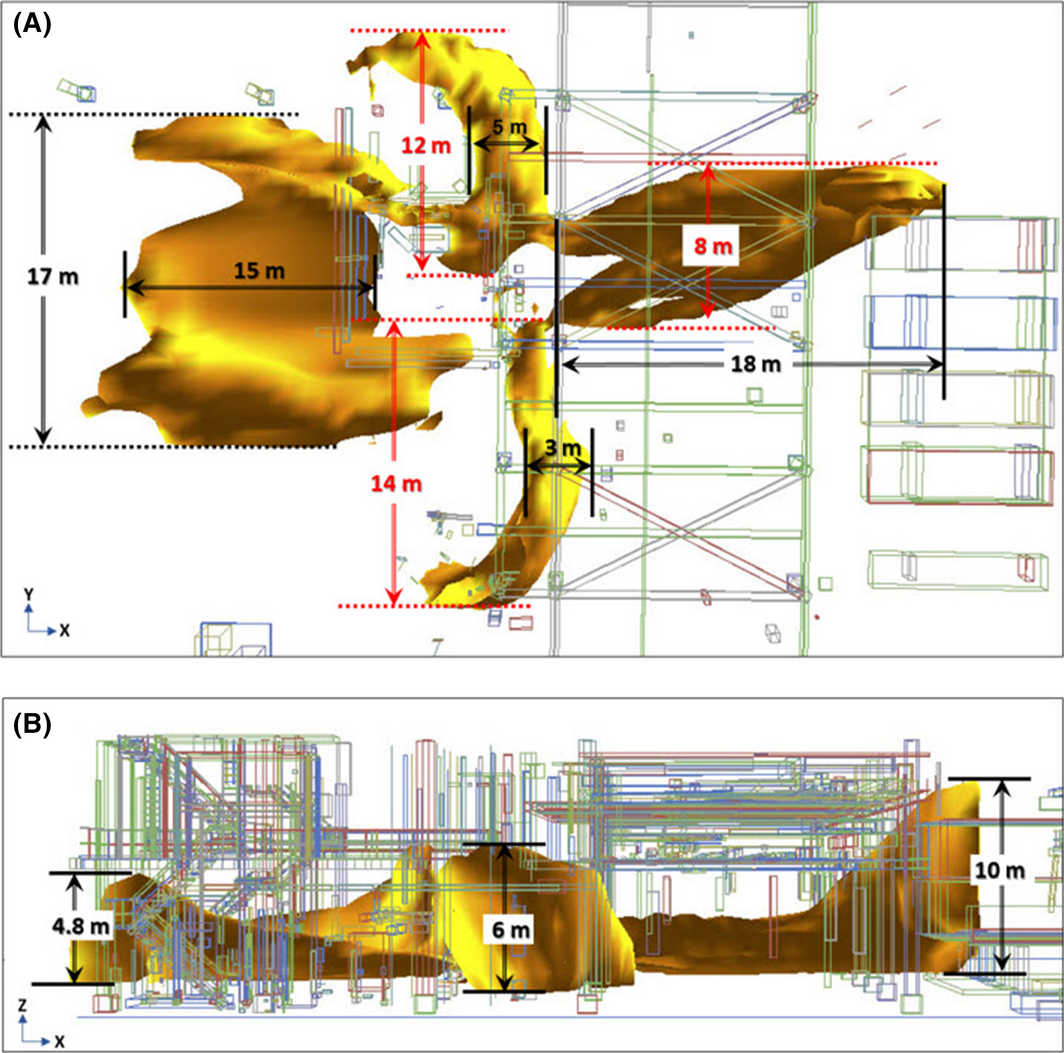
The area of temperature distribution at 1 m high was the widest, showing that the facilities and devices in this region are most affected by heat. In addition, centered on the melting temperature of iron, 1811 K, the temperature distribution form and size were minutely segmented, as shown in Figures 9 and 10. These two figures indicate that the domain under temperature distribution within the melting point range of iron was fairly wide; the maximum height range was from 4.8 to 10 m in the +Z direction (Fig. 10B), the maximum width range from the leak point was 17 m in the ±Y direction (Fig. 10A), and the maximum length range was 18 m in the ±X direction (Fig. 10A).

Figure 9. Volume of distribution of 1811 K as a result of jet fire simulation: (A) isometric view, (B) top view.

Figure 10. Volume size of distribution of 1811 K: (A) size through the top view and (B) size through the side view on the Y-axis.

Radiant Flux

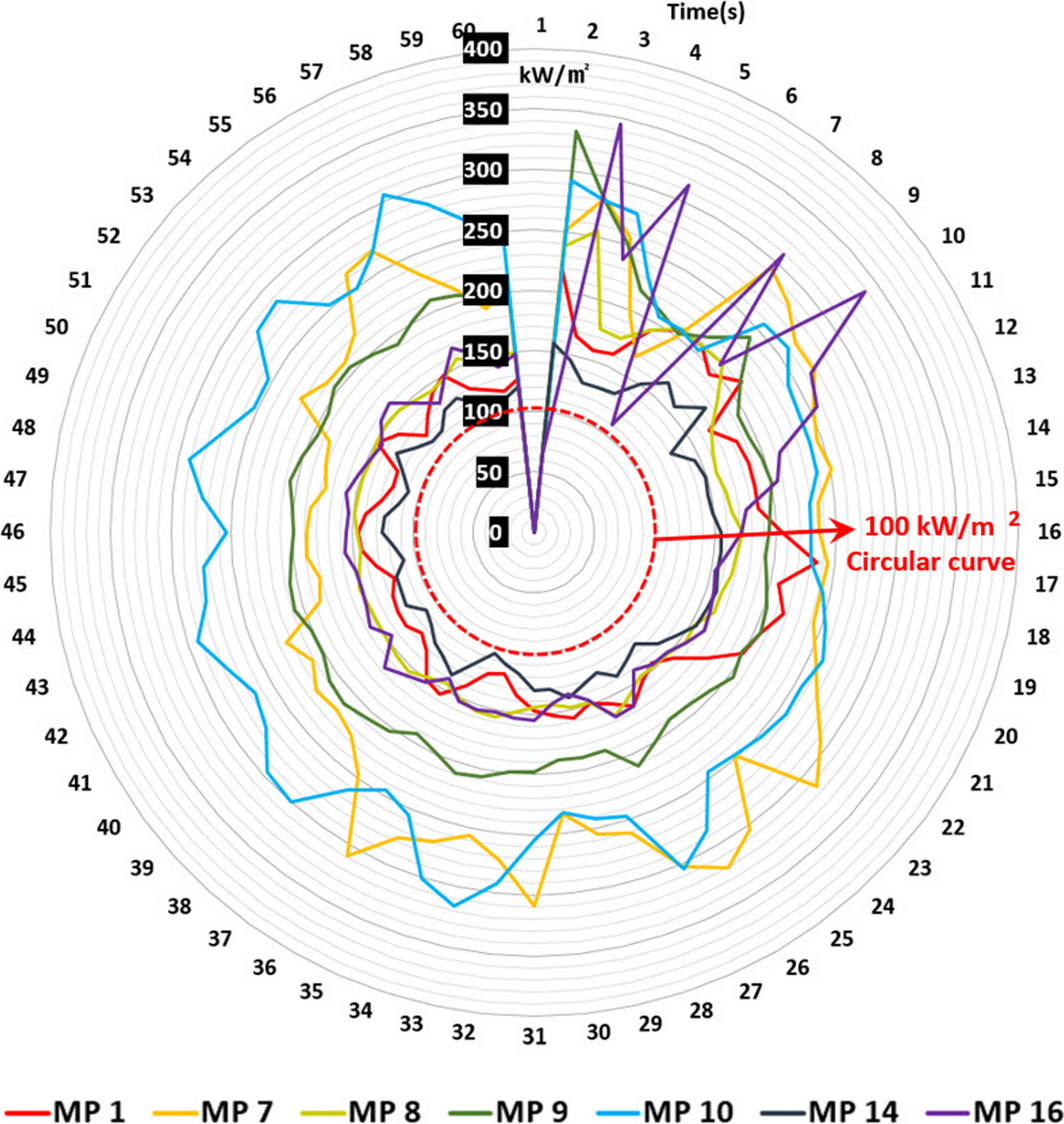
To evaluate the value of radiant heat and the jet fires effect on it, in the simulation domain, the points of interest – monitoring points (MPs) – were set as shown in Table 2. Each MP was set based on the leak point (coordinates: X:56.6, Y:73.6, Z:2.8), human height, and the positional density of process facilities and devices. Each MP was set at 2 m high and 4 m high with a certain displacement in the X-axis and Y-axis direction. The detailed coordinates and values of MPs are in Table 2.

Table 2. Monitor point (MP) and coordinate within the simulation domain

Type		Coordinate
		X-axis (m)	Y-axis (m)	Z-axis (m)
Leak position		56.6	73.6	2.8
MP	MP 7	48.3	72	2
	MP 1	56.4	72	2
	MP 10	70	72	2
	MP 14	56	72	4
	MP 8	62.3	72	4
	MP 9	67.7	72	4
	MP 16	73.4	72	4

Table 2 shows that there are three MPs at 2 m high, with a distance from MP 7 to MP 10 at 21.7 m. There are four MPs at 4 m above from the leak point, and the distance between MP 14 and MP 16 is 18 m. For the outcome of the simulation, the radiant heat at each MP was evaluated.

When the radiant heat reaches 15.8 kW/m², an operator within a structure may not function, and this heat may be delivered to other devices and under a radiant heat of 19.9 kW/m², humans may feel pain within 2 sec and under a radiant heat of 37.5 kW/m², facilities and devices can be damaged [24, 25]. The aforementioned standard of damage was compared with the outcome of this damage, and all MPs in this simulation had radiant heat values over 100 kW/m² (Fig. 11). This value has the worst effect on humans, facilities, and devices, and facilities and devices in this domain may receive severe secondary damage, possibly leading to a critical accident.

Figure 11. Monitoring points (MPs) to show the effect of radiant heat: (A) MP location 2 m above the ground, (B) 4 m above the ground.

Comparison with the Phast Results

As the Process Hazard Analysis Software Tool (Phast) by DNVGL is widely used for jet fire and flare simulations in the chemical and petrochemical industry, version 7.11 was used for comparison of its heat radiation results with those of KFX for the same scenario. The program uses a model based on Chamberlain and Johnsons model for heat radiation calculation from a jet fire. It is important to validate simulated results with experiments, but experimental results are usually difficult to obtain; thus, we chose the newest Phast version because the program has been extensively validated with real flare and jet fire experiments, such as Chamberlain, Johnson, Bennett, and Thornton field tests [23]. The software was also compared with a H₂ jet fire experiment with modification [26].

For Phast, input values are as following:

• 900 kg H₂ inventory with 60-sec fixed duration release (to match the 15.0 kg/sec discharge rate);
• 2.03 m/sec wind speed with F air stability; and
• 400 kW/m² maximum surface emissive power (default).

From the calculation, some important values were reported as follows:

• Jet velocity: 1272.5 m/sec;
• Fraction of heat radiated: 0.14; and
• Surface emissive power: 344 kw/m².

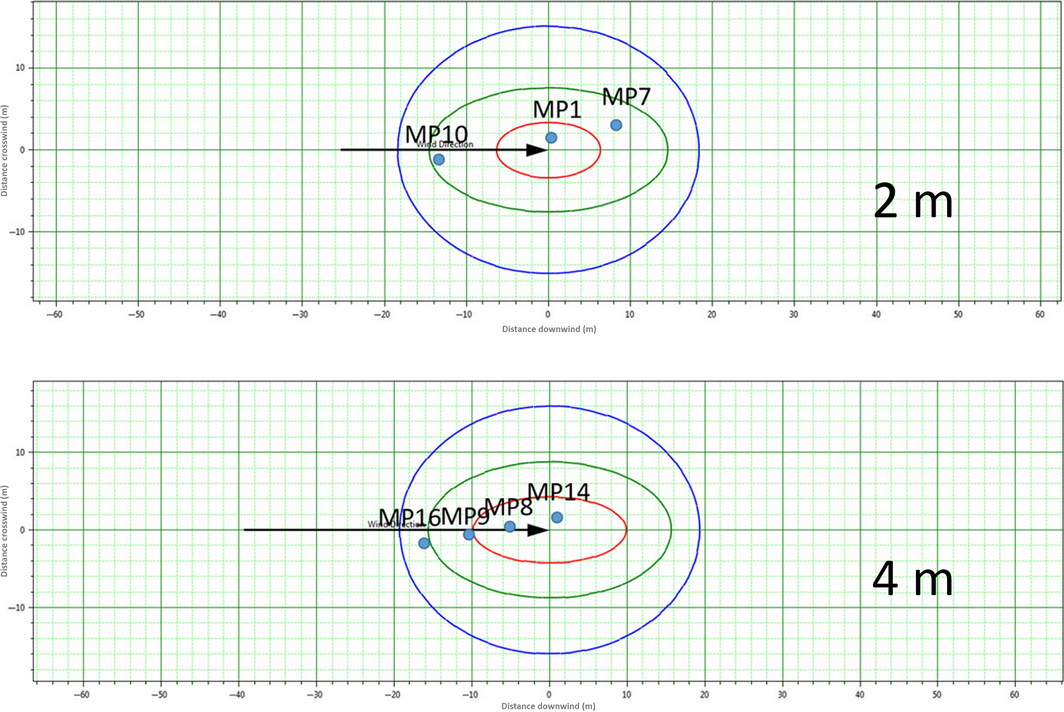
For comparison, varying heat radiation results from KFX were averaged for 1 min. Phast gives a definitive result for each MP because Phast does not assume effects from surrounding equipment or flame propagation; rather, it uses a definitive cone shape for its jet fire. Phast cannot handle obstacles, heat reflection from surrounding geometry, and so on. The heat radiation results are shown in Figure 12. The results of the comparison are shown in Table 3 and exhibit good agreements within ±50% except for MP 14. The reason for the difference in the MP 14 results is the hindrance effect because MP 14 is located right behind a structure, and therefore receives less heat radiation. This shows that the KFX CFD code can give better predictions in case of a complex geometry where accurate predictions are needed.

Figure 12. Intensity radii for jet Fire by Phast for the monitoring points (2, 4 m height). From inside – Red: 200 kW/m2; Green: 100 kW/m2; Blue: 200 kW/m2.

Table 3. Heat radiation results from Kameleon FireEX (KFX) and Phast

MP	Coordinates for Phast (moved)			Heat radiation (kW/m2)
	X-axis (m)	Y-axis (m)	Z-axis (m)	KFX (averaged)	Phast
Origin	0	0	2.8	N.A.	N.A.
MP 1	−0.2	−1.6	2	158	223
MP 7	−8.3	−1.6	2	240	344
MP 8	5.7	−1.6	4	162	208
MP 9	11.1	−1.6	4	206	157
MP 10	13.4	−1.6	2	261	116
MP 14	−0.6	−1.6	4	132	334
MP 16	16.8	−1.6	4	171	99

Conclusions

The aim of this study was to apply the CFD modeling on a hydrogen jet fire during the RHDS process in an oil refinery, where a large amount of high-pressure hydrogen is consumed, to compute the flame, temperature, and radiant heat. As a result of simulation, the volume of the hydrogen jet fire expanded rapidly from ignition to 3 sec, expanded irregularly from 3 to 9 sec, and fell under the equilibrium state after 9 sec to maintain a steady form of the flame. Thereafter, the maximum height of the flame was 22 m (+Z), the maximum width was 30 m (±Y), and the maximum length was 47 m (±X). To evaluate the temperature distribution by flame in more detail, the height under the influence of flame was segmented by 1 m from 1 to 5 m in the +Z direction. As a result, the area of temperature distribution at the domain from the ground to 1 m high was the widest. The domino effect related to the temperature of flame was also evaluated by analyzing the domain of 1811 T – the melting point of iron. To analyze the maximum range of this domain, the maximum height range of 10 m (+Z), the maximum width range of 17 m (±Y), and the maximum length range of 18 m (±X) were evaluated. For evaluation of radiant heat, the regions affected by the flame at 2 m high and 4 m high were selected, and seven MPs were set as the points of interest. The results indicated that the radiant heat at all MPs exceeded 100 kW/m². By comparing the outcome of radiant heat with the standard damage level, the outcome of the study indicated that the radiant heat effect has critical consequences for humans, facilities, and devices.

A comparison of the results with those of Phast 7.11 was presented to show that the present approach exhibited good agreement with the tool. Furthermore, the approach can be superior in regions where obstacles play an important role.

Finally, the risk analysis methodology for jet fire using CFD in this study provided a preliminary virtual analysis of the consequences of a high-risk fire accident extracted through the qualitative risk assessment of a process plant with a great deal of hazardous material under high pressure and high temperature. Thus, it may be applied to generate contingency plans or prepare safety measures. Furthermore, it fundamentally reflects the outcome of accidents in the design stage of processing, allowing for the efficient application of passive fire protection (PFP) to prevent and minimize secondary accidents that may occur during firefighting.

Nomenclature

B

buoyancy

C₁, C₂

constant in k-ε model

C_D

discharge coefficient

e_T

total internal energy [J/kg]

F_liq

exchange of momentum between liquid and gas phase

f₁, f₂

functions in low Reynolds number model

f_i

mass forces which the gas is influenced

f_u

low-Reynolds number correction factor

g

gravitational acceleration [m/sec²]

k

turbulent kinetic energy [J/kg]

k_I

conductivity

P

production of turbulent kinetic energy [W/m³]

p

absolution pressure[pa]

Q_gs

heat transport from solid to gas phase

Q_Rad,f

net radiative transfer to the gas phase

R_ι

chemical source term

R_liq

rate of liquid to gas phase transition

R_t

turbulent Reynolds number

S_liq

net heat transfer from the liquid phase

Y_ι

species mass fraction

V_ιj

molecular diffusion velocity of species ι in the direction j

Greek letters

δ

Kronecker delta

ε

dissipation of the turbulent kinetic energy [W/m³]

κ

second viscosity coefficient

μ_eff

effective diffusion coefficient

μ_t

turbulence diffusion coefficient

ρ

gas density [kg/m³]

τ_ij

tensor [N/m²]

Subscripts

eff

effective

i, j

index

ι

species

liq

liquid phase

Superscripts

—

mean, time-averaged quantities

″

fluctuation, Favre-averaged quantities

~

mean, Favre-averaged quantities

References

1. Hord, J.1978. Is hydrogen a safe fuel?Int. J. Hydrogen Energy3:157–176.
2. Lim, H.2014. The direction and prospect of hydrogen fuel cells industry. Korea Gasnewspaper Co. Ltd. Available at: http://www.gasnews.com/news/articleView.html?idxno=67327
3. Alileche, N., V. Cozzani, G. Reniers, and L. Estel. 2015. Thresholds for domino effects and safety distances in the process industry: a review of approaches and regulations. Reliab. Eng. Syst. Saf.143:74–84.
4. Gomez-Mares, M., L. Zarate, and J. Casal. 2008. Jet fires and the domino effect. Fire Saf. J.43:583–588.
5. Salzano, E., and V. Cozzani. 2005. The analysis of domino accidents triggered by vapor cloud explosions. Reliab. Eng. Syst. Saf.90:271–284.
6. Darbra, R., A. Palacios, and J. Casal. 2010. Domino effect in chemical accidents: main features and accident sequences. J. Hazard. Mater.183:565–573.
7. Kikukawa, S., H. Mitsuhashi, and A. Miyake. 2009. Risk assessment for liquid hydrogen fueling stations. Int. J. Hydrogen Energy34:1135–1141.
8. Zhiyong, L., P. Xiangmin, and M. Jianxin. 2010. Harm effect distances evaluation of severe accidents for gaseous hydrogen refueling station. Int. J. Hydrogen Energy35:1515–1521.
9. Brennan, S., D. Makarov, and V. Molkov. 2009. LES of high pressure hydrogen jet fire. J. Loss Prev. Process Ind.22:353–359.
10. Deimling, L., V. Weiser, A. Blanc, N. Eisenreich, G. Billeb, and A. Kessler. 2011. Visualisation of jet fires from hydrogen release. Int. J. Hydrogen Energy36:2360–2366.
11. Vembe, B., K. Rian, J. Holen, N. Lilleheie, B. Grimsmo, and T. Myhrvold. 2001. Kameleon FireEx 2000 theory manual. Computational Industry Technologies AS, Trondheim, Norway.
12. Evanger, T., and T. Holmås. 2005. Kameleon FireEx – an Advanced Computational System for Calculation of Fire Structure Interaction. Fabig Technical Newsletter.
13. Magnussen, B., T. Evanger, B. Vembe, N. Lilleheie, B. Grimsmo, B. Velde et al. 2010. SPE International Conference on Health, Safety, and the Environment in Oil and Gas Exploration and Production. Norway.
14. Byggstöyl, S., N. Lilleheie, and B. Magnussen. 1987. Strategy for Inclusion of Chemical Kinetics into the Eddy Dissipation Concept. in IX Task Leaders Meeting-Energy Conservation in Combustion, IEA.
15. Vembe, B., N. Lilleheie, J. Holen, B. Magnussen, B. Velde, G. Linke et al. 1998. International Gas Research Conference 1998, Pp. 429–437.
16. Antonioni, G., G. Spadoni, and V. Cozzani. 2009. Application of domino effect quantitative risk assessment to an extended industrial area. J. Loss Prev. Process Ind.22:614–624.
17. Korea Occupational Safety and Health Agency. 2008. Manual for Petrochemical unit screening technique. Korea.
18. Mingguang, Z., and J. Juncheng. 2008. An improved probit method for assessment of domino effect to chemical process equipment caused by overpressure. J. Hazard. Mater.158:280–286.
19. American Institute of Chemical Engineers. Center for Chemical Process Safety. 2000. Guidelines for chemical process quantitative risk analysis. New York, U.S.
20. Glassman, I.1996. Combustion. Academic Press, San Diego, CA.
21. Shah, N. G.1979. Jet Fire Computational Fluid Dynamic Simulations: Validation from an Industrial & Consultancy Perspective. These. Imperial College London (University of London)
22. Computational Industry Technologies. 2014. KFXTM furcifer user manual. Computational Industry Technologies, Norway.
23. Malkeson, S. P., T. Jones, and R. English. 2015. The computation of radiation heat transfer. 25th International Colloquium on the Dynamics of Explosions and Reactive Systems, Leeds, UK, 2015.
24. American Petroleum Institute. Division of Refining. 1982. Guide for pressure-relieving and depressuring systems. Washington, D.C. USA.
25. Kayes, P., and B. Mundial. 1985. Manual of industrial hazard assessment techniques. Technica.
26. Lutostansky, E., L. Creitz, S. Jung, J. Schork, D. Worthington, and Y. Xu. 2013. Modeling of underground hydrogen pipelines. Process Saf. Prog.32:212–216.