Iber — River modelling simulation tool

Resumen

Para dar respuesta a los requerimientos en materia de aguas definidos en las directrices, reglamentos y recomendaciones existentes en la legislación española, los cuales están mayoritariamente basados en directivas europeas, se ha desarrollado una herramienta de modelización numérica del flujo de agua en lámina libre en 2 dimensiones. La herramienta, llamada Iber, combina un módulo hidrodinámico, un módulo de turbulencia y un módulo de transporte de sedimentos, y utiliza el método de volúmenes finitos para resolver las ecuaciones correspondientes. Al módulo de cálculo se le ha adaptado una interfaz que se basa en el software de preproceso y posproceso GiD, desarrollado por CIMNE. El resultado es una herramienta de modelización numérica del flujo de agua y sedimentos en ríos y estuarios, que utiliza esquemas numéricos avanzados especialmente estables y robustos en cualquier situación pero especialmente adecuados para flujos discontinuos y, en concreto, para cauces torrenciales y regímenes irregulares.

Abstract

The recent requirements of Spanish regulations and directives, on their turn based on European directives, have led to the development of a new two dimensional open channel flow modelling tool. The tool, named Iber, combines a hydrodynamic module, a turbulence module and a sediment transport module, and is based in the finite volume method to solve the involved equations. The simulation code has been integrated in a pre-process and post-process interface based on GiD software, developed by CIMNE. The result is a flow and sediment modelling system for rivers and estuaries that uses advanced numerical schemes, robust and stable, which are especially suitable for discontinuous flows taking place in torrential and hydrologically irregular rivers.

Palabras clave

Flujo en lámina libre ; Aguas someras ; Modelización de procesos fluviales ; Inundaciones

Keywords

Open channel flow ; Shallow water ; Fluvial processes modelling ; Flood modelling

1. Introducción

La modelación matemática del flujo de agua en un río consiste en predecir los valores que toman las variables hidráulicas (calado, velocidades, caudal, etc.) a partir de la resolución mediante métodos numéricos de unas ecuaciones obtenidas con una serie de hipótesis. Para el estudio de los efectos de la propagación de avenidas en ríos se pueden utilizar modelos unidimensionales o bidimensionales. La necesidad de estudiar cada vez fenómenos más complejos, y la observación que en la naturaleza se encuentran muchas situaciones donde el flujo parece ser efectivamente bidimensional —es decir, predominan las dimensiones horizontales sobre la vertical—, junto con la creciente capacidad y velocidad de los ordenadores, ha llevado al uso de ecuaciones y esquemas bidimensionales (ecuaciones de aguas someras). Actualmente existe una variedad de herramientas para la resolución del flujo de agua en lámina libre en 2 dimensiones. Algunas de las más consolidadas, como Mike-21, Sobek o Tuflow2D, utilizan esquemas en diferencias finitas, lo que conlleva limitaciones en la flexibilidad de la malla y en el cálculo de soluciones con discontinuidades. Otras, como Telemac2D, los distintos módulos de cálculo de SMS y FLO-2D, utilizan elementos finitos, lo que permite más flexibilidad en la malla de cálculo al trabajar con mallas no estructuradas. La tendencia actual se decanta claramente hacia la metodología de volúmenes finitos, aprovechando los importantes desarrollos habidos en las últimas décadas con este tipo de esquemas para las ecuaciones de las aguas someras (ver por ejemplo [1] y [2] ). Algunas de las herramientas disponibles y que utilizan volúmenes finitos son Infoworks, Guad2D, las últimas versiones de Mike-21 e Iber.

Iber es un modelo matemático bidimensional para la simulación del flujo en ríos y estuarios desarrollado a partir de la colaboración del Grupo de Ingeniería del Agua y del Medio Ambiente, GEAMA (Universidade da Coruña ), del Grupo de Ingeniería Matemática (Universidade de Santiago de Compostela ), del Instituto Flumen (Universitat Politècnica de Catalunya y Centre Internacional de Mètodes Numèrics en Enginyeria) y promovido por el Centro de Estudios Hidrográficos del CEDEX. Iber es un modelo numérico desarrollado directamente desde la administración pública española en colaboración con las universidades mencionadas y diseñado para ser especialmente útil a las necesidades técnicas específicas de las confederaciones hidrográficas en la aplicación de la legislación sectorial vigente en materia de aguas. Algunos de los campos de aplicación de la versión actual de Iber son:

• Simulación del flujo en lámina libre en cauces naturales.
• Evaluación de zonas inundables. Cálculo de las zonas de flujo preferente.
• Cálculo hidráulico de encauzamientos.
• Cálculo hidráulico de redes de canales en lámina libre.
• Cálculo de corrientes de marea en estuarios.
• Estabilidad de los sedimentos del lecho.
• Procesos de erosión y sedimentación por transporte de material granular.

Iber se desarrolló a partir de 2 herramientas de modelización numérica bidimensional ya existentes, Turbillón y CARPA (cuya metodología se puede encontrar por ejemplo en Cea et al. [3] y Bladé et al. [4] , respectivamente), ambas con el método de volúmenes finitos, que fueron integradas en un único código ampliado con nuevas capacidades. El modelo Iber consta de diferentes módulos de cálculo acoplados entre sí. En su primera versión se incluye un módulo hidrodinámico, un módulo de turbulencia y un módulo de transporte de sedimentos, de granulometría uniforme, por carga de fondo y por carga en suspensión. En sucesivas versiones del modelo se irán complementando y ampliando estos módulos y se desarrollarán otros nuevos. Entre las líneas prioritarias de desarrollo de Iber a corto plazo se encuentran los modelos de transporte de mezclas de sedimento, los modelos de hábitat fluvial y los modelos de calidad de aguas. Iber es un modelo de uso libre que se puede descargar de la página web www.iberaula.es , donde se ofrece documentación adicional, soporte a través de un foro de discusión y cursos de formación.

2. Modelo numérico

2.1. Ecuaciones

El módulo hidrodinámico de Iber resuelve las ecuaciones de St. Venant bidimensionales, incorporando los efectos de la turbulencia y rozamiento superficial por viento:

${\begin{array}{l}{\frac {\partial h}{\partial t}}+{\frac {\partial hU_{x}}{\partial x}}+{\frac {\partial hU_{y}}{\partial y}}=0\\{\frac {\partial }{\partial t}}\left(hU_{x}\right)+{\frac {\partial }{\partial x}}\left(hU_{x}^{2}+g{\frac {h^{2}}{2}}\right)+{\frac {\partial }{\partial y}}\left(hU_{x}U_{y}\right)=-gh{\frac {\partial Z_{b}}{\partial x}}+{\frac {{\tau }_{s,x}}{\rho }}-{\frac {{\tau }_{b,x}}{\rho }}+{\frac {\partial }{\partial x}}\left({\nu }_{t}h{\frac {\partial U_{x}}{\partial x}}\right)+{\frac {\partial }{\partial y}}\left({\nu }_{t}h{\frac {\partial U_{x}}{\partial y}}\right)\\{\frac {\partial }{\partial t}}\left(hU_{y}\right)+{\frac {\partial }{\partial x}}\left(hU_{x}U_{y}\right)+{\frac {\partial }{\partial y}}\left(hU_{y}^{2}+g{\frac {h^{2}}{2}}\right)=-gh{\frac {\partial Z_{b}}{\partial y}}+{\frac {{\tau }_{s,y}}{\rho }}-{\frac {{\tau }_{b,y}}{\rho }}+{\frac {\partial }{\partial x}}\left({\nu }_{t}h{\frac {\partial U_{y}}{\partial x}}\right)+{\frac {\partial }{\partial y}}\left({\nu }_{t}h{\frac {\partial U_{y}}{\partial y}}\right)\end{array}}$

en donde h es el calado, U_x, U_y son las velocidades horizontales promediadas en profundidad, g es la aceleración de la gravedad, ρ es la densidad del agua, Z_b es la cota del fondo, τ_s es la fricción en la superficie libre debida al rozamiento producido por el viento, τ_b es la fricción debida al rozamiento del fondo y ν_t es la viscosidad turbulenta. La fricción de fondo se evalúa mediante la fórmula de Manning como:

${\tau }_{b,x}=\rho gh{\frac {n^{2}U_{x}\left|U\right|^{2}}{h^{4/3}}}{\mbox{ }}{\tau }_{b,y}=$$\rho gh{\frac {n^{2}U_{y}\left|U\right|^{2}}{h^{4/3}}}$

La fuerza de rozamiento realizada por el viento sobre la superficie libre se calcula a partir de la velocidad del viento a 10 m de altura, utilizando para ello la ecuación de Van Dorn [5] :

${\tau }_{s,x}=\rho C_{VD}\left|V_{10}\right|V_{x,10}{\mbox{ }}{\tau }_{s,y}=$$\rho C_{VD}\left|V_{10}\right|V_{y,10}$

donde, V_X,10,V_Y,10 son las 2 componentes de la velocidad del viento a 10 m de altura, |V₁₀| es el módulo de la velocidad del viento a 10 m de altura y C_VD es un coeficiente de arrastre superficial que se calcula en función de la velocidad del viento a partir de la siguiente expresión:

$\left|V_{10}\right|<5,6m/s\rightarrow C_{VD}=1,2\cdot {10}^{-6}$ $\left|V_{10}\right|\geq 5,6m/s\rightarrow C_{VD}=1,2\cdot {10}^{-6}+$$2,25\cdot {10}^{-6}{\left(1-{\frac {5,6}{\left|V_{10}\right|}}\right)}^{2}$

Todas las funciones y parámetros que aparecen en las ecuaciones hidrodinámicas (incluyendo el coeficiente de Manning y la velocidad del viento) pueden imponerse de forma variable tanto espacial como temporalmente.

La viscosidad turbulenta se calcula mediante modelos de turbulencia específicos para las ecuaciones de aguas someras promediadas en profundidad. Iber incluye 3 modelos de turbulencia promediados en profundidad: el modelo parabólico, un modelo de longitud de mezcla y el modelo k-ɛ de Rastogi y Rodi [6] . En el modelo parabólico se calcula la viscosidad turbulenta como:

${\nu }_{t}=0,068u_{f}h{\mbox{ }}u_{f}={\sqrt {{\tau }_{b}/\rho }}$

siendo u_f la velocidad de fricción de fondo. Utilizando la fórmula de Manning para calcular la fricción de fondo se obtiene la siguiente expresión para la viscosidad turbulenta:

${\nu }_{t}=0,068{\sqrt {g}}n\left|U\right|h^{5/6}$

En el modelo de longitud de mezcla para aguas someras, la viscosidad turbulenta se calcula mediante la siguiente expresión:

${\nu }_{t}={\left[min\left(0,267\kappa h,\kappa d_{wall}\right)\right]}^{2}{\sqrt {2S_{ij}S_{ij}+{\left(2,34{\frac {u_{f}}{\kappa h}}\right)}^{2}}}{\mbox{ }}S_{ij}=$${\frac {1}{2}}\left({\frac {\partial U_{i}}{\partial x_{j}}}+\right.$$\left.{\frac {\partial U_{j}}{\partial x_{i}}}\right)$

en donde κ = 0,41 es la constante de von Karman y d_wall es la distancia desde el punto considerado a la pared más cercana. El modelo k-ɛ de Rastogi y Rodi [6] resuelve una ecuación de transporte para la energía cinética turbulenta k y para la tasa de disipación de energía turbulenta ɛ :

${\frac {\partial k}{\partial t}}+{\frac {\partial U_{x}k}{\partial x}}+$${\frac {\partial U_{y}k}{\partial y}}={\frac {\partial }{\partial x_{j}}}\left(\left(\nu +\right.\right.$$\left.\left.{\frac {{\nu }_{t}}{{\sigma }_{k}}}\right){\frac {\partial k}{\partial x_{j}}}\right)+$$2{\nu }_{t}S_{ij}S_{ij}+c_{k}{\frac {u_{f}^{3}}{h}}-\epsilon$

${\frac {\partial \epsilon }{\partial t}}+{\frac {\partial U_{x}\epsilon }{\partial x}}+$${\frac {\partial U_{y}\epsilon }{\partial y}}={\frac {\partial }{\partial x_{j}}}\left(\left(\nu +\right.\right.$$\left.\left.{\frac {{\nu }_{t}}{{\sigma }_{\epsilon }}}\right){\frac {\partial \epsilon }{\partial x_{j}}}\right)+$$c_{\epsilon 1}{\frac {\epsilon }{k}}2{\nu }_{t}S_{ij}S_{ij}+$$c_{\epsilon }{\frac {u_{f}^{4}}{h^{2}}}-c_{\epsilon 2}{\frac {{\epsilon }^{2}}{k}}$

${\nu }_{t}=c_{\mu }{\frac {k^{2}}{\epsilon }}{\mbox{ }}c_{k}=$$c_{f}^{-1/2}{\mbox{ }}c_{\epsilon }=3,6c_{k}^{3/2}c_{\epsilon 2}c_{\mu }^{1/2}{\mbox{ }}c_{f}=$${\frac {{\tau }_{b}}{\rho }}{\frac {1}{\left|U\right|^{2}}}$

$c_{\mu }=0,09{\mbox{ }}c_{\epsilon 1}=1,44{\mbox{ }}c_{\epsilon 2}=$$1,92{\mbox{ }}{\sigma }_{k}=1,0{\mbox{ }}{\sigma }_{\epsilon }=$$1,31$

2.2. Condiciones de contorno

Iber distingue entre contornos cerrados (tipo pared) y contornos abiertos por los cuales entra y sale el agua del dominio de cálculo. En los contornos cerrados se puede imponer o una condición de deslizamiento libre o una condición de fricción de pared. Con la condición de deslizamiento libre se desprecia el rozamiento generado por los contornos sobre el fluido. Si se considera relevante el efecto del rozamiento generado por el contorno se debe utilizar una condición de contorno tipo fricción. La velocidad tangencial a la pared puede expresarse como una función de la velocidad de fricción de pared (u_* ) y de la distancia a la pared como:

$\left|U\right|={\frac {u_{\ast }}{0,4}}Ln\left(E\cdot {\frac {du_{\ast }}{\nu }}\right)$

donde d es la distancia en perpendicular a la pared y E es un parámetro cuyo valor depende de las características del flujo. Para el cálculo de E se consideran condiciones de flujo turbulento liso, turbulento rugoso, y transición entre turbulento liso y rugoso, tal como se especifica en la tabla 1 .

Tabla 1. Fricción de pared. K_s es la altura de rugosidad de la pared

Tipo de régimen	${\textstyle K_{S}^{+}=K_{S}u_{\ast }/\nu }$	${\textstyle \left|u\right|={\frac {u_{\ast }}{\kappa }}Ln\left(E\cdot d^{+}\right)}$
Turbulento liso	KS+<5	E=9, 0
Transición liso-rugoso	5<KS+<70	E=0,11+0,033⋅KS+−1
Turbulento rugoso	KS+>70	E=30/KS+

Respecto a los contornos abiertos, se consideran diferentes alternativas en función del régimen hidráulico en el contorno. En los contornos de entrada se fija el caudal de agua y se asume que la dirección del flujo es perpendicular al contorno. En caso de que el flujo entre en régimen supercrítico, se impone adicionalmente el calado. La distribución del caudal unitario a lo largo del contorno se realiza de forma proporcional al calado en cada punto del mismo según la expresión q_n  = C  · h^5/3 , donde C es una constante que asegura que la integral del caudal unitario q_n a lo largo del contorno considerado es igual al caudal total de entrada.

En los contornos de salida se impone el nivel de la lámina de agua en caso de que se produzca un régimen subcrítico, mientras que no es necesario imponer ninguna condición en el caso de que el régimen sea supercrítico. En los contornos de salida se considera asimismo la posibilidad de introducir una relación de curva de gasto que defina la relación entre la cota de la lámina de agua y el caudal específico desaguado en cada punto del contorno.

Por último, se incluye la posibilidad de definir contornos abiertos tipo marea, en los cuales se impone una cota de la lámina de agua variable en el tiempo. En estos contornos se fija únicamente la cota de la lámina cuando el agua sale del dominio de cálculo (marea vaciante), y se impone adicionalmente la dirección del flujo de forma perpendicular al contorno cuando el agua entra en el dominio (marea entrante).

2.3. Condiciones internas

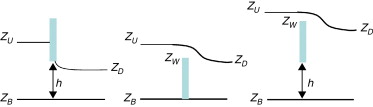
Las condiciones internas se utilizan para modelar estructuras hidráulicas tipo compuertas, vertederos o puentes que entran en carga. En estos casos las ecuaciones de St. Venant dejan de ser válidas por incumplirse las hipótesis de presión hidrostática y velocidad uniforme en profundidad, y por lo tanto es más adecuado calcular la relación entre el caudal y la pérdida de carga a través de dichas estructuras mediante ecuaciones de descarga específicas. En Iber se consideran condiciones internas de flujo bajo compuerta y de flujo sobre vertedero en lámina libre. El flujo a través de tableros de puentes anegados se puede calcular como la combinación de las 2 condiciones anteriores. En este caso el caudal total desaguado se obtiene como la suma del caudal bajo compuerta y del caudal sobre vertedero. Las ecuaciones de desagüe y variables utilizadas en cada caso se especifican en la tabla 2 (donde C_dg es el coeficiente de desagüe para compuerta libre, C_dg’ es el coeficiente de desagüe para compuerta sumergida, C_dw es el coeficiente de desagüe del vertedero y B es el ancho de paso de la estructura) y en la figura 1 .

Tabla 2. Ecuaciones utilizadas en las condiciones internas, siempre y cuando se cumpla Z_U-Z_B > h

Compuerta - Libre	(ZD−ZB)/(ZU−ZB)<0, 67	Q=CdgBh2g(ZU−ZB)
Compuerta - Transición	0, 67<(ZD−ZB)/(ZU−ZB)<0, 80	Q=CdgBh6g(ZU−ZD)
Compuerta - Anegada	(ZD−ZB)/(ZU−ZB)>0, 80	Q=C'dgBh2g(ZU−ZD)
Vertedero - Libre	(ZD−ZB)/(ZU−ZB)<0, 67	Q=CdwB(ZU−Zw)1,5
Vertedero - Anegado	(ZD−ZB)/(ZU−ZB)>0, 67	Q=2,6 Cdw B(ZD−Zw)(ZU−Zw)0,5

Figura 1. Definición esquemática de las variables utilizadas en la imposición de condiciones internas. Compuerta sin vertedero (izquierda), vertedero sin compuerta (centro) y combinación compuerta-vertedero (derecha).

2.4. Esquemas numéricos

Las ecuaciones de aguas someras y las del modelo k-ɛ se resuelven mediante el método de volúmenes finitos para mallas bidimensionales no estructuradas. Los esquemas numéricos utilizados en Iber son especialmente apropiados para la modelización de cambios de régimen y de frentes seco-mojado (frentes de inundación). El análisis de los algoritmos de resolución empleados en Iber excede los objetivos de este artículo, y se puede encontrar una descripción detallada de aquellos en Bermúdez et al. [7] , LeVeque [8] , Roe [9] y Vázquez-Cendón [2] .

La discretización del dominio espacial se realiza con volúmenes finitos en mallas no estructuradas, admitiéndose estas mixtas formadas por elementos triangulares y cuadrangulares. El flujo convectivo se discretiza mediante esquemas descentrados de tipo Godunov, concretamente el esquema descentrado de Roe [9] , así como su extensión a orden 2 con el limitador de pendiente Minmod [2] para evitar oscilaciones en regiones con máximos o mínimos locales. El término que incluye la pendiente del fondo se discretiza de forma descentrada con el fin de evitar oscilaciones espurias de la lámina libre cuando se trabaja con terrenos complejos [7] . El resto de términos fuente, incluidos los de difusión turbulenta, se discretizan con un esquema centrado.

Para el tratamiento de los frentes seco-mojado se define una tolerancia seco-mojado, de forma que si el calado en un volumen finito es menor a dicha tolerancia, el elemento se considera seco y no se incluye en el cálculo. La altura de agua nunca se fuerza a cero, con el fin de evitar pérdidas de masa en el interior del dominio de cálculo. De esta manera se define el frente de inundación como el límite entre las zonas con calado inferior a la tolerancia seco-mojado y las zonas con calado superior a dicho límite. En el frente de inundación se impone una condición de reflexión, que consiste en imponer a cero tanto la velocidad perpendicular al frente como el gradiente de la lámina de agua en dicha dirección.

2.5. Interfaz de preproceso y posproceso

La interfaz de usuario de un programa de simulación numérica es de gran importancia, y en el caso particular de la modelación bidimensional puede resultar clave dada la cantidad y la variedad de datos de entrada que se requieren. La interfaz de Iber está realizada en base al programa GiD [10] , [11]  and [12] , desarrollado por el Centre Internacional de Mètods Numèrics en Enginyeria (CIMNE). GiD es un programa de preproceso y post proceso para simulaciones numéricas que está diseñado para ser adaptado y personalizado según los requisitos del modelo numérico. El resultado es una herramienta flexible y amigable con el usuario. Muchas de las capacidades disponibles en la interfaz de Iber son intrínsecas de GiD, pero muchas otras han sido desarrolladas para dotar al modelo de las herramientas específicas que se necesitan para simulación numérica de flujos a lámina libre en aguas poco profundas [13] . De entre los desarrollos específicos para el preproceso destaca la importación desde un archivo georreferenciado de la rugosidad de Manning asociada a usos del suelo y su asignación automática a los elementos de la malla.

Uno de los procesos que requieren mayor tiempo y esfuerzo a la hora de desarrollar un estudio de simulación numérica del flujo en ríos es la generación de la malla de cálculo. Un río tiene una geometría irregular y la construcción de una malla eficiente no es evidente. Es deseable que la malla sea irregular, con el fin de minimizar el número de elementos con transiciones suaves. Para ello son muy adecuados los métodos de mallado basados en el error cordal (máxima distancia entre el terreno original y la malla). Por ello Iber incorpora las capacidades estándar de mallado de GiD, como la creación de mallas estructuradas y no estructuradas, de triángulos y de cuadriláteros, mediante el uso de diversos algoritmos de mallado. Adicionalmente se han desarrollado herramientas de creación y edición de mallas que se adaptan a las necesidades de los estudios de hidráulica fluvial.

En el caso de que el terreno forme una superficie suficientemente suave, es posible importar el archivo del MDT como una única superficie. Iber considera las superficies como entidades NURBS (Non Uniform Rational B-Splines). Este método puede proporcionar mallas de gran calidad cuando la superficie resultante está bien condicionada. Por el contrario, si el terreno tiene irregularidades importantes, como por ejemplo edificios, es posible que no se pueda representar como una superficie NURBS, o que su aproximación no sea adecuada y la superficie se pliegue sobre sí misma, produciéndose por lo tanto errores en el mallado. Para topografías que presentan irregularidades o complejidades se implementó la metodología de creación de geometrías en formato RTIN (Regular Triangular Irregular Network) adaptando la propuesta presentada en Evans et al. [14] . Las topografías resultantes permiten obtener mallas de gran calidad y robustez, aunque con presencia de direcciones dominantes (fig. 2 ).

Figura 2. Malla de cálculo formada por una Red Irregular de Triángulos Rectángulos (RTIN).

Por último, se incorpora una herramienta que permite, una vez creada la malla de cálculo, modificar la cota de los nodos de los elementos de la malla a partir de un modelo digital del terreno en formato ASCII de Arc/Info (fig. 3 ).

Figura 3. Menú Iber_Herramientas y un ejemplo de edición de nodos de una malla.

2.6. Capacidades adicionales

La base del modelo Iber son los módulos que calculan la hidrodinámica y la turbulencia, descritos en los apartados anteriores. La herramienta completa tiene, como se menciona en el apartado 2.1, la posibilidad de incluir en las ecuaciones del modelo los efectos de las precipitaciones y del transporte de sedimentos. Aunque hacer una explicación detallada de estas capacidades no forma parte de los objetivos de este artículo, sí resulta interesante describirlos de manera concisa.

En el módulo de transporte de sedimentos se resuelven las ecuaciones de transporte por carga de fondo y por carga en suspensión. Teniendo en cuenta ambos modos de transporte se calcula la evolución de la cota del fondo debido a procesos de sedimentación y erosión mediante la ecuación de Exner. En todos los casos se consideran granulometrías uniformes.

El caudal sólido de fondo se calcula mediante formulaciones empíricas en función de la tensión de fondo. El módulo de transporte de sedimentos por carga de fondo incluye las siguientes características:

• Umbral de movimiento de Shields.
• Formulaciones para caudal sólido de fondo.
• Meyer Peter-Müller con corrección de Wong-Parker (D = 2-30 mm) [15] .
• Van Rijn (D = 0,2-2 mm) [16] .
• Corrección por pendiente de fondo en inicio del arrastre (tensión crítica en talud) [17] .
• Corrección por pendiente de fondo en transporte sólido (magnitud y dirección) [17] .
• Separación de tensiones de Einstein por formas de fondo y grano.
• Condiciones de contorno tipo sedimentograma (caudal sólido de fondo variable en tiempo).
• Condición de cota de fondo no erosionable (puntos fijos).

El transporte en suspensión se calcula resolviendo la ecuación de convección-difusión promediada en profundidad para la concentración de sedimento, incluyendo un término de deposición/resuspensión que modela el intercambio de sedimento entre el lecho y la carga en suspensión. Las principales características de este módulo son:

• Incorporación de transporte por difusión turbulenta.
• Término de deposición/resuspensión.
• Cálculo de la concentración de sedimento en suspensión según las formulaciones de:
• Van Rijn [18] .
• Smith McLean [19] .
• Ariathurai [20] .
• Cálculo de la velocidad de sedimentación de las partículas según van Rijn [18]
• Condición de contorno de concentración de sedimento en suspensión variable en tiempo.

En Iber es posible considerar el aporte de masa de agua generado por un episodio de precipitación variable en el tiempo y en el espacio. Para ello se pueden definir diferentes hietogramas en diferentes zonas del dominio de estudio. En la simulación de procesos de precipitación puede ser necesario considerar la infiltración de agua en el terreno no saturado. La modelización de la infiltración de agua superficial en el terreno es especialmente importante en la simulación de la transformación de lluvia en escorrentía. Para calcular la infiltración potencial se implementan 3 modelos de infiltración comúnmente utilizados: el modelo de Green-Ampt, el modelo de Horton y el modelo lineal.

Así mismo, Iber incorpora la posibilidad de realizar las simulaciones de manera que faciliten la delimitación de la vía de intenso desagüe, un requisito que la normativa española exige para los estudios de determinación de los mapas de inundabilidad.

3. Validaciones

En esta sección se presentan algunas validaciones experimentales del modelo Iber con el fin de mostrar las capacidades del modelo y la precisión que se puede esperar de sus resultados en diferentes tipos de aplicaciones.

3.1. Escala de peces de hendidura vertical

Una escala de peces es un dispositivo diseñado para posibilitar la migración de las especies piscícolas río arriba a través de obstáculos transversales como pueden ser azudes o presas. Las escalas de hendidura vertical consisten en un canal dividido en diferentes piscinas separadas por paredes verticales con una hendidura vertical a través de la cual los peces puedan desplazarse de piscina en piscina. En este tipo de escalas de peces las velocidades verticales son muy pequeñas excepto en la hendidura, y el campo de velocidad es muy homogéneo en profundidad, por lo que el flujo puede simularse adecuadamente con un modelo basado en las ecuaciones de St. Venant 2D. Debido a las elevadas pendientes de este tipo de dispositivos (habitualmente entre el 5 y el 10%) y a la elevada velocidad del agua en las hendiduras verticales, el flujo es altamente turbulento, y por lo tanto se hace indispensable utilizar un modelo de turbulencia tipo k-ɛ para una correcta modelización del campo de velocidades y de las zonas de recirculación que se producen en las piscinas [21] .

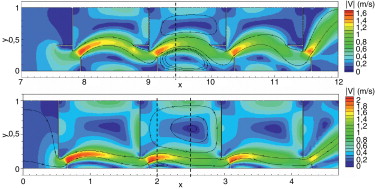
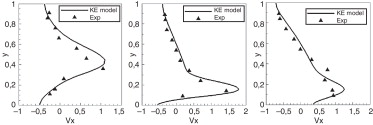
Para validar el modelo hidrodinámico y de turbulencia se modelizó el flujo en 2 diseños de escalas de hendidura vertical y se compararon los campos de velocidad con los obtenidos experimentalmente en Puertas et al. [22] . La figura 4 muestra la geometría de los diseños utilizados, así como el campo de velocidad y líneas de corriente calculadas para un caudal de 65 l/s. Para discretizar cada una de las geometrías que se muestran en la figura 4 se utilizó una malla no estructurada formada por aproximadamente 11.000 volúmenes finitos, con un tamaño medio de elemento de 4 cm² . Si se utiliza el modelo k-ɛ para calcular las tensiones turbulentas el modelo predice adecuadamente las zonas de recirculación y las velocidades máximas que se producen en las piscinas, como puede observarse en la comparación numérico experimental que se muestra en la figura 5 para 3 secciones transversales: una en el diseño T1 y 2 en el diseño T2.

Figura 4. Vista en planta de los campos de velocidad en 2 tipos de escala de peces de hendidura vertical. Diseños T1 (arriba) y T2 (abajo).

Figura 5. Secciones transversales de velocidad longitudinal, experimental y numérica, en diferentes secciones de la piscina. Diseño T1 en x = 9,46 m (izquierda), diseño T2 en x = 2,0 m (centro) y diseño T2 en x = 2,6 m (derecha).

3.2. Rotura de presa

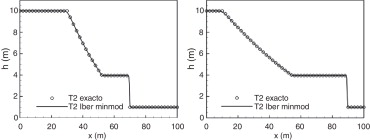
El cálculo de las zonas afectadas por la rotura total o parcial de una presa o de una balsa de contención es una posible aplicación de los modelos de aguas someras bidimensionales, que proporcionan en estos casos una buena relación entre precisión en los resultados y complejidad del modelo de cálculo. Un test utilizado habitualmente para evaluar la capacidad de un modelo numérico para resolver los cambios de régimen ligados a este tipo de problemas es el análisis de la rotura de presa instantánea unidimensional, para la cual existe solución analítica. Aunque el test de rotura instantánea unidimensional es geométricamente sencillo, desde el punto de vista numérico implica que el modelo debe ser capaz de resolver cambios de régimen y ondas de choque de forma estable y precisa. Los esquemas numéricos implementados en Iber (de tipo Godunov) son especialmente adecuados para el cálculo de este tipo de flujos. La figura 6 compara los resultados numéricos con la solución analítica para un test de rotura instantánea de presa 1D, considerando unos calados de 10 m y de 1 m a cada lado de la presa. Para el cálculo numérico se ha utilizado una malla de 200 elementos. Como puede observarse, el modelo es capaz de predecir con gran precisión la solución analítica, sin crear ningún tipo de inestabilidad numérica en la onda de choque.

Figura 6. Rotura de presa 1D instantánea. Perfiles longitudinales de calado en 2 instantes de tiempo calculados con Iber (línea continua) y solución analítica (círculos).

3.3. Cruce de calles

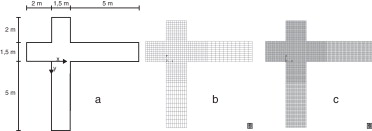
Durante un episodio de lluvia en una ciudad, una parte de la precipitación acaba circulando por la superficie de las calles y es un factor importante a tener en cuenta desde el punto de vista de la seguridad de vehículos y peatones. Los modelos de aguas someras en 2 dimensiones permiten obtener información de gran interés para la comprensión y análisis de este problema. Para comprobar la eficacia del modelo en este tipo de casos se realizó una validación experimental en la que se utilizó una instalación del Laboratorio de Modelos Reducidos de la Sección de Ingeniería Hidráulica e Hidrológica del Departamento de Ingeniería Hidráulica, Marítima y Ambiental de la Universitat Politècnica de Catalunya, construida para el estudio de la distribución de caudales en un cruce de calles [23] . La instalación consiste en 2 canales de 1,5 m de ancho que se cruzan perpendicularmente. La pendiente de los canales es variable excepto en la zona del cruce, donde la solera es horizontal. Los 2 canales disponen de alimentación de agua independiente, y existen vertederos para aforo del caudal tanto en las 2 entradas como en las 2 salidas. La geometría en planta de la instalación se puede observar en la figura 7 a.

Figura 7. a) Geometría en planta de la instalación del cruce de calles. b) Malla empleada para la campaña experimental. c) Malla para las simulaciones.

Para el estudio de los campos de calados y velocidades se realizó una campaña de medidas. El campo de velocidades se midió con la ayuda de un correntímetro electromagnético bidimensional. El mismo aparato sirvió para la determinación de niveles de agua utilizándolo a modo de limnímetro. Se tomaron medidas en un total de 720 puntos, con un espaciado de 0,15 m a lo ancho de las calles, también 0,15 m de espaciado longitudinal en la zona del cruce y 1,5 m aguas arriba y aguas abajo del mismo, y 0,30 m de espaciado longitudinal en el resto (fig. 7 b). Para la simulación numérica se utilizó una malla 3 veces más densa, pero de manera que cada punto de medida coincidiera con un volumen finito para facilitar la comparación, obteniéndose un total de 6.480 elementos (fig. 7 c).

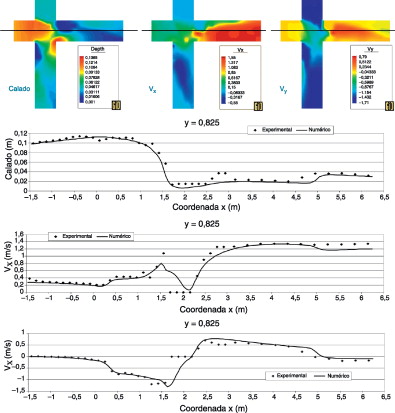
En la figura 8 se presenta la comparación numérico-experimental de calados y velocidades en forma de perfiles longitudinales por líneas paralelas al eje x de la instalación.

Figura 8. Comparación numérico-experimental según el eje x.

4. Aplicaciones

4.1. Cálculo de velocidades en un tramo de río con azud y escala de peces

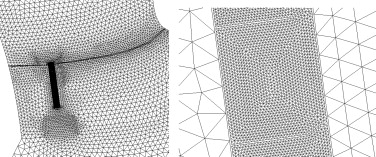
El uso de mallas no estructuradas formadas por elementos de 3 y 4 lados permite el mallado de geometrías complejas de manera muy eficiente. Esto resulta muy adecuado en problemas en los que existen patrones de flujo con escalas espaciales muy diferentes, ya que permite optimizar el número de elementos de la malla y su tamaño. En la figura 9 se muestran distintos detalles de la malla utilizada para el cálculo hidrodinámico de una tramo de río de aproximadamente 1 km de longitud en el que existe un azud con una escala de peces de hendidura vertical. La malla está compuesta por elementos de tamaños comprendidos desde los 100 cm² en las piscinas de la escala de peces, hasta los 100 m² en el cauce del río. De esta manera es posible calcular el funcionamiento hidráulico de la escala acoplado al del azud, para diferentes combinaciones de caudal del río y nivel de la lámina aguas abajo del azud. Esto permite evaluar al mismo tiempo el porcentaje de caudal del río que se desvía por la escala, el campo de velocidades y calados en las piscinas y el efecto llamada, todos ellos factores de los que depende el correcto funcionamiento de una escala de peces.

Figura 9. Malla de volúmenes finitos no estructurada. Vista general del azud y la escala (izquierda) y detalle de una de las piscinas de la escala (derecha).

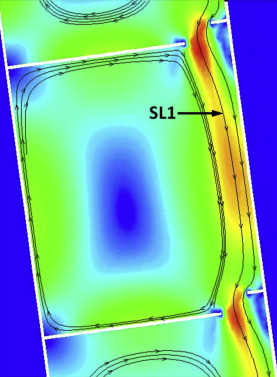
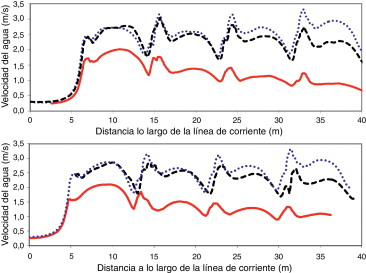
La velocidad del agua a lo largo de la línea de corriente SL1 (figura 10 ) que atraviesa la escala de peces, para caudales del río de 30 y 60 m³ /s, combinados con distintos niveles de la lámina aguas abajo del azud, se muestra en la figura 11 . Puede observarse claramente que la velocidad del agua es prácticamente independiente del caudal, lo cual es un comportamiento característico de las escalas de peces de hendidura vertical [22] , pero está influenciada de forma importante por el nivel de la superficie libre aguas abajo del azud, que en este caso viene determinada por el nivel de marea, por hallarse el azud muy próximo a la desembocadura del río.

Figura 10. Líneas de corriente en la escala de peces. SL1 indica la línea correspondiente a los perfiles de la figura 11 .

Figura 11. Velocidad del agua a lo largo de la línea de corriente SL1 que atraviesa la escala de peces para caudales del río de 30 m3 /s (arriba) y de 60 m3 /s (abajo). Niveles aguas abajo correspondientes a bajamar (puntos), marea media (líneas) y pleamar (continua).

4.2. Cálculo de zonas inundables en un tramo de río con un puente anegado

La resistencia al flujo que generan estructuras transversales al cauce de un río como vertederos, compuertas o tableros de puentes es de gran importancia en el cálculo de zonas inundables. En este ejemplo se calcula el campo de calados y velocidades en condiciones de avenida en un tramo del río Sarria (Lugo) en el cual existe un puente. En el tramo considerado existen además motas de encauzamiento que se deben considerar en el modelo numérico.

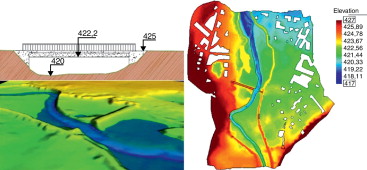
Para modelizar los efectos del puente se introducen los taludes transversales y estribos como una sobreelevación del MDT utilizado en el modelo (fig. 12 ). El tablero se introduce mediante una condición interna tipo combinación compuerta-vertedero, de forma que en caso de que la lámina de agua toque la parte inferior del tablero, el caudal que pasa bajo el tablero se calcula mediante una ecuación de descarga tipo compuerta, y si el agua supera la cota superior del tablero, el caudal que pasa sobre el tablero se calcula mediante una ecuación de descarga tipo vertedero (tabla 2 ).

Figura 12. Sección transversal con vista 3D del talud del puente (izquierda), y MDT utilizado en el modelo numérico donde puede observarse el trazado de las motas de protección frente a inundaciones (derecha).

Respecto a las motas longitudinales de encauzamiento, en el caso de que puedan ser rebasadas por el agua debido a que su cota de coronación no es lo suficientemente elevada, es necesario introducirlas como parte del MDT (fig. 12 ). En este caso es necesario que los elementos de la malla en torno a la mota sean lo suficientemente finos como para definir en detalle la coronación de la mota; en caso contrario, el error en los resultados puede ser importante. En caso de que las motas no vayan a ser superadas por el agua pueden modelizarse como contornos tipo pared, en cuyo caso la malla de cálculo únicamente se extiende en la zona comprendida entre motas (fig. 13 ).

Figura 13. Extensión de la inundación y altura de la lámina de agua calculada considerando motas rebasables definidas mediante una sobreelevación del MDT (izquierda) y motas no rebasables definidas como contornos tipo pared (derecha).

El cálculo de zonas inundables se realiza para un caudal de 370 m³ /s correspondiente a un período de retorno de 100 años. El coeficiente de Manning se fija a 0,03 en el cauce principal y 0,05 en las llanuras de inundación. En la figura 13 se muestra la extensión de la zona inundada calculada con 2 modelos en los que se han introducido respectivamente las motas como condiciones de contorno tipo pared (motas no rebasables) y como sobreelevación del MDT (motas rebasables). Para el caudal de cálculo considerado la hipótesis de mota no rebasable es correcta en la margen izquierda pero no en la margen derecha, donde la altura de la mota es inferior al nivel alcanzado por el agua. En la figura 13 puede observarse claramente el efecto sobre el flujo generado por el puente, que produce sobreelevaciones de la lámina de agua del orden de 3 m.

4.3. Canal de eslalon dentro del cauce de un río

Dentro de un proyecto de recuperación del río Segre, en Cataluña, tras las afecciones a este río debidas al proyecto de la presa de Rialb, se llevó a cabo el estudio hidráulico del río en el entorno del canal de eslalon de Ponts (Noguera), que se encuentra a unos 3 km aguas abajo de la presa [24] . Para la delimitación del canal de eslalon se dispone una estructura longitudinal de escollera en el centro del río, con el objetivo de dividir el cauce en 2 zonas: el canal de eslalon por la derecha y el retorno por la izquierda. En el lado correspondiente al canal de eslalon se disponen otras estructuras de escollera para conseguir el flujo adecuado para la práctica del piragüismo. La complejidad de la geometría suponía un reto para la creación de la malla así como para el cálculo hidrodinámico. La discretización del campo de eslalon se realizó mediante una malla irregular, con unas zonas de malla estructurada en cuadriláteros y otras de malla no estructurada de elementos triangulares. El número total de elementos de la malla es de 19.062. En la figura 14 se puede ver un detalle.

Figura 14. Detalle de la malla de cálculo del canal de piragüismo.

El coeficiente de rugosidad de Manning utilizado en el cálculo bidimensional es n = 0,028. Este coeficiente es inferior al que se utilizaría en un cálculo unidimensional debido a que la resistencia ocasionada por la geometría de los bloques de escollera está implícitamente considerada al introducir en detalle la geometría de dichos bloques. La condición de contorno aguas arriba es el caudal de estudio, y aguas abajo se determinó la cota de la lámina de agua a imponer con un cálculo en régimen permanente del tramo aguas abajo.

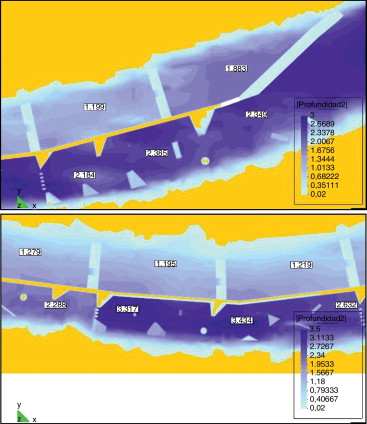
Dos de los objetivos del estudio eran asegurar que para el caudal de estudio (33 m³ /s, que corresponde a la dotación del Canal d’Urgell más el caudal ecológico) dos terceras partes pasen por el canal de eslalon (derecha del dique central) y el resto por el canal de retorno (izquierda), y también conocer aproximadamente el flujo (calados y velocidades) en el canal de eslalon y el canal de retorno para comprobar que son adecuados para la práctica del piragüismo. Los resultados indican que las estructuras transversales de escollera provocan un cierto escalonado de la lámina de agua. Ello es así ya que los límites entre los tramos están formados por estrechamientos que producen la aceleración del flujo hacia aguas abajo y una sobreelevación de la lámina hacia aguas arriba, como se puede apreciar en la figura 15 . Un escalonado similar se produce en el canal de retorno, debido a las estructuras transversales.

Figura 15. Calados en el canal de eslalon con las geometrías de escolleras propuesta.

4.4. Estudio del efecto de una infraestructura en los niveles de inundación

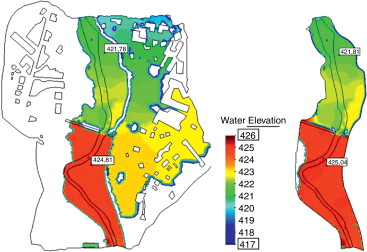
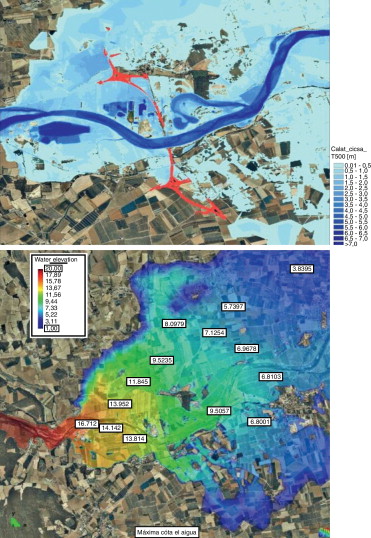
Una de las aplicaciones habituales de los modelos hidrodinámicos bidimensionales es el estudio de la influencia de las infraestructuras en los niveles de agua y extensión de la inundación en zonas llanas. La figura 16 muestra el tipo de resultados que se puede obtener con Iber en un estudio de este tipo, correspondiente al efecto de la carretera C-31 en la inundación del río Fluvià. A la izquierda se muestran calados en formato GIS y a la derecha la cota de la lámina de agua. En este caso el estudio se realizó en régimen variable, utilizando un hidrograma con un caudal punta de 3.390 m³ /s y una malla RTIN.

Figura 16. Estudio de los efectos hidráulicos de una nueva carretera sobre el río Fluvià.

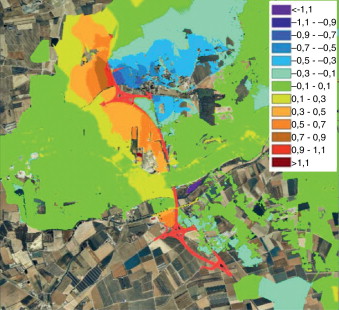
Una de las características de Iber es la exportación de resultados en distintos formatos, entre ellos el formato ASCII de ArcInfo, que permite obtener y tratar los resultados en un entorno GIS y comparar el funcionamiento hidráulico de distintos escenarios. De esta manera, en la figura 17 se observan las diferencias en la cota de la lámina de agua (sobreelevaciones) obtenidas con 2 geometrías distintas pero utilizando la misma malla de base.

Figura 17. Comparación de escenarios. La leyenda indica diferencias en la cota de la lámina de agua.

5. Conclusiones

El uso del método de volúmenes finitos para el cálculo del flujo de agua, sedimentos y turbulencia se ha mostrado adecuado para el desarrollo de una herramienta de aplicación en la resolución de problemas ingenieriles. Iber resuelve las ecuaciones de la hidrodinámica, la turbulencia y el transporte de sedimentos con esquemas explícitos descentrados, lo que lo hace particularmente eficaz para el cálculo de flujos discontinuos (resaltos hidráulicos, frentes de onda), pero sin quitarle capacidad ni precisión en zonas con soluciones más suaves como es el flujo en un estuario.

Los esquemas numéricos utilizados en Iber se han integrado en una potente interfaz de preproceso y posproceso como es GiD, constituyendo el conjunto una herramienta efectiva para dar respuesta a los requerimientos actuales, en cuanto a modelización numérica de procesos fluviales, de la legislación española.

Agradecimientos

A los autores les gustaría agradecer al Laboratorio de Hidráulica del Centro de Estudios Hidrográficos del CEDEX, en especial a su director Luis Balairón y a los investigadores Ángel Lara, David López y Juan José Rebollo, por su confianza en el proyecto y su colaboración.

Bibliografía

1. [1] M.E. Vázquez-Cendón; Improved treatment of source terms in upwind schemes for the shallow water equations in channels with irregular geometry; J. Comput. Phys., 148 (1999), pp. 497–526
2. [2] E.F. Toro; Riemann Solvers and Numerical Methods for Fluid Dynamics. A Practical Introduction; Springer Verlag, Berlin (2009)
3. [3] L. Cea, J. Puertas, M.-E. Vázquez-Cendón; Depth averaged modelling of turbulent shallow water flow with wet-dry fronts; Arch. Comput. Methods Eng., 14 (2007), pp. 303–341
4. [4] E. Bladé, M. Gómez, M. Sánchez-Juny, J. Dolz; Preserving steady-state in one-dimensional finite-volume computations of river flow; J. Hydraul. Eng., 134 (2008), pp. 1343–1347
5. [5] W.C. Van Dorn; Wind stress on an artificial pond; J. Mar. Res., 12 (1953), pp. 249–276
6. [6] A.K. Rastogi, W. Rodi; Predictions of heat and mass transfer in open channels; J. Hydraul. Div. - ASCE, 104 (1978), pp. 397–420
7. [7] A. Bermúdez, A. Dervieux, J.-A. Desideri, M.E. Vázquez; Upwind schemes for the two-dimensional shallow water equations with variable depth using unstructured meshes; Comp. Meth. Appl. Mech. Eng., 155 (1998), pp. 49–72
8. [8] R.J. LeVeque; Finite Volume Methods for Hyperbolic Problems; Cambridge University Press, Cambridge (2002)
9. [9] P.L. Roe; Discrete models for the numerical analysis of time-dependent multidimensional gas dynamics; J. Compt. Phys., 63 (1986), pp. 458–476
10. [10] R. Ribó, M. Pasenau, E. Escolano, J. Pérez, A. Coll, A. Melendo, et al.; GiD Reference Manual; CIMNE, Barcelona (2007)
11. [11] R. Ribó, M. Pasenau, E. Escolano, J. Pérez, A. Coll, A. Melendo, et al.; GiD User Manual; CIMNE, Barcelona (2007)
12. [12] R. Ribó, M. Pasenau, E. Escolano, J. Pérez, A. Coll, A. Melendo, et al.; GiD Customization Manual; CIMNE, Barcelona (2007)
13. [13] G. Corestein, E. Bladé, L. Cea, A. Lara, E. Escolano, A. Coll; Iber, a river dynamics simulation tool; M. Pasenau, E. Escolano, J. Suit, A. Coll, A. Melendo, A. Monros (Eds.), et al. , GiD 2010. 5th Conference on Advances and Applications of GID. Monografía CIMNE M118, International Center for Numerical Methods and Engineering, Barcelona (2010), p. 87
14. [14] W. Evans, D. Kirkpatrick, G. Townsend; Right-triangulated irregular networks; Algorithmica, 30 (2001), pp. 264–286
15. [15] M. Wong, G. Parker; Reanalysis and correction of bedload relation of Meyer Peter and Müller using their own database; J. Hydraul. Eng., 132 (2006), p. 1159
16. [16] L.C. van Rijn; Sediment transport. Part I: Bed load transport; J. Hydraul. Eng., 110 (1984), p. 1431
17. [17] D.D. Apsley, P.K. Stansby; Bed-load sediment transport on large slopes: model formulation and implementation within a RANS solver; J. Hydraul. Eng., 134 (2008), p. 1440
18. [18] L.C. van Rijn; Sediment transport. Part II: Suspended load transport; J. Hydraul. Eng., 110 (1984), p. 1613
19. [19] M.H. Garcia; Sedimentation Engineering: Processes, Measurements, Modeling and Practice. ASCE Manuals and Reports on Engineering Practice No. 110; American Society Civil Engineering Publications (2008)
20. [20] R. Ariathurai, K. Arulanandan; Erosion rates of cohesive soils; J. Hydraul. Div., 104 (1978), pp. 279–283
21. [21] L. Cea, L. Pena, J. Puertas, M.-E. Vázquez-Cendón, E. Peña; Application of several depth averaged turbulence models to simulate flow in vertical slot fishways; J. Hydraul. Eng., 133 (2007), pp. 160–172
22. [22] J. Puertas, L. Pena, T. Teijeiro; An experimental approach to the hydraulics of vertical slot fishways; J. Hydraul. Eng., 130 (2004), pp. 10–23
23. [23] L.S. Nanía Escobar; Metodología Numérico-Experimental para el Análisis del Riesgo Asociado a la Escorrentía Pluvial en una Red de Calles; Universitat Politècnica de Catalunya, Barcelona (1999)
24. [24] Estudio Hidráulico del Río Segre en el Entorno del Canal de Eslalon de Ponts (Noguera); DEHMA, Barcelona (2003)