Simultaneous effects of slip and MHD on peristaltic blood flow of Jeffrey fluid model through a porous medium

Abstract

In this article, the simultaneous effects of slip and Magnetohydrodynamics (MHD) on peristaltic blood flow of Jeffrey fluid model have been investigated in a non-uniform porous channel. The governing equation of blood flow for Jeffrey fluid model is solved with the help of long wavelength and creeping flow regime. The solution of the resulting differential equation is solved analytically and a closed form solution is presented. The impact of all the physical parameters is plotted for velocity profile and pressure rise. Nowadays, Magnetohydrodynamics is applicable in various magnetic drug targeting for cancer diseases and also very helpful to control the flow. The present analysis is also described for Newtonian fluid ${\textstyle \left({\lambda }_{1}\rightarrow 0\right)}$ as a special case of our study. It is observed that magnitude of the velocity is opposite near the walls due to slip effects whereas similar behavior has been observed for magnetic field.

Keywords

Magnetohydrodynamics; Blood flow; Slip effects; Jeffrey fluid; Porous medium

Nomenclature

${\textstyle {\tilde {u}}{\mbox{,}}{\tilde {v}}}$- axial and transverse velocity

${\textstyle {\tilde {x}}{\mbox{,}}{\tilde {y}}}$- coordinate axis

${\textstyle {\tilde {p}}}$- pressure

M- Hartmann number

${\textstyle B_{0}}$- magnetic field

${\textstyle b({\tilde {x}})}$- half width of the channel

${\textstyle K\left(\ll 1\right)}$- constant

${\textstyle C}$- wave velocity

${\textstyle {\tilde {t}}}$- time

${\textstyle {\tilde {a}}}$- wave amplitude

${\textstyle A_{1}}$- Rivilin-Erickson tensor

k- porosity parameter

${\textstyle S}$- stress tensor

Greek symbols

${\textstyle \delta }$- wave number

${\textstyle \phi }$- amplitude ratio

${\textstyle \lambda }$- wavelength

${\textstyle \mu }$- dynamic viscosity

${\textstyle \rho }$- fluid density

${\textstyle \beta }$- slip parameter

${\textstyle {\lambda }_{1}}$- ratio b/w relaxation to retardation time

${\textstyle {\lambda }_{2}}$- delay time

${\textstyle \gamma }$- shear rate

1. Introduction

Blood flow (or Hemodynamics) problems have received a considerable attention due to its major importance in physio-pathology. For a long time, blood is treated as a vital fluid. Blood circulation performs various types of function in a human body such as transport of nutrients, transport of oxygen, removal of metabolic products and removal of carbon dioxide. Blood circulation is divided into three types such as capillary circulation, systemic circulation and microcirculation. Blood consists of various types of formed elements and plasma which includes red blood cells (RBC), white blood cells (WBC) and platelets. In normal circumstances, blood depicts laminar characteristics, that is why, the velocity of the blood is higher in the middle of the vessel/channel as compared to the walls. Velocity of the blood can be measured in different ways like laser Doppler anemometry or video-capillary micro-scoping with frame to frame analysis. Several authors investigated blood flow problems in various geometrical aspects with different biological fluids [1], [2], [3], [4], [5] and [6].

On the other hand, Magnetohydrodynamics is also very helpful and applicable in different magnetic drug targeting like cancer diseases etc. Magnetohydrodynamics is also applicable in various engineering problems such as electromagnetic casting, liquid–metal cooling of nuclear reactors, continuous casting process of metals and plasma confinement. The decrements in blood pressure may cause to reduce the flow rate of blood and also it is noticed that the blood flow is affected by the presence of magnetic field because the red blood cell is a major bio-magnetic substance. In view of the above discussion many researchers studied MHD by developing different modeling. Investigation on blood flow under the external applied magnetic field has been reported by Sinha and Misra [7]. Sud et al. [8] analyzed the effect of a moving magnetic field on blood. Very recently researchers investigated nanoparticles separation technology which shows that magnetic field can be used to isolate a wide range of nano particles out of plasma with a minimum amount of manipulation [9]. Moreover, it should be noted that flow of blood in a porous artery is significantly influenced by the external magnetic field. In fact, the ratio between the total volume of the medium and volume of the void space is referred as porosity. Porous medium is considered as a material volume that contains a solid matrix with an interconnected void.

Peristaltic flow is also an important mechanism that can be found in a human body. It is generally a contraction and suspension of smooth muscles in a living body such as digestive system, urine transport from kidney to bladder, chyme in the gastrointestinal tract and vasomotion of tiny blood vessels. Different Mechanical devices work on the principle of peristalsis such as finger pumps, heart lung machine and roller pumps. Mekheimer and Al-Arabi [10] investigated the nonlinear peristaltic motion of MHD flow through a porous medium. Later, Mekheimer [11] again considered the effects of magnetic field on peristaltic blood flow of couple stress fluid in a non-uniform channel. He analyzed that the pressure behaves as an increasing function due to magnetic field while its behavior seems opposite for couple stress fluid parameter. Akbar [12] analyzed the blood flow of Prandtl fluid model in tapered stenosed arteries. Sreenadh et al. [13] discussed the pumping characteristics of peristaltic flow of Jeffrey fluid in an inclined channel having permeable walls. Ramesh and Devakar [14] studied the slip effects for the flows of Casson fluid model and obtained the analytic solutions. Extensive literature on the present topic can be found from the references [15], [16], [17], [18], [19], [20], [21], [22], [23] and [24].

A review on the literature bears witness that in various blood flow problems, less attention has been given to investigate the flows in the presence of slip. However, the effects of slip can be found in various applications such as internal cavities and polishing of artificial heart valves. The slip effects are divided into two types namely, rare field gases and fluid having elastic characteristics. Akbar et al. [25] studied the heat transfer on peristaltic flow of Williamson fluid model in an inclined asymmetric channel under the influence of slip condition. Recently, Akbar et al. [26] examined the thermal and velocity slip effects on peristaltic flow with carbon nanotubes in an asymmetric channel under the effects of magnetic field. Adesanya [27] investigated the velocity slip and temperature jump on free convective flow of heat generating fluid through a porous vertical channel. Some pertinent studies on the present topic can be found from the list of Refs. [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40], [41], [42], [43], [44], [45], [46], [47] and [48] and therein.

With the above analysis in mind, the aim of this present study was to analyze the slip effects on MHD peristaltic blood flow of Jeffrey fluid through a non-uniform porous channel. This analysis may provide a good understanding about blood flow in a diseased blood vessel and also beneficial under various pathological situation. The governing equation of blood flow for Jeffrey fluid model is obtained with the help of continuity equation and momentum equation. The resulting differential equation is solved analytically by taking the approximation of long wavelength and creeping flow regime. The impact of all the physical parameters is plotted and discussed. Mathematical and graphical comparison has also been made between Newtonian and non-Newtonian fluid. This paper is summarized as follows: after the introduction in Sections 1 and 2 characterizes the mathematical formulation of the problem, while Section 3 describes the solution methodology and finally, Section 4 is devoted to numerical results and discussion.

2. Mathematical formulation

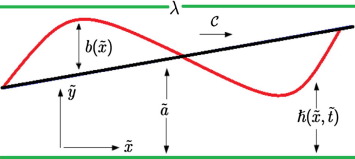
Let us consider the peristaltic motion of Jeffrey fluid (treated as Blood) through a two dimensional non-uniform channel with sinusoidal wave propagating toward down of its walls. The fluid is electrically conducting in such a way that, an external magnetic field ”${\textstyle B_{0}}$” is applied to it. Cartesian coordinate system is selected in such a way that ${\textstyle {\tilde {x}}-}$axis is considered along the center line in the direction of wave propagation and ${\textstyle {\tilde {y}}-}$axis is transverse to it (see Fig. 1). The geometry of the wall surface is defined as

$\hslash ({\tilde {x}}{\mbox{,}}{\tilde {t}})=b({\tilde {x}})+$${\tilde {a}}sin{\frac {2\pi }{\lambda }}({\tilde {x}}-C{\tilde {t}}){\mbox{,}}$

(1)

where

$b({\tilde {x}})=b_{0}+K{\tilde {x}}{\mbox{.}}$

(2)

Figure 1. Geometry of the flow problem.

The governing equation of continuity and momentum equation for incompressible, irrotational laminar Blood flow of Jeffrey fluid model in the presence of applied magnetic field can be written as

${\frac {\partial {\tilde {u}}}{\partial {\tilde {x}}}}+{\frac {\partial {\tilde {v}}}{\partial {\tilde {y}}}}=$$0{\mbox{,}}$

(3)

$\rho \left({\frac {\partial {\tilde {u}}}{\partial {\tilde {t}}}}+\right.$$\left.{\tilde {u}}{\frac {\partial {\tilde {u}}}{\partial {\tilde {x}}}}+\right.$$\left.{\tilde {v}}{\frac {\partial {\tilde {u}}}{\partial {\tilde {y}}}}\right)+$${\frac {\partial {\tilde {p}}}{\partial {\tilde {x}}}}=\mu \left({\frac {\partial S_{{\tilde {x}}{\tilde {x}}}}{\partial {\tilde {x}}}}+\right.$$\left.{\frac {\partial S_{{\tilde {x}}{\tilde {y}}}}{\partial {\tilde {y}}}}\right)-$$\sigma B_{0}{\tilde {u}}-{\frac {\mu }{\overline {k}}}{\tilde {u}}{\mbox{,}}$

(4)

$\rho \left({\frac {\partial {\tilde {v}}}{\partial {\tilde {t}}}}+\right.$$\left.{\tilde {u}}{\frac {\partial {\tilde {v}}}{\partial {\tilde {x}}}}+\right.$$\left.{\tilde {v}}{\frac {\partial {\tilde {v}}}{\partial {\tilde {y}}}}\right)+$${\frac {\partial {\tilde {p}}}{\partial {\tilde {y}}}}=\mu \left({\frac {\partial S_{{\tilde {y}}{\tilde {x}}}}{\partial {\tilde {x}}}}+\right.$$\left.{\frac {\partial S_{{\tilde {y}}{\tilde {y}}}}{\partial {\tilde {y}}}}\right)-$$\sigma B_{0}{\tilde {v}}-{\frac {\mu }{\overline {k}}}{\tilde {v}}{\mbox{.}}$

(5)

The stress tensor for the Jeffrey fluid is defined as

$S={\frac {\mu }{1+{\lambda }_{1}}}\left({\overset {\cdot }{\gamma }}+\right.$$\left.{\lambda }_{2}{\ddot {\gamma }}\right){\mbox{.}}$

(6)

Now, it is convenient to define the non-dimensional quantities

${\begin{array}{rl}&x={\frac {\tilde {x}}{\lambda }}{\mbox{,}}\quad y={\frac {\tilde {y}}{b_{0}}}{\mbox{,}}\quad t={\frac {C{\tilde {t}}}{\lambda }}{\mbox{,}}\quad u={\frac {\tilde {u}}{C}}{\mbox{,}}\quad v={\frac {\tilde {v}}{C\delta }}{\mbox{,}}\quad p={\frac {{\tilde {p}}b_{0}^{2}}{\mu \lambda C}}{\mbox{,}}\quad h={\frac {\hslash }{b_{0}}}{\mbox{,}}\quad \phi ={\frac {\tilde {a}}{b_{0}}}{\mbox{,}}\quad \nu ={\frac {\mu }{\rho }}{\mbox{,}}\\&Re={\frac {\rho Cb_{0}}{\mu }}{\mbox{,}}\quad S={\frac {b_{0}}{\mu C}}S{\mbox{,}}\quad \delta ={\frac {b_{0}}{\lambda }}{\mbox{,}}\quad k={\frac {\overline {k}}{b_{0}}}{\mbox{,}}\quad {\overset {\cdot }{\gamma }}={\frac {{\overset {\cdot }{\gamma }}b_{0}}{C}}{\mbox{,}}\quad M={\sqrt {\frac {\sigma }{\mu }}}B_{0}b_{0}{\mbox{.}}\end{array}}$

(7)

Let us consider the assumption of long wavelength ${\textstyle \left(0\ll \lambda \rightarrow \infty \right)}$ and low Reynolds number ${\textstyle \left(Re\rightarrow 0\right)}$ approximations. Using Eq. (7) in Eqs. (3), (4), (5) and (6) we get the resulting equations in simplified form

${\frac {\partial p}{\partial x}}={\frac {1}{1+{\lambda }_{1}}}{\frac {{\partial }^{2}u}{\partial y^{2}}}-$$M^{2}u-{\frac {1}{k}}u{\mbox{,}}$

(8)

subject to their respective slip boundary conditions

${\begin{array}{rl}&{\frac {\partial u}{\partial y}}=0{\mbox{,}}\quad y=0{\mbox{,}}\\&u(y)+\beta {\frac {\partial u}{\partial y}}=0{\mbox{,}}\quad y=h{\mbox{,}}\end{array}}$

(9)

where ${\textstyle h=1+{\frac {Kx\lambda }{b_{0}}}+\phi sin2\pi (x-t)}$.

3. Solution of the problem

The exact solution of Eq. (8) can be written as

$u(y)={\frac {dp/dx\left(cosh\quad Ny{\sqrt {1+{\lambda }_{1}}}-cosh\quad Nh{\sqrt {1+{\lambda }_{1}}}-{\sqrt {1+{\lambda }_{1}}}N\beta sinh\quad Nh{\sqrt {1+{\lambda }_{1}}}\right)}{N^{2}\left(cosh\quad Nh{\sqrt {1+{\lambda }_{1}}}+{\sqrt {1+{\lambda }_{1}}}N\beta sinh\quad Nh{\sqrt {1+{\lambda }_{1}}}\right)}}{\mbox{.}}$

(10)

The instantaneous volume rate is defined as

$Q(x{\mbox{,}}t)={\int }_{0}^{h}u(y)dy{\mbox{.}}$

(11)

The pressure gradient can be calculated with the help of above equation, and we get

${\frac {dp}{dx}}=-{\frac {dp/dx\left(h{\sqrt {1+{\lambda }_{1}}}N\quad cosh\quad N\quad h{\sqrt {1+{\lambda }_{1}}}+(-1+h(1+{\lambda }_{1})N^{2}\beta )sinh\quad N\quad h{\sqrt {1+{\lambda }_{1}}}\right)}{{\sqrt {1+{\lambda }_{1}}}N^{3}\left(cosh\quad N\quad h{\sqrt {1+{\lambda }_{1}}}+{\sqrt {1+{\lambda }_{1}}}N\quad \beta sinh\quad N\quad h{\sqrt {1+{\lambda }_{1}}}\right)}}{\mbox{,}}$

(12)

where

$N={\sqrt {M^{2}+{\frac {1}{k}}}}{\mbox{.}}$

(13)

The non dimensional form of Pressure rise ${\textstyle \left(\Delta P_{L}\right)}$ at the wall along the whole length of the non-uniform channel ${\textstyle \left(L\right)}$ is given by

$\Delta P_{L}={\int }_{0}^{L/\lambda }\left({\frac {dp}{dx}}\right)dx{\mbox{.}}$

(14)

3.1. Special case: Newtonian fluid

The above results can be reduced to Newtonian fluid by taking ${\textstyle {\lambda }_{1}\rightarrow 0}$ in Eq. (10) as a special case of our study. The solution of velocity profile for Newtonian fluid can be written as

$u(y)={\frac {dp/dx\left(cosh\quad Ny-cosh\quad Nh-N\beta sinh\quad Nh\right)}{N^{2}\left(cosh\quad Nh+N\beta sinh\quad Nh\right)}}{\mbox{,}}$

(15)

and with no-slip effects ${\textstyle \left(\beta =0\right)}$, it can be written as

$u(y)={\frac {dp/dx\left(cosh\quad Ny-cosh\quad Nh\right)}{N^{2}\left(cosh\quad Nh\right)}}{\mbox{.}}$

(16)

4. Numerical results and discussion

In this section, the graphical and numerical results of all the pertinent parameters are discussed and plotted for velocity profile and pressure rise against slip parameter ${\textstyle \left(\beta \right)}$, Hartmann number ${\textstyle \left(M\right)}$ and porosity parameter ${\textstyle \left(k\right)}$. Numerical computation has been used to evaluate the expression of pressure rise for the following parametric values: ${\textstyle K=5\times {10}^{-5}{\mbox{,}}L/\lambda =1\quad cm{\mbox{,}}\quad b_{0}=}$$1\times {10}^{-2}\quad cm$. The volume flow rate ${\textstyle Q(x{\mbox{,}}t)}$ is periodic in ${\textstyle \left(x-t\right)}$ and it can be written as

$Q={\overline {Q}}+\phi sin2\pi \left(x-t\right){\mbox{.}}$

(17)

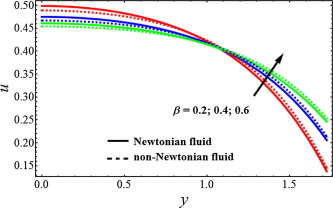
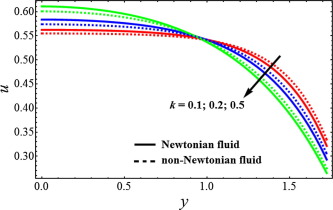
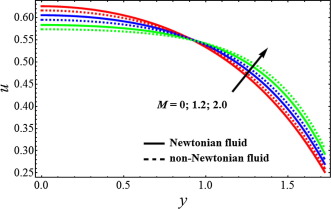
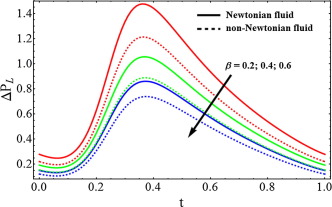
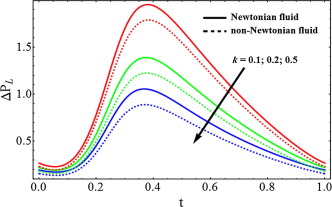
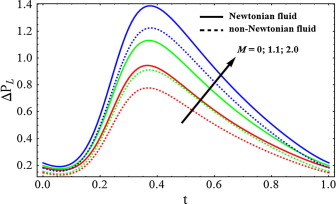
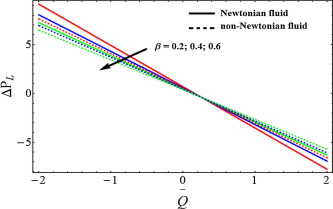
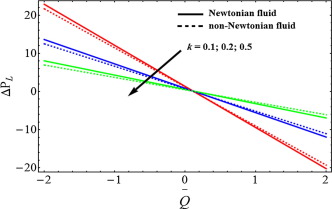
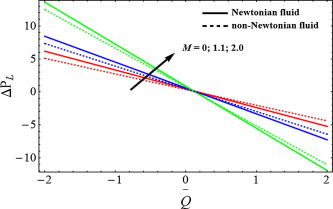
Figure 2, Figure 3 and Figure 4 is sketched for velocity profile against Newtonian and non-Newtonian fluid. It is depicted from Fig. 2 that when the slip parameter ${\textstyle \left(\beta \right)}$ increases, then the velocity profile shows opposite behavior near the walls of the channel while the velocity for Newtonian fluid case is lower. From Fig. 3, we can analyze that due to porosity parameter ${\textstyle \left(k\right)}$, the velocity of the fluid behaves as an decreasing function near the wall of the channel. It can be observed from Fig. 4 that when the Hartmann number ${\textstyle \left(M\right)}$ increases the velocity of the fluid decreases. Figure 5, Figure 6 and Figure 7 has been plotted for pressure rise. The maximum pressure rise can be achieved by taking ${\textstyle {\overline {Q}}=0}$, in Eq. (17). It is depicted from Fig. 5 that due to slip effects the pressure decreases, while the pressure rise for Newtonian case is higher in magnitude as compared to non-Newtonian fluid. Fig. 6 shows the variation of Weissenberg number ${\textstyle \left(We\right)}$ on pressure rise. It can be noticed from this figure that the pressure rise decreases due to increment in the porosity parameter ${\textstyle \left(k\right)}$. It can be visualized from Fig. 7 that when the Hartmann number ${\textstyle \left(M\right)}$ increases, the pressure rise increases. To understand the pumping characteristics on blood flow, Figure 8, Figure 9 and Figure 10 is sketched. It can be noticed from Fig. 8 that due to slip effects the pumping rate decreases in retrograde pumping region ${\textstyle \left(\Delta P_{L}>0{\mbox{,}}{\overline {Q}}<0\right)}$, while its behavior has been observed opposite in co-pumping region ${\textstyle \left(\Delta P_{L}<0{\mbox{,}}{\overline {Q}}>0\right)}$. It can also be observed from Fig. 9 that the pumping rate increases when the porosity parameter ${\textstyle \left(k\right)}$ increases in co-pumping region ${\textstyle \left(\Delta P_{L}<0{\mbox{,}}{\overline {Q}}>0\right)}$, whereas pumping rate decreases in retrograde pumping region ${\textstyle \left(\Delta P_{L}>0{\mbox{,}}{\overline {Q}}<0\right)}$. It can be scrutinized from Fig. 10 due to effects of Hartmann number ${\textstyle \left(M\right)}$, the pumping rate increases in retrograde pumping region ${\textstyle \left(\Delta P_{L}>0{\mbox{,}}{\overline {Q}}<0\right)}$, but its behavior starts changing in co-pumping region and opposite behavior has been observed.

Figure 2. Velocity profile for different values of slip parameter ${\textstyle \left(beta\right)}$, when ${\textstyle M=1{\mbox{,}}k=0.5{\mbox{,}}\phi =0.6}$.

Figure 3. Velocity profile for different values of porosity parameter ${\textstyle \left(k\right)}$, when ${\textstyle M=1{\mbox{,}}\beta =0.4{\mbox{,}}\phi =0.6}$.

Figure 4. Velocity profile for different values of Hartmann number ${\textstyle \left(M\right)}$, when ${\textstyle \beta =0.4{\mbox{,}}k=0.5{\mbox{,}}\phi =0.6}$.

Figure 5. Pressure rise for different values of slip parameter ${\textstyle \left(\beta \right)}$, when ${\textstyle M=1{\mbox{,}}k=0.5{\mbox{,}}\phi =0.6}$.

Figure 6. Pressure rise for different values of porosity parameter ${\textstyle \left(k\right)}$, when ${\textstyle M=1{\mbox{,}}\beta =0.4{\mbox{,}}\phi =0.6}$.

Figure 7. Pressure rise for different values of Hartmann number ${\textstyle \left(M\right)}$, when ${\textstyle \beta =0.4{\mbox{,}}k=0.5{\mbox{,}}\phi =0.6}$.

Figure 8. Pressure rise vs   average volume flow rate for different values of slip parameter ${\textstyle \left(\beta \right)}$, when ${\textstyle M=1{\mbox{,}}k=0.5{\mbox{,}}\phi =0.6}$.

Figure 9. Pressure rise vs   average volume flow rate for different values of porosity parameter ${\textstyle \left(k\right)}$, when ${\textstyle M=1{\mbox{,}}\beta =0.4{\mbox{,}}\phi =0.6}$.

Figure 10. Pressure rise vs   average volume flow rate for different values of Hartmann number ${\textstyle \left(M\right)}$, when ${\textstyle \beta =0.4{\mbox{,}}k=0.5{\mbox{,}}\phi =0.6}$.

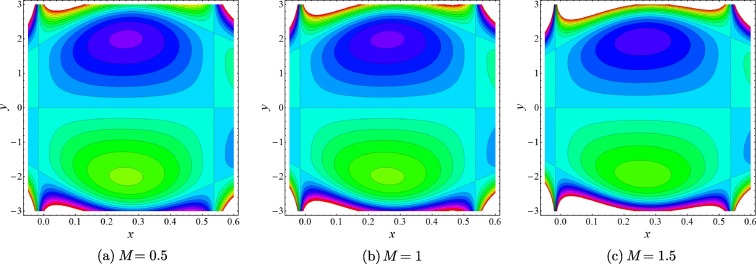
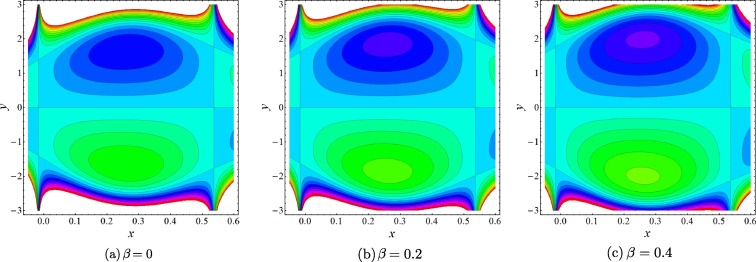
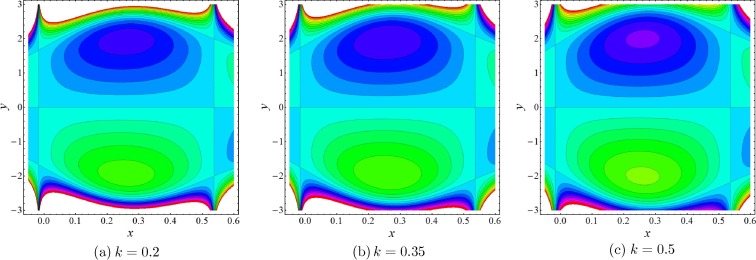
The next most engrossing mechanism of peristaltic blood flow is trapping which is taken under consideration by drawing stream lines against various physical parameters. For this purpose Figure 11, Figure 12 and Figure 13 has been plotted. It is generally a formulation of internally circulating bolus that is enclosed by various stream lines. stream lines are very helpful to understand the relation between velocity and pressure in an inviscid fluid. It is depicted from Fig. 11 that when the Hartmann number ${\textstyle \left(M\right)}$ increases the magnitude of the bolus decreases slowly whereas the bolus also reduces in numbers. It can be noticed from Fig. 12 that when the slip parameter ${\textstyle \left(\beta \right)}$ increases the number of trapping bolus increases. From Fig. 13, we can observe that due to porosity parameter ${\textstyle \left(k\right)}$, the size of the trapping bolus increases, while the number of bolus also increases.

Figure 11. Stream lines for various values of Hartmann number ${\textstyle \left(M\right)}$, when ${\textstyle \phi =0.6{\mbox{,}}\beta =0.4{\mbox{,}}k=0.5}$.

Figure 12. Stream lines for various values of slip parameter ${\textstyle \left(\beta \right)}$, when ${\textstyle \phi =0.6{\mbox{,}}k=0.5{\mbox{,}}M=1}$.

Figure 13. Stream lines for various values of porosity parameter ${\textstyle \left(k\right)}$, when ${\textstyle \phi =0.6{\mbox{,}}\beta =0.4{\mbox{,}}M=1}$.

5. Conclusion

In this article, the simultaneous effects of slip and MHD on blood flow of Jeffrey fluid model through a porous medium have been investigated. The governing equation flow problem is modeled by taking the approximation of long wavelength and creeping flow regime. The solution of the resulting differential equation has been solved analytically and a closed form solution is presented. The major outcomes of the present analysis are as follows:

• Velocity of fluid depicts same behavior for slip parameter and Hartmann number.
• Pressure rise decreases due to slip effects and porosity parameter.
• Pressure rise increases due to Hartmann number.
• The present analysis can also be reduced to Newtonian fluid by taking ${\textstyle {\lambda }_{1}\rightarrow 0}$ as a special case of our study.
• The present analysis reveals many engrossing behavior that warrants further study on various biological fluids for blood flow problems.

References

1. [1] G.J. Tortora, B. Derrickson; The cardiovascular system: the blood; Principles of Anatomy and Physiology, 13th. John Wiley & Sons (2015)
2. [2] J.S. Fieldman, D.H. Phong, Y.S. Aubin, L. Vinet, Rheology, Biology and Mechanics of Blood Flows, Part II: Mechanics and Medical Aspects, 2007.
3. [3] G.J. Tortora, B. Derrickson; The Cardiovascular System: Blood Vessels and Hemodynamics, Laminar Flow Analysis, John Wiley & Sons (2012)
4. [4] L.M. Srivastava, V.P. Srivastava; Peristaltic transport of blood: Casson model II; J. Biomech., 17 (1984), pp. 821–829
5. [5] J.C. Misra, S.K. Pandey; Peristaltic transport of blood in small vessels: study of a mathematical model; Comput. Math. Appl., 43 (2002), pp. 1183–1193
6. [6] K.S. Mekheimer; Peristaltic flow of a couple stress fluid in an annulus: application of an endoscope; Physica A, 387 (2008), pp. 2403–2415
7. [7] A. Sinha, J.C. Misra; MHD flow of blood through a dually stenosed artery: effects of viscosity variation, variable hematocrit and velocity slip; Can. J. Chem. Eng., 92 (2014), pp. 23–31
8. [8] V.K. Sud, G.S. Sekhon, R.K. Mishra; Pumping action on blood by a magnetic field; Bull. Math. Biol., 39 (1977), pp. 385–390
9. [9] S. Ibsen, A. Sonnenberg, C. Schutt, R. Mukthavaram, Y. Yeh, I. Ortac, M.J. Heller; Recovery of drug delivery nanoparticles from human plasma using an electrokinetic platform technology; Small, 11 (2015), pp. 5088–5096
10. [10] K.S. Mekheimer, T.H. Al-Arabi; Nonlinear peristaltic transport of MHD flow through a porous medium; Int. J. Math. Math. Sci., 2003 (2003), pp. 1663–1682
11. [11] K.S. Mekheimer; Peristaltic flow of blood under effect of a magnetic field in a non-uniform channels; Appl. Math. Comput., 153 (2004), pp. 763–777
12. [12] N.S. Akbar; Blood flow analysis of Prandtl fluid model in tapered stenosed arteries; Ain Shams Eng. J., 5 (2014), pp. 1267–1275
13. [13] S. Sreenadh, K. Komala, A.N.S. Srinivas; Peristaltic pumping of a power Law fluid in contact with a Jeffrey fluid in an inclined channel with permeable walls; Ain Shams Eng. J. (2015) http://dx.doi.org/10.1016/j.asej.2015.08.019 (in press)
14. [14] K. Ramesh, M. Devakar; Some analytical solutions for flows of Casson fluid with slip boundary conditions; Ain Shams Eng. J., 6 (2015), pp. 967–975
15. [15] J.C. Misra, A. Sinha, G.C. Shit; Mathematical modeling of blood flow in a porous vessel having double stenoses in the presence of an external magnetic field; Int. J. Biomath., 4 (2011), pp. 207–225
16. [16] K.S. Mekheimer, A.N. Abdel-Wahab; Net annulus flow of a compressible viscous liquid with peristalsis; J. Aerospace Eng., 25 (2011), pp. 660–669
17. [17] N.S. Akbar, S. Nadeem; Exact solution of peristaltic flow of biviscosity fluid in an endoscope: a note; Alexandria Eng. J., 53 (2014), pp. 449–454
18. [18] N.S. Akbar, S. Nadeem, M. Ali; Jeffrey fluid model for blood flow through a tapered artery with a stenosis; J. Mech. Med. Biol., 11 (2011), pp. 529–545
19. [19] M.M. Rashidi, N. Kavyani, S. Abelman; Investigation of entropy generation in MHD and slip flow over a rotating porous disk with variable properties; Int. J. Heat Mass Transfer, 70 (2014), pp. 892–917
20. [20] M.M. Rashidi, E. Erfani; Analytical method for solving steady MHD convective and slip flow due to a rotating disk with viscous dissipation and Ohmic heating; Eng. Comput., 29 (2012), pp. 562–579
21. [21] N.S. Akbar; Mhd Eyring Prandtl fluid flow with convective boundary conditions in small intestines; Int. J. Biomath., 6 (2013), p. 1350034
22. [22] K.S. Mekheimer; Peristaltic flow of a magneto-micropolar fluid: effect of induced magnetic field; J. Appl. Math. (2008) doi: http://dx.doi.org/10.1155/2008/570825
23. [23] N.S. Akbar, S. Nadeem, Z.H. Khan; Numerical simulation of peristaltic flow of a Carreau nanofluid in an asymmetric channel; Alexandria Eng. J., 53 (2014), pp. 191–197
24. [24] K.S. Mekheimer, M.H. Haroun, M.A. El Kot; Induced magnetic field influences on blood flow through an anisotropically tapered elastic artery with overlapping stenosis in an annulus; Can. J. Phys., 89 (2011), pp. 201–212
25. [25] N.S. Akbar, T. Hayat, S. Nadeem, S. Obaidat; Peristaltic flow of a Williamson fluid in an inclined asymmetric channel with partial slip and heat transfer; Int. J. Heat Mass Transfer, 55 (2012), pp. 1855–1862
26. [26] N.S. Akbar, S. Nadeem, Z.H. Khan; Thermal and velocity slip effects on the MHD peristaltic flow with carbon nanotubes in an asymmetric channel: application of radiation therapy; Appl. Nanosci., 4 (2014), pp. 849–857
27. [27] N.S. Akbar, M. Raza, E. Ellahi; CNT suspended CuO+H₂O nano fluid and energy analysis for the peristaltic flow in a permeable channel; Alexandria Eng. J., 54 (2015), pp. 623–633
28. [28] A. Yldrm, S.A. Sezer; Effects of partial slip on the peristaltic flow of a MHD Newtonian fluid in an asymmetric channel; Math. Comput. Model., 52 (2010), pp. 618–625
29. [29] N.S. Akbar, Z.H. Khan; Heat transfer analysis of the peristaltic instinct of biviscosity fluid with the impact of thermal and velocity slips; Int. Commun. Heat Mass, 58 (2014), pp. 193–199
30. [30] S. Hina; MHD peristaltic transport of Eyring-Powell fluid with heat/mass transfer, wall properties and slip conditions; J. Magn. Magn. Mater., 404 (2016), pp. 148–158
31. [31] N.F. Fauzi, S. Ahmad, I. Pop; Stagnation point flow and heat transfer over a nonlinear shrinking sheet with slip effects; Alexandria Eng. J., 54 (2015), pp. 929–934
32. [32] R. Ellahi, S.U. Rahman, S. Nadeem, K. Vafai; The blood flow of Prandtl fluid through a tapered stenosed arteries in permeable walls with magnetic field; Commun. Theor. Phys., 63 (2015), p. 353358
33. [33] R. Ellahi; The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: analytical solutions; Appl. Math. Model., 37 (2013), p. 14511467
34. [34] S. Rashidi, M. Dehghan, R. Ellahi, M. Riaz, M.T. Jamal-Abad; Study of stream wise transverse magnetic fluid flow with heat transfer around an obstacle embedded in a porous medium; J. Magn. Magn. Mater., 378 (2015), p. 128137
35. [35] Noreen Sher Akbar, M. Raza, R. Ellahi; Interaction of nanoparticles for the peristaltic flow in an asymmetric channel with the induced magnetic field; Eur. Phys. J. Plus, 129 (2014), p. 155
36. [36] A. Zeeshan, R. Ellahi, M. Hassan; Magnetohydrodynamic flow of water/ethylene glycol based nanofluids with natural convection through a porous medium; Eur. Phys. J. Plus, 129 (2014), p. 261
37. [37] A. Zeeshan, R. Ellahi; Series solutions for nonlinear partial differential equations with slip boundary conditions for non-Newtonian MHD fluid in porous space; Appl. Math. Inf. Sci., 7 (2013), pp. 257–265
38. [38] R. Ellahi, M. Hameed; Numerical analysis of steady non Newtonian flows with heat transfer analysis, MHD and nonlinear slip effects; Int. J. Numer. Methods, 22 (2012), pp. 24–38
39. [39] R. Ellahi, M. Mubashir Bhatti, Arshad Riaz, Mohsen Sheikholeslami; Effects of magnetohydrodynamics on peristaltic flow of jeffrey fluid in a rectangular duct through a porous medium; J. Porous Media, 17 (2014), pp. 143–157
40. [40] A. Afsar Khan, R. Ellahia, M. Mudassar Gulzar, Mohsen Sheikholeslami; Effects of heat transfer on peristaltic motion of Oldroyd fluid in the presence of inclined magnetic field; J. Magn. Magn. Mater., 372 (2014), pp. 9–106
41. [41] Noreen Sher Akbar, M. Raza, R. Ellahi; Influence of induced magnetic field and heat flux with the suspension of carbon nanotubes for the peristaltic flow in a permeable channel; J. Magn. Magn. Mater., 381 (2015), pp. 405–415
42. [42] M.S. Kandelousi, Rahmat Ellahi; Simulation of ferrofluid flow for magnetic drug targeting using the lattice Boltzmann method; Z. Naturforsch. A, 70 (2015), pp. 115–124
43. [43] A. Sinha, G.C. Shit, N.K. Ranjit; Peristaltic transport of MHD flow and heat transfer in an asymmetric channel: effects of variable viscosity, velocity-slip and temperature jump; Alexandria Eng. J., 54 (2015), pp. 691–704
44. [44] M. Abdulhameed, W. Varnhorn, I. Hashim, R. Roslan; The unsteady flow of a third-grade fluid caused by the periodic motion of an infinite wall with transpiration; Alexandria Eng. J., 54 (2015), pp. 1233–1241
45. [45] A. Sinha; MHD flow and heat transfer of a third order fluid in a porous channel with stretching wall: application to hemodynamics; Alexandria Eng. J., 54 (2015), pp. 1243–1252
46. [46] H. Sakuma, T. Taniyama, K. Ishii, Y. Kitamoto, Y. Yamazaki; Analysis of atomic arrangement in magnetic Fe–Pt nanoparticles; J. Magn. Magn. Mater., 300 (2006), pp. 284–292
47. [47] J.C. Misra, A. Sinha; Effect of thermal radiation on MHD flow of blood and heat transfer in a permeable capillary in stretching motion; Heat Mass Transfer, 49 (2013), pp. 617–628
48. [48] M. Mustafa, S. Hina, T. Hayat, A. Alsaedi; Slip effects on the peristaltic motion of nanofluid in a channel with wall properties; ASME J. Heat Transfer, 135 (2013), p. 041701