Resumen
Este artículo presenta un estudio numérico utilizando el programa ANSYS para análisis de conexiones de acero tipo «T» denominadas «T-Stub», en las cuales puede darse el fenómeno de acción de palanca. El efecto de apalancamiento en los tornillos de la placa ha sido estudiado antes, pero la localización de las fuerzas de palanca ha sido simplificada. El efecto del espesor de las placas de conexión «T-Stub» en las áreas de contacto entre ellas y un soporte rígido ha sido investigado en este artículo diferentemente de lo que se encuentra en la literatura técnica, en que dicho fenómeno es estudiado entre bases flexibles. La conexión ha sido discretizada con elemento de sólido 3D y elementos de interfaz. En los análisis realizados se adoptan diferentes espesores de la placa y tornillos de diámetros distintos en los cuales se ha aplicado una precarga. En este artículo se presenta una discusión sobre la magnitud de los esfuerzos en los tornillos y la extensión del área de contacto efectiva entre la placa y un soporte rígido.
Abstract
This paper presents a numerical study of «T-Stub» steel connections using FEM analyses. In such connections prying action phenomenon may take place. Prying action effect on the bolts has been studied before but the location of the prying action forces has always been simplified. The effect of the thickness of «T-Stub» flanges on contact areas between flanges and support base is investigated in this paper. A 3D finite element model is used and interface elements are employed for the investigation. Nonlinear FE analyses are undertaken on connection with different flange thickness and bolt preload with two bolts. Nonlinear gap elements are used as interfaces. Discussion and conclusions on contact areas and stresses, prying action distributions and resultant of loads on bolts in the «T-Stub» connections are presented.
Palabras clave
Conexión «T-Stub» ; Tensiones de contacto ; Acción de apalancamiento ; Esfuerzos en los tornillos
Keywords
«T-Stub» connections ; Contact stresses ; Prying action ; Stresses on bolts
1. Introducción
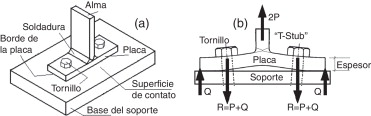
Las conexiones «T-Stub», tal como se muestra en la figura 1 a, son miembros generalmente sometidos a tensión. Los estudios [1] muestran que los tornillos en este tipo de conexión pueden estar sujetos a altas tracciones debido a un fenómeno llamado «acción de palanca». Este fenómeno se asocia a la rigidez a la flexión de la placa de conexión «T-Stub», conforme se muestra en la figura 1 b. La acción de apalancamiento es un fenómeno físico debido a la excentricidad entre la aplicación de la fuerza externa (2P) y la línea de resistencia de los tornillos. La acción de apalancamiento (Q) aumenta las fuerzas que actúan sobre los tornillos (R = P + Q) y por tanto deben ser consideradas para un diseño correcto de las conexiones «T-Stub» [2] and [3] . Según Kulak [1] , una carga externa de tracción aplicada en la conexión «T-Stub» con precarga en los tornillos reduce la presión de contacto entre la placa y la base de apoyo. Sin embargo, las fuerzas adicionales de tracción dependen de la rigidez a la flexión de la placa. Modelos analíticos (fig. 1 b) para el diseño de conexión «T-Stub», propuestos por Douty y McGuire [4] , Struik y deBack [5] y Nair [6] , consideran la acción de fuerzas de apalancamiento (Q) concentradas en una línea en el borde de la placa de conexión «T-Stub». Este enfoque ha sido adoptado por muchas normas [7] , [8] and [9] , pero no se corresponde con la realidad del fenómeno de apalancamiento en las conexiones «T-Stub».
|
|
|
Figura 1. a) Conexión de acero «T-Stub». b) Modelo analítico usual. |
El trabajo publicado por Swanson, Kokan y Leon [10] muestra cualitativamente la distribución de la acción de las fuerzas de apalancamiento sobre el área de contacto entre la placa de conexión «T-Stub» y la base de apoyo, aunque utilizando una base con la misma rigidez de la placa. Otros trabajos [11] and [12] también adoptan modelos experimentales en los cuales se usan 2 conexiones «T-Stub» idénticas ligadas a través de las placas. Sin embargo eso no se corresponde con la realidad, pues las conexiones «T-Stub» generalmente se ligan a partes de mayor rigidez. En este trabajo se hace un análisis cualitativo y cuantitativo de la distribución de la fuerza de contacto de conexiones «T-Stub» con apoyo en una superficie rígida, conforme se muestra en la figura 1 , con el propósito de aproximarse a una situación más real cuando se utiliza el «T-Stub» para conectar, por ejemplo, las vigas a las columnas o los tirantes a las vigas.
La determinación precisa de la posición de la fuerza de contacto es importante, porque tal posición puede influir en el dimensionamiento de los tornillos de las conexiones «T-Stub». La localización más precisa de la fuerza de apalancamiento puede ser realizada usando un modelo numérico sofisticado en elementos finitos, el cual permitirá conocer de forma más realista los esfuerzos en los tornillos de las conexiones «T-Stub». La nomenclatura aquí adoptada de las partes componentes de una conexión «T-Stub» se detallada en la figura 1 . Este artículo es producto de una investigación en curso en el Departamento de Ingeniería Civil de la Universidad de Brasilia (UnB) para la verificación numérica y experimental del comportamiento de los conectores de acero del tipo «T-Stub» [13] .
2. Conexiones de acero «T-Stub»
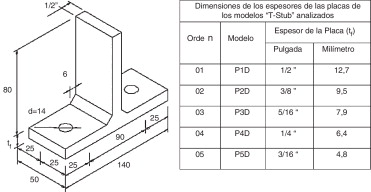
El objetivo del presente artículo es la investigación, mediante métodos numéricos, de la influencia del espesor de la placa de la conexión «T-Stub» en: a) las fuerzas de apalancamiento; b) la distribución de esas fuerzas en el contacto placa-soporte de base, y c) en la aparición de fuerzas de tracción adicionales en los tornillos. Todas las investigaciones que se presentan en este artículo se basan en la simulación numérica de los diversos modelos de conexión «T-Stub» representados en la figura 2 . El los «T-Stub» considerados en este estudio se han utilizado 2 tornillos (fig. 1 ) y placas de espesores variables cuyas dimensiones y sus respectivas denominaciones se definen en la figura 2 .
|
|
|
Figura 2. Dimensiones «T-Stub» (en milímetros). |
En la misma figura 2 se muestra el detalle de la perforación de 14 mm de diámetro para la colocación de los tornillos y las distancias a los bordes de la placa, según recomendaciones de la Norma de Proyecto de Estructuras de Acero, NBR8800:2008 [8] . El espesor del alma de todos los conectores «T-Stub» es 1/2″ (12,7 mm). La soldadura de conexión entre alma y placa es una soldadura en ángulo y tiene el tamaño de pierna de 6 mm, como se muestra en la figura 2 . Las propiedades del acero utilizado son: módulo de elasticidad (E) = 205.000 MPa, y coeficiente de Poisson (ν) = 0,3; las tensiones de límite elástico son de 300 MPa para la placa y alma, y de 466 MPa para los tornillos.
3. El modelo de elementos finitos
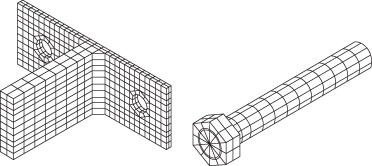
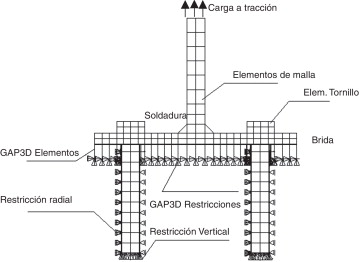
Para las simulaciones numéricas se ha usado el programa de elementos finitos (EF) comercial ANSYS [14] . Para la discretización de la conexión «T-Stub» y de los tornillos se han utilizado los EF SOLID-45 disponibles en la biblioteca de elementos del programa mencionado con 3 grados de libertad por nodo. La malla de EF tiene 776 elementos sólidos y 2.141 nodos. Todos los modelos tienen la misma malla, pero el espesor de la placa cambia de un modelo a otro (como se especifica en la fig. 2 ). Una unión perfecta es asumida en la interfaz entre la cabeza de los 2 tornillos y la placa. La malla de EF se muestra en la figura 3 .
|
|
|
Figura 3. Mallas de EF para la conexión «T-Stub» con los tornillos. |
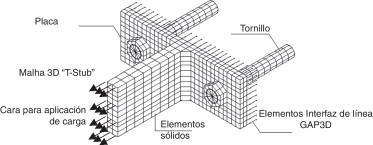
Los elementos de la interfaz se colocan entre la base de apoyo y la placa para conocer la región de contacto real entre ambas. Estos elementos tienen como finalidad no solamente captar las áreas de contacto, sino también evaluar las fuerzas de contacto. Se ha utilizado el elemento GAP3D de la librería del programa ANSYS [14] para los elementos de la interfaz. Esos elementos son unidimensionales con 3 grados de libertad, definiendo el contacto punto a punto entre las superficies. El elemento GAP3D tiene solamente capacidad de soportar fuerzas de compresión en la dirección normal a las superficies. Aunque el elemento de la interfaz tiene la capacidad de considerar la fricción entre 2 superficies, en este estudio la fricción no es considerada. La interfaz GAP3D se representa como líneas y se señala en la figura 4 . Para simular una base de apoyo rígida se impone en los elementos de interfaz una rigidez a la compresión muy alta. Se utilizan un total de 333 elementos GAP3D (fig. 4 ).
|
|
|
Figura 4. Malla completa del «T-Stub» para los modelos P1D, P2D, P3D, P4D y P5D. |
4. Cargas aplicadas
En la figura 5 se presenta una sección transversal del modelo EF. La carga aplicada y las restricciones en desplazamientos también están representadas en esa figura. Es posible apreciar también el detalle de la malla de los tornillos y las líneas que representan los elementos de interfaz. El desplazamiento longitudinal de los tornillos se permite a lo largo de la longitud del tornillo. En los elementos de interfaz GAP3D un nodo se fija en la placa de conexión y el otro nodo está anclado en la base, simulando un apoyo rígido. Los elementos GAP3D se distribuyen en los nodos de la malla en la interfaz como se muestra en la figura 6 . El contacto entre la placa de conexión y la base de apoyo soporta la precarga aplicada en los tornillos y una eventual acción de «apalancamiento» que es producida por la carga de tracción externa aplicada en el alma del conector «T-Stub». Para el estudio actual, las cargas aplicadas en los tornillos se han considerado 2 casos de carga denominados «caso 1» y «caso 2»: el primero sin precarga, y el segundo con una precarga de 45 kN en los tornillos (22,5 kN en cada tornillo, según el código NBR8800:1986 [8] ) antes de la aplicación de la carga externa de tracción. En los modelos EF es importante aplicar las cargas respetando la secuencia de realización del montaje de la conexión. En el caso 1, donde los tornillos no se precargan, el modelo EF es sometido exclusivamente a la carga externa de tracción. En el caso 2, la precarga en los tornillos es la primera solicitación y posteriormente se aplica la carga externa de tracción. En todos los análisis, la carga externa de tracción se incrementa monotónicamente en 4 pasos de carga de 40 hasta 160 kN. En el caso 2, la primera fase de carga es la precarga y después los 4 pasos de carga externa, para un total de 5 fases de carga. Consecuentemente, el caso 1 tiene solamente 4 fases de carga. Obsérvese que la carga externa de tracción es aplicada uniformemente sobre todos los nodos en la cara del alma del «T-Stub» conforme se muestra en las Figura 4 and Figura 5 . Las cargas y precargas asociadas con cada caso de carga se resumen en la tabla 1 .
|
|
|
Figura 5. Malla de los elementos de la interfaz y del contorno. |
|
|
|
Figura 6. Identificación de ejes y nodos de la malla en la interfaz de contacto. |
| Modelos de elementos finitos (EF) | Pasos de carga (PC) | Precarga | Incrementos de carga de tracción (kN) |
|---|---|---|---|
| 5 modelos EF con 2 tornillos | |||
| Caso 1 | 4 PC | 0,00 | 40-80-120-160 |
| Caso 2 | 5 PC = Precarga + 4 | 45 kN | 40-80-120-160 |
5. Resultados numéricos
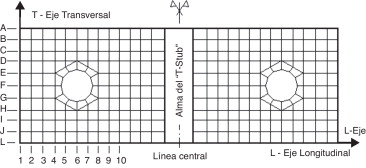
Para el análisis de los resultados numéricos se ha utilizado la nomenclatura de identificación de nodos presentada en la figura 6 . La malla resultante está compuesta en su mayoría por cuadrados regulares de aproximadamente 5 mm de lado. Tres parámetros son examinados de la salida de los datos numéricos.
- Distribución de las fuerzas de contacto en la placa.
- Resultante de las fuerzas de contacto y su ubicación.
- Resultante de fuerzas que actúan sobre los tornillos.
6. Distribución de las fuerzas de contacto en las placas de los «T-Stub» para el caso 1
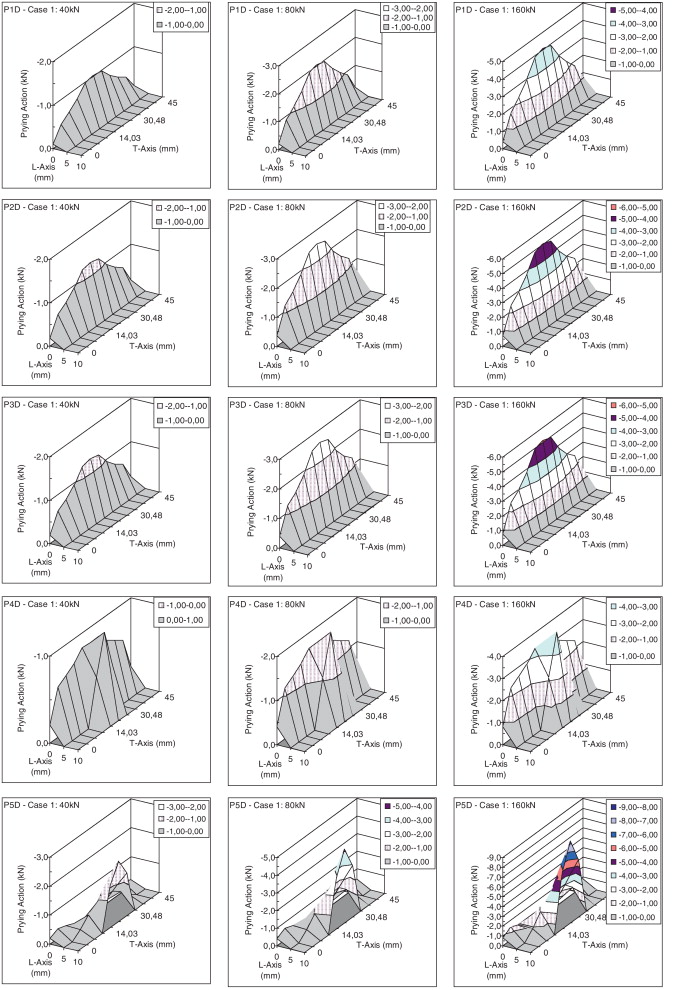
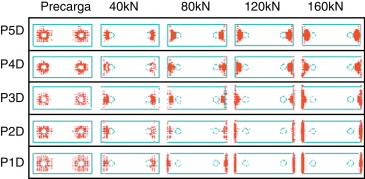
La figura 7 presenta las magnitudes y la distribución de las fuerzas de contacto entre las superficies de la placa de conexión «T-Stub» y la base de apoyo rígido. Los valores de la fuerza de contacto son tomados directamente de los elementos de interfaz. Debido a la limitación de espacio en la figura 7 , el eje L se limita al rango [0,10] —cuando las fuerzas de contacto son significativas—. Debe tenerse en cuenta que la perforación del tornillo comienza a 18 mm del borde de la placa (25-14/2, véase fig. 2 ). En la figura 7 , a pesar de la no linealidad causada por la presencia de los elementos de la interfaz, se nota la proporcionalidad entre las fuerzas de contacto y las cargas aplicadas.
|
|
|
Figura 7. Distribución de la acción de apalancamiento para el caso 1 (sin precarga). |
La distribución de la fuerza de contacto muestra una concentración en el eje longitudinal en el rango [0,10] y muestra similitudes a pesar de la variación del espesor de la placa. Para los modelos P1D, P2D y P3D (placas más gruesas), la fuerza de contacto se concentra a lo largo de la dirección del eje T, en el borde de la placa en el rango [0,5] del eje L. Para P4D y P5D, la distribución de la fuerza de contacto presenta una concentración en el borde de la placa, pero también alrededor de la cabeza del tornillo y en el rango [0,10] del eje L. En el origen del eje L y a lo largo de la dirección transversal, la concentración de las fuerzas de contacto se encuentra en la franja correspondiente a la cabeza del tornillo. En las esquinas de la placa las tensiones de contacto son muy reducidas. Para espesores de placas más delgados (P4D y P5D) las distribuciones de concentración se presentan muy cerca de la cabeza del tornillo.
7. Distribución de fuerzas de contacto en las placas de los «T-Stub» para el caso 2
En este caso, la no linealidad debido a los elementos de interfaz es más notable. La aplicación de la precarga produce un ajuste de la placa contra la base de apoyo. Cuando la carga externa de tracción actúa sobre la placa, las fuerzas de contacto (generadas por la precarga del tornillo) tienden a disminuir. No debe perderse de vista que, en este caso, la tracción se aplica en 4 pasos subsecuentes de carga, de tal forma que solo después de la primera fase de carga se consigue en el sistema una tracción comparable con la precarga del tornillo.
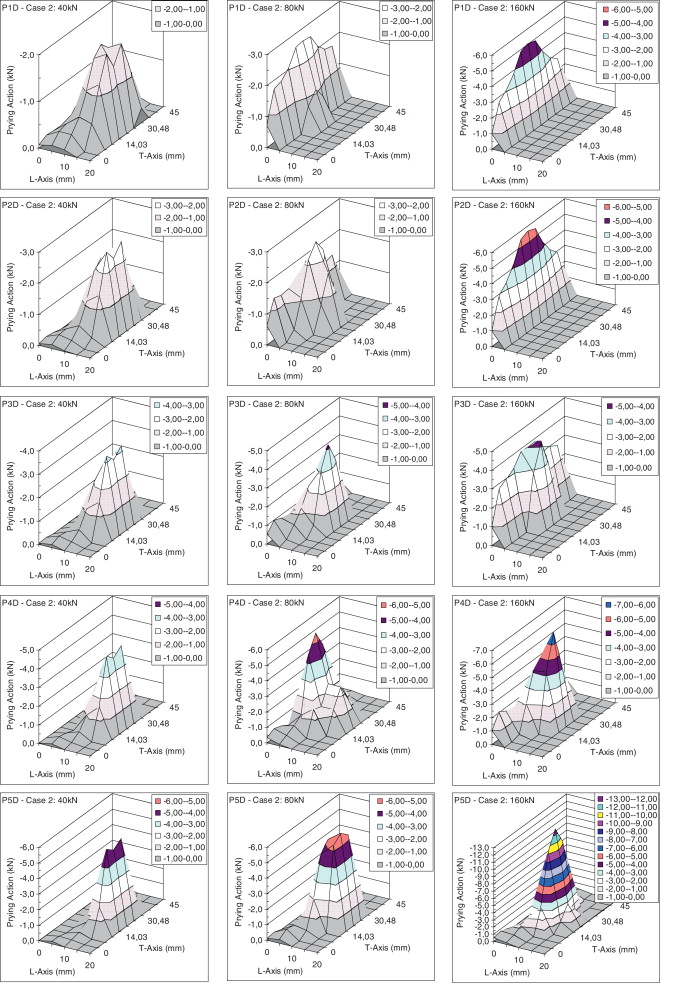
La figura 8 muestra la magnitud y la distribución de las fuerzas de contacto entre la superficie de la placa de conexión «T-Stub» y la base de soporte rígido. Como en el caso 1, los valores de la fuerza de contacto se toman directamente de los elementos de interfaz en la figura 8 . Para ahorrar espacio en la figura 8 , las observaciones están limitadas al rango [0,20] del eje L, en el cual las fuerzas de contacto son significativas.
|
|
|
Figura 8. Distribución de la acción de apalancamiento para el caso 2 (precarga). |
8. Resultante de las fuerzas de contacto en las placas de los «T-Stub»
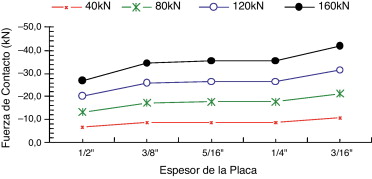
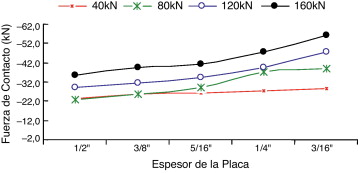
El análisis de las fuerzas de contacto, en las Figura 7 and Figura 8 , muestra que espesores de placa más delgados dan lugar a fuerzas de contacto más grandes, confirmando lo que hay en la literatura [1] y puede ser igualmente observado en las Figura 9 and Figura 10 , la primera asociada al caso 1 (sin precarga en los tornillos) y la segunda relacionada con el caso 2 (con precarga en los tornillos). Tales figuras trazan la resultante de las fuerzas de contacto (RFC) en función del espesor de la placa. Debido a la simetría, el valor RFC es la suma de todas las fuerzas de contacto en un solo lado de la placa. El RFC crece con la disminución del espesor. El signo negativo está asociado a las fuerzas de compresión entre la placa y la base de apoyo.
|
|
|
Figura 9. Variación de la resultante en función del espesor de la placa: caso 1. |
|
|
|
Figura 10. Variación de la resultante en función del espesor de la placa: caso 2. |
9. Distribución y localización de las fuerzas de contacto sobre las placas de los «T-Stub»
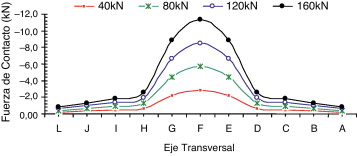
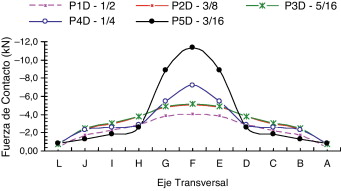
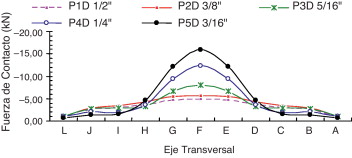
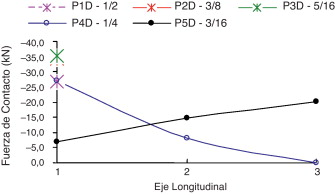
La distribución de la fuerza de contacto a lo largo del eje transversal T se puede ver en las Figura 11 , Figura 12 and Figura 13 y 14–16, respectivamente, para el caso 1 y el caso 2. En las Figura 11 and Figura 12 se muestra la distribución de las RFC a lo largo de la dirección del eje T, respectivamente, para espesores de la placa de 1/16 «(placa delgada P5D) y 1/2» (placa gruesa P1D). Dichas resultantes RFC se obtienen a través de la suma de las fuerzas de contacto a lo largo del eje L. Por ejemplo, en la figura 11 el nivel de carga de 160 kN y una resultante (RFC) de 12 kN (correspondiente a la letra F) es la suma de todas las fuerzas de contacto en los puntos de F-1, F-2, y F-3 (a lo largo del eje L) en la malla definida en la figura 6 . Se debe tener en cuenta que las resultantes están más concentradas cerca de la cabeza del tornillo cuando la placa es delgada. Por otra parte, cuando la placa es más gruesa, como se muestra en la figura 12 , las resultantes están menos concentradas y se extienden por el eje T. Para ahorrar espacio, solo se grafican los espesores de la placa más delgada y más gruesa que se muestra en las Figura 11 and Figura 12 , respectivamente.
|
|
|
Figura 11. Resultante de las fuerzas a lo largo del eje transversal de P5D: caso 1. |
|
|
|
Figura 12. Fuerzas resultantes de contacto a lo largo del eje T para P1D: caso 1. |
|
|
|
Figura 13. Fuerzas resultantes de contacto a lo largo del eje T-160 kN: caso 1. |
|
|
|
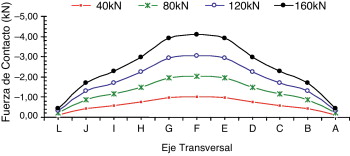
Figura 14. Fuerza resultante de contacto a lo largo del eje T para P5D: caso 2. |
|
|
|
Figura 15. Resultante de la fuerza de contacto a lo largo del eje T para P1D: caso 2. |
|
|
|
Figura 16. Resultante de la fuerza de contacto a lo largo del eje T para 160 kN: caso 2. |
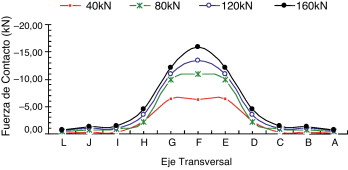
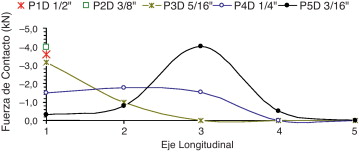
En la figura 13 se resume la distribución y la magnitud de la RFC, teniendo en consideración los espesores de placa para el nivel de carga de 160 kN. Las Figura 14 , Figura 15 and Figura 16 son equivalentes para el caso 2. En estas figuras, las magnitudes de las fuerzas RFC son más altas que en las Figura 11 , Figura 12 and Figura 13 , y esto se debe a la precarga en los tornillos. Las Figura 17 and Figura 18 muestran la variación de la fuerza de contacto a lo largo del eje longitudinal (L) en función del espesor de la placa para los casos 1 y 2, respectivamente, considerando una carga de tracción de 160 kN.
En la figura 17 se nota que cuando no se aplica la precarga (caso 1), las fuerzas de contacto se concentran en la posición-1 (borde de la placa en la figura 6 ). Esto es aplicable para las placas gruesas P1D, P2D y P3D. Sin embargo, en la figura 17 , para las placas más delgadas, P4D y P5D, la distribución de fuerzas de contacto es muy diferente. En estos casos, las fuerzas de contacto no se concentran a lo largo del borde de las placas (origen de eje L). Para P4D, la distribución de la fuerza de contacto disminuye desde el borde hacia la línea del tornillo (posición 3, a lo largo del eje T, en la figura 6 ) y para la placa más delgada, P5D, la distribución de la RFC aumenta hacia a la línea del tornillo. Cabe comentar que las RFC están a 1,16 y 6,57 mm del borde de la placa, respectivamente, para P4D y P5D. Con respecto al caso 2, un cambio significativo se observa en la distribución de las fuerzas de contacto en la dirección longitudinal. Debido a la precarga en los tornillos, las placas de conexión «T-Stub» tienen áreas de contacto más grandes que en el caso 1. Las fuerzas de contacto, en el caso 2, dependen de la rigidez de la placa y de la carga externa a la tracción aplicada en el alma.
|
|
|
Figura 17. Fuerza de contacto a lo largo del eje L para 160 kN: caso 1. |
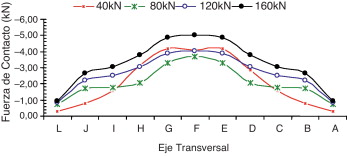
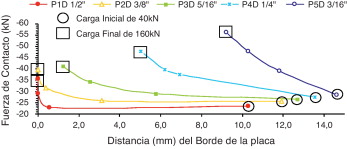
En la figura 18 se presenta la distribución de las fuerzas de contacto para el caso 2 para el nivel de carga de 160 kN. En la tabla 2 se muestran las magnitudes y las ubicaciones de las RFC para el caso 2, y las curvas correspondientes se muestran en la figura 19 . Se puede observar que, para las placas más delgadas, las RFC están más cerca de las cabezas de los tornillos que para las placas más gruesas. A medida que la carga de tracción externa aumenta, la localización de las RFC cambia de ubicación. Para las conexiones «T-Stub» P1D y P2D y nivel de carga de 160 kN, las fuerzas de contacto se desplazan desde el interior de la placa hasta el borde de ella (a lo largo del eje longitudinal). Para las otras conexiones «T-Stub» también hay un movimiento en la ubicación de las RFC en dirección del borde. Las posiciones de las RFC se pueden observar en la tabla 2 y en la figura 19 .
|
|
|
Figura 18. Fuerza de contacto a lo largo del eje L para 160 kN: caso 2. |
| Incremento de carga | P1D - 1/2″ | P2D - 3/8″ | P3D - 5/16″ | P4D - 1/4″ | P5D - 3/16″ | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Posición (mm) | Carga (kN) | Posición (mm) | Carga (kN) | Posición (mm) | Carga (kN) | Posición (mm) | Carga (kN) | Posición (mm) | Carga (kN) | |
| 40 kN | 10,30 | −23,5 | 11,90 | −25,8 | 12,66 | −26,5 | 13,55 | −27,4 | 14,61 | −28,3 |
| 80 kN | 0,57 | −22,9 | 3,10 | −25,9 | 5,76 | −29,1 | 6,95 | −37,4 | 11,80 | −39,1 |
| 120 kN | 0,00 | −29,0 | 0,39 | −31,6 | 2,53 | −34,3 | 6,22 | −39,7 | 10,29 | −47,7 |
| 160 kN | 0,00 | −35,7 | 0,00 | −39,7 | 1,21 | −41,4 | 5,04 | −47,7 | 9,22 | −56,4 |
|
|
|
Figura 19. Resultante de fuerza de contacto y distancia al borde de la placa: caso 2. |
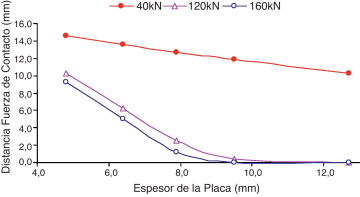
En la figura 20 se presentan las distancias de las RFC al borde de las placas para cada espesor y para distintos niveles de carga. Para cargas pequeñas el comportamiento es prácticamente lineal. Con el aumento gradual de la carga se hace evidente la no linealidad. Debe tenerse en cuenta que para 120 y 160 kN con placas más gruesas (mayor rigidez), las posiciones de las RFC están en el borde de la placa, tal como se has adoptado en los modelos tradicionales de acción de apalancamiento en conexiones «T-Stub» [1] , [2] , [3] , [4] , [5] , [6] , [7] , [8] , [9] , [10] , [11] and [12] . La variación de las posiciones de las RFC se presenta en la figura 21 .
|
|
|
Figura 20. Distancia de las RFC hasta al borde vs espesor de la placa: caso 2. |
|
|
|
Figura 21. Evolución de la distribución de la fuerza de contacto para el caso 2. |
10. Fuerza actuante en el tornillo de las conexiones «T-Stub»
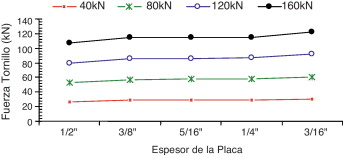
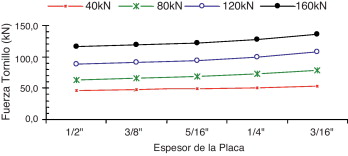
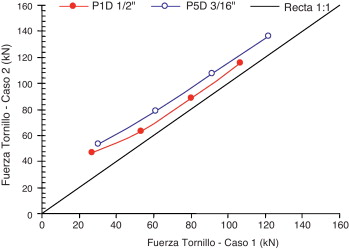
A partir de los análisis realizados en este artículo se observa que la fuerza que actúa sobre el tornillo de conexión «T-Stub» varía con el espesor de la placa. Por simplicidad se denominará «FT» a la fuerza que actúa sobre el tornillo. Solamente se han considerado los rangos de espesor de placas considerados en esta investigación (fig. 1 ). Los análisis confirman que cuanto más delgada es la placa, mayor es la fuerza en el tornillo. Obviamente, esta última afirmación debe tener un límite, pues una placa muy delgada no puede producir ningún apalancamiento. La variación de la FT en función de los espesores de la placa está representada en la figura 22 y en la tabla 3 para el caso 1. En la figura 23 y la tabla 4 se muestra la variación de la FT para el caso 2. En esas tablas, la diferencia entre los valores de las columnas A y B representan las fuerzas adicionales en cada tornillo debido al efecto de apalancamiento (cuyo valor es igual a las RFC). Para la conexión P1D y P5D (tabla 1 ), la relación entre la FT en el caso 2 y en el caso 1 puede verse en la figura 24 . Los otros casos están entre las curvas mostradas en la figura 24 . Debe tenerse en cuenta que la FT en el caso 2 es mayor que en el caso 1.
|
|
|
Figura 22. Relación de la fuerza en uno tornillo y el espesor de la placa: caso 1. |
| Unidad → | (kN) | (kN) | (kN) | (kN) | ||||
|---|---|---|---|---|---|---|---|---|
| Alma → | 40 | 80 | 120 | 160 | ||||
| (A) → | 20 | 40 | 60 | 80 | ||||
| Espesor ↓ | (B) | (C) | (B) | (C) | (B) | (C) | (B) | (C) |
| 1/2 | 27,50 | 7,50 | 52,70 | 12,70 | 79,70 | 19,70 | 108,00 | 28,00 |
| 3/8 | 28,19 | 8,19 | 56,56 | 16,56 | 85,75 | 25,75 | 115,40 | 35,40 |
| 5/16 | 28,20 | 8,20 | 58,20 | 18,20 | 85,80 | 25,80 | 116,09 | 36,09 |
| 1/4 | 28,21 | 8,21 | 58,20 | 18,20 | 87,02 | 27,02 | 116,09 | 36,09 |
| 3/16 | 31,52 | 11,52 | 61,05 | 21,05 | 92,10 | 32,10 | 122,80 | 42,80 |
A: fuerza en el tornillo sin el efecto de apalancamiento; B: fuerza estimada en el tornillo con el efecto de apalancamiento; C = B – A: fuerza de contacto RFC debido al efecto de apalancamiento.
|
|
|
Figura 23. Relación de la fuerza en uno tornillo y el espesor de la placa: caso 2. |
| Unidad → | (kN) | (kN) | (kN) | (kN) | ||||
|---|---|---|---|---|---|---|---|---|
| Alma → | 40 | 80 | 120 | 160 | ||||
| Precarga→ | 22,5 | 22,5 | 22,5 | 22,5 | ||||
| (A) → | 42,5 | 62,5 | 82,5 | 102,5 | ||||
| Espesor ↓ | (B) | (C) | (B) | (B) | (B) | (B) | (B) | (B) |
| 1/2 | 43,50 | 23,50 | 62,90 | 22,90 | 89,00 | 29,00 | 115,70 | 35,70 |
| 3/8 | 45,80 | 25,80 | 65,90 | 25,90 | 91,60 | 31,60 | 119,70 | 39,70 |
| 5/16 | 46,50 | 26,50 | 69,10 | 29,10 | 94,30 | 34,30 | 121,40 | 41,40 |
| 1/4 | 47,40 | 27,40 | 77,40 | 37,40 | 99,70 | 39,70 | 127,70 | 47,70 |
| 3/16 | 48,30 | 28,30 | 79,10 | 39,10 | 107,70 | 47,70 | 136,40 | 56,40 |
A: fuerza en el tornillo sin el efecto de apalancamiento; B: fuerza estimada en el tornillo con el efecto de apalancamiento; C = B – A: fuerza de contacto RFC debido al efecto de apalancamiento.
|
|
|
Figura 24. Relación entre la RFC en el caso 2 y el caso 1. |
11. Conclusión
De los resultados numéricos presentados, teniendo en cuenta exclusivamente el rango de espesores de la placa de conexión «T-Stub» (fig. 1 ) de 1/2″ (12,7 mm), 3/4″ (9,5 mm), 5/16″ (7,9 mm), 1/4″ (6,4 mm) y 3/16″ (4,8 mm), con 2 tornillos de fijación en base rígida, se extraen las siguientes conclusiones:
- El valor de la fuerza de apalancamiento sobre los tornillos depende del nivel de la carga aplicada en la alma de la conexión «T-Stub», de la rigidez a la flexión de la placa y, en consecuencia, del espesor de la placa.
- En la dirección longitudinal (eje L en la figura 6 ), la posición de la resultante de la fuerza de contacto (RFC) (y, por tanto, la fuerza de apalancamiento) no siempre es en el borde de la placa, como se supone por muchos modelos simplificados adoptados en la literatura.
- La posición de las RFC es función del espesor de la placa, del valor de la carga aplicada y del valor de la precarga aplicada en los tornillos. Por lo tanto, los modelos matemáticos adoptados en la literatura con la posición de contacto entre el borde de la placa del «T-Stub» y la base de apoyo no representan adecuadamente el fenómeno de apalancamiento que genera el aumento de la fuerza de los tornillos de fijación en la «T-Stub».
- En la dirección transversal, la posición de la fuerza de apalancamiento está en la cercanía a la cabeza del tornillo.
- La fuerza ejercida sobre el tornillo depende de la carga aplicada, del espesor de la placa y, consecuentemente, de la rigidez a la flexión de la placa del conector «T-Stub».
Por último, es importante señalar que los estudios experimentales que se están llevando a cabo en la Universidad de Brasilia (UnB) deben confirmar los resultados obtenidos por los modelos numéricos aquí presentados.
Agradecimientos
Este artículo es parte de una investigación en curso en la Universidad de Brasilia (UnB). Los autores quieren expresar sus agradecimientos al CNPq (Consejo Brasileño Nacional de Desarrollo Científico y Tecnológico) y a la CAPES (Comité Brasileño para el Curso de Posgrado en Educación Superior) por los apoyos financieros recibidos para el desarrollo de estos estudios.
Bibliografía
- [1] G.L. Kulak, J.W. Fisher, J.H.A. Struik; Guide to Design Criteria for Bolted and Riveted Joints; (2nd ed.)American Institute of Steel Construction Edition, Chicago (2001)
- [2] T.V. Galambos; Basic Steel Design with LRFD; Prentice Hall, Upper Saddle River, New Jersey (1996)
- [3] L.F.L. Ribeiro; Estudo do Comportamento Estrutural de Ligações Parafusadas Viga-coluna com Placa de Topo [Tesis doctoral]; Escola de Eng. de São Carlos, USP (1998)
- [4] R.T. Douty, W. McGuire; High strength bolted moment connections; J. Constr. Steel Res, 91 (1965) ST2
- [5] J.H.A. Struik, J. deBack; Tests on Bolted T-Stub with respect to a Bolted Beam-to-Column Connections. Report 6-69-13; Stevin Laboratory, Detf University of Technology, Detf, the Netherlands (1969)
- [6] R.S. Nair, P.C. Birkemoe, W.H. Munse; High Strength Bolts Subjected to Tension and Prying. Structural Research Series 353; Departament of Civil Engineering, University of Illinois, Urbana (1969)
- [7] American Society of Civil Engineers (ASCE), Commentary on Plastic Design. Manual 41, New York, 1971.
- [8] Associação Brasileira de Normas Técnicas, NB-8800:1986. Projeto e Execução de Estruturas de Aço de Edifícios», Rio de Janeiro, 1986.
- [9] Ministério do Desenvolvimento da Indústria e Comércio, Manual Brasileiro para Cálculo de Estruturas Metálicas, Segunda Edição, São Paulo, 1980.
- [10] J.A. Swanson, D.S. Kokan, R.T. Leon; Advanced finite element modelling of bolted T-stub connection components; J. Constr. Steel Res, 58 (2002), pp. 1015–1031
- [11] A. Loureiro, R. Gutiérrez, J.M. Reinosa, A. Moreno; Axial stiffness prediction of non-preloaded T-Stub: An analytical frame approach; J. Constr. Steel Res, 66 (2010), pp. 1516–1522
- [12] A.M. Girão Coelho, S.K.F. Bijlaard, N. Gresnigt, L.S. Silva; Experimental assessment of the behaviour of bolted T-Stub connections made up of welded plates; J. Constr. Steel Res, 60 (2004), pp. 269–311
- [13] C.A.S. Freitas; Estudo Experimental, Numérico e Analítico do Efeito Alavanca em Conexões Metálicas Tipo T [dissertação de Mestrado]; Universidade de Brasília, Brasília (2005)
- [14] ANSYS; Analysis System; Houston, PA, USA (2002)
Document information
Published on 28/02/14
Accepted on 19/07/12
Submitted on 28/02/12
Volume 30, Issue 1, 2014
DOI: 10.1016/j.rimni.2012.07.005
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?