Nonlinear dynamical model for the assessment of the seismic behaviour of ferrocement houses

Resumen

En este trabajo se evalúa el comportamiento cíclico de un prototipo de vivienda de ferrocemento, ensamblado mediante muros prefabricados de pared delgada, con la finalidad de identificar sus parámetros estructurales y proponer un modelo dinámico no lineal para simular el comportamiento de viviendas bajo movimientos sísmicos. Para ello se construyó un prototipo a escala real 1:1 y se probó bajo carga cíclica. De los resultados experimentales se obtuvieron: el comportamiento histerético, la rigidez elástica, la resistencia a cortante, la resistencia máxima, la ductilidad, la capacidad de disipación de energía, el amortiguamiento y el coeficiente de capacidad de disipación de energía; todos ellos, parámetros necesarios para la evaluación dinámica de la vivienda de ferrocemento bajo movimientos sísmicos. Al final se implementó el modelo dinámico no lineal de Bouc-Wen-Baber-Noori (BWBN). Este modelo permitió realizar la evaluación sísmica de la vivienda prefabricada de ferrocemento bajo sismos ocurridos.

Abstract

This article evaluates the cyclic behaviour of a prototype of a precast ferrocement house, which is assembled using precast thin walls, in order to identify its structural parameters and propose a nonlinear dynamical model which is able to simulate the behaviour of those houses when subjected to seismic loading. For this purpose, a full-scale precast ferrocement house was tested under cyclic loading conditions. From the experimental results, the hysteretic behaviour, the elastic stiffness, the shear resistance, the maximum strength, the ductility, the energy dissipation, the equivalent damping and its coefficient of energy dissipation were assessed; those parameters are needed in order to evaluate the dynamic behaviour of ferrocement dwellings when subjected to earthquakes. At the end, the Bouc-Wen-Baber-Noori (BWBN) model of hysteresis was implemented. The model allowed performing the seismic evaluation of the precast ferrocement house under seismic activity.

Plavras-chave

Ferrocemento ; Carga cíclica ; Ductilidad ; Modelo de Bouc-Wen-Baber-Noori ; Diseño sismorresistente

Keywords

Ferrocement ; Cyclic loading ; Ductility ; Bouc-Wen-Baber-Noori model ; Earthquake resistant design

1. Introducción

La actividad sísmica propia del planeta Tierra ha hecho necesario crear materiales resistentes no solo bajo cargas estáticas sino también bajo dinámicas. Los terremotos nos han mostrado la precariedad de algunos materiales bajo cargas repetitivas y nos obligan a generar nuevos materiales y sistemas para la construcción sismorresistente de viviendas. Los sistemas estructurales basados en muros prefabricados de ferrocemento han demostrado alta resistencia [1]  and [2] , baja fragilidad sísmica [1] y sustentabilidad para el medio ambiente [3] . Estos sistemas habitualmente consisten en paredes construidas a partir de muros prefabricados de pared delgada o de muros gruesos construidos in situ tipo sandwich[3]  and [4] . Los sistemas con muros prefabricados de pared delgada permiten versatilidad arquitectónica, la autoconstrucción y/o la industrialización y rápida construcción, en especial para viviendas temporales en caso de desastres naturales [2] , [5] , [6] , [7] , [8] , [9] , [10]  and [11] . Las dimensiones típicas de muros prefabricados de ferrocemento oscilan entre 500 y 1.000 mm de ancho, 2.000 a 2.400 mm de altura y de 10 a 50 mm de espesor. La resistencia y la ductilidad de los muros prefabricados de ferrocemento son suministradas por un conjunto de mallas de alambres y barras de acero de refuerzo embebidos en un mortero requerido de alta resistencia. En algunos lugares del mundo se ha utilizado el ferrocemento como solución de vivienda, como en los casos del archipiélago malayo, las islas de Sumatra, Sri Lanka, Nueva Guinea, México, India, Tailandia, EE.UU., Cuba, Haití, Brasil y Colombia.

Las primeras aplicaciones registradas en elementos constructivos para la edificación datan de principios de los años cuarenta, cuando el ingeniero y arquitecto Pier Luigi Nervi [12] redescubre las propiedades excepcionales del ferrocemento: elasticidad, flexibilidad y resistencia. Inicialmente lo utiliza para la construcción de barcos de pesca de 165 toneladas, tanques de almacenamiento y losas de entrepiso y finalmente construye la cubierta del salón principal del palacio de exposiciones de Turín, Italia, con una luz de 96 m de longitud. Más tarde, Castro [5] y Olvera [7] construyeron casas de uno y dos pisos utilizando muros prefabricados de pared delgada en México. En la India, en 1983, Gokhale [6] documentó un sistema para la construcción de viviendas llamado «Catone». En 1994, Wainshtok-Rivas [8] construyó las primeras viviendas de ferrocemento en Cuba. Naaman [2] publicó en 2000 los resultados de sus investigaciones desarrolladas en casas de ferrocemento en la Universidad de Michigan. Exploró las ventajas del ferrocemento desde el punto de vista de la industrialización, con el fin de permitir el desarrollo y la difusión de los beneficios de este material. Bedoya-Ruiz [1] publicó en 2005 una investigación experimental y analítica sobre muros prefabricados de pared delgada y viviendas de ferrocemento. Actualmente, en Cuba y en Haití se construyen más de 30.000 viviendas a partir de muros prefabricados de pared delgada de ferrocemento como solución a la destrucción de viviendas que causó el huracán Sandy de 2012 en Cuba, y en Haití después del terremoto de 2010 [11] . En esta última la construcción de las viviendas se hace por autoconstrucción, mientras que en Cuba ha sido industrializada.

Un método de análisis estructural habitual para realizar el diseño sismorresistente de este tipo de viviendas es el método de la fuerza horizontal equivalente (MFHE). Por ejemplo, Bedoya-Ruiz [13] y Wainshtok-Rivas [14] implementaron este método con el fin de obtener las fuerzas sísmicas generadas sobre una vivienda construida con muros prefabricados de pared delgada de ferrocemento ubicadas en una zona de actividad sísmica intermedia y alta. Bedoya-Ruiz et al. [15] propusieron un modelo dinámico no lineal para evaluar la vulnerabilidad sísmica de las viviendas de ferrocemento, permitiendo construir escenarios de daño para las diferentes zonas de actividad sísmica estudiadas. Recientemente, Ortiz et al. [16] implementaron metodologías de optimización para capturar la no linealidad exhibida por los muros de ferrocemento bajo carga cíclica, y Bedoya-Ruiz et al. [17] realizaron una investigación experimental y analítica sobre el comportamiento bajo carga cíclica de muros prefabricados de pared delgada de ferrocemento.

En este estudio se propone un modelo dinámico no lineal a partir de ensayos de carga cíclica realizados sobre un prototipo a escala real de una vivienda de ferrocemento estructurada con muros prefabricados de pared delgada. Inicialmente se describen los materiales y el ensayo de carga cíclica. Seguidamente se obtienen los parámetros estructurales característicos y necesarios del ferrocemento para desarrollar el modelo dinámico no lineal. Finalmente se compara el modelo teórico con los resultados experimentales.

2. Descripción del prototipo y ensayo

2.1. Descripción de los materiales

Para la construcción de los muros prefabricados de pared delgada de ferrocemento que componen las paredes del prototipo de vivienda, se utilizó un mortero y un tejido de mallas de alambre. El mortero se fabricó con cemento Portland tipo i , arena de uso habitual en la elaboración de mezclas para concreto reforzado, agua y aditivo superplastificante en las siguientes proporciones en peso: relación arena–cemento de 1:2, relación agua–cemento de 0,40, aditivo superplastificante al 1% del peso del cemento (para mejorar la manejabilidad y penetrabilidad del mortero a través del refuerzo) y el refuerzo distribuido en la matriz cementante consistió de 6 capas de malla hexagonal de doble torsión con una abertura de 31,75 mm (esta malla fue colocada longitudinalmente). La superficie específica de las mallas de refuerzo fue de 0,0314mm² /mm³ y la fracción de volumen fue de 0,39% y, adicionalmente, en los extremos de cada muro se colocó una barra de acero de refuerzo #2 (diámetro = 6,35mm) (fig. 1 ).

Figura 1. Composición de la armadura y mallado de los muros prefabricados de ferrocemento.

La resistencia a compresión del mortero (${\textstyle f_{cm}^{'}}$ ) a los 28 días fue de 33 MPa, el módulo de elasticidad (E_c ) del compuesto fue de 11.050 MPa, el esfuerzo de cedencia (σ_ry ) de la malla de refuerzo fue de 282 MPa, y su módulo de elasticidad de (E_r ) 81 GPa. El esfuerzo a la fluencia de las barras #2 fue de 420 MPa.

2.2. Descripción del prototipo

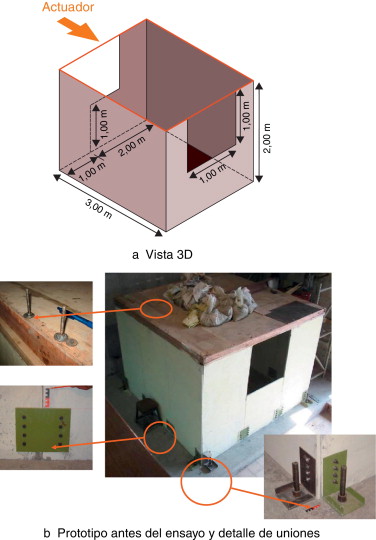
El prototipo fue construido con muros prefabricados de pared delgada de ferrocemento. Cada muro tiene 1,0 m de ancho, 2,0 m de altura y 20 mm de espesor. Con estos muros se construyeron cada una de las paredes del prototipo de vivienda. El prototipo tiene 3,0 m de largo y 3,0 m de ancho y una altura de 2,0 m. Cada barra #2 fue roscada en los extremos superiores para sujetar los muros a la estructura de cubierta mediante tuercas. En la parte inferior los muros fueron anclados a una cimentación rígida de concreto mediante platinas de acero. En la figura 2 a se muestra el esquema en 3D y en la figura 2 b el prototipo antes del ensayo, con la estructura de cubierta, la cual fue elaborada a partir de vigas rígidas de madera longitudinal y transversalmente. Posteriormente, la cubierta fue cargada con sacos de arena uniformemente distribuidos para simular las cargas gravitacionales habituales en este tipo de vivienda. La figura 2 b también detalla los medios de unión implementados en el prototipo.

Figura 2. Vista general de un prototipo de vivienda de ferrocemento.

2.3. Instrumentación e historia de carga sobre el prototipo

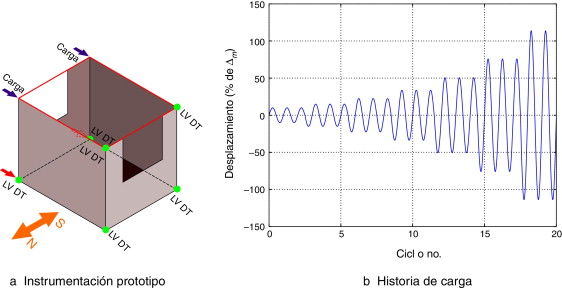
Para medir los desplazamientos laterales se utilizó un conjunto de sensores de movimiento (LVDT, según sus siglas en inglés). Todos los datos de carga y deformación fueron registrados en un computador. En la figura 3 a, las flechas de color azul indican puntos de aplicación de fuerzas, las flechas rojas indican puntos de medición de desplazamiento en la base y los puntos verdes indican puntos de medición de desplazamiento lateral en la parte superior del prototipo. En la figura 3 a se muestra la distribución de LVDT. El prototipo fue sometido a una historia de carga cíclica usando un actuador hidráulico. En la figura 3 b se muestra la historia de carga cíclica que le fue aplicada, donde Δ_m representa el desplazamiento correspondiente a la carga máxima.

Figura 3. Configuración del ensayo.

3. Resultados experimentales. Resistencia a carga cíclica

3.1. Comportamiento histerético y resistencia

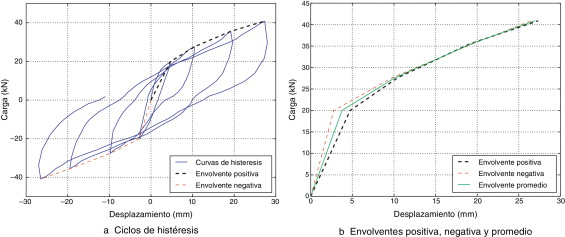
En la figura 4 a se muestra la relación carga-desplazamiento. Se puede observar que el sistema gana resistencia y exhibe muy poco estrangulamiento. En la figura 4 b se muestran cada una de las envolventes de los lazos de histéresis y la envolvente promedio, que se ajusta bien.

Figura 4. Ciclos de histéresis y envolventes.

Las envolventes obtenidas a partir de los ensayos cíclicos mostraron una capacidad de carga lateral de 40,88 kN. Usando la norma ASTM E2126–11 [18] y las envolventes de los ciclos de histéresis, se calcularon parámetros estructurales de la casa de ferrocemento, que se muestran en la tabla 1 .

Tabla 1. Parámetros calculados a partir de los ensayos de carga cíclica de acuerdo a la norma ASTM E2126–11

Rigidez elástica (Ki )	Resistencia elástica a cortante (νpeak )	Carga de cedencia (Pyield )	Carga absoluta máxima (Ppeak )	Despl. último (Δu )	Despl. de cedencia (Δyield )	Ductilidad (μ  = Δu /Δyield )
kN/mm	kN/m	kN	kN	mm	mm
5,33	13,63	32,23	40,88	26,91	6,05	4,45

3.2. Disipación de energía y amortiguamiento

En la actualidad, los diseños estructurales se basan en análisis de fragilidad, los cuales buscan que los elementos estructurales disipen la energía transmitida por fuerzas dinámicas externas por medio de histéresis con el fin de incrementar el margen de seguridad de dichos elementos y evitar una falla súbita o un estado de daño frágil del material.

Una forma de cuantificar la cantidad de energía que disipa una estructura cuando se le somete a cargas cíclicas o dinámicas es calculando el área encerrada por los ciclos de histéresis (fig. 4 a). Otra forma de evaluar la capacidad de un material en términos de disipación de energía es por medio del cálculo del amortiguamiento viscoso equivalente (ξ_eq ), que se define como [19]  and [20] :

$\xi _{eq}={\frac {E_{i}}{4\pi \left(E_{e}\right)_{i}}}\cdot 100\%$

( 1)

donde E_i representa la energía disipada por el elemento estructural en el ciclo de carga i   -ésimo, y ${\textstyle \left(E_{e}\right)_{i}}$ es la energía potencial elástica almacenada en un sistema lineal elástico equivalente cuando se alcanza el desplazamiento máximo en el ciclo i -ésimo en condiciones estáticas.

Se puede calcular la energía disipada en el ciclo i -ésimo E_i a partir de los ciclos de histéresis experimentales. La energía potencial elástica almacenada en un sistema lineal elástico ${\textstyle \left(E_{e}\right)_{i}}$ está dada por el área bajo la curva de carga versus el desplazamiento obtenida en los ensayos cíclicos. Esta viene dada por el área de un triángulo rectángulo cuya base es igual al desplazamiento máximo positivo medido en el modelo ${\textstyle \left(\Delta _{max}\right)_{i}}$ y cuya altura ${\textstyle \left(P_{m}\right)_{i}}$ es la carga pico promedio del ciclo analizado, es decir:

$\left(P_{m}\right)_{i}={\frac {\left|\left(P_{max}\right)_{i}\right|+\left|\left(P_{min}\right)_{i}\right|}{2}}$

( 2)

donde ${\textstyle \left(P_{max}\right)_{i}}$ y ${\textstyle \left(P_{min}\right)_{i}}$ representan los valores máximos y mínimos que alcanza la carga en el ciclo i   -ésimo. Con estos datos, la energía ${\textstyle \left(E_{e}\right)_{i}}$ se puede calcular como sigue:

$\left(E_{e}\right)_{i}={\frac {\left(P_{m}\right)_{i}\left(\Delta _{max}\right)_{i}}{2}}$

( 3)

La tabla 2 muestra las energías E_i y ${\textstyle \left(E_{e}\right)_{i}}$ , las derivas y el amortiguamiento viscoso equivalente para cada nivel de derivas.

Tabla 2. Disipación de energía y amortiguamiento viscoso equivalente

Ciclo	Ei (kN·mm)	Ee (kN·mm)	Deriva (%)	ξeq (%)
1	69,6075	47,4000	0,19	11,69
2	306,4601	144,7478	0,51	16,85
3	853,4850	348,7455	0,98	19,47
4	1301,398	571,7068	1,37	18,11

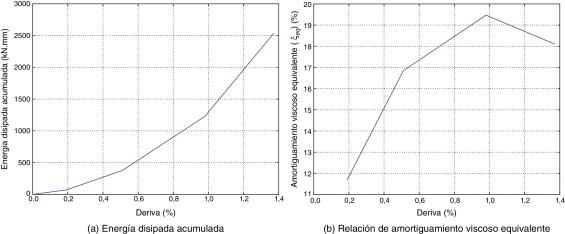
La figura 5 muestra la energía disipada acumulada y el amortiguamiento viscoso equivalente como una función de la deriva. El sistema alcanza mayor disipación de energía con el incremento en los desplazamientos. Además, el amortiguamiento viscoso equivalente está por encima de los valores usuales para sistemas a base de concreto.

Figura 5. Energía de disipación y amortiguamiento del prototipo de ferrocemento.

El modelo exhibió pérdida de energía. Sin embargo, la forma redondeada de los ciclos de histéresis y el área encerrada por dichos ciclos sugieren que el sistema tiene buena capacidad de disipación de energía conforme la deriva aumenta. La forma de los ciclos de histéresis efectivamente determina la habilidad de la vivienda para disipar energía cuando es sometida a cargas mas allá de su rango lineal. Por otro lado, se puede observar un pequeño grado de estrangulamiento (pinching) en el centro de las curvas de histéresis debido a la apertura y cierre de las grietas que se generaron en la superficie de los muros, lo cual afecta la habilidad del sistema para disipar energía. Estos efectos se tendrán en cuenta en el modelo dinámico no lineal propuesto más adelante.

3.3. Coeficiente de capacidad de disipación de energía

El coeficiente de capacidad de disipación de energía (R_μ ) es un concepto orientado al diseño que aproxima el comportamiento no lineal de sistemas estructurales cuando son sometidos a cargas sísmicas. Dicho coeficiente se usa en la mayoría de los reglamentos de construcción sismorresistente con el fin de reducir la magnitud de las cargas evaluadas desde un punto de vista elástico.

Con el fin de determinar R_μ , se empleó el modelo propuesto por Takada et al. [21] , el cual es independiente del período de la estructura:

$R_{\mu }=\varepsilon {\sqrt {2\mu -1}}$

( 4)

donde μ es la ductilidad y ɛ es un factor de ajuste que representa el grado de desviación de la relación R_μ versus μ   de la expresión de energía ${\textstyle {\sqrt {2\mu -1}}}$ . Algunos resultados obtenidos a partir de simulaciones de Monte Carlo indican que el valor promedio de ɛ varía entre 1,05 y 1,34 (véanse Miranda y Bertero [22] y Takada et al. [21] para más detalles). Tomando ɛ = 1,05, se tiene que R_μ = 2,95, y tomando ɛ = 1,34, se tiene que R_μ = 3,77; estos valores de R_μ son similares a aquellos usados por Wainshtok Rivas [14] para el diseño sismorresistente de viviendas prefabricadas de ferrocemento en Cuba.

4. Modelo dinámico no lineal

El modelo de histéresis de Bouc-Wen-Baber-Noori (BWBN) (Baber y Wen [23] , Baber y Noori [24] ) es uno de los modelos más populares en el área de dinámica estructural debido a que no solo es capaz de modelar efectos de degradación en el material, sino que también simula el efecto de estrangulamiento (pinching) . El modelo ha sido usado en una amplia variedad de aplicaciones, tales como vibración de estructuras de concreto [25] , estructuras de madera [26]  and [27] , entre otros.

Considere un sistema de un solo grado de libertad que posee una componente de fuerza de restauración histerética y un componente de amortiguamiento viscoso, descrito por la ecuación diferencial:

${\ddot {x}}(t)+2\xi \omega _{0}{\dot {x}}(t)+\alpha \omega _{0}^{2}x(t)+(1-\alpha )\omega _{0}^{2}z(t)=u(t)$

( 5)

con condiciones iniciales ${\textstyle {\dot {x}}(0)=v_{0}}$ y ${\textstyle {\ddot {x}}(0)=a_{0}}$ ; donde ${\textstyle v_{0}}$ y a₀ representan la velocidad y la aceleración inicial del sistema, x (t ) denota el desplazamiento en el tiempo t   , ${\textstyle \omega _{0}^{2}:=k_{i}/m}$ es el cuadrado de la frecuencia pseudonatural del sistema no lineal, m es la masa del sistema, ξ es la relación de amortiguamiento viscoso, u (t ) es la excitación externa (aceleración) y α  : = k_f /k_i es la relación de rigidez de postcedencia k_f a rigidez de precedencia (elástica) k_i . La componente histerética está gobernada por el desplazamiento histerético z , que viene dado por la siguiente ecuación diferencial:

${\begin{array}{l}\displaystyle {\dot {z}}(t)=\\\displaystyle =h(t){\frac {A(t){\dot {x}}(t)-\nu (t)\left(\beta \vert {\dot {x}}(t)\vert \vert z(t)\vert ^{n-1}z(t)+\gamma {\dot {x}}(t)\vert z(t)\vert ^{n}\right)}{\eta (t)}}\end{array}}$

( 6)

con condición inicial z (0) = 0. Los parámetros β , γ y n controlan la forma de los ciclos de histéresis, y los parámetros ν (t ), η (t ) y h (t ) están asociados con las funciones de degradación de resistencia, rigidez y el fenómeno de estrangulamiento, respectivamente. Dichas funciones de degradación están definidas en función de la energía histerética absorbida ɛ (t ):

$\nu (t):=\nu _{0}+\delta _{\nu }\varepsilon (t)\quad A(t):=A_{0}-\delta _{A}\varepsilon (t)\quad \eta (t):=\eta _{0}+\delta _{\eta }\varepsilon (t)$

( 7)

La función de pinching h (t ) viene dada por la siguiente ecuación:

$h(t):=1-\varsigma _{1}(t)exp\left(-{\frac {(z(t)sign({\dot {x}}(t))-qz_{u})^{2}}{(\varsigma _{2}(t))^{2}}}\right)$

( 8)

donde z_u es el valor último de z ,

$z_{u}={\frac {1}{\nu (t)(\beta +\gamma )}}n$

( 9)

y

${\begin{array}{l}\displaystyle \varsigma _{1}(t):=(1-exp\left(-p\varepsilon (t)\right))\varsigma _{0}\quad \varsigma _{2}(t):=(\psi _{0}+\delta _{\psi }\varepsilon (t))(\lambda +\\\displaystyle +\varsigma _{1}(t)).\end{array}}$

( 10)

Las constantes p , q , ς₀ , ψ₀ , δ_ψ y λ definen la forma y la severidad del pinching .

4.1. Identificación de parámetros del modelo de BWBN para la casa de ferrocemento

Se empleó una nueva metodología propuesta por [16] , que usa la optimización multiobjetivo por medio de algoritmos evolutivos para la identificación de los parámetros de modelos de histéresis tipo Bouc-Wen. El conjunto de parámetros por identificar lo representa el vector p :

${\mbox{p}}=\left[\xi ,\alpha ,\beta ,\gamma ,n,\nu _{0},\delta _{\nu },A_{0},\delta _{A},\eta _{0},\delta _{\eta },p,\zeta _{0},\psi _{0},\delta _{\psi },\lambda ,q\right]^{T}$

( 11)

La tabla 3 muestra los resultados del proceso de identificación. Los primeros dos parámetros (m , k_i ) se obtuvieron a partir del ensayo experimental.

Tabla 3. Parámetros identificados del modelo de histéresis de BWBN para la casa prefabricada de ferrocemento. Unidades: masa [kg], rigidez inicial [kN/mm], relación de amortiguamiento viscoso [%]; los otros parámetros son adimensionales.

Parámetro	Valor
m	1,060
ki	5,73
ξ	14,50
α	0,1759
β	0,3272
γ	−0,1730
n	1,6180
ν0	0,5214
δν	1,2473
A0	0,9827
δA	−0,4370
η0	0,8210
δη	3,8806
p	1,7267
ζ0	−7,3316
ψ0	0,0031
δψ	−0,4493
λ	3,1319
q	-1,1645

Se puede observar que el valor de ξ es similar al calculado en la sección 3.2 , y está dentro del rango mostrado en la figura 5 (b).

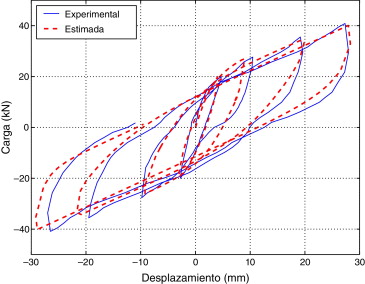
La figura 6 compara las histéresis obtenidas experimentalmente y la generada por el modelo matemático. Se puede observar un muy buen ajuste entre las dos curvas, lo cual demuestra que los parámetros estimados son buenos para propósitos de simulación. El desplazamiento experimental máximo fue 27,97 mm, y el desplazamiento máximo estimado fue 29,16 mm, lo cual representa un error del 4%. También se puede observar que los efectos de degradación fueron bien modelados por el modelo propuesto.

Figura 6. Respuesta experimental y estimada del sistema.

4.2. Evaluación sísmica de la casa prefabricada de ferrocemento

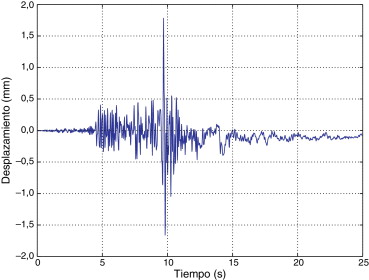
Con el fin de evaluar la capacidad del modelo para estimar los desplazamientos que sufre la vivienda cuando se aplica a la estructura una excitación externa aleatoria, el sistema de un solo grado de libertad equivalente fue sometido al sismo de 1994 de Northridge [28] , y se usaron los parámetros registrados en la tabla 3 en el modelo matemático de BWBN. En la figura 7 se muestra la respuesta simulada de la vivienda de ferrocemento.

Figura 7. Respuesta estimada de la casa de ferrocemento cuando es sometida al sismo de 1994 de Northridge.

Los códigos de diseño sísmico en muchos países buscan mantener bajo control el daño de una estructura cuando esta es sometida a sismos de diferente magnitud. Para cada nivel de intensidad se pueden predecir diferentes escenarios de daño. En Colombia, para la construcción de viviendas que usen sistemas estructurales prefabricados, basados en muros de pared delgada, la deriva máxima entre pisos debe ser inferior a 1/200; esto es aplicable a todo tipo de escenarios de daño y zonas de actividad sísmica (desde 0,05 g hasta 0,9 g). En este caso, el desplazamiento máximo permisible para la casa de ferrocemento usada en la campaña experimental es de 10 mm, y el desplazamiento máximo calculado usando como señal de entrada el sismo de 1994 de Northridge (intensidad: 0,8 g) fue de 1,78 mm, el cual es un 82% menos que el desplazamiento máximo permisible de acuerdo al Reglamento Colombiano de Construcción Sismo Resistente [29] .

5. Conclusiones

En este artículo se presentó el comportamiento histerético exhibido por un prototipo de vivienda a escala real construido con muros prefabricados de ferrocemento de pared delgada y se propuso un sistema dinámico de un solo grado de libertad con características de degradación y estrangulamiento (pinching) para la evaluación del comportamiento no lineal de la estructura.

A partir del ensayo de carga cíclica se identificaron los parámetros para la evaluación estructural del sistema. Se determinó la rigidez elástica, la resistencia a cortante, la resistencia máxima, la ductilidad, la capacidad de disipación de energía, el amortiguamiento y el coeficiente de capacidad de disipación de energía. El coeficiente de disipación de energía permitirá diseñar este tipo de sistemas de vivienda de acuerdo con los reglamentos de construcción sismorresistente.

El modelo dinámico no lineal propuesto se ajusta bien a la respuesta experimental bajo cargas aleatorias y es estructuralmente robusto para el análisis sísmico no lineal de las viviendas de ferrocemento.

La evaluación sísmica de la vivienda prefabricada de ferrocemento, utilizando el modelo no lineal propuesto y sismos reales, reveló un comportamiento satisfactorio en términos de carga-deflexión del prototipo ensayado, que exhibió desplazamientos máximos por debajo del 80% del máximo permisible, en este caso comparado con el Reglamento Colombiano de Construcción Sismo Resistente.

Agradecimientos

Este estudio fue desarrollado dentro del proyecto de investigación: «Estudio y comportamiento sísmico de estructuras de materiales económicos de construcción, tales como el ferrocemento y otros materiales, por medio del análisis experimental y el análisis numérico determinista y estocástico», Proyecto DIMA, código HERMES No. 12870. Los autores agradecemos a la Universidad Nacional de Colombia, sede Manizales, al Laboratorio de Estructuras de la Universidad Nacional de Colombia, sede Manizales, y demás entidades por el apoyo brindado para la ejecución de este estudio.

References

1. [1] D. Bedoya-Ruiz; Estudio de resistencia y vulnerabilidad sísmicas de viviendas de bajo costo estructuradas con ferrocemento. Ph. D. dissertation;; Universidad Politécnica de Catalunya (2005)
2. [2] A.E. Naaman; Ferrocement and laminated cementitious composites. Michigan: Ed.; 3000, Techno Press (2000)
3. [3] D. Bedoya-Ruiz; Experiencias sobre residuos agro-industriales en la construcción de vivienda de ferrocemento; Capítulo de Libro: Aprovechamiento de residuos agro-industriales como fuentes sostenibles de materiales de construcción. Cap. 23. CYTED, acción VALORES y Universidad Politécnica de Valencia. Editorial UPV (2011)
4. [4] El-Deps, M.K., Machado, Jr., de Hanai, J.B. y Takeya, T. Ferrocement sandwich walls: Research projects by the Sao Carlos Group (Brazil). En ferrocement 6: Lambot symposium, proceeding of the sixth international symposium on ferrocemento. Editor: A.E. Naaman. Univesity de Michigan, Ann Arbour. Junio. pp. 493-506.
5. [5] J. Castro; Application of ferrocement in low-cost housing in Mexico; American Concrete Institute, 61 (1979), pp. 143–146
6. [6] V.G. Gokhale; System built ferrocemento housing; J. Ferrocement, 13 (1) (1983), pp. 37–42
7. [7] Olvera López, A. Applications of prefabricated ferrocement housing in Mexico. En ferrocement 6: Lambot symposium, proceeding of the sixth international symposium on ferrocemento. Editor: A.E. Naaman. Univesity de Michigan, Ann Arbour. Junio. pp. 95-108.
8. [8] H. Wainshtok Rivas; Low-cost housing built with ferrocement precast elements; J. Ferrocement, 24 (1) (1994), pp. 29–34
9. [9] A. Abdullah; Applications of ferrocement as a low-cost construction material in Malaysia; J. Ferrocement, 25 (2) (1995), pp. 123–127
10. [10] Machado, Jr., E. F. Building system for low-cost ferrocement housing. En ferrocement 6: Lambot symposium, proceeding of the sixth international symposium on ferrocemento. Editor: A.E. Naaman. Univesity de Michigan, Ann Arbour. Junio. pp. 129-138.
11. [11] ECOSUR. Red para el hábitat económico y ecológico, 2014 [consultado 15 Oct 2013]. Disponible en www.ecosur.org .
12. [12] P.L. Nervi; Ferrocement: Its characteristics and potentialities; Library translation No. 60, Cement and Concrete association, London (1956) July
13. [13] D. Bedoya-Ruiz, J. Farbiarz, J. Hurtado, Ll y Pujades; Ferrocemento: un acercamiento al dise no sismo resistente; Monografías de Ingeniería sísmica, Centro Internacional de Métodos Numéricos (CIMNE) (2002)
14. [14] H. Wainshtok Rivas; Model seismic resistant ferrocement houses; J. Ferrocement, 34 (2) (2004), pp. 363–371
15. [15] D. Bedoya-Ruiz, J. Hurtado, Ll y Pujades; Experimental and analytical research on seismic vulnerability of low-cost ferrocement dwelling houses; Struct. Infrastruct. Eng., 6 (1-2) (2010), pp. 55–62
16. [16] G.A. Ortiz, D.A. Álvarez, D. y Bedoya-Ruiz; Identification of Bouc-Wen type models using multi-objective optimization algorithms; Comput. Struct., 114-115 (1) (2013), pp. 121–132
17. [17] D. Bedoya-Ruiz, G.A. Ortiz, D.A. Alvarez; Behaviour under cyclic loading of precast ferrocement thin walls: An experimental and analytical research; Rev. Ing. Invest. UNAL, 34 (1) (2014), pp. 29–35
18. [18] ASTM Standard E2126-11. Standard test methods for cyclic (reversed) load test for shear resistance of vertical elements of the lateral force resisting systems for buildings. Tech. Rep.; ASTM International; PA, USA; 2011.
19. [19] M.J.N. Priestley; Seismic design and retrofit of bridges; John Wiley & Sons Inc (1996) ISBN 978-0471579984
20. [20] Chopra, A. K.; Dynamics of Structures; Theory and Applications to Earthquake Engineering. Berkeley (3^rd ed.), Prentice Hall Inc, California, USA (2006)
21. [21] T. Takada, H.H.M. Hwang, M. y Shinozuka; Response modification factor for multiple-degree-of-freedom systems; Proceedings of the 9^th World Conference on Earthquake Engineering5 (1988), pp. 129–134
22. [22] E. Miranda, V. y Bertero; Evaluation of strength reduction factors for earthquake-resistant design; Earthq. Spectra, 10 (2) (1994), pp. 357–379
23. [23] T.T. Baber, Y.K. y Wen; Random Vibration of hysteretic degrading systems; J. Eng. Mech., 107 (6) (1981), pp. 1069–1087
24. [24] T.T. Baber, M.H. y Noori; Random Vibration of Degrading, Pinching Systems; J. Eng. Mech., 111 (8) (1985), pp. 1010–1026
25. [25] S.K. Kunnath, J.B. Mander, L. y Fang; Parameter identification for degrading and pinched hysteretic structural concrete systems; Eng. Struct., 19 (3) (1997), pp. 224–232
26. [26] G.C. Foliente; Hysteresis Modeling of Wood Joints and Structural Systems; J. Struct. Eng., 121 (6) (1995), pp. 1013–1022
27. [27] N. Ajavakom, C.H. Ng, F. y Ma; Performance of nonlinear degrading structures: Identification, validation, and prediction; Comput. Struct., 86 (7-8) (2008), pp. 652–662
28. [28] CESMD. Center for Engineering Strong Motion Data [consultado 15 Oct 2013]. Disponible en: http://www.strongmotioncenter.org/cgi-bin/CESMD/search1.pl; 2013. Northridge earthquake (1994), Santa Monica. Station 24538.
29. [29] Asociación Colombiana de Ingeniería Sísmica AIS. Reglamento Colombiano de Construcción Sismo Resistente NSR-2010. Tech. Rep.; AIS; Bogotá, Colombia; 2010.