Simulation of a pultrusion process of composite material profiles reinforced with carbon fiber for aeronautical applications

1 Introducción

El presente documento se enmarca dentro del proyecto PULTRUBEAM, que tiene por objetivo madurar la tecnología de Pultrusión, para la fabricación de forma continua y fuera de autoclave de perfiles estructurales en material compuesto, utilizando como refuerzo un tejido no entrelazado (non-crimp fabric o NCF).

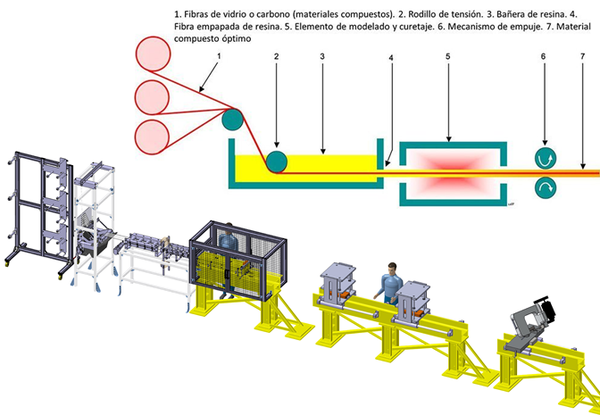
El proceso de Pultrusión puede ser entendido de forma resumida observando la Figura 1. En una primera etapa se encuentra la zona donde se posicionan los rollos de refuerzo de fibra de carbono “Non Crimp Fabric” (NCF), a continuación un sistema de guiado lo conduce hasta la cubeta de impregnación, donde se aplica un baño de resina, para posteriormente entrar en la zona de rodillos. En una primera zona los rodillos de impregnación eliminan el exceso de resina a la vez que aseguran el impregnado del interior del tejido gracias a la aplicación de presión. Posteriormente el perfil atraviesa una segunda zona de rodillos donde se realiza el conformado. El curado del perfil se produce dentro de un molde cerrado (hilera), y a continuación se procede a un corte a la medida que requiera su aplicación. En la zona de tiro un sistema de arrastre proporciona la tracción necesaria para poder llevar a cabo todo el proceso, que se desarrolla de forma continua y permite fabricar perfiles a una velocidad constante.

La zona de estudio en lo relativo a la modelización con modelos de elementos finitos (FEM) será la zona de la hilera, pues en ella se lleva a cabo el calentamiento de las placas para el curado de la resina, que provoca un endurecimiento de la misma. Este calentamiento ha demostrado en etapas anteriores que induce la deformación de los moldes influyendo considerablemente a la forma del perfil. Además, en ella se lleva a cabo la polimerización o curado de la resina, reacción química en la que se produce una reorganización de los enlaces atómicos que provoca el endurecimiento de la resina. Este proceso se inicia gracias a la aplicación de temperatura sobre los moldes cerrados utilizando placas calefactoras, tres para el molde inferior y otras tres para el superior. Al finalizar el curado, el perfil ya posee las propiedades mecánicas y de calidad finales.

Son numerosas las variables que intervienen durante el proceso de pultrusión, por lo que, con el fin de proporcionar un conocimiento detallado del proceso que permita seleccionar los valores óptimos, se ha recurrido a la creación de modelos FEM, con el que se pueda simular el proceso, y que utilizaremos como herramienta de predicción y análisis de diversos aspectos relativos al proceso.

En concreto se desea conocer el nivel de esfuerzos y deformaciones que aparecen en la fibra y en los moldes como consecuencia de la dilatación térmica que tiene lugar al incrementar la temperatura. Al dilatarse las piezas, aparecen esfuerzos de contacto que deben ser evaluados. También se desea comprobar qué zonas de la hilera tienden a separarse entre ellas o por el contrario a contactar, dependiendo de su localización. El software elegido para el desarrollo del modelo es Patran/Nastran, por ser adecuado para esta simulación, especialmente por su capacidad de incorporar gap lineales como método efectivo para simular los contactos y para el análisis detallado del molde se he seleccionado el software Abaqus/CAE 6.13.2. por su capacidad de simular procesos no lineales, potencia de cálculo y por ser adecuado para análisis térmicos.

Figura 1. Proceso de pultrusión.

Por último, con el fin de proporcionar un conocimiento detallado del proceso, que permita seleccionar los valores óptimos, se ha recurrido a la creación de un modelo FEM, con el que se pueda simular el proceso de curado, y que utilizaremos como herramienta de predicción y análisis de grado de curado. El software elegido también es Abaqus/CAE 6.10.2.

El método será implementado para estudiar y deducir el grado de curado para dos especímenes diferentes: un perfil rectangular plano para desarrollar el proceso y un perfil de sección en L como demostrador.

2 Formulación termomecánica

2.1 Formulación del balance energético

De acuerdo con la ecuación de conducción de calor de Fourier y con la ley de conservación de la energía, el modelo matemático aplicable a la reacción de curado queda establecido por la ecuación para el balance energético [1, 2]:

Figura 2.Volumen de control.

${\frac {\partial }{\partial t}}\int _{V}^{}\rho udV=-\int _{S}^{}{\phi }_{conv}\cdot ndS-\int _{S}^{}{\phi }_{diff}\cdot ndS+\int _{S}^{}{u}_{genn}\cdot dV$

Esta ecuación pude ser reescrita, en coordenadas cartesianas tanto para el molde como para el composite asumiendo que la densidad del material es constante, el calor específico así como la conductividad del material en todas su direcciones, considerándose despreciable el cambio debido a la polimerización de la resina. Los subíndices c y m corresponden al perfil de material compuesto y al molde metálico respectívamente.

${\rho }_{m}{Cp}_{m}\left({\frac {\partial T}{\partial t}}\right)={k}_{x,m}{\frac {{\partial }^{2}T}{\partial {x}^{2}}}+{k}_{y,m}{\frac {{\partial }^{2}T}{\partial {y}^{2}}}+{k}_{z,m}{\frac {{\partial }^{2}T}{\partial {z}^{2}}}\quad \quad \quad \quad \quad \quad \quad (1)$

${\rho }_{c}{Cp}_{c}\left({\frac {\partial T}{\partial t}}+u{\frac {\partial T}{\partial z}}\right)=$

Donde T es la temperatura del sistema, t es el tiempo de la simulación, C_p es el calor específico, u la velocidad del de desplazamiento del perfil en el molde de pultrusión, ρ la densidad y k_x, k_y y k_z son las conductividades en las direcciones x, y, z del sistema. Las propiedades del material compuesto se calculan mediante la regla de las mezclas [3]:

${\rho }_{c}=\left(1-{V}_{r}\right){\rho }_{f}+{V}_{r}{\rho }_{r}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (3)$

${Cp}_{c}={\frac {\left(1-{V}_{r}\right){\rho }_{f}{Cp}_{f}+{V}_{r}{\rho }_{r}{Cp}_{r}}{{\rho }_{c}}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\,(4)$

${k}_{i,c}={\frac {{k}_{r}{k}_{f}{\rho }_{c}}{\left(1-{V}_{r}\right){\rho }_{f}{k}_{f}+{V}_{r}{\rho }_{r}{k}_{r}}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (5)$

Donde V es la fracción en volumen. El proceso de curado de la resina se lleva a cabo mediante una reacción química, llamada polimerización, que se inicia gracias al aumento de temperatura inducido por los moldes sobre la fibra situada dentro de la hilera. Durante esta polimerización o curado de la resina, se produce una reorganización de los enlaces atómicos, que tiene como resultado un endurecimiento de la misma. Esta reacción es exotérmica, por lo que implicará un aumento adicional de la temperatura en la fibra, al liberarse energía en forma de calor, introducida en la ecuación (2) con el término Q.

2.2 Formulación de la cinética de reacción

El flujo de calor interno “Q” generado por la reacción exotérmica en un instante “t”, se puede expresar de la siguiente manera [3]:

$Q={V}_{r}{\rho }_{c}{H}_{tr}{R}_{r}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (6)$

Donde:

• V_r es la fracción volumétrica de resina respecto al volumen total

• ρ_r es la densidad de la resina (kg/m³)

• H_tr: calor total de la reacción de curado (J/Kg)

• R_r: “rate” de curado de la resina en el instante “t” (1/s)

El grado de curado de la resina (α) en un instante “t” se define como el cociente entre la cantidad de calor generado durante la reacción de curado hasta el instante “t” (H(t)), y el calor total generado en el curado completo (H_tr):

$\alpha ={\frac {H(t)}{{H}_{tr}}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,(7)$

El grado de curado por lo tanto es un valor que varía entre 0 y 1, indicando el porcentaje de resina que ya ha completado el ciclo de curado en un determinado instante. R_r se define como la variación del grado de curado con el tiempo, y se puede expresar empíricamente, mediante un modelo cinético de curado, como una función de la temperatura K(T) multiplicada por una función del grado de curado f(α):

${R}_{r}\left(\alpha ,T\right)={\frac {\partial \alpha }{\partial t}}={\frac {1}{{H}_{tr}}}{\frac {\partial H(t)}{\partial t}}=K\left(T\right)\cdot f\left(\alpha \right)\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (8)$

La función K(T) se define mediante la relación de Arrhenius:

$K\left(T\right)={K}_{o}{e}^{-{\frac {E}{RT}}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\,(9)$

Donde:

• Ko: constante propia de la resina (1/s)

• E: energía de activación de la resina para iniciar el curado (J/mol)

• R: constante universal de los gases (J/mol ºK)

• T: temperatura (ºK)

• n: n-ésimo coeficiente de la reacción de polimerización

En cuando a la función α, existen diversos modelos cinéticos de curado para su definición:

• f(α)=(1-α): Modelo de primer orden

• f(α)=(1-α)ⁿ: Modelo de n-ésimo orden

• f(α)=(1-α)ⁿ(1+Kα): Modelo de n-ésimo orden con autocatalización

• f(α)= α^m(1-α)ⁿ: Modelo Prout-Tompkins de n-ésimo orden con autocatalización

En este caso se ha escogido el modelo de primer orden [4], por lo que el rate de curado se puede obtener como:

${\textstyle K\left(T\right)={K}_{o}{e}^{-{\frac {E}{RT}}}{(1-\alpha )}^{}}$

(10)

Las constantes H_tr, K_o y E se pueden obtener mediante tests DSC con metodología estándar ASTM E698 aplicando el método Kissinger [5].

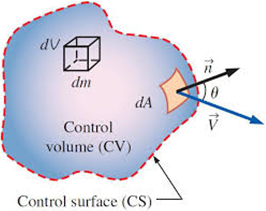
Con el fin de conocer el grado de curado en cada punto de la hilera, es necesario implementar un método numérico basado en incrementos, aplicados sobre un cierto volumen de control de la resina [5], que simula el proceso del paso del material compuesto a través de la hilera. Los datos de partida son las temperaturas en la fibra, que han sido obtenidos en puntos distanciados 9mm dentro de la hilera, al ser éste el tamaño de malla utilizado en la simulación FEM. Partiendo de la condición inicial en la que α₀=0 (grado de curado nulo), después de un incremento de tiempo Δt, el grado de curado α en el primer intervalo se obtiene como:

${\alpha }_{1}={\alpha }_{o}+\Delta \alpha ={\alpha }_{o}+\left({\frac {\Delta \alpha }{\Delta t}}\right)\Delta t\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (11)$

De forma genérica para un intervalo i:

${\alpha }_{i}={\alpha }_{i-1}+\Delta \alpha ={\alpha }_{i-1}+\left({\frac {\Delta \alpha }{\Delta t}}\right)\Delta t\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,(12)$

donde Δα/Δt es el rate de curado R_r, que como se expuso anteriormente, puede expresarse como función de α y de T (Arrhenius), luego sustituyendo en la anterior expresión se obtiene:

${\textstyle {\alpha }_{i}={\alpha }_{i-1}+{K}_{o}{e}^{-{\frac {E}{RT}}}{(1-\alpha )}^{}\Delta t\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\,(13)}$

Como la temperatura es conocida gracias a los análisis previos con FEM, el único dato que falta para poder calcular α es el incremento de tiempo de cada intervalo, el cual es constante durante el proceso, y se obtiene como:

${\textstyle \Delta t={\frac {l}{u}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (14)}$

Donde:

• u: velocidad de tirado

• l: longitud del volumen de control considerado

Como se expuso anteriormente, para el análisis se considera una longitud l igual al tamaño de mallado de la fibra en el FEM. El incremento del grado de curado en un intervalo i es:

$\Delta \alpha ={\alpha }_{i}-{\alpha }_{i-1}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (15)$

Una vez conocidos Δα y Δt, se puede obtener el flujo térmico (W/m³) generado por el curado durante el intervalo:

$Q={V}_{r}{\rho }_{c}{H}_{tr}{R}_{r}={V}_{r}{\rho }_{c}{H}_{tr}{\frac {{\Delta \alpha }^{i}}{\Delta t}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (16)$

Este flujo genera a su vez un incremento en la temperatura de la resina, que se puede cuantificar empleando la siguiente ecuación, que lo relaciona con el flujo másico del proceso:

$Q=[({Cp}_{r}\cdot \Delta T+{C}_{L})\cdot {\overset {\cdot }{m}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\,(17)$

Donde:

• Q: flujo térmico generado (w/m³)

• C_pr: calor específico de la resina (J/KgºK)

• C_L: calor latente de la resina (J/Kg)

• ṁ: flujo másico (Kg/s)

El incremento de temperatura se obtiene despejando de la anterior ecuación (17):

$\Delta T={\frac {Q}{{\overset {\cdot }{m}}{Cp}_{r}}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\,(18)$

Se establece la hipótesis de que no hay cambio de fase, por lo que el calor latente es nulo por considerarse despreciable. El flujo másico es la masa que sale de la hilera por unidad de tiempo, luego se obtiene como:

${\overset {\cdot }{m}}={\rho }_{r}\cdot A\cdot u\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (19)$

Donde:

• ρ_r es la densidad de la resina (kg/m³)

• A: área de salida de la hilera (m²)

• u: velocidad de tirado(m/s)

Una vez conocido el incremento de temperatura (ΔT) producido en el intervalo i debido a la reacción de curado, es posible calcular un nuevo grado de curado corregido α_c. Se hace la hipótesis de que este calor tarda un tiempo igual a Δt en ser liberado, por lo que ΔT se añade a la temperatura de la hilera obtenida en el FEM para el intervalo siguiente (i+1).De esta forma, el cálculo del grado de curado corregido para el intervalo i+1 se hace considerando una temperatura T_i+1+ΔT. A continuación se resume el proceso de cálculo completo paso a paso:

1. Conocida la temperatura de la resina en un punto de la hilera, se puede calcular su grado de curado (α).

2. Conocido α se obtiene el flujo térmico liberado por la reacción de curado (Q).

3. Este flujo Q provoca un incremento de temperatura ΔT que puede ser cuantificado.

4. Dicho ΔT se añade a la temperatura del siguiente intervalo porque tarda en generarse un tiempo igual a Δt.

5. En el siguiente intervalo se obtiene un grado de curado corregido (α_c), considerando T+ΔT.

Por lo tanto, gracias a este método, siendo conocido el perfil de temperaturas de la fibra dentro de la hilera, es posible obtener el grado de curado en cada punto.

3 Modelos numéricos

Los modelos aquí desarrollados corresponden a los casos de pultrusión de perfil plano y de pultrusión de perfil en L. Ambos casos fueron analizados desde el punto de vista termomecánico y termoquímico para estudiar los parámetros del proceso y predecir el grado de curado.

3.1 Pultrusión de perfil plano rectangular. Caso de validación

3.1.1 Descripción del proceso

El perfil plano rectangular fue fabricado en una hilera de pultrusión especialmente diseñada para obtener el perfil. El perfil fabricado y que se ha simulado está formado por tres capas de Non Crimp Fabric (NCF) Saertex 30004156 cuadriaxiales creando el siguiente laminado (0/45/90/-45/0/45/90/-45/0/45/90/-45) con un espesor teórico de 3mm y 170mm de ancho y con la resina (V_f=50%) SICOMIN SR 1331 con endurecedor SH 166 y acelerante SX AC 1MI. El material del molde de pultrusión es acero al carbono TOOLOX 33^®. Las propiedades de los materiales y los valores relativos a la cinética de la reacción [6] de la resina se muestran en las siguientes tablas (Tabla 1 y Tabla 2).

Tabla 1.Propiedades de los materiales

Material	ρ[Kg/m3]	Cp[J/Kg·K]	ki[W/m·K]	αx,y[⁰C-1]
Perfil	993	1100	2.02	1.22·10-6
TOOLOX33®	7860	460	35	1.31·10-5

Tabla 2.Parámetros de cinética de la resina

Vr[%]	ρ[Kg/m3]	Htr[J/Kg]	ko[1/s]	E[J/mol]
Resina	1170	360200	5538494	70670

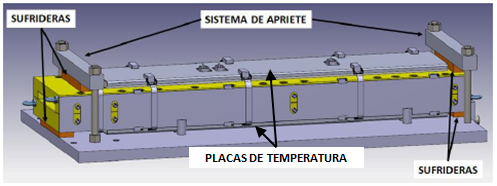
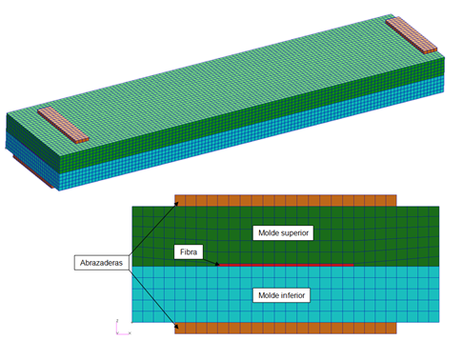
La geometría del modelo se muestra en la siguiente figura. El calentamiento del molde de pultrusión se realiza mediante seis placas calefactoras colocadas en la parte superior e inferior del molde de pultrusión en contacto directo con el acero.

Figura 3.Molde de pultrusión para perfil plano.

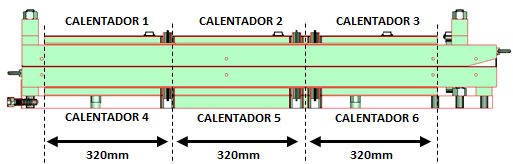
Para poder obtener una temperatura de transición vítrea T_g por encima de 120ºC para la resina de SICOMIN se establece un tiempo de 6min a 140ºC dentro de la hilera lo cual es aceptable para el proceso buscado. La geometría se ha ajustado a la de las placas existentes en el laboratorio; la distancia de la primera placa (Calentador 1) a la entrada del molde es de 140mm, mientras que la distancia de (Calentador 3) a la salida es de 60mm. La anchura de todas las placas es de 150mm, y su longitud de 320mm. Se establecen estos parámetros como los iniciales de operación para la resina y para definir las simulaciones del proceso. Se opta por las condiciones de operación que se muestran en la tabla 3:

Tabla 3. Condiciones de operación para molde con perfil plano

T1[⁰C]	T2[⁰C]	T3[⁰C]	T4[⁰C]	T5[⁰C]	T6[⁰C]
70	140	140	70	140	140

3.1.2 Modelo termomecánico perfil plano

El modelo termomecánico se ha realizado con el software NASTRAN-PATRAN simulando contactos entre las piezas del molde y el perfil con gaps lineales. Se ha creado un FEM, utilizando PATRAN 2012, que está compuesto por las siguientes piezas: abrazaderas, molde inferior, molde superior y perfil de fibra. En las figuras 4 y 5 se puede apreciar varias vistas de los componentes del FEM.

Para el mallado de las piezas con elementos sólidos, se ha definido un tamaño de elemento de 10mm con el elemento sólido CHEXA, un hexaedro con 8 nodos lineales. Se define una temperatura inicial para todas los piezas igual a la temperatura ambiente del laboratorio, fijada en 20ºC aplicándola a todos los nodos del modelo. Los apoyos del modelo, definidos mediante SPCs aplicadas en los nodos correspondientes a abrazaderas y centradores. Según el eje longitudinal el molde inferior se apoya en una placa vertical (no modelizada) en la zona trasera que sirve como tope. Según el eje transversal “x”: el molde inferior se apoya en cuatro cilindros (no modelizados) en los laterales. Se definen SPCs en los nodos que ocupan la superficie de los cilindros. Según el eje vertical “z”: ambos moldes se apoyan en cuatro abrazaderas fijas (modelizadas). Se definen SPCs en los nodos exteriores de las abrazaderas. En las abrazaderas se establecen gaps lineales de contacto.

Los campos de temperatura se han aplicado suponiendo que se ha alcanzado un estado estacionario bajo una evolución lineal. Se definen tres zonas diferenciadas:

• En la entrada de la hilera una primera zona a 70ºC que correspondiente a la primera placa calefactora.

• A continuación una segunda zona a 140ºC, que corresponde a la segunda y tercera placas.

• Se establece la hipótesis de que las abrazaderas conservan su temperatura inicial de 20ºC.

3.1.2.1 Resultados y discusión

La configuración de temperaturas considerada en todos los análisis es de 70ºC en la primera placa y 140ºC en la segunda y tercera. Se procede al análisis del FEM completo con el perfil, que se verá afectada por la dilatación de los moldes, los cuales causarán un estado de deformaciones en ella que se desea conocer y cargas aplicadas sobre el perfil. Para ello se obtienen los desplazamientos verticales y relativos en cada pareja de puntos (1-4, 2-5 y 3-6) en cada una de las secciones de perfil a lo largo del molde (Figura 6 y Figura 7).

Figura 4. Configuración de placas térmicas para molde de pultrusión para perfil plano.

Figura 5. FEM termomecánico de molde de pultrusión para perfil plano.

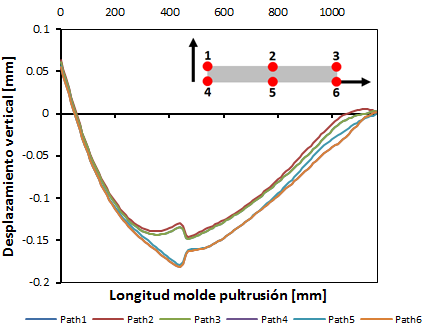
Figura 6. Gráficas de desplazamientos verticales de perfil plano.

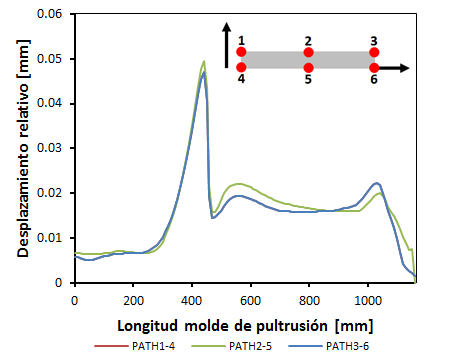
Figura 7. Gráficas de desplazamientos verticales relativos de perfil plano.

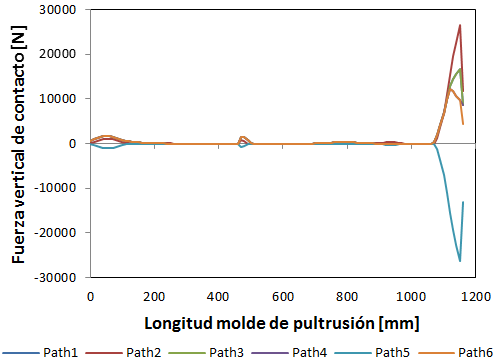
Las cargas verticales de contacto entre el molde y el perfil en cada uno de los puntos definidos anteriormente se muestran en la Figura 8.

Figura 8. Gráficas de fuerzas verticales de contacto sobre el perfil plano.

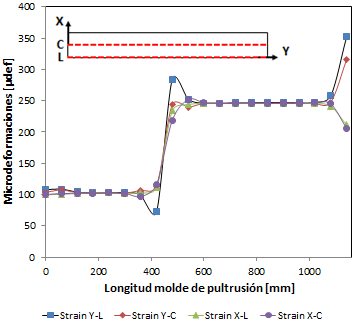
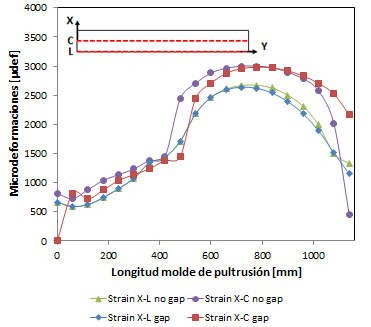
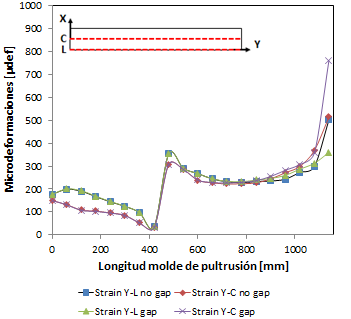
Las microdeformaciones en el plano del perfil se muestran en la figura 9.

Figura 9. Gráficas de microdeformaciones del perfil demostrador.

Se observa que las zonas de diferente temperatura provocan microdeformaciones que pueden ser consideradas constantes pero con niveles bajos de microdeformaciones, produciéndose un escalón en la zona de transición debidos al cambio de temperatura y un aumento al final del molde. Este comportamiento se puede ver también reflejado en las fuerzas de contacto que sufre la fibra como se observa en la Figura 8 Por lo tanto, la dilatación del molde debido a sus condiciones de contorno provoca un riesgo de gripado de la fibra al final del molde de pultrusión. Ante estos resultados se observa que es conveniente relajar las condiciones de contorno de la sufridera a la salida del perfil para reducir las cargas de presión y aumentar la estabilidad térmica con un incremento de espesor de los moldes de la hilera de pultrusión.

3.1.3 Modelo termoquímico perfil plano

Se ha creado un FEM no lineal transitorio (Coupled temp-displacement y Response Transient) utilizando ABAQUS/CAE 6.13.2, compuesto por tres piezas: molde inferior, molde superior y perfil de fibra. Se ha simulado el desplazamiento forzado de la fibra dentro del molde, manteniendo fijo este, definiendo una velocidad de desplazamiento de 2mm/s con el fin de obtener una temperatura de transición vítrea objetivo de 120ºC y un grado de curado >95%. Para cada “step” del modelo, se ha considerado una transferencia térmica perfecta entre molde y fibra así como entre las partes del molde por conducción y convección no forzada entre el molde y el ambiente en las zonas no aisladas (frontal delantero y trasero del molde). La conductancia térmica existente entre el molde y la fibra se define estableciendo la hipótesis de que el aire dentro del molde actúa como medio a través del cual se trasmite la energía calorífica. Por lo tanto se utiliza un valor de conductancia del aire igual a 3640 W/m²/ºC [7].

3.1.3.1 Resultados y discusión

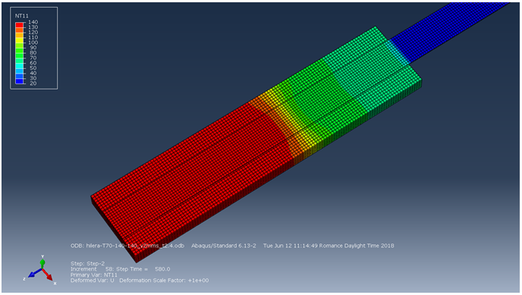
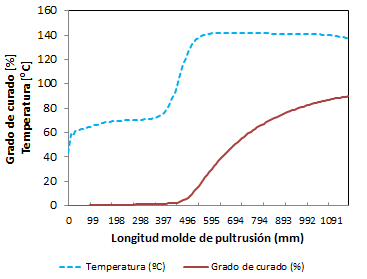
El campo térmico alcanzado con la evolución del grado de curado junto con la temperatura corregida debido al incremento de temperatura por el calor de reacción se muestra en las Figuras 10 y 11.

Figura 10. Campo térmico alcanzado en perfil plano.

Figura 11. Grado de curado y perfil de temperaturas alcanzado en perfil plano.

Los resultados de correlación de grado de curado se muestran en la siguiente tabla. Se evalúan los ensayos realizados a probetas de material fabricado mediante pultrusión [8] y predicción con FEM mostradas en la siguiente tabla.

Tabla 4. Correlación de Grado de curado para perfil plano

Informe	α PULTRUSION(%)	α DFEM(%)	DIFF(%)
Ci0221/18	96.40	89.77	7
CI0222/18	97.70	89.77	9
CI0223/18	97.10	89.77	8
PROMEDIO	97.07	89.77	8

Se puede concluir que para las condiciones de operación elegidas, las pruebas de pultrusión el grado de curado (α) se aproxima al ideal. Los valores de α obtenidos por pultrusión son similares a las obtenidos de los ensayos aunque un 8% por debajo del obtenido en las pruebas de fabricación, lo cual indica que la reacción puede ser de n-enésimo orden. Sin embargo, se valida el procedimiento seguido para la predicción teórica de grado de curado alcanzado para el proceso de pultrusión.

3.2 Pultrusión de perfil rigidizador para componentes aeronáuticos. Caso de demostrador

3.2.1 Descripción del proceso

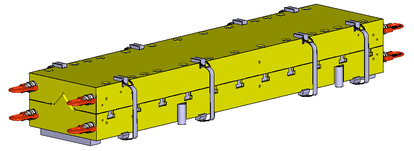
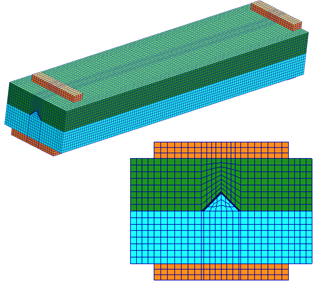
El proceso mantiene los parámetros de operación validados en el estudio de la fabricación del perfil plano del capítulo 3.1 y los parámetros de material definidos en las Tablas 1 y 2 así como cargas térmicas y condiciones de contorno. El molde de pultrusión se ha modificado para atender a las conclusiones obtenidas a partir del modelo termomecánico anterior. La hilera ha sido modificada aumentando el espesor de cada molde a 80mm (Figura 12) y cambiando el material de esta a un acero comercial para moldes W360 [9] de mayor dureza y estabilidad térmica con mejores acabados superficiales después de las operaciones de mecanizado (Tabla 5).

Tabla 5.Propiedades acero W360

Material	ρ[Kg/m3]	Cp[J/Kg·K]	ki[W/m·K]	αx,y[⁰C-1]
W360	7860	460	31.5	1.11·10-5

Figura 12.Molde de pultrusión para perfil rigidizador.

Al igual que en la simulación anterior, se han usado las mismas placas para obtener el campo de temperaturas del perfil manteniéndose la posición de cada una de ellas en el molde superior e inferior. Para completar la simulación se han realizado tres modelos: dos modelos termomecánicos: un modelo no lineal complejo del molde para el estudio del proceso de calentamiento y un modelo similar al modelo termomecánico anterior para evaluar las cargas sobre el perfil y el modelo termoquímico para evaluar el grado de curado del perfil. La cavidad del perfil se ha adecuado al espesor real de 2.5mm obtenidos de las pruebas de fabricación para el perfil plano. Para los cilindros centradores colocados en el molde inferior se ha realizado un encaje con holgura en la dirección de tiro del perfil para evitar grandes esfuerzos por dilatación.

3.2.2 Modelo termomecánico de demostrador no lineal de calentamiento

El modelo detallado está compuesto por las siguientes piezas: molde inferior, molde superior, sufrideras, cilindros, tornillos y tuercas. Debido al gran número de partes y elementos que generaría este modelo, y teniendo en cuenta que existe simetría en el plano longitudinal, se simplifica el modelo a la mitad mediante condiciones de simetría, estableciendo una frontera adiabática en el plano de simetría del modelo. En la Figura 13 se puede apreciar una vista general. Los elementos sólidos son del tipo C3D8T, un hexaedro con 8 nodos para análisis térmico combinado con desplazamientos. Se usa como software ABAQUS/CAE 6.13.2 con una solución Explicit, para incluir efectos no lineales en el modelo.

Figura 13.Modelo FEM detallado para el molde de pultrusión para perfil rigidizador.

3.2.2.1 Resultados y discusión

Todos los resultados pertenecen al último step del proceso de solución no lineal donde se ha alcanzado la condición de equilibrio estacionario considerando el fin del proceso transitorio. Los esfuerzos máximos que se muestran en la figura 14 se alcanzan en las sufrideras y en la zona de contacto debido al gripado o contacto por clivaje de la hilera. Son esfuerzos conservativos y con un orden de magnitud alto (600MPa) aunque no son reales debido a que están asociados a condiciones de contorno restrictivas.

Figura 14.Máximos esfuerzos del molde de pultrusión para perfil rigidizador.

Con respecto al campo térmico alcanzado (figura 14), existe una discontinuidad térmica entre las placas en el área de transición de 70ºC a 140ºC. La discontinuidad es pequeña y beneficia la transición fluida. El resto de la estructura alcanza la temperatura de operación satisfactoriamente.

Figura 14.Campo térmico del molde de pultrusión para perfil rigidizador.

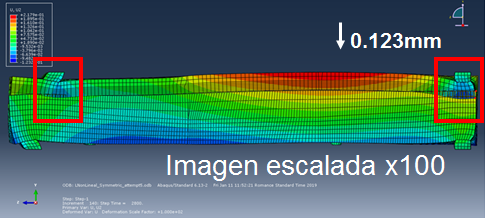
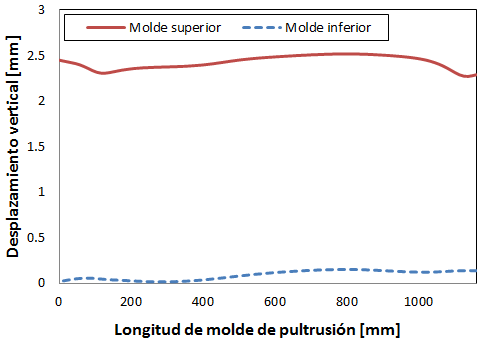
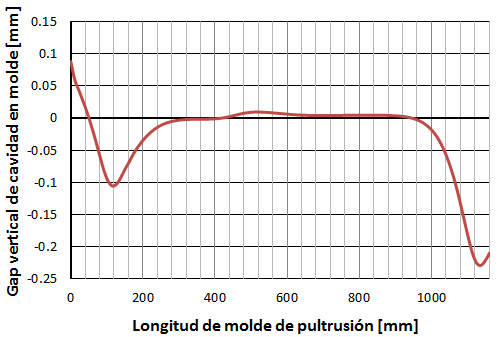
Para el análisis, se muestra el desplazamiento vertical, U2, al ser el más influyente en la capacidad operativa del molde de pultrusión. En las figuras 15 y 16 se observa que se reduce el espesor del canal de pultrusión en 0.123mm al final de la hilera debido al contacto con la sufridera, ya previsto. Por otro lado la reducción al inicio de la hilera es muy pequeña. Las figuras 18 y 19 muestran el desplazamiento absoluto y el gap existente en la cavidad entre el molde superior y el inferior. El gap de la zona inicial se reduce 0.1mm, mientras que la zona final se reduce 0.22mm, orden de magnitud de una capa sin compactar de NCF. La mayoría de la cavidad permanece con un gap constante sin desviaciones. Las sufrideras son las áreas donde puede haber problemas de gripado con el perfil según el modelo. Una posible mitigación sería reducir el apriete en las sufrideras liberando un gap de 0.12mm para evitar gripados.

Figura 15.Campo térmico del molde de pultrusión para perfil rigidizador.

Figura 16.Campo térmico del molde de pultrusión para perfil rigidizador.

Figura 17. Desplazamiento vertical del molde de pultrusión para perfil rigidizador.

Figura 18.Desplazamiento vertical relativo (gap de la cavidad) del molde de pultrusión para perfil rigidizador.

3.2.3 Modelo termomecánico de demostrador

El modelo termomecánico para el demostrador se ha realizado acorde a las características definidas en el apartado 3.1.2 pero actualizando la geometría y condiciones de contorno definidas en 3.2.1 para la simulación del proceso de fabricación para el demostrador. Dentro del estudio termomecánico, se ha valorado las recomendaciones del modelo no lineal descrito en el apartado anterior, estudiando la influencia de establecer un gap de 0.12mm en la sufridera superior en la zona de salida del perfil.

Figura 19.FEM termomecánico de molde de pultrusión para perfil demostrador.

3.2.3.1 Resultados y discusión

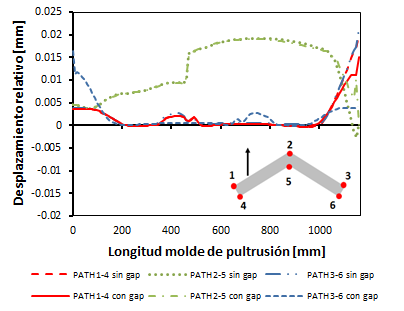
Se procede al análisis del FEM completo con el perfil, que se verá afectada por la dilatación de los moldes, los cuales causarán un estado de deformaciones en ella que se desea conocer y cargas aplicadas sobre el perfil. Para ello se obtienen los desplazamientos relativos en cada pareja de puntos (1-4, 2-5 y 3-6) comparando entre modelo sin gap o con gap de 0.12mm aplicado en la abrazadera trasera del molde para compensar las dilataciones debido al campo térmico (Figura 20).

Figura 20. Gráficas de desplazamientos verticales relativos de perfil demostrador.

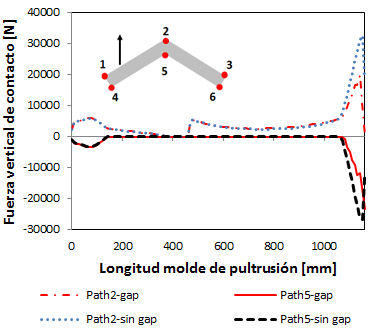
Las cargas verticales de contacto entre el molde y el perfil en cada uno de los puntos definidos anteriormente se muestran en la Figura 21.

Figura 21. Gráficas de fuerzas verticales de contacto sobre el perfil demostrador.

Las microdeformaciones en el plano del perfil se muestran en las Figura 22a y 22b. Las diferentes zonas de temperatura provocan diferente nivel de microdeformaciones que pueden ser considerados constantes aunque existe para el caso de demostrador cierto comportamiento no lineal con niveles importantes de microdeformaciones, produciéndose un escalón en la zona de transición debidos al cambio de temperatura y disminución en la dirección transversal y un aumento en la dirección axial al final del molde. Las fuerzas de contacto que sufre la fibra como se observa en la Figura 21. La dilatación del molde debido a sus condiciones de contorno provoca un riesgo de gripado de la fibra al final del molde de pultrusión.

Se observa que al introducir un gap, recomendado en la simulación de validación, las fuerzas de contacto disminuyen al igual que las microdeformaciones (Figura 22).

Figura 22a. Gráficas de microdeformaciones del perfil demostrador en dirección transversal.

Figura 22. Gráficas de microdeformaciones del perfil demostrador en dirección longitudinal.

Ante estos resultados cabe destacar que, como se valoró para el perfil plano, es conveniente relajar las condiciones de contorno de la sufridera a la salida del perfil para reducir las cargas de presión y aumentar la estabilidad térmica con un aumento de espesor de los moldes de la hilera de pultrusión.

3.2.4 Modelo termoquímico perfil demostrador

Al igual que con el perfil de validación, se ha simulado el desplazamiento forzado de la fibra dentro del molde, manteniendo fijo este bajo las mismas premisas. Esto es, una velocidad de desplazamiento de 2mm/s con el fin de obtener una temperatura de transición vítrea objetivo de 120ºC y un grado de curado >95%. Además, se ha simulado el proceso bajo el mismo perfil de temperaturas pero aumentando la velocidad a 3 y 5mm/s para observar la dependencia con el parámetro de la velocidad de pultrusión en el punto 2. Finalmente, se ha realizado la evaluación de grado de curado y perfil térmico en el punto 2 y 6 del perfil demostrador y evaluar la influencia de la forma y el espesor del perfil sobre el curado a v=2mm/s.

3.2.4.1 Resultados y discusión

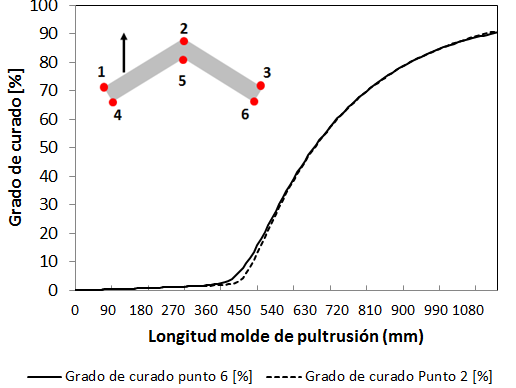
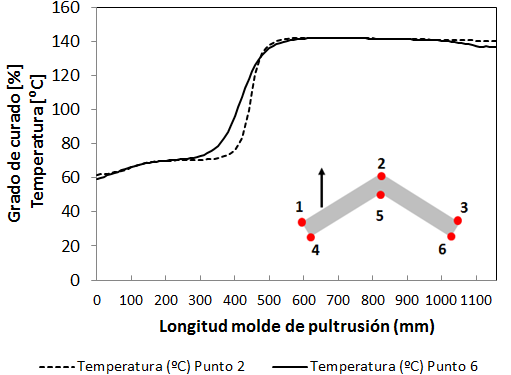
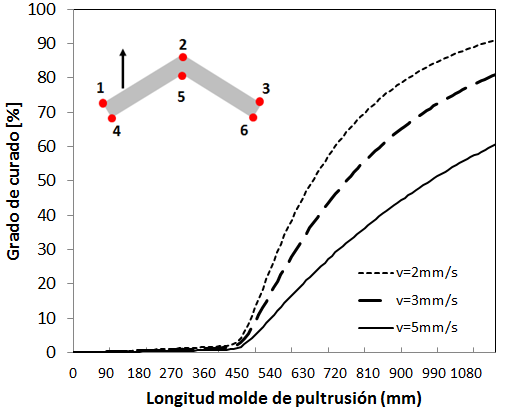
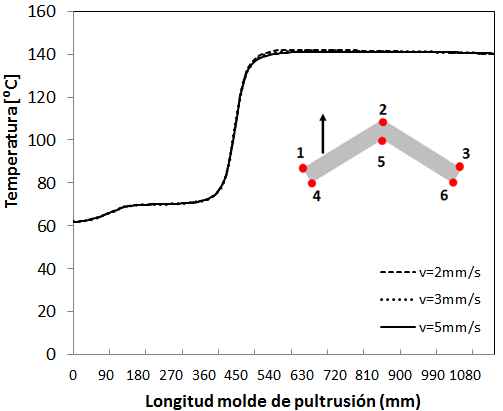
El campo térmico alcanzado y la evolución del grado de curado junto con la temperatura corregida debido al incremento de temperatura por el calor de reacción se muestran en las Figuras 23, 24 y 25. Para el grado de curado y la evolución de temperaturas sobre el perfil se han obtenido resultados para dos puntos del perfil, en concreto para los puntos 2 y 6. En las figuras 26 y 27 se muestra la comparativa del perfil de temperaturas y grado de curado en el punto 2 a diferentes velocidades.

Figura 23. Campo térmico alcanzado en perfil plano.

Los resultados de correlación de grado de curado se muestran en la tabla 4. Se evalúan los ensayos realizados a probetas de material fabricado mediante pultrusión [11] y predicción con FEM mostradas en la siguiente tabla.

Tabla 6. Correlación de Grado de curado para perfil plano

Informe	α PULTRUSION(%)	α DFEM(%)	DIFF(%)
PUNTO 2	99.0	90.99	8.1%
PUNTO 6	99.0	90.42	8.7%

Se puede concluir que, al igual que para el perfil plano, para las condiciones de operación elegidas el grado de curado (α) se aproxima al de las pruebas de pultrusión realizadas. Los valores de α obtenidos por pultrusión son similares a los predichos con el modelo DFEM con una desviación del 8%, lo cual, valida el procedimiento seguido para la predicción teórica de grado de curado alcanzado para el proceso de pultrusión.

Figura 24. Grado de curado alcanzado en perfil demostrador v=2mm/s puntos 2 y 6.

Figura 25. Perfil de temperaturas alcanzado en perfil demostrador v=2mm/s puntos 2 y 6.

Figura 26. Grado de curado alcanzado en perfil demostrador para diferentes velocidades en punto 2.

Figura 27. Perfil de temperaturas alcanzado en perfil demostrador para diferentes velocidades en punto 2.

El estudio a diferentes velocidades concluye que en el proceso de pultrusión, el fenómeno de conducción de calor (k∂²T/∂x²) domina al fenómeno de convección (u·∂T/∂x) del balance energético desarrollado. Se demuestra que el perfil de temperaturas alcanza un estado estacionario a diferentes temperaturas prácticamente similar siendo el tiempo de estancia del perfil en el molde, Δt ecuación (13), lo que determina el grado de curado del perfil, siendo mucho menor para altas velocidades.

Por otro lado para v=2mm/s, el perfil de temperatura en el punto 2 se desplaza hacia la derecha con respecto al punto 6 en la zona de transición de temperatura pero alcanza la máxima temperatura al igual que el punto 6 debido al pequeño espesor del perfil y la efectividad del fenómeno de conducción. Para el grado de curado la evolución es similar no apareciendo dependencia con el espesor del perfil.

4 Conclusiones

Se ha desarrollado y estudiado la simulación termomecánica y termoquímica de un proceso de pultrusión para un perfil rigidizador antipandeo de sección en L para aplicaciones aeronáuticas en estructuras como HTP y VTP.

En el caso de perfil plano, usado como estudio para la validación de la simulación, se desarrollaron simulaciones termomecánicas para obtener los desplazamientos y esfuerzos sobre el molde y la influencia de estos sobre el perfil obteniéndose las fuerzas de contacto y microdeformaciones asociadas a la carga térmica. Además se realizó la simulación termoquímica obteniéndose el grado de curado y el perfil de temperaturas asociado al proceso de pultrusión. Los modelos fueron evaluados encontrándose que la estabilidad dimensional del molde de pultrusión demostró ser una propiedad muy importante debido al riesgo de gripado del perfil dentro del molde al disminuir el gap a la salida del proceso de pultrusión, recomendando aumentar el gap en las condiciones de contorno para disminuir el riesgo. Posteriormente, implementando estos resultados en un proceso de pultrusión real, se comparó el grado de curado obtenido para un perfil plano fabricado por pultrusión encontrándose una buena correlación entre el grado de curado obtenido en la simulación y el perfil fabricado. Esto demostró un alto grado de confiabilidad en la simulación numérica.

Como segundo paso, se desarrolló una simulación similar pero para un perfil rigidizador de sección en L. Aumentando el alcance del estudio, se realizaron las simulaciones termomecánicas sin introducir el gap e introduciendo el gap para ver la influencia sobre el perfil, observando disminuciones de fuerzas de contacto y aumento de gap en la zona conflictiva con riesgo de gripado. Finalmente se predijo el grado de curado comparando dos puntos del perfil y un estudio de la influencia de la velocidad de pultrusión sobre el perfil de temperaturas y el grado de curado. Se obtuvo como conclusión que para perfiles con bajo espesor el grado de curado se mantiene prácticamente constante debido a la alta influencia del fenómeno de conducción respecto al convectivo. Finalmente, el perfil de temperatura se mantiene similar independientemente de la velocidad pero el grado de curado varía mucho con respecto a la velocidad, siendo de extrema importancia el tiempo que pasa el perfil dentro de la hilera ya que el grado de curado disminuye linealmente con la velocidad, un 11% a 3mm/s y un 33% a 5mm/s respecto al proceso a 2mm/s.

Agradecimientos

Este trabajo es parte del proyecto Pultrubeam que ha sido otorgado por el Centro de Desarrollo Tecnológico Industrial (CDTI) bajo la convocatoria INTERCONECTA 2016. Este proyecto ha sido cofinanciado por el Fondo Europeo de Desarrollo Regional (FEDER), dentro del Programa Operativo de Crecimiento Inteligente 2014-2020.

También agradecer Titania todo el trabajo llevado a cabo en el ámbito de la experimentación dentro del proyecto.

Referencias

[1] Zhang, Xu, Huang. Effect of cure cycle on curing process and hardness for epoxy resin. EXPRESS Polymer Letters 3(9):534-541 (2009)

[2] I. Baran, J.H. Hattel and Cem C. 3D thermo-chemical-mechanical analysis of the pultrusion process. Proceedings of the 34th Risø International Symposium on Materials Science: Processing of fibre composites - challenges for maximum materials performance, pág 169-176 (2013)

[3] P Akishin, E Barkanov and A. Bondarchuk. 2nd International Conference on Innovative Materials, Structures and Technologies, 96 (2015) 012012, pág. 101 (2015)

[4] Hardis, Ricky, "Cure kinetics characterization and monitoring of an epoxy resin for thick composite structures" (2012).Graduate Theses and Dissertations. 12608, [https:/lib.dr.iastate.edu/etd/12608 https:/lib.dr.iastate.edu/etd/12608] (2012)

[5] Standard Test Method for Kinetic Parameters for Thermally Unstable Materials Using Differential Scanning Calorimetry and the Flynn/Wall/Ozawa Method, ASTM E698 - 18

[6] Barkanov, Akishin, Miazza, Galvez. Numerical Simulation of Pultrusion Processes: Algorithms' Comparative Study. In: Proceedings of the10th International Conference on Composite Science and Technology, Portugal, Lisbon, 2-4 pp.1-12 September, 2015.

[7] Yunus Cengel, 2007. Transferencia de calor y masa

[8] J. M. Bayo, Raúl Páez. Informe Técnico ITC 20161269 pultrubeam 2017_v4.pdf, pág. 261 (2018).

[9] BÖLER W360 ISOBLOCK. W360 datasheet.pdf, pág. 11 (2018).

[10] J. M. Bayo, Raúl Páez. Informe Técnico ITC 20161269 pultrubeam 2018_v1.pdf, pág. 231 (2019).