Prony's method and matrix pencil method performance on determining the complex natural resonance frequencies of a linear system

Resumen

La caracterización de un sistema físico es un asunto de suma importancia para abordar algunos problemas de la física aplicada y de la ingeniería. Las frecuencias complejas de resonancia de un sistema, las cuales están incluidas en su respuesta impulsiva son parte característica de dicho sistema y ayudan a describirlo. Son pocos los trabajos escritos en idioma inglés que muestran una comparación entre los métodos discretos que extraen las frecuencias complejas de resonancia a través del estudio de la respuesta impulsiva del sistema que se esté estudiando. Mucho menos común es encontrar este tipo de estudios comparativos escritos en idioma castellano. Dada esta situación, en este trabajo de investigación se describen, prueban y comparan algunos de los métodos numéricos discretos más importantes para estimar las frecuencias naturales complejas de resonancia de un sistema, a través del estudio de su respuesta impulsiva en diferentes escenarios de simulación. De acuerdo con los resultados obtenidos, el método del haz de matrices con filtro SVD es el método menos sensible al ruido, mientras que el método Prony y sus diferentes versiones son los más eficientes desde el punto de vista computacional. Se discuten los escenarios de simulación que podrían ser más adecuados para cada método.

Palabras clave: Resonancias naturales complejas, método del haz de matrices, método de Prony, descomposición en valores singulares, método de mínimos cuadrados totales

Abstract

Characterization of a physical system is an important issue to approach some applied physics and engineering problems. The complex natural resonance frequencies of the system which are included in its impulsive response are characteristic of such system and are part of its description. Few works written in English language show a comparison among discrete methods that extract natural complex frequencies from a system impulsive response. Much less common is to find works written in Spanish language about this important research topic. Given this situation, important discrete numeric methods to estimate the complex natural resonance frequencies of a system through its impulsive response are described, tested and compared in different simulation scenarios in this document. According to the obtained results, the matrix pencil method with a SVD filter is the less sensitive method to the noise, while the Prony method and its different versions are the fastest ones. Scenarios that could be more suitable for each method are discussed.

Keywords: Complex Natural Resonances (CNRs), Matrix Pencil (MP) method, Prony's method, Singular Value Decomposition (SVD), Total Least Square (TLS) method

1. Introducción

El estudio de un sistema físico a partir de su respuesta impulsiva es un asunto relevante y vigente en el mundo de la física aplicada y la ingeniería. La respuesta impulsiva de un sistema lineal invariante en el tiempo contiene las denominadas frecuencias naturales complejas de resonancia (FCNR), distintivas de dicho sistema, a partir de las cuales el sistema puede ser identificado sin necesidad de conocer a priori su constitución interna.

Entre las técnicas más utilizadas para estimar las FCNR de un sistema dado (en el dominio del tiempo) se reconocen dos grandes métodos, a saber: el método de Prony y el método de haz de matrices, los cuales son algoritmos con un fundamento teórico que no está basado en el análisis de Fourier. Vale la pena mencionar que en el dominio de la frecuencia existen otros métodos, ver por ejemplo [1], los cuales, sin embargo, no serán motivo de estudio en este trabajo. La versión original del método de Prony fue propuesta por Gaspard Riche de Prony en 1795 [2-3] y la del método del haz de matrices por Y. Hua y T.K. Sarkar en 1989 [4]. A partir de entonces y hasta la fecha de hoy, se han planteado nuevas versiones de ambos métodos, algunas de las cuales han demostrado ser más robustas en presencia de ruido [5-9].

Si bien el método de Prony fue concebido originalmente para tratar de modelar el fenómeno de expansión de los gases y el método del haz de matrices recibió al principio una atención especial en el campo de la tecnología de radar para la identificación de blancos no amigables en un contexto militar, en el proceso de revisión bibliográfica realizada durante el desarrollo de este trabajo se encontró una gran utilidad práctica de las distintas versiones de ambos métodos, para aplicaciones tan disímiles como las siguientes: determinación de las frecuencias naturales de oscilación de una red eléctrica [10], detección de fallas y monitoreo de armónicos de la red de suministro de potencia eléctrica [11-13], monitoreo de armónicos de convertidores electrónicos de sistemas de potencia eléctrica [14], estudio de los sistemas de control [15], procesamiento de señales de radar [16-21], detección de armas de mano escondidas en la ropa [22-23], diseño y análisis de metamateriales [24-25], diseño de líneas de transmisión y análisis de antenas de microondas [26-27], monitoreo y diagnóstico biomédico [28-32], procesamiento de imágenes de resonancia magnética nuclear [33-35], microscopía de superresolución [36], medición no invasiva de glucosa en sangre mediante microondas [37], así como análisis y procesamiento de señales provenientes de sistemas de audio[38], telescopios astronómicos [39], detectores de ondas gravitacionales [40], sonar [41-43], sismógrafos [44] y medidores de fuerzas de Coriolis [45].

Vale la pena mencionar las aplicaciones que realizan el proceso de detección e identificación de un objeto en calidad de dispersor electromagnético a partir de su respuesta impulsiva [16-25], ya que los métodos numéricos estudiados en este trabajo son los que comunmente son utilizados para dichos procesos de detección e identificación. Para estas aplicaciones, el conjunto de elementos físicos conformados por el objeto dispersor, la señal impulsiva que lo excita y su respectiva respuesta es lo que de ahora en adelante llamaremos sistema lineal. Visto el dispersor como un sistema, su respuesta impulsiva tiene como rasgo distintivo estar compuesta por un conjunto de FCNR dadas por $s_{n}=-\sigma _{n}+\jmath \omega _{n}$, las cuales permiten, entre otras cosas, identificar unívocamente al propio objeto y en conjunto con cierto conocimiento previo, caracterizarlo desde un punto de vista físico. Las FCNR propias de un objeto dispersor electromagnético se correlacionan directamente con su geometría y constitución material y se distribuyen sobre el plano complejo formando “ramas” simétricas respecto del eje real con cierto orden y separación que es también característico del objeto. Los objetos “altamente” resonantes, como por ejemplo un dipolo metálico, poseen un cojunto de FCNR que se alojan en ramas muy próximas al eje imaginario, alejándose de éste a medida que aumenta la frecuencia. Las FCNR de los objetos “suavemente” resonantes, en cambio, como por ejemplo una esfera metálica, se alojan en ramas que se separan mucho más notablemente del eje imaginario [46]. La extracción de las componentes imaginarias $\omega _{n}$ de estas FCNR no puede realizarse con precisión usando el análisis de Fourier por que al seccionar la función del sistema $H(s)$ con el plano $\sigma =0$ para obtener a $H(\omega )$, las $\omega _{n}$ pueden quedar “escondidas” o aliased, lo cual se observa en mayor medida para sistemas suavemente resonantes en comparación con los altamente resonantes [29].

También vale la pena agregar que por lo general el conjunto de valores de ${\textstyle \omega _{n}}$ no son múltiplos de una frecuencia armónica natural fundamental como suele indicar la teoría de Fourier para señales periódicas, sino que más bien están distribuidas de manera arbitraria en el espectro, donde su valor es característico del sistema que se esté estudiando.

Aún dado el gran auge del uso del método de Prony, del método del haz de matrices y de sus variantes, no abundan las publicaciones arbitradas acerca del desempeño comparativo de dichos métodos en idioma castellano. Durante el proceso de revisión bibliográfica, en idioma castellano solo se consiguió el contexto histórico en el cual se crea el método de Prony, su descripción y su comparación con el método de la descomposición armónica de Pisarenko [47]. También se encontraron en idioma castellano algunas publicaciones en las que se aplica el método de Prony para modelar una falla en una central termonuclear [48], para la determinación de las frecuencias naturales de oscilación de una red eléctrica de potencia [49-50], para el procesamiento de imágenes de alta resolución [51] y para la creación de un software para la predicción del valor de acciones financieras [52].

Incluso en idioma inglés, son escasos los estudios comparativos publicados en revistas arbitradas acerca del desempeño de cada una de las variantes del método de Prony y del método del haz de matrices en diferentes escenarios de simulación. Entre los estudios comparativos encontrados durante el trabajo de revisión pueden citarse [30,40,53-55], en los cuales se examinan solamente alguna de las versiones de los métodos de Prony y del haz de matrices en algunos escenarios de simulación particulares. Entre estos estudios, uno de los más detallados que se encontró fue el descrito en [30], el cual muestra el desempeño de varios métodos generalmente utilizados en sistemas de análisis de señales bio-médicas, pero probando solo una de las versiones del método de Prony y del método del haz de matrices, sin tomar en cuenta el tiempo de cálculo de cada algoritmo, sin variar la frecuencia de muestreo y además variando los niveles de ruido en un rango no tan amplio como en el trabajo de investigación realizado en nuestro artículo. Otro trabajo de relevancia, de alta rigurosidad y enfoque estadístico, en el cual se muestra el desempeño de varias variantes del método de Prony y una variante del haz de matrices para diferentes números de muestras, sin variar la frecuencia de muestreo y tampoco el nivel de ruido presente en las señales que se estudian, se reporta en [40].

Vale la pena agregar que también durante el proceso de revisión bibliográfica se encontró un importante estudio analítico no comparativo del desempeño particular del método de Prony [56], en el cual se estudia la precisión teórica de dicho método en presencia de ruido.

Con base en el contexto anterior, con la intención de realizar un pequeño aporte al conocimiento y documentarlo en idioma castellano nos planteamos describir, analizar y comparar mediante simulación el desempeño de cinco métodos derivados de las teorías originales de Prony y del haz de matrices, a saber: el método de Prony clásico, el método de Prony con filtrado a través de la descomposición de valores singulares (DVS), el método de Prony usando mínimos cuadrados totales, el método del haz de matrices sin filtro y el método del haz de matrices con filtrado usando DVS. Para ello ponemos a prueba cada método en dos escenarios distintos de simulación, uno en el que se usan distintos niveles de ruido añadido y otro en el que se prueban distintas frecuencias de muestreo, ambos para una ventana de observación constante. En cada caso se registran los tiempos de cómputo de cada método. Luego, a partir de este trabajo comparativo, se determinan los escenarios más favorables para cada método, con los fines de proveer información valiosa que puede servir para desarrollar aplicaciones en los campos de la física y la ingeniería en general.

2. Breve descripción de los cinco métodos estudiados.

En este apartado describiremos brevemente las prescripciones de los métodos de Prony clásico, de haz de matrices y sus derivados. Específicamente revisaremos los fundamentos matemáticos de los métodos de Prony, de Prony con filtrado de valores singulares, de Prony con mínimos cuadrados, de haz de matrices y de haz de matrices con filtrado de valores singulares. Todos estos métodos se implementan en el dominio del tiempo y permiten estimar las frecuencias naturales complejas de resonancia de un sistema lineal invariante en el tiempo (LIT). Las frecuencias naturales complejas de un sistema LIT coinciden con los polos de la respuesta ${\textstyle H(s)}$ del sistema.

La respuesta impulsiva $h(t)$ de un sistema lineal está compuesta por una combinación lineal de $N'$ cosenos amortiguados de la forma

$h(t)=\sum _{n=1}^{N'}|r_{n}|e^{-\sigma _{n}t}\cos(\omega _{n}t+\phi _{n})=\sum _{n=1}^{N'}\Re \left\{r_{n}e^{s_{n}t}\right\}$

(1)

que a su vez forma un par transformado con la función $H(s)$ del sistema:

$h(t)=\sum _{n=1}^{N'}\Re \left\{r_{n}e^{s_{n}t}\right\}\Leftrightarrow$ $\sum _{n=1}^{N'}{\frac {1}{2}}\left({\frac {r_{n}}{s-s_{n}}}+{\frac {r_{n}^{\ast }}{s-s_{n}^{\ast }}}\right)=H(s)$

(2)

donde $N'=N/2$, siendo $N$ el número par de frecuencias naturales complejas de resonancia del sistema, ${\textstyle r_{n}}$ y ${\textstyle r_{n}^{\ast }}$, con ${\textstyle r_{n}=|r_{n}|e^{\jmath \phi _{n}}}$, son residuos complejos, y ${\textstyle s_{n}}$ y ${\textstyle s_{n}^{\ast }}$ son los polos complejos del sistema también llamados frecuencias complejas naturales de resonancia, con $s_{n}=-\sigma _{n}+\jmath \omega _{n}$ y $\sigma _{n}>0$, donde el símbolo ${\textstyle \ast }$ denota conjugación.

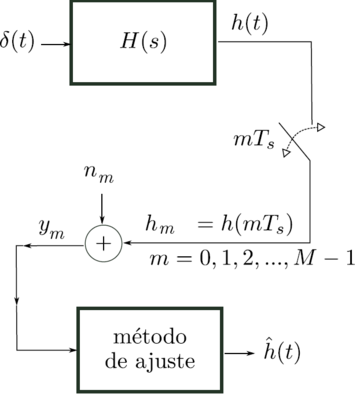
Los métodos de Prony y de haz de matrices en todas sus versiones, son métodos de estimación mediante ajuste numérico que parten de un número finito, dígase ${\textstyle M}$, de muestras de ${\textstyle h(t)}$ tal cual se muestra en la Figura 1.

Figura 1. Sistema de reconstrucción de la respuesta impulsiva de un sistema lineal

En la Figura 1, el sistema lineal $H(s)$ es estimulado con un impulso $\delta (t)$ ideal. Como resultado, el sistema responde produciendo a la salida una respuesta impulsiva de la forma dada por la ecuación (1). Luego, la respuesta $h(t)$ del sistema es muestreada a una tasa $T_{s}$ uniforme: $h_{m}=h(mT_{s})$. Las muestras $h_{m}$, contaminadas con ruido $n_{m}$ en parte proveniente del propio sistema y en parte de tipo numérico, dan lugar a la señal $y_{m}$:

$y_{m}=y(mT_{s})=\displaystyle \sum _{n=1}^{N}r_{n}e^{s_{n}mT_{s}}+n_{m}=$ $\displaystyle \sum _{n=1}^{N}r_{n}{z_{n}}^{m}+n_{m}$

(3)

con ${\textstyle m=0,1,2,\ldots ,M-1}$, y donde ${\textstyle z_{n}=e^{s_{n}T_{s}}}$ son los polos de ${\textstyle H(z)}$, y a su vez ${\textstyle H(z)}$ es la representación discreta del sistema ${\textstyle H(s)}$.

El conjunto de muestras $\{y_{m}\}$ alimenta al algoritmo de estimación o método de ajuste objeto de estudio en este trabajo, el cual permite estimar las frecuencias complejas naturales de resonancia ${\hat {s}}_{n}$ a partir de las cuales finalmente se construye una estimación de la respuesta impulsiva que se denominará de aquí en adelante ${\hat {h}}(t)$.

2.1 Método de Prony clásico

Gaspard Riche de Prony creó el método que hoy lleva su nombre en la última parte del siglo XVIII [2] para tratar de modelar el fenómeno de expansión de los gases. Prony asumió originalmente que el número ${\textstyle N}$ de frecuencias complejas naturales era conocido y la señal ${\textstyle y(t)}$ bajo estudio tenía un ruido añadido despreciable, de modo que la condición ${\textstyle h(t)\approx y(t)}$ se cumplía.

El primer paso del algoritmo de Prony consiste en organizar las muestras ${\textstyle h_{m}}$ obtenidas a partir del muestreo uniforme de la señal ${\textstyle y(t)}$, con ${\textstyle m=0,1,2,\ldots ,M-1}$, en un vector columna ${\textstyle \mathbf {h} }$:

${\mathbf {h} }=\left(h_{0},h_{1},\ldots ,h_{M-1}\right)^{\mathit {H}}$

(4)

donde el superíndice ${\textstyle {\mathit {H}}}$ denota conjugación transpuesta. Luego, tomando en cuenta que en ausencia de ruido ${\textstyle y_{m}=h_{m}=h(mT_{s})}$, el valor de cada muestra puede expandirse a partir de la ecuación (3) de la forma

${\begin{array}{rlcl}h_{0}~=&r_{1}&+...+&r_{N}\\h_{1}~=&r_{1}e^{s_{1}T_{s}}&+...+&r_{N}e^{{(s_{N})}T_{s}}\\\vdots ~=&\\h_{m}~=&r_{1}e^{s_{1}mT_{s}}&+...+&r_{N}e^{{(s_{N})}mT_{s}}\\\vdots ~=&\\h_{M-1}~=&r_{1}e^{s_{1}(M-1)T_{s}}&+...+&r_{N}e^{(s_{N})(M-1)T_{s}}\end{array}}$

(5)

o de forma más compacta

${\begin{array}{rclcccl}h_{0}&=&r_{1}&+&\ldots &+&r_{N}\\h_{1}&=&r_{1}z_{1}&+&\ldots &+&r_{N}z_{N}\\\vdots &=&\\h_{m}&=&r_{1}z_{1}^{m}&+&\ldots &+&r_{N}z_{N}^{m}\\\vdots &=&\\h_{M-1}&=&r_{1}z_{1}^{(M-1)}&+&\ldots &+&r_{N}z_{N}^{(M-1)}\end{array}}$

(6)

donde ${\textstyle \{z_{n}\}}$, con ${\textstyle n=1,2,\ldots ,N}$, y ${\textstyle z_{n}=e^{s_{n}T_{s}}}$ son los polos de ${\textstyle H(z)}$. Por otra parte, ${\textstyle H(z)}$ es la representación discreta del sistema original ${\textstyle H(s)}$.

El sistema de ecuaciones dado por (6) contiene ${\textstyle 2N}$ incógnitas: ${\textstyle N}$ residuos complejos desconocidos y ${\textstyle N}$ polos ${\textstyle \{z_{n}\}}$ desconocidos. Por esa razón se requiere un número ${\textstyle M}$ de muestras mayor o igual a ${\textstyle 2N}$ para resolver dicho conjunto de ecuaciones para ${\textstyle \{r_{n}\}}$ y ${\textstyle \{z_{n}\}}$.

Luego, los valores de ${\textstyle \{r_{n}\}}$ y ${\textstyle \{z_{n}\}}$ se estiman tal que, mediante la técnica de mínimos cuadrados, con la ${\textstyle {\hat {h}}(t)}$ obtenida, se minimice el error ${\textstyle \xi }$ dado por

$\xi ={\sqrt {\sum _{m=0}^{M-1}\left({\hat {h}}_{m}-h_{m}\right)^{2}}}$

Posteriormente, el método de Prony prosigue con los tres pasos siguientes:

1. La solución de un sistema lineal algebraico de ecuaciones de por lo menos orden ${\textstyle N}$, para los coeficientes ${\textstyle \{a_{n}\}}$ del sistema ${\textstyle H(z)}$:

   $H(z)={\frac {b_{0}z^{K}+b_{1}z^{K-1}+\ldots +b_{K-1}z+b_{K}}{a_{0}z^{N}+a_{1}z^{N-1}+\ldots +a_{N-1}z+a_{N}}}={\frac {N(z)}{D(z)}}$

donde se asume que ${\textstyle a_{0}=1}$ y ${\textstyle K<N}$. Observe que los ceros del polinomio en el denominador son los polos o frecuencias naturales de ${\textstyle H(z)}$.

2. El cálculo de las ${\textstyle N}$ raíces ${\textstyle \{z_{n}\}}$ del polinomio característico ${\textstyle D(z)}$:

   ${\begin{array}{rl}D(z)=a_{0}z^{N}+a_{1}z^{N-1}+\ldots +a_{N}=&0\\=a_{0}(z-z_{N})(z-z_{N-1})\times \ldots \times (z-z_{1})=&0\\=a_{0}\Pi _{n=1}^{N}(z-z_{n})=&0\end{array}}$

   (7)

3. La solución de un sistema de ${\textstyle N}$ ecuaciones algebraicas para los residuos ${\textstyle \{r_{n}\}}$.

Estos pasos se explican de manera detallada a continuación.

Para comenzar la estimación de coeficientes ${\textstyle \{a_{n}\}}$, el sistema dado por la ecuación (6) se multiplica sucesivamente por ${\textstyle (a_{N},a_{N-1},\ldots ,a_{1},a_{0})^{H}}$ como se indica a continuación:

${\begin{array}{crlll}{a_{N}}~\times &(h_{0}&=r_{1}&+\ldots +&r_{N})\\{\vdots }~~~~\times &(h_{1}&=r_{1}z_{1}&+\ldots +&r_{N}z_{N})\\{a_{0}}~~\times &\vdots &&&{\vdots }\\&(h_{m}&=r_{1}z_{1}^{m}&+\ldots +&r_{N}z_{N}^{m})\\&\vdots &=&&{\vdots }\\&(h_{M-1}&=r_{1}z_{1}^{(M-1)}&+\ldots +&r_{N}z_{N}^{(M-1)})\end{array}}$

(8)

entonces, también se puede realizar el proceso iniciándolo en la fila siguiente

${\begin{array}{crlll}&(h_{0}&=r_{1}&+\ldots +&r_{N})\\{a_{N}}~\times &(h_{1}&=r_{1}z_{1}&+\ldots +&r_{N}z_{N})\\{\vdots }~~~~\times &\vdots &&&{\vdots }\\{a_{0}}~~\times &(h_{m}&=r_{1}z_{1}^{m}&+\ldots +&r_{N}z_{N}^{m})\\&\vdots &=&&{\vdots }\\&(h_{M-1}&=r_{1}z_{1}^{(M-1)}&+\ldots +&r_{N}z_{N}^{(M-1)})\end{array}}$

(9)

y así sucesivamente, hasta la última fila como se observa a continuación

${\begin{array}{ccrll}&&(h_{0}&=r_{1}&+...+r_{N})\\&&(h_{1}&=r_{1}z_{1}&+...+r_{N}z_{N})\\&&\vdots &=&\\{a_{N}}&\times &(h_{m}&=r_{1}z_{1}^{m}&+...+r_{N}z_{N}^{m})\\{\vdots }&\times &\vdots &=&\\{a_{0}}&\times &(h_{M-1}&=r_{1}z_{1}^{(M-1)}&+...+r_{N}z_{N}^{(M-1)})\end{array}}$

(10)

Si nos centramos ahora en el sistema que resulta de completar la operación de multiplicación de la ecuación (8) y se suman los términos en cada lado de las ${\textstyle N+1}$ primeras ecuaciones, se obtiene:

$a_{N}h_{0}+\ldots +a_{0}h_{N}=$ $a_{N}(r_{1}+\ldots +r_{N})+\ldots +a_{0}(r_{1}z_{1}^{N}+\ldots +r_{N}z_{N}^{N})$

(11)

la cual puede ser reordenada como

$a_{N}h_{0}+\ldots +a_{0}h_{N}=$ $(a_{N}r_{1}+\ldots +a_{0}r_{1}z_{1}^{N})+$ $(a_{N}r_{2}+\ldots +a_{0}r_{2}z_{2}^{N})+$ $\ldots +(a_{N}r_{N}+\ldots +a_{0}r_{N}z_{N}^{N})$

(12)

Luego de notar que los términos del lado derecho de la ecuación (12) son todas versiones del polinomio característico (7), puede escribirse que

$a_{N}h_{0}+\ldots +a_{0}h_{N}=0$

(13)

Luego, esta ecuación puede generalizarse mediante la repetición de un proceso similar aplicado a todos los sistemas lineales que van desde (8) hasta (10), para obtener:

$a_{N}h_{m}+a_{N-1}h_{m+1}+\ldots +a_{0}h_{m+N}=0$ ${\mbox{para }}\quad m=0,1,\ldots ,M-N-1$

(14)

por eso, un sistema de ${\textstyle M-N}$ ecuaciones lineales con ${\textstyle N-1}$ incógnitas puede escribirse:

${\begin{array}{rl}a_{N}h_{0}+\ldots +a_{0}h_{N}=&0\\a_{N}h_{1}+\ldots +a_{0}h_{N+1}=&0\\\vdots &\\a_{N}h_{M-N-1}+\ldots +a_{0}h_{M-1}=&0\end{array}}$

(15)

Luego, recordando que ${\textstyle a_{0}=1}$, el sistema de ecuaciones (15) puede ser escrito nuevamente, con la forma

${\begin{array}{rl}a_{N}h_{0}+\ldots +a_{1}h_{N-1}~=&-h_{N}\\a_{N}h_{1}+\ldots +a_{1}h_{N}~=&-h_{N+1}\\\vdots &\\a_{N}h_{M-N-1}+\ldots +a_{1}h_{M-2}~=&-h_{M-1}\end{array}}$

(16)

Y éste a su vez, puede ser reescrito en la forma matricial siguiente

$\underbrace {\begin{pmatrix}h_{0}&h_{1}&\ldots &h_{N-1}\\h_{1}&h_{2}&\ldots &h_{N}\\\vdots &\vdots &\vdots &\vdots \\h_{M-N-1}&h_{M-N-2}&\ldots &h_{M-2}\end{pmatrix}} _{\mathbf {H} }\underbrace {\begin{pmatrix}a_{N}\\a_{N-1}\\\vdots \\a_{1}\end{pmatrix}} _{\mathbf {a} }=$ $\underbrace {\begin{pmatrix}-h_{N}\\-h_{N+1}\\\vdots \\-h_{M-1}\end{pmatrix}} _{\mathbf {b} }$

(17)

donde ${\textstyle \mathbf {H} }$ es una matriz de Hankel de orden ${\textstyle (M-N)\times N}$, ${\textstyle \mathbf {b} }$ es el vector ${\textstyle (M-N)\times 1}$ de valores conocidos, ambos construidos a partir de las muestras ${\textstyle h_{m}}$ de ${\textstyle h(t)}$, mientras que ${\textstyle \mathbf {a} }$ es el vector incógnita con los coeficientes ${\textstyle a_{n}}$, con ${\textstyle n=1,2,\ldots ,N}$ del polinomio característico de ${\textstyle H(z)}$.

Como la ecuación (17) representa un sistema de ecuaciones linealmente independientes con más ecuaciones que incógnitas no hay manera de encontrar una solución exacta para el vector ${\textstyle \mathbf {a} }$. La mejor estimación del vector ${\textstyle \mathbf {a} }$ se obtiene, sin embargo, mediante la técnica de aproximación por mínimos cuadrados [57] de la forma:

$\mathbf {a} =\mathbf {H} ^{+}\mathbf {b}$

(18)

donde ${\textstyle \mathbf {H} ^{+}=({\mathbf {H} ^{H}}\mathbf {H} )^{-1}\mathbf {H} ^{H}}$ es la inversa de Moore-Penrose, o pseudo-inversa, de la matriz ${\textstyle \mathbf {H} }$.

Una vez que los valores de ${\textstyle \{a_{n}\}}$ son obtenidos, las frecuencias naturales (discretas) ${\textstyle \{z_{n}\}}$ del sistema ${\textstyle H(z)}$ podrían estimarse encontrando las raíces del polinomio característico dado por (7).

A partir de ${\textstyle \{z_{n}\}}$ las frecuencias complejas naturales de resonancia ${\textstyle \{s_{n}\}}$ pueden estimarse, ya que ${\textstyle z_{n}=e^{s_{n}T_{s}}=e^{-\sigma _{n}T_{s}}e^{\pm \jmath \omega _{n}T_{s}}}$, y además se cumple que ${\textstyle |z_{n}|=e^{-\sigma _{n}T_{s}}}$ y que ${\textstyle \angle z_{n}=\pm \omega _{n}T_{s}}$, entonces

$s_{n}={\frac {\ln {(z_{n})}}{T_{s}}}$

(19)

Finalmente, de ser necesario, el sistema de ecuaciones de la ecuación (6) puede ser utilizado para estimar los ${\textstyle N}$ residuos ${\textstyle \{r_{n}\}}$ y construir la señal estimada ${\textstyle {\hat {h}}(t)}$:

$\underbrace {\begin{pmatrix}1&1&\ldots &1\\z_{1}&z_{2}&\ldots &z_{N}\\\vdots &\vdots &\vdots &\vdots \\z_{1}^{m}&z_{2}^{m}&\vdots &z_{N}^{m}\\\vdots &\vdots &\vdots &\vdots \\z_{1}^{M-1}&z_{2}^{M-1}&\ldots &z_{N}^{M-1}\\\end{pmatrix}} _{\mathbf {Z} }\underbrace {\begin{pmatrix}r_{1}\\r_{2}\\\vdots \\r_{N}\end{pmatrix}} _{\mathbf {r} }=\underbrace {\begin{pmatrix}h_{0}\\h_{1}\\\vdots \\h_{m}\\\vdots \\h_{M-1}\end{pmatrix}} _{\mathbf {h} }$

(20)

Y de aquí

$\mathbf {r} =\mathbf {Z} ^{+}\mathbf {h}$

(21)

donde ${\textstyle \mathbf {Z} ^{+}}$ es la matriz inversa de Moore-Penrose de ${\textstyle \mathbf {Z} }$, que a su vez es una matriz de Vandermonde transpuesta.

2.2 Método de Prony clásico utilizando filtrado con descomposición en valores singulares (DVS)

Cuando el número exacto de frecuencias naturales complejas de ${\textstyle h_{m}}$ se desconoce y además el ruido ${\textstyle n_{m}}$ no se puede despreciar, el método clásico de Prony en general falla. Para remediar este inconveniente se puede proceder, suponiendo un valor máximo de polos ${\textstyle N_{\mathrm {MAX} }}$ inicial, a filtrar el ruido mediante una descomposición en valores singulares de la matriz de Hankel del sistema antes de aplicar el método de Prony clásico [5]. Una versión similar a esta estrategia se conoce con el nombre de método de Kumaresan-Tufts [6,40].

En este método, así como en el método clásico de Prony, se procede primero a la creación de una matriz de Hankel como ${\textstyle \mathbf {H} }$ en la ecuación (17), pero que esta vez designaremos como ${\textstyle \mathbf {Y} }$ debido a la presencia del ruido, la cual tiene la siguiente estructura

${\mathbf {Y} }={\begin{pmatrix}y_{0}&y_{1}&...&y_{(N_{\mathrm {MAX} }-1)}\\y_{1}&y_{2}&...&...\\y_{2}&y_{3}&...&...\\.&.&...&...\\.&.&...&y_{M-3}\\y_{(M-N_{\mathrm {MAX} }-1)}&.&...&y_{M-2}\\\end{pmatrix}}$

de dimensiones ${\textstyle (M-N_{\mathrm {MAX} })\times N_{\mathrm {MAX} }}$ tal que ${\textstyle N_{\mathrm {MAX} }>N}$.

Luego, la matriz ${\textstyle \mathbf {Y} }$ es factorizada mediante DVS de la forma

$\mathbf {Y} =\mathbf {U} \mathbf {\Sigma } {\mathbf {V} }^{\mathit {H}}$

(22)

donde ${\textstyle \mathbf {U} }$ es una matriz unitaria de dimensiones ${\textstyle (M-N_{\mathrm {MAX} })\times (M-N_{\mathrm {MAX} })}$ cuyas columnas son los autovectores de ${\textstyle \mathbf {Y} \mathbf {Y} ^{\mathit {H}}}$, ${\textstyle \mathbf {V} }$ es una matriz de dimensiones ${\textstyle (N_{\mathrm {MAX} }+1)\times (N_{\mathrm {MAX} }+1)}$ cuyas columnas son los autovectores de ${\textstyle \mathbf {Y} ^{\mathit {H}}\mathbf {Y} }$ y ${\textstyle \mathbf {\Sigma } }$ es una matriz diagonal de dimensiones ${\textstyle (M-N_{\mathrm {MAX} })\times (N_{\mathrm {MAX} }+1)}$ la cual contiene los valores singulares de ${\textstyle \mathbf {Y} }$ (raíz cuadrada de los autovalores de ${\textstyle {\mathbf {Y} }^{\mathit {H}}{\mathbf {Y} }}$ ) ordenados en forma descendente tal que ${\textstyle \sigma _{1}>\sigma _{2}>...>\sigma _{N_{\mathrm {MAX} }+1}}$ [9,58].

Debido a la presencia de ruido, el número de valores singulares no nulos en ${\textstyle \mathbf {\Sigma } }$ se incrementa más allá del orden ${\textstyle N}$ del sistema, el cual no se conoce a priori. Los valores singulares originales de la matriz “limpia” ${\textstyle \mathbf {H} }$ son perturbados por el ruido en ${\textstyle \mathbf {Y} }$ y además otros valores singulares adicionales aparecen en el proceso. Dada esta situación, los errores que se deben al ruido pueden suprimirse por medio de la eliminación de los valores singulares espurios de la matriz ${\textstyle \mathbf {\Sigma } }$ [6,40].

Con base en este principio y tomando en cuenta que los valores singulares asociados al ruido poseen menor potencia, se establece una tolerancia ${\textstyle T}$ relativa al máximo valor singular ${\textstyle \sigma _{1}}$ a partir de un umbral ${\textstyle \sigma _{T}}$ de acuerdo a la siguiente ecuación

${\frac {\sigma _{T}}{\sigma _{1}}}\approx 10^{-p}$

(23)

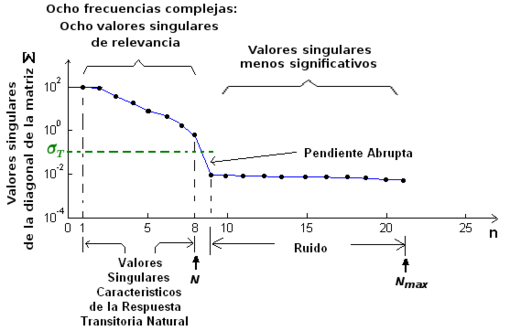
donde ${\textstyle p}$ es el número de dígitos significativos en los datos debido a la resolución esperada, ${\textstyle T}$ es la tolerancia relativa admitida, y ${\textstyle \sigma _{T}}$ es el umbral de filtrado. Es natural esperar que el número de valores singulares ${\textstyle \sigma _{n}}$ que cumplen con la condición ${\textstyle \sigma _{n}>\sigma _{T}}$ coincida con ${\textstyle N}$ en condiciones ideales. Por otra parte, los valores singulares que cumplen con la condición ${\textstyle \sigma _{n}<\sigma _{T}}$ se consideran espurios. Un ejemplo de aplicación de este procedimiento para determinar el número verdadero de polos del sistema analizado se muestra en la Figura 2, donde ya se ha calculado el valor de ${\textstyle \sigma _{T}}$, umbral con el cual se determina el número de polos del sistema, que en este caso particular mostrado en la figura resulta ser ${\textstyle N=8}$.

Figura 2. Caso típico de los valores singulares de la diagonal de la matriz $\mathbf {\Sigma }$ en función de la $n-$ésima posición en la diagonal de dicha matriz, para una respuesta transitoria $y(t)$ que proviene de un sistema lineal de ocho polos

Seguidamente, utilizando este criterio los valores singulares de la matriz ${\textstyle \mathbf {\Sigma } }$ con una tolerancia relativa inferior a ${\textstyle T}$ se reemplazan con ceros, para generar una matriz ${\textstyle \mathbf {\Sigma ^{\prime }} }$, la cual podría interpretarse como una matriz ${\textstyle \mathbf {\Sigma } }$ de bajo nivel de ruido o “limpia” [5]. Con esta nueva matriz ${\textstyle \mathbf {\Sigma ^{\prime }} }$ se crea luego una matriz de Hankel ${\textstyle \mathbf {Y^{\prime }} }$ de bajo nivel de ruido o “limpia” a partir de la expresión

$\mathbf {Y^{\prime }} ={\mathbf {U} }{\mathbf {\Sigma ^{\prime }} }{{\mathbf {V} }^{H}}$

(24)

Usando la matriz ${\textstyle \mathbf {Y^{\prime }} }$ en lugar de ${\textstyle \mathbf {H} }$ en la ecuación (18) se obtiene el vector ${\textstyle \mathbf {a} }$ con los coeficientes del polinomio característico de ${\textstyle H(z)}$ de la forma:

$\mathbf {a} =\mathbf {Y^{\prime }} ^{+}\mathbf {b}$

a partir de lo cual se siguen todos los pasos subsiguientes del método clásico de Prony.

2.3 Método de Prony usando mínimos cuadrados totales

El uso del método de mínimos cuadrados totales en conjunto con el método de Prony, descrito en la presente sección, presupone que el número ${\textstyle N}$ de frecuencias naturales se conoce a priori y que la señal bajo análisis está contaminada de ruido. En este método se aplica una descomposición DVS a la matriz ${\textstyle {\mathbf {Y} }}$ ampliada de la forma ${\textstyle [\mathbf {Y} ,-\mathbf {b} ]}$ [7,8].

La modificación sustancial planteada surge cuando no se propone resolver directamente el sistema de ecuaciones ${\textstyle \mathbf {Y} \mathbf {a} =\mathbf {b} }$, sino el sistema ${\textstyle [{\mathbf {Y} },{-\mathbf {b} }][{\mathbf {a} }^{\mathit {H}}~~-1]^{^{\mathit {H}}}=0}$.

Como la matriz aumentada ${\textstyle [\mathbf {Y} ,-\mathbf {b} ]}$ contiene muestras contaminadas con ruido, se la expande mediante una descomposición en valores singulares de la forma [59]:

$[\mathbf {Y} ,-\mathbf {b} ]=\mathbf {U} \mathbf {\Sigma } \mathbf {V} ^{\mathit {H}}$

(25)

Luego, comprobamos que la matriz ${\textstyle \mathbf {V} }$ de (25) puede representarse como

$\mathbf {V} ={\begin{pmatrix}\mathbf {V_{pp}} &~\mathbf {v_{pq}} \\\mathbf {v_{qp}} &~v_{qq}\\\end{pmatrix}}$

donde ${\textstyle \mathbf {v_{pq}} }$ es el último vector columna de ${\textstyle \mathbf {V} }$ sin su último elemento, ${\textstyle \mathbf {v_{qp}} }$ es el último vector fila de ${\textstyle \mathbf {V} }$ sin su último elemento, y ${\textstyle v_{qq}}$ es el elemento faltante de ambos vectores. Y el vector ${\textstyle -v_{qq}^{-1}{\mathbf {v_{pq}} }}$ contiene los coeficientes del polinomio característico de Prony dado en la ecuación (7) [8]:

${\mathbf {a} }\approx -v_{qq}^{-1}{\mathbf {v_{pq}} }$

A partir de aquí se aplican los pasos subsiguientes del método de Prony clásico.

2.4 Método de haz de matrices en ausencia de ruido

El método de haz de matrices o de haz de funciones generalizado (GPOF) es un método de un solo paso de cálculo, el cual permite estimar los polos discretos ${\textstyle \{z_{n}\}}$ del sistema ${\textstyle H(z)}$ como los autovalores generalizados de un haz lineal de matrices de la forma:

$\mathbf {H_{2}} -\lambda \mathbf {H_{1}}$

(26)

donde las matrices ${\textstyle \mathbf {H_{1}} }$ y ${\textstyle \mathbf {H_{2}} }$ se derivan de la matriz aumentada de Hankel ${\textstyle [\mathbf {H} ,-\mathbf {b} ]}$, de dimensiones ${\textstyle (M-N)\times (N+1)}$

${[\mathbf {H} ,-\mathbf {b} ]}={\begin{pmatrix}h_{0}&h_{1}&..&h_{N}\\h_{1}&h_{2}&..&h_{N+1}\\.&.&..&.\\.&.&..&.\\.&.&..&.\\h_{M-N-1}&&..&h_{M-1}\\\end{pmatrix}}_{(M-N)\times ({N+1})}$

Las matrices ${\textstyle \mathbf {H_{1}} }$ y ${\textstyle \mathbf {H_{2}} }$ se construyen a partir de ${\textstyle [\mathbf {H} ,-\mathbf {b} ]}$ eliminando de esta la segunda y la primera columna, respectivamente:

${\mathbf {H_{1}} }={\begin{pmatrix}h_{0}&h_{1}&...&h_{N-1}\\h_{1}&h_{2}&...&...\\h_{2}&h_{3}&...&...\\.&.&...&...\\.&.&...&h_{M-3}\\h_{M-N-1}&.&...&h_{M-2}\\\end{pmatrix}}_{(M-N)\times N}$

${\mathbf {H_{2}} }={\begin{pmatrix}h_{1}&h_{2}&...&h_{N}\\h_{2}&h_{3}&...&...\\h_{3}&h_{4}&...&...\\.&.&...&...\\.&.&...&h_{M-2}\\h_{M-N}&.&...&h_{M-1}\\\end{pmatrix}}_{(M-N)\times N}$

Fácilmente se comprueba que las matrices ${\textstyle \mathbf {H_{1}} }$ y ${\textstyle \mathbf {H_{2}} }$ pueden ser factorizadas de la forma [4]:

$\mathbf {H_{1}} =\mathbf {Z_{1}RZ_{2}}$

(27)

$\mathbf {H_{2}} =\mathbf {Z_{1}RZ_{0}Z_{2}}$

(28)

donde

$\mathbf {Z_{1}} ={\begin{pmatrix}1&1&\ldots &1\\z_{1}&z_{2}&\ldots &z_{N}\\\vdots &\vdots &\ldots &\vdots \\z_{1}^{M-N-1}&z_{2}^{M-N}&\ldots &z_{N}^{M-1}\end{pmatrix}}_{(M-N)\times N}$

(29)

$\mathbf {R} ={\begin{pmatrix}r_{1}&0&\ldots &0\\0&r_{2}&\ldots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\vdots &r_{N}\end{pmatrix}}_{N\times N}$

(30)

$\mathbf {Z_{0}} ={\begin{pmatrix}z_{1}&0&\ldots &0\\0&z_{2}&\ldots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\vdots &z_{N}\end{pmatrix}}_{N\times N}$

(31)

$\mathbf {Z_{2}} ={\begin{pmatrix}1&z_{1}&\ldots &z_{1}^{N-1}\\1&z_{2}&\ldots &z_{2}^{N-1}\\\vdots &\vdots &\ldots &\vdots \\1&z_{N}&\ldots &z_{N}^{N-1}\end{pmatrix}}_{N\times N}$

(32)

Ahora bien, combinando apropiadamente las ecuaciones (27) y (28) se obtiene:

$\mathbf {H_{1}^{+}} \mathbf {H_{2}} =\mathbf {Z_{2}^{+}} \mathbf {Z_{0}} \mathbf {Z_{2}}$

(33)

donde ${\textstyle \mathbf {H_{1}^{+}} }$ es la pseudoinversa de Moore-Penrose de ${\textstyle \mathbf {H_{1}} }$:

$\mathbf {H_{1}^{+}} =\left({\mathbf {H_{1}^{\mathit {H}}} }\mathbf {H_{1}} \right)^{-1}\mathbf {H_{1}^{\mathit {H}}}$

(34)

De la inspección de la ecuación (33), puede concluirse que los autovalores de ${\textstyle \mathbf {H_{1}^{+}} \mathbf {H_{2}} }$ son los autovalores de la matriz diagonal ${\textstyle \mathbf {Z_{0}} }$ dado que ${\textstyle \mathbf {Z_{2}^{+}} \mathbf {Z_{0}} \mathbf {Z_{2}} }$ es una forma de diagonalización de la matriz ${\textstyle \mathbf {H_{1}^{+}} \mathbf {H_{2}} }$. Por tanto, los autovalores de la matriz ${\textstyle \mathbf {H_{1}^{+}} \mathbf {H_{2}} }$ son iguales a los elementos de la matriz ${\textstyle \mathbf {Z_{0}} }$ que de acuerdo a la ecuación (31) son las raíces ${\textstyle z_{n}}$ que se desea estimar.

Una vez obtenidas las raíces ${\textstyle z_{n}}$, las frecuencias naturales complejas ${\textstyle s_{n}}$ pueden determinarse como ${\textstyle s_{n}=\ln(z_{n})/\Delta t}$.

2.5 Método de haz de matrices en presencia de ruido

La estrategia que describiremos a continuación también se conoce como método de haz de matrices con mínimos cuadrados totales [58], y se utiliza cuando las muestras están contaminadas de ruido y además el número ${\textstyle N}$ de frecuencias naturales complejas del sistema bajo estudio se desconoce. Con este método los polos discretos ${\textstyle z_{n}}$ del sistema ${\textstyle H(z)}$ se estiman también en un solo paso como solución del problema generalizado de autovalores del haz lineal de matrices de la forma:

$\mathbf {Y_{2}} -\lambda \mathbf {Y_{1}}$

(35)

donde las matrices ${\textstyle \mathbf {Y_{1}} }$ y ${\textstyle \mathbf {Y_{2}} }$ se derivan de la matriz de Hankel ${\textstyle \mathbf {Y} }$ de dimensiones ${\textstyle (M-L)\times (L+1)}$, construida a partir de las muestras ${\textstyle y_{m}=h_{m}+n_{m}}$ (Figura 1):

${\mathbf {Y} }={\begin{pmatrix}y_{0}&y_{1}&..&y_{L}\\y_{1}&y_{2}&..&y_{(L+1)}\\.&.&..&.\\.&.&..&.\\y_{M-L-2}&.&..&y_{M-2}\\y_{M-L-1}&&..&y_{M-1}\\\end{pmatrix}}_{(M-L)\times ({L+1})}$

(36)

donde ${\textstyle L}$ se conoce como parámetro del haz, y se utiliza para eliminar algunos de los efectos del ruido presente en los datos. Los valores recomendados de ${\textstyle L}$ se ubican en el rango entre ${\textstyle M/3}$ y ${\textstyle M/2}$. Para estos valores de ${\textstyle L}$ la varianza de los valores estimados de ${\textstyle z_{n}}$ debida al ruido ha resultado mínima [9].

La matriz ${\textstyle \mathbf {Y_{1}} }$ se construye por medio de la eliminación de la última columna de ${\textstyle \mathbf {Y} }$, mientras que la matriz ${\textstyle \mathbf {Y_{2}} }$ se construye mediante la eliminación de la primera columna de ${\textstyle \mathbf {Y} }$:

${\mathbf {Y_{1}} }={\begin{pmatrix}y_{0}&y_{1}&...&y_{L-1}\\y_{1}&y_{2}&...&y_{L}\\y_{2}&y_{3}&...&y_{L+1}\\.&.&...&...\\y_{M-L-2}&.&...&y_{M-3}\\y_{M-L-1}&.&...&y_{M-2}\\\end{pmatrix}}_{(M-L)\times L}$

${\mathbf {Y_{2}} }={\begin{pmatrix}y_{1}&y_{2}&...&y_{L}\\y_{2}&y_{3}&...&y_{L+1}\\y_{3}&y_{4}&...&y_{L+2}\\.&.&...&...\\y_{M-L-1}&.&...&y_{M-2}\\y_{M-L}&.&...&y_{M-1}\\\end{pmatrix}}_{(M-L)\times L}$

Debido a la presencia de ruido en las muestras, ${\textstyle L-N}$ polos matemáticos falsos aparecen, acompañando las ${\textstyle N}$ frecuencias naturales complejas propias del sistema. Una descomposición DVS de ${\textstyle \mathbf {Y} }$ permite discriminar las frecuencias naturales de los polos espurios. En efecto:

$\mathbf {Y} =\mathbf {U} \mathbf {\Sigma } \mathbf {V^{\mathit {H}}}$

(37)

donde vale la pena recordar que ${\textstyle \mathbf {\Sigma } }$ es una matriz diagonal de dimensiones ${\textstyle (M-L)\times (L+1)}$ la cual contiene los valores singulares de ${\textstyle \mathbf {Y} }$ ordenados de forma descendente tal que ${\textstyle \sigma _{1}>\sigma _{2}>...>\sigma _{L+1}}$ [9,58].

Definiendo una tolerancia ${\textstyle T}$ tal como se hizo en la Sección 2.1 (ecuación (23)), se construye la matriz diagonal cuadrada ${\textstyle \mathbf {\Sigma } _{\mathit {T}}}$ de dimensiones ${\textstyle T\times T}$ con los ${\textstyle T}$ valores singulares más significativos de la matriz ${\textstyle \mathbf {Y} }$, y luego las matrices rectangulares truncadas ${\textstyle {\mathbf {U} _{\mathit {T}}}}$ y ${\textstyle {\mathbf {V} _{\mathit {T}}}}$, por medio de la supresión de todas las columnas más allá de la ${\textstyle T}$-ésima columna de ${\textstyle \mathbf {U} }$ y ${\textstyle \mathbf {V} }$, respectivamente.

Por medio de la eliminación de la última fila de la matriz ${\textstyle \mathbf {V} _{\mathit {T}}}$ se crea la matriz ${\textstyle \mathbf {V_{1}} }$ y mediante la eliminación de la primera fila de ${\textstyle \mathbf {V} _{\mathit {T}}}$ se crea la matriz ${\textstyle \mathbf {V_{2}} }$. Las matrices obtenidas ${\textstyle \mathbf {V_{1}} }$ y ${\textstyle \mathbf {V_{2}} }$ cumplen con la relación

$\mathbf {Y_{1}} =\,\mathbf {U} _{\mathit {T}}\mathbf {\Sigma } _{\mathit {T}}{\mathbf {V_{1}} }^{\mathit {H}}$ $\mathbf {Y_{2}} =\,\mathbf {U} _{\mathit {T}}\mathbf {\Sigma } _{\mathit {T}}{\mathbf {V_{2}} }^{\mathit {H}}$

Luego, tomando en cuenta que el problema de autovalores generalizado ${\textstyle (L\times T)\Rightarrow (T\times T)}$:

$\mathbf {Y_{2}} -\lambda \mathbf {Y_{1}} \Rightarrow \mathbf {Y_{1}^{+}} \mathbf {Y_{2}} -\lambda \mathbf {I}$

(38)

es equivalente al problema ordinario de autovalores dado por

$\mathbf {V_{2}^{\mathit {H}}} -\lambda \mathbf {V_{1}^{\mathit {H}}} \Rightarrow \mathbf {V_{1}^{{\mathit {H}}^{+}}} \mathbf {V_{2}} ^{\mathit {H}}-\lambda \mathbf {I}$

(39)

los polos ${\textstyle z_{n}}$ del sistema ${\textstyle H(z)}$ se estiman como los autovalores de la matriz ${\textstyle {\mathbf {V_{1}^{{\mathit {H}}^{+}}} }{\mathbf {V_{2}} }^{\mathit {H}}}$ [9].

3. Resultados

Con la intención de comparar su desempeño, a continuación se presentan los resultados obtenidos a partir de la programación en MATLAB de los métodos descritos en la Sección 2 en diferentes escenarios de simulación. Como señal de prueba se usó una compuesta de la suma de cuatro cosenos amortiguados de la forma:

$y(t)=r_{1}e^{-\sigma _{1}t}\cos(\omega _{1}t)+r_{2}e^{-\sigma _{2}t}\cos(\omega _{2}t)+\ldots$ $\dots +r_{3}e^{-\sigma _{3}t}\cos(\omega _{3}t)+r_{4}e^{-\sigma _{4}t}\cos(\omega _{4}t)+n(t)$

(40)

donde tanto la potencia de ruido blanco Gausiano ${\textstyle n(t)}$ así como los valores de las frecuencias naturales complejas ${\textstyle s_{n}=-\sigma _{n}\pm \jmath \omega _{n}}$, con ${\textstyle \sigma _{n}>0}$, y sus residuos ${\textstyle r_{n}}$ asociados fueron definidos ad hoc para cada experimento.

3.1 Comparación del desempeño de cada algoritmo en presencia de diferentes niveles de ruido añadido

Este primer experimento fue realizado con la idea de examinar la precisión de cada uno de los métodos numéricos presentados en la Sección 2 en la estimación de las frecuencias naturales complejas asociadas al sistema lineal bajo estudio en presencia de diferentes niveles de ruido blanco Gausiano añadido. Para realizar este experimento, se seleccionó una señal ${\textstyle y(t)}$ de la forma dada por la ecuación (40) con ${\textstyle r_{1}=10}$, ${\textstyle r_{2}=5}$, ${\textstyle r_{3}=r_{4}=0}$, ${\textstyle \sigma _{1}=1.1}$, ${\textstyle \omega _{1}=2\pi }$, ${\textstyle \sigma _{2}=1.4}$ y ${\textstyle \omega _{2}=4\pi }$. Nótese que dado que ${\textstyle r_{3}=r_{4}=0}$, cada algoritmo, de ser exitoso, solo debe estimar las frecuencias naturales complejas ${\textstyle s_{1}}$, ${\textstyle s_{2}}$, ${\textstyle s_{5}}$ y ${\textstyle s_{6}}$.

En este experimento se utilizó un formato numérico de doble precisión para la estimación de los valores de ${\textstyle s_{1}}$, ${\textstyle s_{2}}$, ${\textstyle s_{5}}$ y ${\textstyle s_{6}}$. La señal ${\textstyle y(t)}$ fue muestreada desde ${\textstyle t_{0}=0}$ hasta ${\textstyle t_{f}=Mt_{s}}$, con ${\textstyle M=}$ 80, con una frecuencia de muestreo de ${\textstyle f_{s}=11}$, correspondiente a un tiempo de muestreo de ${\textstyle t_{s}=1/f_{s}=1/11}$.

Para los métodos de haz de matrices con filtro DVS, y de Prony con filtro DVS, se utilizó un número máximo de componentes de la matriz diagonal ${\textstyle {\mathbf {Z} _{0}}}$ de ${\textstyle N_{\mathrm {MAX} }=50}$. El factor de truncamiento ${\textstyle T}$ se fijó en ${\textstyle T=4}$, mientras que el parámetro del haz de matrices ${\textstyle L}$ se fijó en ${\textstyle L=[5M/12]=33}$ donde la utilización de los corchetes, en este caso, simbolizan la función parte entera.

Por otra parte, para los métodos de Prony clásico y con mínimos cuadrados totales, así como para el de haz de matrices sin filtro DVS, se fijó el número de frecuencias naturales complejas a calcular en ${\textstyle N=T=4}$.

Una vez definidos los valores de entrada, cada algoritmo fue corrido en presencia de ruido un número de ${\textstyle K=200}$ veces para 20 valores distintos de la relación señal a ruido, desde SNR=10 hasta SNR=153. Con los valores estimados de ${\textstyle {\hat {s}}_{1}}$ (${\textstyle {\hat {\sigma }}_{1}}$ y ${\textstyle {\hat {\omega }}_{1}}$) se estimaron, a su vez, las varianzas normalizadas ${\textstyle \mathrm {Var} ({\hat {\sigma }}_{1})/\sigma _{1}^{2}}$ y ${\textstyle \mathrm {Var} ({\hat {\omega }}_{1})/\omega _{1}^{2}}$ para cada valor de SNR a partir de las ecuaciones:

$\mathrm {Var} ({\hat {\sigma }}_{1})={\dfrac {\displaystyle \sum _{k=1}^{K}({\hat {\sigma }}_{1,k}-{\bar {\sigma }}_{1})^{2}}{K-1}}$

(41)

$\mathrm {Var} ({\hat {\omega }}_{1})={\dfrac {\displaystyle \sum _{k=1}^{K}({\hat {\omega }}_{1,k}-{\bar {\omega }}_{1})^{2}}{K-1}}$

(42)

donde ${\textstyle {\hat {\sigma }}_{1,k}}$ y ${\textstyle {\hat {\omega }}_{1,k}}$ son los valores estimados de ${\textstyle \sigma _{1}}$ y ${\textstyle \omega _{1}}$ en la ${\textstyle k}$-ésima corrida realizada, mientras que ${\textstyle {\bar {\sigma }}_{1}}$ y ${\textstyle {\bar {\omega }}_{1}}$ son los respectivos promedios aritméticos de ${\textstyle {\hat {\sigma }}_{1}}$ y ${\textstyle {\hat {\omega }}_{1}}$, estimados en ${\textstyle K=200}$ realizaciones.

Los resultados obtenidos se presentan en las Figuras 3 y 4. En tales figuras se han trazado las curvas de ${\textstyle \left(\mathrm {Var} ({\hat {\sigma }}_{1})/\sigma _{1}^{2}\right)^{-1}}$ y ${\textstyle \left(\mathrm {Var} ({\hat {\omega }}_{1})/\omega _{1}^{2}\right)^{-1}}$, respectivamente, en ambos casos como una función de la relación señal a ruido (SNR), para cada uno de los métodos analizados, de manera similar a la realizada en [4].

Figura 3. Valor de $\left[\mathrm {Var} ({\hat {\sigma }}_{1})/\sigma _{1}^{2}\right]^{-1}$ en decibelios versus la relación señal a ruido (SNR) en decibelios, para cada uno de los métodos estudiados

Figura 4. Valor de $\left[\mathrm {Var} ({\hat {\omega }}_{1})/\omega _{1}^{2}\right]^{-1}$ en decibelios versus la relación señal a ruido (SNR) en decibelios, para cada uno de los métodos estudiados

3.2 Comparación del desempeño de cada algoritmo para distintas frecuencias de muestreo

Este segundo experimento fue realizado con la idea de examinar la precisión de cada uno de los métodos numéricos presentados en la Sección 2 cuando se estiman las frecuencias naturales complejas de un sistema en presencia de un nivel de ruido añadido fijo, al utilizar distintas frecuencias de muestreo ${\textstyle f_{s}}$. Para realizar este experimento, se utilizó una señal ${\textstyle y(t)}$ tal que ${\textstyle r_{1}=10}$, ${\textstyle r_{2}=r_{3}=r_{4}=0}$, con ${\textstyle \sigma _{1}=1.1}$ y ${\textstyle \omega _{1}=2\pi }$. En este caso cada algoritmo debe estimar las frecuencias complejas ${\textstyle s_{1}}$ y ${\textstyle s_{1}^{\ast }}$ del sistema lineal. Para realizar este experimento, se utlizó un ruido del tipo Gausiano blanco ${\textstyle n(t)}$ con una potencia relativa apropiada para proveer una relación señal a ruido resultante de SNR=60 dB.

Para todas las simulaciones realizadas en este experimento se utilizó un formato numérico de doble precisión. La señal ${\textstyle y(t)}$ fue muestreada en una ventana de observación que va desde ${\textstyle t_{0}=0}$ hasta ${\textstyle t_{f}=4}$, para un rango de frecuencias de muestreo (${\textstyle f_{s}}$) que va desde ${\textstyle {f_{s}}_{MIN}=2.5}$ hasta ${\textstyle {f_{s}}_{\mathrm {MAX} }=27}$. Para lograr esta condición hubo que cambiar para cada simulación el número de muestras ${\textstyle M}$, tal que se cumpliese ${\textstyle M=[{f_{s}}(t_{f}-t_{0})]}$ con la idea de mantener la ventana de observación constante para cada valor de ${\textstyle f_{s}}$ utilizado en cada simulación.

Para las simulaciones realizadas en este experimento con el método de Prony con filtro DVS y para el haz de matrices con filtro DVS, se fijó el número máximo de componentes ${\textstyle N_{\mathrm {MAX} }}$ de la matriz diagonal ${\textstyle {\mathbf {Z} _{0}}}$ en ${\textstyle N_{\mathrm {MAX} }=20}$, mientras que el parámetro del haz de matrices ${\textstyle L}$ se fijó en ${\textstyle L=[5M/12]=33}$, para un factor de truncamiento ${\textstyle T=2}$ pues son dos las frecuencias complejas naturales a calcular.

Por otra parte, para las simulaciones realizadas con el método de Prony clásico, con el método de Prony con mínimos cuadrados totales y con el método del haz de matrices sin filtro DVS, se utilizó un número de frecuencias naturales complejas ${\textstyle N=2}$.

Luego, para cincuenta valores de frecuencia de muestreo ${\textstyle f_{s}}$ equiespaciadas, desde ${\textstyle f_{s}=2.5}$ hasta ${\textstyle f_{s}=27.5}$ se muestra el inverso de las varianzas normalizadas ${\textstyle \mathrm {Var} ({\hat {\sigma }}_{1})/\sigma _{1}^{2}}$ y ${\textstyle \mathrm {Var} ({\hat {\omega }}_{1})/\omega _{1}^{2}}$, donde ${\textstyle \mathrm {Var} ({\hat {\sigma }}_{1})}$ y ${\textstyle \mathrm {Var} ({\hat {\omega }}_{1})}$ están definidas por las ecuaciones (41) y (42) para ${\textstyle K=40}$ realizaciones. Como resultado, en las Figuras 5 y 6 se muestran las gráficas de los valores ${\textstyle \left(\mathrm {Var} ({\hat {\sigma }}_{1})/\sigma _{1}^{2}\right)^{-1}}$ y ${\textstyle (\mathrm {Var} \left({\hat {\omega }}_{1})/\omega _{1}^{2}\right)^{-1}}$ en función de la frecuencia ${\textstyle f_{s}}$ de muestreo, para cada algoritmo bajo estudio.

Figura 5. Valor de $\left[\mathrm {Var} ({\hat {\sigma }}_{1})/\sigma _{1}^{2}\right]^{-1}$ en decibelios versus la frecuencia de muestreo $f_{s}$, para cada uno de los métodos estudiados

Figura 6. Valor de $\left[\mathrm {Var} ({\hat {\omega }}_{1})/\omega _{1}^{2}\right]^{-1}$ en decibelios versus la frecuencia de muestreo $f_{s}$, para cada uno de los métodos estudiados

3.3 Comparación de los tiempos de cómputo que cada algoritmo necesita para determinar las frecuencias naturales complejas de un sistema dado

Este experimento fue realizado con el objetivo de comparar el tiempo de cómputo de cada algoritmo para estimar las ocho frecuencias naturales complejas que forman parte de la señal ${\textstyle y(t)}$ dada por la ecuación (40) variando la ventana temporal de observación de la señal y manteniendo constante la tasa de muestreo.

En este experimento la señal ${\textstyle y(t)}$ fue construida artificialmente usando los siguientes valores: ${\textstyle r_{1}=10}$, ${\textstyle r_{2}=7}$, ${\textstyle r_{3}=3}$, ${\textstyle r_{4}=1}$, ${\textstyle \sigma _{1}=1.1}$, ${\textstyle \sigma _{2}=1.4}$, ${\textstyle \sigma _{3}=2}$, ${\textstyle \sigma _{4}=3}$, ${\textstyle \omega _{1}=2\pi }$, ${\textstyle \omega _{2}=4\pi }$, ${\textstyle \omega _{3}=6\pi }$ y ${\textstyle \omega _{4}=10\pi }$ usando un formato numérico de doble precisión para todos los cómputos.

Las muestras de ${\textstyle y(t)}$ fueron tomadas durante cuatro ventanas temporales de duración distinta, desde ${\textstyle t_{0}=0}$ hasta ${\textstyle t_{f}=Mt_{s}}$, con ${\textstyle M=\{100,200,300,400\}}$, usando en todos los casos la misma frecuencia de muestreo de ${\textstyle f_{s}=11}$, correspondiente a un tiempo de muestreo de ${\textstyle t_{s}=1/f_{s}=1/11}$.

Para las simulaciones realizadas en este experimento con el haz de matrices con filtro DVS y con el método de Prony con filtro DVS, se utilizó un número máximo de componentes de la matriz diagonal ${\textstyle {\mathbf {Z} _{0}}}$ de ${\textstyle N_{\mathrm {MAX} }=20}$. El parámetro del haz de matrices se fijó para cada caso en ${\textstyle L=[5M/12]}$ y el factor de truncamiento se fijó en ${\textstyle T=8}$.

Por otra parte, para las estimaciones realizadas con los métodos de Prony clásico, de Prony con mínimos cuadrados totales y de haz de matrices sin filtro DVS, se fijó un número de frecuencias naturales complejas a estimar de ${\textstyle N=T=8}$.

En la Tabla 1 se muestra el tiempo de cómputo en milisegundos empleado por cada algoritmo durante la estimación de la frecuencias naturales complejas ${\textstyle s_{n}}$ según el número ${\textstyle M}$ de muestras tomadas a ${\textstyle y(t)}$.

Tabla 1. Tiempo de cómputo en milisegundos empleado por cada algoritmo durante la estimación de la frecuencias $s_{n}$ según el número $M$ de muestras tomadas a $y(t)$

Algoritmo	${\textstyle M=100}$	${\textstyle M=200}$	${\textstyle M=300}$	${\textstyle M=400}$
Prony clásico	0.00029	0.00033	0.00039	0.00045
Prony con DVS	0.00165	0.00218	0.00490	0.00427
Prony con mínimos cuadrados totales	0.00167	0.00434	0.01150	0.02474
Haz de matrices	0.00616	0.04337	0.13920	0.27570
Haz de matrices con DVS	0.00460	0.02660	0.07272	0.17300

4. Análisis de resultados

Del análisis comparativo de los resultados observados de todas las simulaciones realizadas durante el desarrollo de este trabajo, puede concluirse que, en presencia de bajos niveles de ruido, todos los métodos estudiados son capaces de estimar las frecuencias naturales de resonancia del sistema bajo estudio. Sin embargo, del análisis comparativo de los resultados expuestos en la Sección 3.1, en las Figuras 3 y 4, puede concluirse que el método convencional más preciso y robusto cuando la señal ${\textstyle y(t)}$ está contaminada con ruido es el método de haz de matrices convencional con descomposición DVS. Este resultado es consistente con los estudios reportados en [4], en los cuales se observa que la precisión de los resultados provenientes de este método está muy cerca del límite de Cramer-Rao, el cual es el límite teórico de máxima precisión posible para este tipo de algoritmos estudiados.

Del estudio realizado en la misma Sección 3.1 llama la atención el buen desempeño que tiene el método de Prony cuando utiliza como insumo una matriz ${\textstyle \mathbf {Y} }$ que se ha limpiado mediante una descomposición DVS. También es importante resaltar la significativa diferencia de tolerancia al ruido que tiene el método de haz de Matrices con y sin filtrado DVS, pues al no utilizar la descomposición DVS, el método de haz de Matrices pierde capacidad de tolerar al ruido presente en las muestras.

De los resultados mostrados en la Sección 3.2, particularmente en las Figuras 5 y 6, pudo constatarse que en la medida en que la frecuencia de muestreo aumenta dentro de una misma ventana de observación, la precisión que brinda cada una de las versiones de los métodos de Prony y de haz de matrices aumenta, con la excepción del método de Prony clásico que más bien parece mejorar su desempeño en la medida en que la frecuencia de muestreo ${\textstyle f_{s}}$ se aproxima a ${\textstyle 6\omega _{1}/(2\pi )}$ (Figura 6). De hecho, de acuerdo a la información presentada en estas gráficas, el método de Prony clásico puede brindar una mejor precisión que varios de los métodos utilizados si es pequeña la cantidad de muestras que se dispone dentro de una ventana de observación.

Otro aspecto interesante que puede observarse comparando los resultados de las Figuras 3 y 4, y también comparando los resultados de las Figuras 5 y 6, es que, en general, la precisión con la que los métodos analizados calculan el factor de amortiguamiento ${\textstyle \sigma _{1}}$ es menor que la con la que calculan la frecuencia angular de resonancia ${\textstyle \omega _{1}}$. También llama la atención el desempeño del método de Prony clásico cuando, en presencia de poco ruido añadido, casi iguala la precisión del método de haz de matrices con SVD para el cálculo de ${\textstyle \omega _{1}}$, mientras que el mismo método de Prony clásico es el menos preciso para el cálculo de ${\textstyle \sigma _{1}}$ bajo las mismas condiciones. La mayoría de estas observaciones son consistentes con las realizadas en el estudio comparativo presentado en [54].

Del estudio realizado en la Sección 3.3, pudo constatarse a través de los resultados expuestos en la Tabla 1, que las distintas versiones basadas en el método de Prony son más rápidas en el cálculo que los métodos que utilizan la teoría del haz de Matrices. Esta diferencia en la velocidad de cálculo se incrementa en la medida en que el número de muestras utilizadas se hace más grande. De acuerdo al análisis realizado al código del programa que se elaboró, este fenómeno se debe a que las rutinas de MATLAB que calculan las raíces del polinomio característico de Prony son más rápidas que las rutinas que calculan los autovalores de las matrices dadas para el haz de matrices. Estos resultados son congruentes con el estudio presentado en [38], en el cual se menciona la dificultad de utilizar el método del haz de matrices en la medida en que se incrementa el número de muestras ${\textstyle M}$ tomadas a la señal ${\textstyle y(t)}$.

5. Conclusiones y recomendaciones

La respuesta impulsiva de un sistema lineal tiene como rasgo distintivo un conjunto de frecuencias naturales complejas de resonancia las cuales le son propias. Durante el desarrollo de este trabajo, se estudiaron y probaron en distintos escenarios de simulación, algunos de los más importantes algoritmos de cálculo numérico que existen para estimar tales frecuencias complejas naturales del sistema. Entre estos algoritmos, se probó el método de Prony clásico, el método de Prony con filtrado usando descomposición en valores singulares, el método de Prony usando mínimos cuadrados totales, el método de haz de matrices sin filtro y el método de haz de matrices con filtrado mediante descomposición en valores singulares. También durante el desarrollo de este trabajo, se realizó una revisión bibliográfica que evidenció la importancia que tienen estos métodos en diferentes aplicaciones de la física y de la ingeniería.

Se evaluó y comparó mediante simulación la precisión obtenida en la estimación de las frecuencias naturales complejas ${\textstyle s_{n}}$ de cada uno de los algoritmos en presencia de ruido. Pudo concluirse que el método de haz de matrices con descomposición y filtrado DVS es el más robusto en presencia ruido de los métodos convencionales estudiados, tal y como sugiere la bibliografía revisada. De hecho, es difícil encontrar un algoritmo que supere este desempeño pues su precisión está muy cerca del límite teórico de precisión de Cramer-Rao [4] para algoritmos de este tipo. Por tanto, el método del haz de matrices puede utilizarse en aplicaciones en que el tiempo de cálculo no sea una variable crítica a tomar en cuenta, debido a su excelente precisión en ambientes de medición ruidosos.

El notable desempeño en presencia de ruido del método del haz de matrices con descomposición DVS se debe, justamente, a la descomposición y filtrado DVS, la cual permite discriminar y eliminar los valores singulares asociados al ruido presente en la matriz ${\textstyle \mathbf {Y} }$. De hecho, el método pierde su robustez cuando no se utiliza la descomposición DVS. En este mismo sentido, cuando se utiliza filtrado a partir de una descomposición DVS en el método de Prony clásico en presencia de ruido se obtiene un desempeño comparable al del método haz de matrices.

La frecuencia de muestreo y el número de muestras utilizadas para crear la matriz ${\textstyle \mathbf {Y} }$ son variables importantes cuando se quiere aumentar la precisión de la estimación de cada frecuencia natural compleja con ruido presente. A excepción del método de Prony clásico, los métodos estudiados en los escenarios dados aumentan su precisión cuando la frecuencia de muestreo aumenta.

Por otra parte, el método clásico de Prony y sus variantes presentaron mayor velocidad de cálculo que los métodos basados en un haz de matrices, debido a que las rutinas utilizadas para el cálculo de las raíces del polinomio característico de Prony son más rápidas que las que estiman los autovalores de las matrices definidas para el método de haz de matrices. Esto podría indicar que si la relación señal a ruido fuese lo suficientemente alta y si se tiene una aplicación que necesite realizar el cálculo de ${\textstyle s_{n}}$ tan rápido como sea posible, el método de Prony y sus variantes pudiesen ser más apropiados que el método del Haz de Matrices y sus variantes.

Agradecimientos

Proyecto financiado por el Concurso de Proyectos Regulares de Investigación, año 2019, código LPR19-03, Universidad Tecnológica Metropolitana, Santiago de Chile.

Referencias

[1] Lee W., Sarkar T.K., Moon H., Salazar-Palma M. Computation of the natural poles of an object in the frequency domain using the Cauchy method. IEEE Antennas and Wireless Propagation Letters, 11:1137-1140, 2012.

[2] Prony R. Essai éxperimental et analytique: Sur les lois de la dilatabilité de fluides élastique et sur celles de la force expansive de la vapeur de l'alkool à différentes températures. Journal de l'École Polytechnique, 1:24-76, 1795.

[3] Easley D. Prony's method: Determining the number of exponential modes and the optimal sample period. MSc. Thesis, Oklahoma State University, United States of America, 1982.

[4] Hua Y., Sarkar T.K. Generalized pencil-of-function method for extracting poles of an EM system from its transient response. IEEE Transactions on Antennas and Propagation, 37(2):229-234, 1989.

[5] Younan N.H., Taylor C.D. On using the SVD-Prony method to extract poles of an EM system from its transient response. Electromagnetics, 11(2):223-233, 1991.

[6] Porat B., Friedlander B. On the accuracy of the Kumaresan-Tufts method for estimating complex damped exponentials. IEEE Transactions on Acoustics, Speech, and Signal Processing, 35(2):231-235, 1987.

[7] Rahman M.D., Yu K.B. Total least square approach for frequency estimation using linear prediction. IEEE Transactions on Acoustics Speech and Signal Processing, 35(10):1440-1454, 1987.

[8] Gavin H.P. Total least squares. Duke University, Fall 2017. http://people.duke.edu/~hpgavin/SystemID/CourseNotes/TotalLeastSquares.pdf.

[9] Sarkar T.K., Pereira O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials. IEEE Antennas and Propagation Magazine, 37(1):48-55, 1995.

[10] Crow M.L., Singh A. The matrix pencil for power system modal extraction. IEEE Transaction on Power Systems, 20(1):501-502, 2005.

[11] Xu M.M., Xiao L.Y., Wang H.F. A Prony-based method of locating short-circuit fault in DC distribution system. 2nd IET Renewable Power Generation Conference (RPG 2013), 1-4, 9-11 September 2013.

[12] Yang L., Jiao, Z., Kang, X., Wang, X. A novel matrix pencil method for real-time power frequency phasor estimation under power system transients. 12th IET International Conference on Developments in Power System Protection (DPSP 2014), 12-32, 31 March-3 April 2014.

[13] Tawfik M.M., Morcos M.M. On the use of Prony method to locate faults in loop systems by utilizing modal parameters of fault current. IEEE Transactions on Power Delivery, 20(1):532-534, 2005.

[14] Costa F.F., Fernandes D.A., De Almeida L.A.L., Naidu S.R. Prony's method versus FFT for analyzing power converters signals. 2005 European Conference on Power Electronics and Applications, 11-14 September 2005.

[15] Chen J., Fu P., Méndez-Barrios C., Niculescu S., Zhang, H. Stability and instability intervals of polynomially dependent systems: An matrix pencil analysis. 2017 American Control Conference (ACC), 24-26 May 2017.

[16] Tesche F. On the analysis of scattering and antenna problems using the singularity expansion technique. IEEE Transactions on Antennas and Propagation, 21(1):53-62, 1973.

[17] Hua Y., Sarkar T.K. A discussion of E-pulse method and Prony's method for radar target resonance retrieval from scattered field. IEEE Transactions on Antennas and Propagation, 37(7):944-946, 1989.

[18] Sabio V. Target recognition in ultra-wideband sar imagery. Army Research Laboratory TAD-A283 462, 1994.

[19] Andreev M.V., Drobakhin O.O. Feature of Prony's method application for natural frequencies estimation from the frequency response. 2016 8th International Conference on Ultrawideband and Ultrashort Impulse Signals (UWBUSIS), 5-11 September 2016.

[20] Yoshizawa A., Uchida S. A discriminant-based RMSE improvement technique for classical Prony method in small array radars. 2020 17th European Radar Conference (EuRAD), pp. 298-301, 10-15 January 2021.

[21] Drissi K.E.K., Poljak D. The matrix pencil method applied to smart monitoring and radar. 17th International Conference on Computational Methods and Experimental Measurements, 13-24, 5-7 May 2015.

[22] Harmer S.W., Andrews D.A., Rezgui N.D., Bowring N.J. Detection of handguns by their complex natural resonant frequencies. IET Microwaves, Antennas Propagation, 4(9):1182-1990, 2010.

[23] Harmer S.W., Cole S.D., Bowring N. J., Rezgui N. D., Andrews D. On body concealed weapon detection using a phased antenna array. Progress In Electromagnetics Research, 124:187-210, 2012.

[24] Li M., Li S., Yu Y., Ni X., Chen R. Design of random and sparse metalens with matrix pencil method. Optics Express, 26:24702-24711, 2018.

[25] Kokkinos T., Adve R.S., Sarris C.D. Spectral analysis of negative refractive index metamaterials utilizing signal processing techniques and time-domain simulations. IEEE/ACES International Conference on Wireless Communications and Applied Computational Electromagnetics, pp. 409-412, 3-7 April 2005.

[26] Singh A. Analysis of leaky wave antennas using the matrix pencil method. MSc. Thesis. Conconcordia University (Canada), 2014.

[27] Sabett K.F., Katehi L.P.B., Sarabandi K. Wavelet-based CAD modeling of microstrip discontinuities using least square Prony's method. 1997 IEEE MTT-S International Microwave Symposium Digest, 1799-1802, 8-13 June 1997.

[28] Avramenko D.V., Andrejev V.G. Spectral estimation of the photoplethysmographic signal by the double sided Prony method. 2019 8th Mediterranean Conference on Embedded Computing (MECO), 1-4, 10-14 June 2019.

[29] Bhuiyan M., Malyarenko E.V., Pantea M.A., Seviaryn F.M., Maev R.G. Advantages and limitations of using matrix pencil method for the modal analysis of medical percussion signals. IEEE Transactions on Biomedical Engineering, 60(2):417-426, 2013.

[30] Hossein Q., Hojjat A. A comparative study of signal processing methods for structural health monitoring. Journal of Vibroengineering, 18(4):2186-2204, 2016.

[31] Fernández A., de Santiago L., López Guillén E., Rodríguez Ascariz J.M., Miguel Jiménez J.M., Boquete L. Coding Prony’s method in MATLAB and applying it to biomedical signal filtering. BMC Bioinformatics, 19(451):2186-2204, 2018.

[32] Pushkareva A.V., Markuleva M.V. The research of noise stability of the Prony's method while processing of cardiological time series. 2019 International Multi-Conference on Engineering, Computer and Information Sciences (SIBIRCON), 0476–0479, 21-27 October 2019.

[33] Fricke S.N., Seymour J.D., Battistel M.D., Freedberg D.I., Eads C.D., Augustine M.P. Data processing in NMR relaxometry using the matrix pencil. Journal of Magnetic Resonance, 313:106704, 2020.

[34] Bauman G., Bieri O. Matrix pencil decomposition of time-resolved proton MRI for robust and improved assessment of pulmonary ventilation and perfusion. Magnetic Resonance in Medicine, 77(1):336-342, 2016.

[35] Wang Y., Lee H., Apte D. Quantitative NMR spectroscopy by matrix pencil methods. International Journal of Imaging Systems and Technology, 4(3):201-206, 1992.

[36] Ehler M., Kunis S., Peter T., Richter C. A randomized multivariate matrix pencil method for superresolution microscopy. Electronic Transactions on Numerical Analysis, 51:63-74, 2019.

[37] Li Q., Xiao X., Kikkawa T. Noninvasive blood glucose level detection based on matrix pencil method and artificial neural network. Journal of Electrical Engineering & Technology, 16(4):2183-2190, 2021.

[38] Laroche J. The use of the matrix pencil method for the spectrum analysis of musical signals. The Journal of the Acoustical Society of America, 94:1958-1965, 1993.

[39] Avramenko D.V., Andrejev V.G. Spectral analysis of light reflections from cosmic objects by the modified Prony's method. 2018 7th Mediterranean Conference on Embedded Computing (MECO), 1-4, 10-14 June 2018.

[40] Berti E., Cardoso V., González J.A., Sperhake U. Mining information from binary black hole mergers: A comparison of estimation methods for complex exponentials in noise. Physical Review D, 75(12):124017, 2007.

[41] Adve R. Target identification using matrix pencil. Final report, University of Toronto (Canada), 2017.

[42] Chaparro-Arce D., Gallego A., Albarracin-Vargas F., Gutierrez C., Vega F., Pedraza C. Matrix pencil method applied to the compression of audio data in naval operations. 2020 IEEE International Conference on Computational Electromagnetics (ICCEM), 254-256, 24-26 August 2020.

[43] Chaparro-Arce D., Gutierrez S., Gallego A., Gutierrez C., Vega F., Pedraza C. Extraction of complex natural resonances of ships acoustic signals using matrix pencil method. 2020 IEEE Colombian Conference on Communications and Computing (COLCOM), 1-4, 7-8 August 2020.

[44] Persichkin A., Shpilevoy A. About the method of estimating the parameters of seismic signals. IKBFU’s Vestnik Theoretical and Experimental Physics, 10:122-125, 2015.

[45] Li M., Henry M. Signal processing methods for coriolis mass flow metering in two-phase flow conditions. 2016 IEEE International Conference on Industrial Technology (ICIT), 690-695, 14-17 March 2016.

[46] Zaky Y.Y., Fortino N., Dauvignac J.-Y., Seyfert F., Olivi M., Baratchart L. Comparison of SEM methods for poles estimation from scattered field by canonical. 2020 IEEE Radar Conference (RadarConf20), 1-6, 21-25 September 2020.

[47] Hidalgo P. Métodos de Prony y Pisarenko para análisis espectral. BSc. Tesis, Escuela Politécnica Nacional (Ecuador), 1985.

[48] Castillo R., Ortiz J., Calleros G. Análisis de estabilidad de los eventos ocurridos en Laguna Verde. Memorias del XVI Congreso Anual de la SNM/XXIII Reunión Anual de la SMSR, 1-13, 2005.

[49] Issouribehere P.E., Barbero J.C., Issouribehere F., Rodríguez J. Análisis de oscilaciones subsincrónicas derivadas de fallas en sistemas de 500 KV. Experiencias de aplicación del Método de Prony. XIV Encuentro Regional Iberoamericano de la Cigré, 2011.

[50] Issouribehere P.E., Barbero J.C., Issouribehere F. Desarrollo de una herramienta computacional para la detección de modos de oscilación en sistemas de potencia basada en el análisis de Prony. XV Encuentro Regional Iberoamericano de la Cigré, 2013.

[51] Quiroz C. Aplicaciones del modelo autoregresivo y del algoritmo de Prony. MSc. Tesis, Instituto Politécnico Nacional (Mexico), 2002.

[52] Arizaga-Jasso A. Análisis de predicción de tendencia en acciones financieras empleando el método de Prony. MSc. Thesis, Instituto Tecnológico y de Estudios Superiores de Occidente (Mexico), 2020.

[53] Almunif A., Fan L., Miao Z. A tutorial on data-driven eigenvalue identification: Prony analysis, matrix pencil, and eigensystem realization algorithm. International Transactions on Electrical Energy Systems, 30(4):1-17, 2020.

[54] Sarrazin F., Sharaiha A., Pouliguen P., Chauveau J., Collardey S., Potier P. Comparison between matrix pencil and Prony methods applied on noisy antenna responses. 2011 Loughborough Antennas and Propagation Conference, 1-4, 14-15 November 2011.

[55] Sarrazin F., Chauveau J., Pouliguen P., Potier P., Sharaiha A. Accuracy of singularity expansion method in time and frequency domains to characterize antennas in presence of noise. IEEE Transactions on Antennas and Propagation, 62(3):1261-1269, 2014.

[56] Lee J.H., Cho Y.S., Jeong J.H. Performance analysis of the LS Prony method for estimating parameters of damped sinusoids. IET Radar, Sonar and Navigation, 13(11):1918–1933, 2019.

[57] Leon S.J. Linear Algebra with its applications. 9th Edition, Pearson, 2015.

[58] Rao S.M., Vechinski D.A. Chapter 4 - Finite conducting bodies: TDIE solution. Time Domain Electromagnetics, Rao S.M. (Ed.), Academic Press, pp. 97-129, 1999.

[59] Brunton S.L., Kutz J.N. Data-driven science and engineering: Machine learning, dynamical systems and control. Cambridge University Press, 2019.