Resumen
El análisis dinámico incremental es una poderosa herramienta para evaluar la vulnerabilidad y el riesgo sísmico de edificios. Permite calcular el daño global de estructuras para diferentes aceleraciones máximas del terreno y representar este resultado por medio de curvas de daño. Dichas curvas se utilizan para evaluar el riesgo sísmico a nivel urbano. Aunque el uso de este método en un entorno probabilista requiere un considerable esfuerzo computacional, este debe ser el método de referencia para el cálculo de las mencionadas curvas. Sin embargo, resulta de interés práctico disponer de un método más sencillo que utilice, por ejemplo, el análisis estático no lineal incremental (pushover analysis) para evaluar la vulnerabilidad sísmica y el riesgo de los edificios, que permita obtener resultados similares a los obtenidos usando el análisis dinámico incremental. Haciendo referencia a los métodos basados en la capacidad y la demanda, habitualmente se han utilizado opiniones de expertos para definir los umbrales de los estados de daño a partir del punto de plastificación y del desplazamiento máximo espectral identificado en el espectro de capacidad bilineal. Por lo tanto, en el artículo se propone un nuevo procedimiento para la definición de los umbrales de los estados de daño, con base en la degradación de la rigidez de la estructura. El problema se aborda mediante un método totalmente probabilista utilizando la simulación por Monte Carlo con el fin de comparar de una manera rigurosa los resultados obtenidos con los proporcionados por el análisis dinámico incremental.
Abstract
The incremental dynamic analysis is a powerful tool for evaluating the seismic vulnerability and risk of buildings. It allows calculating the global damage of structures for different peak ground accelerations, PGA, and representing this result by means of damage curves. Such curves are currently used to obtain seismic risk scenarios at urban level. Even if the application of this method in a probabilistic environment requires a relevant computational effort, this has to be the reference method for determining those curves. Nevertheless, it would be of high practical interest to have a simpler method based, for instance, on pushover analysis, for assessing the seismic vulnerability and risk of buildings, which allows obtaining results similar to those based on the incremental dynamic analysis. Referring to the capacity-spectrum-based-methods, expert opinions have been used in previous researches for defining damage states thresholds starting from the yielding and the ultimate spectral displacement identified in the bilinear capacity spectrum. Therefore, we propose in this article a new procedure for defining the damage states thresholds, based on the stiffness degradation of reinforced concrete building, and a fully probabilistic approach is tackled by means of Monte Carlo simulations. It is demonstrated in the paper that the obtained results are in good agreement with those calculated using the incremental dynamic analysis.
Palabras clave
Análisis dinámico incremental ; Análisis pushover ; Método de Monte Carlo
Keywords
Incremental dynamic analysis ; Pushover analysis ; Monte Carlo method
1. Introducción
Para evaluar el riesgo sísmico de las estructuras existentes debe establecerse cuál es el grado de daño producido por un terremoto. Existen diversas metodologías para el cálculo de dicho grado de daño como, por ejemplo, el método del índice de vulnerabilidad en el que se define la acción sísmica por medio de la escala macrosísmica europea EMS-98 [1] , y el comportamiento estructural se describe por medio de un índice de vulnerabilidad [2] , [3] , [4] , [5] and [6] . Otra metodología ampliamente usada se basa en el método del espectro de capacidad propuesto en las referencias [7] and [8] y ha sido ampliamente investigada, mejorada y aplicada [9] , [10] , [11] , [12] , [13] , [14] and [15] . En este método, la acción sísmica se define por medio del espectro de respuesta elástico, mientras que la capacidad del edificio se define por medio del espectro de capacidad, suponiendo que la respuesta estructural está contenida principalmente en el primer modo de vibración. El espectro de capacidad se calcula mediante un análisis estático no lineal incremental, conocido comúnmente como pushover analysis (PA por sus siglas en inglés). El método del espectro de capacidad ha sido posteriormente modificado para incluir los efectos de los modos más altos de vibración [16] , [17] and [18] . Dicho método se aplicó en varios estudios anteriores con el fin de calcular el riesgo sísmico de zonas urbanas [19] , [20] and [21] , donde se siguen los desarrollos realizados en el proyecto RISK-UE [22] , en el que los umbrales de los estados de daño se definen a partir de la opinión de expertos [4] and [23] con base en los desplazamientos de plastificación y último del espectro de capacidad. Aunque este enfoque es útil para evaluaciones a gran escala, puede proporcionar resultados que no están de acuerdo con los obtenidos por medio del análisis dinámico incremental, que es la herramienta de referencia para evaluar la vulnerabilidad y el riesgo sísmico de edificios. Este procedimiento permite calcular el daño global de estructuras para diferentes intensidades y, además, representarlo por medio de curvas de daño. Dichas curvas son utilizadas en muchos métodos para la obtención de escenarios probabilistas de riesgo sísmico a nivel urbano.
En este artículo se muestra cómo, con una nueva definición de los umbrales de los estados de daño con base en la degradación de la rigidez del edificio, calculada a partir de las derivadas primera y segunda del espectro de capacidad, el método puede ser mejorado. Esta nueva definición de los umbrales de daño se ilustra usando un edificio de 3 plantas de hormigón armado teniendo en cuenta las incertidumbres relacionadas con el riesgo sísmico y las propiedades mecánicas de los materiales. Se demuestra, considerando un riguroso enfoque probabilista, que hay un mejor acuerdo entre los resultados obtenidos mediante un cálculo dinámico y un cálculo estático.
2. Descripción del edificio estudiado
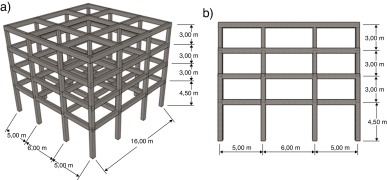
El edificio estudiado es de hormigón armado, tiene 4 niveles y 3 vanos y se muestra en la figura 1 junto con sus dimensiones. Debido a su simetría puede ser representado mediante un modelo bidimensional utilizando un solo pórtico (figura 1 b) cuyas características se muestran en la tabla 1 .
|
|
|
Figura 1. Edificio estudiado (a) y el modelo 2 D del edificio (b). |
| Columnas | Vigas | |||||
|---|---|---|---|---|---|---|
| Nivel | b (m) | h (m) | ρ | b (m) | h (m) | ρ |
| 1 | 0,5 | 0,5 | 0,03 | 0,45 | 0,6 | 0,0066 |
| 2 | 0,5 | 0,5 | 0,02 | 0,45 | 0,6 | 0,0066 |
| 3 | 0,45 | 0,45 | 0,015 | 0,45 | 0,6 | 0,0066 |
| 4 | 0,4 | 0,4 | 0,015 | 0,45 | 0,6 | 0,0066 |
El material de las vigas y de las columnas del modelo estructural sigue la regla de histéresis de Takeda modificada [24] . Las superficies de fluencia se definen por medio del diagrama de interacción de flexo-compresión para las columnas y de momento-curvatura para las vigas. Las cargas aplicadas y el diseño de los elementos estructurales siguen las recomendaciones dadas por el Eurocódigo 2 (EC2) [25] para estructuras de hormigón armado y del Eurocódigo 8 (EC8) para considerar las cargas sísmicas. Los valores característicos de las propiedades mecánicas del hormigón y del acero son valores utilizados comúnmente en el diseño de tales edificios. Las normas de diseño requieren valores característicos de resistencia de los materiales obtenidos durante el proceso de control de calidad, a partir de ensayos de compresión y tracción en las muestras de hormigón y acero, respectivamente. Por medio de estos ensayos, la resistencia a compresión del hormigón, fc , y el módulo de elasticidad del acero, Es , se pueden modelizar como variables aleatorias, lo que es muy útil debido al enfoque probabilista de este artículo. La tabla 2 muestra la media, la desviación estándar y el coeficiente de variación, cdv, de estas variables aleatorias. Se supone que estas siguen una distribución normal. Otras posibles incertidumbres, como las relacionadas con la formación de grietas y el aplastamiento del hormigón, el endurecimiento por deformación y la resistencia final de acero o debidas a efectos como la participación de la losa, las variaciones de fuerza axial sobre la carga de la columna, solo para nombrar unas pocas, pueden ser también incluidas en el análisis probabilista estructural. Sin embargo, en este artículo solo consideramos las incertidumbres de las variables dadas en la tabla 2 .
| μ | σ | cdv | |
|---|---|---|---|
| fc (kPa) | 2.1 E04 | 2.1 E03 | 0,1 |
| Es (kPa) | 2 E08 | 2 E07 | 0,1 |
A continuación se utiliza la estructura descrita con el fin de ilustrar el procedimiento de evaluación del comportamiento sísmico que se propone en el artículo.
3. Análisis dinámico incremental
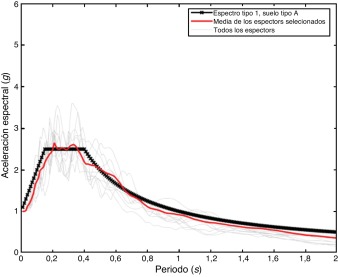
El análisis dinámico no lineal (NLDA, por sus siglas en inglés) usando un acelerograma proporciona la historia de la respuesta temporal de un edificio. De esta historia se pueden obtener las características máximas de la respuesta de la estructura, como el desplazamiento en el techo o el índice de daño global de acuerdo a un cierto criterio. Si se escala el acelerograma para diferentes incrementos de la aceleración máxima del terreno (PGA, por sus siglas en inglés) y para cada incremento se realiza un NLDA, se puede obtener una curva que relaciona el PGA (medida de intensidad) con cualquier medida de la respuesta estructural, por ejemplo, el desplazamiento máximo en el techo, la deriva de piso, un índice de daño, etc. Una curva que relaciona una medida de intensidad del sismo con un índice de daño global de la estructura se denomina curva de daño. Cuando, en lugar de un solo acelerograma, se utilizan varios de ellos para realizar los análisis dinámicos no lineales y se hacen estadísticas con los resultados obtenidos, nos enfrentamos a un análisis dinámico incremental (IDA, por sus siglas en inglés) [26] . Resumiendo, el IDA permite obtener la respuesta dinámica no lineal de una estructura para un grupo de terremotos que se escalan a diferentes medidas de intensidad como, por ejemplo, la aceleración máxima del terreno (PGA). Este procedimiento ha sido extendido para incluir las incertidumbres en las propiedades estructurales [27] , [28] , [29] and [30] . Una fuente importante de incertidumbre radica en los parámetros del terremoto [31] , [32] , [33] , [34] and [35] . Por esto, de acuerdo con el enfoque de simulación probabilista que se emplea en este artículo, se describe la acción sísmica como una variable aleatoria. Para ello han sido seleccionados 10 terremotos de la base de datos europea [36] , cuyos espectros se pueden ver en la figura 2 . Esta figura, además, muestra el espectro medio y el espectro tipo 1 para un suelo tipo A del Eurocódigo 8 (EC8) [37] . Los terremotos se han seleccionado de tal manera que la media de sus espectros minimice el error cuadrático medio en un intervalo de periodos dado. La figura 2 muestra que el procedimiento que se ha utilizado para la selección de acelerogramas compatibles con una zona sísmica, representada por una forma espectral, permite obtener un buen ajuste. La lista de estos terremotos y de sus principales características se muestra en la tabla 3 .
|
|
|
Figura 2. Espectros de respuesta calculados a partir del procedimiento con base en el espectro medio. |
| Nombre de la estación | Fecha | Epicentro | Profundidad (km) | Magnitud (Ms) | Geología local | Distancia epicentral (km) | |
|---|---|---|---|---|---|---|---|
| N | E | ||||||
| San Rocco | 15.09.1976 | 46.29 | 13.20 | 15 | 6,06 | Suelo rígido | 17 |
| San Rocco | 15.09.1976 | 46.32 | 13.16 | 12 | 5,98 | Suelo rígido | 17 |
| Kotor Nas Rakit | 24.05.1979 | 42.23 | 18.76 | 5 | 6,34 | Roca | 21 |
| Auleta | 23.11.1980 | 40.78 | 15.33 | 16 | 6,87 | Roca | 25 |
| Ponte Corvo | 07.05.1984 | 41.73 | 13.90 | 8 | 5,79 | Roca | 31 |
| Matelica | 26.09.1997 | 43.03 | 12.86 | 6 | 5,9 | Roca | 20 |
| Tricarico | 05.05.1990 | 40.65 | 15.92 | 12 | 5,6 | Roca | 20 |
| Izmit-M-Istasyonu | 13.09.1999 | 40.70 | 30.02 | 13 | 5,9 | Suelo rígido | 13 |
| Bolu-Bayindirlik | 12.11.1999 | 40.76 | 31.14 | 14 | 7,3 | Suelo rígido | 39 |
| Athens-Papagos | 07.09.1999 | 38.13 | 23.54 | 9 | 5,6 | Roca | 26 |
Hancock et al. [38] han estudiado varios métodos para determinar el número óptimo de acelerogramas requeridos para realizar análisis dinámicos inelásticos. Ellos llegan a la conclusión de que el número de eventos que deben considerarse depende de las medidas de daño que se consideran y también de su predictibilidad. La mayoría de estos métodos se basan en la magnitud y la forma espectral. No obstante, en este trabajo no estamos interesados en la obtención de un número óptimo de acelerogramas, sino en obtener una medida de la incertidumbre en la respuesta estructural de las estructuras sometidas a acciones sísmicas. Por esta razón se ha realizado una selección de los acelerogramas con base en la diferencia cuadrática entre la media de un grupo de espectros de respuesta y el espectro objetivo, en este caso el tipo 1 suelo tipo A del EC8; los acelerogramas correspondientes a estos espectros han sido previamente normalizados a 1 g. El cálculo tiene su base en la diferencia absoluta acumulada entre el espectro objetivo y el espectro promedio en varios puntos; estos puntos están separados por intervalos de periodo iguales a 0,01 s.
Con el fin de incluir las incertidumbres relacionadas con las características estructurales se utiliza el método de Monte Carlo. Es bien conocido que la variabilidad espacial entre las características de los elementos estructurales influye en gran medida en los resultados [39] . Por lo tanto, se ha generado, para todas las columnas de un mismo nivel del edificio, una muestra aleatoria de la resistencia a la compresión de hormigón, fc , y, para cada columna del mismo nivel, una muestra aleatoria del módulo de elasticidad del acero, Es . Se ha utilizado el mismo criterio para generar muestras aleatorias de las características de los materiales de las vigas de un mismo nivel. Es importante observar que las muestras correspondientes a cada nivel son independientes. Esta consideración se debe al hecho de que, por lo general, los elementos estructurales de la misma planta están hechos de la misma mezcla de hormigón. Las propiedades de la armadura se han supuesto como independientes de elemento a elemento. Cabe destacar que en la modelación se ha considerado al límite elástico de resistencia del acero, fy , función del módulo de elasticidad Es . Aunque el objetivo de este artículo es la evaluación del riesgo sísmico de un edificio individual, el estudio se podría extender a estructuras existentes en zonas urbanas teniendo en cuenta la variabilidad de las características estructurales de edificio a edificio para la misma tipología estructural [40] . Posteriormente, se han generado muestras aleatorias de las propiedades mecánicas de los materiales y se han realizado una serie de análisis dinámicos no lineales para los diferentes acelerogramas linealmente escalados para PGA que van desde 0,1 a 1,4 g en intervalos de 0,1 g. Se ha utilizado el método del hipercubo latino para generar muestras aleatorias de las propiedades de los materiales y la combinación de estas con los acelerogramas [41] ; se han llevado a cabo 1.000 NLDA para cada PGA.
Se han propuesto varios índices de daño para los elementos de estructuras de hormigón armado a partir de un post-proceso de la respuesta dinámica no lineal [42] , [43] , [44] , [45] , [46] , [47] , [48] and [49] . En este trabajo se ha utilizado el índice de daño de Park y Ang [43] porque permite incluir el efecto del daño en los elementos debido tanto al desplazamiento máximo alcanzado como a la disipación de energía histerética. La siguiente ecuación muestra cómo se calcula el índice de daño de Park y Ang a nivel de elementos estructurales:
|
|
( 1) |
donde μm y μu son la ductilidad máxima y última, respectivamente. De acuerdo con las condiciones de diseño de la estructura se ha seleccionado un valor μu = 2,5. β es un parámetro positivo que representa el efecto de los ciclos de carga en el daño estructural. Se ha seleccionado un valor igual a 0,05, tanto para flexión como para compresión. Eh es la energía histerética disipada, y Fy y δy son la carga y el desplazamiento de fluencia, respectivamente. El índice de daño global de la estructura, DI es una media ponderada de los índices de daño de los elementos considerando como pesos la relación entre la energía histerética disipada por cada elemento y la energía histerética total disipada por la estructura [36]
|
|
( 2) |
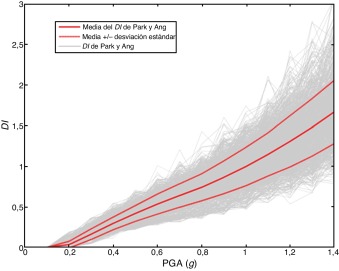
donde DI es el índice de daño global obtenido a partir del análisis dinámico de la estructura, λi es la relación entre la energía de histerética disipada por un elemento E y la energía histerética total disipada por la estructura. La figura 3 muestra la evolución del DI en función de la aceleración máxima del terreno PGA, teniendo en cuenta las incertidumbres relacionadas con las propiedades mecánicas de los materiales y la acción sísmica.
|
|
|
Figura 3. Gráficos de los índices de daño global representados en función de la PGA (curvas de daño), calculados mediante análisis no lineal dinámico para la estructura de la figura 1 . |
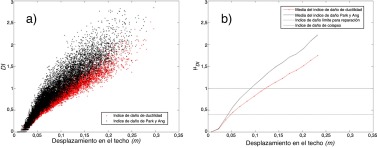
De acuerdo con la calibración original del índice de daño realizado por Park et al. [50] , un valor de 0,4 indica que el coste de la reparación de la estructura supera el coste de reemplazarla por completo, mientras que un índice de daño de 1 indica colapso. Por esta razón, en este artículo, cuando el índice de daño de Park y Ang es mayor que 1, su valor se fija en 1, puesto que a mayor PGA, la desviación estándar del índice de daño disminuye, lo que indica que la probabilidad de que ocurra colapso tiende a 1. El índice de daño de Park y Ang también puede relacionarse con el desplazamiento máximo al nivel del techo, tal como se muestra en la figura 4 . Además, en la figura 4 b se muestra el DI global correspondiente al caso en que solo se tuviera en cuenta la contribución del primer término de la ecuación de Park y Ang; se le denomina índice de daño de ductilidad. En la misma figura se muestran también los valores medios de ambos índices de daño y los límites de 0,4 (correspondiente a la posibilidad de reparación) y 1 (correspondiente a colapso).
|
|
|
Figura 4. a) Índice de daño debido a la ductilidad e índice de daño de Park y Ang representados en función del desplazamiento en el techo. b) Gráficas de los valores medios de los mismos índices y valores límites de reparación y de colapso de la estructura. |
4. Índice de daño obtenido a partir del análisis pushover
Cuando se consideran incertidumbres en las propiedades de los materiales, el IDA es una manera de obtener curvas de probabilidad de daño muy cara desde el punto de vista computacional. Por tanto, sería interesante desarrollar un procedimiento que pueda utilizar los resultados de un análisis estático no lineal, realizado en un entorno probabilista, con el fin de obtener curvas de daños similares a las calculadas mediante el análisis dinámico no lineal. Obviamente, es importante conservar la valiosa información que se obtiene del IDA, no solo por considerar las incertidumbres en las propiedades mecánicas de los materiales, sino también en la acción sísmica. El análisis estático incremental, PA, y el método de N2 [11] , en combinación con la metodología para calcular las curvas de fragilidad propuesta en las referencias [20] and [51] , es una herramienta potente y simplificada para el cálculo de curvas de probabilidad de daño similares a las calculadas usando el IDA probabilista.
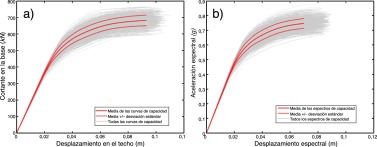
Como se mencionó anteriormente, el primer paso necesario para desarrollar la metodología simplificada es el PA que consiste en aplicar una carga horizontal sobre la estructura de acuerdo con un patrón de fuerzas y calcular su respuesta aumentando el valor de las fuerzas hasta que se alcance el colapso estructural. De esta manera se obtiene una curva que relaciona el desplazamiento en el techo con el cortante en la base del edificio llamada curva de capacidad. De acuerdo con el enfoque probabilista, es necesario llevar a cabo un gran número de PA y, por lo tanto, es apropiado utilizar un procedimiento para obtener automáticamente el límite de carga horizontal que se debe aplicar sobre la estructura. Satyarno propone que se realice un análisis no lineal incremental adaptativo que establece el límite de carga horizontal como una función de la rigidez tangente y, por consiguiente, de la frecuencia asociada al primer modo de vibración, que se calcula para cada incremento de carga [52] . Por lo tanto, en cada paso se calcula el primer modo de vibración para determinar la forma de la carga en altura. Una descripción detallada de este procedimiento se puede encontrar en los manuales del programa Ruaumoko [53] , que se ha utilizado en este trabajo para calcular la respuesta estática y dinámica estructural en régimen no lineal. De acuerdo con los valores de la tabla 1 , se han generado 1.000 grupos de muestras con distribución gaussiana, considerando la variabilidad espacial de la misma forma que en el apartado anterior. La figura 5 muestra las 1.000 curvas de capacidad que se han calculado mediante los PA, cuyas características, de rigidez elástica, desplazamiento máximo, cortante en la base máxima, etc., son variables aleatorias.
|
|
|
Figura 5. Curvas de capacidad y espectros de capacidad del edificio estudiado considerando las propiedades mecánicas de los materiales como variables aleatorias. |
De acuerdo con las metodologías expuestas en HAZUS [54] y en el ATC-40 [55] , es posible evaluar el riesgo sísmico de las estructuras a partir de su curva de capacidad y de la amenaza sísmica expresada en términos del espectro de respuesta. Este enfoque puede ser muy útil cuando se compara el método para calcular el riesgo que utiliza el espectro de capacidad con el método que utiliza el NLDA por varias razones: 1) el esfuerzo computacional de la realización de un PA es bajo cuando se compara con el requerido por un análisis dinámico no lineal; 2) el volumen de cálculos para encontrar una función que relaciona la respuesta del edificio con la demanda es menor cuando se hace a partir del PA que cuando se hace a partir del NLDA; 3) el post-proceso para calcular los índices globales de daño es muy simple en el método basado en el PA en comparación con el post-proceso requerido por el NLDA.
El procedimiento de ATC-40 y del método de N2 para calcular la respuesta de una estructura requiere la transformación de las curvas de capacidad en espectros de capacidad. Esta transformación permite relacionar el desplazamiento espectral con la aceleración espectral por medio de las siguientes ecuaciones:
|
|
( 3) |
El subíndice i se refiere a los incrementos de carga aplicada sobre la estructura durante el PA; sdi es el desplazamiento espectral; δi es el desplazamiento en el tejado del edificio; PF1 es el factor de participación modal correspondiente al primer modo de vibración; sai es la aceleración espectral expresada en g; Vi es el cortante en la base; W es el peso de la estructura, y α1 es el coeficiente de masa modal del primer modo de vibración. Mediante el uso de las ecs.(3), las 1.000 curvas de capacidad que se muestran en la figura 5 a se transforman en los 1.000 espectros de capacidad de la figura 5 b.
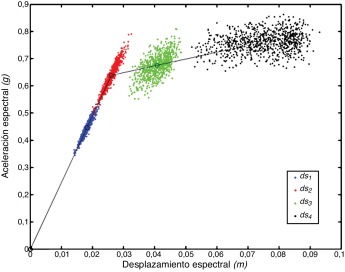
El espectro de capacidad se puede representar en un formato bilineal útil para definir los estados de daño. Las hipótesis para calcular el espectro de capacidad bilineal son: 1) el área bajo la curva bilineal debe ser igual al área del espectro de capacidad original; 2) las coordenadas del punto de desplazamiento máximo deben ser las mismas en las dos curvas; 3) la pendiente de la rama inicial debe ser igual en ambas curvas. En diferentes estudios se ha propuesto el cálculo de los daños estructurales a partir de estados de daño, dsi , que predefinen el daño sísmico en función del desplazamiento espectral de la estructura. En HAZUS [40] se definen 4 estados de daño: leve , moderado , extensivo y completo . La descripción de dichos estados de daño depende del tipo de estructura. Por ejemplo, el estado de daño leve para estructuras de hormigón armado se describe como el inicio de la fisuración por esfuerzo cortante o momento flector en vigas y columnas [54] . Los estados de daño también se pueden definir de una manera simplificada a partir de la representación bilineal del espectro de capacidad mediante los valores (Dy , Ay ) y (Du , Au ) asociados al desplazamiento de fluencia y último del espectro de capacidad, respectivamente [20] and [51] . Los desplazamientos espectrales para los 4 umbrales de daño se definen de acuerdo a las siguientes ecuaciones con base en opinión de expertos [12] , [13] , [14] , [15] , [29] and [30] :
|
|
( 4) |
En la figura 6 se muestran los espectros de capacidad bilineales y los estados de daño obtenidos desde una perspectiva probabilista. El siguiente paso consiste en obtener las curvas de fragilidad correspondientes que representan la probabilidad de alcanzar o superar un estado de daño como una función del desplazamiento espectral. Para obtener las curvas de fragilidad, en este artículo se consideran las siguientes hipótesis: 1) en cada umbral de daño, la probabilidad de ocurrencia de la curva de fragilidad correspondiente se fija en 50%; 2) las curvas de fragilidad siguen una función de probabilidad cumulativa lognormal descrita por la siguiente ecuación:
|
|
( 5) |
|
|
|
Figura 6. Umbrales de los estados de daño representados como variables aleatorias, calculados a partir de opinión de expertos (ecs.(4)). |
donde sd es la variable independiente y representa el desplazamiento espectral y es la desviación estándar del logaritmo natural de la variable dsi , y 3) para cada desplazamiento espectral asociado a los umbrales de daño, la probabilidad de exceder cada estado de daño se calcula suponiendo que estos siguen una distribución de probabilidad binomial.
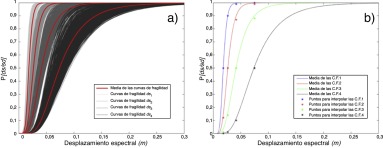
La figura 7 a muestra las 1.000 curvas de fragilidad para cada estado de daño calculadas después de aplicar las hipótesis descritas. Además, las curvas de fragilidad promedio y los puntos calculados a partir de la distribución binomial (hipótesis 3), utilizados para llevar a cabo la interpolación de las curvas de fragilidad, se muestran en la figura 7 b.
|
|
|
Figura 7. a) Curvas de fragilidad. b) Curvas de fragilidad media junto con los puntos particulares calculados con la distribución binomial para la interpolación de las curvas de fragilidad. |
El índice de daño global esperado de la estructura, DI , se calcula a partir de las probabilidades de ocurrencia de cada estado de daño que se obtienen a partir de las curvas de fragilidad. DI se obtiene como la media ponderada de dichas probabilidades, que razonablemente asigna más peso a los estados de daño más altos y que se calcula usando la siguiente ecuación [14] , [20] and [51] :
|
|
( 6) |
donde n es el número de los estados de daño considerados no nulos que, en este caso, es igual a 4, y P (dsi ) es la probabilidad de ocurrencia de dsi . DI será, como en el caso del análisis dinámico, el índice de daño global de la estructura.
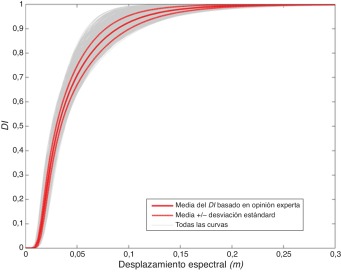
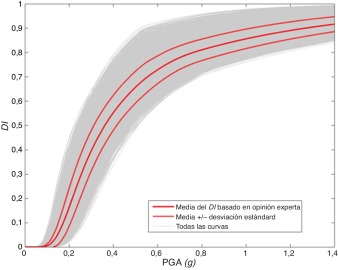
La figura 8 muestra el DI calculado a partir de las curvas de fragilidad de la figura 7 a. Las curvas de la figura 8 se conocen como curvas de vulnerabilidad debido a que dependen del desplazamiento espectral pero no tienen en cuenta la acción sísmica. Para hacer que dependan de la acción sísmica se tiene que calcular el punto de desempeño, el cual es una medida del desplazamiento máximo esperado en una estructura dada una demanda sísmica representada en términos del espectro de respuesta. Este espectro se puede escalar para diferentes niveles de intensidad, como en el análisis dinámico incremental.
|
|
|
Figura 8. Curvas de vulnerabilidad mostrando los índices de daño representados en función del desplazamiento espectral; los cálculos se han hecho considerando las propiedades mecánicas de los materiales como variables aleatorias. |
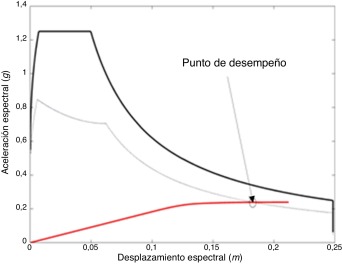
El procedimiento utilizado para calcular el punto de desempeño es el del ATC-40 [55] , que tiene en cuenta la reducción del espectro de respuesta elástico por la ductilidad de la estructura. La figura 9 ilustra este procedimiento.
|
|
|
Figura 9. Punto de desempeño para un determinado espectro (método propuesto en el capítulo 8 del ATC-40). |
Este procedimiento se aplica a todas las curvas de capacidad y los espectros de respuesta elástica correspondientes a los acelerogramas utilizados en el IDA. De esta manera, el índice de daño puede ser expresado como una función de la aceleración pico, PGA, tal como se muestra en la figura 10 . Puesto que se ha incluido el efecto de la acción sísmica, ahora estas curvas se llaman curvas de daño. Es importante señalar que el procedimiento del ATC-40 [55] ha sido aplicado para las mismas PGA que los utilizados en el análisis dinámico.
|
|
|
Figura 10. Índices de daños representados en función de la aceleración máxima del terreno. Se han considerado las incertidumbres relacionadas con las propiedades mecánicas de los materiales y con las características de la acción sísmica. |
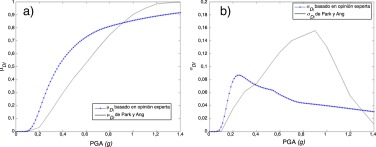
En la figura 11 a,b se comparan la media y la desviación estándar de los índices de daño calculados mediante el método de RISK-UE (cuya base es el análisis estático) con el índice de daño de Park y Ang. Claramente, se puede ver que el índice de daño obtenido con el primer enfoque, con base en el PA, no estima con suficiente precisión el índice de daño obtenido con el análisis dinámico. Por esta razón se propone una nueva técnica para mejorar los resultados obtenidos a partir del análisis pushover .
|
|
|
Figura 11. a) Curvas de daño medio. b) Desviación estándar de los índices de daño. Las figuras muestran la comparación probabilista entre los resultados obtenidos mediante análisis dinámico, utilizando el índice de daño de Park y Ang, y mediante análisis pushover , utilizando los límites de los estados de daño de las ecs.(4). |
5. Índice de daño con base en la degradación espectral
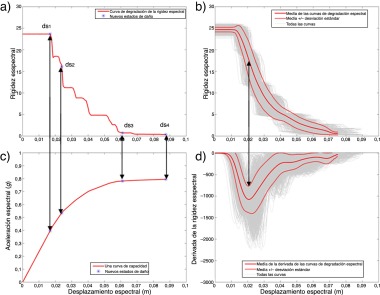
Los umbrales de los estados de daño calculados mediante las ecs.(4) pueden sobreestimar o incluso subestimar los daños, en algunos casos, dependiendo de cómo empieza a ocurrir el daño. Por ejemplo, el ds1 , que se define como 0,7ds2 y se supone constante, puede variar de un edificio a otro. Por esta razón se propone aquí calcular los estados de daño en función de la derivada del espectro de capacidad, que se denominará en este artículo rigidez espectral . Para ello, se propone localizar el umbral del estado de daño leve , ds1 , en el punto donde la rigidez espectral, asociada a la elasticidad, comienza a degradarse, como se puede ver en la figura 12 a.
|
|
|
Figura 12. Nueva definición de los umbrales de los estados de daño. a) Curva de rigidez espectral y su correspondiente espectro de capacidad. b) Las 1000 curvas de rigidez espectral simuladas por Monte Carlo y sus derivadas. |
Se propone calcular el umbral del estado moderado , ds2 , a partir de la curva de rigidez espectral media. Un ejemplo de dicha curva, correspondiente a la estructura estudiada, se muestra en la parte superior de la figura 12 b. Se calcula la derivada numérica de la curva de rigidez espectral media y se determina el desplazamiento espectral correspondiente a su valor mínimo. Para dicho desplazamiento se calcula la rigidez espectral media y se divide por la rigidez espectral media asociada a la elasticidad. Se obtiene así un porcentaje que se utiliza para encontrar el desplazamiento espectral relacionado con el estado de daño 2 para cada espectro de capacidad simulado. Como regla general, el estado de daño moderado se encuentra en un punto donde la curva de rigidez espectral degrada a un valor entre el 40 y el 70% de la rigidez espectral asociada a la elasticidad. Por ejemplo, en el caso del edificio estudiado, este porcentaje es el 68% de la rigidez espectral asociada a la elasticidad. Es importante señalar que la definición propuesta del estado de daño moderado , ds2 , deberá efectuarse utilizando la derivada de la curva de degradación espectral media ya que, como se puede ver en la figura 12 a, cada curva de rigidez espectral tiene varias secciones con rigidez constante cuyas derivadas son cero, es decir, varios valores mínimos locales.
El umbral del estado daño extensivo , ds3 , se encuentra en el punto inicial de la última parte constante de cada curva de rigidez espectral, tal como se muestra en la figura 12 a. Por último, el umbral de daño de colapso , ds4 , corresponde al desplazamiento espectral final.
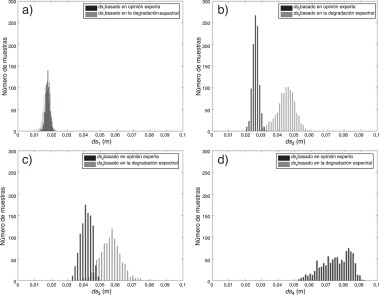
Los nuevos umbrales de los estados de daño se comparan con los obtenidos a partir de la opinión de los expertos de una manera probabilista por medio de los histogramas de la figura 13 . Estos histogramas muestran que los estados de daño ds1 obtenidos con el nuevo método son inferiores a los obtenidos mediante el uso de opiniones de los expertos, y que los estados de daño ds2 y ds3 son superiores. Con los nuevos estados de daño se calculan las curvas de fragilidad utilizando ahora las siguientes hipótesis:
- Para el umbral del estado leve , ds1 , se supone que la probabilidad de superar su curva de fragilidad correspondiente se fija en un 5% con el fin de evitar que la contribución del estado leve se produzca antes del inicio de la degradación de la rigidez, lo que produciría un retraso en la curva de daño. Para los umbrales de los estados de daño ds2 y ds3 , la probabilidad de exceder sus curvas de fragilidad correspondiente es del 50%; para el umbral del estado de daño de colapso , la probabilidad de exceder sus curvas de fragilidad se fija en el 95%, debido a que una probabilidad del 50% indicaría que el colapso no ha ocurrido. Sin embargo, basados en el método adaptativo aplicado para calcular las curvas de capacidad, se sabe que en realidad un mecanismo de colapso se ha producido para este desplazamiento espectral.
- Las curvas de fragilidad siguen una función lognormal de probabilidad acumulativa descrita por la ec.(5).
- Para cada desplazamiento espectral asociado a los umbrales de daño, la probabilidad de exceder cada estado de daño se calcula suponiendo que siguen una distribución de probabilidad binomial.
|
|
|
Figura 13. Comparación entre los umbrales de los estados de daño obtenidos con las ecs.(4) (opiniones de expertos) y el método de degradación de rigidez. |
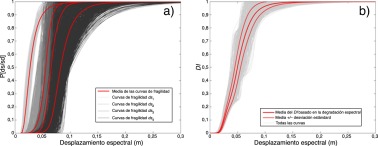
La figura 14 a muestra las nuevas curvas de fragilidad calculadas con las hipótesis descritas y, basados en la ec.(6), se calculan los correspondientes índices de daño que se muestran en la figura 14 b.
|
|
|
Figura 14. Nuevas curvas de fragilidad y de vulnerabilidad obtenidas mediante el método de degradación de la rigidez. |
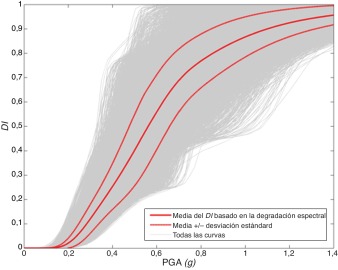
Finalmente, se calcula el punto de desempeño siguiendo el procedimiento del ATC-40 [55] , que tiene en cuenta la reducción del espectro de respuesta elástico debido a la ductilidad del edificio. Es decir, se cruza la capacidad y la demanda para obtener curvas de daño que dependan de la capacidad estructural y de la demanda sísmica. En la figura 15 se muestran los nuevos índices de daño como una función de la PGA.
|
|
|
Figura 15. Nuevos curvas de daño obtenidas utilizando el método de degradación de la rigidez. En esta figura hay 20.000 curvas de daño. Los índices de daño se han representado en función de la aceleración máxime del terreno, PGA. |
6. Discusión de resultados
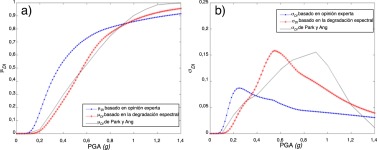
Las curvas de daño obtenidas con el método propuesto con base en criterios estáticos y utilizando la degradación de la rigidez se ajustan mejor a las curvas de daño calculadas mediante el método dinámico no lineal que las obtenidas con base en la opinión de expertos [4] , [14] , [20] and [51] . Los resultados obtenidos se comparan, desde una perspectiva probabilista, con las curvas de daños calculadas con IDA, en términos de la media y de la desviación estándar que se muestran en la figura 16 a,b, respectivamente.
|
|
|
Figura 16. a) Comparación entre las curvas de daño calculadas mediante análisis dinámico y el índice de Park y Ang y mediante análisis pushover , con los límites de los estados de daño definidos por la ec.(4) (opinión de expertos) y por el método de degradación de la rigidez. b) Comparación de la desviación estándar del daño para los mismos casos. Los resultados corresponden a la estructura mostrada en la figura 1 . |
Estos resultados muestran claramente el buen ajuste de las curvas de daño obtenidas con el nuevo método. En términos de valores medios, el método que utiliza la opinión de expertos sobreestima el daño inicial dentro del rango de la PGA desde 0 a 0,9 g. Es importante observar que un índice de daño igual a 0,4 corresponde a una PGA de 0,25 g con el método inicial, mientras que con el IDA y el método nuevo este índice de daño se produce a 0,55 g. Este hecho demuestra que el método basado en la opinión de los expertos es excesivamente conservador. En términos de desviación estándar, para los valores que están entre 0 y 0,35 g, el método inicial también es muy conservador, mientras que, para valores más altos, es no conservador; con el nuevo método, incluso en términos de la desviación estándar, los resultados se ajustan mejor a los resultados dinámicos no lineales.
7. Conclusiones
En este trabajo se ha evaluado el riesgo sísmico de un edificio de hormigón armado teniendo en cuenta las incertidumbres en las características mecánicas de los materiales (la resistencia a compresión del hormigón y el módulo de elasticidad del acero) y en las de la acción sísmica. Todas estas características se han tratado como variables aleatorias. Se han utilizado 2 enfoques para evaluar los daños esperados del edificio: el primero con base en el análisis dinámico incremental y el segundo en el análisis pushover . Una conclusión importante es que, a pesar de trabajar con métodos avanzados de análisis no lineal de estructuras, los resultados muestran incertidumbres significativas si se tiene en cuenta el carácter aleatorio de las variables de entrada. Con el objetivo de mejorar la evaluación del daño mediante métodos de análisis estático no lineal, ha sido propuesto un nuevo procedimiento para definir los umbrales de los estados de daño que consiste en utilizar la degradación de la rigidez que se puede observar en la derivada de la curva de capacidad. Los resultados obtenidos con este nuevo enfoque muestran un mejor acuerdo con el análisis dinámico que los que utilizan los umbrales de los estados de daño con base en opinión de expertos.
Una de las conclusiones más relevantes de este trabajo es que, siempre que los procedimientos descritos se utilizan para evaluar el daño sísmico esperado de una estructura, los parámetros que influyen en las curvas de daño de las estructuras deben ser considerados como aleatorios. Se ha visto que la consideración probabilista de estos parámetros genera incertidumbres significativas en la respuesta sísmica. Procedimientos simplificados deterministas basados en los valores característicos de las variables conducen generalmente a resultados conservadores. Pero algunas simplificaciones, por ejemplo en la definición de las acciones sísmicas y en la estimación de los estados de daño sísmico, pueden subestimar el daño que puede ocurrir en una estructura.
En este artículo se ha estudiado una estructura baja y simétrica mediante el nuevo método. En los edificios altos y/o asimétricos deben hacerse consideraciones que tengan en cuenta los efectos de los modos de vibración superiores [56] , [57] , [58] , [59] , [60] , [61] and [62] , entre otros. Estas consideraciones permitirán ampliar el alcance del método propuesto para evaluar el riesgo sísmico de estructuras más complejas.
Una de las principales aplicaciones de los resultados obtenidos en este artículo es la estimación de escenarios probabilistas de riesgo sísmico que requieren curvas probabilistas definidas de manera paramétrica, por su media y su desviación estándar. Finalmente, las principales ventajas del nuevo método son: 1) el esfuerzo de cálculo es menor que en el caso del IDA probabilista; 2) si la amenaza sísmica cambia, el método de análisis dinámico requiere llevar a cabo nuevos análisis dinámicos no lineales, paso que no es necesario en el caso en que se aplique el nuevo método; 3) el método propuesto también permite considerar las incertidumbres relacionadas no solo al comportamiento estructural, sino también al riesgo sísmico.
Agradecimientos
Este trabajo fue financiado en parte por el Instituto Geológico de Cataluña (IGC), por el Gobierno español y por la Comisión Europea con fondos FEDER, a través de los proyectos de investigación: CGL2008-00869/BTE, CGL2011-23621, CGL2011-29063, INTERREG POCTEFA 2007-2013/73/08 y DESURBS-FP7-2011-261652.
Bibliografía
- [1] G. Grünthal; European Macroseismic Scale 1998, EMS-98, Cahiers du Centre Européen de Géodynamique et de Séismologie; Conseil de L’Europe (1998), p. 15
- [2] A.H. Barbat, F. Yépez, J.A. Canas; Damage scenarios simulation for RISK assessment in urban zones; Earthquake Spectra, 2 (3) (1996), pp. 371–394
- [3] A.H. Barbat, U. Mena, F. Yépez; Evaluación probabilista del riesgo sísmico en zonas urbanas; Rev. Int. Metodos Numer. Calc. Diseño Ing., 14 (2) (1998), pp. 247–268
- [4] S. Lagomarsino, S. Giovinazzi; Macroseismic and mechanical models for the vulnerability and damage assessment of current buildings; Bull. Earthquake Eng., 4 (4) (2006), pp. 415–443
- [5] N. Lantada, J. Irrizari, A.H. Barbat, X. Goula, A. Roca, T. Susagna, et al.; Seismic hazard and risk scenarios for Barcelona, Spain, using the Risk-UE vulnerability index method; Bull. Earthquake Eng., 8 (2010), pp. 201–229
- [6] A.H. Barbat, M.L. Carreño, O.D. Cardona, M.C. Marulanda; Evaluación holística del riesgo sísmico en zonas urbanas; Rev. Int. Metodos Numer. Calc. Diseño Ing., 27 (1) (2011), pp. 3–27
- [7] S.A. Freeman, J.P. Nicoletti, J.V. Tyrell; Evaluations of existing buildings for seismic RISK — A case study of Puget Sound Naval Shipyard, Bremerton, Washington; Proc. 1 st U.S. National Conference of Earthquake Engineering, EERI, Berkeley (1975)
- [8] S.A. Freeman; Development and use of capacity spectrum method; Proc. 6 th U.S. National Conference of Earthquake Engineering, EERI, Seattle (1998)
- [9] P. Fajfar, P. Gaspersic; The N2 method for the seismic damage analysis of RC buildings; Earthquake Eng. Struct. Dyn., 25 (1) (1996), pp. 31–46
- [10] A.K. Chopra, R.K. Goel; Capacity-demand-diagram methods for estimating seismic deformation of inelastic structures: SDOF systems. PEER Report 1999/02 Berkeley; Pacific Earthquake Engineering Research Center, University of California (1999)
- [11] P. Fajfar; Capacity spectrum based on inelastic demand spectra; Earthquake Eng. Struct. Dyn., 28 (9) (1999), pp. 979–993
- [12] A.H. Barbat, L.G. Pujades, N. Lantada, R. Moreno; Performance of buildings under earthquakes in Barcelona, Spain; Comput. Aided Civ. Infrastruct. Eng., 21 (2006), pp. 573–593
- [13] A.H. Barbat, S. Lagomarsino, L.G. Pujades; Vulnerability assessment of dwelling buildings; C. Sousa, X. Goula, A. Roca (Eds.), Assessing and Managing Earthquake Risk, Springer (2006), pp. 115–134
- [14] A.H. Barbat, M.L. Carreño, L.G. Pujades, N. Lantada, O.D. Cardona, M.C. Marulanda; Seismic vulnerability and risk evaluation methods for urban areas. A review with application to a pilot area; Struct. Infrastruct. Eng., 6 (1-2) (2010), pp. 17–38
- [15] J. Irrizari, N. Lantada, L.G. Pujades, A.H. Barbat, X. Goula, T. Susagna, et al.; Ground-shaking scenarios and urban risk evaluation of Barcelona using the Risk-UE capacity spectrum based method; Bull. Earthquake Eng., 9 (2011), pp. 441–466
- [16] A.K. Chopra, R.K. Goel; A modal pushover analysis procedure to estimate seismic demand for unsymmetric-plan buildings; Earthquake Eng. Struct. Dyn., 33 (8) (2004), pp. 903–927
- [17] A.K. Chopra, R.K. Goel, C. Chintanapakdee; Evaluation of a modified MPA procedure assuming higher modes as elastic to estimate seismic demands; Earthquake Spectra, 20 (3) (2004), pp. 757–778
- [18] M. Kreslin, P. Fajfar; The extended N2 method considering higher mode effects in both plan and elevation; Bull. Earthquake Eng., 10 (2) (2012), pp. 695–715
- [19] A.H. Barbat, L.G. Pujades, N. Lantada, R. Moreno; Seismic damage evaluation in urban areas using the capacity spectrum method: Application to Barcelona; Soil Dyn. Earthquake Eng., 28 (10-11) (2008), pp. 851–865
- [20] N. Lantada, L.G. Pujades, A.H. Barbat; Vulnerability index and capacity spectrum based methods for urban seismic RISK evaluation. A comparison; Nat. Hazard. Rev., 51 (3) (2009), pp. 501–524
- [21] L.G. Pujades, A.H. Barbat, R. González-Drigo, J. Avila, S. Lagomarsino; Seismic performance of a block of buildings representative of the typical construction in the Eixample district in Barcelona (Spain); Bull. Earthquake Eng., 10 (1) (2012), pp. 331–349
- [22] RISK-EU; An advanced approach to earthquake RISK scenarios with applications to different European towns; European Project ENV K4-2000-00513 (2000)
- [23] Z.V. Milutinovic, G.S. Trendafiloski; RISK-UE: An advanced approach to earthquake RISK scenarios with applications to different European towns WP4: Vulnerability of current buildings; European Project EVK4-CT-2000-00014 (2003)
- [24] S. Otani; Inelastic analysis of RC frame structures; J. Struct. Div., ASCE., 100 (7) (1974), pp. 1433–1449
- [25] CEN. Eurocode 2; Design of concrete structures – Part 1: General-common rules for building and civil engineering structures; European Committee for Standardization (2004)
- [26] D. Vamvatsikos, C.A. Cornell; The incremental dynamic analysis; Earthquake Eng. Struct. Dyn., 31 (3) (2002), pp. 491–514
- [27] D. Vamvatsikos, M. Fragiadakis; Incremental dynamic analysis for estimating seismic performance sensitivity and uncertainty; Earthquake Eng. Struct. Dyn., 39 (2) (2010), pp. 141–163
- [28] Y.F. Vargas, L.G. Pujades, A.H. Barbat, J.E. Hurtado; Pushover analysis and incremental dynamic analysis. A probabilistic comparison; Computational Methods in Stochastic Dynamic Analysis, 2, Springer (2011), p. 2013
- [29] Y.F. Vargas, L.G. Pujades, A.H. Barbat, J.E. Hurtado; Capacity, fragility and damage in reinforced concrete buildings: A probabilistic approach; Bull. Earthquake Eng., 11 (6) (2013), pp. 2007–2032
- [30] Y.F. Vargas, A.H. Barbat, L.G. Pujades, J.E. Hurtado; Probabilistic seismic risk evaluation of reinforced concrete buildings; Structures and Buildings, 167 (6) (2013), pp. 327–336
- [31] N.A. Abrahamson, P.G. Somerville, C.A. Cornell; Uncertainty in numerical ground motion predictions; Proceedings of the 4 st U.S. National Conference of Earthquake Engineering, EERI (1991), pp. 407–416
- [32] J.J. Bommer, H. Crowley; The influence of ground motion variability in earthquake loss modelling; Bull. Earthquake Eng., 4 (3) (2006), pp. 231–248
- [33] J.J. Bommer, P.J. Stafford, J.E. Alarcón, S. Akkar; The influence of magnitude range on empirical ground-motion prediction; Bull. Seismol. Soc. Am., 97 (2007), pp. 2152–2170
- [34] D. Arroyo, M. Ordaz; On the forecasting of ground-motion parameters for probabilistic seismic hazard analysis; Earthquake Spectra, 27 (1) (2011), pp. 1–21
- [35] J.J. Egozcue, A.H. Barbat, J.A. Canas, J. Miquel, E. Banda; A method to estimate occurrence probabilities in low seismic activity regions; Earthquake Eng. Struct. Dyn., 20 (1) (1991), pp. 43–60
- [36] Ambraseys N., Smit P., Sigbjornsson R., Suhadolc P., Margaris B. (2004). Internet-Site for European Strong-Motion Data, European Commission, Research-Directorate General, Environment and Climate Programme [consultado 17 Abr 2011]. Disponible en: http://www.isesd.hi.is/ESD_Local/frameset.htm
- [37] CEN. Eurocode 8; Design of structures for earthquake resistance; Part 1: General rulesseismic actions and rules for building, European Committee for Standardization (2004)
- [38] J. Hancock, J.J. Bommer, P.J. Sttaford; Numbers of scaled and matched accelerograms required for inelastic dynamic analyses; Earthquake Eng. Struct. Dyn., 37 (14) (2008), pp. 1585–1607
- [39] P. Franchin, P. Pinto, R. Pathmanathan; Confidence factor?; J. Earthquake Eng., 14 (7) (2010) 1989-1007
- [40] H. Crowley, J.J. Bommer, R. Pinho, J.F. Bird; The impact of epistemic uncertainty on an earthquake loss model; Earthquake Eng. Struct. Dyn., 34 (14) (2005), pp. 1635–1685
- [41] J.E. Hurtado, A.H. Barbat; Monte Carlo techniques in computational stochastic mechanics; Arch. Comput. Meth. Eng., 5 (1) (1998), pp. 3–30
- [42] H. Banon, D. Veneziano; Seismic safety of reinforced concrete members and structures; Earthquake Eng. Struct. Dyn., 10 (2) (1982), pp. 179–193
- [43] Y.-J. Park, A.H.-S. Ang; Mechanistic seismic damage model for reinforced concrete; J. Struct. Eng.-ASCE, 111 (4) (1985), pp. 722–739
- [44] M.S.L. Roufaiel, C. Meyer; Analytical model of hysteretic behaviour of RC frames; J. Struct. Eng.-ASCE, 113 (3) (1987), pp. 429–457
- [45] J.M. Bracci, A.M. Reinhorn, J.B. Mander, S.K. Kunnath; Deterministic for seismic damage evaluation of reinforced concrete structures, National Center for Earthquake Engineering Research. NCEER-89-0033; State University of New York, Buffalo (1989)
- [46] E. Cosenza, G. Manfredi, R. Ramasco; The use of damage functionals in earthquake engineering: A comparison between different methods; Earthquake Eng. Struct. Dyn., 22 (10) (1993), pp. 855–868
- [47] S. Oller, A.H. Barbat; Moment-curvature damage model for bridges subjected to seismic loads; Comput. Meth. Appl. Mech. Eng., 195 (2006), pp. 4490–4511
- [48] J. Faleiro, S. Oller, A.H. Barbat; Plastic-damage seismic model for reinforced concrete frames; Comput. Struct., 86 (7-8) (2008), pp. 581–597
- [49] J. Faleiro, S. Oller, A.H. Barbat; Plastic-damage analysis of reinforced concrete frames; Eng. Computations, 27 (1) (2010), pp. 57–83
- [50] Y.-J. Park, A.H.-S. Ang, Y. Kwei-Wen; Seismic damage analysis of reinforced concrete buildings; J. Struct. Eng.-ASCE, 111 (4) (1985), pp. 740–757
- [51] Y.F. Vargas, L.G. Pujades, A.H. Barbat, J.E. Hurtado; Evaluación probabilista de la capacidad, fragilidad y daño sísmico en edificios de hormigón armado; Rev. Int. Metodos Numer. Calc. Diseño Ing, 29 (2) (2013), pp. 63–78
- [52] I. Satyarno; Adaptive pushover analysis for the seismic assessment of older reinforced concrete buildings [doctoral thesis]; Department of Civil Engineering, University of Canterbury, Christchurch, New Zealand (2000)
- [53] A.J. Carr; Ruaumoko-Inelastic Dynamic Analisys Program. Department of Civil Engineering; University of Canterbury, Christchurch, New Zealand (2000)
- [54] FEMA; HAZUS Earthquake loss estimation methodology; Federal Emergency Management Agency, Washington, DC (1999)
- [55] ATC-40; Seismic evaluation and retrofit of concrete buildings; Applied Technology Council, Redwood City, California (1996)
- [56] A.H. Barbat, L.M. Bozzo; Seismic analysis of base isolated buildings; Arch. Computat Methods Eng, 4 (2) (1997), pp. 153–192
- [57] M. Poursha, F. Khoshnoudian, A.S. Moghadam; A consecutive modal pushover procedure for estimating the seismic demands of tall buildings; Eng. Struct., 31 (2) (2009), pp. 591–599
- [58] R. Bento, C. Bhatt, R. Pinho; Using nonlinear static procedures for seismic assessment of the 3 D irregular SPEAR building; Earthquake and Structures, 1 (2) (2010), pp. 177–195
- [59] J.C. Reyes, A.K. Chopra; Evaluation of three-dimensional modal pushover analysis for unsymmetric-plan buildings subjected to two components of ground motion; Earthquake Eng. Struct. Dyn., 40 (13) (2011), pp. 1475–1494
- [60] J. Reyes, A.K. Chopra; Three-dimensional modal pushover analysis of building subjected to two components of ground motions, including its evaluation for tall buildings; Earthquake Eng. Struct. Dyn., 40 (7) (2011), pp. 789–806
- [61] C. Bhatt, R. Bento; Assessing the torsional response of existing RC building using the extended N2 method; Bull. Earthquake Eng., 9 (4) (2011), pp. 1183–1201
- [62] K. Fujii; Nonlinear static procedure for multi-story asymmetric building considering bi-directional excitation; J. Earthquake Eng., 15 (2) (2011), pp. 245–273
Document information
Published on 01/03/16
Accepted on 17/11/14
Submitted on 17/07/13
Volume 32, Issue 1, 2016
DOI: 10.1016/j.rimni.2014.11.001
Licence: Other
Share this document
claim authorship
Are you one of the authors of this document?