Hybrid Discontinuous Galerkin method for perturbations of the modified Helmholtz equation

1 Introduction

The modified Helmholtz equation appears in a common physical model, and its numerical solution remains an active line of research. See the discussion in Yaman & zdemir [1] and the recent Yaman et al [2]. In the former, an integral equation method is proposed for the numerical solution. In this work, a Galerkin approach is preferred for the numerical solution of perturbations of the modified Helmholtz equation.

The classical Galerkin approach is the continuous Galerkin, Finite Element Method (FEM). A recent and attractive alternative is the Discontinuous Galerkin (DG) method. Unlike FEM, it is locally conservative and ${\textstyle H^{p}}$-adaptative. On the downside, the application of the Discontinuous Galerkin Method to elliptic problems usually leads to underdetermined linear systems, and penalization or suitable constraints are required. Moreover, Discontinuous Galerkin methods are more expensive because of the need for numerical fluxes at the edges of the mesh elements, thus yielding more coupled unknowns than FEM. See Riviere [3] and Di Pietro & Ern [4] for a thorough exposition.

These shortcomings of the DG method can be addressed in part by its descendant, the Hybrid Discontinuous Galerkin Method (HDG), Bui-Tahn [5]. The numerical flux is hybridized, introducing additional unknowns on the edges of the mesh, which reduces the coupling between elements. The global solution is then obtained by solving small and independent linear systems on each element.

For the elliptic problem under study, we use a simple, physically motivated hybrid numerical flux that yields a well-posed linear system. This is guaranteed by the dominant reaction term in the modified Helmholtz equation.

The outline is as follows. In Section 2, we follow the HDG methodology and introduce a first-order system associated with the perturbed modified Helmholtz equations. Then, we delve into the discretization of the first-order system and show that the resulting finite-dimensional problem is well posed. Numerical tests are presented in Section 3. First, we illustrate its performance as a Poisson solver in a preliminary comparison with a leading method in the literature. Accurate approximations are also shown for some benchmark Helmholtz problems in Coastal Ocean Modeling. In all examples, we highlight approximations on coarse meshes. We close our exposition with conclusions and future work.

2 Numerical solution of the modified Helmholtz equation

In what follows, we build on the theoretical and numerical aspects of the finite element method (FEM) as presented, for instance, in the text [6].

2.1 A first order system for perturbations of the modified Helmholtz equation

For a bounded Lipschitz domain ${\textstyle \Omega }$ in ${\textstyle \mathbb {R} ^{d}}$, let us consider the diffusion-advection-reaction equation for the unknown function ${\textstyle u}$,

$-\nabla \cdot (\mathbf {D} \nabla u)+\mathbf {v} \cdot \nabla u+cu=b.$

(1)

The diffusion term is uniformly elliptic, that is ${\textstyle \mathbf {D} (x)}$ is symmetric and there exist constants ${\textstyle 0<\lambda {<\Lambda }}$ such that for almost all ${\textstyle x\in \Omega }$

$\lambda \vert \xi \vert ^{2}\leq \xi ^{T}\mathbf {D} (x)\xi \leq \Lambda \vert \xi \vert ^{2},\quad \xi \in \mathbb {R} ^{d}.$

(2)

Also, assume that ${\textstyle \mathbf {v} \in \left(L^{\infty }(\Omega ))\right)^{d}}$, and ${\textstyle c,\,b\in L^{\infty }(\Omega )}$.

For ${\textstyle \mathbf {v} =0}$ and ${\textstyle c>0}$, equation (1) is known as the modified Helmholtz equation. To construct a Discontinuous Galerkin approximation, a first step is to construct a hyperbolic-like first-order system. A small advection term is allowed; the smallness condition is made precise below.

Define the new variable (flux) ${\textstyle \mathbf {z} =-\mathbf {D} \nabla u}$. Since the matrix ${\textstyle \mathbf {D} }$ is invertible, ${\textstyle \nabla u=-\mathbf {D} ^{-1}\mathbf {z} }$, we obtain the following system

$\nabla u+\mathbf {D} ^{-1}\mathbf {z} =\mathbf {0}$ $\nabla \cdot \mathbf {z} -\mathbf {v} \cdot \left(\mathbf {D} ^{-1}\mathbf {z} \right)+cu=b$

Let ${\textstyle m=d+1}$, and ${\textstyle \mathbf {e} ^{i}}$ be the ${\textstyle i-}$th canonical vector. Define

${\mathcal {K}}=\left({\begin{matrix}\mathbf {D} ^{-1}&\mathbf {0} \\-\mathbf {v} ^{T}\mathbf {D} ^{-1}&c\end{matrix}}\right),$

${\mathcal {A}}_{i}=\left({\begin{matrix}\mathbf {0} &\mathbf {e} ^{i}\\\left(\mathbf {e} ^{i}\right)^{T}&0\end{matrix}}\right),\quad i=1,2,\ldots ,d,$

$\mathbf {u} :=\left({\begin{matrix}\mathbf {z} \\u\end{matrix}}\right),\quad \mathbf {f} :=\left({\begin{matrix}\mathbf {0} \\b\end{matrix}}\right).$

The system becomes

$\sum _{i=1}^{d}{\mathcal {A}}_{i}\partial _{i}\mathbf {u} +{\mathcal {K}}\mathbf {u} =\mathbf {f} .$

(3)

2.2 A Hybrid Discontinuous Galerkin Method

Here we introduce the essentials of HDG, for full details see Bui-Thanh [5].

For any matrix ${\textstyle \mathbf {M} }$, we denote by ${\textstyle \mathbf {M} _{i},\,\mathbf {M} ^{j}}$ its row ${\textstyle i}$ and column ${\textstyle j}$ respectively.

Let us define

$F_{i}(\mathbf {u} ):=(({\mathcal {A}}_{1})_{i}\mathbf {u} ,\ldots ,({\mathcal {A}}_{d})_{i}\mathbf {u} ),\quad i=1,2,\ldots ,m,$

and

$F(\mathbf {u} ):=\left[{\begin{array}{c}F_{1}(\mathbf {u} )\\\vdots \\F_{m}(\mathbf {u} )\\\end{array}}\right].$

We apply operators component-wise. For instance, for the divergence operator, we have,

$\nabla \cdot F(\mathbf {u} ):=\left[{\begin{array}{c}\nabla \cdot F_{1}(\mathbf {u} )\\\vdots \\\nabla \cdot F_{m}(\mathbf {u} )\\\end{array}}\right].$

We can write system (3) in the form

$\nabla \cdot F(\mathbf {u} )+\mathbf {B} \mathbf {u} =\mathbf {f} ,$

(4)

Assume we have a valid element partition of the domain ${\textstyle \Omega }$. In DG, functions are approximated locally in each element by polynomials, then coupled with others in adjacent elements by means of a numerical flux. The basic process is as follows.

Let ${\textstyle \tau }$ be an element in the partition. Compute the ${\textstyle (L^{2})^{m}}$ inner product on ${\textstyle \tau }$ of each side of (4) with a test function ${\textstyle \mathbf {v} }$, to obtain

$(\nabla \cdot F(\mathbf {u} ),\mathbf {v} )_{\tau }{+}(\mathbf {B} \mathbf {u} ,\mathbf {v} )_{\tau }=(\mathbf {f} ,\mathbf {v} )_{\tau }{.}$

(5)

Denoting the inner product in th eboundary of ${\textstyle \tau }$ by ${\textstyle \langle \cdot ,\cdot \rangle _{\partial \tau }}$ we obtain after integrating by parts,

$-(F(\mathbf {u} ),\nabla \mathbf {v} )_{\tau }{+\langle }F(\mathbf {u} )\cdot \mathbf {n} ,\mathbf {v} \rangle _{\partial \tau }+(B\mathbf {u} ,\mathbf {v} )_{\tau }=(\mathbf {f} ,\mathbf {v} )_{\tau }{.}$

(6)

Continuity is not enforced at the boundary of adjacent elements. Therefore, the boundary term ${\textstyle F(\mathbf {u} )}$ is replaced with a boundary numerical flux ${\textstyle F^{*}(\mathbf {u} ^{*})}$ where ${\textstyle \mathbf {u} ^{*}\equiv \mathbf {u} ^{*}(\mathbf {u} ^{-},\mathbf {u} ^{+})}$ solves a Riemann problem with Cauchy data ${\textstyle \mathbf {u} ^{-},\,\mathbf {u} ^{+}}$. As is standard, the – superscript denotes limits from the interior of ${\textstyle e}$, and the ${\textstyle +}$ superscript, limits from the exterior. In this context, element ${\textstyle \tau }$ is denoted by ${\textstyle \tau ^{-}}$ and the outer normal ${\textstyle \mathbf {n} }$ by ${\textstyle \mathbf {n} ^{-}}$.

To hybridize the flux, and break the coupling, ${\textstyle \mathbf {u} ^{*}}$ is regarded as an extra unknown to be solved on the skeleton (the set of element edges ${\textstyle {\mathcal {F}}}$) of the mesh. Renaming ${\textstyle \mathbf {u} ^{*}}$ as ${\textstyle {\hat {\mathbf {u} }}}$ and ${\textstyle F^{*}}$ as ${\textstyle {\hat {F}}}$, the problem is to propose a suitable hybrid numerical flux ${\textstyle {\hat {\mathbf {F} }}(\mathbf {u} )}$.

Let us apply this scheme to equation (1) under the following condition

$c-{\frac {1}{2}}\mathbf {v} \cdot \left(\mathbf {D} ^{-1}\mathbf {v} \right)\geq 0.$

(7)

This condition implies a dominant reaction term, which yields a tamed advection. Consequently, the diffusive flux is assumed to be continuous across any interface. Instead of the Riemann problem solution approach, we set the hybrid flux

${\hat {\mathbf {F} }}\cdot \mathbf {n} =\left({\begin{matrix}{\hat {u}}\mathbf {n} \\\mathbf {z} \cdot \mathbf {n} +u-{\hat {u}}\end{matrix}}\right).$

(8)

Notice the dependence only in the unknown ${\textstyle {\hat {u}}}$.

For each element ${\textstyle \tau }$, the DG local unknown ${\textstyle \mathbf {u} }$ and the extra trace unknown ${\textstyle {\hat {u}}}$ need to satisfy

$-(F(\mathbf {u} ),\nabla \mathbf {v} )_{\tau }{+\langle }{\hat {F}}\cdot \mathbf {n} ,\mathbf {v} \rangle _{\partial \tau }+(\mathbf {B} \mathbf {u} ,\mathbf {v} )_{\tau }=(\mathbf {f} ,\mathbf {v} )_{\tau },$

(9)

This is complemented by a weak jump condition in the skeleton. Namely, for each edge ${\textstyle e}$

$(\lbrack \lbrack \mathbf {z} \cdot \mathbf {n} +u-{\hat {u}}\rbrack \rbrack ,w)_{e}=0,$

(10)

where ${\textstyle \mathbf {v} }$ in (9), ${\textstyle w}$ in (10) are polynomial test functions defined on elements ${\textstyle \tau }$ and edges ${\textstyle e}$ respectively.

Here, ${\textstyle \lbrack \lbrack \cdot \rbrack \rbrack }$ is the jump operator,

$\lbrack \lbrack (\cdot )\rbrack \rbrack =(\cdot )^{-}+(\cdot )^{+}.$

On each element, we are led to solving the equations (9) and (10). Let us show that this finite-dimensional problem is well-posed by showing that under null data, the solution is the trivial one.

Lemma. Assume condition (7) holds. If ${\textstyle f(x)=0}$ and ${\textstyle {\hat {u}}=0}$ on ${\textstyle {\mathcal {F}}}$, then ${\textstyle u=0,\mathbf {z} =\mathbf {0} }$ in ${\textstyle \Omega }$.

Proof.

Let us split the test function in the form ${\textstyle \mathbf {v} =(\mathbf {w} ,w)}$. The equation (9) using the hybrid flux can be written as

$-(u,\nabla \cdot \mathbf {w} )_{\tau }{+}({\hat {u}},\mathbf {w} \cdot \mathbf {n} )_{\partial \tau }+(\mathbf {D} ^{-1}\mathbf {z} ,\mathbf {w} )_{\tau }=0$ (11) $-(\mathbf {z} ,\nabla w)_{\tau }{+}(\mathbf {z} \cdot \mathbf {n} +u-{\hat {u}},w)_{\partial \tau }+(cu-\mathbf {v} \cdot \left(\mathbf {D} ^{-1}\mathbf {z} \right),w)_{\tau }=(f,w)_{\tau }$ (12)

By integration by parts in (12)

$(\nabla \cdot \mathbf {z} ,w)_{\tau }{+}(u,w)_{\partial \tau }+(cu-\mathbf {v} \cdot \left(\mathbf {D} ^{-1}\mathbf {z} \right),w)_{\tau }=0.$

(13)

Let ${\textstyle \mathbf {w} =\mathbf {z} ,w=u}$, and add equations (11) and (13) to obtain

$(\mathbf {D} ^{-1}\mathbf {z} ,\mathbf {z} )_{\tau }{+}(u,u)_{\partial \tau }+(cu-\mathbf {v} \cdot \left(\mathbf {D} ^{-1}\mathbf {z} \right),u)_{\tau }=0$

.

Notice that in the boundary term, ${\textstyle u}$ is the inner limit ${\textstyle u^{-}}$.

We are led to

$0=(\mathbf {D} ^{-1}\mathbf {z} ,\mathbf {z} )_{\tau }{+}(u^{-},u^{-})_{\partial \tau }+(cu-\mathbf {v} \cdot \left(\mathbf {D} ^{-1}\mathbf {z} \right),u)_{\tau }$ $\geq {\frac {1}{2}}(\mathbf {D} ^{-1}\mathbf {z} ,\mathbf {z} )_{\tau }{+}(u^{-},u^{-})_{\partial \tau }+(c-{\frac {1}{2}}\mathbf {v} \cdot \left(\mathbf {D} ^{-1}\mathbf {v} \right),u^{2})_{\tau }\geq 0$

Hence, ${\textstyle u^{-}=0}$ on ${\textstyle \partial \tau }$, and ${\textstyle \mathbf {z} =\mathbf {0} }$ in ${\textstyle \tau }$. Equation (11) becomes

$-(u,\nabla \cdot \mathbf {w} )_{\tau }=0.$

Integrating by parts

$-(u^{-},\mathbf {w} \cdot \mathbf {n} )_{\partial \tau }+(\nabla u,\mathbf {w} )_{\tau }=0.$

$(\nabla u,\mathbf {w} )_{I}=0.$

Since ${\textstyle \mathbf {w} }$ is arbitrary, ${\textstyle \nabla u=0}$, and consequently ${\textstyle u\equiv 0}$ in each element ${\textstyle u}$.

We conclude that ${\textstyle u=0,\mathbf {z} =\mathbf {0} }$ in ${\textstyle \Omega }$. ${\textstyle \blacksquare }$

Remark. Notice that the result is valid for Poisson problems, ${\textstyle c=0}$, ${\textstyle \mathbf {v} =\mathbf {0} }$.

3 Numerical results

Here, we illustrate some numerical results on a variety of problems, where the perturbed modified Helmholtz equation HDG solver serves as the computational engine.

The full code of the numerical implementation is available on GitHub:

https://github.com/Danalie/Hibrid-Discontinuos-Galerkin-DG2

We will test benchmark problems in rectangular geometries and regular meshes for simplicity.

We use the classical element functions on the reference segment ${\textstyle [-1,1]}$ for 1D applications. We denote by ${\textstyle HDG_{p}}$ a ${\textstyle p}$-order bilinear approximation. In 2D, ${\textstyle HDG_{2},HDG_{4}}$ refer to basis functions on the reference square ${\textstyle [-1,1]\times [-1,1]}$, as products of first-order and second-order one-dimensional 1D basis functions, respectively.

To report the accuracy of the approximation, we use the Root Mean Square Error (RMSE). Sometimes, we normalize by the corresponding norm of the exact solution to obtain the Normalized Root Mean Square Error (NRMSE).

3.1 Poisson problems

For ${\textstyle c=0}$ and ${\textstyle \mathbf {v} =0}$ in (1) we have the pure diffusion equation

$-\nabla \cdot (\mathbf {D} \nabla u)=b.$

To illustrate the HDG method with continuous diffusion numerical flux, as a Poisson solver, we consider ${\textstyle \mathbf {D} }$ as the identity matrix.

First a smooth Dirichlet Problem for Poisson's equation on the domain ${\textstyle \Omega =(0,1)\times (0,1)}$,

$-\Delta p=0,(x,y)\in \Omega ,$ $p(x,y)=1+x+y+xy,(x,y)\in \partial \Omega {.}$

The exact solution is ${\textstyle p(x,y)=1+x+y+xy}$. The numerical solution using ${\textstyle HDG_{2}}$ on a ${\textstyle 10\times 10}$ grid yields ${\textstyle RMSE=0}$ to machine precision; no further refinement is necessary.

The DG method is ${\textstyle H^{p}}$-adaptative. Local high order is straightforward, and accurate approximations are possible on coarse meshes. For instance, we use ${\textstyle HDG_{4}}$ for the Dirichlet problem

$-\Delta p=-6,\quad (x,y)\in \Omega =(0,1)\times (0,1),$ $p(x,y)=1+x^{2}+2y^{2},\quad (x,y)\in \partial \Omega {.}$

On a ${\textstyle 10\times 10}$ grid the ${\textstyle RMSE}$ is again zero to machine precision.

A preliminary comparison with the method in [7]. The latter relies on an internal-penalty numerical flux requiring a penalty parameter chosen heuristically, see (34) therein. Accuracy is shown in an exhaustive list of test problems. The simplest of such is the Dirichlet problem

$-\Delta q=2\pi ^{2}\sin(\pi x)\sin(\pi y),\mathbf {x} \in \Omega =(0,1)^{2},$ $q=0,\mathbf {x} \in \partial \Omega ,$

with analytic solution is ${\textstyle q_{e}=\sin(\pi x)\sin(\pi y)}$. Our solution is in Table 1.

Tabla. 1 Convergence of the two-dimensional Poisson problem using the Root means square error (RMSE). ${\mathcal {P}}$ is the order of approximation

Elements by dimension	$HDG_{2}$	${\mathcal {P}}$	$HDG_{4}$	${\mathcal {P}}$
20	0.0051	1.97	5.71e-5	2.94
30	0.0022	2.07	1.7e-5	2.98
50	0.00079	2.00	3.7e-6	2.98
70	0.00041	1.94	1.34e-6	3.01
100	0.00022	1.74	4.57e-7	3.01
150	8.93e-5	2.22	1.34e-7	3.02

By inspection of Figure 7 in [7], it is apparent that our results compare favorably. A full comparison is to be carried out.

3.2 Helmholtz equation

We consider two benchmark problems in Coastal Ocean Modeling (COM) that lead to Helmholtz equations. A comparison is made with the Finite Volume (FVCOM) as presented in Chen et al [8]. Therein, FVCOM is applied for the modeling of tidal simulation in a semienclosed basin with tidal forcing at the open boundary under near-resonance conditions.

Here we apply HDG to illustrate the accurate simulation of the troublesome near resonance case. We remark that for the Helmholtz equation, condition (7) is not valid. Nevertheless, the numerical results are highly satisfactory.

3.2.1 A Rectangular Channel

Consider a fluid layer of uniform density that propagates along a channel aligned with the ${\textstyle x-}$direction. More precisely, a semienclosed narrow channel with length ${\textstyle L}$ and variable depth ${\textstyle H(x)}$ and a closed boundary at ${\textstyle x=L_{1}}$ and an open boundary at ${\textstyle x=L}$.

Neglecting Coriolis force and advection of momentum, the governing equations modeling tidal waves propagation in the semienclosed channel (see Figure 1) are given as

${\frac {\partial u}{\partial t}}+g{\frac {\partial \zeta }{\partial x}}=0;\quad {\frac {\partial \zeta }{\partial t}}+g{\frac {\partial uH}{\partial x}}=0;\quad (x,t)\in (L_{1},L)\times (0,T).$

Here, ${\textstyle H(x)}$ is the total water depth, ${\textstyle g}$ is acceleration due to gravity, ${\textstyle u}$ is speed in the ${\textstyle x-}$direction, and ${\textstyle \zeta }$ is sea-level elevation.

Figura 1: Configuration of the semienclosed channel.

Assuming harmonic solutions,

$\zeta =\zeta _{0}(x)e^{-i\sigma t},\quad u=u_{0}(x)e^{-i\sigma t},$

we obtain the one dimensional Helmholtz problem for ${\textstyle \zeta _{0}}$

$(H\zeta _{0}')'+{\frac {\sigma ^{2}}{g}}\zeta _{0}=0.$

(14)

We specify a periodic tidal forcing with amplitude ${\textstyle A}$ at the mouth of the channel,

$\zeta _{0}(L)=A,$

and a no-flux boundary condition at the wall,

$H(L_{1})\zeta _{0}'(L_{1})=0.$

Let the channel depth decrease linearly toward the end of the channel, so that ${\textstyle H(x)}$ can be written as

$H(x)={\frac {xH(L)}{L}}.$

It is readily seen that (14) is a Bessel's equation. With the given boundary conditions, the analytic solution is given by

$\zeta _{0}(x)=A{\frac {Y_{0}^{\prime }(2k{\sqrt {L_{1}}})J_{0}(2k{\sqrt {x}})-J_{0}^{\prime }(2k{\sqrt {L_{1}}})Y_{0}(2k{\sqrt {x}})}{Y_{0}^{\prime }(2k{\sqrt {L_{1}}})J_{0}(2k{\sqrt {L}})-J_{0}^{\prime }(2k{\sqrt {L_{1}}})Y_{0}(2k{\sqrt {L}})}}$

where

$k:={\frac {\sigma {\sqrt {L}}}{\sqrt {gH(L)}}},$

${\textstyle J_{0},Y_{0}}$ are the Bessel's functions of degree zero and one respectively.

To compare with the HDG approximation, we solve the system,

$\zeta _{0}^{\prime }+H^{-1}z=0$ $z^{\prime }-{\frac {\sigma ^{2}}{g}}\zeta _{0}=0.$

Here we have defined ${\textstyle z=-H\zeta _{0}^{\prime }}$ in (14).

The following parameters are considered for a channel very close to resonance.

$L=300km,\,L_{1}=10km,\,H(L)=20.1m,\,\sigma ={\frac {2\pi }{12.42\cdot 3600s}},\,A=1cm.$

The HDG method is applied using nodal polynomials of degree 2 (${\textstyle {\mbox{HDG}}_{2}}$). It is compared with the FV method and the analytic solution. For consistency with the FV method, we consider the approximation at the middle point ${\textstyle x_{i}}$ of the element ${\textstyle I_{i}=[x_{i-{\frac {1}{2}}},x_{i+{\frac {1}{2}}}]}$. As illustrated in Table 4, a second-order approximation with HDG in a coarse resolution is of greater quality than FV.

Tabla. 2 Relative root mean square error for ${\mbox{HDG}}_{2}$ and FV.

Elements	NRMSE${\textstyle (HDG_{2})}$	NRMSE${\textstyle (FV)}$
10	0.180784	22.3052
20	0.0748017	0.585413
40	0.0235224	0.553751
80	0.00684013	0.43336
160	0.00187985	0.297118
320	0.000495726	0.181964
640	0.000127432	0.102475
1280	$0.0000324$	0.0546902

The analytic solution describes a standing wave with a node point near the closed side of the channel. As expected, the reproduction of these features by HDG is accurate. See Figure 2

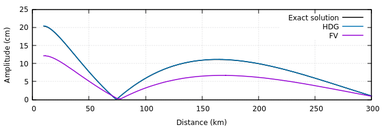
Figura 2: Solution for the rectangular channel near resonance case, with HDG nodal with polynomials of degree 2 and 80 elements.

Remark. As pointed out in Chen et al [8], regardless of the numerical method, a proper selection of horizontal resolution recover accurately this tidal resonance problem. We argue that the accuracy attained by HDG in coarse meshes yields a better choice.

3.2.2 A Sector Channel

Now consider a flat bottom channel in the form of a semicircular section, which in polar coordinates is defined from ${\textstyle 0}$ to ${\textstyle L}$ in the radial direction and from ${\textstyle -\alpha /2}$ to ${\textstyle \alpha /2}$ in the angular direction.

The semicircular line of radius ${\textstyle L}$ corresponds to an open border, while along the semicircular line of radius ${\textstyle L_{1}}$ and the two sides, they are closed, (Figure 3).

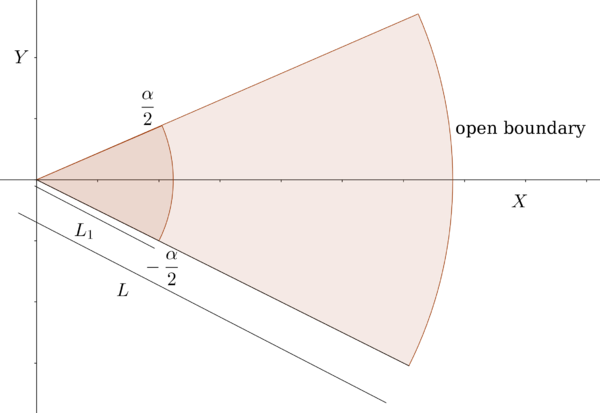
Figura 3: Semienclosed sector channel in the polar region $L_{1}\leq r\leq L$, $-{\frac {\alpha }{2}}\leq \theta \leq {\frac {\alpha }{2}}$. The sector is open at $r=L$ and closed elsewhere.

The following equations govern the nonrotating tidal oscillation,

${\frac {\partial V_{r}}{\partial t}}=-g{\frac {\partial \eta }{\partial r}},$ (15) ${\frac {\partial V_{\theta }}{\partial t}}=-g{\frac {\partial \eta }{r\partial \theta }},$ (16) ${\frac {\partial \eta }{\partial t}}+{\frac {\partial rV_{r}H_{0}}{r\partial r}}+{\frac {\partial V_{0}H_{0}}{r\partial \theta }}=0.$ (17)

${\textstyle H_{0}}$ is the constant water depth, ${\textstyle V_{r},V_{\theta }}$ are the radial and angular ${\textstyle r,\theta }$ velocity components, and ${\textstyle \eta }$ is the free surface water elevation.

Assuming a harmonic solution,

$\eta =Re(\eta _{0}(r,\theta )e^{-it(\omega t-{\frac {\pi }{2}})}),$

we can reduce the equations (15-17) to an elliptic equation

${\frac {\partial ^{2}\eta _{0}}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial \eta _{0}}{\partial r}}+{\frac {1}{r^{2}}}{\frac {\partial ^{2}\eta _{0}}{\partial \theta ^{2}}}+{\frac {\omega ^{2}}{gH_{0}}}\eta _{0}=0.$

(18)

The physical boundary conditions are as follows

1. At the open mouth of the channel, a harmonic tidal forcing is assumed,

$\eta _{0}(r,\theta )={\overline {A}}\cos \left(m\pi {\frac {\theta +{\frac {\alpha }{2}}}{\alpha }}\right),\quad \lbrace L\rbrace \times \left(-{\frac {\alpha }{2}},{\frac {\alpha }{2}}\right),$

2. On the solid walls, null flux is prescribed,

$-K\nabla \eta _{0}(r,\theta )=0,\quad \lbrace L_{1}\rbrace \times \left({\frac {-\alpha }{2}},{\frac {\alpha }{2}}\right)\bigcup (L_{1},L)\times \left\lbrace -{\frac {\alpha }{2}}\right\rbrace \bigcup (L_{1},L)\times \left\lbrace {\frac {\alpha }{2}}\right\rbrace {.}$

The analytic solution of this boundary-value problem is:

$\eta _{0}(r,\theta )={\overline {A}}{\frac {Y_{v}^{\prime }(L_{1}\kappa )J_{v}(r\kappa )-J_{v}^{\prime }(L_{1}\kappa )Y_{v}(r\kappa )}{Y_{v}^{\prime }(L_{1}\kappa )J_{v}(L\kappa )-J_{v}^{\prime }(L_{1}\kappa )Y_{v}(L\kappa )}}\cos \left({\frac {m\pi }{\alpha }}(\theta +{\frac {\alpha }{2}})\right)$

where

$v={\frac {m\pi }{\alpha }},\kappa ={\frac {\omega }{\sqrt {gH_{0}}}},$

${\textstyle J_{v},Y_{v}}$ are the ${\textstyle v}$ th-order Bessel function of the first and second types.

Let us show the HDG solution in the rectangular domain ${\textstyle (L_{1},L]\times (-\alpha /2,\alpha /2)}$.

Let ${\textstyle \nabla }$ denote the gradient with respect to ${\textstyle (r,\theta )}$ and let

$K:=\left({\begin{matrix}1&0\\0&{\frac {1}{r^{2}}}\end{matrix}}\right).$

Equation (18) becomes a perturbation of the two-dimensional Helmholtz equation,

$-\nabla \cdot (K\nabla \eta _{0})-(r^{-1},0)\cdot \nabla \eta _{0}-{\frac {\omega ^{2}}{gH_{0}}}\eta _{0}=0.$

(19)

We apply the fourth order (${\textstyle {\mbox{HDG}}_{4}}$) scheme developed above for a near-resonance case. The geometric parameter values are:

$H_{0}=1m,\,\alpha ={\frac {\pi }{4}},\,L_{1}=90km,\,m=1.0,\,\omega ={\frac {2\pi }{12.42\cdot 3600}}{\frac {1}{s}},\,L=158km,{\overline {A}}=1cm.$

Figure (4) compares the analytic and numerical solutions. The relative mean square error is shown in Table 3.

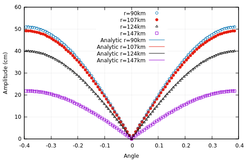
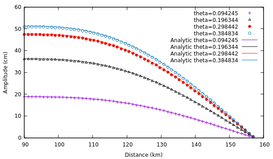
Figura 4: Comparison between the analytic solution to the sector problem with the ${\mbox{HDG}}_{4}$ solution using $30\times 50$ elements. a) Solution for some $r$ values, b) Solution for some $\theta$ values.

Tabla. 3 Relative root mean square error for ${\mbox{HDG}}_{4}$ and FV.

Elements	NRMSE${\textstyle (HDG_{4})}$	NRMSE${\textstyle (FV)}$
${\textstyle 5\times 5}$	0.441213	0.920939
${\textstyle 10\times 10}$	0.009879	0.887757
${\textstyle 35\times 35}$	0.0026408	0.803039
${\textstyle 40\times 40}$	0.00115041	0.794262

Remark. Noteworthy, the ${\textstyle 10\times 10}$ ${\textstyle {\mbox{HDG}}_{4}}$ solution is of grater quality that the ${\textstyle 40\times 40}$ FV solution. In regards to execution time, the former is attained in half a second on a personal laptop. A solution of the same quality would require in the order of minutes with the Finite Volume Method in a much finer mesh.

4 Conclussions

We have introduced a first-order system formulation for a regularly perturbed Modified Helmholtz equation. A discretization is derived by means of the Hybrid Discontinuous Galerkin method with an ad-hoc numerical flux. The well-posedness of the finite-dimensional HDG discrete linear system follows from a dominant reaction condition.

The preliminary comparison with a leading Poisson solver shows promise as a competitive alternative. Research on this is ongoing.

The proposed HDG discrete method is also applied to Helmholtz's problems arising from coastal ccean modeling. It outperforms the Finite Volume method commonly used in this setting.

The application to irregular regions with more general meshes is more elaborate but straightforward. Also, a parallel computing implementation is desired. Both tasks are left for future work.

BIBLIOGRAPHY

[1] Yaman, Olha Ivanyshyn and zdemir, Gazi. (2021) "Numerical solution of a generalized boundary value problem for the modified Helmholtz equation in two dimensions", Volume 190. Elsevier. Mathematics and Computers in Simulation 181–191

[2] Ivanyshyn Yaman, Olha and zdemir, Gazi. (2025) "An interior inverse generalized impedance problem for the modified Helmholtz equation in two dimensions", Volume 105. Wiley Online Library. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik 1 e202300711

[3] Riviere, Béatrice. (2008) "Discontinuous Galerkin methods for solving elliptic and parabolic equations: theory and implementation". SIAM

[4] Di Pietro, Daniele Antonio and Ern, Alexandre. (2011) "Mathematical aspects of discontinuous Galerkin methods", Volume 69. Springer Science & Business Media

[5] Bui-Thanh, Tan. (2015) "From Godunov to a unified hybridized discontinuous Galerkin framework for partial differential equations", Volume 295. Elsevier. Journal of Computational Physics 114–146

[6] Gockenbach, Mark S. (2006) "Understanding and implementing the finite element method". SIAM

[7] Fischer, Nils L and Pfeiffer, Harald P. (2022) "Unified discontinuous Galerkin scheme for a large class of elliptic equations", Volume 105. APS. Physical Review D 2 024034

[8] Chen, Changsheng and Huang, Haosheng and Beardsley, Robert C and Liu, Hedong and Xu, Qichun and Cowles, Geoffrey. (2007) "A finite volume numerical approach for coastal ocean circulation studies: Comparisons with finite difference models", Volume 112. Wiley Online Library. Journal of Geophysical Research: Oceans C3