Change of effective properties of concrete by alkali-silica reaction

Resumo

No presente trabalho, desenvolve-se um modelo de simulação computacional das propriedades efetivas do concreto sob ação da reação álcali-sílica. Obtém-se uma representação computacional a partir da análise da reação química e de técnicas de homogeneização. A reação álcali-sílica forma um gel que altera as propriedades efetivas do concreto e pode levar a danificação de estruturas, especialmente das barragens de usinas hidrelétricas. O modelo desenvolvido é composto de 3 fases, geração do elemento representativo do concreto, formação e difusão do gel pela reação álcali-sílica e homogeneização do material final. A primeira fase é o desenvolvimento do elemento representativo do concreto que é simulada a partir da curva granulométrica e utiliza-se um algoritmo de detecção de colisão computacional para elipses. Para modelar o comportamento da evolução química, usa-se um modelo baseado nas equações da cinética química, através da Lei de Guldberg - Waage, e em modelos de difusão do gel desenvolvidos para a malha do elemento representativo do concreto. Para modelar a variação das propriedades efetivas, usa-se modelos de homogeneização (Método de Reuss, Método de Voigt, Método Auto-consistente e Método de Mori-Tanaka) para prever, assim, os coeficientes de elasticidade do material compósito. A combinação dos modelos permitiu prever a evolução e a danificação do material ao longo do tempo e analisar a influência da fração volumétrica dos agregados no tempo de vida útil do concreto.

Palavras-chave: Métodos de homogeneização, método de Mori-Ranaka, método Auto-Consistente, reação álcali-sílica, concreto e patologias

Abstract

The present work develops a model of computer simulation of the actual properties of concrete under the action of alkali-silica reaction. Obtains a computational representation from the analysis of the chemical reaction and homogenenization techniques. Alkali-Silica reaction forms a gel that changes the effective properties of concrete and can lead to damage to structures, especially of hydroelectric dams. The model consists of three phases, generation of representative element of concrete, gel formation and dissemination by alkali-silica reaction and homogeneization of the final material. The first stage is the development of representative concrete element that is simulated from the granulometric curve and uses a computacional collision detection algorithm to ellipses. To model the behavior of chemical evolution, it uses a system based on equations of chemical kinetics, known as Guldberg - Waage Law and uses a gel diffusion model developed to mesh of representative element of concrete. To model the variation of the effective properties, it uses homogenization schemes (Reuss method, Voigt Method, Self-Consistent method and Mori-Tanaka method) to provide, thus, elasticity coefficientes of the composite material. The combination of the models allowed to predict the evolution and damage to the material over time and analyze the influence of the volume fraction of agregates in the lifetime of concrete.

Keywords: Homogenization methods, Mori-Tanaka method, self-consistent method. Alkali-Silica reaction, concrete and pathologies

1. Introdução

As barragens das Usinas Hidrelétricas são construídas, majoritariamente, com concreto, o qual é um material que pode sofrer ação da reação álcali-sílica. Tal fenômeno danifica o material ao longo do tempo, pois resulta na formação de um gel, expansivo sob a ação da água, que diminui as propriedades mecânicas efetivas da barragem ao longo do tempo. Além disso, o surgimento do gel inicia um processo de microfissura que danifica o material podendo chegar ao caso de colapsá-lo.

Os estudos referentes a patologias do concreto, como a reação álcali-sílica, já estão presentes na literatura técnica desde 1940. Entre eles, podem-se citar os seguintes trabalhos que tratam da reação proposta: Balbo et al [1] o qual propõe um modelo para geração, difusão e dano químico causado pelo gel da reação álcali-sílica a partir da cinética da reação química e da difusão realizada pelo gel. Glasser and Kataoka [2] e Glasser [3] discutem a cinética da reação álcali sílica. Hobbs [4] propõe um primeiro modelo para a expansão do gel na argamassa. Pesavento et al [5] propõe um modelo matemático combinando a ação da água, a reação química e o carregamento mecânico para descrever a degradação do material pela reação química.

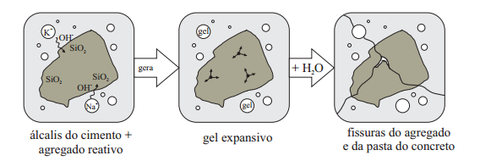
A reação álcali-sílica é uma das reações álcali-agregado. Esta reação específica ocorre quando há agregado reativo, juntamente com a disponibilidade de álcalis provenientes do cimento Portland, além de um alto grau de umidade. Esta umidade é responsável por tornar disponíveis os álcais e hidroxilas que por sua vez quebram as ligações do tipo siloxano e silanol que estão presentes no agregado reativo. Este quebra leva a formação de um gel que absorve água e expande. Tal representação pode ser observada na Figura 1 que apresenta a formação do gel, que por sua vez se expande e causa as fissuras.

Figura 1. Formação, expansão do gel e fissura do agregado e pasta do cimento [1]

A reação álcali-sílica consiste inicialmente dos íons hidroxilas ${\textstyle OH^{-}}$ que reagem com a superfície do agregado, rompendo as ligações do tipo siloxano ${\textstyle \equiv Si-O-Si\equiv }$, formando ligações do tipo silanol ${\textstyle \equiv Si-OH}$ [6].

$\equiv Si-O-Si\equiv +R^{+}+OH^{-}\rightarrow \equiv Si-O-R+H-O-Si\equiv$

(1)

Nesta reação, ${\textstyle R^{+}}$ denota os íons alcalinos sódio ${\textstyle Na^{+}}$ e potássio ${\textstyle K^{+}}$. Na sequência, os íons hidroxila continuam o ataque, desta vez nas ligações do tipo silanol, de acordo com:

$\equiv Si-OH+R^{+}+OH^{-}\rightarrow \equiv Si-O-R+H_{2}O.$

(2)

O gel álcali-sílico ${\textstyle \equiv Si-O-R\equiv }$ é formado nestas etapas.

O objetivo deste artigo é apresentar a simulação realizada para a evolução das propriedades efetivas do concreto. Para isso, a abordagem utilizada será utilizar as técnicas de homogeneização para prever os valores efetivos a partir das propriedades e das quantidades de gel existentes no concreto ao longo do tempo.

A simulação é realizada em um elemento representativo do concreto (RVE), gerado a partir da análise dos constituintes do concreto (argamassa e agregados graúdos). Para a simulação se tornar adequada, foram necessárias quatro fases:

Os resultados encontrados mostram que a combinação dos dois modelos (formação e difusão do gel) permite prever a evolução e a danificação do material ao longo do tempo e analisar a influência da fração volumétrica dos agregados no tempo de vida útil do concreto.

Na sequência, são apresentados os principais conceitos e os principais resultados obtidos para cada fase.

2. Representação computacional do concreto - RVE

Para a simulação discutida aqui, foi considerado o concreto formado como uma mistura heterogênea de argamassa e agregados graúdos. Além disso, a escala de trabalho escolhida foi a macroscópica, por evidenciar essas duas fases e, posteriormente, a presença do gel.

Para obter as propriedades físicas do material, foi realizada uma simulação a partir da curva granulométrica, em um teste descrito pela norma ABNT NBR 7211:2004 [7]. Esta curva apresenta uma função de distribuição de partículas do solo, descrevendo a variabilidade destes partículas, os quais existem em diferentes tamanhos e em proporções varidas. O ensaio de peneiramento é realizado de acordo coma norma ABNT NBR NM 248:2003 [8], com peneiras padronizadas pela norma ABNT NBR ISO 3310-1:2010 [9]. Para gerar computacionalmente o RVE, os agregados graúdos foram aproximados por elipses e posicionados a partir de uma adaptação do algoritmo de detecção de colisão, proposto por Choi [12]. A descrição detalhada sobre a geração do RVE pode ser encontrado em Pianezzer et al [10].

Este modelo permitiu gerar o RVE para diferentes quantidades de agregado. Esse parâmetro é conhecido como fração volumétrica, o qual na Figura 2 exemplifica-se o RVE gerado para ${\textstyle f_{ag}=60\%}$. Vários RVEs foram gerados para diferentes frações volumétricas.

Figura 2. Elemento representativo do concreto gerado com fração volumétrica de 60%

3. Formação e difusão do gel pela reação álcali-sílica

A partir das equações 1 e 2 que representam, respectivamente, a quebra das ligações do tipo siloxano e a formação do gel álcali-sílico, foi possível modelar a evolução dos componentes para cada ponto do elemento representativo do concreto. Para isso, foi solucionada a equação que representa a Lei de Guldberg - Waage, que representa a velocidade da reação proporcional ao produto das concentrações molares dos reagentes em cada ponto da malha, ao longo do tempo. Também acoplou-se um modelo de difusão do gel ao longo do tempo.

O modelo desenvolvido permitiu obter a concentração de gel presente no RVE ao longo do tempo. Para isso, foram plotados tais concentrações para o período de 1, 3, 5, 7 e 9 anos após o início do processo.

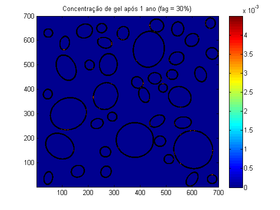
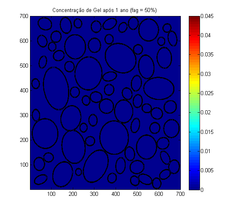
Figura 3. Mudança da concentração de gel após 1 ano

A Figura 3 mostra a mudança da concentração de gel após 1 ano. Como a reação teve pouco tempo para acontecer, a geração de gel ainda não é perceptível.

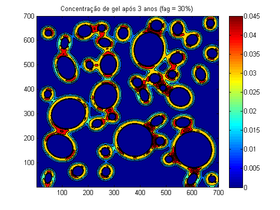
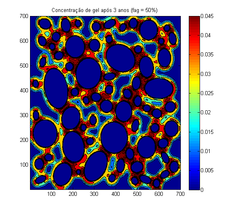
Figura 4. Mudança da concentração após 3 anos

Após 3 anos, como mostra a Figura 4, a mudança na concentração de gel passa a ser significativa. Entre 1 e 3 anos, a evolução do gel acontece de forma mais rápida do que nos anos iniciais. O mapa de concentração de gel permite verificar que a formação de gel ocorre próximo aos agregados graúdos, os quais são responsáveis pela reação por conta da maior disponibilidade de silanol do que a argamassa.

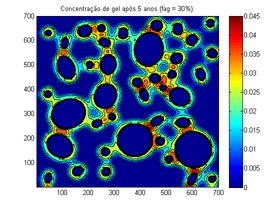
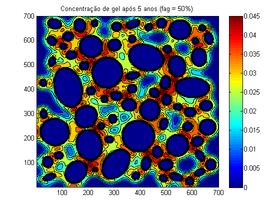
Figura 5. Mudança da concentração após 5 anos

A Figura 5 mostra a evolução após 5 anos, período médio da simulação no qual a quantidade de gel atinge sua quantidade máxima antes de começar a se estabilizar.

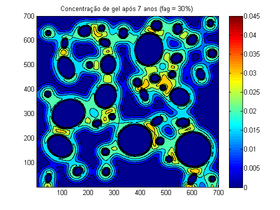
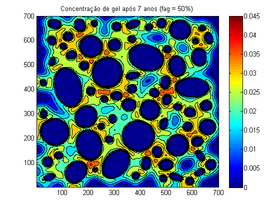
Figura 6. Mudança da concentração após 7 anos

A Figura 6 apresenta a evolução após 7 anos. Como o modelo simulado acopla um modelo de difusão, a medida que o tempo passa a quantidade de gel tende a se estabilizar, ao invés de crescer indefinidamente.

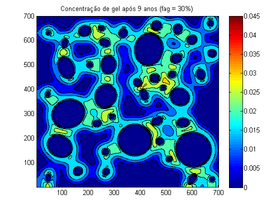
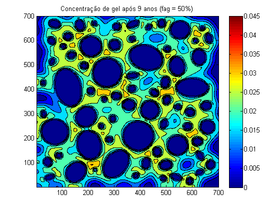
Figura 7. Mudança da concentração após 9 anos

A Figura 7 apresenta a evolução após 9 anos. A partir desta fase, a quantidade de gel se estabilizou e o modelo não apresenta mais variação significativa na mudança de gel. Os parâmetros do modelo estão ajustados para uma quantidade limitada de sílica, o qual age como um fator limitante da reação. Ao aumentar a quantidade de sílica, os gráficos se comportam de forma similar. Entretanto, o tempo para se estabilizar tende a aumentar.

4. Técnicas de homogeneização

Para análise das propriedades efetivas, foi utilizado as técnicas de homogeneização os quais permitem prever tais propriedades a partir daquelas dos constituintes. Os métodos utilizados como análise foi o Método de Reuss, o Método de Voigt, o Método autoconsistente e o Método de Mori-Tanaka.

Para determinar as propriedades do agregado graúdo (inclusão), assumiu-se da literatura [11], que o mesmo possui módulo de elasticidade de ${\textstyle 5.10^{4}MPa}$ e coeficiente de Poison de ${\textstyle 1.3x10^{-1}}$. Além disso, considerou-se que as inclusões comportam-se como isotrópicas. Isso significa que o tensor de flexibilidade é definido a partir das constantes de Engenharia. Para os valores utilizados, foi possível determinar o tensor de flexibilidade para a inclusão, ${\textstyle \mathbf {S_{ag}} }$ e ao inverter este tensor obteve-se o tensor de elasticidade ${\textstyle \mathbf {C_{ag}} }$. De maneira equivalente, obteve-se o módulo de elasticidade e o coeficiente de Poisson para a argamassa e para o gel.

4.1 Descrição das técnicas de homogeneização utilizadas

4.1.1 Método de Voigt

O método de Voigt é um dos mais simples esquemas de homogeneização de material compósito. A utilidade deste modelo reside no fato de que hoje ele representa um limite superior (Limite superior de Voigt) para o valor do módulo de elasticidade de um material compósito, de maneira que representa valores superestimados para esta informação. O modelo de Voigt encontra o tensor homogeneizado através da expressão dada pela Equação ${\textstyle \displaystyle \mathbf {C} ^{h}=f_{i}\mathbf {C} _{i}+f_{m}\mathbf {C} _{m}.}$ Nesta equação ${\textstyle \mathbf {C} _{ag}}$ e ${\textstyle \mathbf {C} _{ar}}$ representam as propriedades da inclusão e da matriz como indicados pela seção anterior. O parâmetro ${\textstyle f}$, discutido anteriormente, diz respeito à fração volumétrica do compósito, sendo ${\textstyle f_{ag}}$ a fração volumétrica de agregados graúdos indicando a porcentagem de agregados presentes no volume do concreto.

4.1.2 Método de Reuss

O método de Reuss representa um limite inferior para o valor do tensor de elasticidade efetivo do material compósito. Conhecendo as informações extraídas da inclusão e da matriz, o modelo de Reuss encontra o tensor homogeneizado através da Equação ${\textstyle \displaystyle \mathbf {C} ^{h}=[f_{i}\mathbf {C} _{i}^{-1}+f_{m}\mathbf {C} _{m}^{-1}]^{-1}.}$

4.1.3 Método auto-consistente

O método auto-consistente utiliza o tensor de Eshelby [13] para o cálculo das propriedades efetivas. Esse tensor já foi calculado para diversos formatos de inclusão e no exemplo apresentado aqui os agregados graúdos foram aproximados como circulares [14]. O tensor de Eshelby para inclusões circulares é dado de maneira explícita através da Equação (3):

$\displaystyle E_{ijkl}={\frac {5\nu -1}{15(1-\nu )}}\delta _{ij}\delta _{kl}+{\frac {4-5\nu }{15(1-\nu )}}(\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}),$

(3)

no qual ${\textstyle \delta _{ij}}$ representa o Delta de Kronicker que retorna 1 no caso em que os índices são iguais e 0 caso contrário. Além disso, o método depende do cálculo de ${\textstyle A_{ag}}$ dado por: ${\textstyle \displaystyle \mathbf {A} _{ag}=(\mathbf {C} _{ar}-\mathbf {C} _{ag})^{-1}:\mathbf {C} _{ar}}$ e do cálculo do tensor de concentração dado por ${\textstyle \displaystyle \gamma =A_{ag}:(A_{ag}-\mathbf {E} )^{-1}}$ Assim, o tensor de elasticidade homogeneizado pelo método é dado pela Equação ${\textstyle \displaystyle {\overline {\mathbf {C} }}=\mathbf {C} _{ar}+f_{ag}(\mathbf {C} _{ag}-\mathbf {C} _{ar}):\gamma {.}}$

4.1.4 Método de Mori-Tanaka

O esquema de homogeneização pelo método de Mori-Tanaka apresenta a estimativa para o tensor de elasticidade, dada por ${\textstyle \displaystyle {\overline {\mathbf {C} }}=[(f_{ar}\mathbf {C} _{ar}+f_{ag}\mathbf {C} _{ag}:\gamma ):(f_{ar}\mathbf {I} +f_{ag}\gamma )]^{-1},}$ no qual, ${\textstyle \mathbf {I} }$ representa a matriz identidade e os outros parâmetros são os mesmos do método anterior [14].

5. Resultados encontrados

5.1 Técnicas de homogeneização aplicadas sem a presença de gel

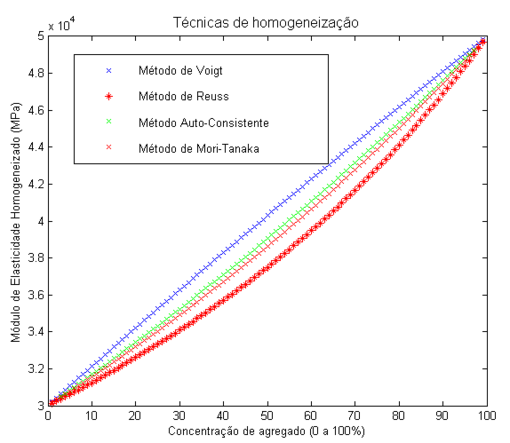
Antes de analisar a influência do gel, foram simulados, a partir dos métodos de homogeneização escolhidos, a mudança nas propriedades efetivas em função da fração volumétrica de agregados graúdos. Os resultados obtidos podem ser verificados na Figura 8. Pelo gráfico, é possível notar que o Método de Voigt e o Método de Reuss são os limites superior e inferior, respectivamente, para o valor previsto do módulo de elasticidade. Mas vale resaltar que tais modelos são considerados insatisfatórios por conta de sua variabilidade. No pior caso, para ${\textstyle f_{ag}=55\%}$ a diferença entre as previsões é de ${\textstyle 2.81x10^{3}}$, o que representa, aproximadamente, ${\textstyle 7\%}$ de desvio do valor correto.

Entretanto, tais modelos servem para validar os resultados encontrados pelos métodos mais atuais, o método Auto-Consistente e o método de Mori-Tanaka. Tais modelos são mais precisos para o real valor das propriedades efetivas, mostrando uma variabilidade entre eles de ${\textstyle 4.30x10^{2}}$, o que representa, aproximadamente, ${\textstyle 1\%}$ de desvio do valor correto.

Figura 8. Técnicas de homogeneização aplicadas para o concreto constituído de argamassa e agregados graúdos.

5.2 Técnicas de homogeneização aplicadas com a presença de gel

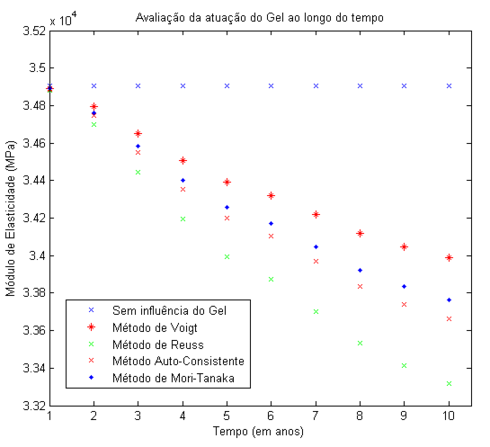
As técnicas de homogeneização foram utilizadas considerando-se a mistura de argamassa e gel como matriz e o gel como inclusão. A Figura 9 apresenta o resultado, em forma de gráfico, encontrado. A título de comparação foi ilustrado o valor do módulo de elasticidade médio obtido sem a influência do gel e a variação o módulo de elasticidade obtido pelos 4 métodos pesquisados a partir da influência do gel.

Figura 9. Avaliação da influência do gel para $f_{a}g=30\%$. (Vários métodos)

A Figura 9 continua apresentando o limite superior de Voigt e o limite inferior de Reuss e os métodos mais atuais. Além disso, como, ao longo destes 10 anos, o gel está se expandindo e se difundindo dentro do RVE, o módulo de elasticidade tende a diminuir por conta das falta de resistência deste material. Esse é um processo lento, visto que a perda de elasticidade do material é, no primeiro ano, de 0.41%, chegando a 3.28% no pior caso.

Além disso, os resultados mostram uma variabilidade máxima de 1.99% entre os piores métodos (Reuss e Voigt) e uma variabilide máxima de 0.30% entre os melhores métodos (Auto-Consistente e Mori-Tanaka).

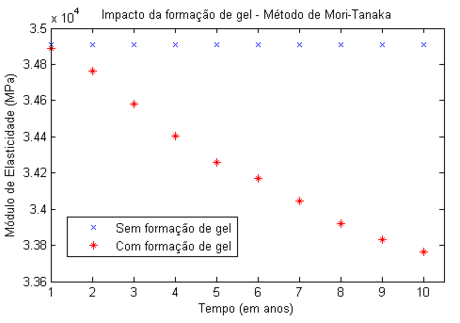
A Figura 10 mostra a avaliação da influência do gel apenas para o Método de Mori-Tanaka, comparando-o com o modelo sem a formação do gel.

Figura 10. Avaliação da influência do gel para $f_{a}g=30\%$ (Método de Mori-Tanaka).

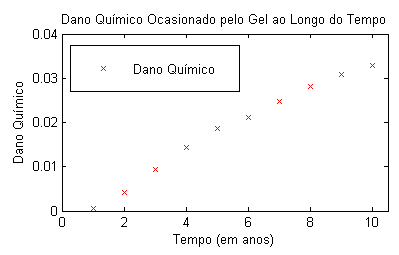
A Figura 11 apresenta a evolução do dano químico causado pelo gel. O dano é uma variável que pode ser obtida a partir de ${\textstyle \mathbf {E} =(1-D)\mathbf {E} _{0}}$. Além do dano químico, outras variáveis afetam a danificação de estruturas, como o dano ocasionado por carregamento constante, entre outros.

Figura 11. Avaliação do dano químico

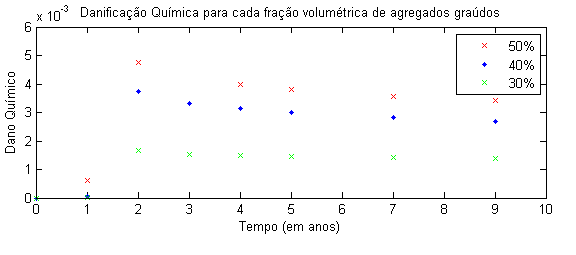
Também foram realizadas simulações para diferentes valores de fração volumétrica de agregados, para analisar a influência desta quantidade na danificação do material ao longodo tempo e no tempo de vida útil do concreto. Os resultados comparados, para o método de Mori-Tanaka estão representados na Figura 12.

Figura 12. Influência de diferentes frações volumétricas de agregados na danificação do material

Os resultados obtidos mostram que a diferença na danificação de um elemento representativo do concreto com 30% para 50% é de, cerca de, 2.85x o valor de danificação.

6. Considerações finais

Este trabalho apresenta uma metodologia que pode ser aplicada para obter as propriedades efetivas do concreto ao longo do tempo. As fases de desenvolvimento da metodologia - geração do elemento representativo do concreto, formação e difusão do gel pela reação álcali-sílica e homogeneização do material final - podem ser aplicadas para atingir o objetivo proposto, como indicam os resultados. Com a divisão proposta pela metodologia, cada fase pode ser aperfeiçoada independente para modelos mais confiáveis para cada dificuldade analisada. A escolha de certos métodos, aproximações e hipóteses, como a Lei de Guldberg - Waage ou a escolha de agregados elípticos, pode ser alterada sem que a metodologia em sua forma final sofra alteração.

Referências

[1] Balbo F.A.N., et. al. An application to the diffusion equation in a model for the damage in concrete due to alkali-silica reaction. Applied Mathematical Sciences (Ruse), 9(83):4135-4147, 2015.

[2] Glasser L.D., Kataoka N. Some observations on the rapid chemical test for potentially reactive aggregate. Cement and Concrete Research, 11(2):191-196, 1982.

[3] Glasser L.D. Osmotic pressure and the swelling of gels. Cement and Concrete Research, 9(4):515-517, 1979.

[4] Hobbs D.W. The alkali-silica reaction - a model for predicting expansion in mortar. Magazine of Concrete Research, 33:208-220, 1981.

[5] Pesavento F., Gawin D., Wyrzykowski M., Schrefler B A., Simoni L. Modeling alkali-silica reaction in non-isothermal, partially saturated cement based materials. Computer Methods in Applied Mechanics and Engineering, 225–228:95-115, 2012.

[6] Dron R., Brivot F. Thermodynamic and kinetic approach to the alkali-silica reaction. Part 1: Concepts. Cement and Concrete Research, 22(5):941-948, 1992.

[7] Associação Brasileira de Normas Técnicas. NBR 7211:2004: Agregados para concreto - Especificação, Rio de Janeiro, 2004.

[8] Associação Brasileira de Normas Técnicas. NBR 248:2003: Agregados - Determinação da composição granulométrica, Rio de Janeiro, 2003.

[9] Associação Brasileira de Normas Técnicas. NBR 3310-1:2010: Peneiras de ensaio - Requisitos técnicos e verificação, Rio de Janeiro, 2010.

[10] Pianezzer G.A., et al. Um algoritmo para geração do elemento representativo do concreto com agregados graúdos em formato elíptico. Revista Sodebras, 8(86):11-15, 2013.

[11] Teixeira M.R. A contribution to the numerical modeling of the heterogeneity of concrete with the elements free Galerkin method. Thesis, São Paulo, 2011.

[12] Choi Y., et. al. Continuous collision detection for elliptic disks. HKU CS Tech. Report, 2005.

[13] Eshelby J.D. The determination of the elastic field of an ellipsoidal inclusion and related problem. Proc. of Roy. Soc., 241(1226):376-396, 1957.

[14] Li S., Wang G. Introduction to micromechanics and nanomechanics. World Scientific, pp. 516, 2008.