Drag on a slip spherical particle moving in a couple stress fluid

Abstract

The creeping motion of a rigid slip sphere in an unbounded couple stress fluid is investigated. The linear slip boundary condition and the vanishing couple stress condition are applied on the surface of the sphere. A simple formula for the drag force acting on a slip sphere translating in an unbounded couple stress fluid is obtained. Special cases of the deduced drag formula are concluded and compared with analogous results in the literature. The normalized drag force experienced by the fluid on the slip sphere is represented graphically and the effects of slip parameter and viscosity coefficients are discussed.

Keywords

Drag formula; Couple stress fluid; Slip condition

1. Introduction

The theory of couple stress fluids has been introduced by Stokes [1] and [2] to avoid the inadequacy of the classical Navier–Stokes model describing the correct behavior of some types of fluids with microstructure such as animal blood flow, chemical suspensions, and liquid crystals [3] and [4]. In the developed theory of fluids with couple stresses, it is considered that the surface of a portion of the fluid medium is affected on by a stress vector in addition to a couple stress vector [1]. The presence of non-symmetric stress tensor, body couples, and couple stress tensor, depending on the curvature twist rate tensor, distinguishes the model of couple stress fluids. Mathematically, the motion of a couple stress fluid is governed by an equation similar to the classical Navier–Stokes equation but with higher order and the constitutive equations are characterized by two tensors representing the stresses and the couple stresses [2].

Fluids with microstructure can also be described by another model, namely micropolar fluids, introduced by Eringen. Many authors have utilized the model of micropolar theory to physical problems of fluids with microstructure such as blood flow. A general expression for the drag force experienced by a micropolar fluid on an axisymmetric body has been derived by Ramkissoon and Majumdar [3]. They applied their derived formula to discuss the flow of micropolar fluid past a sphere. Hoffmann et al. [4] discussed the drag on a sphere in micropolar fluids assuming non-homogeneous boundary condition for the microrotation vector. Shu and Lee [5] derived fundamental solutions for micropolar fluids due to a point force and a point couple and applied their results to obtain the drag force acting on a solid sphere that translates in a low-Reynolds number micropolar flow. Deo and Shukla [6] studied the problem of creeping flow of a micropolar liquid past a fluid sphere with non-homogeneous boundary condition for microrotation. They discussed the drag force acting on the fluid sphere with respect to the material parameters. Ashmawy [7] obtained a general formula for the drag on a sphere placed in a creeping unsteady micropolar fluid flow.

Many other researchers have investigated viscous fluid flow problems through the use of Navier–Stokes equations. Felderhof [8] studied the steady motion of a viscous incompressible fluid with spinning particles using no-slip boundary condition. Lindgren [9] investigated the motion of a sphere in a viscous liquid at Reynolds numbers considerably less than one. Also, Liao [10] applied the homotopy analysis method to give approximate solutions for viscous fluid flow past a sphere using no-slip condition.

Although too many researchers considered viscous and micropolar fluid flows, less attention has been given recently to the model of couple stress fluids. Pralhad and Schultz [11] investigated the problem of blood flow in a stenosed tube using the couple stress model. Reddy et al. [12] studied the blood flow between the clogged artery and the catheter using the model of couple stress fluid. The same authors studied the problem of blood flow through unsymmetric stenosed tapered artery in the presence of catheter [13] using the model of couple stress fluids. Naduvinamani et al. [14] discussed the effect of surface roughness on the hydrodynamic lubrication of couple stress squeeze film between a sphere and a flat plate. Devakar and Iyengar [15] studied the motion of a couple stress fluid between two parallel plates. Iyengar and Vani discussed the slow rotational motion of a couple stress fluid between two confocal oblate spheroids [16]. The oscillatory flow of an incompressible couple stress fluid through an annulus with mild constriction at the outer wall is studied by Srinivasacharya and Srikanth [17]. Devakar et al. [18] applied the slip condition to the Couette and Poiseuille couple stress fluid flows.

The classical no-slip boundary condition has been applied extensively in the field of fluid dynamics. However, in the last century numerous studies have been established that the no-slip condition may not always occur and that the slippage of fluid particles on the surface of the rigid boundary can take place [19] and [20]. Recently, a linear slip boundary condition stating that the fluid tangential velocity relative to the solid boundary is proportional to the shearing stress acting at the contact point has been proposed and applied to many fluid problems either viscous or micropolar [21], [22], [23], [24], [25], [26], [27], [28] and [29].

Based on the above mentioned literature review and to the best knowledge of the author, the influence of the drag force experienced by a couple stress fluid on a moving sphere, utilizing linear slip condition, has not been investigated yet. In the present work, we investigate the slow steady motion of a slip spherical particle in an unbounded incompressible couple stress fluid. The velocity slip boundary condition is applied on the surface of the rigid boundary. Also, it is assumed that the couple stress vanishes on the surface of the sphere. The drag force experienced by the couple stress fluid on the surface of the sphere using slip condition is obtained and represented graphically.

2. Formulation of the problem

The field equations governing a slow steady motion of an incompressible couple stress fluid, in the absence of body forces and body couples, are [1] and [2]

$q_{i{\mbox{,}}i}=0{\mbox{,}}$

(2.1)

$\mu q_{\mbox{i,jj}}-\eta q_{i{\mbox{,}}jjkk}-p_{{\mbox{,}}i}=$$0{\mbox{,}}$

(2.2)

where q_i is the velocity vector and p represents the fluid pressure at any point in the fluid flow. The classical viscosity coefficient μ has the dimensions M/LT while the couple stress viscosity parameters η and η′ have the dimensions of momentum, namely ML/T. These material constants are constrained to the following restrictions [2].

$\mu \geqslant 0{\mbox{,}}\eta \geqslant 0{\mbox{,}}\eta \geqslant {\eta }^{'}$

(2.3)

To completely describe the problem governed by (2.1) and (2.2), a set of six boundary conditions are needed. Three boundary conditions on the velocity, namely slip conditions, and three boundary conditions on couple stresses are provided.

The following slip boundary condition is imposed on the surface of the spherical particle, r = r₀, [22]

${\beta }_{0}(q_{i}-U\quad {\hat {e}}_{z})=(I-n_{k}n_{k})\quad (n_{j}t_{ji})\quad on\quad r=$$r_{0}{\mbox{,}}$

(2.4)

where ${\textstyle {\hat {e}}_{z}}$ is the unit vector along z-direction, n_j is the unit normal to the boundary pointing into the fluid and I is the unit dyadic. In addition, the parameter β₀ is termed the slip coefficient which is varying from zero to infinity. This parameter depends only on the nature of the fluid flow and the material of the boundary. The classical case of no-slip condition can be recovered as a special case when the slip parameter approaches infinity while the perfect slip is deduced when the slip parameter vanishes.

The remaining proposed boundary condition is the vanishing couple stress on the surface of the sphere. This means that the mechanical interaction at the boundary is equivalent to a force distribution only [2]

$n_{j}m_{ji}=0{\mbox{,}}\quad on\quad r=r_{0}{\mbox{.}}$

(2.5)

The stress tensor t_ij and the couple stress tensor m_ij can be written as [1] and [2]

$t_{ij}=-p\quad {\delta }_{ij}+\quad 2\mu \quad d_{ij}-$${\frac {1}{2}}\quad \quad e_{ijk}\quad m_{sk{\mbox{,}}s}{\mbox{,}}$

(2.6)

$m_{ij}=m{\delta }_{ij}+4(\eta \quad {\omega }_{j{\mbox{,}}i}+$${\eta }^{'}\quad {\omega }_{i{\mbox{,}}j}){\mbox{,}}$

(2.7)

where m is the trace of the couple stress tensor. The deformation rate tensor d_ij   and the vorticity vector ${\textstyle {\omega }_{i}}$ are given by

$d_{ij}={\frac {1}{2}}(q_{i{\mbox{,}}j}+q_{j{\mbox{,}}i})\quad {\omega }_{i}\quad =$${\frac {1}{2}}\quad e_{ijk}\quad q_{k{\mbox{,}}j}{\mbox{.}}$

(2.8)

Also, δ_ij and e_ijk are denoting the Kronecker delta and the alternating tensor, respectively.

Consider the steady creeping motion of an incompressible couple stress fluid extending to infinity; that is, the fluid region is assumed to be unbounded. We assume that a solid sphere of radius, r₀, is allowed to translate in an infinite region filled with a couple stress fluid. The velocity of the sphere is supposed to be constant of magnitude U directed along z-direction.

Working with the spherical polar coordinates (r, θ, ϕ), the velocity vector can take the form

${\overset {\rightarrow }{q}}=(u(r{\mbox{,}}\theta ){\mbox{,}}v(r{\mbox{,}}\theta ){\mbox{,}}0){\mbox{.}}$

(2.9)

The stream function ψ(r, θ) can be used such that

$u(r{\mbox{,}}\theta )={\frac {-1}{r^{2}sin\theta }}{\frac {\partial \psi }{\partial \theta }}{\mbox{,}}\quad v(r{\mbox{,}}\theta )=$${\frac {1}{rsin\theta }}{\frac {\partial \psi }{\partial r}}{\mbox{.}}$

(2.10)

Thus, the governing equations (2.2) reduce to

${\frac {\partial p}{\partial r}}+{\frac {\mu }{r^{2}sin\theta }}{\frac {\partial }{\partial \theta }}E^{2}\psi -$${\frac {\eta }{r^{2}sin\theta }}{\frac {\partial }{\partial \theta }}E^{4}\psi =$$0{\mbox{,}}$

(2.11)

${\frac {1}{r}}{\frac {\partial p}{\partial \theta }}-{\frac {\mu }{rsin\theta }}{\frac {\partial }{\partial r}}E^{2}\psi +$${\frac {\eta }{rsin\theta }}{\frac {\partial }{\partial r}}E^{4}\psi =$$0{\mbox{,}}$

(2.12)

where

$E^{2}={\frac {{\partial }^{2}}{\partial r^{2}}}+{\frac {1}{r^{2}}}{\frac {{\partial }^{2}}{\partial {\theta }^{2}}}-$${\frac {cot\theta }{r^{2}}}{\frac {\partial }{\partial \theta }}{\mbox{.}}$

Eliminating the pressure appearing in the two equations (2.11) and (2.12), we obtain

$E^{4}(E^{2}-{\lambda }^{2})\quad \psi (r{\mbox{,}}\theta )=$$0{\mbox{,}}$

(2.13)

where ${\textstyle {\lambda }^{2}=\mu /\eta {\mbox{.}}}$

The parameter ${\textstyle \beta =r_{0}{\sqrt {\mu /\eta }}=r_{0}\lambda }$ is denoting the couple stress parameter where the length-dependent parameter ${\textstyle {\sqrt {\eta /\mu }}}$ is a characteristic measure of the polarity of the couple stress fluids model. For the case of non-polar fluids, the length-dependent parameter becomes identically zero.

3. Solution of the problem

In order to obtain the solution of the differential equation (2.13), the superposition principle is used by assuming that ψ = ψ₁ + ψ₂ such that

$E^{4}\quad {\psi }_{1}(r{\mbox{,}}\theta )=0{\mbox{,}}$

(3.1)

$(E^{2}-{\lambda }^{2})\quad {\psi }_{2}(r{\mbox{,}}\theta )=$$0{\mbox{.}}$

(3.2)

The well known solutions of the differential equations (3.1) and (3.2), regular at infinity, have the forms

${\psi }_{1}(r{\mbox{,}}\theta )={\frac {1}{2}}\left({\frac {A}{r}}+\right.$$\left.Br\right){sin}^{2}\theta {\mbox{,}}$

(3.3)

${\psi }_{2}(r{\mbox{,}}\theta )={\frac {C}{2}}\left(1+{\frac {1}{\lambda r}}\right)e^{-\lambda r}{sin}^{2}\theta {\mbox{.}}$

(3.4)

Therefore, the general solution of Eq. (2.13) is

$\psi (r{\mbox{,}}\theta )={\frac {1}{2}}\left({\frac {A}{r}}+\right.$$\left.Br+C\left\{1+{\frac {1}{\lambda r}}\right\}\quad e^{-\lambda r}\right){sin}^{2}\theta {\mbox{.}}$

(3.5)

Substituting into expressions (2.10), we get

$\quad u(r{\mbox{,}}\theta )=-\quad \left({\frac {A}{r^{3}}}+\right.$$\left.{\frac {B}{r}}+C\left\{{\frac {1}{r^{2}}}+{\frac {1}{\lambda r^{3}}}\right\}\quad e^{-\lambda r}\right)cos\theta {\mbox{,}}$

(3.6)

$\quad v(r{\mbox{,}}\theta )={\frac {1}{2}}\left(-{\frac {A}{r^{3}}}+\right.$$\left.{\frac {B}{r}}-C\left\{{\frac {\lambda }{r}}+{\frac {1}{r^{2}}}+\right.\right.$$\left.\left.{\frac {1}{\lambda r^{3}}}\right\}\quad e^{-\lambda r}\right)sin\theta {\mbox{.}}$

(3.7)

Also, the non-vanishing component of the vorticity vector is found to be

$\quad {\omega }_{\phi }(r{\mbox{,}}\theta )={\frac {1}{4}}\left(-\right.$$\left.{\frac {2B}{r^{2}}}+C{\lambda }^{2}\left\{{\frac {1}{r}}+\right.\right.$$\left.\left.{\frac {1}{\lambda r^{2}}}\right\}\quad e^{-\lambda r}\right)sin\theta {\mbox{.}}$

(3.8)

Substituting for ${\textstyle \psi (r{\mbox{,}}\theta )}$ into Eqs. (2.11) and (2.12) and then integrating, we obtain the pressure at any point in the fluid as

$p(r{\mbox{,}}\theta )=-{\frac {\mu \quad B}{r^{2}}}cos\theta {\mbox{.}}$

(3.9)

The imposed slip boundary condition (2.4) and the vanishing couple stress condition (2.5) applied on the surface of the spherical particle reduce to

$u(r_{0}{\mbox{,}}\theta )=U\quad cos\theta {\mbox{,}}$

(3.10)

${\beta }_{0}\lbrace v(r_{0}{\mbox{,}}\theta )+Usin\theta \rbrace =$$t_{r\theta }(r_{0}{\mbox{,}}\theta ){\mbox{,}}$

(3.11)

$m_{r\phi }(r_{0}{\mbox{,}}\theta )=0{\mbox{.}}$

(3.12)

To employ the proposed boundary conditions (3.10), (3.11) and (3.12), we use the constitutive equations (2.6) and (2.7) to obtain the stress and couple stress components as

${\begin{array}{rl}t_{rr}=&-p+2\mu \quad {\frac {\partial u}{\partial r}}\\=&\mu \quad \left({\frac {6A}{r^{4}}}+{\frac {3B}{r^{2}}}+C\left\{{\frac {2\lambda }{r^{2}}}+{\frac {6}{r^{3}}}+{\frac {6}{\lambda r^{4}}}\right\}\quad e^{-\lambda r}\right)cos\theta {\mbox{,}}\end{array}}$

(3.13)

${\begin{array}{rl}t_{r\theta }=&\mu \left({\frac {1}{r}}{\frac {\partial u}{\partial \theta }}-{\frac {v}{r}}+{\frac {\partial v}{\partial r}}\right)-{\frac {1}{2}}\left({\frac {1}{r}}{\frac {\partial m_{\theta \phi }}{\partial \theta }}+{\frac {\partial m_{r\phi }}{\partial r}}+{\frac {2m_{r\phi }+m_{\phi r}}{r}}\right)\\=&\mu \quad \left({\frac {3A}{r^{4}}}+C\left\{{\frac {\lambda }{r^{2}}}+{\frac {3}{r^{3}}}+{\frac {3}{\lambda r^{4}}}\right\}\quad e^{-\lambda r}\right)sin\theta {\mbox{,}}\end{array}}$

(3.14)

$m_{r\phi }=\quad \left\{(2\eta +{\eta }^{'})\quad \left({\frac {2B}{r^{3}}}-\right.\right.$$\left.\left.{\lambda }^{2}C\left\{{\frac {1}{r^{2}}}+{\frac {1}{\lambda r^{3}}}\right\}\quad e^{-\lambda r}\right)-\right.$$\left.\eta \quad {\frac {{\lambda }^{3}C}{r}}\quad e^{-\lambda r}\right\}sin\theta {\mbox{,}}$

(3.15)

$m_{\phi \quad r}=\left\{(\eta +2{\eta }^{'})\quad \left({\frac {2B}{r^{3}}}-\right.\right.$$\left.\left.{\lambda }^{2}C\left\{{\frac {1}{r^{2}}}+{\frac {1}{\lambda r^{3}}}\right\}\quad e^{-\lambda r}\right)-\right.$$\left.{\eta }^{'}\quad {\frac {{\lambda }^{3}C}{r}}\quad e^{-\lambda r}\right\}sin\theta {\mbox{,}}$

(3.16)

$m_{\theta \phi }=(\eta -{\eta }^{'})\quad \left(-\right.$$\left.{\frac {2B}{r^{3}}}+{\lambda }^{2}C\left\{{\frac {1}{r^{2}}}+\right.\right.$$\left.\left.{\frac {1}{\lambda r^{3}}}\right\}\quad e^{-\lambda r}\right)cos\theta {\mbox{,}}$

(3.17)

Applying the boundary conditions (3.10), (3.11) and (3.12), we obtain

$A={\frac {{Ur}_{0}^{3}}{2}}\left\{{\frac {\xi }{\left(\xi +3\right)}}+\right.$$\left.{\frac {3\alpha \quad (\xi +2)\quad }{{\beta }^{2}\quad (\xi +3)}}\left({\frac {(\xi +3)({\beta }^{2}+2\beta +2)-{\beta }^{2}}{\alpha +\beta (\xi +3)}}\right)\right\}{\mbox{,}}$

(3.18)

$B={\frac {-3{Ur}_{0}}{2}}\left\{1+{\frac {\alpha \quad (\xi +1)-\quad \beta }{\quad \alpha +\beta \quad (\xi +3)}}\right\}{\mbox{,}}$

(3.19)

$C={\frac {-3{Ur}_{0}^{2}\alpha \quad (\xi +2)}{\quad \beta (\alpha +\beta \quad (\xi +3))}}e^{\beta }{\mbox{,}}$

(3.20)

where

$\alpha ={\frac {2+\tau }{2+\tau +\beta }}{\mbox{,}}\quad \quad \quad \quad \xi =$${\frac {r_{0}{\beta }_{0}}{\mu }}{\mbox{,}}\quad \tau ={\frac {{\eta }^{'}}{\eta }}{\mbox{,}}\quad \beta =$$\lambda r_{0}{\mbox{.}}$

4. Drag force on a sphere

The drag force experienced by a couple stress fluid extending to infinity on a spherical particle translating in it, along its direction of motion, is evaluated using the following integral formula [30]

$F_{z}=2\pi \quad r_{0}^{2}{\int }_{0}^{\pi }{\left(t_{rr}cos\theta -t_{r\theta }sin\theta \right)}_{r=r_{0}}\quad sin\theta \quad d\theta {\mbox{,}}$

(4.1)

Substituting the expressions (3.13) and (3.14) into the above formula, we obtain

$F_{z}=4\pi \mu \quad B{\mbox{,}}$

(4.2)

From the expression (3.5), we find that

$B=2{\underset {r\rightarrow \infty }{lim}}{\frac {\psi }{r{sin}^{2}\theta }}{\mbox{,}}$

(4.3)

Substituting from (4.3) into (4.2), we arrive at the formula

$F_{z}=8\pi \mu \quad \quad {\underset {r\rightarrow \infty }{lim}}{\frac {\psi }{r{sin}^{2}\theta }}{\mbox{.}}$

(4.4)

Formula (4.4) is similar to that obtained by Happel and Brenner for Newtonian viscous fluids [31]. A similar formula for the drag in the case of micropolar fluids has been provided by Ramkissoon and Majumdar [3] in the form

$D=4\pi \quad (2\mu +\kappa )\quad \quad {\underset {r\rightarrow \infty }{lim}}{\frac {\psi }{r{sin}^{2}\theta }}{\mbox{,}}$

(4.5)

where κ is the micropolarity parameter that characterizes the model of micropolar fluids.

Now, we aim to apply the general formula (4.4) to our boundary value problem governed by (2.1), (2.2), (2.3), (2.4) and (2.5) to evaluate the drag force experienced by the couple stress fluid on the surface of the slip spherical object.

Substituting for the constant B from (3.19) into Eq. (4.2), we obtain

$F_{z}=-6\pi \mu \quad r_{0}U\left\{1+{\frac {\alpha (\xi +1)-\beta }{\alpha +\beta \quad (\xi +3)}}\right\}{\mbox{.}}$

(4.6)

Later formula (4.6) represents the drag force experienced by a couple stress fluid on the surface of a slip spherical object translating in it. This formula generalizes the results given by Stokes [32] and Basset [33]. It can be noticed from the drag formula (4.6) that the couple stress parameter β   contributes considerably on the drag force and this can also be concluded from the numerical results. As this parameter approaches infinity (i.e. when the length-dependent parameter ${\textstyle {\sqrt {\eta /\mu }}}$ vanishes), the couple stress features disappear and the case of classical non-polar fluids occurs.

In other words, the drag force acting on a non-slip sphere moving in a couple stress fluid obtained by Stokes [32] can be recovered from our formula (4.6) as a limiting case when ξ → ∞ to get

$F_{z}=-6\pi \mu \quad r_{0}U\left\{1+{\frac {\alpha }{\beta \quad }}\right\}{\mbox{,}}$

(4.7)

Another special case can be concluded from the formula (4.6) by taking the limit as η → 0 (i.e. β → ∞) to recover the drag on a slip sphere moving in a viscous fluid obtained by Basset [33]

$F_{z}=-6\pi \mu \quad r_{0}U\left\{{\frac {\xi +2}{\xi +3}}\right\}{\mbox{.}}$

(4.8)

Moreover, the drag force acting on a non-slip sphere moving in a viscous fluid can be deduced from (4.6) by taking the limits as η → 0 and ξ → ∞

$F_{z}=-6\pi \mu \quad r_{0}U{\mbox{.}}$

(4.9)

5. Numerical results

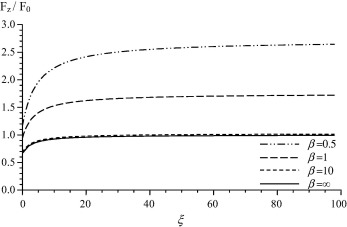
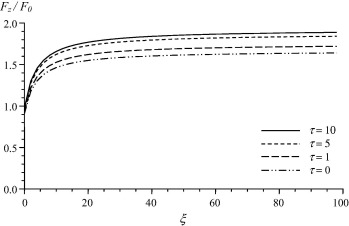
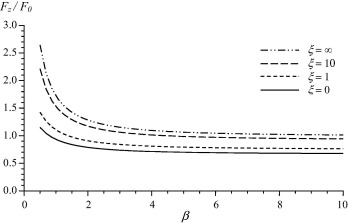
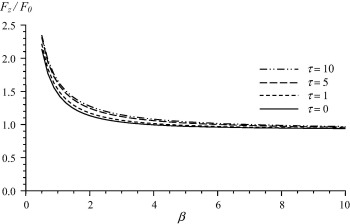
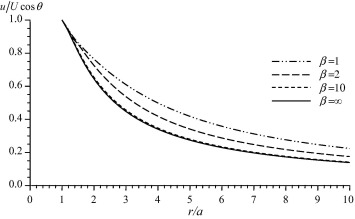
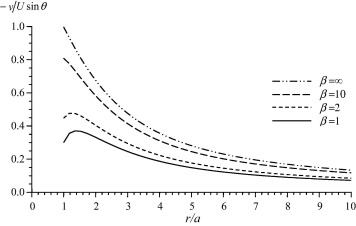
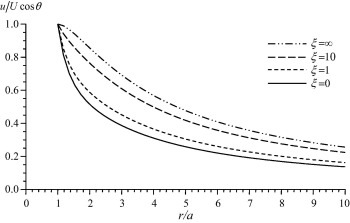
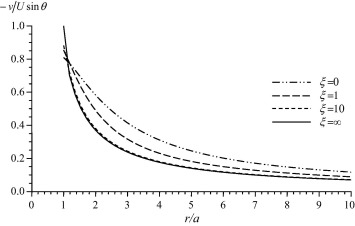
In this section, we represent the normalized drag force F_z/F₀, where ${\textstyle F_{0}=-6\pi \mu \quad r_{0}U{\mbox{,}}}$ experienced by the couple stress fluid on the slip spherical particle numerically. The effect of the couple stress viscosity parameter, β, on the drag is discussed in Fig. 1. It is observed that as β increases (i.e. as η decreases), the normalized drag force decreases and that the contribution of this viscosity parameter on the drag is remarkable. Also, the values of drag force of the present problem are compared with the results of Basset [33] where β is approaching infinity. It is concluded that the values of the resistance of couple stress fluids exceed considerably its values in the classical viscous fluids. Fig. 2 shows the variation of the normalized drag force versus the slip parameter for different values of the couple stress viscosity ratio τ = η′/η. It is noticed that the increase in the parameter τ results in an increase in the drag. The effect of the slip parameter can be observed from Fig. 3. In this figure, a comparison between our results and the analogous results of Stokes [32] with no-slip (i.e. ξ → ∞) is demonstrated. It can be seen that the drag values in the presence of slip are less than its values in the case of no-slip. In addition, it can be observed that the increase in the slip parameter increases the drag force and the no-slip case can be reached when the slip parameter approaches infinity. Fig. 4, presents the variation of the normalized drag force versus the couple stress parameter β for different values of the viscosity ratio τ. It is noticed that the increase of τ results in a slight increase in the drag. The main reason of this slight effect on the drag is that the couple stress viscosity parameter η appears also in the non-dimensional parameter β which is varying as presented in Fig. 4. The distributions of the velocity components against the distance from the obstacle for different values of β are shown in Figure 5 and Figure 6. It is observed, as expected, that far from the spherical particle the values of the velocity decrease. Also, the effect of the slip parameter on the velocity components is shown in Figure 7 and Figure 8. It can be noticed that the increase in the slip values increases the radial velocity while it decreases the transverse velocity. The same observation of Figure 5 and Figure 6 is also noticed in Figure 7 and Figure 8.

Figure 1. Drag force variation with the slip parameter ξ for τ = 1.

Figure 2. Drag force variation with the slip parameter ξ for β = 1.

Figure 3. Drag force variation with the couple stress parameter β for τ = 1.

Figure 4. Drag force variation with the couple stress parameter β for ξ = 10.

Figure 5. Variation of the radial velocity with the displacement for ξ = 10 and τ = 1.

Figure 6. Variation of the transverse velocity with the displacement for ξ = 10 and τ = 1.

Figure 7. Variation of the radial velocity with the displacement for β = 1 and τ = 1.

Figure 8. Variation of the transverse velocity with the displacement for β = 1 and τ = 1.

6. Conclusion

The slow steady motion of a rigid sphere in a couple stress fluid with the effect of slip boundary condition is investigated. The drag force acting on the slip spherical particle is evaluated and some special cases are recovered and compared with analogous results. The effects of the couple stress viscosity parameters and the slip coefficient on the fluid flow are discussed. It is concluded that the increase in the couple stress viscosity parameter β (i.e. the decrease of η) decreases the normalized drag force. This means that the resistance of couple stress fluids exceeds the resistance of classical viscous fluids. Also, as expected, it is observed that the values of the drag force acting on a slip sphere increase with the increase in the slip parameter. It can be also concluded that far from the obstacle the values of the velocity decrease.

References

1. [1] V.K. Stokes; Couple stresses in fluids; Phys. Fluids, 9 (1966), pp. 1709–1715
2. [2] V.K. Stokes; Theories of Fluids with Microstructure; Springer, New York (1984)
3. [3] H. Ramkissoon, S.R. Majumdar; Drag on an axially symmetric body in the Stokes’ flow of micropolar fluid; Phys. Fluids, 19 (1976), pp. 16–21
4. [4] K.H. Hoffmann, D. Marx, N.D. Botkin; Drag on spheres in micropolar fluids with nonzero boundary conditions for microrotations; J. Fluid Mech., 590 (2007), pp. 319–330
5. [5] J.-J. Shu, J.S. Lee; Fundamental solutions for micropolar fluids; J. Eng. Math., 61 (2008), pp. 69–79
6. [6] S. Deo, P. Shukla; Creeping flow of micropolar fluid past a fluid sphere with non-zero spin boundary condition; Int. J. Eng. Technol., 1 (2012), pp. 67–76
7. [7] E.A. Ashmawy; A general formula for the drag on a sphere placed in a creeping unsteady micropolar fluid flow; Meccanica, 47 (2012), pp. 1903–1912
8. [8] B.U. Felderhof; Steady-state hydrodynamics of a viscous incompressible fluid with spinning particles; J. Chem. Phys., 135 (2011), pp. 234901–234906
9. [9] E.R. Lindgren; The motion of a sphere in an incompressible viscous fluid at Reynolds Numbers considerably less than one; Phys. Scr., 60 (1999), pp. 97–110
10. [10] S. Liao; On the viscous flow past a sphere: a simplified description; Commun. Nonlinear Sci. Numer. Simulat., 4 (1999), pp. 104–109
11. [11] R.N. Pralhad, D.H. Schultz; Modeling of arterial stenosis and its applications to blood diseases; Math. Biosci., 190 (2004), pp. 203–220
12. [12] J.V.R. Reddy, D. Srikanth, S.K. Murthy; Mathematical modelling of couple stresses on fluid flow in constricted tapered artery in the presence of slip velocity – Effects of catheter; Appl. Math. Mech., 35 (2014), pp. 947–958
13. [13] J.V. Ramana Reddy, D. Srikanth, S.V.S.S.N.V.G. Krishna Murthy; Mathematical modelling of pulsatile flow of blood through catheterized unsymmetric stenosed artery – effects of tapering angle and slip velocity; Eur. J. Mech. B/Fluids, 48 (2014), pp. 236–244
14. [14] N.B. Naduvinamani, P.S. Hiremath, G. Gurubasavaraj; Effect of surface roughness on the couple-stress squeeze film between a sphere and a flat plate; Tribol. Int., 38 (2005), pp. 451–458
15. [15] M. Devakar, T.K.V. Iyengar; Run up flow of a couple stress fluid between parallel plates; Non-Linear Anal.: Model Control, 15 (2010), pp. 29–37
16. [16] T.K.V. Iyengar, V.G. Vani; Flow of an incompressible couple stress fluid in the region between two slowly rotating confocal oblate spheroids; Global J. Math. Sci.: Theory Practical, 4 (2012), pp. 337–352
17. [17] D. Srinivasacharya, D. Srikanth; Steady streaming effect on the flow of a couple stress fluid through a constricted annulus; Arch. Mech., 64 (2012), pp. 137–152
18. [18] M. Devakar, D. Sreenivasu, B. Shankar; Analytical solutions of couple stress fluid flows with slip boundary conditions; Alex. Eng. J., 53 (2014), pp. 723–730
19. [19] S. Richardson; On the no-slip boundary condition; J. Fluid Mech., 59 (1973), pp. 707–719
20. [20] D.K. Hutchins, M.H. Harper, R.L. Felder; Slip correction measurements for solid spherical particles by modulated dynamic light scattering; Aerosol Sci. Technol., 22 (1995), pp. 202–218
21. [21] A. Thompson, S.M. Troian; A general boundary condition for liquid flow at solid surfaces; Nature, 389 (1997), pp. 360–362
22. [22] H.J. Keh, C.H. Huang; Slow motion of axisymmetric slip particles along their axes of revolution; Int. J. Eng. Sci., 42 (2004), pp. 1621–1644
23. [23] F. Yang; Slip boundary condition for viscous flow over solid surfaces; Chem. Eng. Comm., 197 (2010), pp. 544–550
24. [24] E.A. Ashmawy; Slip at the surface of a general axi-symmetric body rotating in a viscous fluid; Arch. Mech., 63 (2011), pp. 341–361
25. [25] E.A. Ashmawy; Unsteady rotational motion of a slip spherical particle in a viscous fluid; ISRN Math. Phys., 2012 (2012), pp. 1–8
26. [26] H.H. Sherief, M.S. Faltas, E.A. Ashmawy; Stokes flow between two confocal rotating spheroids with slip; Arch. Appl. Mech., 82 (2012), pp. 937–948
27. [27] E.A. Ashmawy; Unsteady Couette Flow of a Micropolar Fluid with Slip; Meccanica, 47 (2012), pp. 85–94
28. [28] H.H. Sherief, M.S. Faltas, E.A. Ashmawy, M.G. Nashwan; Slow motion of a slip spherical particle along the axis of a circular cylindrical pore in a micropolar fluid; J. Mol. Liq., 200 (2014), pp. 273–282
29. [29] H.H. Sherief, M.S. Faltas, E.A. Ashmawy, A.M. Abdel-Hameid; Parallel and perpendicular flows of a micropolar fluid between slip cylinder and coaxial fictitious cylindrical shell in cell models; Eur. Phys. J. Plus, 129 (2014), pp. 1–16
30. [30] L.D. Landau, E.M. Lifshitz; Fluid Mechanics: Course of Theoretical Physics, vol. 6, Butterworth-Heinemann, Oxford (1995)
31. [31] J. Happel, H. Brenner; Low Reynolds Number Hydrodynamics; Noordhoff Int. Publish, Leyden (1973)
32. [32] V.K. Stokes; Effects of couple stresses in fluids on the creeping flow past a sphere; Phys. Fluids, 14 (1971), pp. 1580–1582
33. [33] A.B. Basset; A Treatise on Hydrodynamics, vol. 2, Dover, New York (1961)