An innovative approach for planning and execution of pre-experimental runs for Design of Experiments

Abstract

This paper addresses the study of the pre-experimental planning phase of the Design of Experiments (DoE) in order to improve the final product quality. The pre-experimental planning phase includes a clear identification of the problem statement, selection of control factors and their respective levels and ranges. To improve production quality based on the DoE a new approach for the pre-experimental planning phase, called Non-Conformity Matrix (NCM), is presented. This article also addresses the key steps of the pre-experimental runs considering a consumer goods manufacturing process. Results of the application for an industrial case show that this methodology can support a clear definition of the problem and also a correct identification of the factor ranges in particular situations. The proposed new approach allows modeling the entire manufacturing system holistically and correctly defining the factor ranges and respective levels for a more effective application of DoE. This new approach can be a useful resource for both research and industrial practitioners who are dedicated to large DoE projects with unknown factor interactions, when the operational levels and ranges are not completely defined.

JEL classification

L660

Keywords

Pre-experimental runs;Non-Conformity Matrix;Design of Experiments

1. Introduction

Design of Experiments (DoE) is one of the most powerful tools for process improvement and optimization in the scientific and engineering disciplines. It is widely used to develop robust processes, so that they are less affected by external sources of variability. Objectives of DoE are to study the performance of processes and systems and to better understand the behavior of the process factors, as well as their impact on the quality characteristics of the product and process under analysis. In other words, experiments are performed to (Montgomery, Keatsa, Perrya, Thompsonb, & Messinab, 2000):

• Determine which controllable factors have most influence on the response(s);
• Determine where to set the significant controllable factors in order to assure that the response(s) are close to their target value;
• Determine where to set the significant controllable factors in order to assure that the effects of the uncontrollable and noise factors on the response(s) are minimal.

Application of DoE in process improvements can result in improved process yields, reduced process variability and reduced overall costs (Montgomery, 2008). Over the past many years, industries have successfully applied DoE to improve process performance and reduce variability (Javorsky et al., 2014 ;  Montgomery et al., 2000). However, other applications of DoE are also realized in the areas of product development (Fowlkes & Creveling, 1996) and performance optimization of automation technologies (Subulan & Cakmakci, 2011).

DoE consists of three important phases: pre-experimental planning; execution of the experiments; and statistical analysis of the data collected. Pre-experimental planning is a key phase for the successful implementation of the experiments because final conclusions largely depend on the way in which the experiments are planned. At the end of the pre-experimental planning phase, it is expected that the objectives of the experiment, the selection of response variables, factors and their levels and ranges required are clearly defined.

Definition of the problem and selection of factors and their levels and ranges are thus critical steps in any DoE analysis. Incorrect identification of the problem will lead to final recommendations that are not meaningful. Typically, in order to define and characterize the problem, cause-and-effect-diagram and Failure Mode and Effect Analysis techniques are applied as simple and straightforward methods to identify potential design factors. However, these techniques are applied once the region of interest is identified (Taguchi, Chowdhury, & Wu, 2005). In order to better identify this region, a Systems Engineering tool called Non-Conformity Matrix (NCM) is presented in this paper. This tool enables to model the entire system (e.g. industrial process) holistically, also allowing a systematic analysis of the interactions between its elements that, in our particular case, are the non-conformities identified along the production process.

After the region of interest is clearly defined, it is important to select the right factors and ranges that will be the subject of optimization through DoE, thus improving the quality of the final product. Factors are the input variables of a process that affect directly the response variables. In order to select factors and their levels and ranges, it is required that the experimenter has a deep process knowledge, based on a combination of practical experience and theoretical understanding, as well as historical data and/or previous experimental results, though, even considering all these information, there are still particular situations where the correct identification of factor levels and ranges is hard to accomplish. This might be due to a variety of causes, such as a certain immaturity of the process, a random behavior of the factor levels and ranges each time the production is run or even to the presence of unpredictable noise factors. The ideal way to address these problems consists in performing the pre-experimental runs to identify the factor levels and ranges for the above-discussed situations. In fact Czitrom (2003) and Coleman and Montgomery (1993) have also mentioned that if additional information is required on factor levels and ranges it is advisable to consider performing pre-experimental runs.

The objective of this paper is to study the pre-experimental planning phase of the DoE for an industrial case in order to improve the final product quality. The pre-experimental planning phase includes: (1) a clear identification of the problem, that was better achieved with the help of the NCM, as well as (2) the correct selection of control factors and their respective levels and ranges. Furthermore, application to the industrial case comprises studying practical problems typically faced while performing pre-experimental runs and selecting factor levels and ranges, highlighting the most important problems and cautions that should be taken into account at this phase of the experiment.

In the following sections, a brief introduction is presented on Design of Experiments and the techniques used in the pre-experimental planning phase. Also in this section an overview of the basics and principles of the Non-Conformity Matrix (NCM) is presented. Then, a comprehensive study is provided for the experimenters (scientists or engineers) in order to determine when the pre-experimental runs are required and what the key steps for its successful implementation are.

2. Guidelines for Design of Experiments (DoE)

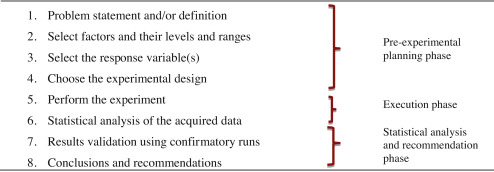
The successful implementation of DoE is comprised of eight steps, as summarized in Table 1. The first four steps are normally termed as the pre-experimental planning phase (Montgomery, 2008).

Table 1. Guidelines for design of experiments.

The pre-experimental planning phase is one of the most important and critical phases of a DoE analysis that compromises the validity of the final results. In this phase, the statisticians or consultants, who design the experiments together with engineers and experimenters, have to bridge a gap in experience, available resources and knowledge. The current paper discusses in detail what is critical in steps I and II from Table 1, applying the defined procedures to an industrial example.

2.1. Pre-experimental planning phase techniques

Cause-and-effect-diagram techniques (Ishikawa diagrams), Quality Functional Deployment (QFD), and Failure Mode and Effects Analysis (FMEA) are typically used in the pre-experimental planning phase (Fahmy et al., 2012; Montgomery, 2008 ;  Taguchi et al., 2005) to identify potential design factors. These techniques are often applied once the region of interest (where DoE is performed) is identified (Taguchi et al., 2005). In cause-and-effect-diagrams, first, all the controllable and uncontrollable factors that could influence the quality of the product are identified. This process is normally held in brainstorming sessions bringing together process engineers, quality engineers and line operators, and then these factors are hierarchically organized. This technique is also referred as fishbone diagram, because the effect of interest is drawn along the spine of the diagram and the causes are written along the ribs. The causes listed in the fishbone diagram are a big help in the correct identification of the potential failure modes.

FMEA can also be used instead of cause-and-effect diagram with additional advantages of identifying the seriousness of effects, how frequently effects occur, and how they can be detected. These metrics are represented by a risk priority number (RPN) for each effect and are calculated on a subjective basis (Fahmy et al., 2012).

Another technique that can be utilized to develop process matrix exhibiting interactions between the system elements is Quality Functional Deployment (QFD) (Browning, 2001). This technique is a four-phase process: understanding customer requirements (product planning), develop design planning matrix, develop process planning matrix, and develop operations planning matrix (Hassan et al., 2010 ;  Taguchi et al., 2005).

The technique proposed in this paper to identify potential key area consists of a systems engineering tool called Non-Conformity Matrix (NCM). This matrix models the entire system holistically, presenting the cause-and-effect relations between the system elements in a matrix form. The proposed tool, once compared to the more traditional quality tools, has three additional advantages: (i) Identification of the region of interest by analyzing the entire manufacturing system (QFD has been used for similar purpose, however in different context); (ii) Cause-and-effect relations are identified in a systematic and innovative manner, i.e. if the relations need to be updated then they can be easily modified; (iii) It also allows applying mathematical operations and algorithms to the matrix, thus reinforcing what are the most relevant interactions between the elements.

2.2. Non-Conformity Matrix

The Non-Conformity Matrix (NCM) is a Design Structure Matrix (DSM) (Browning, 2001 ;  Eppinger and Browning, 2012) based tool developed to systematize all non-conformities (NCs) originated along a production line in a matrix form, highlighting relations and interactions between them. This is the first time that DSM based methodology is used for the process improvement phase. Tavares, Farooq, Araújo, and Nóvoa (2013) developed a ten-step methodology for the application of a NCM to a manufacturing system. Applying the DSM principles on a NCM tool allows identifying clusters of NCs for prioritizing quality improvement actions. Farooq, Tavares, Nóvoa, and Araújo (2014) discusses comprehensively how a NCM is built and what are the relevant phases of this process in order to effectively capture the knowledge from the industry experts. The ultimate goal is to use this tool to highlight critical manufacturing process points and then applying quality improvement techniques to improve the final product quality.

3. Industrial application

Three-piece tin plate aerosol cans are a mass produced product in the consumer goods packaging industry. Although the aerosol can seems simple at a first glance, customer requirements are varied and demanding. In fact, a simple aerosol can must satisfy a variety of internal and customer technical requirements including leak tightness, appearance, as well as safety requirements to withstand under certain pressure. Although packaging industries producing this type of aerosol cans are obliged to follow strict international rules and regulations, customers are always demanding for even higher quality levels. Like many such firms, the industry under analysis is also constantly pursuing quality improvement of its products and processes.

Application of DoE to other similar problems in the electronics, pharmaceutical, automotive and semiconductor industries has shown convincing results and successfully found the operational conditions that simultaneously minimize the variation and maintain an average value of the process (Antony, 1999; Javorsky et al., 2014; Konda and Guha, 1998 ;  Montgomery et al., 2000). Therefore, in the case of three-piece tin plate aerosol can, application of DoE to a specific problematic step of the industrial process seemed as the correct approach to improve the final product quality of the manufacturing process. The first step in any DoE implementation is to define clearly the problem statement: in the case under analysis, a NCM was applied to obtain a more thorough understanding of the process, acting as a key input in the pre-experimental planning phase of DoE. In the following sections, first a brief introduction is given about the product and its manufacturing process and then the application of NCM is presented.

3.1. Description of the product

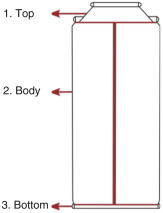
An aerosol can have the objective of containing a product that is dispensed with the aid of a propellant. The product can be dispensed in the form of a mist of liquid particles or foam, depending on the propellant and on the product properties. The aerosol can produced by the company is a three-piece tin plate aerosol can, a simple product composed mainly by three major parts: the top, the bottom and the body, as shown in Fig. 1. The company manufactures both the empty and filled aerosol cans. However, the objective is to improve the final quality of an empty aerosol can, therefore study of the valve, actuator and cup, which are the additional parts in filled aerosol can, are out of scope for this research.

Fig. 1. Three-piece tin plate aerosol can.

3.2. Description of the production process

The complete aerosol manufacturing process is fairly complex and with a high number of intricate steps, but for the current research, a comprehensive understanding of the high-level production processes is sufficient. A three-piece tin plate aerosol can passes successively by the following production areas: primary cutting, varnishing & lithography, secondary cutting and stamping & assembly.

In the primary cutting step of the production process, the tin plate is unrolled from a large coil, straightened and cut into smaller sheets. The top and the bottom are made up from tin-plates with the same thickness whereas the body, according to specifications, has always a relatively lower thickness.

In the varnishing and lithography step, the visual attributes of the aerosol are printed on the tin plate and, according to the customerś requirements, different types of varnish protection are applied to the body before it is cut. The top and the bottom are generally not lithographed.

In the stamping stage, the top and the bottom cup are stamped from a tin-plate sheet. These parts are then transported to the assembly line where the body, which is generally not lithographed, is winded to give a cylindrical shape and then welded. Then the cylindrical shape is assembled together with the top and bottom parts via seaming joints (one seaming joint between top and body, and another seaming joint between bottom and body).

3.3. Non-Conformity Matrix

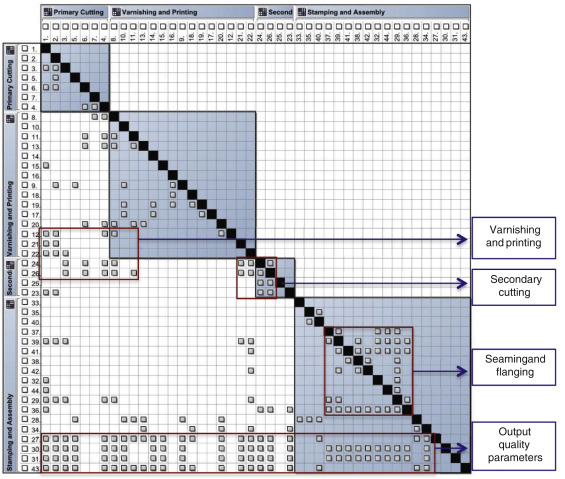
The application of NCM to the three-piece tin plate aerosol can has begun through modeling the entire production system in fine detail, highlighting all the quality control points and the NCs traced in each of the quality control points. Fig. 2 shows a 44 × 44 NCM obtained after interviewing comprehensively the experts of the industry (Farooq et al., 2013 ;  Farooq et al., 2014). NCM is an N × N square matrix with corresponding rows and columns. The matrix elements represent non-conformities and are listed in time sequence from left to right in the horizontal axis. Non-conformities in the vertical axis represent the same elements as in horizontal axis from top to bottom. Off-diagonal cells indicate the dependency of one non-conformity on other non-conformity. Reading across a row shows input sources; reading down a column shows output sinks. When a non-conformity depends on another non-conformity, then the corresponding matrix cell is marked with 1 otherwise left blank.

Fig. 2. Non-Conformity Matrix – before applying mathematical operations.

Fig. 3 shows a NCM obtained after application of the sequencing algorithms. These algorithms are applied within each of the high-level production process, so that the non-conformities remain within their production process. Furthermore, type of the sequencing algorithm applied is the lower block triangular matrix algorithm that organizes most of the NCs below the diagonal. The NCs that remained above the diagonal show complex feedback relations. Moreover, these mathematical algorithms identified four important clusters of NCs. Varnishing and Printing NCs are influenced mainly by primary cutting NCs. Secondary cutting NCs are influenced mainly by varnishing and printing NCs and also Secondary cutting NCs. Flanging and seaming NCs are mainly influenced by themselves, which is called modularity. Finally, it can also be seen that the output quality parameters, which logically appear at the matrix end, are influenced by NCs generated all along the production process.

Fig. 3. Non-Conformity Matrix – after applying mathematical operations.

Among the four key areas highlighted, the most influenced area (output quality parameters) was further analyzed through Pareto Chart analysis. The analysis, which is made hidden due to confidentiality clause, has shown that the high majority of aerosol can defects is due to problems related with the welding process. Therefore, welding process was elected as the primary area of analysis to further improve the final quality of the process.

The second step of DoE is to select the right factors to analyze, as well as their levels and ranges. In the case under analysis, this step involved a complete understanding of the welding process. In fact, after a careful analysis of this process, experimenters found that the current operating conditions of the welding process could be significantly improved, thus enabling a finer control of the process. Furthermore, due to the presence of a considerably number of noise factors, it was not possible to replicate similar operating conditions each time the production is run and it was not possible to define the correct ranges of the selected welding factors unambiguously.

In order to solve this problem, an approach of pre-experimental runs was put in place, enabling a better definition of the ranges of the factors. As to what should be the correct levels of the factors, they were initially set based on expert opinion and process knowledge. In the next sections, the approach used is further explained.

4. An approach to selecting factors and their levels and ranges

The NCM and Pareto Chart analysis facilitated the process of identifying the key areas of the manufacturing process that required particular attention, also helping in a better definition of the problem. These analyses, together with brainstorming with key experts, helped in listing down the controllable, uncontrollable and noise factors that affect the problem. At a second stage, and after all the factors have been identified, brainstorming further reduced the number of factors, simplifying the subsequent DoE analysis. Table 2 shows the final list of identified controllable factors, which corresponds to the first part of step II of DoE in Table 1.

Table 2. Control factors.

Welding current

Welding force

Welding speed

Space between welding bodies

The second part of step II of DoE is to select factor levels and ranges, which are inputs to the experiments that determine the magnitude and direction of each factors effect on the response variable(s), therefore directly affecting the results. If the factor levels and ranges are not correctly chosen, the subsequent statistical analysis and final recommendations might be misleading.

Selection of factor levels and ranges has to go through an iterative process. The first iterations of factor levels and ranges may contain experimental design with too many experimental runs and might not be practically feasible. Therefore, it may require reducing the experimental runs based on available resources and experimental objectives. The tools used for a comprehensive selection of factor levels and ranges are experimental objectives, theoretical knowledge, expert opinion, process knowledge, available resources, previous experimental results and performing pre-experimental runs (Czitrom, 2003 ;  Montgomery, 2008).

Generally, factor levels and ranges are selected based on the definition of the factors, namely whether it is a quantitative factor or a qualitative factor. For the current industrial case and as shown in Table 2, only quantitative factors are applicable. As the objective of the experiment was to determine whether or not the factor has an effect on the response variable, the size and direction (sign) of the effect, as well as to potentially study the curvature in the response, three levels for each factor were selected. Furthermore, it was the first time such experiments were performed in this industry and therefore it was required to design and start with a simple model.

In order to select a proper range for a quantitative factor, process knowledge, previous experimental results and expert opinion are required. However, in the current industrial example, it was not possible to clearly identify the factor ranges due to presence of noise factors (e.g. coil properties) and also due to the reason that the process is not completely controlled. Therefore, in order to overcome these problems, it is advisable to proceed with pre-experimental runs, further explained in the following section.

4.1. Pre-experimental runs

Pre-experimental runs are the experiments that are performed on specific situations. It is therefore essential to know when they are required. Pre-experimental runs should be performed before designed experiments, if the tools (process knowledge, expert opinion, experimental objectives, theoretical knowledge and previous experiments) are not sufficient enough to define clearly the levels and ranges of a factor. Explicitly, there are the following two cases when pre-experimental runs are required:

• When it is not completely known that a quantitative factor will have a linear (2 levels) or a non-linear (3 or more levels) response and also the objective of the experiment is depending on the natural effect of the factor. Generally, two levels are studied if the objective of the experiment is to determine whether or not the factor has an effect (size and direction) on the response. Three or more levels are studied if the objective of the experiment is to study also the full relation with the response;
• When it is not possible to define clearly the range of the levels for quantitative factors, and it is required to explore the process behavior over a wide area of factor ranges.

Practically, selection of factors and their levels and ranges, and selection of response variable(s) are done simultaneously or in reverse order as shown in Table 1. However, if it is required to perform pre-experimental runs, then it is recommended to select response variable(s) and study measurement system(s) prior to selecting factor levels and ranges. This is because the response variable(s) and measurement system(s) help in studying the process behavior and defining the correct factor levels and ranges. Furthermore, it is also recommended to list down all the noise factors before performing pre-experimental runs and then note down their values during the tests. These noise factors should be controlled as far as possible, in order to assure that they will have almost the same values while performing the pre-experimental runs as well as on the designed experiment, enabling a better identification of factor levels and ranges. Due to confidentiality clause, response variable(s), measurement system(s) and noise factor(s) are made hidden for the current industrial application.

A brainstorming session was conducted with the experts in order to estimate the values of selected factors. This helped in saving some time during pre-experimental runs implementation because it has provided valuable hints to set the factor around estimated values. The selected factors and estimated factors’ values are shown in Table 3.

Table 3. Control factors and their estimated values.

Control factors	Estimateda values (low-high)
Welding current	598–611
Welding force	117–130
Welding speed	151–169
Space between welding bodies	3.9–5.2

a. Due to confidentiality clause, the exact figures are not presented (a scale of certain value is adopted).

Table 4 defines comprehensively the guidelines used for the implementation of pre-experimental runs.

Table 4. Guidelines for pre-experimental runs.

1.	Calibration of the selected response variable(s) and measurement system(s);
2.	Note down the values for all the possible noise factor(s);
3.	Adjust the machine to standard operating condition and start producing the units;
4.	Note down the standard values for all control factors when satisfactory units are produced;
5.	Increase first control factor from the standard value intermittentlya until the factor reaches a maximum value while still producing relatively good units by analyzing the response variable(s);
6.	Maintain all other factors at the standard values for maximum or minimum values;
7.	Note down the value of the factor, this is the factors maximum value;
8.	Decrease the same control factor from the standard value intermittentlya until the factor reaches a minimum value while still producing relatively good units by analyzing the response variable(s);
9.	Note down the value of the factor, this is the factors minimum value;
10.	The range for two levels can be defined by low level (minimum factor value) and high level (maximum factor value);
11.	The range for three levels can be defined by low level (minimum factor value), center point (standard value) and high level (maximum factor value);
12.	Adjust the minimum and maximum values so that the standard value is at the center of both, which is highly recommended. However there are situationsb when standard value might not be adjusted at the center, therefore maintain the settings to non-central values.
13.	If the factor is required to perform with more than three levels then take more center points between the levels or take points where there is a region of interest;

a. Increase the value of control factor by 5%, 10%, … of its value or randomly depending upon the objective of the experiment.

b. It is dependent on the objective of the experiment.

After successful implementation of the pre-experimental runs for the industrial case, ranges for all the selected control factors were clearly identified as shown in Table 5.

Table 5. Control factors’ ranges.

Control factors	Lowa	Standarda	Higha
Welding current	611	650	666
Welding force	104	112	115
Welding speed	120	151	166
Space between welding bodies	0.25	5.2	13

a. Due to confidentiality clause, the exact figures are not presented (a scale of certain value is adopted).

The registered range of each control factor was then successfully modeled, in order to assist the selection of the experimental design (fourth step in DoE), and subsequently, the performance of the selected experiment (fifth step in DoE). These steps are not part of the current paper and therefore are considered future work.

5. Conclusions

A clear definition of the problem and a correct selection of factor levels and ranges are one of the key elements in any DoEs implementation. FMEA, QFD and cause-and-effect techniques have long been used as key tools for identifying the potential design factors during the pre-experimental planning phase of the DoE, provided that a region of interest was identified. For the same purpose and in order to better identify this region, a new Systems Engineering tool is introduced in this paper, termed Non-Conformity Matrix (NCM), a tool that is used for the first time in a quality improvement project. This tool models the entire system holistically, highlighting key problematic areas of the manufacturing system, through a systematic analysis of the interactions between the non-conformities identified along the production process.

The NCM methodology is then applied to the three-piece tin plate aerosol can product of a large consumer goods packaging industry. The industry under analysis is constantly considering improving its manufacturing process and final quality of its products, namely aerosol cans. Application of the NCM together with Pareto chart analysis have shown that a high majority of the problems occurred due to the welding process, which is one of the key elements in the improvement of the final product quality. However, while studying the welding process in detail for the DoE, it was found that due to the unknown behavior of noise factors and also due to the fact that the process is not completely monitored and controlled, it was not possible to clearly define the factor ranges. This particular problem was solved by the successful implementation of pre-experimental runs, thus further defining the appropriate ranges for all the factors.

Future directions involve the execution of the following three important aspects:

• Execution of the next steps of a DoE implementation (Table 2), thus providing a valuable input to what should be the best operating conditions for the welding process that minimize the non-conformities of three-piece tin plate aerosol cans, as well as increase the productivity.
• Formulating the Cost of Quality model that receives input from DoE and evaluate per unit cost based on non-conforming units sent to the customer and failure costs. In this particular study relation between external and internal failure costs, and quality of non-conformance shipped to the customer on the global cost savings for acceptance sampling will be explored.
• Extrapolating this methodology into a general framework that can be applied to other industries and products.

Acknowledgements

The authors acknowledge Colep, an international leading manufacturer of aerosol cans, which is engaged with the Engineering Design and Advanced Manufacturing (EDAM) focus area of the MIT-Portugal Program in a Research Program. Muhammad Arsalan Farooq acknowledges support from the Foundation for Science and Technology, under the research Grant SFRH/BD/51579/2011. Further thanks to the MIT-Portugal Program (www.mitportugal.org).

References

1. Antony, 1999 J. Antony; Improving the wire bonding process quality using statistically designed experiments; Microelectronics Journal, 30 (2) (1999), pp. 161–168
2. Browning, 2001 T.R. Browning; Applying the design structure matrix to system decomposition and integration problems: a review and new directions; IEEE Transactions on Engineering Management, 48 (3) (2001), pp. 292–306
3. Coleman and Montgomery, 1993 D.E. Coleman, D.C. Montgomery; Industrial experiment a systematic approach to planning for a designed industrial experiment; Technometrics (1993), pp. 1–12
4. Czitrom, 2003 V. Czitrom; Guidelines for selecting factors and factor levels for an industrial designed experiment; Handbook of Statistics (2003), pp. 3–32
5. Eppinger and Browning, 2012 S.D. Eppinger, T.R. Browning; Design structure matrix methods and applications; MIT Press, Cambridge, MA (2012)
6. Fahmy et al., 2012 R. Fahmy, R. Kona, R. Dandu, W. Xie, G. Claycamp, S. Hoag; Quality by design I: Application of failure mode effect analysis (FMEA) and Plackett-Burman design of experiments in the identification of “main factors” in the formulation and process design space for roller-compacted ciprofloxacin hydrochloride immediat; AAPS PharmSciTech, 13 (4) (2012), pp. 1243–1254
7. Farooq et al., 2013 A. Farooq, S.M.O. Tavares, H. Nóvoa, A. Araújo; Evaluation of a Non-Conformity Matrix complexity using components modularity metrics; 15th International Dependency and Structure Modelling Conference, DSM, Carl Hanser Verlag GmbH & Co. KG, Melbourne (2013), pp. 19–25
8. Farooq et al., 2014 A. Farooq, S.M.O. Tavares, H. Nóvoa, A. Araújo; An application of Knowledge Management in Design Structure Matrix for a process improvement phase; 16th International Dependency and Structure Modelling Conference, DSM, Carl Hanser Verlag GmbH & Co. KG, Paris (2014)
9. Fowlkes and Creveling, 1996 W.Y. Fowlkes, C.M. Creveling; Engineering methods for robust product design: Using taguchi methods in technology and product development; Journal of Product Innovation Management, 13 (3) (1996), p. 279
10. Hassan et al., 2010 A. Hassan, A. Siadata, J.-Y. Dantana, P. Martina; Conceptual process planning – An improvement approach using QFD, FMEA, and ABC methods; Robotics and Computer-Integrated Manufacturing, 26 (4) (2010), pp. 392–401
11. Javorsky et al., 2014 J. Javorsky, M. Franchetti, H. Zhang; Determining the optimal parameters of bonding polyvinylchloride to stainless steel in automotive applications with the use of full factorial design of experiment; CIRP Journal of Manufacturing Science and Technology, 7 (2) (2014), pp. 151–158
12. Konda and Guha, 1998 R. Konda, A. Guha; Design of experiments to study and optimize process performance; International Journal of Quality & Reliability Management, 16 (1) (1998), pp. 56–71
13. Montgomery, 2008 D.C. Montgomery; Design and analysis of experiments; (7th ed.)Wiley, New York (2008)
14. Montgomery et al., 2000 D.C. Montgomery, J.B. Keatsa, L.A. Perrya, J.R. Thompsonb, W.S. Messinab; Using statistically designed experiments for process development and improvement: an application in electronics manufacturing; Robotics and Computer-Integrated Manufacturing, 16 (1) (2000), pp. 55–63
15. Subulan and Cakmakci, 2011 K. Subulan, M. Cakmakci; A feasibility study using simulation-based optimization and Taguchi experimental design method for material handling—Transfer system in the automobile industry; International Journal of Advanced Manufacturing Technology, 59 (5–8) (2011), pp. 433–443
16. Taguchi et al., 2005 G. Taguchi, S. Chowdhury, Y. Wu; Taguchis quality engineering handbook; John Wiley & Sons, Inc., Hoboken, NJ (2005)
17. Tavares et al., 2013 S.M.O. Tavares, A. Farooq, A. Araújo, H. Nóvoa; Application of non-conformity matrix to predict system interactions in complex quality problems. Flexible Automation and Intelligent Manufacturing; Springer International Publishing, Switzerland (2013), pp. 839–851